A Hidden Side of the Conformational Mobility of the Quercetin Molecule Caused by the Rotations of the O3H, O5H and O7H Hydroxyl Groups: In Silico Scrupulous Study

Abstract

In this study at the MP2/6-311++G(2df,pd)//B3LYP/6-311++G(d,p) level of quantum-mechanical theory it was explored conformational variety of the isolated quercetin molecule due to the mirror-symmetrical hindered turnings of the O3H, O5H and O7H hydroxyl groups, belonging to the A and C rings, around the exocyclic C–O bonds. These dipole active conformational transformations proceed through the 72 transition states (TSs; C₁ point symmetry) with non-orthogonal orientation of the hydroxyl groups relatively the plane of the A or C rings of the molecule (HO7C7C8/HO7C7C6 = ±(89.9–93.3), HO5C5C10 = ±(108.9–114.4) and HO3C3C4 = ±(113.6–118.8 degrees) (here and below signs ‘±’ corresponds to the enantiomers)) with Gibbs free energy barrier of activation ΔΔG_TS in the range 3.51–16.17 kcal·mol⁻¹ under the standard conditions (T = 298.1 K and pressure 1 atm): ΔΔG_TS^O7H (3.51–4.27) < ΔΔG_TS^O3H (9.04–11.26) < ΔΔG_TS^O5H (12.34–16.17 kcal mol⁻¹). Conformational dynamics of the O3H and O5H groups is partially controlled by the intramolecular specific interactions O3H…O4, C2′/C6′H…O3, O3H…C2′/C6′, O5H…O4 and O4…O5, which are flexible and cooperative. Dipole-active interconversions of the enantiomers of the non-planar conformers of the quercetin molecule (C₁ point symmetry) is realized via the 24 TSs with C₁ point symmetry (HO3C3C2C1 = ±(11.0–19.1), HC2′/C6′C1′C2 = ±(0.6–2.9) and C3C2C1′C2′/C3C2C1′C6′ = ±(1.7–9.1) degree; ΔΔG_TS = 1.65–5.59 kcal·mol⁻¹), which are stabilized by the participation of the intramolecular C2′/C6′H…O1 and O3H…HC2′/C6′ H-bonds. Investigated conformational rearrangements are rather quick processes, since the time, which is necessary to acquire thermal equilibrium does not exceed 6.5 ns.

1. Introduction

Quercetin molecule is one of the important flavonoids and has a broad range of anti-oxidant, anti-inflammation and others therapeutic actions [1,2,3,4,5,6,7]. This compound, which consists of (A + C) and B rings and five OH hydroxyl groups at the 3, 3′, 4′, 5 and 7 positions [8,9,10,11,12,13], is usually gained from plants, vegetables and fruits like blueberries, apples, green tea, wine and onion. At the same time, it possesses low solubility in water and poor permeability in physiological solutions, which limits its application in the pharmaceutical field [14]. It was the object of the theoretical analysis, in particular with the application of the quantum-chemical methods [11,15].

In our previous study it was found by using the quantum-mechanical (QM) calculations at the MP2/6-311++G(2df,pd)//B3LYP/6-311++G(d,p) level of QM theory that isolated quercetin molecule is very conformationally mobile structure and so can acquire 48 stable conformers, among which there are 24 planar (C_s point symmetry) and 24 non-planar (C₁ point symmetry) with Gibbs free energy ranging from 0.00 to 25.30 kcal·mol⁻¹ under standard conditions and with a dipole moment, which varies from 0.35 to 9.87 Debye [16]), which can interconvert into each other through the rotations of its non-deformable (A + C) and B rings around the C2–C1′ bond [17,18,19,20].

At this, all possible conformers can be divided into four different subfamilies, depending on the orientations of the (A + C) and B rings and 5 hydroxyl groups of the quercetin molecule: subfamily I—conformers 1–12; subfamily II—conformers 13–18, 20, 23, 24, 26, 29 and 30; subfamily III—conformers 19, 21, 22, 25, 27, 28, 31–36 and subfamily IV—conformers 37–48 (see Figure 2 in the paper [16]). Planar conformers belong to the subfamilies I and III, non-planar ones—to the subfamilies II and IV.

However, despite the intensive theoretical investigations of the conformational properties of the quercetin molecule [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27], information according the fundamental mechanisms of the conformational transitions, which are caused by the torsional mobility of its hydroxyl groups around the exocyclic C–O bonds, remains very restricted.

In this study we pursued the goal to investigate the conformational mobility of the quercetin molecule, which is defined by the rotations of the O3H, O5H and O7H hydroxyl groups around the exocyclic C3–O3, C5–O5 and C7–O7 bonds through the transitions states, and also to establish the pathways of the interconversion of the enantiomers of all its non-planar conformers.

Importance of such set of the task is caused by the torsional mobility of the O3H and O5H hydroxyl groups, which is mostly responsible for the formation of the three conformational subfamilies, while the torsional mobility of the O7H hydroxyl group plays the role at this of the additional “multiplier” of the conformational states. The multifunctionality of the quercetin molecule of natural origin is usually associated with its conformational diversity [2,7,8,10].

Many of the biological molecules (and quercetin in this case is not the exception) commonly have various enantiomers, which differently effect on living systems. Notably, that opposite to the objects of the non-living nature, the “R” and “L” forms in them have different part of the observance. Thus, in particular, native proteins contain only “L” amino acids, while nucleic acids—only “R” sugar residues.

It is also known that among drugs very often only one of the enantiomers is responsible for the desired physiological effects, while another enantiomer is less important or even leads to genuinely opposite effect. That is why very often the drug is based only on one enantiomer in order to increase its activity and eliminate ‘side effects’. So, it is important to know the possible ways of the interconversion of the enantiomers of the biomolecules between each other [28,29].

As a result of this in-depth in silico investigation at the MP2/6-311++G(2df,pd)//B3LYP/6-311++G(d,p) level of QM theory, we defined all possible conformational pathways of the rotations of the O3H, O5H and O7H hydroxyl groups, and also their physico-chemical characteristics such as geometrical, in particular symmetrical, energetic and polar, which are reflecting the details of the biological mechanisms of action of the quercetin molecule. Intramolecular specific contacts, H-bonds and attractive van der Waals (vdW) contacts, which assist these biologically-important processes and represent biologically important structural attribute of the quercetin molecule [16,17], have also been explored in detail.

2. Computational Methods

Calculations of the geometries of the conformers and transition states (TSs) of their interconversions, followed by the calculations of their vibrational spectra scaled by a factor of 0.9668 [30], have been performed at the B3LYP/6-311++G(d,p) level of QM theory [31,32,33] by Gaussian’09 program package [34]. This quantum-chemical level of theory has been approved to show adequate results at the studies of heterocyclic compounds [35,36].

Intrinsic reaction coordinate (IRC) calculations has been performed using Hessian-based predictor-corrector integration algorithm [37] by following in the forward and reverse directions from each TS, containing one and only one imaginary frequency in the vibrational spectra.

All calculations have been provided for the quercetin molecule as its intrinsically inherent property.

Electronic and Gibbs free energies under standard conditions have been calculated at the MP2/6-311++G(2df,pd)//B3LYP/6-311++G(d,p) level of QM theory [38,39,40].

The time τ_99.9%, which is needed for reaching the 99.9% of the equilibrium concentration of the reactant and product has been calculated by the formula [41]:

$${\tau }_{99.9\%}=\frac{ln{10}^3}{k_f+k_r},$$

(1)

where forward k_f and reverse k_r rate constants for the conformational transitions have been obtained by the formula [41]:

$$k_{f,r}=\Gamma \cdot \frac{k_{B}T}{h}{e}^{-\frac{\Delta \Delta G_{f,r}}{RT}},$$

(2)

where Γ—Wigner’s coefficient, accounting tunneling [42]:

$$\Gamma =1+\frac{1}{24}{\left(\frac{h{\nu }_i}{k_{B}T}\right)}^2,$$

(3)

where k_B—Boltzmann’s constant, h—Planck’s constant, ΔΔG_f,r—Gibbs free energy of activation for the conformational transition in the forward (f) and reverse (r) directions and ν_i—magnitude of the imaginary frequency of the vibrational mode at the TSs.

The lifetime τ of the conformers has been obtained using the formula:

τ = 1/k_r.

(4)

The topology of the electron density was analyzed by AIM’2000 program package [43,44], based on the Bader’s quantum theory of “Atoms in Molecules” (QTAIM). For this purpose it was used wave functions received at the B3LYP/6-311++G(d,p) level of QM theory.

Energies of the unusual intramolecular CH···O H-bonds and OH…HC dihydrogen bonds [45] and attractive O···O vdW contacts [16,17] have been calculated by the empirical Espinosa–Molins–Lecomte (EML) formula [46,47]:

E_{CH···O/OH···HC/O···O} = 0.5·V(r),

(5)

where V(r)—value of a local potential energy at the (3, −1) BCP.

The energies of the classical intramolecular OH···O H-bonds have been received by the Nikolaienko–Bulavin–Hovorun (NBH) formula [48]:

E_OH···O = −3.09 + 239·ρ,

(6)

where ρ—the electron density at the (3, −1) BCP of the H-bond.

In this work standard numeration of the atoms of the quercetin molecule was used [16,17] (see Scheme 1).

3. Results and Discussion

Aiming to achieve the goal set in this work and obtain maximally possible information according to the conformational properties of the quercetin molecule, which is connected with the mirror-symmetric turnings of the hydroxyl groups in the 3, 5 and 7 positions around the corresponding exocyclic C–O bonds, we localized all possible 72 TSs (24 for each hydroxyl group—O3H, O5H and O7H), which were controlling these processes (see for more details Figure 1, Figure 2, Figure 3 and Figure 4 and

Table 1. Energetic, polar, structural and kinetic characteristics of the conformational transitions in the isolated quercetin molecule via the mirror-symmetrical rotations of the O7H hydroxyl group around the C7–O7 bond through the transition states with a non-perpendicularly oriented O7H group, obtained at the MP2/6-311++G(2df,pd)//B3LYP/6-311++G(d,p) level of quantum-mechanical (QM) theory under standard conditions (see Figure 1).

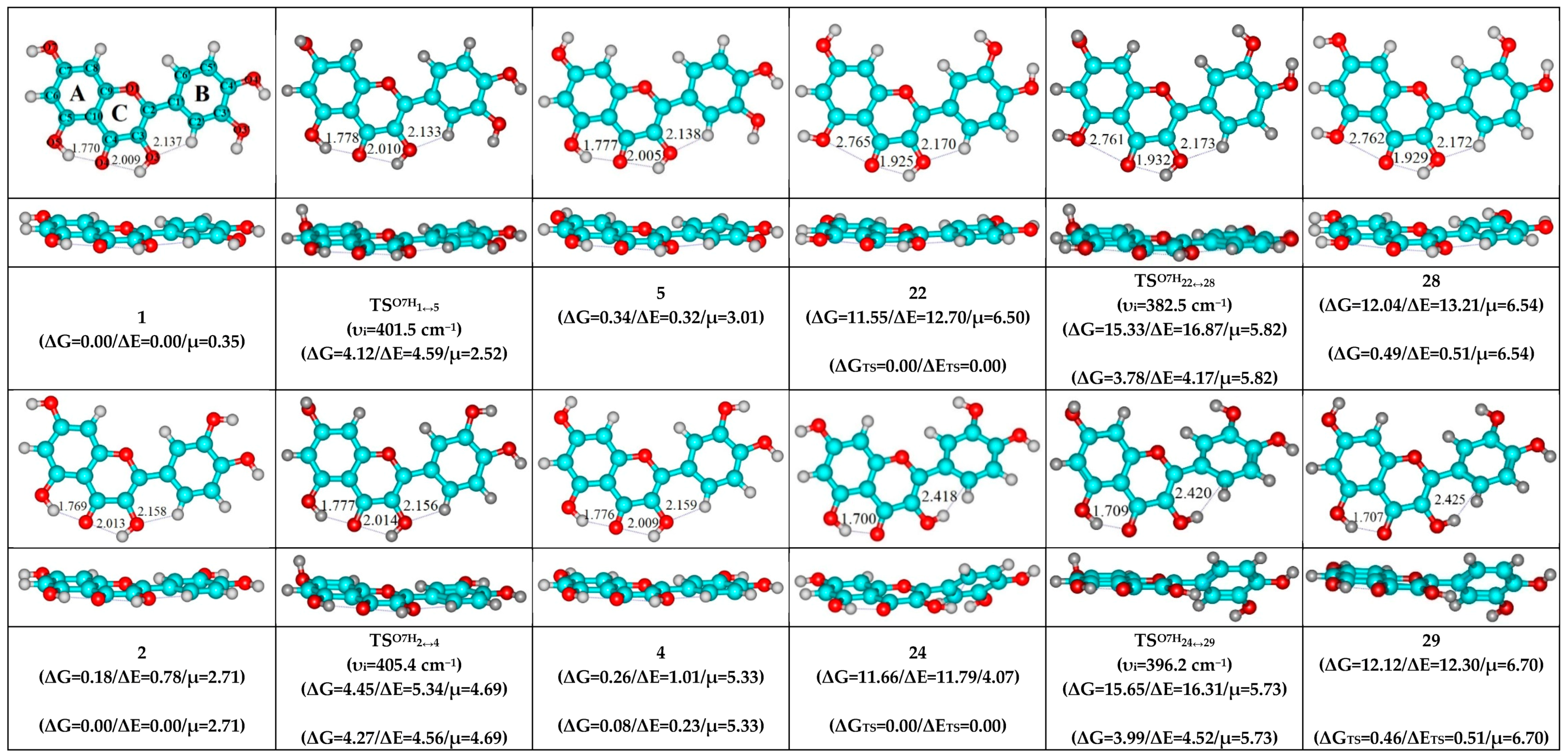
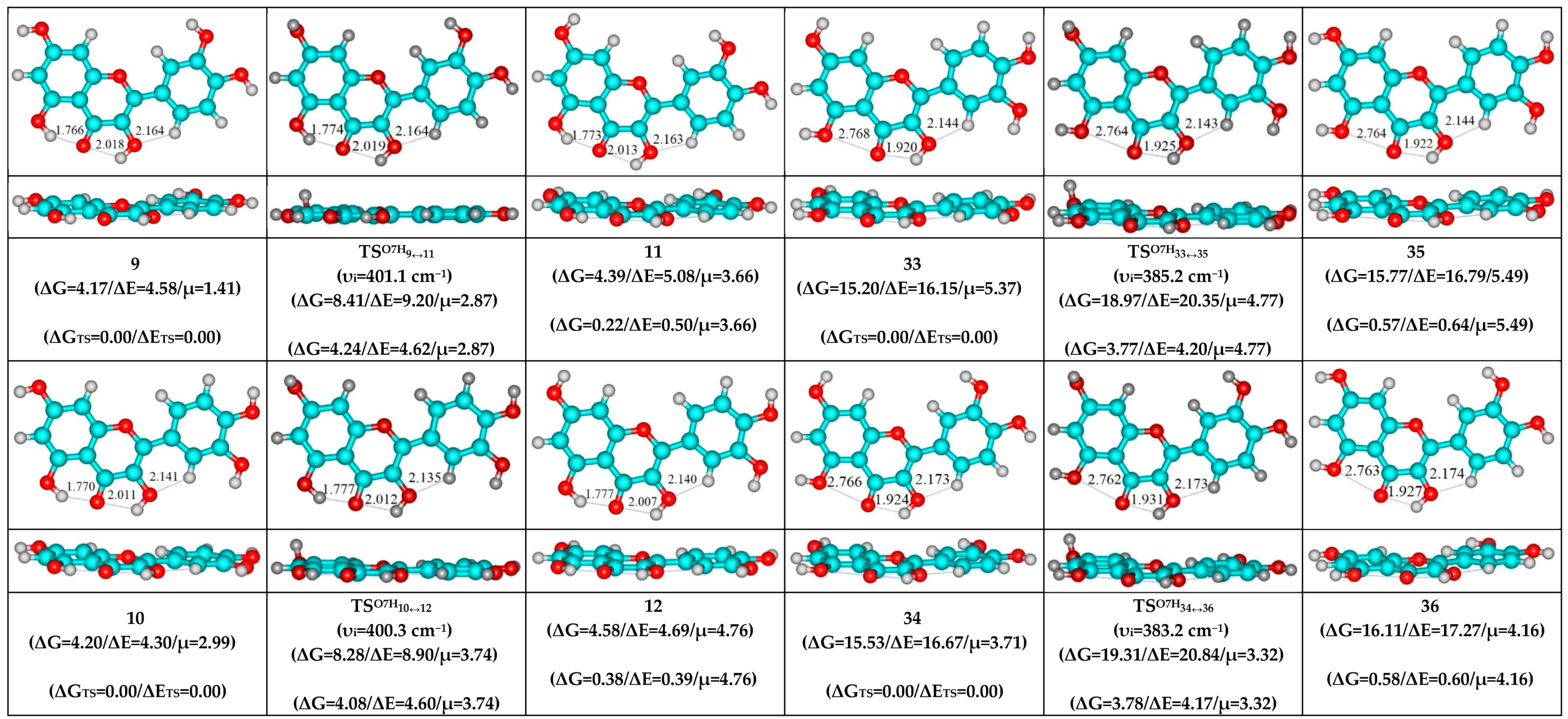
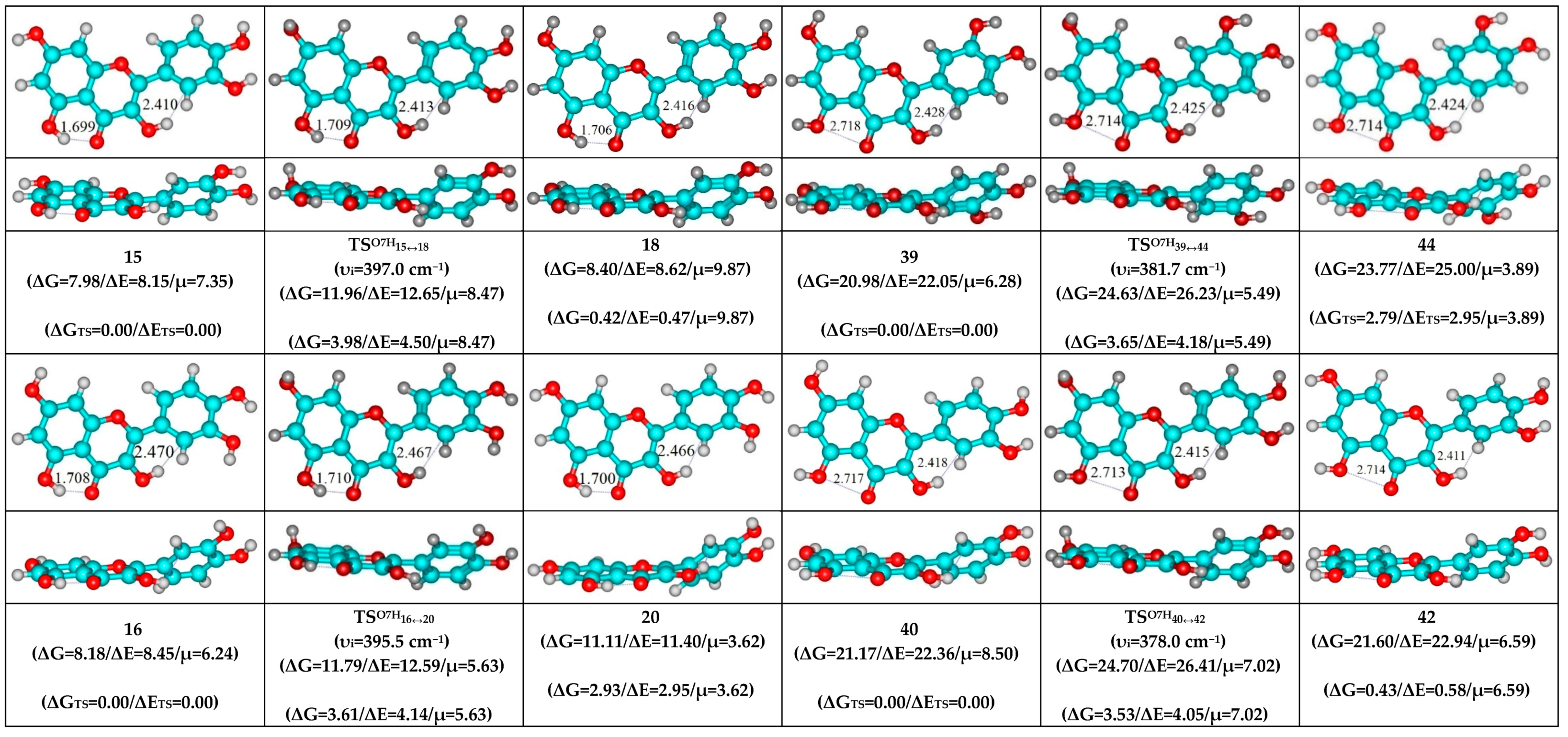
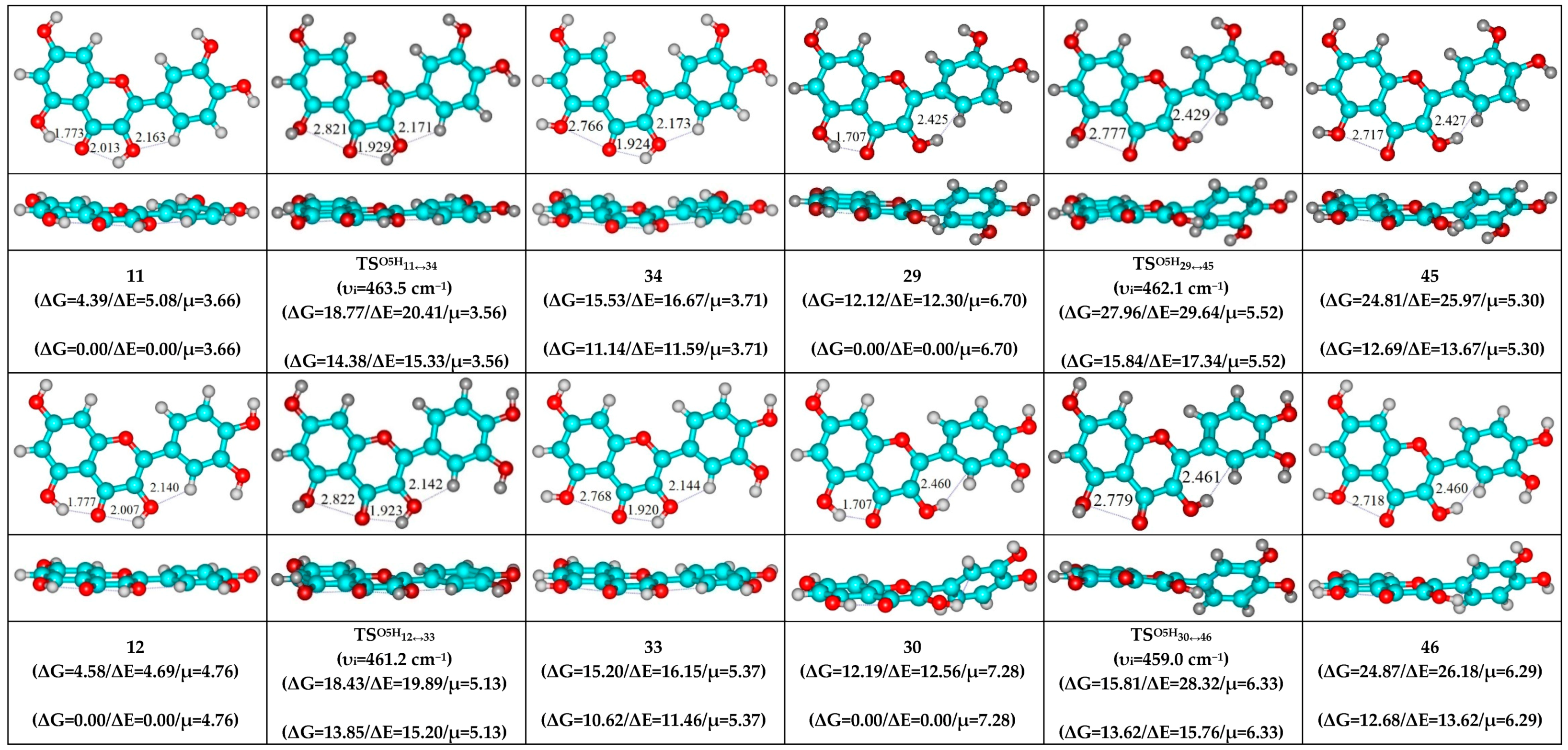
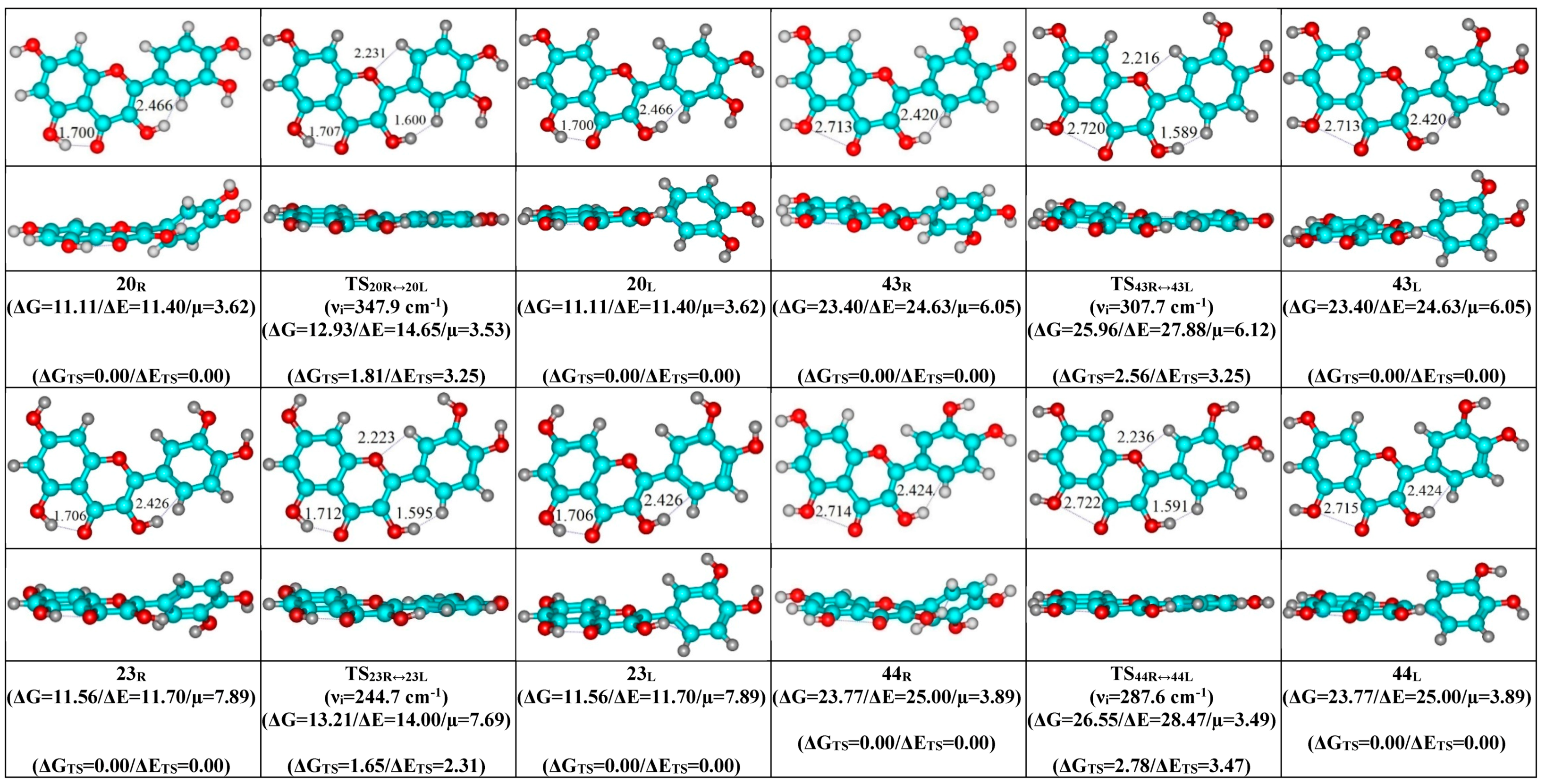
Conformational Transition	µTS a	νi b	∆G c	∆E d	∆∆GTS e	∆∆ETS f	∆∆G g	∆∆E h	kf i	kr j	τ99.9% k	τ l	HO7C7C8/HO7C7C6 m
1↔5	2.52	401.5	0.34	0.32	4.12	4.59	3.78	4.27	6.72 × 109	1.20 × 1010	3.70 × 10−10	8.36 × 10−11	±90.6
2↔4	4.69	405.4	0.08	0.23	4.27	4.56	4.19	4.32	5.23 × 109	5.99 × 109	6.16 × 10−10	1.67 × 10−10	±90.8
3↔6	4.57	400.9	0.28	0.53	4.11	4.63	3.83	4.10	6.87 × 109	1.10 × 1010	3.86 × 10−10	9.07 × 10−11	±89.9
7↔8	6.11	401.0	0.34	0.37	3.88	4.59	3.54	4.22	1.01 × 1010	1.79 × 1010	2.46 × 10−10	5.59 × 10−11	±90.3
9↔11	2.87	401.1	0.22	0.50	4.24	4.62	4.02	4.12	5.48 × 109	8.00 × 109	5.12 × 10−10	1.25 × 10−10	±90.1
10↔12	3.74	400.3	0.38	0.39	4.08	4.60	3.71	4.22	7.17 × 109	1.34 × 1010	3.35 × 10−10	7.45 × 10−11	±90.3
13↔23	6.44	395.1	3.97	4.04	3.98	4.52	0.01	0.48	8.50 × 109	6.94 × 1012	9.94 × 10−13	1.44 × 10−13	±89.9
14↔17	7.92	399.3	0.35	0.36	3.98	4.52	3.63	4.16	8.57 × 109	1.54 × 1010	2.88 × 10−10	6.49 × 10−11	±90.4
15↔18	8.47	397.0	0.42	0.47	3.98	4.50	3.56	4.03	8.61 × 109	1.75 × 1010	2.65 × 10−10	5.72 × 10−11	±90.1
16↔20	5.63	395.5	2.93	2.95	3.61	4.14	0.68	1.19	1.59 × 1010	2.24 × 1012	3.06 × 10−12	4.47 × 10−13	±90.3
19↔25	2.54	385.9	0.60	0.79	3.78	4.40	3.18	3.61	1.19 × 1010	3.28 × 1010	1.55 × 10−10	3.05 × 10−11	±93.0
21↔31	2.26	385.4	0.74	0.88	3.91	4.38	3.17	3.50	9.62 × 109	3.36 × 1010	1.60 × 10−10	2.98 × 10−11	±93.3
22↔28	5.82	382.5	0.49	0.51	3.78	4.17	3.24	3.66	1.18 × 1010	2.95 × 1010	1.67 × 10−10	3.39 × 10−11	±92.3
24↔29	5.73	396.2	0.46	0.51	3.99	4.52	3.53	4.01	8.46 × 109	1.84 × 1010	2.57 × 10−10	5.43 × 10−11	±93.3
26↔30	4.82	395.0	0.45	0.44	4.02	4.53	3.57	4.08	7.93 × 109	1.70 × 1010	2.77 × 10−10	5.88 × 10−11	±90.2
27↔32	5.97	385.0	0.59	0.62	3.79	4.16	3.20	3.55	1.16 × 1010	3.14 × 1010	1.61 × 10−10	3.18 × 10−11	±92.7
33↔35	4.77	385.2	0.57	0.64	3.77	4.20	3.20	3.56	1.20 × 1010	3.16 × 1010	1.58 × 10−10	3.16 × 10−11	±92.8
34↔36	3.32	383.2	0.58	0.60	3.78	4.17	3.20	3.57	1.18 × 1010	3.16 × 1010	1.59 × 10−10	3.17 × 10−11	±92.5
37↔43	5.89	378.4	2.62	2.71	3.51	3.97	0.89	1.26	1.87 × 1010	1.56 × 1012	4.37 × 10−12	6.40 × 10−13	±92.3
38↔41	3.94	379.3	0.46	0.66	3.63	4.15	3.17	3.49	1.53 × 1010	3.33 × 1010	1.42 × 10−10	3.00 × 10−11	±92.8
39↔44	5.49	381.7	2.79	2.95	3.65	4.18	0.86	1.23	1.47 × 1010	1.63 × 1012	4.20 × 10−12	6.13 × 10−13	±92.8
40↔42	7.02	378.0	0.43	0.58	3.53	4.05	3.10	3.46	1.80 × 1010	3.72 × 1010	1.25 × 10−10	2.69 × 10−11	±92.6
45↔47	4.33	379.3	0.42	0.54	3.54	4.03	3.12	3.49	1.78 × 1010	3.63 × 1010	1.28 × 10−10	2.76 × 10−11	±92.5
46↔48	5.03	445.0	0.43	0.61	3.57	4.10	3.14	3.49	1.68 × 1010	3.48 × 1010	1.34 × 10−10	2.88 × 10−11	±92.7

^a The dipole moment of the transition state (TS), Debye. ^b The imaginary frequency at the TS of the conformational transition, cm⁻¹. ^c The Gibbs free energy of the initial relatively the terminal conformer of the quercetin molecule (T = 298.15 K), kcal·mol⁻¹. ^d The electronic energy of the initial relatively the terminal conformer of the quercetin molecule, kcal·mol⁻¹. ^e The Gibbs free energy barrier for the forward conformational transformation of the quercetin molecule, kcal·mol⁻¹. ^f The electronic energy barrier for the forward conformational transformation of the quercetin molecule, kcal·mol⁻¹. ^g The Gibbs free energy barrier for the reverse conformational transformation of the quercetin molecule, kcal·mol⁻¹. ^h The electronic energy barrier for the reverse conformational transformation of the quercetin molecule, kcal·mol⁻¹. ⁱ The rate constant for the forward conformational transformation, s⁻¹. ^j The rate constant for the reverse conformational transformation, s⁻¹. ^k The time necessary to reach 99.9% of the equilibrium concentration between the reactant and the product of the reaction of the conformational transformation, s. ^l The lifetime of the product of the conformational transition, s. ^m The dihedral angle, which describes at the TS the orientation of the O7H hydroxyl group relatively the A ring of the quercetin molecule, degree; sings “±” correspond to enantiomers.

,

Table 2. Energetic, polar, structural and kinetic characteristics of the conformational transitions in the isolated quercetin molecule via the mirror-symmetrical rotations of the O5H hydroxyl group around the C5–O5 bond through the transition states with a non-perpendicularly oriented O5H group, obtained at the MP2/6-311++G(2df,pd)//B3LYP/6-311++G(d,p) level of QM theory under standard conditions (see Figure 2) *.

Conformational Transition	µTS	νi	∆G	∆E	∆∆GTS	∆∆ETS	∆∆G	∆∆E	kf	kr	τ99.9%	τ	HO5 C5C10 a
1↔25	2.71	445.0	11.68	12.45	14.41	15.69	2.00	2.48	1.96 × 102	2.49 × 1011	2.77 × 10−11	4.01 × 10−12	±110.9
2↔31	1.69	443.5	12.08	12.63	14.85	15.78	2.77	3.15	9.37 × 101	6.80 × 1010	1.02 × 10−10	1.47 × 10−11	±111.0
3↔28	5.85	445.1	11.79	12.66	14.57	15.83	2.78	3.18	1.51 × 102	6.71 × 1010	1.03 × 10−10	1.49 × 10−11	±111.1
4↔21	3.79	462.2	11.26	11.52	14.51	15.24	3.25	3.72	1.69 × 102	3.07 × 1010	2.25 × 10−10	3.26 × 10−11	±109.0
5↔19	2.54	461.0	10.74	11.34	13.86	15.16	3.12	3.82	5.04 × 102	3.81 × 1010	1.81 × 10−10	2.62 × 10−11	±108.9
6↔22	6.20	463.9	11.02	11.62	14.24	15.43	3.28	3.81	2.64 × 102	2.89 × 1010	2.39 × 10−10	3.46 × 10−11	±109.1
7↔32	5.70	445.9	11.62	12.65	14.39	15.80	2.77	3.15	2.08 × 102	6.88 × 1010	1.00 × 10−10	1.45 × 10−11	±111.1
8↔27	7.05	461.7	10.69	11.66	13.87	15.33	3.18	3.66	4.97 × 102	3.44 × 1010	2.01 × 10−10	2.90 × 10−11	±109.1
9↔36	3.38	444.9	11.94	12.69	14.72	15.86	2.78	3.17	1.17 × 102	6.68 × 1010	1.03 × 10−10	1.50 × 10−11	±111.0
10↔35	4.78	445.0	11.57	12.49	14.33	15.67	2.76	3.17	1.92 × 102	5.87 × 1010	1.18 × 10−10	1.70 × 10−11	±111.0
11↔34	3.56	463.5	11.14	11.59	14.38	15.33	3.24	3.74	2.09 × 102	3.12 × 1010	2.22 × 10−10	3.21 × 10−11	±109.0
12↔33	5.13	461.2	10.62	11.46	13.85	15.20	3.23	3.74	5.14 × 102	3.18 × 1010	2.18 × 10−10	3.15 × 10−11	±108.9
13↔43	5.57	446.8	15.81	16.97	16.17	17.79	0.36	0.82	1.01 × 101	3.97 × 1012	1.74 × 10−12	2.52 × 10−13	±114.2
14↔44	4.58	445.9	15.81	16.97	16.16	17.76	0.35	0.79	1.03 × 101	4.06 × 1012	1.70 × 10−12	2.46 × 10−13	±114.3
15↔42	6.47	443.3	13.62	14.79	16.16	17.82	2.54	3.02	1.02 × 101	9.94 × 1010	6.95 × 10−11	1.01 × 10−11	±114.4
16↔38	5.12	458.6	12.66	13.58	15.78	17.26	3.12	3.68	1.96 × 101	3.80 × 1010	1.82 × 10−10	2.63 × 10−11	±112.3
17↔39	7.06	461.6	12.67	13.66	15.83	17.32	3.16	3.67	1.83 × 101	3.59 × 1010	1.92 × 10−10	2.79 × 10−11	±112.3
18↔40	8.61	458.5	12.77	13.74	15.85	17.38	3.07	3.64	1.75 × 101	4.11 × 1010	1.68 × 10−10	2.44 × 10−11	±112.4
20↔41	3.22	443.1	10.19	11.29	12.75	14.35	2.56	3.06	3.24 × 103	9.70 × 1010	7.12 × 10−11	1.03 × 10−11	±114.3
23↔37	7.06	462.6	9.22	10.22	12.34	13.88	3.12	3.66	6.61 × 103	3.78 × 1010	1.83 × 10−10	2.64 × 10−11	±112.3
24↔47	3.71	446.8	13.57	14.72	16.17	17.78	2.60	3.06	1.01 × 101	9.10 × 1010	7.59 × 10−11	1.10 × 10−11	±114.2
26↔48	4.82	440.5	13.56	14.67	16.11	17.73	2.55	3.06	1.12 × 101	9.87 × 1010	7.00 × 10−11	1.01 × 10−11	±114.3
29↔45	5.52	462.1	12.69	13.67	15.84	17.34	3.15	3.67	1.78 × 101	3.62 × 1010	1.91 × 10−10	2.76 × 10−11	±112.3
30↔46	6.33	459.0	12.68	13.62	15.76	17.29	3.08	3.67	2.04 × 101	4.09 × 1010	1.69 × 10−10	2.44 × 10−11	±112.3

* See definitions in the footnote of Table 1. ^a The dihedral angle, which describes at the TS the orientation of the O5H hydroxyl group relatively the A ring of the quercetin molecule, degree.

,

Table 3. Energetic, polar, structural and kinetic characteristics of the conformational transitions in the isolated quercetin molecule via the mirror-symmetrical rotations of the O3H hydroxyl group around the C3–O3 bond through the transition states with a non-perpendicularly oriented O3H group, obtained at the MP2/6-311++G(2df,pd)//B3LYP/6-311++G(d,p) level of QM theory under standard conditions (see Figure 3) *.

Conformational Transition	µTS	νi	∆G	∆E	∆∆GTS	∆∆ETS	∆∆G	∆∆E	kf	kr	τ99.9%	τ	HO3 C3C4 a	C3C2 C1′C2′/C3C2 C1′C6′ b
1↔20	2.77	274.2	11.11	11.40	9.16	9.61	−1.95	−1.80	1.26 × 106	1.78 × 1014	3.88 × 10−14	5.61 × 10−15	±118.6	±32.0
2↔14	5.04	326.5	7.78	7.25	9.53	9.47	1.75	2.21	6.96 × 105	3.54 × 1011	1.95 × 10−11	2.83 × 10−12	±114.1	±31.9
3↔13	5.40	330.4	7.34	7.11	9.20	9.46	1.86	2.35	1.21 × 106	2.95 × 1011	2.34 × 10−11	3.39 × 10−12	±113.8	±29.4
4↔17	7.71	329.3	8.05	7.38	9.85	9.64	1.80	2.26	4.10 × 105	3.29 × 1011	2.10 × 10−11	3.04 × 10−12	±114.3	±32.2
5↔16	5.45	278.6	7.84	8.13	9.19	9.70	1.36	1.57	1.20 × 106	6.70 × 1011	1.03 × 10−11	1.49 × 10−12	±118.6	±32.5
6↔23	7.46	335.1	11.03	10.62	9.38	9.62	−1.65	−0.99	8.99 × 105	1.11 × 1014	6.22 × 10−14	9.00 × 10−15	±113.7	±30.8
7↔15	6.95	324.7	7.06	7.06	9.04	9.32	2.01	2.26	1.59 × 106	2.27 × 1011	3.04 × 10−11	4.40 × 10−12	±113.6	±30.5
8↔18	9.37	328.3	7.14	7.16	9.21	9.53	2.07	2.36	1.19 × 106	2.07 × 1011	3.34 × 10−11	4.84 × 10−12	±113.7	±31.3
9↔24	3.36	328.8	7.49	7.21	9.27	9.49	1.77	2.29	1.08 × 106	3.42 × 1011	2.02 × 10−11	2.93 × 10−12	±114.2	±29.9
10↔26	4.47	284.1	7.54	7.82	9.12	9.51	1.59	1.69	1.36 × 106	4.57 × 1011	1.51 × 10−11	2.19 × 10−12	±117.4	±31.5
11↔29	5.93	333.3	7.73	7.22	9.49	9.54	1.76	2.33	7.49 × 105	3.49 × 1011	1.98 × 10−11	2.86 × 10−12	±114.1	±31.2
12↔30	2.71	288.7	7.61	7.87	9.23	9.66	1.61	1.78	1.14 × 106	4.39 × 1011	1.57 × 10−11	2.28 × 10−12	±117.3	±32.1
19↔38	3.75	301.8	9.76	10.37	11.08	11.98	1.33	1.62	5.00 × 104	7.17 × 1011	9.64 × 10−12	1.39 × 10−12	±118.8	±32.2
21↔39	5.33	351.6	9.46	9.52	11.12	11.74	1.66	2.23	4.80 × 104	4.19 × 1011	1.65 × 10−11	2.38 × 10−12	±114.8	±32.1
22↔37	7.07	359.0	9.23	9.22	11.08	11.74	1.85	2.52	5.19 × 104	3.05 × 1011	2.26 × 10−11	3.27 × 10−12	±114.1	±31.3
25↔41	2.53	298.0	9.62	10.24	11.03	11.85	1.41	1.61	5.41 × 104	6.15 × 1011	1.12 × 10−11	1.62 × 10−12	±118.8	±31.7
27↔40	8.24	346.3	9.22	9.24	11.26	11.63	2.04	2.39	3.80 × 104	2.20 × 1011	3.14 × 10−11	4.55 × 10−12	±114.4	±31.2
28↔43	6.21	354.7	11.36	11.42	10.99	11.68	−0.37	0.26	6.04 × 104	1.30 × 1013	5.32 × 10−13	7.70 × 10−14	±114.2	±29.7
31↔44	1.73	351.6	11.51	11.59	10.39	10.86	−1.12	−0.72	1.64 × 105	4.55 × 1013	1.52 × 10−13	2.20 × 10−14	±114.8	±32.1
32↔42	6.03	343.1	9.06	9.20	11.13	11.58	2.07	2.38	4.69 × 104	2.08 × 1011	3.33 × 10−11	4.82 × 10−12	±114.3	±30.4
33↔46	6.07	310.8	9.67	10.03	11.20	11.79	1.53	1.76	4.10 × 104	5.13 × 1011	1.35 × 10−11	1.95 × 10−12	±117.7	±31.9
34↔45	4.65	356.8	9.28	9.30	10.98	11.65	1.70	2.35	6.15 × 104	3.91 × 1011	1.77 × 10−11	2.56 × 10−12	±114.5	±31.5
35↔48	5.03	307.1	9.53	10.00	11.08	11.74	1.55	1.74	4.99 × 104	4.88 × 1011	1.42 × 10−11	2.05 × 10−12	±117.7	±31.2
36↔47	3.52	352.8	9.12	9.24	10.83	11.56	1.71	2.33	7.88 × 104	3.86 × 1011	1.79 × 10−11	2.59 × 10−12	±113.9	±30.1

* See definitions in the footnote of Table 1. ^a The dihedral angle, which describes at the TS the orientation of the O3H hydroxyl group relatively the C ring of the quercetin molecule, degree. ^b The dihedral angle, which describes the mutual orientation of the (A+C) and B rings of the quercetin molecule accordingly each other, degree.

,

Table 4. Energetic, polar, structural and kinetic characteristics of the interconversions of the enantiomers of the non-planar conformers of the isolated quercetin molecule via the quasi-planar TSs with C₁ point symmetry, obtained at the MP2/6-311++G(2df,pd)//B3LYP/6-311++G(d,p) level of QM theory under standard conditions (see Figure 4) *.

Interconversion of Enantiomers	µTS	νi	∆∆GTS	∆∆ETS	kf,r	τ99.9%	τ	HO3C3C2C1′ a	HC2′/C6′C1′C2 b	C3C2C1′C2′/C3C2C1′C6′ c
13R/L↔13L/R	5.47	266.3	4.98	5.56	1.48 × 109	2.34 × 10−9	6.78 × 10−10	±14.6	±0.7	±7.6
14R/L↔14L/R	5.92	256.6	4.01	5.92	7.51 × 109	4.60 × 10−10	1.33 × 10−10	±15.7	±0.6	±7.7
15R/L↔15L/R	7.31	227.0	5.27	5.68	8.87 × 108	3.89 × 10−9	1.13 × 10−9	±18.1	±0.7	±8.4
16R/L↔16L/R	6.20	344.0	5.17	6.72	1.11 × 109	3.10 × 10−9	8.99 × 10−10	±16.4	±2.9	±7.7
17R/L↔17L/R	8.57	250.1	5.21	5.92	9.82 × 108	3.52 × 10−9	1.02 × 10−9	±18.0	±0.6	±9.1
18R/L↔18L/R	9.79	221.3	5.33	5.82	8.00 × 108	4.32 × 10−9	1.25 × 10−9	±19.1	±0.7	±8.7
20R/L↔20L/R	3.53	347.9	1.81	3.25	3.22 × 1011	1.07 × 10−11	3.11 × 10−12	±16.2	±2.8	±7.7
23R/L↔23L/R	7.69	244.7	1.65	2.31	4.06 × 1011	8.52 × 10−12	2.47 × 10−12	±16.1	±0.6	±8.1
24R/L↔24L/R	3.89	268.7	4.96	5.64	1.53 × 109	2.25 × 10−9	6.52 × 10−10	±16.0	±0.7	±8.2
26R/L↔26L/R	4.73	326.0	5.49	6.50	6.37 × 108	5.43 × 10−9	1.57 × 10−9	±15.9	±2.3	±7.7
29R/L↔29L/R	6.52	263.7	5.09	5.85	1.22 × 109	2.83 × 10−9	8.19 × 10−10	±17.5	±0.7	±8.7
30R/L↔30L/R	7.19	322.1	5.54	6.65	5.88 × 108	5.88 × 10−9	1.70 × 10−9	±16.1	±2.4	±7.7
37R/L↔37L/R	7.17	270.5	5.02	5.65	1.38 × 109	2.51 × 10−9	7.26 × 10−10	±12.6	±0.6	±7.0
38R/L↔38L/R	4.02	328.0	5.53	6.50	5.98 × 108	5.78 × 10−9	1.67 × 10−9	±15.6	±2.3	±8.0
39R/L↔39L/R	6.02	282.3	5.04	5.73	1.33 × 109	2.60 × 10−9	7.53 × 10−10	±13.4	±0.7	±7.6
40R/L↔40L/R	8.61	241.6	5.20	5.67	1.01 × 109	3.43 × 10−9	9.93 × 10−10	±14.0	±0.6	±7.2
41R/L↔41L/R	2.21	339.2	5.51	6.44	6.27 × 108	5.51 × 10−9	1.60 × 10−9	±14.8	±0.7	±7.7
42R/L↔42L/R	6.82	256.9	5.13	5.58	1.13 × 109	3.05 × 10−9	8.82 × 10−10	±13.1	±0.7	±6.8
43R/L↔43L/R	6.12	307.7	2.56	3.25	8.97 × 1010	3.85 × 10−11	1.11 × 10−11	±11.0	±0.7	±6.3
44R/L↔44L/R	3.49	287.6	2.78	3.47	6.14 × 1010	5.62 × 10−11	1.63 × 10−11	±13.3	±0.7	±7.6
45R/L↔45L/R	4.90	277.7	4.96	5.70	1.53 × 109	2.25 × 10−9	6.52 × 10−10	±13.4	±0.7	±7.4
46R/L↔46L/R	6.21	312.2	5.59	6.44	5.35 × 108	6.46 × 10−9	1.87 × 10−9	±14.8	±1.8	±7.7
47R/L↔47L/R	3.40	308.0	4.75	5.56	2.22 × 109	1.56 × 10−9	4.51 × 10−10	±12.1	±0.7	±6.9
48R/L↔48L/R	4.93	315.5	5.59	6.35	5.35 × 108	6.46 × 10−9	1.87 × 10−9	±14.6	±1.7	±1.7

* See definitions in the footnote of Table 1. Subscripts “R” and “L” denotes “Right” and “Left” enantiomers. ^a The dihedral angle, which forms the O3H hydroxyl group accordingly the C ring of the quercetin molecule, degree. ^b The dihedral angle, which forms the C2′H/C6′H groups accordingly the B ring of the quercetin molecule, degree. ^c The dihedral angle, which describes the mutual orientation of the (A+C) and B rings of the quercetin molecule, degree. Sings “±” correspond to enantiomers.

and

Table 5. Electron-topological, geometrical and energetic characteristics of the intramolecular specific interactions (H-bonds and attractive van der Waals contacts) in the revealed TSs between the quercetin molecule conformers obtained at the B3LYP/6-311++G(d,p) level of QM theory in the continuum with ε = 1 (see Figure 1, Figure 2, Figure 3 and Figure 4 and Table 1, Table 2, Table 3 and Table 4).

Transition State	AH···B H-Bond/AH···HB Dihydrogen H-Bond/A···B vdW Contact	EAH···B/EAH···HB/EA··B a	ρ b	Δρ c	dA···B d	dH···B/dH···H e	AH···B f	C3C2C1′C6′ g
1	2	3	4	5	6	7	8	9
TSO7H1↔5	O5H...O4	6.42	0.040	0.124	2.659	1.778	147.0	179.5
	O3H...O4	3.24	0.026	0.103	2.625	2.010	118.8
	C2′H...O3H *	4.07	0.018	0.077	2.879	2.133	123.9
TSO7H2↔4	O5H...O4	6.45	0.040	0.124	2.658	1.777	147.0	−0.5
	O3H...O4	3.20	0.026	0.103	2.626	2.014	118.7
	C6′H...O3H *	3.86	0.018	0.073	2.892	2.156	123.3
TSO7H3↔6	O5H...O4	6.52	0.040	0.124	2.655	1.773	147.0	−3.2
	O3H...O4	3.13	0.026	0.102	2.630	2.020	118.4
	C6′H...O3H *	3.80	0.017	0.072	2.898	2.163	123.2
TSO7H7↔8	O5H...O4	6.50	0.040	0.124	2.656	1.775	147.0	177.8
	O3H...O4	3.12	0.026	0.102	2.629	2.021	118.4
	C2′H...O3H *	3.87	0.018	0.074	2.882	2.156	122.4
TSO7H9↔11	O5H...O4	6.50	0.040	0.124	2.656	1.774	147.0	−2.4
	O3H...O4	3.14	0.026	0.102	2.629	2.019	118.5
	C6′H...O3H *	3.80	0.017	0.072	2.895	2.164	122.9
TSO7H10↔12	O5H...O4	6.44	0.040	0.124	2.658	1.777	147.0	179.1
	O3H...O4	3.21	0.026	0.103	2.626	2.012	118.7
	C2′H...O3H *	4.03	0.018	0.076	2.885	2.135	124.1
TSO7H13↔23	O5H...O4	8.24	0.047	0.135	2.604	1.709	148.2	−42.3
	O3H…C6′ *	2.47	0.013	0.046	3.068	2.422	124.0
TSO7H14↔17	O5H...O4	8.20	0.047	0.135	2.605	1.710	148.2	−43.1
	O3H…C6′ *	2.45	0.013	0.046	3.064	2.426	123.3
TSO7H15↔18	O5H...O4	8.25	0.047	0.135	2.604	1.709	148.2	137.2
	O3H…C2′ *	2.48	0.013	0.046	3.063	2.413	124.4
TSO7H16↔20	O5H...O4	8.20	0.047	0.135	2.605	1.710	148.2	137.7
	O3H…C2′ *	2.35	0.012	0.045	3.052	2.467	118.8
TSO7H19↔25	O5...O4 *	2.91	0.012	0.049	2.765	-	-	179.7
	O3H...O4	4.60	0.032	0.117	2.571	1.923	121.1
	C2′H...O3H *	3.98	0.018	0.075	2.886	2.141	123.8
TSO7H21↔31	O5...O4 *	2.92	0.012	0.049	2.764	-	-	−0.1
	O3H...O4	4.55	0.032	0.116	2.572	1.926	120.9
	C6′H...O3H *	3.76	0.017	0.071	2.901	2.166	123.2
TSO7H22↔28	O5...O4 *	2.94	0.012	0.049	2.761	-	-	−2.4
	O3H...O4	4.46	0.032	0.116	2.575	1.932	120.7
	C6′H...O3H *	3.71	0.017	0.070	2.907	2.173	123.2
TSO7H24↔29	O5H...O4	8.23	0.047	0.135	2.604	1.709	148.2	−42.4
	O3H…C6′ *	2.47	0.013	0.046	3.065	2.420	123.9
TSO7H26↔30	O5H...O4	8.22	0.047	0.135	2.605	1.710	148.2	137.4
	O3H…C2′ *	2.37	0.012	0.045	3.057	2.457	120.1
TSO7H27↔32	O5...O4 *	2.93	0.012	0.049	2.762	-	-	178.7
	O3H...O4	4.43	0.031	0.115	2.575	1.934	120.6
	C2′H...O3H *	3.79	0.017	0.072	2.891	2.165	122.4
TSO7H33↔35	O5...O4 *	2.92	0.012	0.049	2.764	-	-	179.4
	O3H...O4	4.57	0.032	0.117	2.572	1.925	121.0
	C2′H...O3H *	3.95	0.018	0.074	2.892	2.143	124.1
TSO7H34↔36	O5...O4 *	2.93	0.012	0.049	2.762	-	-	−1.7
	O3H...O4	4.48	0.032	0.116	2.574	1.931	120.7
	C6′H...O3H *	3.71	0.017	0.070	2.903	2.173	122.9
TSO7H37↔43	O5...O4 *	3.26	0.013	0.055	2.712	-	-	−42.7
	O3H…C6′ *	2.44	0.013	0.046	3.079	2.423	124.8
TSO7H38↔41	O5...O4 *	3.25	0.013	0.055	2.714	-	-	137.6
	O3H…C2′ *	2.35	0.012	0.045	3.061	2.465	119.7
TSO7H39↔44	O5...O4 *	3.25	0.013	0.055	2.714	-	-	−43.1
	O3H…C6′ *	2.44	0.013	0.046	3.072	2.425	124.0
TSO7H40↔42	O5...O4 *	3.26	0.013	0.055	2.713	-	-	137.2
	O3H…C2′ *	2.46	0.013	0.046	3.070	2.415	124.9
TSO7H45↔47	O5...O4 *	3.26	0.013	0.055	2.713	-	-	−42.7
	O3H…C6′ *	2.45	0.013	0.046	3.075	2.422	124.6
TSO7H46↔48	O5...O4 *	3.25	0.013	0.055	2.714	-	-	137.3
	O3H…C2′ *	2.36	0.012	0.045	3.065	2.456	120.8
TSO5H1↔25	O5...O4 *	2.98	0.012	0.045	2.821	-	-	−178.7
	O3H...O4	4.60	0.032	0.117	2.571	1.923	121.1
	C2′H...O3H *	4.00	0.018	0.075	2.884	2.139	123.8
TSO5H2↔31	O5...O4 *	2.98	0.012	0.045	2.820	-	-	1.9
	O3H...O4	4.55	0.032	0.116	2.572	1.926	120.9
	C2′H...O3H *	3.78	0.017	0.072	2.899	2.165	123.2
TSO5H3↔28	O5...O4 *	2.99	0.012	0.045	2.818	-	-	1.3
	O3H...O4	4.45	0.032	0.116	2.575	1.933	120.7
	C2′H...O3H *	3.73	0.017	0.071	2.905	2.171	123.2
TSO5H4↔21	O5...O4 *	2.97	0.012	0.044	2.823	-	-	1.9
	O3H...O4	4.57	0.032	0.116	2.572	1.925	120.9
	C2′H...O3H *	3.76	0.017	0.071	2.900	2.167	123.1
TSO5H5↔19	O5...O4 *	2.97	0.012	0.044	2.823	-	-	−178.7
	O3H...O4	4.63	0.032	0.117	2.570	1.921	121.1
	C2′H...O3H *	3.99	0.018	0.075	2.885	2.139	123.8
TSO5H6↔22	O5...O4 *	2.99	0.012	0.045	2.820	-	-	1.4
	O3H...O4	4.49	0.032	0.116	2.574	1.930	120.7
	C6′H...O3H *	3.74	0.017	0.071	2.904	2.169	123.2
TSO5H7↔32	O5...O4 *	2.99	0.012	0.045	2.818	-	-	−178.4
	O3H...O4	4.43	0.031	0.115	2.576	1.934	120.6
	C2′H...O3H *	3.80	0.017	0.072	2.889	2.163	122.4
TSO5H8↔27	O5...O4 *	2.99	0.012	0.045	2.821	-	-	−178.3
	O3H...O4	4.46	0.032	0.116	2.574	1.932	120.6
	C2′H...O3H *	3.80	0.017	0.072	2.889	2.163	122.4
TSO5H9↔36	O5...O4 *	2.99	0.012	0.045	2.819	-	-	1.6
	O3H...O4	4.48	0.032	0.116	2.575	1.931	120.7
	C6′H...O3H *	3.73	0.017	0.071	2.901	2.171	122.8
Transition State	AH···B H-Bond/AH···HB Dihydrogen H-Bond/A···B vdW Contact	EAH···B/EAH···HB/EA··B a	ρ b	Δρ c	dA···B d	dH···B/dH···H e	AH···Bf	C3C2C1′C6′ g
TSO5H10↔35	O5...O4 *	2.98	0.012	0.045	2.820	-	-	−178.8
	O3H...O4	4.57	0.032	0.116	2.572	1.925	121.0
	C2′H...O3H *	3.97	0.018	0.075	2.890	2.142	124.1
TSO5H11↔34	O5...O4 *	2.98	0.012	0.045	2.821	-	-	1.7
	O3H...O4	4.51	0.032	0.116	2.573	1.929	120.8
	C6′H...O3H *	3.73	0.017	0.071	2.901	2.171	122.9
TSO5H12↔33	O5...O4 *	2.98	0.012	0.045	2.822	-	-	−178.8
	O3H...O4	4.60	0.032	0.117	2.571	1.923	121.0
	C2′H...O3H *	3.97	0.018	0.075	2.890	2.142	124.1
TSO5H13↔43	O5...O4 *	3.27	0.014	0.050	2.774	-	-	−42.4
	O3H…C6′ *	2.45	0.013	0.046	3.075	2.422	124.6
TSO5H14↔44	O5...O4 *	3.26	0.014	0.049	2.776	-	-	−43.1
	O3H…C6′ *	2.44	0.013	0.046	3.071	2.426	123.9
TSO5H15↔42	O5...O4 *	3.26	0.014	0.049	2.774	-	-	137.6
	O3H…C2′ *	2.48	0.013	0.046	3.067	2.412	124.7
TSO5H16↔38	O5...O4 *	3.24	0.014	0.049	2.780	-	-	137.1
	O3H…C2′ *	2.33	0.012	0.045	3.064	2.470	119.6
TSO5H17↔39	O5...O4 *	3.24	0.014	0.049	2.779	-	-	−43.2
	O3H…C6′ *	2.42	0.013	0.045	3.074	2.430	123.8
TSO5H18↔40	O5...O4 *	3.25	0.014	0.049	2.777	-	-	136.6
	O3H…C2′ *	2.43	0.013	0.045	3.073	2.420	124.7
TSO5H20↔41	O5...O4 *	3.25	0.014	0.049	2.777	-	-	137.7
	O3H…C2′ *	2.36	0.012	0.045	3.058	2.464	119.6
TSO5H23↔37	O5...O4 *	3.24	0.014	0.049	2.777	-	-	−43.7
	O3H…C6′ *	2.42	0.013	0.045	3.084	2.431	124.7
TSO5H24↔47	O5...O4 *	3.25	0.014	0.049	2.775	-	-	−42.5
	O3H…C6′ *	2.48	0.013	0.046	3.072	2.421	124.5
TSO5H26↔48	O5...O4 *	3.25	0.014	0.049	2.776	-	-	137.6
	O3H…C2′ *	2.38	0.012	0.045	3.062	2.454	120.7
TSO5H29↔45	O5...O4 *	3.25	0.014	0.049	2.777	-	-	−43.6
	O3H…C6′ *	2.40	0.013	0.045	3.080	2.429	124.4
TSO5H30↔46	O5...O4 *	3.24	0.014	0.049	2.779	-	-	136.5
	O3H…C2′ *	2.34	0.012	0.045	3.069	2.461	120.8
TSO3H1↔20	O5H...O4	8.54	0.049	0.136	2.600	1.699	148.7	149.8
	C2′H...O3H *	2.92	0.014	0.050	2.941	2.369	111.3
TSO3H2↔14	O5H...O4	8.54	0.049	0.136	2.600	1.699	148.7	−31.9
	C2′H...O3H *	2.89	0.014	0.050	2.950	2.376	111.6
TSO3H3↔13	O5H...O4	8.58	0.049	0.136	2.598	1.697	148.7	−29.4
	C2′H...O3H *	2.99	0.014	0.051	2.948	2.353	113.0
TSO3H4↔17	O5H...O4	8.31	0.048	0.135	2.605	2.382	111.4	−32.2
	C2′H...O3H *	2.86	0.014	0.049	2.953	1.925	120.9
TSO3H5↔16	O5H...O4	8.31	0.048	0.135	2.605	1.707	148.6	149.3
	C2′H...O3H *	2.88	0.014	0.050	2.943	2.376	111.0
TSO3H6↔23	O5H...O4	8.37	0.048	0.135	2.603	1.705	148.6	−30.8
	C6′H...O3H *	2.92	0.014	0.050	2.952	2.368	112.2
TSO3H7↔15	O5H...O4	8.37	0.048	0.135	148.747	1.698	148.7	150.8
	C2′H...O3H *	2.92	0.014	0.050	2.937	2.365	111.4
TSO3H8↔18	O5H...O4	8.35	0.048	0.135	2.604	1.705	148.6	150.0
	C2′H...O3H *	2.90	0.014	0.050	2.940	2.374	111.0
TSO3H9↔24	O5H...O4	8.57	0.049	0.136	2.599	1.698	148.7	−29.9
	C6′H...O3H *	2.95	0.014	0.051	2.947	2.361	112.4
TSO3H10↔26	O5H...O4	8.54	0.049	0.136	2.599	1.699	148.7	150.3
	C2′H...O3H *	2.94	0.014	0.051	2.943	2.363	111.8
TSO3H11↔29	O5H...O4	8.35	0.048	0.135	2.604	1.705	148.6	−31.2
	C6′H...O3H *	2.89	0.014	0.049	2.951	2.376	111.7
TSO3H12↔30	O5H...O4	8.32	0.048	0.135	2.605	1.706	148.6	149.5
	C2′H...O3H *	2.91	0.014	0.050	2.945	2.371	111.5
TSO3H19↔38	O5...O4 *	3.19	0.013	0.054	2.723	-	-	149.5
	C2′H...O3H *	2.87	0.014	0.049	2.946	2.377	111.1
TSO3H21↔39	O5...O4 *	3.18	0.013	0.054	2.724	-	-	−32.1
	C6′H...O3H *	2.83	0.014	0.048	2.957	2.388	111.3
TSO3H22↔37	O5...O4 *	3.19	0.013	0.054	2.723	-	-	−31.3
	C6′H...O3H *	2.85	0.014	0.049	2.959	2.382	111.8
TSO3H25↔41	O5...O4 *	3.22	0.013	0.054	2.719	-	-	150.0
	C2′H...O3H *	2.91	0.014	0.050	2.943	2.370	111.4
TSO3H27↔40	O5...O4 *	3.19	0.013	0.054	2.723	-	-	150.0
	C2′H...O3H *	2.87	0.014	0.049	2.944	2.380	110.9
TSO3H28↔43	O5...O4 *	3.21	0.013	0.054	2.719	-	-	−29.7
	C6′H...O3H *	2.93	0.014	0.050	2.954	2.364	112.7
TSO3H31↔44	O5...O4 *	3.18	0.013	0.054	2.724	-	-	−32.1
	C6′H...O3H *	2.83	0.014	0.048	2.957	2.388	111.3
TSO3H32↔42	O5...O4 *	3.21	0.013	0.054	2.720	-	-	150.9
	C2′H...O3H *	2.91	0.014	0.050	2.942	2.371	111.3
TSO3H33↔46	O5...O4 *	3.19	0.013	0.054	2.723	-	-	149.7
	C2′H...O3H *	2.89	0.014	0.050	2.948	2.373	111.5
TSO3H34↔45	O5...O4 *	3.19	0.013	0.054	2.723	-	-	−31.5
	C6′H...O3H *	2.83	0.014	0.048	2.957	2.387	111.3
TSO3H35↔48	O5...O4 *	3.22	0.013	0.054	2.719	-	-	150.4
	C2′H...O3H *	2.93	0.014	0.050	2.946	2.365	111.9
TSO3H36↔47	O5...O4 *	3.21	0.013	0.054	2.720	-	-	−30.1
	C6′H...O3H *	2.90	0.014	0.050	2.952	2.371	112.1
TS13R↔13L	O5H...O4	8.37	0.048	0.135	2.603	1.705	148.4	−7.6
	O3H...HC6′ *	4.81	0.023	0.075	2.496	1.592	155.4
	C2′H...O1 *	4.74	0.019	0.090	2.619	2.218	99.3
TS14R↔14L	O5H...O4	8.33	0.048	0.135	2.605	1.707	148.4	−7.7
	O3H...HC6′ *	4.77	0.023	0.075	2.490	1.590	154.6
	C2′H...O1 *	4.72	0.019	0.090	2.617	2.234	98.3
TS15R↔15L	O5H...O4	8.37	0.048	0.135	2.603	1.705	148.4	171.9
	O3H...HC2′ *	4.67	0.022	0.074	2.500	1.603	153.9
	C6′H...O1 *	4.69	0.019	0.089	2.627	2.233	98.9
TS16R↔16L	O5H...O4	8.09	0.047	0.134	2.610	1.715	148.3	171.2
	O3H...HC2′ *	4.67	0.023	0.074	2.502	1.601	155.4
	C6′H...O1 *	4.66	0.019	0.089	2.631	2.234	99.2
TS17R↔17L	O5H...O4	8.10	0.047	0.134	2.610	1.714	148.3	−9.1
	O3H...HC6′ *	4.73	0.023	0.074	2.493	1.600	153.2
	C2′H...O1 *	4.71	0.019	0.089	2.621	2.241	98.1
TS18R↔18L	O5H...O4	8.16	0.047	0.134	2.608	1.712	148.3	170.8
	O3H...HC2′ *	4.58	0.022	0.073	2.496	1.612	151.5
	C6′H...O1 *	4.64	0.019	0.088	2.631	2.239	98.9
TS20R↔20L	O5H...O4	8.30	0.048	0.135	2.605	1.707	148.4	171.3
	O3H...HC2′ *	4.68	0.023	0.074	2.502	1.600	155.5
	C6′H...O1 *	4.69	0.019	0.089	2.629	2.231	99.2
TS23R↔23L	O5H...O4	8.18	0.047	0.134	2.608	1.712	148.3	−8.1
	O3H...HC6′ *	4.78	0.023	0.075	2.493	1.595	154.2
	C2′H...O1 *	4.69	0.019	0.089	2.624	2.223	99.2
TS24R↔24L	O5H...O4	8.36	0.048	0.135	2.603	1.705	148.4	8.2
	O3H...HC6′ *	4.77	0.023	0.075	2.497	1.597	154.8
	C2′H...O1 *	4.71	0.019	0.089	2.624	2.219	99.5
TS26R↔26L	O5H...O4	8.32	0.048	0.135	2.605	1.707	148.4	171.4
	O3H...HC2′ *	4.70	0.023	0.074	2.499	1.597	155.3
	C6′H...O1 *	4.70	0.019	0.089	2.626	2.235	98.8
TS29R↔29L	O5H...O4	8.16	0.047	0.134	2.608	1.712	148.3	−8.2
	O3H...HC6′ *	4.76	0.023	0.075	2.497	1.597	154.6
	C2′H...O1 *	4.67	0.019	0.089	2.627	2.223	99.5
TS30R↔30L	O5H...O4	8.11	0.047	0.134	2.610	1.714	148.3	171.3
	O3H...HC2′ *	4.69	0.023	0.074	2.499	1.598	155.1
	C6′H...O1 *	4.66	0.019	0.089	2.629	2.238	98.8
TS37R↔37L	O5...O4 *	3.20	0.013	0.054	2.722	-	-	−7.0
	O3H...HC6′ *	4.82	0.023	0.075	2.501	1.591	156.8
	C2′H...O1 *	4.68	0.019	0.089	2.624	2.221	99.4
TS38R↔38L	O5...O4 *	13.75	0.047	0.134	2.725	-	-	171.2
	O3H...HC2′ *	4.67	0.023	0.074	2.507	1.602	156.0
	C6′H...O1 *	4.66	0.019	0.089	2.633	2.235	99.3
TS39R↔39L	O5...O4 *	3.17	0.013	0.054	2.726	-	-	−7.6
	O3H...HC6′ *	4.80	0.023	0.075	2.502	1.593	156.6
	C2′H...O1 *	4.70	0.019	0.089	2.621	2.236	98.4
TS40R↔40L	O5...O4 *	3.19	0.013	0.054	2.723	-	-	−172.5
	O3H...HC2′ *	4.69	0.023	0.074	2.505	1.601	155.6
	C6′H...O1 *	4.63	0.019	0.088	2.631	2.235	99.1
TS41R↔41L	O5...O4 *	3.20	0.013	0.054	2.722	-	-	171.6
	O3H...HC2′ *	4.68	0.023	0.074	2.507	1.599	156.6
	C6′H...O1 *	4.66	0.019	0.088	2.631	2.232	99.3
TS42R↔42L	O5...O4 *	3.21	0.013	0.054	2.720	-	-	−172.9
	O3H...HC2′ *	4.71	0.023	0.074	2.506	1.600	156.3
	C6′H...O1 *	4.67	0.019	0.089	2.628	2.232	99.1
TS43R↔43L	O5...O4 *	3.21	0.013	0.054	2.720	-	-	6.3
	O3H...HC6′ *	4.84	0.023	0.075	2.503	1.589	157.8
	C2′H...O1 *	4.73	0.019	0.090	2.620	2.216	99.4
TS44R↔44L	O5...O4 *	3.20	0.013	0.054	2.722	-	-	7.6
	O3H...HC6′ *	4.84	0.023	0.075	2.500	1.591	156.8
	C2′H...O1 *	4.71	0.019	0.090	2.620	2.236	98.3
TS45R↔45L	O5...O4 *	3.19	0.013	0.054	2.723	-	-	7.5
	O3H...HC6′ *	4.79	0.023	0.075	2.504	1.595	156.7
	C2′H...O1 *	4.66	0.019	0.088	2.628	2.221	99.6
TS46R↔46L	O5...O4 *	3.18	0.013	0.054	2.724	-	-	171.6
	O3H...HC2′ *	4.69	0.023	0.074	2.503	1.598	156.0
	C6′H...O1 *	4.63	0.019	0.088	2.631	2.238	98.9
TS47R↔47L	O5...O4 *	3.21	0.013	0.054	2.720	-	-	6.9
	O3H...HC6′ *	4.81	0.023	0.075	2.505	1.592	157.6
	C2′H...O1 *	4.70	0.019	0.089	2.625	2.216	99.7
TS48R↔48L	O5...O4 *	3.20	0.013	0.054	2.721	-	-	171.7
	O3H...HC2′ *	4.70	0.023	0.074	2.503	1.598	156.2
	C6′H...O1 *	4.66	0.019	0.089	2.628	2.235	98.9

^a Energy of the AH···B/AH···HB/A···B specific contact, calculated by Espinose–Molins–Lecomte (Espinosa, Molins and Lecomte, 1998; Mata, Alkorta, Espinosa and Molins, 2011; marked with an asterisk) or Nikolaienko–Bulavin–Hovorun (Nikolaienko, Bulavin and Hovorun, 2011) formulas, kcal·mol⁻¹. ^b The electron density at the (3, −1) BCP of the specific contact, a.u. ^c The Laplacian of the electron density at the (3, −1) BCP of the specific contact, a.u. ^d The distance between the A and B atoms of the AH···B/A···B specific contact, Å. ^e The distance between the H and B/H atoms of the AH···B/AH···HB specific contact, Å. ^f The H-bond angle, degree. ^g Dihedral angle between the (A + C) and B rings, degree.

). This enabled us to receive a complete picture of the conformational mobility and to obtain a number of interesting physico-chemical regularities.

Thus, all established TSs (C₁ point symmetry; Figure 1, Figure 2 and Figure 3, Table 1, Table 2 and Table 3 and Table 5) have non-orthogonal structure—corresponding dihedral angles, which describe the orientation of the OH hydroxyl groups according the rings, to which they are covalently bonded, lie in the range ±(89.9–93.3)/±(108.9–114.4)/±(113.6–118.8) degrees (sings “±” correspond to enantiomers). This fact is connected with the asymmetrical surrounding of the lone electron pairs of the oxygen atom of the hydroxyl groups. In the process of the turning via the TSs it was not observed deformation of the hydroxyl groups or rings, with which they are bounded. In other words, these fragments of the quercetin molecule could be considered as non-deformational, rigid rotators. Turning of the O5H and O7H around the 180 degree around the C5–O5 and C7–O7 bonds practically do not change the geometry of the molecule. At the same time, the torsional mobility of the O3H hydroxyl group is closely connected with the torsional mobility of the B ring around the C2–C1′ bond (Figure 1, Figure 2 and Figure 3, Table 1, Table 2 and Table 3 and Table 5).

Interestingly, that TSs, which control the torsional mobility of the O3H and O5H hydroxyl groups, are stabilized by the intramolecular specific interactions (Figure 2, Figure 3 and Table 5). The same effects are not characteristic for the rotation of the O7H hydroxyl group (Figure 1).

In the first case for the O3H hydroxyl group turning—there are non-standard [45] C2′H/C6′H...O3H H-bonds (2.86–2.99/2.83–2.95 kcal·mol⁻¹); in the second case—attractive O4...O5 vdW contact (2.91–3.27 kcal·mol⁻¹). It should be noted that energies of these interactions in TSs are higher, than in the corresponding conformers—starting in the first case and terminal—in the second case [16].

It attracts attention that at the TSs^O7H, where O7H hydroxyl group is not involved in the intramolecular specific interactions, the energy of all others specific interactions (O5H…O4, O3H…O4, O3H…C2′/C6′, C2′/C6′H…O3 and O4…O5), especially of two first, slightly changes (no more than by 5%) in comparison with the analogous values for the starting or terminal conformers. It points on the fact, that strictly saying, specific intramolecular contacts are not interactions, which are localized at the defined set of atoms and are dependent on the conformational state of the whole molecule.

It was observed interesting dependencies of the influence of the rotation of the hydroxyl group around the C–O bond on the energy of the specific intramolecular interactions for the TSs^O5H (Figure 2, Table 2 and Table 5). In the case of the conformational transitions in the non-planar conformers of the quercetin molecule this influence on the energies of the O3H…C2′/C6′ H-bonds and attractive O4…O5 vdW contacts could be neglected, since it is insignificant. Transition of the O5H hydroxyl group at the TSs of the planar conformers caused insignificant increasing of the energy (by 0.07 kcal mol⁻¹) of the O4…O5 contact in comparison with the final conformers. At the same time, the energy of the O3H…O4 H-bond significantly increased (by 40%) in comparison with the analogous values for the starting conformers, and the energy of the C2′/C6′H…O3 H-bonds remained almost unchangeable (Table 5).

At the transition of the O3H group at the TSs, the energy of the C2′/C6′H…O3 H-bonds decreased by 25%, and energy of the O5H…O4 H-bonds increased by 30% in comparison with the analogous value for the starting conformers. At the same time, the energy of the attractive O4…O5 vdW contacts increased by 0.3% in comparison with the analogous value for the starting conformers (Table 5).

Under standard conditions the activation barriers of the Gibbs free energies ∆∆G_TS form the following order of priority: ΔΔG_TS^O7H (3.51–4.24) < ΔΔG_TS^O3H (9.04–11.26) < ΔΔG_TS^O5H (12.34–16.17 kcal mol⁻¹; Table 1, Table 2 and Table 3). It became understandable from the mentioned above, why the value of the Gibbs free energy barrier for the forward conformational transformation ΔΔG_TS^O5H is the largest—at the corresponding TSs the most strong O5H…O4 H-bonds (6.47–8.62 kcal·mol⁻¹) was absent and could not be compensated by the present attractive O4…O5 vdW contact (2.97–3.27 kcal·mol⁻¹) and increasing of the energy of the unusual [45] C2′H/C6′H...O3 H-bond on 1.3 kcal mol⁻¹ (Table 5). Value of the ΔΔG_TS^O7H was the smallest, since in this case there were no specific intramolecular interactions. Value for the ΔΔG_TS^O3H possessed a middle value, since the absence of the O3H…O4 H-bond (3.12–4.56 kcal·mol⁻¹) was partially compensated by the non-standard [45] C2′H/C6′H...O3 H-bonds (2.85–2.95 kcal·mol⁻¹; Table 5).

By analyzing the rearrangement of the specific intramolecular contacts (H-bonds and vdW contacts) it was established that in the case of the rotation of the O7H hydroxyl group these contacts remained (Figure 1, Figure 2 and Figure 3, Table 5). In particular, in the case of the interconversion of the planar conformers of the quercetin molecule there were three specific contacts:

-

O5H…O4, O3H…O4 and C2′H…O3 H-bonds (initial conformer, TS, terminal conformer; 1↔5, 7↔8 and 10↔12);

-

O5H…O4, O3H…O4 and C6′H…O3 H-bonds (initial conformer, TS, terminal conformer; 2↔4, 3↔6 and 9↔11);

-

O5…O4 vdW contact and O3H…O4, C2′H…O3 H-bonds (initial conformer, TS, terminal conformer; 19↔25, 27↔32 and 33↔35);

-

O5…O4 vdW contact and O3H…O4, C6′H…O3 H-bonds (initial conformer, TS, terminal conformer; 21↔31, 22↔28 and 34↔36).

In the case of the interconversion of the non-planar conformers there were two specific contacts:

-

O5H…O4 and O3H…C6′ H-bonds (initial conformer, TS, terminal conformer; 13↔23, 14↔17 and 24↔29);

-

O5H…O4 and O3H…C2′ H-bonds (initial conformer, TS, terminal conformer; 15↔18, 16↔20 and 26↔30);

-

O5…O4 vdW contact and O3H…C6′ H-bond (initial conformer, TS, terminal conformer; 37↔43, 39↔44 and 45↔47);

-

O5…O4 vdW contact and O3H…C2′ H-bond (initial conformer, TS, terminal conformer; 38↔41, 40↔42 and 46↔48).

Notably, that for each set of the specific intramolecular contacts, there were three transitions.

In the case of the rotation of the O5H hydroxyl group the set of intramolecular specific contacts (3 H-bonds) transformed into the set of 1 vdW contact and 2 H-bonds for the interconversions of the planar conformers:

-

O5H…O4, O3H…O4 and C2′H…O3 H-bonds (initial conformer) → O5…O4 vdW contact and O3H…O4, C2′H…O3 H-bonds (TS, terminal conformer; 1↔25, 3↔28, 5↔19, 7↔32, 8↔27, 10↔35 and 12↔33);

-

O5H…O4, O3H…O4 and C6′H…O3 H-bonds (initial conformer) → O5…O4 vdW contact and O3H…O4, C6′H…O3 H-bonds (TS, terminal conformer; 2↔31, 4↔21, 6↔22, 9↔36 and 11↔34).

A set of two intramolecular contacts (2 H-bonds) transformed into another set (1 vdW contact and 1 H-bond) for the interconversions of the non-planar conformers:

-

O5H…O4 and O3H…C6′ H-bonds (initial conformer) → O5…O4 vdW contact and O3H…C6′ H-bonds (TS, terminal conformer; 13↔43, 14↔44, 17↔39, 23↔37, 24↔47 and 29↔45);

-

O5H…O4 and O3H…C2′ H-bonds (initial conformer) → O5…O4 vdW contact and C6′H…O3 H-bonds (TS, terminal conformer; 15↔42, 16↔38, 18↔40, 20↔41, 26↔48 and 30↔46).

Finally, the most exotic situation was observed at the interconversion of the conformers, which all were non-planar, through the rotation of the O3H hydroxyl group—at this, three intramolecular specific contacts (3 H-bonds/1 vdW contact and 2 H-bonds) transformed into two (2 H-bonds/1 vdW contact and 1 H-bond):

-

O5H…O4, O3H…O4 and C2′H…O3 H-bonds (initial conformer) → O5H…O4, C2′H…O3H H-bonds (TS) → O5H…O4 and O3H…C2′ H-bonds (terminal conformer; 1↔20, 5↔16, 7↔15, 8↔18, 10↔26 and 12↔30);

-

O5H…O4, O3H…O4 and C6′H…O3 H-bonds (initial conformer) → O5H…O4, C6′H…O3H H-bonds (TS) → O5H…O4 and O3H…C6′ H-bonds (terminal conformer; 2↔14, 3↔13, 4↔17, 6↔23, 9↔24 and 11↔29);

-

O5…O4 vdW contact and O3H…O4, C2′H…O3 H-bonds (initial conformer) → O5…O4 vdW contact and C2′H…O3H H-bond (TS) → O5…O4 vdW contact and O3H…C2′ H-bond (terminal conformer; 19↔38, 25↔41, 27↔40, 32↔42, 33↔46 and 35↔48);

-

O5…O4 vdW contact and O3H…O4 and C6′H…O3 H-bonds (initial conformer) → O5…O4 vdW contact and C6′H…O3H H-bond (TS) → O5H…O4 and O3H…C6′ H-bonds (terminal conformer; 21↔39, 22↔37, 28↔43, 31↔44, 34↔45 and 36↔47).

It attracted attention that behavior of the O7H hydroxyl group significantly differed from the other two hydroxyl groups—at its turning on 180 degrees around the C7–O7 bond relative Gibbs free energy of the molecule changed insignificantly (no more than on 0.75 kcal·mol⁻¹) with four exceptions (Table 1). Moreover, dihedral angle HO7C7C8/HO7C7C6, which describes the orientation of this group in the transition state relatively the A ring, differs from the right angle maximally by the 3.4 degree (Table 1).

Since the hydroxyl group was quite polar fragment, it is understandable, that all 72 conformational transitions without exceptions were dipole-active (Figure 1, Figure 2 and Figure 3, Table 1, Table 2 and Table 3). That is, they were accompanied by the significant changing of the dipole moment of the molecule as by the absolute value, so by the spatial orientation.

Revealed conformational processes were in the range from 5.6·10⁻¹⁵ to 1.7·10⁻¹⁰ s—time, which is necessary to acquire thermal equilibrium, did not exceed 6.5 ns (Table 1, Table 2 and Table 3).

The calculations revealed four dynamically unstable conformers—20, 23, 43 and 44 (∆∆G < 0), which was caused by the quite short lifetime (5.6 × 10⁻¹⁵, 9.1 × 10⁻¹⁵, 7.7 × 10⁻¹⁴ and 2.2 × 10⁻¹⁴ s) for the 1↔20, 6↔23, 28↔43 and 31↔44 conformational transitions (Table 3). However, at their immersion into the solution with the dielectric permittivity ε = 4, which corresponded to the interfaces of the biomolecular interactions [16,17], they became dynamically stable with a lifetime 10⁻¹² s (2.8 × 10⁻¹², 5.5 × 10⁻¹², 4.6 × 10⁻¹² and 2.7 × 10⁻¹² s, accordingly).

We also explored interconversions of the enantiomers (two stereoisomers, right (R) and left (L), that are mirror reflections of each other) of the non-planar conformers with C₁ point symmetry—13–18, 20, 23, 24, 26, 29, 30 and 37–48 (Figure 4, Table 4). Enantiomers, as it is known, had the same scalar physico-chemical properties and differed only by the spatial orientation of the dipole moments.

It is quite interesting to consider the structural mechanisms of the interconversion of the enantiomers of the non-planar conformers of the quercetin molecule.

We revealed that the above-mentioned enantiomers could mutually interconvert by the two different pathways from the energetical and topological points of view: first, through the quasi-planar TS and second, through the mirror-symmetric torsional motion of the O3H hydroxyl group through the corresponding planar conformers (with O3H...O4 and C2′/C6′H...O3 H-bond [16]) as intermediate.

Comparison of the activation energy of Gibbs free energies of these two pathways of interconversion indicate that enantiomers of the non-planar conformers of the quercetin molecule most probably mutually interconvert according to the first mechanism—through the quasi-planar TSs with C₁ point symmetry (HO3C3C2C1 = ±(11.0–19.1), HC2′/C6′C1′C2 = ±(0.6–2.9) and C3C2C1′C2′/C3C2C1′C6′ = ±(1.7–9.1) degree; ΔΔG_TS=1.65–5.59 kcal·mol⁻¹; Table 4). This effect was caused by the great structural flexibility of the molecule: there were low-frequency (ν < 100 cm⁻¹) modes in its vibrational spectra, corresponding to the motions of the (A + C) and B rings around the C2–C1′ bond.

We established that the processes of the interconversion of the significantly non-planar enantiomers (C3C2C1′C2′/C6′ 42–44 degree [16]) occurred through the rearrangement of the (A + C) and B rings of the quercetin molecule into the quasi-planar structures. TSs of these transitions had quasi-planar architecture (HO3C3C2C1 = ±(11.0–19.1); HC2′/C6′C1′C2 = ±(0.6–2.9); C3C2C1′C2′/C3C2C1′C6′ = ±(1.7–9.1) degree) and were characterized by the imaginary frequencies, which were in the range 221.3–347.9 cm⁻¹. Gibbs free energy barriers for these reactions were quite low (1.65–5.59 kcal mol⁻¹), that is they were proceeding quite easily (τ_99.9% = 8.52 × 10⁻¹²–6.46 × 10⁻⁹ s; Table 4).

By following the IRC calculations, we established that firstly it occurs by the moving of the O3H hydroxyl groups and C2′H/C6′H groups of the B ring in the opposite directions, followed by the rearrangement of (A + C) and B rings via the rotation around the C2–C1′ bond, leading to the decreasing of their dihedral angles (Table 4). At this, the intramolecular O3H…C2′H/C6′H H-bonds between the (A + C) and B rings switch into the dihydrogen O3H…HC2′/C6′ H-bonds (4.58–4.78/4.70–4.84 kcal mol⁻¹). At this new intramolecular unusual C2′/C6′…O1 H-bond (4.67–4.73/4.63–4.70 kcal mol⁻¹) also arose. Notably, at these transformations the C3C2C1′ and C2′/C6′C1′C2 angles increased (126→130 and 122→125 degrees, respectively) in order to enable the arrangement of the (A + C) and B rings and O3H and C2′H/C6′H hydroxyl groups in the plane. Earlier such H-bonds have been observed in the dozens of the prototropic tautomers, which are isomers differing by the positions of the protons and π-electrons [49], of the quercetin molecule [50]. Their characteristic property is the unusual range of angles of the C2′H/C6′H…O1 H-bonding = 98.1–99.9 degree (Table 5).

It is interesting to note, that planar structures with zero values of the HO3C3C2C1, HC2′/C6′C1′C2 and C3C2C1′C2′/C3C2C1′C6′ angles (point symmetry C_s) were characterized by the presence of the two imaginary frequencies (19.5–40.2 and 466.1–538.6 cm⁻¹), had higher Gibbs free energies (0.69–1.53 kcal mol⁻¹) than quasi-planar TSs, while close values of the dipole moment, and they should be considered as so-called TSs between the just-mentioned non-planar TSs, which control interconversion of the enantiomers of the quercetin molecule (Figure 4 and Table 4).

We are convinced that obtained by us data according the structurally symmetrical mechanisms of the interconversion of the enantiomers of the 24 non-planar conformers of the quercetin molecule are quite important for the understanding of the nature of the stereo-specific interaction of this legendary molecule with molecular targets.

4. Conclusions

As a result of the in silico scrupulous investigation at the MP2/6-311++G(2df,pd)//B3LYP/6-311++G(d,p) level of QM theory, we investigated in details revealed conformational pathways, which are connected with the torsional mobility of the hydroxyl groups at the 3, 5 and 7 positions and interconversion of the enantiomers of the non-planar conformers of the quercetin molecule, and also their structural, energetic and polar physico-chemical characteristics, representing the hidden side of the conformational mobility of the quercetin molecule mentioned in the article title.

• It was established, that conformational mobility of the isolated quercetin molecule, which is connected with the mirror-symmetric torsional mobility of its O3H, O5H and O7H hydroxyl groups, were controlled by the 72 transitions states with the non-orthogonal geometry (C₁ point symmetry). In the cases of the turnings of the O7H and O5H hydroxyl groups, TSs were stabilized by the participation of the specific intramolecular interactions—attractive O4…O5 vdW contacts and C2′/C6′H...O3 H-bonds, respectively. Activation barriers of the Gibbs free energies formed the following series under the standard conditions: ΔΔG_TS^O7H (3.51–4.24) < ΔΔG_TS^O3H (9.04–11.26) < ΔΔG_TS^O5H (12.34–16.17 kcal·mol⁻¹).
• Conformational rearrangement of the O3H and O5H groups was partially controlled by the intramolecular specific interactions O3H…O4, C2′/C6′H…O3, O3H…C2′/C6′, O5H…O4 H-bonds and attractive O4…O5 vdW contacts, which were flexible and cooperative.
• Mutual transformation of the enantiomers of the non-planar conformers of the quercetin molecule realized via the 24 quasi-planar TSs with C₁ point symmetry (ΔΔG_TS = 1.65–5.59 kcal·mol⁻¹), which were supported by the participation of the intramolecular O3H...HC2′/C6′ (~4.7/4.8) and C2′/C6′H…O1 (~4.7 kcal mol⁻¹) H-bonds.
• All investigated conformational transitions were accompanied by the significant changes of the dipole moment of the molecule as by the absolute value, so by the spatial orientation.
• Investigated conformational transformations were quite quick processes—time, which is necessary to acquire thermal equilibrium, did not exceed 6.5 ns.