Closed-Form Solutions for the Form-Finding of Regular Tensegrity Structures by Group Elements

Abstract

An analytical form-finding method for regular tensegrity structures based on the concept of force density is presented. The self-equilibrated state can be deduced linearly in terms of force densities, and then we apply eigenvalue decomposition to the force density matrix to calculate its eigenvalues. The eigenvalues are enforced to satisfy the non-degeneracy condition to fulfill the self-equilibrium condition. So the relationship between force densities can also be obtained, which is followed by the super-stability examination. The method has been developed to deal with planar tensegrity structure, prismatic tensegrity structure (triangular prism, quadrangular prism, and pentagonal prism) and star-shaped tensegrity structure by group elements to get closed-form solutions in terms of force densities, which satisfies the super stable conditions.

1. Introduction

Tensegrity structures refer to the stable structures that are based on the balance between their members in compressive or tensile states. This kind of structure is composed of struts carrying compressive forces and cables carrying tensile forces. The members are prestressed so that the structure gets its shape as well as rigidity in a self-equilibrated state in the absence of external loads [1]. Kennet Snelson designed and constructed the initial tensegrity model in 1947, the concept of which was then introduced by Fuller to define the very type of structure. In the last few decades, tensegrity structures have been widely studied and applied to various fields, such as civil engineering [2,3,4,5], aerospace [6,7], biology [8,9,10], mathematics [11], and robotics [12].

The process of determining the self-equilibrated configuration is known as form-finding [13], which is a necessity for tensegrity structures. The difficulties in solving the form-finding problems of tensegrity structures always lie in finding a self-equilibrated configuration, which satisfies the required specific properties of the structure [14]. A variety of studies about form-finding have been conducted. The existing form-finding methods can be divided into force design and shape design. Theories about force design have been developed a lot, such as searching feasible regions and optimizing internal forces with constraint conditions or given shape [7,15]. Shape design is usually based on force density method, dynamic relaxation method, or nonlinear structural analysis. Schek firstly developed the force density method for the form-finding of cable-nets in 1974 [16]. Following the track, many researchers have extended the concept of force density method [17,18,19,20,21,22]. The dynamic relaxation method has also been applied to tensile structures [23] and tensegrity structures [24]. Nonlinear structural analysis with fictitious material properties has been introduced [25,26]. Existing form-finding methods have been reviewed [27,28,29].

Form-finding methods can also be divided into two broad classes, analytical methods, and numerical methods [30]. Analytical methods are usually used for regular structures with a high level of symmetry, e.g., prismatic tensegrity structures [31,32], or truncated polyhedral tensegrity structures [33,34]. Zhang et al. studied the stability and configuration of symmetric prismatic tensegrity structures [35,36]. Zhang and Ohsaki used group theory and symmetry property of tetrahedral tensegrity structures [37], and Zhang et al. aimed at exploring the self-equilibrium and stability properties of all Z-based and rhombic TRP tensegrities respectively [38,39,40].

Numerical methods may have more extensive applications comparing with analytical methods. Numerical methods with force density concepts have been developed [41,42]. It may also turn into a nonlinear problem that intends to minimize the total length of cables or maximize that of struts [43]. Both dynamic relaxation method and nonlinear structural method, as mentioned, are also placed as numerical methods. Inspired by the dynamic relaxation method, Li et al. developed the Monte Carlo form-finding method for large scale regular and irregular tensegrity structures [13]. An energy method [44] and a marching process [45] for form-finding have been proposed. The genetic algorithm is a representative technique of Darwinian Theory and has been proposed for form-finding [46,47,48,49].

To make tensegrity structures into real applications, it is essential to ensure the stability condition. Maxwell’s rule for structures made of trusses was developed in 1864 [50], and then it was revised by Calladine [51]. Connelly defined the stability condition for tensegrity structures [44]. Deng and Kwan developed an energy-based approach to categorizing of the stability conditions of tensegrity structures [52]. Guest investigated a more natural way to calculate the tangent stiffness matrix [53]. According to Zhang and Ohsaki, the stable status of tensegrity structures can be divided into super-stability and prestress-stability [54]. A tensegrity structure is defined as a super-stable one if it is always stable regardless of the level of prestress and the selection of materials [28], while prestress stability relates to the stiffness matrix and its eigenvalues, as will be discussed later in this paper.

Though numerical methods can deal with more irregular and complicated structures, analytical methods appear to be the most effective way without iteration or the introduction of concepts from other disciplines. Moreover, it provides an opportunity of looking inside the relation between different force densities. Therefore, analytical methods remain optimal, especially when they are applied to regular tensegrities. In most of the previous studies, analytical solutions were deduced by the investigation of self-equilibrium and super-stability conditions. For example, Zhang et al. gave a unified solution for truncated regular tensegrities using the self-equilibrium and stability properties [38,39,40]. Group theory has been developed on structures with a large number of elements [34,35,36]. The method appears to be quite effective for structures with symmetric or periodic property, which are prevalent structural forms in practical engineering [55,56]. This paper follows the idea of group theory and divides the elements into groups to improve computational efficiency. Therefore, the analytical method proposed in this paper has broader applications in regular tensegrity structures comparing to the existing analytical methods.

In this paper, an analytical form-finding method based on the force density method is investigated to get a closed-form solution in terms of force densities. Only the topology and property of structural members are needed in advance. The proposed method can be divided into two main parts, equilibrium analysis and super-stability examination. The paper is organized as follows: Section 2 illuminates the basic concept of force density method and its usage in the process of form-finding, which is followed by the non-degeneracy condition. Section 3 presents the super-stability condition of tensegrity structures. The proposed method is depicted and discussed in Section 4. Examples of a planar tensegrity structure, three kinds of prismatic tensegrity structure (triangular prism, quadrangular prism, and pentagonal prism) and a star-shaped tensegrity structure are given in Section 5 to verify its efficiency and versatility.

2. Force Density Method and Self-Equilibrium Condition

2.1. Assumptions

The analytical method for form-finding bases on the equilibrium condition at the nodes. In this study, the fundamental assumptions for tensegrity structures are adopted as follows [18]:

(a)

Members are connected using pin joints;

(b)

No external loads are included, and the gravity is ignored;

(c)

Member failure is not considered: i.e., struts do not yield and cables do not bear compressive forces;

(d)

The structure is self-equilibrated and free-standing without any support;

(e)

The topology (connectivity between the nodes and members) of the tensegrity structure is known, and the geometrical configuration of the structure can be described in terms of nodal coordinates only.

2.2. Force Density Method

The force density of a structural member k is defined as

$$q_k=\frac{f_k}{l_k}$$

(1)

where f_k and l_k are the force and length of member k, respectively.

We define E as the force density matrix, which can be written directly from the force densities q_k [31,50] as

$$E_{(i,j)}=\{\begin{array}{l}\hspace{0.17em}{\displaystyle \sum _{k\in \phi }{q}_k} \mathrm{for} i=j\\ -q_k \mathrm{for} \mathrm{nodes} i \mathrm{and} j \mathrm{are} \mathrm{connected} \mathrm{by} \mathrm{member} k\\ 0 \mathrm{for} \mathrm{other} \mathrm{cases}\end{array}$$

(2)

where φ denotes the set of members connected to node i. It should be noted that sum of the entries in each row or column of the force density matrix in Equation (2) is zero, which is always true for free-standing structures. The equilibrium condition of tensegrity structures in terms of force density matrix E can be written as

$$\begin{array}{l}Ex=0\\ Ey=0\\ Ez=0\end{array}$$

(3)

where x, y, and z are the coordinates of the structural system. In other words, the equilibrium condition of tensegrity structures can be expressed in terms of force densities.

2.3. Non-Degeneracy Condition

According to Schek [16], matrix E is always square and symmetric, and positive-definite if all members are in tension. So, for cable-nets, which only possess positive values of force densities, E is invertible, and nodal coordinates can be uniquely determined by solving the linear Equation (3) [18]. However, there are struts in tensegrity structures, which means negative elements of E. So, matrix E is invariably singular with rank deficiency. Define the rank deficiency h of E as

$$h=n-\mathrm{rank}(E)$$

(4)

where n is the number of free nodes.

From the equilibrium equations Equation (3), the solution space is spanned by h independent vectors. If h = 1, all nodes degenerate into one node; and if h = 2, it turns into a line passing through the base node; h = 3 and h = 4 forms a two-dimensional and three-dimensional space, respectively [18]. Therefore, to obtain a non-degenerate d-dimensional (d = 2 or 3) tensegrity structure, the rank deficiency h of E should satisfy the following condition

$$h\ge d+1$$

(5)

It should be noticed that Equation (5) is a necessary but not sufficient condition for non-degeneracy of condition tensegrity structures [27,29,44]. The sufficient conditions for tensegrities or self-equilibrated pin-jointed structures were investigated by Zhang and Ohsaki [57], and a rough explanation will be presented in the next section.

3. Stable Conditions

Self-equilibrium analysis and stability properties are the two critical points in the design of tensegrity structures, both of which can be dealt with by investigating the eigenvalues of the force density matrix [37].

A structure is regarded as stable if it satisfies [57]

$$d^{\mathrm{T}}Kd>0$$

(6)

where d is any nodal displacement vector, and K is the tangent stiffness matrix. It should be notable that the rigid-body motions are not included in d. The tangent stiffness matrix K of a tensegrity structure can be divided into two parts

$$K=K^{\mathrm{E}}+K^{\mathrm{G}}$$

(7)

where K^E is the linear stiffness matrix, and K^G is the geometrical stiffness matrix. Substitute Equation (7) into Equation (6)

$$d^{\mathrm{T}}Kd=d^{\mathrm{T}}{K}^{\mathrm{E}}d+d^{\mathrm{T}}{K}^{\mathrm{G}}d>0$$

(8)

An adaptive way to determine whether the stability condition is achieved was proposed [57]. A tensegrity structure is said to be super-stable if it keeps stable with any level of force densities satisfying self-equilibrium without inducing material failure [11,28]. Thus increased force densities only stiffen and stabilize the structure [38]. According to Zhang and Ohsaki, the sufficient super-stability conditions of a tensegrity structure are [54]:

(i)

the geometry matrix is full rank;

(ii)

the matrix E has (d+1) nonzero eigenvalues;

(iii)

the matrix E is positive semi-definite;

where d is the number of the dimension of the tensegrity structure.

For condition (iii), if the matrix E is not positive semi-definite, geometrical stiffness matrix K^G will have negative eigenvalues and become dominant over the linear stiffness matrix K^E at sufficiently large force densities in the elements. So the tangent stiffness matrix K fails to be positive definite, and the structure becomes unstable. Condition (ii) guarantees the self-equilibrium condition. Conditions (ii) and (iii) can be examined by the total number of zero-eigenvalues and the sign of the minimum eigenvalue respectively after eigenvalue decomposition of the force density matrix. According to Zhang [38], condition (i) will be satisfied in most cases if the structure is divisible.

Since the stable conditions of the prestress-stable structure relate to the level of force densities, we consider the super-stability condition for tensegrity structures in this paper.

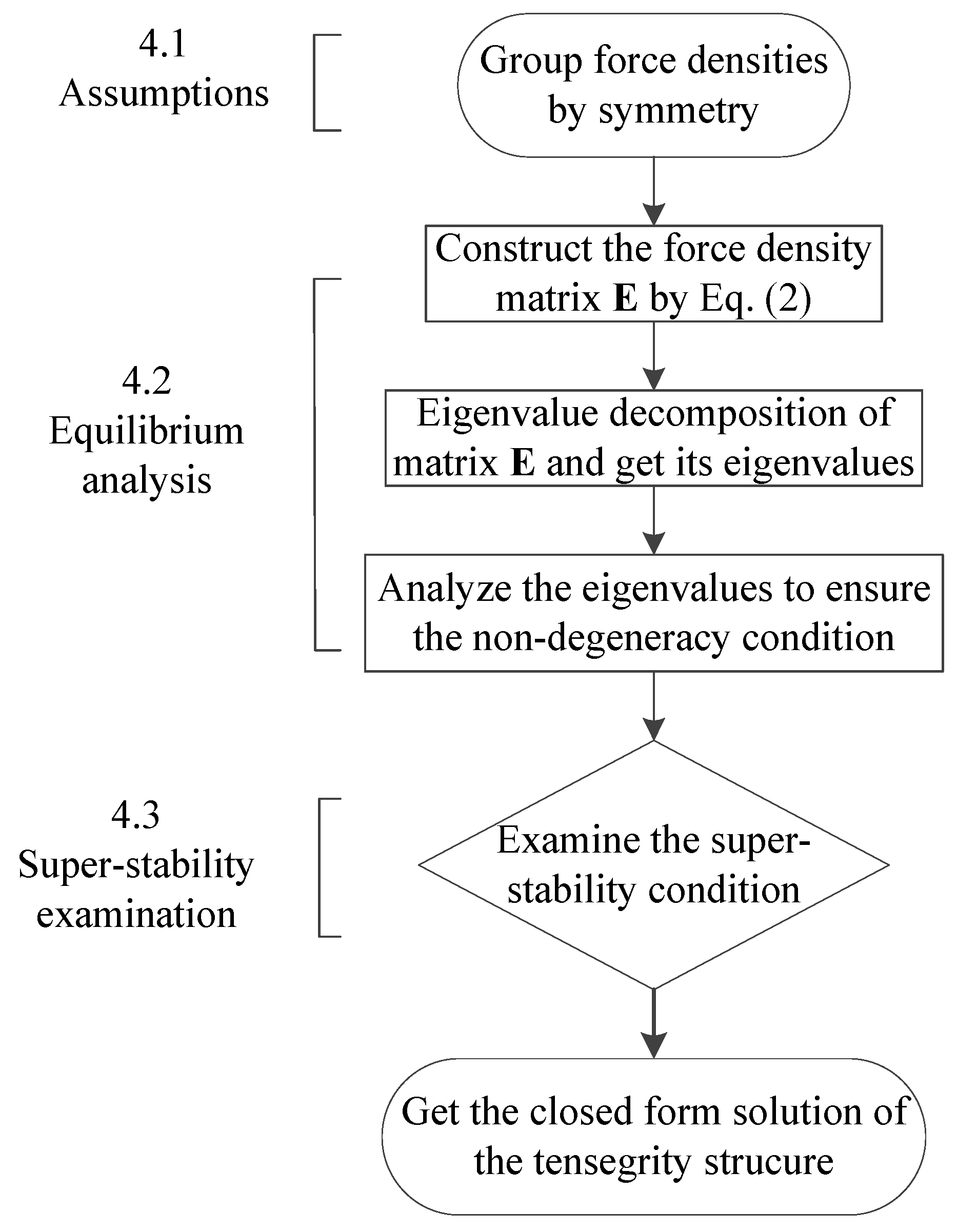
4. Form-Finding Method

In this section, we are going to describe the form-finding method in detail and take a few examples to make it brighter. The process of the analytical form-finding method can be divided into assumptions (Section 4.1), equilibrium analysis (Section 4.2) and super-stability examination (Section 4.3) in terms of force densities. It should be noticed that the method is only suitable for regular and symmetric tensegrity structures. A brief flowchart of this method is presented in Figure 1. Assume that the topology and the type of each member are given.

4.1. Assumptions

Set up force density variables for all members. If the member is a cable, we use numbers as the subscripts, i.e., q₁, q₂, q₃, ...; otherwise, we use letters, i.e., q_s, q_b, ... Moreover, the number of variables of force densities can be reduced by making use of symmetry properties.

4.2. Equilibrium Analysis

As shown in Figure 1, the equilibrium analysis includes three main steps, the construction, decomposition, and ensuring the non-degenerate condition analysis of the force density matrix E. With the force densities assumed, the force density matrix E can be obtained according to Equation (2). Then the eigenvalues λ₁, λ₂, λ₃, ... λ_n of matrix E can be determined by solving the equation [38]

$$\det (\lambda I-E)=0$$

(9)

where I is the unit matrix. The expanded form of Equation (9) is shown as

$$\det (\lambda I-E)={\lambda }^n+A_{n-1}(·){\lambda }^{n-1}+A_{n-2}(·){\lambda }^{n-2}+\dots +A_1(·)\lambda +A_0=0$$

(10)

where A₀(·), A₁(·), ..., A_n-1(·) denote the polynomial functions in terms of the force densities and Equation (10) can be obtained by eigenvalue decomposition.

According to Section 2.3, the non-degeneracy condition has to be achieved to ensure self-equilibrium. Therefore, Equation (5) should be fulfilled. To achieve that, there should exist enough zero eigenvalues. For example, if there is a three-dimensional tensegrity structure, at least four of the eigenvalues should be zero. With the obtained expressions of eigenvalues, we should notice the number of zero eigenvalues before deciding expressions that are definitely greater than zero. Then, for the rest of eigenvalues, the value of which we cannot determine directly by the expressions set one or a few of them equal to zero so that a relationship between force densities can be obtained. The judging process is summarized as follows:

• Step 1: Calculate the rank deficiency h of the force density matrix E (Equation (4)).
• Step 2: Notice the number of expressions that are equal to zero and record it as t₁. Usually, there is only one expression of eigenvalue equal to zero after the decomposition. We assume this eigenvalue as λ₁.
• Step 3: Find all the expressions of eigenvalues that are definitely greater than zero and denote the number of eigenvalues as t₂.
• Step 4: Select a few of the rest expressions of eigenvalues equal to zero. Record the number of expressions that are assumed to zero as t₃, and t₃ + t₁ ≥ h should be satisfied.
• Step 5: Get the relationship between force densities from the equations in Step 4.

4.3. Super-Stability Examination

According to Section 3, the super-stability condition is usually satisfied if conditions (ii) and (iii) are fulfilled. It should be noticed that the non-degeneracy condition is identical to the condition (ii). So only condition (iii) remains to be examined.

The number of all eigenvalues is m, which includes (t₃ + t₁) zero eigenvalues, t₂ positive eigenvalues and (m-t₁-t₂-t₃) uncertain eigenvalues. If all of the uncertain eigenvalues are not less than zero, the structure is super stable. N1, N2, N3, ... represent nodes while M1, M2, ... denote members. A planar tensegrity structure, three types of prismatic tensegrity structures (triangular prism, quadrangular prism, pentagonal prism) and a star-shaped tensegrity structure will be analyzed in the next section.

5. Examples

In this section, examples are presented based on the proposed method. A planar tensegrity structure, three types of prismatic tensegrity structure (triangular prism, quadrangular prism, pentagonal prism) and a star-shaped tensegrity structure are selected as examples. The detailed descriptions of prismatic and star-shaped tensegrity structures can be found in chapters 7 and 8 of reference [57].

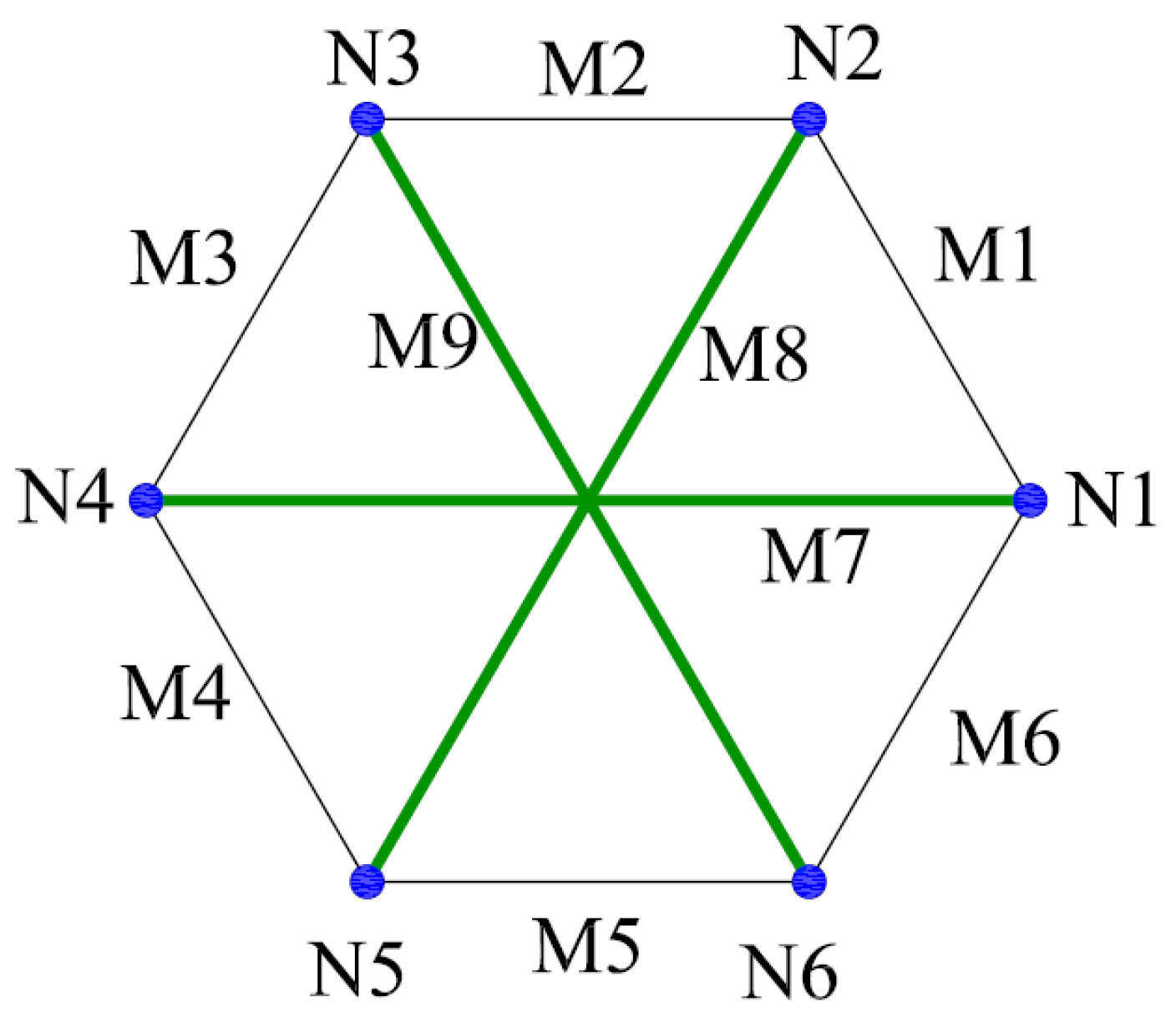
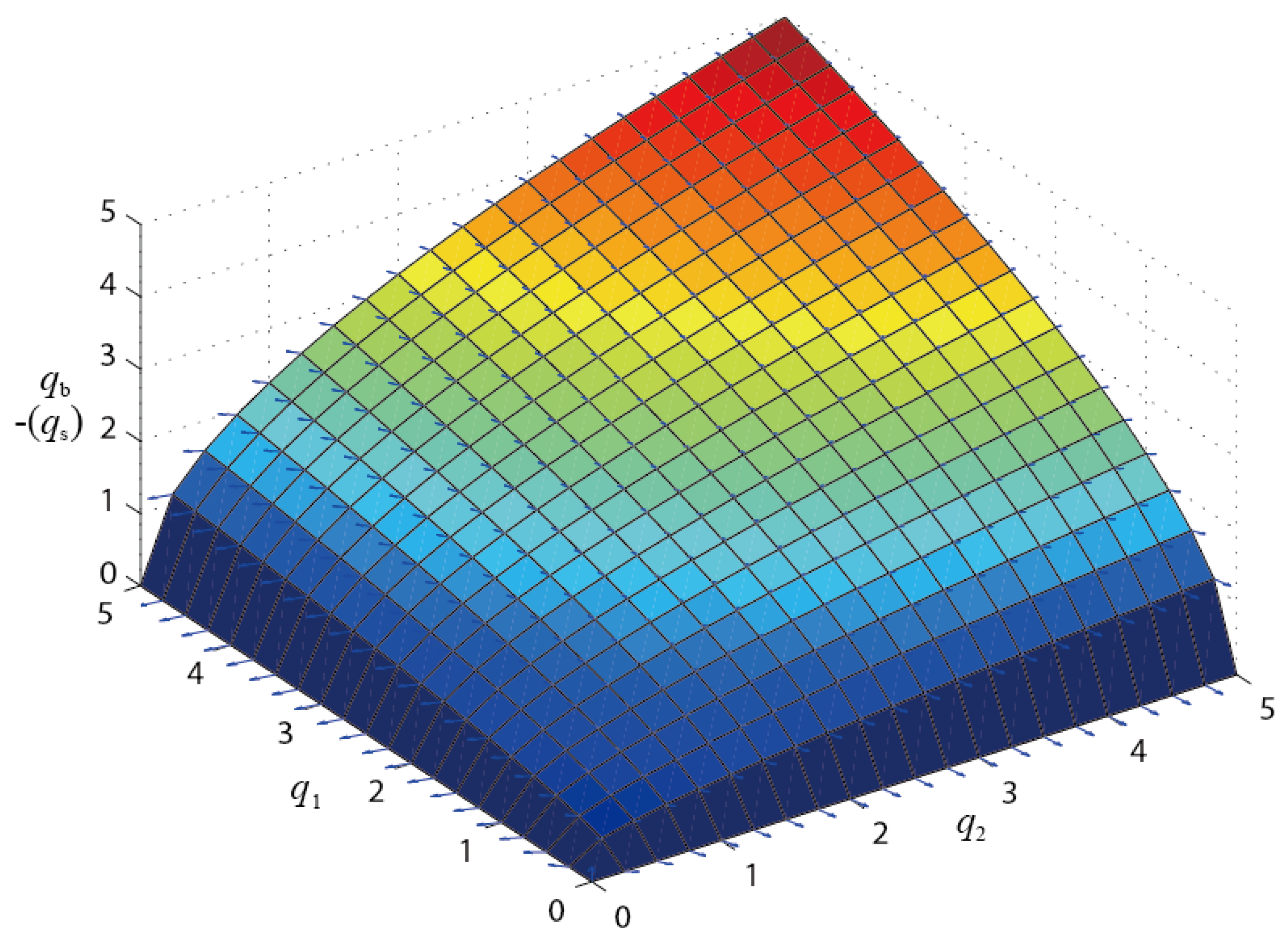
5.1. Planar Tensegrity

For a simple planar tensegrity structure with six cables and three struts, an explicit study is carried out to demonstrate the capability of the investigated method.

Suppose that the tensegrity structure, which is shown in Figure 2, has three kinds of force densities: q₁, q₂, and q_s. q₁ represents the force density of cable elements M1, M3, and M5; q₂ denotes the force density of cable elements M2, M4, and M6; q_s indicates the force density of struts. Then the force density matrix E can be given as

$$E=\left[\begin{array}{cccccc}{q}_1+q_2+q_{\mathrm{s}}& -q_1& 0& -q_{\mathrm{s}}& 0& -q_2\\ -q_1& q_1+q_2+q_{\mathrm{s}}& -q_2& 0& -q_{\mathrm{s}}& 0\\ 0& -q_2& q_1+q_2+q_{\mathrm{s}}& -q_1& 0& -q_{\mathrm{s}}\\ -q_{\mathrm{s}}& 0& -q_1& q_1+q_2+q_{\mathrm{s}}& -q_2& 0\\ 0& -q_{\mathrm{s}}& 0& -q_2& q_1+q_2+q_{\mathrm{s}}& -q_1\\ -q_2& 0& -q_{\mathrm{s}}& 0& -q_1& q_1+q_2+q_{\mathrm{s}}\end{array}\right]$$

(11)

Eigenvalues of the matrix E in Equation (11) are

$$\begin{array}{l} {\lambda }_1=0\\ {\lambda }_2=2(q_1+q_2+q_{\mathrm{s}})\\ {\lambda }_3={\lambda }_5=q_1+q_2+q_{\mathrm{s}}+\sqrt{q_1^2-q_1{q}_2-q_1{q}_s+q_2^2-q_2{q}_{\mathrm{s}}+q_{\mathrm{s}}^2}\\ {\lambda }_4={\lambda }_6=q_1+q_2+q_{\mathrm{s}}-\sqrt{q_1^2-q_1{q}_2-q_1{q}_s+q_2^2-q_2{q}_{\mathrm{s}}+q_{\mathrm{s}}^2}\end{array}$$

(12)

From Equation (12), it should be noticed that q_s is a negative value. Assume that λ₂ is greater than zero. Therefore, λ₃ and λ₅ are always greater than zero. Then assume λ₄ and λ₆ equal to zero, so relationship among q₁, q₂, and q_s is obtained as

$$q_1=-\frac{q_2{q}_{\mathrm{s}}}{q_2+q_{\mathrm{s}}}$$

(13)

To ensure that q₁ is positive, q₂ must be greater than -q_s. q₁ is known by Equation (13), and therefore λ₂ is greater than 0. In conclusion, λ₂, λ₃, and λ₅ in Equation (12) are greater than zero while the other three are equal to zero, which satisfies the super-stability condition of tensegrity structures.

5.2. Three-dimensional prismatic tensegrity structures

5.2.1. Triangular Prism

Suppose that the triangular prism tensegrity structure, shown in Figure 3, has four kinds of force densities: q₁, q₂, q_b, and q_s. q₁ represents the force density of cable element M1, M2, M3; q_b denotes the force density of M4, M5, M6; q₂ denotes the force density of M7, M8, M9, and q_s denotes the force density of struts. Then the force density matrix E can be given as

$$E=\left[\begin{array}{cccccc}2q_1+q_{\mathrm{b}}+q_{\mathrm{s}}& -q_1& -q_1& -q_{\mathrm{s}}& 0& -q_{\mathrm{b}}\\ -q_1& 2q_1+q_{\mathrm{b}}+q_{\mathrm{s}}& -q_1& -q_{\mathrm{b}}& -q_{\mathrm{s}}& 0\\ -q_1& -q_1& 2q_1+q_{\mathrm{b}}+q_{\mathrm{s}}& 0& -q_{\mathrm{b}}& -q_{\mathrm{s}}\\ -q_{\mathrm{s}}& -q_{\mathrm{b}}& 0& 2q_2+q_{\mathrm{b}}+q_{\mathrm{s}}& -q_2& -q_2\\ 0& -q_{\mathrm{s}}& -q_{\mathrm{b}}& -q_2& 2q_2+q_{\mathrm{b}}+q_{\mathrm{s}}& -q_2\\ -q_{\mathrm{b}}& 0& -q_{\mathrm{s}}& -q_2& -q_2& 2q_2+q_{\mathrm{b}}+q_{\mathrm{s}}\end{array}\right]$$

(14)

Eigenvalues of the matrix E in Equation (14) are shown as

$$\begin{array}{l} {\lambda }_1=0\\ {\lambda }_2=2(q_{\mathrm{b}}+q_{\mathrm{s}})\\ {\lambda }_3={\lambda }_5=\frac{3}{2}(q_1+q_2)+q_{\mathrm{s}}+q_{\mathrm{b}}+\frac{1}{2}\sqrt{9q_1^2-18q_1{q}_2+9q_2^2-4q_{\mathrm{b}}{q}_{\mathrm{s}}+4q_{\mathrm{s}}^2+4q_{\mathrm{b}}^2}\\ {\lambda }_4={\lambda }_6=\frac{3}{2}(q_1+q_2)+q_{\mathrm{s}}+q_{\mathrm{b}}-\frac{1}{2}\sqrt{9q_1^2-18q_1{q}_2+9q_2^2-4q_{\mathrm{b}}{q}_{\mathrm{s}}+4q_{\mathrm{s}}^2+4q_{\mathrm{b}}^2}\end{array}$$

(15)

where q₁, q₂, q_b are all positive values, and q_s is negative because of the compression in struts. Set λ₂ equal to zero to satisfy the non-degeneracy condition. Then, we have

$$q_{\mathrm{b}}=-q_{\mathrm{s}}$$

(16)

Thus, it should be noticed that λ₃ and λ₅ are always greater than zero. Set λ₄ and λ₆ also equal to zero. Thus, the relationship among q₁, q₂, q_b, and q_s is obtained as

$$q_1=-\frac{q_2{q}_b+q_{\mathrm{s}}{q}_{\mathrm{b}}+q_2{q}_{\mathrm{s}}}{q_{\mathrm{b}}+3q_2+q_{\mathrm{s}}}$$

(17)

By substituting Equation (16) into Equation (17), we obtain

$$q_{\mathrm{s}}=-\sqrt{3q_1{q}_2}$$

(18)

If both Equation (16) and Equation (17) are satisfied, the structure fulfills the non-degeneracy condition because four eigenvalues are zero. λ₃ and λ₅ in Equation (15) are greater than zero; the other eigenvalues in Equation (15) are all equal to zero so that the structure also satisfies the super-stability condition for tensegrity structures. The results are found the same with analytical solutions derived by Pellegrino and Tibert [27]. The relationship between variables q₁, q₂, and q_s are plotted in the three-dimensional vector graph, shown in Figure 4.

5.2.2. Quadrangular Prism Tensegrity Structure

Suppose that the quadrangular prism tensegrity structure, which is shown in Figure 5, has four kinds of force densities: q₁, q₂, q_b, and q_s. q₁ represents the force density of elements M1, M2, M3, M4; q₂ represents the force density of M5, M6, M7, M8; q_b represents the force density of M9, M10, M11, M12; and q_s represents that of struts. Then the force density matrix E can be given as

$$E=\left[\begin{array}{cccccccc}2q_1+q_{\mathrm{s}}+q_{\mathrm{b}}& -q_1& 0& -q_1& -q_{\mathrm{b}}& -q_{\mathrm{s}}& 0& 0\\ -q_1& 2q_1+q_{\mathrm{s}}+q_{\mathrm{b}}& -q_1& 0& 0& -q_{\mathrm{b}}& -q_{\mathrm{s}}& 0\\ 0& -q_1& 2q_1+q_{\mathrm{s}}+q_{\mathrm{b}}& -q_1& 0& 0& -q_{\mathrm{b}}& -q_{\mathrm{s}}\\ -q_1& 0& -q_1& 2q_1+q_{\mathrm{s}}+q_{\mathrm{b}}& -q_{\mathrm{s}}& 0& 0& -q_{\mathrm{b}}\\ -q_{\mathrm{b}}& 0& 0& -q_{\mathrm{s}}& 2q_2+q_{\mathrm{s}}+q_{\mathrm{b}}& -q_2& 0& -q_2\\ -q_{\mathrm{s}}& -q_{\mathrm{b}}& 0& 0& -q_2& 2q_2+q_{\mathrm{s}}+q_{\mathrm{b}}& -q_2& 0\\ 0& -q_{\mathrm{s}}& -q_{\mathrm{b}}& 0& 0& -q_2& 2q_2+q_{\mathrm{s}}+q_{\mathrm{b}}& -q_2\\ 0& 0& -q_{\mathrm{s}}& -q_{\mathrm{b}}& -q_2& 0& -q_2& 2q_2+q_{\mathrm{s}}+q_{\mathrm{b}}\end{array}\right]$$

(19)

Eigenvalues of the matrix E in Equation (19) are

$$\begin{array}{l} {\lambda }_1=0\\ {\lambda }_2=2(q_{\mathrm{b}}+q_{\mathrm{s}})\\ {\lambda }_3=2(q_1+q_2)+q_{\mathrm{s}}+q_{\mathrm{b}}+\sqrt{4q_1^2-8q_1{q}_2+4q_2^2-2q_{\mathrm{b}}{q}_{\mathrm{s}}+q_{\mathrm{s}}^2+q_{\mathrm{b}}^2}\\ {\lambda }_4=2(q_1+q_2)+q_{\mathrm{s}}+q_{\mathrm{b}}-\sqrt{4q_1^2-8q_1{q}_2+4q_2^2-2q_{\mathrm{b}}{q}_{\mathrm{s}}+q_{\mathrm{s}}^2+q_{\mathrm{b}}^2}\\ {\lambda }_5={\lambda }_7=q_1+q_2+q_{\mathrm{s}}+q_{\mathrm{b}}+\sqrt{q_1^2-2q_1{q}_2+q_2^2+q_s^2+q_b^2}\\ {\lambda }_6={\lambda }_8=q_1+q_2+q_{\mathrm{s}}+q_{\mathrm{b}}-\sqrt{q_1^2-2q_1{q}_2+q_2^2+q_s^2+q_b^2}\end{array}$$

(20)

q₁, q₂ and q_b, the force densities of cable members, are all positive values, and q_s, the force density of struts, is negative. Presume that λ₂ equals to zero. Then

$$q_{\mathrm{b}}=-q_{\mathrm{s}}$$

(21)

It should be noticed that λ₃, λ₅ and λ₇ are always greater than zero. Thus, the sign of λ₁, λ₂, λ₃, λ₅, and λ₇ are determined. Set λ₆ and λ₈ or λ₄ equal to zero.

Case 1: If we assume that λ₆ and λ₈ equal to zero, the relationship among q₁, q₂, q_b, and q_s is obtained as

$$q_1=-\frac{q_2{q}_{\mathrm{b}}+q_{\mathrm{s}}{q}_{\mathrm{b}}+q_2{q}_{\mathrm{s}}}{q_{\mathrm{b}}+2q_{\mathrm{b}}+q_{\mathrm{s}}}$$

(22)

By substituting Equation (21) into Equation (22), we obtain

$$q_{\mathrm{s}}=-\sqrt{2q_1{q}_2}$$

(23)

Bringing Equation (22) and Equation (23) into Equation (20), we obtain λ₄

$${\lambda }_4=2\left(q_1+q_2\right)-\sqrt{4q_1^2+4q_2^2}>0$$

(24)

If both Equation (21) and Equation (23) are satisfied, the structure achieves the non-degenerate condition because four eigenvalues, λ₁, λ₂, λ₆, and λ₈, are zero while the other eigenvalues are greater than zero. So the super-stability condition for tensegrity structures is satisfied.

Case 2: If we set λ₄ equal to zero, the relationship between variables by substituting Equation (21) is shown as

$$q_{\mathrm{b}}=\sqrt{4q_1{q}_2}$$

(25)

Bring Equation (21) and Equation (25) into Equation (20), we obtain λ₆ and λ₈

$$\begin{array}{l}{\lambda }_6={\lambda }_8=q_1+q_2+q_{\mathrm{s}}+q_{\mathrm{b}}-\sqrt{q_1^2-2q_1{q}_2+q_2^2+q_{\mathrm{s}}^2+q_{\mathrm{b}}^2}\\ =q_1+q_2-\sqrt{q_1^2+6q_1{q}_2+q_2^2}>0\end{array}$$

(26)

Therefore, there are only three eigenvalues equal to zero while others are greater than zero. The non-degeneracy condition for tensegrity structures is not fulfilled. The relationship between variables q₁, q₂, and q_s are plotted in the three-dimensional vector graph, shown in Figure 6.

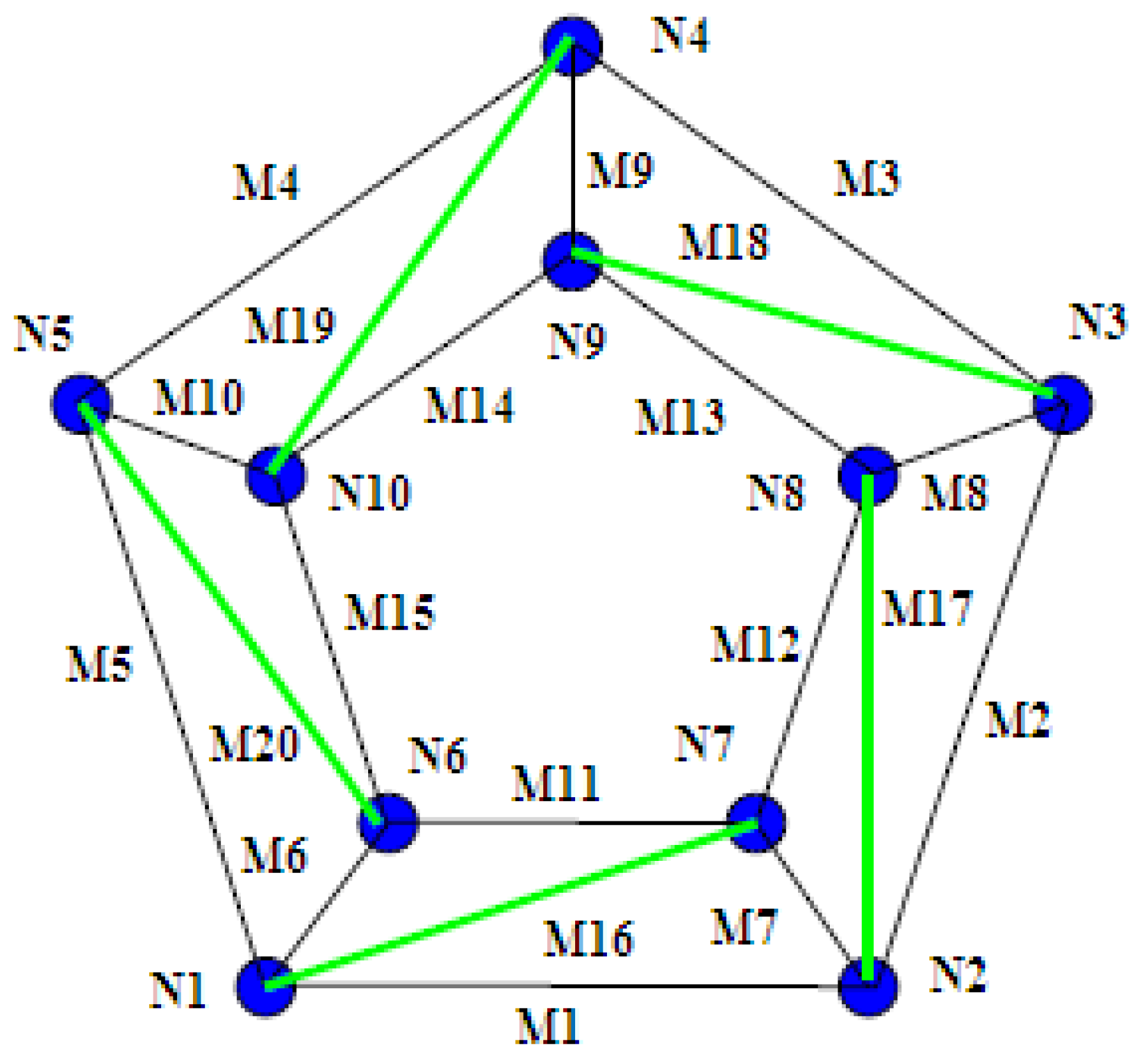
5.2.3. Quadrangular Prism Tensegrity Structure

Suppose that the pentagonal prism tensegrity structure, as shown in Figure 7, has four kinds of force densities, q₁, q₂, q_b, and q_s; q₁ represents the force density of elements M1, M2, M3, M4, M5; q₂ represents the force density of M11, M12, M13, M14, M15; q_b represents the force density of M6, M7, M8, M9, M10; and q_s represents the force density of struts. Then the force density matrix E can be given as

$$E=\left[\begin{array}{cccccccccc}\begin{array}{l}2q_1+q_{\mathrm{b}}\\ +q_{\mathrm{s}}\end{array}& -q_1& 0& 0& -q_1& -q_{\mathrm{b}}& -q_{\mathrm{s}}& 0& 0& 0\\ -q_1& \begin{array}{l}2q_1+q_{\mathrm{b}}\\ +q_{\mathrm{s}}\end{array}& -q_1& 0& 0& 0& -q_{\mathrm{b}}& -q_{\mathrm{s}}& 0& 0\\ 0& -q_1& \begin{array}{l}2q_1+q_{\mathrm{b}}\\ +q_{\mathrm{s}}\end{array}& -q_1& 0& 0& 0& -q_{\mathrm{b}}& -q_{\mathrm{s}}& 0\\ 0& 0& -q_1& \begin{array}{l}2q_1+q_{\mathrm{b}}\\ +q_{\mathrm{s}}\end{array}& -q_1& 0& 0& 0& -q_{\mathrm{b}}& -q_{\mathrm{s}}\\ -q_1& 0& 0& -q_1& \begin{array}{l}2q_1+q_{\mathrm{b}}\\ +q_s\end{array}& -q_{\mathrm{s}}& 0& 0& 0& -q_b\\ -q_{\mathrm{b}}& 0& 0& 0& -q_{\mathrm{s}}& \begin{array}{l}2q_2+q_{\mathrm{b}}\\ +q_{\mathrm{s}}\end{array}& -q_2& 0& 0& -q_2\\ -q_{\mathrm{s}}& -q_{\mathrm{b}}& 0& 0& 0& -q_2& \begin{array}{l}2q_2+q_{\mathrm{b}}\\ +q_{\mathrm{s}}\end{array}& -q_2& 0& 0\\ 0& -q_{\mathrm{s}}& -q_{\mathrm{b}}& 0& 0& 0& -q_2& \begin{array}{l}2q_2+q_{\mathrm{b}}\\ +q_{\mathrm{s}}\end{array}& -q_2& 0\\ 0& 0& -q_{\mathrm{s}}& -q_{\mathrm{b}}& 0& 0& 0& -q_2& \begin{array}{l}2q_2+q_{\mathrm{b}}\\ +q_{\mathrm{s}}\end{array}& -q_2\\ 0& 0& 0& -q_{\mathrm{s}}& -q_{\mathrm{b}}& -q_2& 0& 0& -q_2& \begin{array}{l}2q_2+q_{\mathrm{b}}\\ +q_{\mathrm{s}}\end{array}\end{array}\right]$$

(27)

The first two eigenvalues of the matrix E in Equation (25) are shown as

$$\begin{array}{l} {\lambda }_1=0\\ {\lambda }_2=2(q_{\mathrm{b}}+q_{\mathrm{s}})\end{array}$$

(28)

Set λ2 equal to zero. We obtain

$$q_{\mathrm{b}}=-q_{\mathrm{s}}$$

(29)

Substitute Equation (29) into the other eigenvalues

$$\{\begin{array}{l}{\lambda }_3={\lambda }_7=\frac{5+\sqrt{5}}{4}(q_1+q_2)+\frac{1}{4}\sqrt{(30+10\sqrt{5})(q_1^2+q_2^2)-(60+20\sqrt{5})q_1{q}_2+(40+8\sqrt{5})q_{\mathrm{s}}^2}\\ {\lambda }_4={\lambda }_8=\frac{5+\sqrt{5}}{4}(q_1+q_2)-\frac{1}{4}\sqrt{(30+10\sqrt{5})(q_1^2+q_2^2)-(60+20\sqrt{5})q_1{q}_2+(40+8\sqrt{5})q_{\mathrm{s}}^2}\\ {\lambda }_5={\lambda }_9=\frac{5-\sqrt{5}}{4}(q_1+q_2)+\frac{1}{4}\sqrt{(30-10\sqrt{5})(q_1^2+q_2^2)-(60-20\sqrt{5})q_1{q}_2+(40-8\sqrt{5})q_{\mathrm{s}}^2}\\ {\lambda }_6={\lambda }_{10}=\frac{5-\sqrt{5}}{4}(q_1+q_2)-\frac{1}{4}\sqrt{(30-10\sqrt{5})(q_1^2+q_2^2)-(60-20\sqrt{5})q_1{q}_2+(40-8\sqrt{5})q_{\mathrm{s}}^2}\end{array}$$

(30)

From Equation (30), since q₁, q₂, q_b are all positive values, λ₃, λ₅, λ₇, and λ₉ are always greater than zero. However, the sign of λ₄, λ₆, λ₈ and λ₁₀ cannot be determined yet.

Case 1: Set both λ₄ and λ₈ equal to zero, the relationship among q₁, q₂, q_s is obtained as

$$\frac{2\sqrt{5}}{\sqrt{5}-1}{q}_1{q}_2=q_{\mathrm{s}}^2$$

(31)

Substitute Equation (31) into Equation (30)

$${\lambda }_6={\lambda }_{10}=\frac{5-\sqrt{5}}{4}\left(q_1+q_2\right)-\frac{1}{4}\sqrt{{\left(5-\sqrt{5}\right)}^2{\left(q_1-q_2\right)}^2+80q_1{q}_2}<0$$

(32)

so the structure does not meet the requirement of the super-stability condition.

Case 2: Set λ₆ and λ₁₀ equal to zero, the relationship among q₁, q₂, q_s is obtained as

$$q_{\mathrm{s}}=-\sqrt{\frac{2\sqrt{5}}{\sqrt{5}+1}{q}_1{q}_2}$$

(33)

Substitute Equation (33) into Equation (30), λ₄ and λ₈ are shown as

$${\lambda }_4={\lambda }_8=\frac{5+\sqrt{5}}{4}\left(q_1+q_2\right)-\frac{1}{4}\sqrt{{\left(5+\sqrt{5}\right)}^2{\left(q_1+q_2\right)}^2+80q_1{q}_2}>0$$

(34)

If Equation (32) are satisfied, the structure achieves the non-degeneracy condition because four eigenvalues, λ₁, λ₂, λ₆, and λ₁₀, are zero while the other eigenvalues are greater than zero. So the super-stability condition for tensegrity structures is satisfied. The relationship between variables q₁, q₂ and q_s are plotted in the three-dimensional vector graph, shown in Figure 8.

5.3. Star-Shaped Tensegrity Structure

Suppose that the star-shaped tensegrity structure, as shown in Figure 9, has four kinds of force densities: q₁, q₂, q_b, and q_s. q₁ represents the force density of elements M1, M2, M3; q₂ represents the force density of elements M4, M5, M6; q_b represents the force density of elements M7, M8, M9, M10; and q_s represents that of struts. Then the force density matrix E can be given as

$$E=\left[\begin{array}{cccccccc}{q}_1+q_{\mathrm{b}}+q_{\mathrm{s}}& 0& 0& -q_1& -q_{\mathrm{b}}& -q_{\mathrm{s}}& 0& 0\\ 0& q_1+q_{\mathrm{b}}+q_{\mathrm{s}}& 0& -q_1& 0& -q_{\mathrm{b}}& -q_{\mathrm{s}}& 0\\ 0& 0& q_1+q_{\mathrm{b}}+q_{\mathrm{s}}& -q_1& -q_s& 0& -q_{\mathrm{b}}& 0\\ -q_1& -q_1& -q_1& 3q_1& 0& 0& 0& 0\\ -q_{\mathrm{b}}& 0& -q_{\mathrm{s}}& 0& q_2+q_{\mathrm{b}}+q_{\mathrm{s}}& 0& 0& -q_2\\ -q_{\mathrm{s}}& -q_{\mathrm{b}}& 0& 0& 0& q_2+q_{\mathrm{b}}+q_{\mathrm{s}}& 0& -q_2\\ 0& -q_{\mathrm{s}}& -q_{\mathrm{b}}& 0& 0& 0& q_2+q_{\mathrm{b}}+q_{\mathrm{s}}& -q_2\\ 0& 0& 0& 0& -q_2& -q_2& -q_2& 3q_2\end{array}\right]$$

(35)

The first two eigenvalues of the matrix E in Equation (33) are shown as

$$\begin{array}{l} {\lambda }_1=0\\ {\lambda }_2=2(q_{\mathrm{b}}+q_{\mathrm{s}})\end{array}$$

(36)

Set eigenvalue λ₂ equal to zero. We obtain

$$q_{\mathrm{b}}=-q_{\mathrm{s}}$$

(37)

Substitute Equation (37) into the other eigenvalues

$$\{\begin{array}{l} {\lambda }_3=4q_1\\ {\lambda }_4=4q_2\\ {\lambda }_5={\lambda }_7=\frac{1}{2}(q_1+q_2)+\frac{1}{2}\sqrt{q_1^2+q_2^2-2q_1{q}_2+12q_{\mathrm{s}}^2}\\ {\lambda }_6={\lambda }_8=\frac{1}{2}(q_1+q_2)-\frac{1}{2}\sqrt{q_1^2+q_2^2-2q_1{q}_2+12q_{\mathrm{s}}^2}\end{array}$$

(38)

From Equation (36), since q₁, q₂, q_b are all positive value, λ₃, λ₄, λ₅, and λ₇ are always greater than zero. Set both λ₆ and λ₈ equal to zero, the relationship among q₁, q₂, q_s is obtained as

$$q_{\mathrm{s}}=-\sqrt{\frac{1}{3}{q}_1{q}_2}$$

(39)

If both Equations (35) and (37) are satisfied, the structure achieves the non-degeneracy condition because four eigenvalues are zero while the others are greater than zero in Equation (36) so that the super-stability condition for tensegrity structures is satisfied. The results of structures in Section 5.2 are found to be in good agreement with analytical solutions conjectured by Estrada, which used a unitary value [58]. The relationship between variables q₁, q₂, and q_s are plotted in the three-dimensional vector graph, shown in Figure 10.

6. Conclusions

An analytical method based on the force density method was proposed in this paper to get closed-form solutions for regular tensegrity structures with symmetry. The necessary condition for non-degeneracy of a tensegrity structure is that three or four eigenvalues of the matrix E are zero (two-dimensional tensegrities and three-dimensional tensegrities, respectively). A closed-form solution of the force densities is induced by setting the necessary number of eigenvalues to zero. Then, the super-stability conditions for tensegrity structures are examined.

Several examples were investigated comprehensively in this paper to verify the capability of the proposed technique. A planar tensegrity structure, three types of prismatic tensegrity structure (triangular prism, quadrangular prism, pentagonal prism) and a star-shaped tensegrity structure are included as examples, all of which have regular shapes. After the eigenvalue decomposition of the matrix force density E, a closed-form solution can be conjectured according to the non-degeneracy condition. The closed-form solution can help in understanding the design of regular tensegrity structures in many fields, both in robotics and architecture, as well as deployable structures. Though the proposed method is efficient enough to solve the examples mentioned above, more advanced methods should be developed for form-finding of more complex tensegrities, which will be studied in the future.