Investigation of Magneto Hydro-Dynamics Effects on a Polymer Chain Transfer in Micro-Channel Using Dissipative Particle Dynamics Method
Abstract
:1. Introduction
2. Numerical Simulation
2.1. Magneto-Hydrodynamics
2.1.1. Analytical Solution for MHD in Simple Channel
2.2. Dissipative Particle Dynamics Method
2.3. Polymer Chain
3. Results
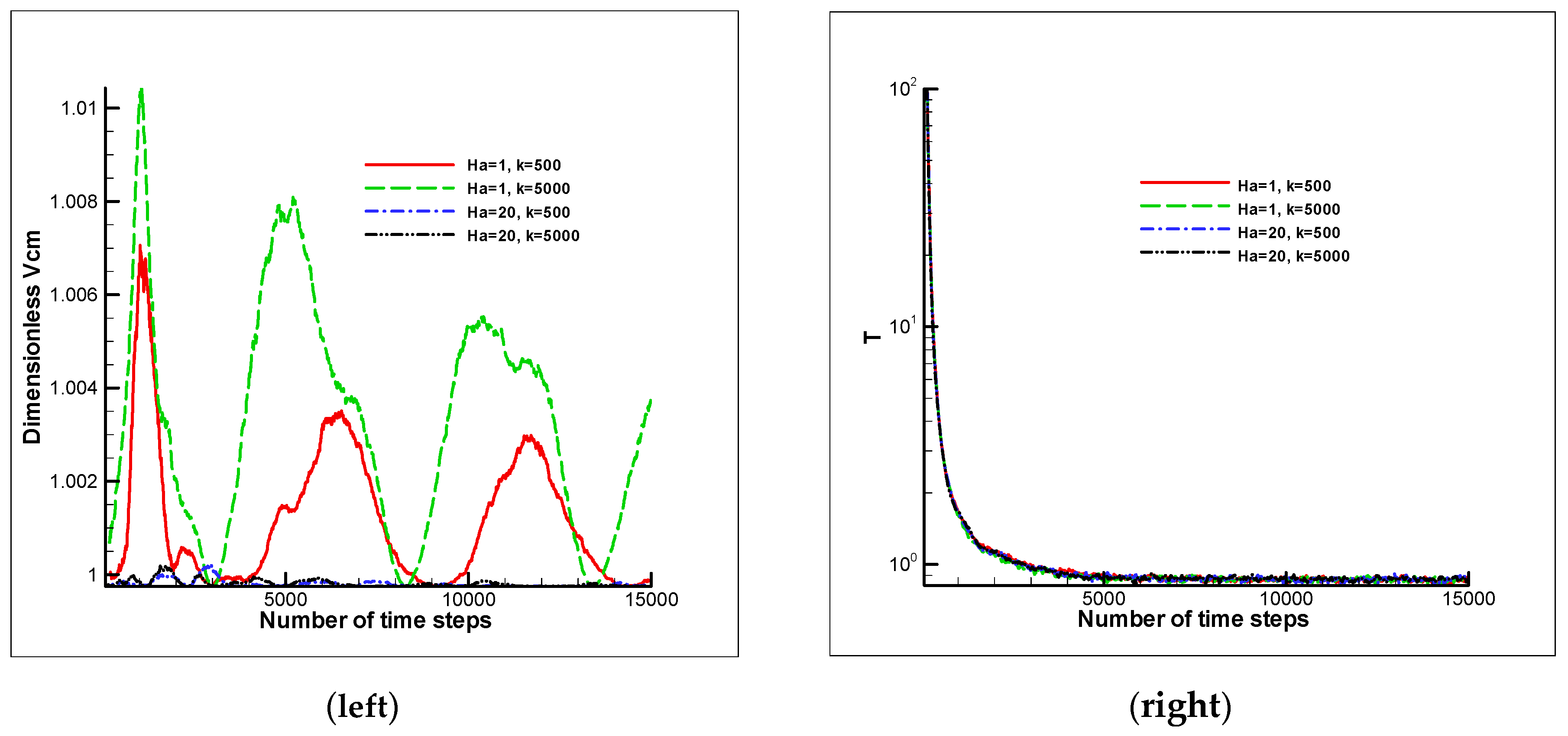
3.1. Validation of MHD-DPD Results with Analytical Solution
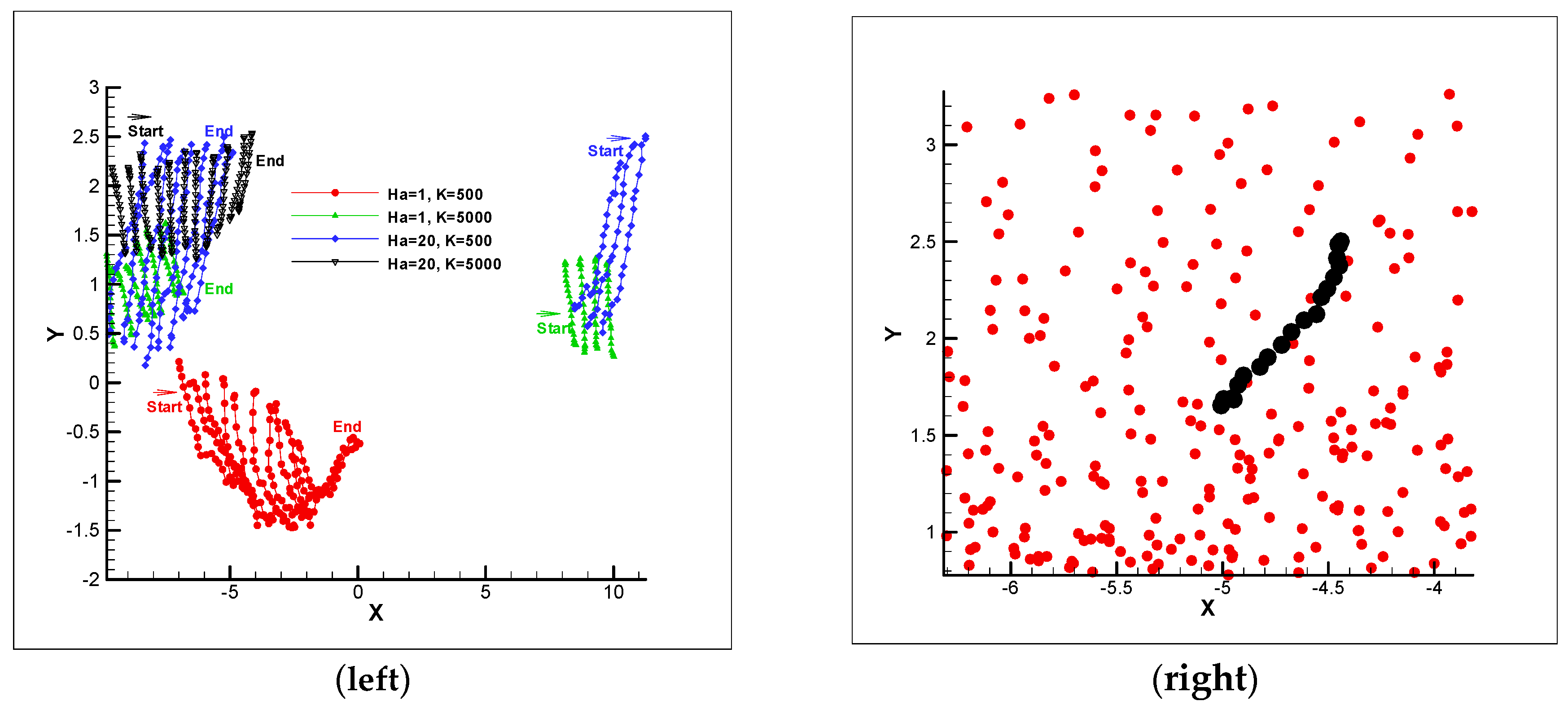
3.2. Short Polymer Chain Transfer in MHD Flow
3.3. Long Polymer Chain Transfer in MHD Flow
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, X.; Pivkin, I.V.; Liang, H. Hydrodynamic effects on flow-induced polymer translocation through a microfluidic channel. Polymer 2013, 54, 4309–4317. [Google Scholar] [CrossRef]
- Xu, Z.; Yang, Y.; Zhu, G.; Chen, P.; Huang, Z.; Dai, X.; Hou, C.; Yan, L.T. Simulating Transport of Soft Matter in Micro/Nano Channel Flows with Dissipative Particle Dynamics. Adv. Theory Simul. 2019, 2, 1800160. [Google Scholar] [CrossRef]
- Li, P.C. Microfluidic Lab-on-A-Chip for Chemical and Biological Analysis and Discovery; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Darbandi, M.; Zakeri, R.; Schneider, G.E. Simulation of Polymer Chain Driven by DPD Solvent Particles in Nanoscale Flows. In Proceedings of the ASME 2010 8th International Conference on Nanochannels, Microchannels, and Minichannels Collocated with 3rd Joint US-European Fluids Engineering Summer Meeting, Montreal, QC, Canada, 1–5 August 2010; pp. 1035–1040. [Google Scholar]
- Chen, C.-W.; Jiang, Y. Computational Fluid Dynamics Study of Magnus Force on an Axis-Symmetric, Disk-Type AUV with Symmetric Propulsion. Symmetry 2019, 11, 397. [Google Scholar] [CrossRef] [Green Version]
- Irandoost Shahrestani, M.; Maleki, A.; Safdari Shadloo, M.; Tlili, I. Numerical Investigation of Forced Convective Heat Transfer and Performance Evaluation Criterion of Al2O3/Water Nanofluid Flow inside an Axisymmetric Microchannel. Symmetry 2020, 12, 120. [Google Scholar] [CrossRef] [Green Version]
- Maleki, A.; Elahi, M.; Assad, M.E.H.; Nazari, M.A.; Shadloo, M.S.; Nabipour, N. Thermal conductivity modeling of nanofluids with ZnO particles by using approaches based on artificial neural network and MARS. J. Therm. Anal. Calorim. 2020. [Google Scholar] [CrossRef]
- Guillouzic, S.; Slater, G.W. Polymer translocation in the presence of excluded volume and explicit hydrodynamic interactions. Phys. Lett. A 2006, 359, 261–264. [Google Scholar] [CrossRef]
- Muthukumar, M.; Kong, C. Simulation of polymer translocation through protein channels. Proc. Natl. Acad. Sci. USA 2006, 103, 5273–5278. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.; Ban, X.; Wang, B.; Wang, X. A Symmetric Particle-Based Simulation Scheme towards Large Scale Diffuse Fluids. Symmetry 2018, 10, 86. [Google Scholar] [CrossRef] [Green Version]
- Ikonen, T.; Bhattacharya, A.; Ala-Nissila, T.; Sung, W. Unifying model of driven polymer translocation. Phys. Rev. E 2012, 85, 051803. [Google Scholar] [CrossRef] [Green Version]
- Jin, H.; Chen, B.; Zhao, X.; Cao, C. Molecular dynamic simulation of hydrogen production by catalytic gasification of key intermediates of biomass in supercritical water. J. Energy Resour. Technol. 2018, 140, 041801. [Google Scholar] [CrossRef]
- Xu, B.; Jin, H.; Li, H.; Guo, Y.; Fan, J. Investigation on the evolution of the coal macromolecule in the process of combustion with Molecular dynamics method. J. Energy Resour. Technol. 2020, 142. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.; Koelman, J. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. EPL (Europhys. Lett.) 1992, 19, 155. [Google Scholar] [CrossRef]
- Zakeri, R.; Lee, E.S. Similar Region in Electroosmotic Flow Rate for Newtonian and non-Newtonian Fluids using dissipative particle dynamics (DPD). In Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014. [Google Scholar]
- Safdari Shadloo, M. Numerical simulation of compressible flows by lattice Boltzmann method. Numer. Heat Transf. Part A Appl. 2019, 75, 167–182. [Google Scholar] [CrossRef]
- Vasheghani Farahani, M.; Foroughi, S.; Norouzi, S.; Jamshidi, S. Mechanistic Study of Fines Migration in Porous Media Using Lattice Boltzmann Method Coupled With Rigid Body Physics Engine. J. Energy Resour. Technol. 2019, 141. [Google Scholar] [CrossRef]
- Almasi, F.; Shadloo, M.; Hadjadj, A.; Ozbulut, M.; Tofighi, N.; Yildiz, M. Numerical simulations of multi-phase electro-hydrodynamics flows using a simple incompressible smoothed particle hydrodynamics method. Comput. Math. Appl. 2019. [Google Scholar] [CrossRef]
- Fatehi, R.; Rahmat, A.; Tofighi, N.; Yildiz, M.; Shadloo, M.S. Density-based smoothed particle hydrodynamics methods for incompressible flows. Comput. Fluids 2019, 185, 22–33. [Google Scholar] [CrossRef]
- Hopp-Hirschler, M.; Shadloo, M.S.; Nieken, U. A smoothed particle hydrodynamics approach for thermo-capillary flows. Comput. Fluids 2018, 176, 1–19. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Oger, G.; Le Touzé, D. Smoothed particle hydrodynamics method for fluid flows, towards industrial applications: Motivations, current state, and challenges. Comput. Fluids 2016, 136, 11–34. [Google Scholar] [CrossRef]
- Hopp-Hirschler, M.; Shadloo, M.S.; Nieken, U. Viscous fingering phenomena in the early stage of polymer membrane formation. J. Fluid Mech. 2019, 864, 97–140. [Google Scholar] [CrossRef]
- Zhang, K.; Manke, C.W. Simulation of polymer solutions by dissipative particle dynamics. Mol. Simul. 2000, 25, 157–166. [Google Scholar] [CrossRef]
- Willemsen, S.; Hoefsloot, H.; Iedema, P. Mesoscopic simulation of polymers in fluid dynamics problems. J. Stat. Phys. 2002, 107, 53–65. [Google Scholar] [CrossRef]
- Pastorino, C.; Kreer, T.; Müller, M.; Binder, K. Comparison of dissipative particle dynamics and Langevin thermostats for out-of-equilibrium simulations of polymeric systems. Phys. Rev. E 2007, 76, 026706. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duong-Hong, D.; Han, J.; Wang, J.S.; Hadjiconstantinou, N.G.; Chen, Y.Z.; Liu, G.R. Realistic simulations of combined DNA electrophoretic flow and EOF in nano-fluidic devices. Electrophoresis 2008, 29, 4880–4886. [Google Scholar] [CrossRef] [PubMed]
- Pan, H.; Ng, T.; Li, H.; Moeendarbary, E. Dissipative particle dynamics simulation of entropic trapping for DNA separation. Sens. Actuators A Phys. 2010, 157, 328–335. [Google Scholar] [CrossRef]
- Masoud, H.; Alexeev, A. Selective control of surface properties using hydrodynamic interactions. Chem. Commun. 2011, 47, 472–474. [Google Scholar] [CrossRef]
- Guo, J.; Li, X.; Liu, Y.; Liang, H. Flow-induced translocation of polymers through a fluidic channel: A dissipative particle dynamics simulation study. J. Chem. Phys. 2011, 134, 134906. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, K.; Vishnyakov, A.; Neimark, A.V. Polymer translocation through a nanopore: DPD study. J. Phys. Chem. B 2013, 117, 3648–3658. [Google Scholar] [CrossRef]
- Ranjith, S.K.; Patnaik, B.; Vedantam, S. Transport of DNA in hydrophobic microchannels: A dissipative particle dynamics simulation. Soft Matter 2014, 10, 4184–4191. [Google Scholar] [CrossRef]
- Zakeri, R. Dissipative particle dynamics simulation of the soft micro actuator using polymer chain displacement in electro-osmotic flow. Mol. Simul. 2019, 45, 1488–1497. [Google Scholar] [CrossRef]
- Mao, J.; Yao, Y.; Zhou, Z.; Hu, G. Polymer translocation through nanopore under external electric field: Dissipative particle dynamics study. Appl. Math. Mech. 2015, 36, 1581–1592. [Google Scholar] [CrossRef]
- Zakeri, R.; Lee, E.S. Simulation of nano polymer chain sensor in electroosmotic flow using dissipative particle dynamics (DPD) method. In Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014. [Google Scholar]
- Alarifi, I.M.; Abokhalil, A.G.; Osman, M.; Lund, L.A.; Ayed, M.B.; Belmabrouk, H.; Tlili, I. MHD flow and heat transfer over vertical stretching sheet with heat sink or source effect. Symmetry 2019, 11, 297. [Google Scholar] [CrossRef] [Green Version]
- Khan, I.; Alqahtani, A.M. MHD Nanofluids in a Permeable Channel with Porosity. Symmetry 2019, 11, 378. [Google Scholar] [CrossRef] [Green Version]
- Laser, D.J.; Santiago, J.G. A review of micropumps. J. Micromech. Microeng. 2004, 14, R35. [Google Scholar] [CrossRef]
- Lim, S.; Choi, B. A study on the MHD (magnetohydrodynamic) micropump with side-walled electrodes. J. Mech. Sci. Technol. 2009, 23, 739–749. [Google Scholar] [CrossRef]
- Kang, H.-J.; Choi, B. Development of the MHD micropump with mixing function. Sens. Actuators A Phys. 2011, 165, 439–445. [Google Scholar] [CrossRef]
- Ito, K.; Takahashi, T.; Fujino, T.; Ishikawa, M. Influences of channel size and operating conditions on fluid behavior in a MHD micro pump for micro total analysis system. J. Int. Counc. Electr. Eng. 2014, 4, 220–226. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.A.; Hristovski, I.R.; Marinaro, G.; Kosel, J. Magnetic Composite Hydrodynamic Pump With Laser-Induced Graphene Electrodes. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Zhou, X.; Gao, M.; Gui, L. A Liquid-Metal Based Spiral Magnetohydrodynamic Micropump. Micromachines 2017, 8, 365. [Google Scholar] [CrossRef] [Green Version]
- Kefayati, G.R.; Gorji-Bandpy, M.; Sajjadi, H.; Ganji, D. Lattice Boltzmann simulation of MHD mixed convection in a lid-driven square cavity with linearly heated wall. Sci. Iran. 2012, 19, 1053–1065. [Google Scholar] [CrossRef] [Green Version]
- Ghahderijani, M.J.; Esmaeili, M.; Afrand, M.; Karimipour, A. Numerical simulation of MHD fluid flow inside constricted channels using lattice Boltzmann method. J. Appl. Fluid Mech. 2017, 10, 1639–1648. [Google Scholar] [CrossRef]
- Javaherdeh, K.; Najjarnezami, A. Lattice Boltzmann simulation of MHD natural convection in a cavity with porous media and sinusoidal temperature distribution. Appl. Math. Mech. 2018, 39, 1187–1200. [Google Scholar] [CrossRef]
- Chaabane, R.; Jemni, A. Lattice Boltzmann approach for MagnetoHydroDynamic convective heat transfer. Energy Procedia 2019, 162, 181–190. [Google Scholar] [CrossRef]
- Jafari, S.; Zakeri, R.; Darbandi, M. DPD simulation of non-Newtonian electroosmotic fluid flow in nanochannel. Mol. Simul. 2018, 44, 1444–1453. [Google Scholar] [CrossRef]
- Elmars, B.; Yu, M.; Ozols, R. Heat and Mass Transfer in MHD Flows; World Scientific: Singapore, 1987; Volume 3. [Google Scholar]
- Gold, R.R. Magnetohydrodynamic pipe flow. Part 1. J. Fluid Mech. 1962, 13, 505–512. [Google Scholar] [CrossRef]
- Asma, M.; Othman, W.; Muhammad, T.; Mallawi, F.; Wong, B. Numerical Study for Magnetohydrodynamic Flow of Nanofluid Due to a Rotating Disk with Binary Chemical Reaction and Arrhenius Activation Energy. Symmetry 2019, 11, 1282. [Google Scholar] [CrossRef] [Green Version]
- Karniadakis, G.; Beskok, A.; Aluru, N. Microflows and Nanoflows: Fundamentals and Simulation; Springer Science & Business Media: Berlin, Germany, 2006; Volume 29. [Google Scholar]
- Jehser, M.; Zifferer, G.; Likos, C.N. Scaling and Interactions of Linear and Ring Polymer Brushes via DPD Simulations. Polymers 2019, 11, 541. [Google Scholar] [CrossRef] [Green Version]
- Nikunen, P.; Karttunen, M.; Vattulainen, I. How would you integrate the equations of motion in dissipative particle dynamics simulations? Comput. Phys. Commun. 2003, 153, 407–423. [Google Scholar] [CrossRef] [Green Version]
- Duong-Hong, D.; Phan-Thien, N.; Fan, X. An implementation of no-slip boundary conditions in DPD. Comput. Mech. 2004, 35, 24–29. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shehzad, S. Magnetohydrodynamic nanofluid convection in a porous enclosure considering heat flux boundary condition. Int. J. Heat Mass Transf. 2017, 106, 1261–1269. [Google Scholar] [CrossRef]
- Yapici, M.K.; Al Nabulsi, A.; Rizk, N.; Boularaoui, S.M.; Christoforou, N.; Lee, S. Alternating magnetic field plate for enhanced magnetofection of iron oxide nanoparticle conjugated nucleic acids. J. Magn. Magn. Mater. 2019, 469, 598–605. [Google Scholar] [CrossRef]







| Variables | aij Different Particles | ajj Same Particles | Number of Particles | Simulation Box (Channel Size) | Time Step | Cut Off Radious | Periodic Boundary Condition | ||
|---|---|---|---|---|---|---|---|---|---|
| Value | 3 | 10 | 4000 | 20 (length) × 50 (height) | 0.001 | 3 | 4.5 | 1 | x-direction |
| Variables | Spring Constant | Number of Beads |
|---|---|---|
| Value | 500, 5000 | 20, 50 |
| Variables | Ha Number | ||
|---|---|---|---|
| Value | 25 | 1 | 1, 2, 7, 10, 20 |
| Spring Constant | Number of Beads | Ha Number | ||||
|---|---|---|---|---|---|---|
| 500 | 20 | 1 | 0.54919 | 0.99985 | 0.87459 | 1.5659 |
| 5000 | 20 | 1 | 0.11650 | 1.00033 | 0.86930 | 0.7998 |
| 500 | 20 | 20 | 0.53191 | 1.00027 | 0.86012 | 1.96924 |
| 5000 | 20 | 20 | 0.11838 | 0.99982 | 0.87195 | 0.78627 |
| 500 | 50 | 1 | 6.7853 | 1.00161 | 0.860313 | 2.9855 |
| 5000 | 50 | 1 | 0.90651 | 1.00477 | 0.86932 | 3.3996 |
| 500 | 50 | 20 | 4.3087 | 0.99984 | 0.86096 | 2.7783 |
| 5000 | 50 | 20 | 0.85215 | 0.99985 | 0.87459 | 1.8455 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zakeri, R.; Sabouri, M.; Maleki, A.; Abdelmalek, Z. Investigation of Magneto Hydro-Dynamics Effects on a Polymer Chain Transfer in Micro-Channel Using Dissipative Particle Dynamics Method. Symmetry 2020, 12, 397. https://doi.org/10.3390/sym12030397
Zakeri R, Sabouri M, Maleki A, Abdelmalek Z. Investigation of Magneto Hydro-Dynamics Effects on a Polymer Chain Transfer in Micro-Channel Using Dissipative Particle Dynamics Method. Symmetry. 2020; 12(3):397. https://doi.org/10.3390/sym12030397
Chicago/Turabian StyleZakeri, Ramin, Moslem Sabouri, Akbar Maleki, and Zahra Abdelmalek. 2020. "Investigation of Magneto Hydro-Dynamics Effects on a Polymer Chain Transfer in Micro-Channel Using Dissipative Particle Dynamics Method" Symmetry 12, no. 3: 397. https://doi.org/10.3390/sym12030397






