Fundamental Solutions for the Coupled KdV System and Its Stability

Abstract

In this paper, we establish exact solutions for the non-linear coupled KdV equations. The exp-function method is used to construct the solitary travelling wave solutions for these equations. The numerical adaptive moving mesh PDEs (MMPDEs) method is also implemented in order to solve the proposed coupled KdV equations. The achieved results may be applicable to some plasma environments, such as ionosphere plasma. Some numerical simulations compared with the exact solutions are provided to illustrate the validity of the proposed methods. Furthermore, the modulational instability is analyzed based on the standard linear-stability analysis. The depiction of the techniques are straight, powerful, robust and can be applied to other nonlinear systems of partial differential equations.

1. Introduction

The nonlinear partial differential equations (NPDEs) are widely used to express a variety of physical circumstances in fields such as biology, economy, engineering, elastic media, meteorology, plasma physics, optics, fluid mechanics and chemical physics, see [1,2,3,4,5,6,7,8,9,10,11,12]. In the last three decades, most researchers have proposed and developed some analytical and numerical methods to find exact and numerical solutions for NPDEs, such as F-expansion method [13], $(\frac{G^{{}^{\prime }}}{G})-$ expansion method [14], homogeneous balance method [15], Jacobi elliptic function method [16], exp-function method [17], sine-cosine method [18], tanh-sech method [19], Lie symmetry analysis [20], RB sub-ODE method [21,22], adaptive moving mesh method [23,24]. Indeed, there are recent developments of symmetry methods to obtain special reduced solutions of NPDEs [25].

The study of non-linear complex waves is very important in various applied sciences, especially in optics, biology, fluid mechanics, engineering, physics, higher-order symmetries, and solid state physics and chemical physics. The Kortweg-de Vries (KdV) equations have been part of an important class of non-linear evolution equations with numerous applications in physics, plasma and engineering fields. All these applications start from a more or less general physical model and end up in the KdV equation by considering a specific limit of the physical problem. In the theory of rogue waves, the nonlinear Schrödinger equation plays a dominant role for waves in deep water, while the KdV equation describes the effects in shallow water. In plasma physics, the KdV equations produce ion-acoustic solutions [26]. Several well-know researchers obtain symmetries because they can be used to obtain systematically exact solutions of the KdV equations [27,28].

This article is concerned with the following coupled KdV equations [29]:

$$\begin{array}{c}{\displaystyle V_t-\alpha V_{xxx}-6\alpha V{V}_x-\beta H{H}_x=0,}\hfill \\ \hfill \\ {\displaystyle H_t+H_{xxx}+3V{H}_x=0,}\hfill \end{array}$$

(1)

subject to

$$\begin{array}{c}{\displaystyle V(-L,t)=f_l(-L,t),H(-L,t)=g_l(-L,t),}\hfill \\ \hfill \\ {\displaystyle V(L,t)=f_R(L,t),H(L,t)=g_R(L,t),\forall t\ge 0,}\hfill \end{array}$$

(2)

where $\alpha$ and $\beta$ are nonzero parameters, $x\in [-L,L],$$f_l,f_R,g_l$ and $g_R$ are functions of $t.$ System (1) was derived by Hirota and Satsuma [29] to describe iterations of water waves with different dispersion relations. Recently, many authors mainly had paid attention to study solutions of coupled equations by using various methods. Among these are the trigonometric function transform method [30], F-expansion method [13], the homotopy perturbation [31] and differential transformation Method [32]. For further methods used to solve system (1), see [33,34] and references therein.

The novelties and the significance of the results in this article are mainly exhibited in three aspects. First, we achieve some new solutions for the coupled KdV Equation (1), utilizing the exp-function method [17,35]. Second, we implement the adaptive moving mesh PDEs (MMPDEs) scheme to solve the coupled KdV Equation (1). We compare these numerical solutions with the exact solutions obtained by the exp-function method. To the best of our knowledge, the proposed methods have not been used to solve Equation (1). Third, the modulation instability is employed in order to study the stability of exact solutions.

2. Summary of the $exp(-\mathbf{\Gamma }(\mathbf{\xi }\left)\right)$-Expansion Method

We give a brief explanation for the $exp(-\mathsf{\Gamma }(\xi \left)\right)$-expansion approach [17,35]. This technique is described in the following steps: Assume that

$$T(\phi ,{\phi }_t,{\phi }_x,{\phi }_{tt},{\phi }_{xx},{\phi }_{xt},\dots \dots \dots )=0,$$

(3)

where $\phi (x,t)$ is an unknown function and T is a polynomial of $\phi$ is a PDE with two independent variables x and t. In order to reduce Equation (3) to an ordinary differential equation (ODE), we introduce the transformation

$$\xi =x\pm wt,\phi (x,t)={\phi }_0\left(\xi \right),$$

(4)

where w is a constant. Expanding the derivatives in Equation (3) using the chain rule leads to the ODE

$$R({\phi }_0,{\phi }_{0,\xi },{\phi }_{0,\xi \xi },{\phi }_{0,\xi \xi \xi },\dots )=0,$$

(5)

where R is a polynomial in ${\phi }_0\left(\xi \right)$ and

$${\phi }_{0,\xi }=\frac{d{\phi }_0}{d\xi },{\phi }_{0,\xi \xi }=\frac{d^2{\phi }_0}{d{\xi }^2},{\phi }_{0,\xi \xi \xi }=\frac{d^3{\phi }_0}{d{\xi }^3},\dots$$

(6)

According to this technique, the solution of Equation (5) is given in the form:

$${\phi }_0\left(\xi \right)=\sum _{k=0}^n{b}_k{e}^{-k\mathsf{\Gamma }\left(\xi \right)},$$

(7)

where the constants $b_0,b_1,b_2,\dots ,b_n$ will be estimated later. Furthermore, $b_n\ne 0,$ and $\mathsf{\Gamma }=\mathsf{\Gamma }\left(\xi \right)$ satisfies the equation

$${\mathsf{\Gamma }}_{\xi }=e^{-\mathsf{\Gamma }\left(\xi \right)}+\mu e^{\mathsf{\Gamma }\left(\xi \right)}+\lambda .$$

(8)

We now turn to present various cases for the solutions of Equation (8).

• If ${\lambda }^2-4\mu >0,\mu \ne 0,$ then
  • $\mathsf{\Gamma }\left(\xi \right)=ln\left(\frac{-\sqrt{({\lambda }^2-4\mu )}tanh\left(\frac{\sqrt{({\lambda }^2-4\mu )}}{2}(\xi +\gamma )\right)-\lambda }{2\mu }\right),$
  • $\mathsf{\Gamma }\left(\xi \right)=ln\left(\frac{-\sqrt{({\lambda }^2-4\mu )}coth\left(\frac{\sqrt{({\lambda }^2-4\mu )}}{2}(\xi +\gamma )\right)-\lambda }{2\mu }\right).$
• If ${\lambda }^2-4\mu <0,\mu \ne 0,$ then
  • $\mathsf{\Gamma }\left(\xi \right)=ln\left(\frac{\sqrt{(4\mu -{\lambda }^2)}tan\left(\frac{\sqrt{(4\mu -{\lambda }^2)}}{2}(\xi +\gamma )\right)-\lambda }{2\mu }\right),$
  • $\mathsf{\Gamma }\left(\xi \right)=ln\left(\frac{\sqrt{(4\mu -{\lambda }^2)}cot\left(\frac{\sqrt{(4\mu -{\lambda }^2)}}{2}(\xi +\gamma )\right)-\lambda }{2\mu }\right).$
• If ${\lambda }^2-4\mu >0,\mu =0,\lambda \ne 0,$ then

  $$\mathsf{\Gamma }\left(\xi \right)=-ln\left(\frac{\lambda }{exp\left(\lambda \right(\xi +\gamma \left)\right)-1}\right).$$

  (9)
• If ${\lambda }^2-4\mu =0,\mu \ne 0,\lambda \ne 0,$ then

  $$\mathsf{\Gamma }\left(\xi \right)=ln\left(-\frac{2\left(\lambda \right(\xi +k)+2}{{\lambda }^2(\xi +\gamma )}\right).$$

  (10)
• If ${\lambda }^2-4\mu =0,\mu =0,\lambda =0,$ then

  $$\mathsf{\Gamma }\left(\xi \right)=ln\left(\xi +\gamma \right),$$

  (11)

  where $\gamma ,\mu ,\lambda$ and w are arbitrary constants. When we insert Equation (7) into Equation (5) and equate the coefficients of the same order of $e^{-\mathsf{\Gamma }\left(\xi \right)},$ we end up with an algebraic system that can be simply solved by using Mathematica to evaluate the values of $b_0,b_1,b_2,\dots ,b_n.$

Stability Analysis

We examine the stability of the achieved traveling wave solutions by using the Hamiltonian system form [36,37], which is

$$\begin{array}{c}{\displaystyle {\rho }_1\left(w\right)={\int }_{-\infty }^{\infty }\frac{1}{2}{\phi }_1^2\left(\xi \right)dx,}\hfill \\ {\displaystyle {\rho }_2\left(w\right)=\frac{1}{2}{\int }_{-\infty }^{\infty }\frac{1}{2}{\phi }_2^2\left(\xi \right)dx,}\hfill \end{array}$$

(12)

where w is the wave speed, ${\rho }_i\left(w\right)$ indicates the momentum and ${\phi }_1$ and ${\phi }_2$ are the obtained traveling wave solutions of the system (1). A sufficient condition for stability is given by

$$\frac{\partial {\rho }_i}{\partial w}>0,\forall i=1,2.$$

(13)

Hence, if conditions (12) and (13) are met, then it is stable on unbounded domains. If conditions (12) and (13) are not satisfied, then it is unstable. The criteria for the stability of traveling wave solutions are discussed here for the system (1) at particular intervals. For more details about the stability of the exact solutions, we refer to [37,38,39] and references therein.

3. The Exact Solution of the Coupled KdV Equations

Consider that the traveling wave solutions of Equation (1) are given by

$$\xi =x+wt⟹V(x,t)=v\left(\xi \right)\mathrm{and}H(x,t)=h\left(\xi \right).$$

(14)

to alter system (1) into the ODEs

$$\begin{array}{c}{\displaystyle w{v}_{\xi }-\alpha v_{\xi \xi \xi }-3\alpha {\left(v^2\right)}_{\xi }-\beta {\left(h^2\right)}_{\xi }=0,}\hfill \\ \hfill \\ {\displaystyle w{h}_{\xi }+h_{\xi \xi \xi }+3v{h}_{\xi }=0,}\hfill \end{array}$$

(15)

Integrating Equation (15) concerning $\xi$ once and neglecting the constant of integration, we have

$$\begin{array}{c}{\displaystyle wv-\alpha v_{\xi \xi }-3\alpha v^2-\beta h^2=0,}\hfill \\ \hfill \\ {\displaystyle w{h}_{\xi }+h_{\xi \xi \xi }+3v{h}_{\xi }=0,}\hfill \end{array}$$

(16)

Balancing the order of $v_{\xi \xi }$ with the exponent of $v^2$ from the first equation of the system (16), gives $N=2$ and the order of $h_{\xi \xi \xi }$ with the exponent of $v{h}_{\xi }$ from the second equation of the system (16), gives $M=2$. Hence, the solutions take the form of

$$\begin{array}{c}{\displaystyle v\left(\xi \right)=\sum _{r=0}^N{a}_r{e}^{-r\mathsf{\Gamma }\left(\xi \right)},}\hfill \\ {\displaystyle h\left(\xi \right)=\sum _{r=0}^M{b}_r{e}^{-r\mathsf{\Gamma }\left(\xi \right)}.}\hfill \end{array}$$

(17)

And then

$$\begin{array}{c}{\displaystyle v\left(\xi \right)=a_0+a_1{e}^{-\mathsf{\Gamma }\left(\xi \right)}+a_2{e}^{-2\mathsf{\Gamma }\left(\xi \right)},}\hfill \\ {\displaystyle h\left(\xi \right)=b_0+b_1{e}^{-\mathsf{\Gamma }\left(\xi \right)}+b_2{e}^{-2\mathsf{\Gamma }\left(\xi \right)},}\hfill \end{array}$$

(18)

where the values of the constants $a_0,a_1,a_2,b_0,b_1$ and $b_2$ are computed later. Substituting Equation (18) into Equation (16) and solving the obtained algebraic system after equating the coefficients of $e^{-r\mathsf{\Gamma }\left(\xi \right)}$, to zero, yields

• Case I

  $$\begin{array}{c}{\displaystyle a_0=\frac{1}{3}(-{\lambda }^2-8\mu -w),a_1=-4\lambda ,a_2=-4,}\hfill \\ {\displaystyle b_0=\frac{\left(\alpha {\lambda }^2+8\alpha \mu +2\alpha w+w\right)}{\sqrt{-6\alpha }\sqrt{\beta }}}\hfill \\ {\displaystyle b_1=-\frac{2\sqrt{-6\alpha }\lambda }{\sqrt{\beta }},b_2=-\frac{2\sqrt{-6\alpha }}{\sqrt{\beta }},}\hfill \end{array}$$

  (19)
• Case II

  $$\begin{array}{c}{\displaystyle a_0=\frac{1}{3}(-{\lambda }^2-2\mu -w),a_1=-2\lambda ,a_2=-2,}\hfill \\ {\displaystyle b_0=-\frac{\lambda \sqrt{-\alpha {\lambda }^2+4\alpha \mu -2\alpha w-w}}{\sqrt{2\beta }}}\hfill \\ {\displaystyle b_1=-\frac{\sqrt{2}\sqrt{-\alpha {\lambda }^2+4\alpha \mu -2\alpha w-w}}{\sqrt{\beta }},b_2=0,}\hfill \end{array}$$

  (20)

Putting $\lambda$ and $\mu$ so that ${\lambda }^2-4\mu >0,$ gives

• From Case I, the exact solutions are given by

$$\begin{array}{c}{\displaystyle V(x,t)=\frac{1}{3}(-{\lambda }^2-8\mu -w)+\frac{8\mu \lambda }{\sqrt{({\lambda }^2-4\mu )}tanh\left(\frac{1}{2}\sqrt{{\lambda }^2-4\mu }(x+x_0+wt)\right)+\lambda }}\hfill \\ {\displaystyle -\frac{16{\mu }^2}{{\left(\sqrt{({\lambda }^2-4\mu )}tanh\left(\frac{1}{2}\sqrt{{\lambda }^2-4\mu }(x+x_0+wt)\right)+\lambda \right)}^2},}\hfill \\ {\displaystyle H(x,t)=\frac{\left(\alpha {\lambda }^2+8\alpha \mu +2\alpha w+w\right)}{\sqrt{-6\alpha }\sqrt{\beta }}+\frac{4\mu \sqrt{-6\alpha }\lambda }{\sqrt{\beta }\left(\sqrt{({\lambda }^2-4\mu )}tanh\left(\frac{1}{2}\sqrt{{\lambda }^2-4\mu }(x+x_0+wt)\right)+\lambda \right)}}\hfill \\ {\displaystyle -\frac{8{\mu }^2\sqrt{-6\alpha }}{\sqrt{\beta }{\left(\sqrt{({\lambda }^2-4\mu )}tanh\left(\frac{1}{2}\sqrt{{\lambda }^2-4\mu }(x+x_0+wt)\right)+\lambda \right)}^2},}\hfill \end{array}$$

(21)

• From Case II

$$\begin{array}{c}{\displaystyle V(x,t)=\frac{1}{3}(-{\lambda }^2-2\mu -w)+\frac{4\mu \lambda }{\sqrt{({\lambda }^2-4\mu )}tanh\left(\frac{1}{2}\sqrt{{\lambda }^2-4\mu }(x+x_0+wt)\right)+\lambda }}\hfill \\ {\displaystyle -\frac{8{\mu }^2}{{\left(\sqrt{({\lambda }^2-4\mu )}tanh\left(\frac{1}{2}\sqrt{{\lambda }^2-4\mu }(x+x_0+wt)\right)+\lambda \right)}^2},}\hfill \\ {\displaystyle H(x,t)=-\frac{\lambda \sqrt{-\alpha {\lambda }^2+4\alpha \mu -2\alpha w-w}}{\sqrt{2\beta }}+\frac{\mu \sqrt{8\left(-\alpha {\lambda }^2+4\alpha \mu -2\alpha w-w\right)}}{\sqrt{\beta }\left(\sqrt{({\lambda }^2-4\mu )}tanh\left(\frac{1}{2}\sqrt{{\lambda }^2-4\mu }(x+x_0+wt)\right)+\lambda \right)},}\hfill \end{array}$$

(22)

Figure 1a,b present the traveling wave solutions Equation (21) with the parameters given by $\alpha =-1.2,\beta =1.2,x_0=-30,w=1.0,\mu =0.5,\lambda =2.5,$$t=0\to 10$ and in the interval $[0,40].$ Figure 2a,b show the traveling wave solutions Equation (22) depicted under the parameters $\alpha =-2.5,\beta =2.5,x_0=-15,w=0.5,\mu =0.10,\lambda =2.0,$$t=0\to 10$ and in the interval $[0,20].$ All of the results are displayed at $t=0\to 10.$ The sufficient conditions of stability (Equations (12) and (13)) are applied, and then we find that all of the obtained solutions are stable in the interval $[0,20].$

The boundary conditions are initially generated from studying the obtained travelling wave solutions at the endpoints. Figure 1a illustrates that the traveling wave solution $V(x,t)$ goes to $-1.75$ at the endpoints of the physical domain and Figure 1b shows that $H(x,t)$ goes to $2.2113$ at the endpoints. While Figure 2a illustrates that the traveling wave solution $V(x,t)$ goes to $-1.3667$ at the endpoints of the physical domain and Figure 2b shows that $H(x,t)$ goes to $\pm 2.8142$ at the endpoints. Hence, we can conclude that

$$\begin{array}{c}{\displaystyle \mathbf{Case}\mathbf{I}:V(x,t)\to -1.75,\mathbf{and}H(x,t)\to 2.2113,\mathbf{as}x\to \pm \infty ,}\hfill \\ {\displaystyle \mathbf{Case}\mathbf{II}:V(x,t)\to -1.3667,\mathbf{and}H(x,t)\to \pm 2.8142,\mathbf{as}x\to \pm \infty .}\hfill \end{array}$$

(23)

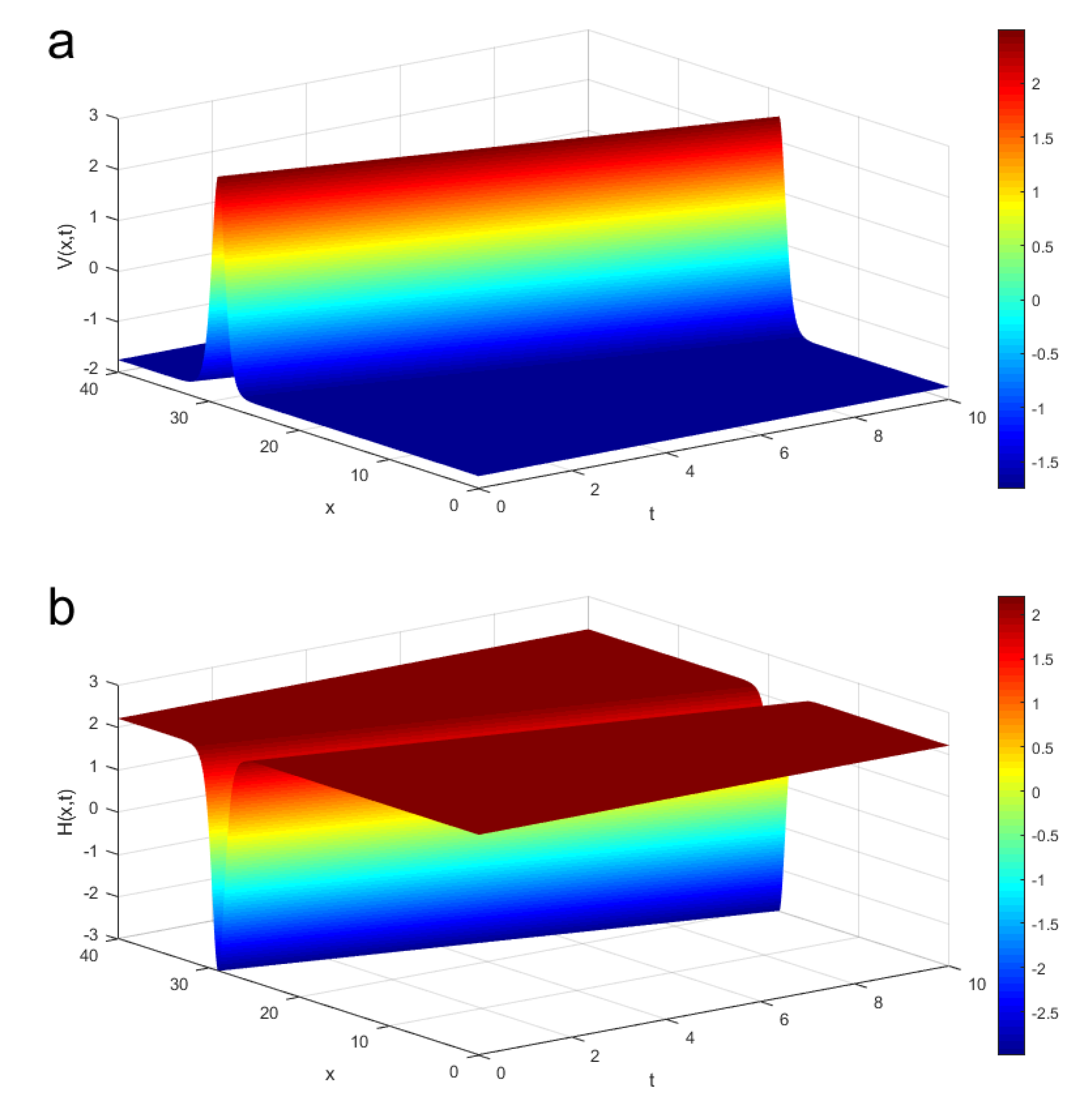
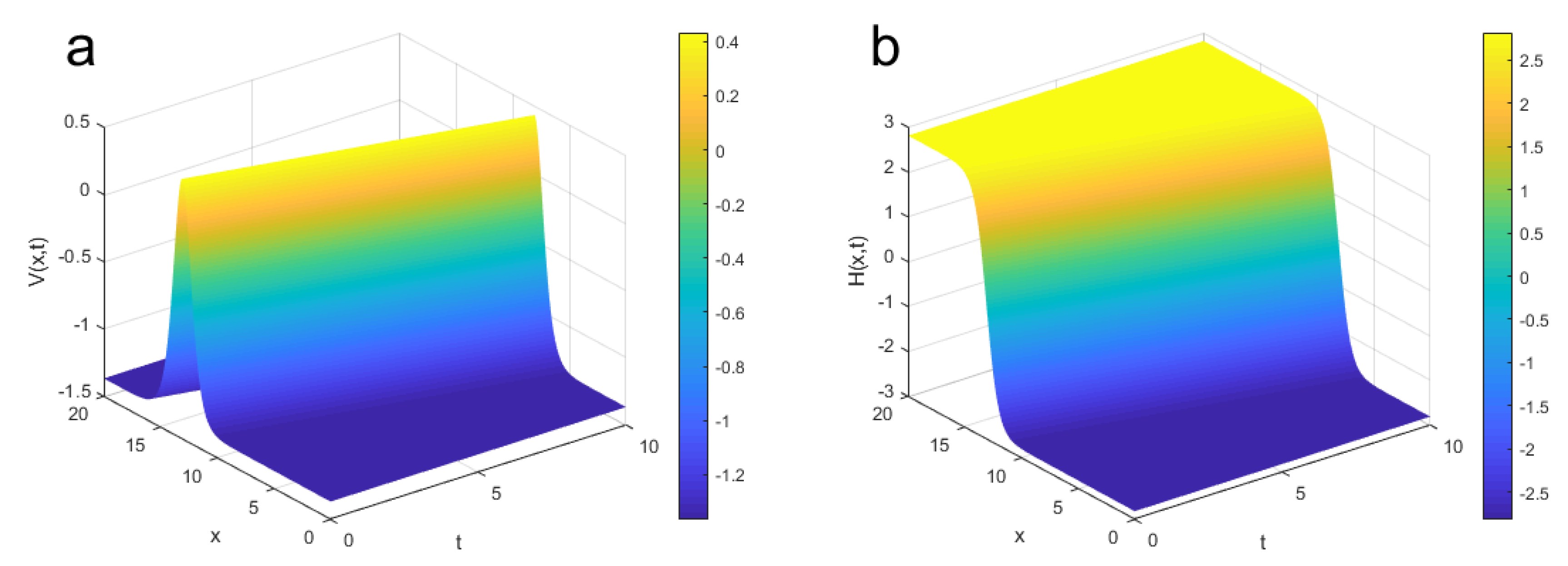
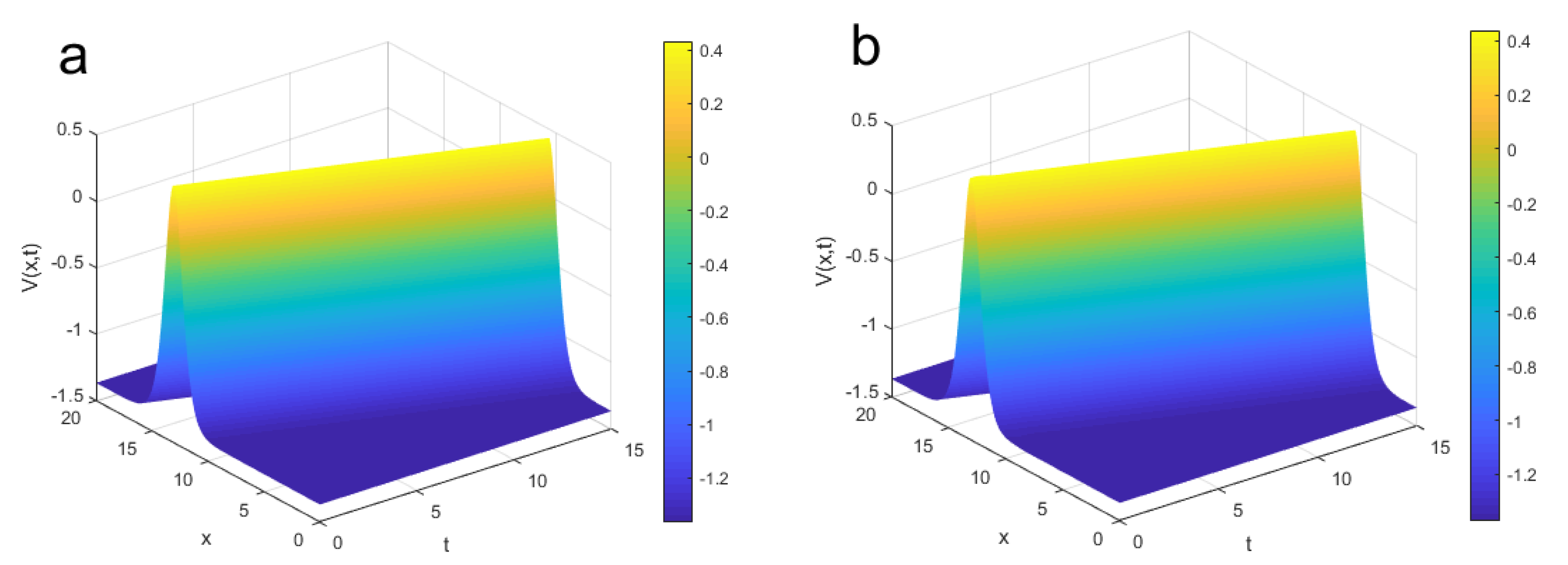
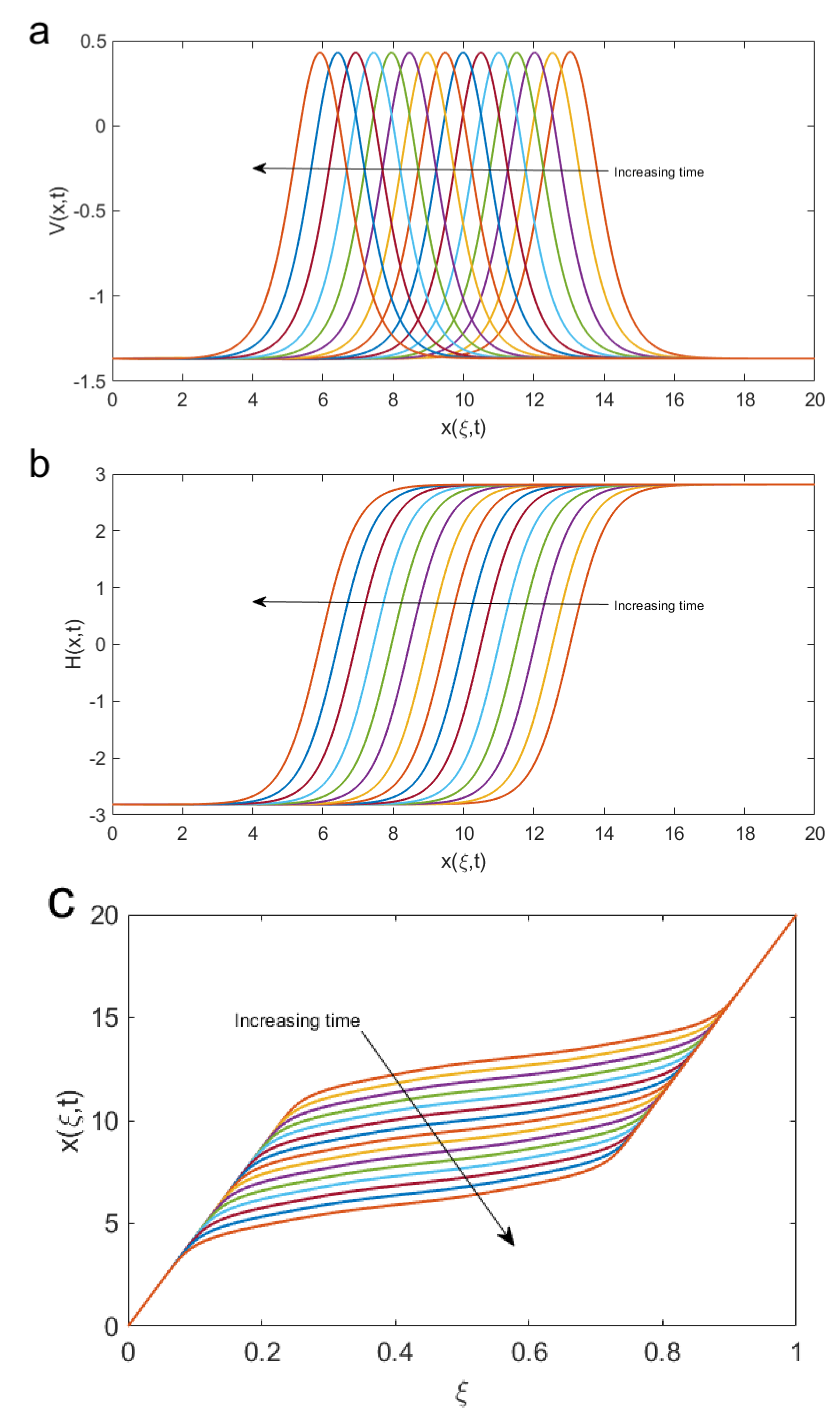
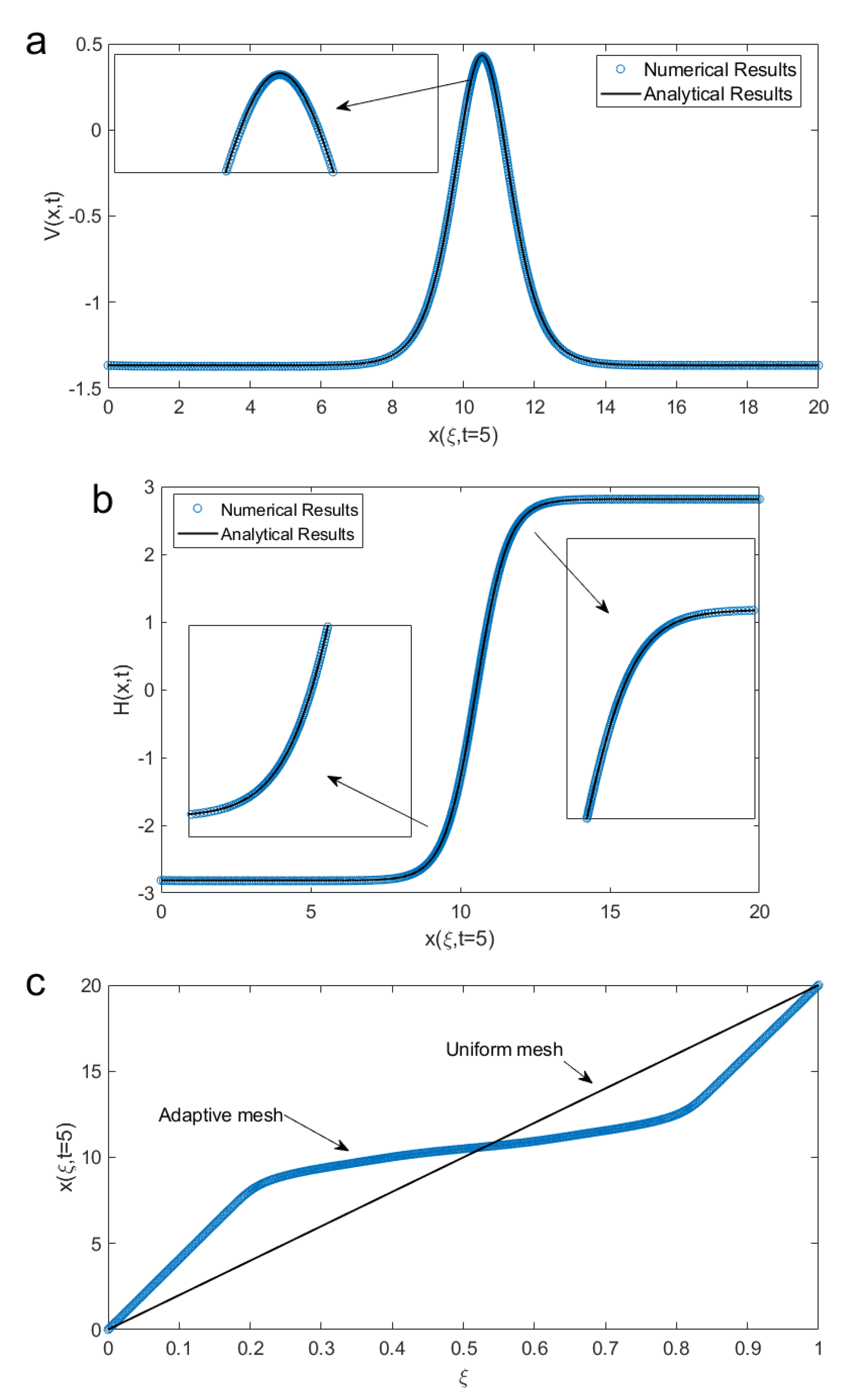
4. Numerical Results

The MMPDEs technique [40] is implemented to extract the numerical solutions of the considered equations. This method can be used to deal with one-dimensional and multi-dimensional PDEs as shown in [40,41,42], respectively. The solutions of the coupled KdV equations are approximated by employing new meshes named gradient flow equations. The main idea of utilizing this approach is to generate new meshes and diminish the error in the solutions by feeding the regions with a high error with more points. The coupled KdV Equation (1) can be simply rewritten by

$$\begin{array}{c}{\displaystyle V_t-\alpha V_{xxx}-6\alpha V{V}_x-\beta H{H}_x=0,}\hfill \\ \hfill \\ {\displaystyle H_t+H_{xxx}+3V{H}_x=0,}\hfill \end{array}$$

(24)

subject to the given boundary values in Equation (23). The corresponding initial data is given by

$$\begin{array}{c}{\displaystyle V(x,0)=\frac{1}{3}(-{\lambda }^2-2\mu -w)+\frac{4\mu \lambda }{\sqrt{({\lambda }^2-4\mu )}tanh\left(\frac{1}{2}\sqrt{{\lambda }^2-4\mu }(x+x_0)\right)+\lambda }}\hfill \\ {\displaystyle -\frac{8{\mu }^2}{{\left(\sqrt{({\lambda }^2-4\mu )}tanh(\frac{1}{2}\sqrt{{\lambda }^2-4\mu }(x+x_0)+\lambda \right)}^2},}\hfill \\ {\displaystyle H(x,0)=-\frac{\lambda \sqrt{-\alpha {\lambda }^2+4\alpha \mu -2\alpha w-w}}{\sqrt{2\beta }}+\frac{\mu \sqrt{8\left(-\alpha {\lambda }^2+4\alpha \mu -2\alpha w-w\right)}}{\sqrt{\beta }\left(\sqrt{({\lambda }^2-4\mu )}tanh(\frac{1}{2}\sqrt{{\lambda }^2-4\mu }(x+x_0)+\lambda \right)},}\hfill \end{array}$$

(25)

The used coordinate transform is expressed as $x=x(\xi ,t):[0,1]\to [-L,L],$ where $x\in [-L,L]$ and $\xi \in [0,1]$ denote the space and computational coordinates, respectively. We use the chain rule to descritise the spatial and temporal derivatives as follows:

$$\begin{array}{c}{\displaystyle V_t-V_x{x}_t-\alpha V_{xxx}-6\alpha V{V}_x-\beta H{H}_x=0,}\hfill \\ \hfill \\ {\displaystyle H_t-H_x{x}_t+H_{xxx}+3V{H}_x=0.}\hfill \end{array}$$

(26)

Now, we rewrite Equation (26) as follows:

$$\begin{array}{c}{\displaystyle V_t-\left(\frac{V_{\xi }}{x_{\xi }}\right)x_t-\alpha V_{xxx}-3\alpha \frac{{V^2}_{\xi }}{x_{\xi }}-\beta \frac{{H^2}_{\xi }}{x_{\xi }}=0,}\hfill \\ \hfill \\ {\displaystyle H_t-\left(\frac{H_{\xi }}{x_{\xi }}\right)x_t+H_{xxx}+3V\frac{H_{\xi }}{x_{\xi }}=0,}\hfill \end{array}$$

(27)

where

$$\begin{array}{c}{\displaystyle V_{xxx}=\frac{1}{x_{\xi }}{\left(\frac{1}{x_{\xi }}{\left(\frac{V_{\xi }}{x_{\xi }}\right)}_{\xi }\right)}_{\xi },}\hfill \\ \hfill \\ {\displaystyle H_{xxx}=\frac{1}{x_{\xi }}{\left(\frac{1}{x_{\xi }}{\left(\frac{H_{\xi }}{x_{\xi }}\right)}_{\xi }\right)}_{\xi }.}\hfill \end{array}$$

(28)

To generate the mesh $x(\xi ,t),$ we use the one dimensional equation [43,44,45]

$$\delta (I-\lambda {\partial }_{\xi \xi })x_t=\frac{1}{\mathsf{\Psi }}{\left(\mathsf{\Psi }{x}_{\xi }\right)}_{\xi },$$

(29)

is utilized with the following boundary conditions

$$x_0=-L,x_{N+1}=L,$$

(30)

where L is half of the length of the physical domain and $\mathsf{\Psi }$ is the monitor function. The initial data that we use is taken

$$x(\xi ,t=0)=(n-1)\Delta x-L,\Delta x=\frac{2L}{N}n=1,2,3,\dots ,N+1.$$

(31)

The relaxation parameter is presented by $\delta$ and $\delta (I-\lambda {\partial }_{\xi \xi })$ is the smoothing operator described by Ceniceros and Hou [46]. The fundamental purpose of $\mathsf{\Psi }(V,H,x)$ is to control the movement of the mesh. A suitable choice for the function $\mathsf{\Psi }$ leads to perfect and acceptable results [43,44,45]. A modified monitor function was developed in [47] as follows:

$$\mathsf{\Psi }(V,H,x)=\sqrt{1+\alpha \left({\left(\frac{1}{x_{\xi }}{\left(\frac{V_{\xi }}{x_{\xi }}\right)}_{\xi }\right)}^2+{\left(\frac{1}{x_{\xi }}{\left(\frac{H_{\xi }}{x_{\xi }}\right)}_{\xi }\right)}^2\right)}.$$

(32)

where $\alpha$ is a positive constant. The semi-discretisation of the spatial derivative converts the coupled KdV equations into $(N+1)$ ODEs easily solved using line methods. The obtained system is numerically integrated using the MATLAB ODE solver (ode15i). The physical domain is firstly separated as follows:

$$x_n<x_{n+1},n=0,1,2,\dots ,N.$$

(33)

The computational coordinates are illustrated by

$${\xi }_n=n\Delta \xi ,\Delta \xi =\frac{1}{N},n=0,1,2,\dots ,N.$$

(34)

We now fix the boundary mesh by $x_0=-L$ and $x_{N+1}=L.$ The interior mesh is completely approximated by resolving Equation (29) with the boundary conditions $x_{t,0}=x_{t,N}=0.$ The discretisation of Equation (28) is simply developed by applying the central finite differences. That is

$$\begin{array}{c}{\displaystyle {\left.V_t\right|}_i-\frac{V_{i+1}-V_{i-1}}{x_{i+1}-x_{i-1}}{\left.x_t\right|}_i=-2\alpha \frac{V_{xx,i+1}-V_{xx,i}}{x_{i+1}-x_{i-1}}-3\alpha \frac{V_{i+1}^2-V_{i-1}^2}{x_{i+1}-x_{i-1}}+\beta \frac{H_{i+1}^2-H_{i-1}^2}{x_{i+1}-x_{i-1}},}\hfill \\ \hfill \\ {\displaystyle {\left.H_t\right|}_i-\frac{H_{i+1}-H_{i-1}}{x_{i+1}-x_{i-1}}{\left.x_t\right|}_i=-2\frac{H_{xx,i+1}-H_{xx,i}}{x_{i+1}-x_{i-1}}-3V_{i+\frac{1}{2}}\frac{H_{i+1}-H_{i-1}}{x_{i+1}-x_{i-1}},}\hfill \end{array}$$

(35)

where

$$\begin{array}{c}{\displaystyle H_{xx,i}=\frac{2}{x_{i+1}-x_{i-1}}\left[\frac{H_{i+1}-H_i}{x_{i+1}-x_i}-\frac{H_i-H_{i-1}}{x_i-x_{i-1}}\right],V_{i+\frac{1}{2}}=\frac{V_{i+1}+V_i}{2},}\hfill \\ {\displaystyle V_{xx,i}=\frac{2}{x_{i+1}-x_{i-1}}\left[\frac{V_{i+1}-V_i}{x_{i+1}-x_i}-\frac{V_i-V_{i-1}}{x_i-x_{i-1}}\right].}\hfill \end{array}$$

(36)

Figure 3 compares the movement of one travelling wave solution for both the exact solution of $V(x,t)$ (left) and the numerical solution of $V(x,t)$ (right) as the time increases from $t=0\to 15.$ In Figure 4, we illustrate the movement of the analytic solution of $H(x,t)$ (left) compared with the movement of the numerical solution of $H(x,t)$ (right) for $t=0\to 15.$ The used parameters are given by $\alpha =-2.5,\beta =2.5,x_0=-15,w=0.5,\mu =0.10,\lambda =2.0,$$t=0\to 10$ and $x=0\to 20.$ The results appear to have approximately the same behaviour. This indicates that the used methods are reliable and can be utilized to solve more nonlinear PDEs. The conditions of the stability are employed and we discover that our results are stable inside the interval $[0,20].$

5. Comparison

The MMPDEs method utterly confirms its validity to be used in dealing with most NLPDEs. In particular, the method gives excellent results for the coupled KdV equations. More specifically, Figure 3 and Figure 4 illustrate a close similarity between the obtained exact and numerical solutions. Figure 5 illustrate that the solution moves as the time increases and seems to be without variations. A satisfactory performance of this approach can be also seen in Figure 6a,b where the numerical solutions mostly agree with the exact ones. This method distributes the points adequately. Therefore, the error is often very small. As a result, this technique can be used to solve several other NLPDEs.

6. Conclusions

In this work, we applied two methods to solve the coupled KdV equations, specifically, the analytical exp-function method and numerical MMPDEs method. We introduced some 2D and 3D plots for some of the obtained solutions. The obtained solutions are stable on the interval [0,20]. The achieved solutions may be applicable for explaining important phenomena in science, namely, in plasma physics and crystal lattices. We are quit sure that these techniques can also be applied to other NPDEs and, therefore, we shall take it up in our future studies.

Now, we summarize the article as follows.

• Constructing some new solutions for coupled KdV equations, using the exp-function method.
• Studying the modulation instability to check the stability of the exact solutions.
• Implementing (numerically) the MMPDEs scheme to solve coupled KdV equations.
• Currently, work is in progress on the application of the proposed two schemes for further coupled systems of NPDEs.