Fingerprints of the Cosmological Constant: Folds in the Profiles of the Axionic Dark Matter Distribution in a Dyon Exterior
Abstract
1. Introduction
2. Description of the Axionic Dark Matter Profiles
2.1. The Total Action Functional
2.2. Background State
2.3. Master Equations of the Axion Electrodynamics
2.4. Static Spacetime with Spherical Symmetry
3. On the Features of the Exact Solution Describing the Dirac Magnetic Monopole in the Spacetime with Cosmological Constant
3.1. Geometrical Aspects and Definition of the Fold
- 1.
- the profile has the central minimum, the barrier on the left of the minimum, and the maximum on the right;
- 2.
- this domain is inside the cosmological horizon, but it is not hidden inside the event horizon, i.e., in this domain.
3.2. Horizons
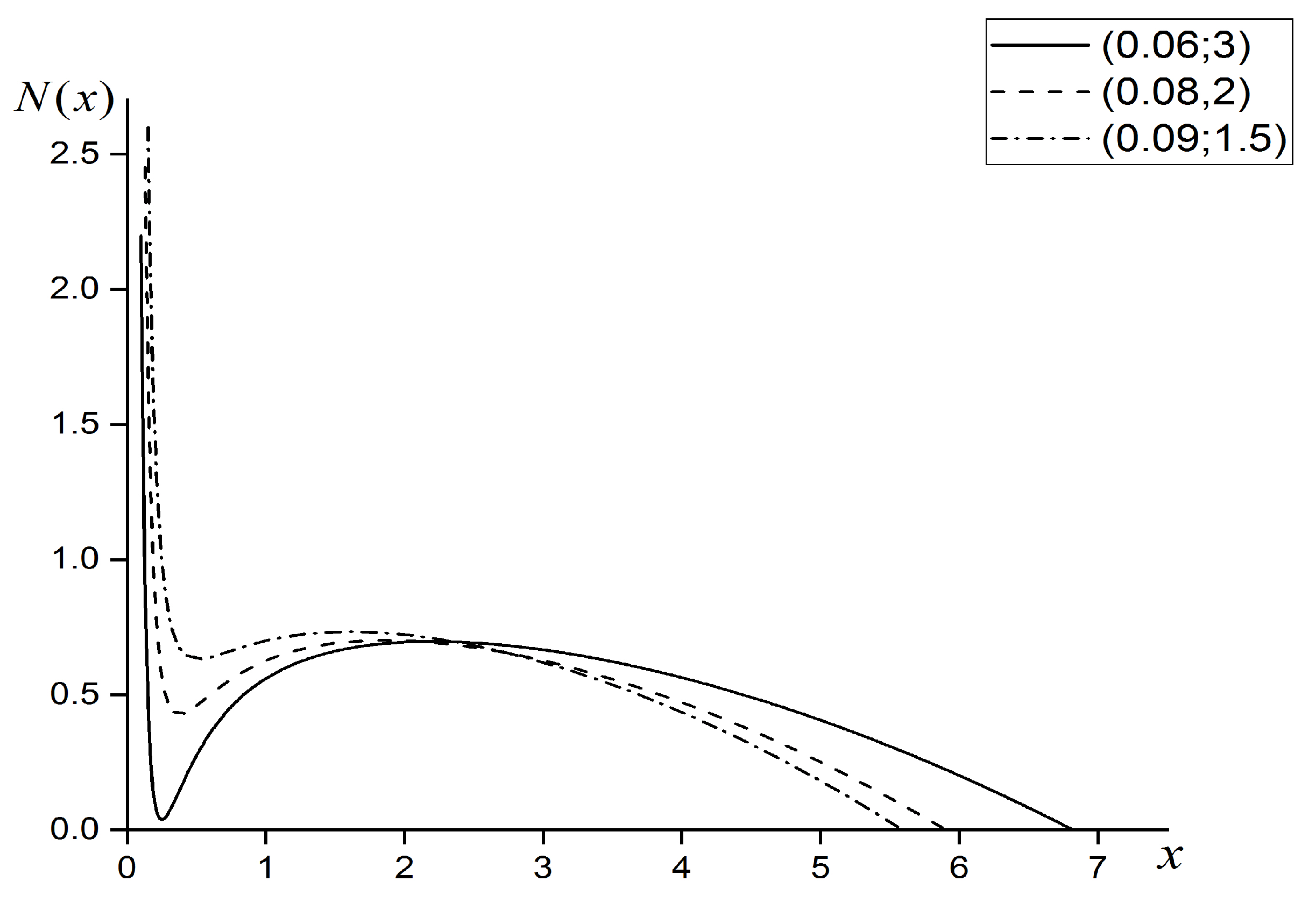
3.2.1. Auxiliary Function Indicating the Number of Horizons
3.2.2. The Case
- When , the mass line crosses the indicated graph in one point, i.e., there is only one (cosmological) horizon.
- When , the mass line is the tangent one with respect to the minimum of this graph, thus, there are two horizons: the double event horizon and the simple cosmological one.
- When , there are three intersection points, thus, there are three horizons: the inner and outer event horizons and the cosmological one.
- When there are two horizons: the simple event horizon and the double cosmological one.
3.2.3. The Case
3.2.4. The Case
- 1.
- , ;
- 2.
- , ;
- 3.
- .
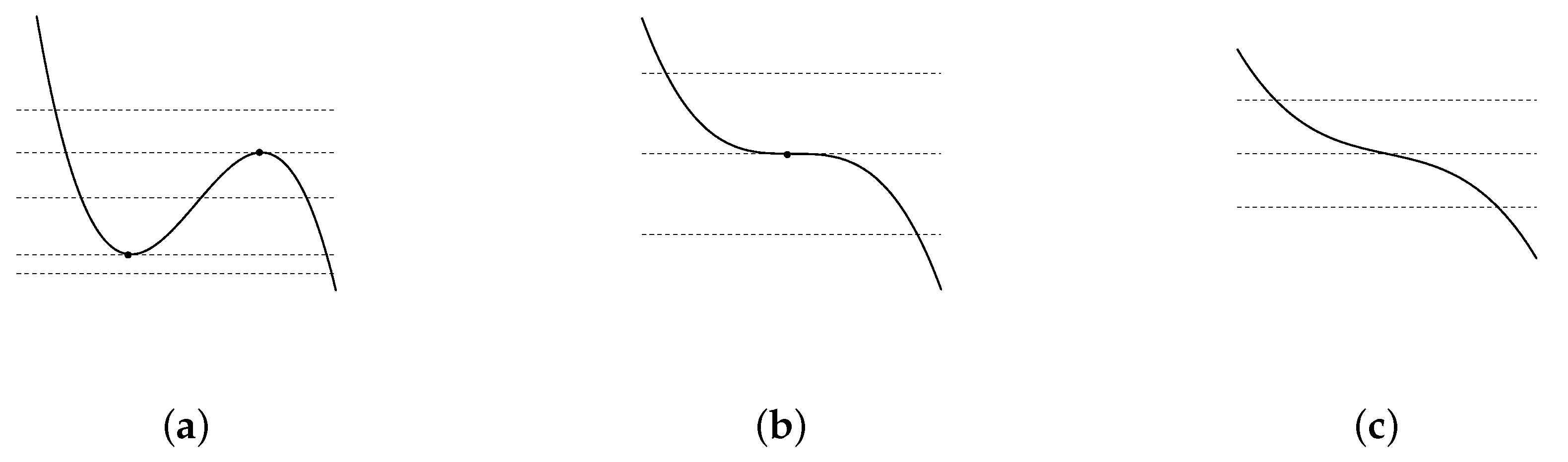
3.3. Folds
- When , the horizontal mass line crosses the graph of the function twice; this means that there are two extrema: the minimum and maximum.
- When , two extrema coincide forming the cubic inflexion point.
- When , the profile is monotonic.
3.4. Final Remarks about the Features of the Spacetime Geometry
3.4.1. The Choice of the Appropriate Scale for the Radial Variable
3.4.2. On the Problem of Naked Singularity and Cosmic Censorship Conjecture
4. Analysis of Solutions to the Key Equation of the Axion Field
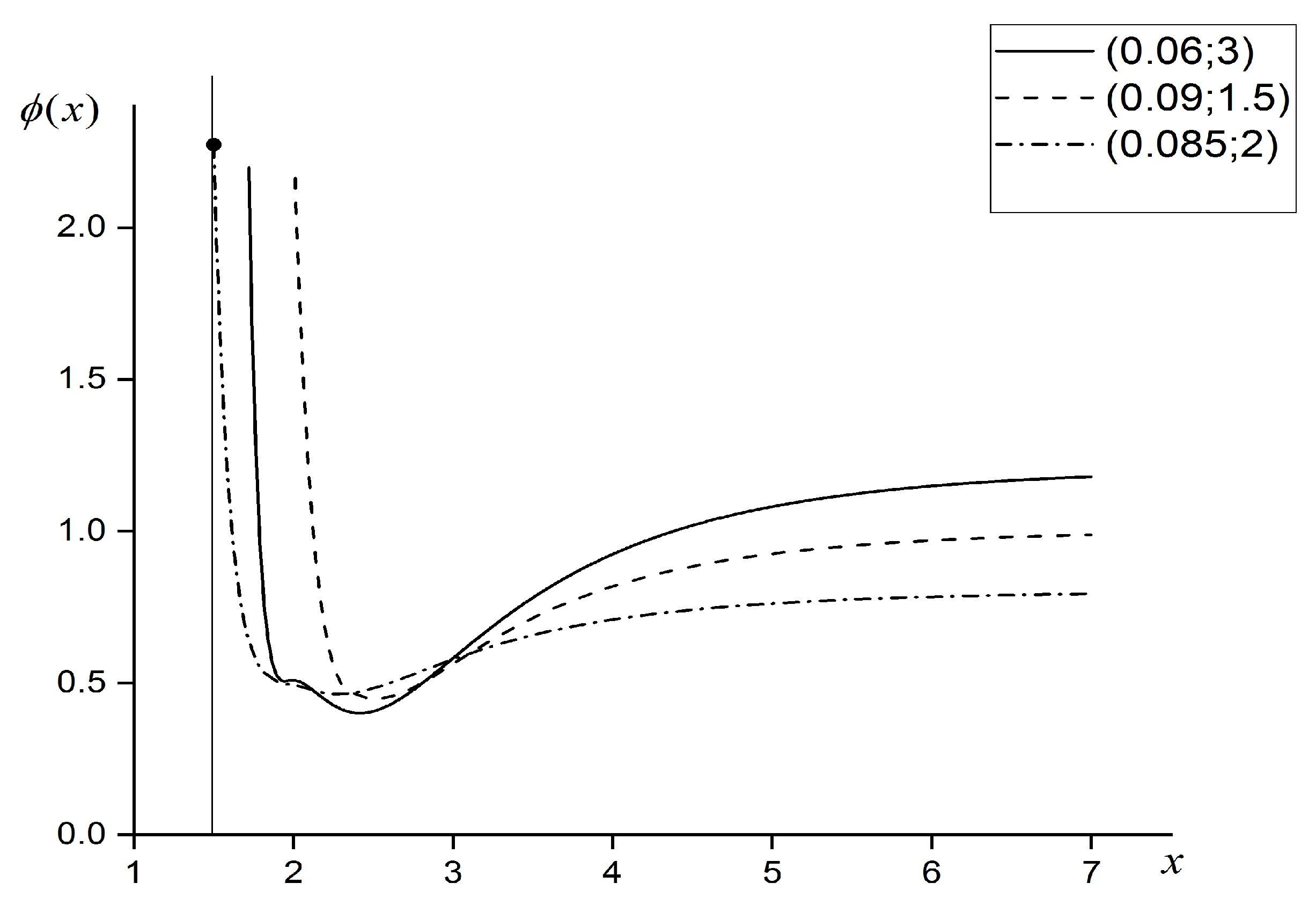
4.1. The Profile of the Axion Field Distribution
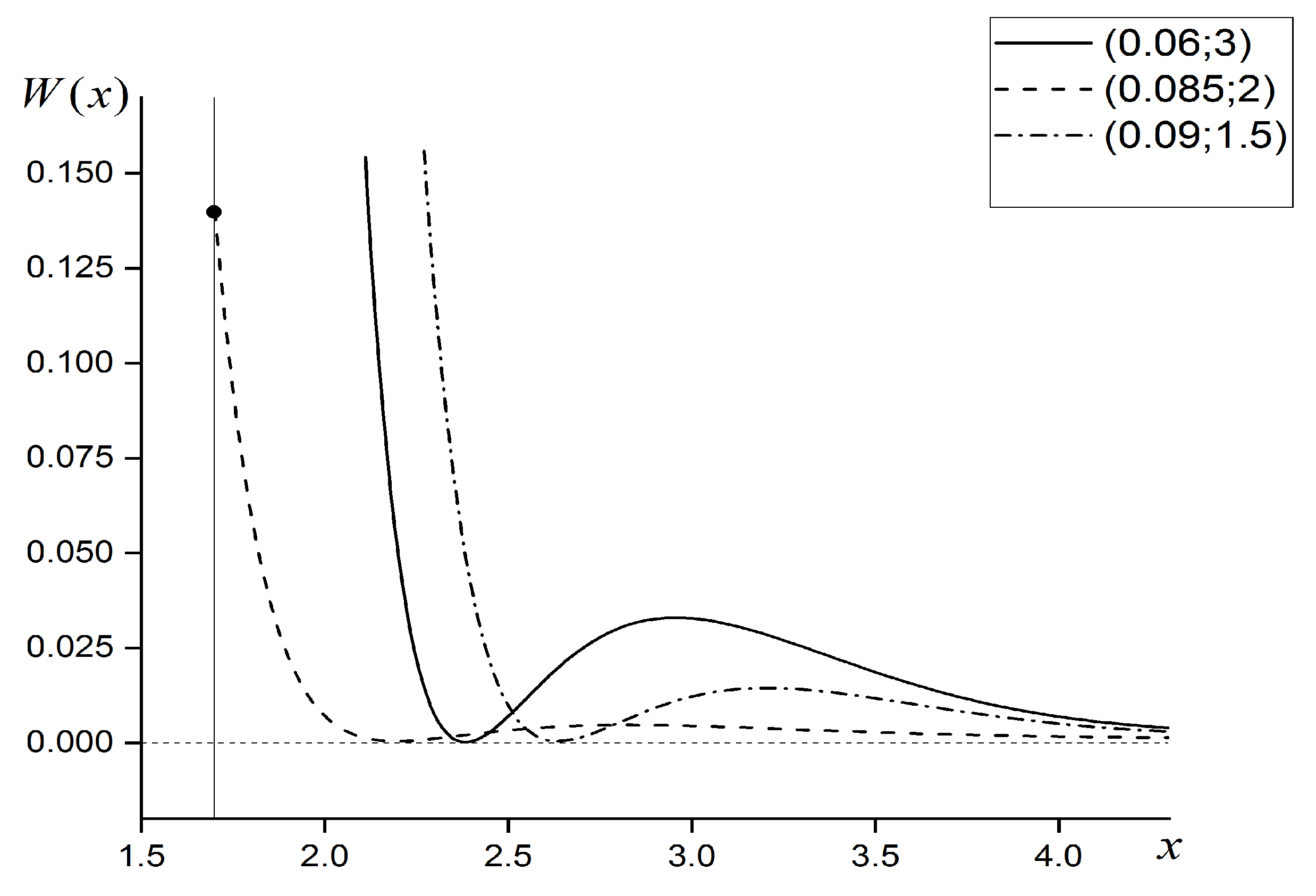
4.2. The Profile of the Energy-Density of the Axionic Dark Matter
4.3. Profiles of the Axionically Induced Electric Field
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Weinberg, S. Cosmology; Oxford University Press: New York, NY, USA, 2008. [Google Scholar]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1–24. [Google Scholar] [CrossRef]
- Carroll, S.M.; Press, W.H.; Turner, E.L. The Cosmological Constant. Annu. Rev. Astron. Astrophys. 1992, 30, 499–542. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The Cosmological Constant and Dark Energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Balakin, A.B.; Zayats, A.E. Dark energy fingerprints in the non-minimal Wu-Yang wormhole structure. Phys. Rev. D 2014, 90, 044049. [Google Scholar] [CrossRef]
- Balakin, A.B.; Lemos, J.P.S.; Zayats, A.E. Regular non-minimal magnetic black holes in spacetimes with a cosmological constant. Phys. Rev. D 2016, 93, 024008. [Google Scholar] [CrossRef]
- Balakin, A.B.; Lemos, J.P.S.; Zayats, A.E. Magnetic black holes and monopoles in a non-minimal Einstein-Yang-Mills theory with a cosmological constant: Exact solutions. Phys. Rev. D 2016, 93, 084004. [Google Scholar] [CrossRef]
- Del Popolo, A. Non-baryonic dark matter in cosmology. Int. J. Mod. Phys. D 2014, 23, 1430005. [Google Scholar] [CrossRef]
- Khlopov, M. Fundamentals of Cosmic Particle Physics; CISP-Springer: Cambridge, UK, 2012. [Google Scholar]
- Deliyergiyev, M.; Del Popolo, A.; Tolos, L.; Le Delliou, M.; Lee, X.; Burgio, F. Dark compact objects: An extensive overview. Phys. Rev. D 2019, 99, 063015. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H.R. CP conservation in the presence of instantons. Phys. Rev. Lett. 1977, 38, 1440–1443. [Google Scholar] [CrossRef]
- Weinberg, S. A new light boson? Phys. Rev. Lett. 1978, 40, 223–226. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of strong P and T invariance in the presence of instantons. Phys. Rev. Lett. 1978, 40, 279–282. [Google Scholar] [CrossRef]
- Preskill, J.; Wise, M.B.; Wilczek, F. Cosmology of the Invisible Axion. Phys. Lett. B 1983, 120, 127–132. [Google Scholar] [CrossRef]
- Abbott, L.F.; Sikivie, P. A Cosmological Bound on the Invisible Axion. Phys. Lett. B 1983, 120, 133–136. [Google Scholar] [CrossRef]
- Dine, M.; Fischler, W. The Not So Harmless Axion. Phys. Lett. B 1983, 120, 137–141. [Google Scholar] [CrossRef]
- Sikivie, P. Axion Cosmology. Lect. Notes Phys. 2008, 741, 19–50. [Google Scholar]
- Battesti, R.; Beltran, B.; Davoudiasl, H.; Kuster, M.; Pugnat, P.; Rabadan, R.; Ringwald, A.; Spooner, N.; Zioutas, K. Axion searches in the past, at present, and in the near future. Lect. Notes Phys. 2008, 741, 199–237. [Google Scholar]
- Steffen, F.D. Dark Matter candidates—Axions, neutralinos, gravitinos, and axinos. Eur. Phys. J. C 2009, 59, 557–588. [Google Scholar] [CrossRef]
- Marsh, D.J.E. Axion Cosmology. Phys. Rept. 2016, 643, 1–79. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Unification of Inflation with Dark Energy in f(R) Gravity and Axion Dark Matter. Phys. Rev. D 2019, 99, 104070. [Google Scholar] [CrossRef]
- Ni, W.-T. Equivalence principles and electromagnetism. Phys. Rev. Lett. 1977, 38, 301–304. [Google Scholar] [CrossRef]
- Sikivie, P. Experimental Tests of the “Invisible” Axion. Phys. Rev. Lett. 1983, 51, 1415–1417. [Google Scholar] [CrossRef]
- Wilczek, F. Two applications of axion electrodynamics. Phys. Rev. Lett. 1987, 58, 1799–1802. [Google Scholar] [CrossRef] [PubMed]
- Sikivie, P.; Yang, Q. Bose-Einstein Condensation of Dark Matter Axions. Phys. Rev. Lett. 2009, 103, 111301. [Google Scholar] [CrossRef]
- Balakin, A.B.; Groshev, D.E. Magnetoelectrostatics of axionically active systems: Induced field restructuring in magnetic stars. Phys. Rev. D 2020, 101, 023009. [Google Scholar] [CrossRef]
- Balakin, A.B.; Groshev, D.E. New application of the Killing vector field formalism: Modified periodic potential and two-level profiles of the axionic dark matter distribution. Eur. Phys. J. C 2020, 80, 145. [Google Scholar] [CrossRef]
- Balakin, A.B.; Groshev, D.E. Polarization and stratification of axionically active plasma in a dyon magnetosphere. Phys. Rev. D 2019, 99, 023006. [Google Scholar] [CrossRef]
- Lee, K.; Nair, V.; Weinberg, E. Black holes in magnetic monopoles. Phys. Rev. D 1992, 45, 2751. [Google Scholar] [CrossRef]
- Astashenok, A.V.; Odintsov, S.D. Supermassive Neutron Stars in Axion F(R) Gravity. Mon. Not. R. Astron. Soc. 2020, 493, 78–86. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Geometric Inflation and Dark Energy with Axion F(R) Gravity. Phys. Rev. D 2020, 101, 044010. [Google Scholar] [CrossRef]
- Penrose, R. Gravitational collapse: The role of general relativity. Nuovo Cimento 1969, 1, 252–276. [Google Scholar]
- Shaikh, R.; Joshi, P.S. Can we distinguish black holes from naked singularities by the images of their accretion disks? JCAP 2019, 10, 064. [Google Scholar] [CrossRef]
- Chakraborty, C.; Kocherlakota, P.; Patil, M.; Bhattacharyya, S.; Joshi, P.S.; Królak, A. Distinguishing Kerr naked singularities and black holes using the spin precession of a test gyro in strong gravitational fields. Phys. Rev. D 2017, 95, 084024. [Google Scholar] [CrossRef]
- Ortiz, N.; Sarbach, O.; Zannias, T. Shadow of a naked singularity. Phys. Rev. D 2015, 92, 044035. [Google Scholar] [CrossRef]
- Kovacs, Z.; Harko, T. Can accretion disk properties observationally distinguish black holes from naked singularities? Phys. Rev. D 2010, 82, 124047. [Google Scholar] [CrossRef]
- Balakin, A.B.; Dehnen, H.; Zayats, A.E. Non-minimal monopoles of the Dirac type as realization of the censorship conjecture. Phys. Rev. D 2009, 79, 024007. [Google Scholar] [CrossRef]
- Balakin, A.B.; Zayats, A.E. Non-minimal Wu-Yang monopole. Phys. Lett. B 2007, 644, 294–298. [Google Scholar] [CrossRef]
- Balakin, A.B.; Dehnen, H.; Zayats, A.E. Non-minimal Einstein-Yang-Mills-Higgs theory: Associated, color and color-acoustic metrics for the Wu-Yang monopole model. Phys. Rev. D 2007, 76, 124011. [Google Scholar] [CrossRef]
- Balakin, A.B.; Zayats, A.E. Ray optics in the field of non-minimal Dirac monopole. Grav. Cosmol. 2008, 14, 86–94. [Google Scholar] [CrossRef]
- Ince, E.L. Ordinary Differential Equations; Dover Publications: New York, NY, USA, 1920. [Google Scholar]
- Borra, E.F.; Deschatelets, D. Measurements of stellar magnetic fields using autocorrelation of spectra. Astron. J. 2015, 150, 146. [Google Scholar] [CrossRef]
- Thorman, A. Polarization of the Balmer-α emission in crossed electric and magnetic fields. J. Quant. Spectrosc. Radiat. Transf. 2018, 207, 8. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balakin, A.; Groshev, D. Fingerprints of the Cosmological Constant: Folds in the Profiles of the Axionic Dark Matter Distribution in a Dyon Exterior. Symmetry 2020, 12, 455. https://doi.org/10.3390/sym12030455
Balakin A, Groshev D. Fingerprints of the Cosmological Constant: Folds in the Profiles of the Axionic Dark Matter Distribution in a Dyon Exterior. Symmetry. 2020; 12(3):455. https://doi.org/10.3390/sym12030455
Chicago/Turabian StyleBalakin, Alexander, and Dmitry Groshev. 2020. "Fingerprints of the Cosmological Constant: Folds in the Profiles of the Axionic Dark Matter Distribution in a Dyon Exterior" Symmetry 12, no. 3: 455. https://doi.org/10.3390/sym12030455
APA StyleBalakin, A., & Groshev, D. (2020). Fingerprints of the Cosmological Constant: Folds in the Profiles of the Axionic Dark Matter Distribution in a Dyon Exterior. Symmetry, 12(3), 455. https://doi.org/10.3390/sym12030455




