1. Introduction
Several recent attempts have been made to extend the exponential distribution in order to increase its versatility for modelling purposes. Among others, the two-parameter exponentiated exponential distribution ([
1,
2,
3] and references therein), and the three-parameter generalised exponential distribution [
4] have been presented as feasible alternatives to the gamma, Weibull and lognormal distributions, although both standard and extended distributions are known to present drawbacks. The latter have been used to analyse lifetime data that present a monotonic (increasing or decreasing) hazard rate function (also known as failure rate function). These distributions are popular among researchers interested in areas such as reliability engineering and software reliability [
5,
6]. Interesting, thorough reviews of the exponential distribution along with its applications may be found in a recent book by Balakrishnan (2019) [
7]. References on extensions of the exponential distribution include Johnson et al. (2019) [
8] and references therein.
The Marshall–Olkin (MO) scheme was originally designed to extend the exponential and Weibull families, and has recently been adapted to obtain new families of distributions; see e.g., Ghitany et al. (2007) [
9], García et al. (2010) [
10], Gómez–Déniz (2010) [
11], Krishna et al. (2013) [
12], Cordeiro et al. (2014) [
13] and García et al. (2016) [
14]. In this respect, Caroni [
15] studied likelihood-based tests for the additional parameter on both families of distributions. An economic reliability test plan for the MO–exponential family has also been studied, in [
16]. Other studies, using diverse methods, have also been undertaken to generalise the Marshall–Olkin scheme [
17].
Inspired by the seminal paper of Marshall and Olkin (1997) [
18], in this paper we introduce a family of three-parameter univariate distributions presenting both decreasing and increasing hazard rates, and include the exponential distribution as a particular case.
Let
be a random sequence given by
where
are random sequences of exponential i.i.d. variables with parameters
and
, respectively, and
.
Let
be the survival function of
; i.e.,
. Then,
Assuming stability for
,
Observe that (
2) yields a mechanism to extend a distribution.
The rest of this paper is organised as follows:
Section 2 presents and discusses general conditions for generalised Marshall–Olkin exponential (GMOE) distributions.
Section 3 then shows some interesting properties of the GMOE distributions. For instance, we show that their hazard rate function is related to the constant hazard rate function of an exponential distribution with parameter
according to the value of
. Secondly, a closed expression for the moments is obtained. Consequently, the mean, variance, skewness coefficient, etc., are easily obtained. Finally, a brief study of the mode location is conducted in
Section 3.
Section 4 presents the expressions for model parameter estimation, and a simulation study is performed to determine the performance of the maximum likelihood estimators with respect to certain sample sizes. Some real-world applications are presented in
Section 5. Finally,
Section 6 and
Section 7 present some extensions of the proposed methodology and the main conclusions drawn, respectively.
2. The Generalised Marshall–Olkin Exponential Distribution
In this section, we introduce the three-parameter generalised Marshall–Olkin exponential (GMOE) distribution, using the mechanism described by (
2).
In order to reach stability in (
2), some initial considerations are needed. Let us denote by
and
the respective survival and cumulative distribution functions (cdfs) of
. For
we have
Thus, its associated cdf is given by
Clearly for any
and
we have
Thus, for
to be a cdf, it is only required that
or equivalently,
Expression (
5) is non-negative for all
x, when
However, if we wish to extend this scheme to cases where
as in the Marshall–Olkin scheme, then it is required that
which is a constraint when
and is true for any
.
Definition 1. A random variable X has the generalised Marshall–Olkin exponential distribution with three parameters denoted by if its cumulative distribution function (cdf) is given by: The probability density function (pdf) corresponding to Equation (7) reduces to which is defined for any set of positive parameters such that .
Remark 1. For we obtain the exponential distribution with parameter . In other words, with the GMO scheme the original family, , can be generalised by the insertion of an additional parameter δ and by the effect of an auxiliary distribution .
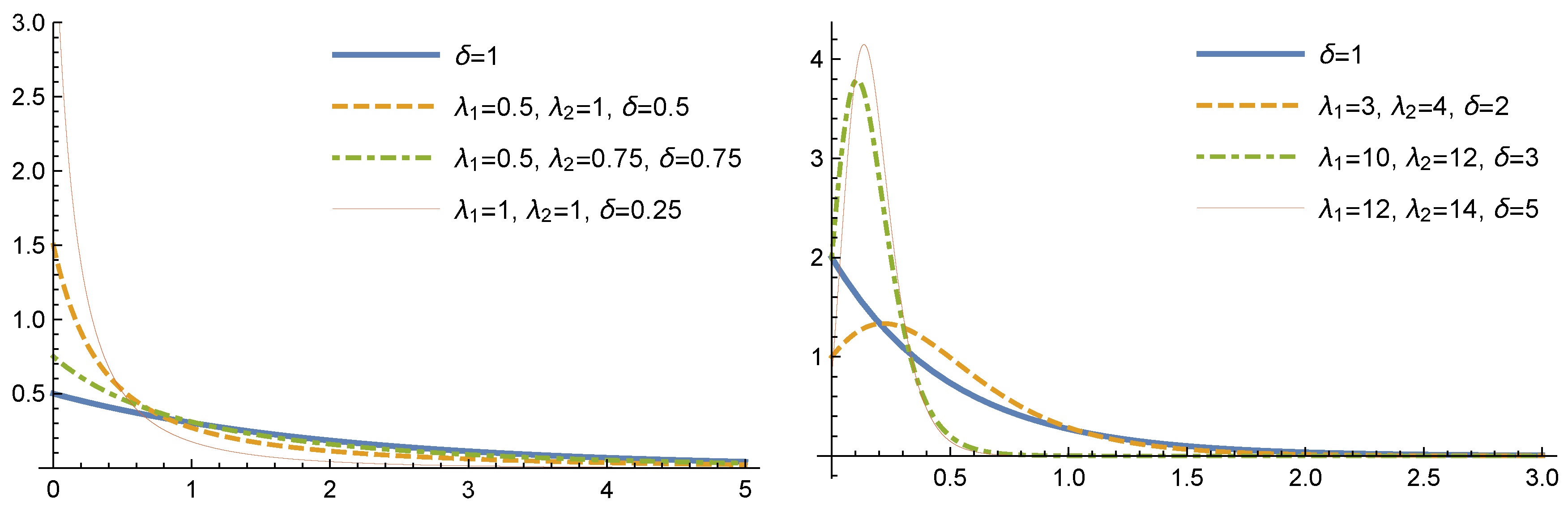
Remark 2. If then (8) reduces to the Marsall–Olkin exponential distribution with parameters and δ. For several values of the parameters
and
the plots of the density function of GMOE distributions are shown in
Figure 1.
3. Some Properties of the GMO–Exponential Distribution
Some important properties of the
distributions are shown in this section. From expression (
3) and given
we can obtain the
qth quantile
of the GMOE distribution as follows. Let
that is,
Then, we rewrite this expression as
or equivalently
where
. Given the real solution of this equation,
,
is the
qth quantile of a
distributed variable. Notice that Equation (
9) has only one positive solution. Additionally, observe that this procedure is useful to obtain the quantile function of the GMOE distribution which is given by
where, when replacing
q by
u,
is the unique solution to (
9). Therefore, if
U is a uniform variate on the interval
, then the random variable
has pdf (
8).
3.1. Moments
The moments of a
–exponential distribution can be written in a closed form with the help of the well-known Hurwitz–Lerch transcendent function,
, which is defined by the expression
and which can also be expressed in an integral form as follows:
Symbolic and numerical evaluations of this function are easily obtained with Mathematica software using the command HurwitzLerchPhi.
Proposition 1. The nth moment of the GMOE distribution is given by Proof. Using expressions (
8) and (
10) and letting
,
Now observe that
can be obtained by parts with
and then
Substituting in (
12) then gives
and the proof is completed. □
Corollary 1. Let X be a GMOE distribution with parameters and δ. Then,
- (i)
- (ii)
In particular,where - (iii)
For a fixed value of the value of its kth moment decreases with and with .
Proof. The proof is immediate and (ii) follows from the identity □
Using (
13)–(
15), the coefficient of variation (CV) and the skewness (
) of
X are given by
Observe that in GMOE distributions with a constant ratio, the and only depend on .
3.2. The Hazard Rate: Reliability Properties
The hazard rate of a
distribution,
, is given by
As
Figure 2 shows, the hazard rate function of the GMOE distribution can take monotonic and quasi-bathtub shapes for different values of the parameters
and
If we denote by the hazard rate of an distribution, the following results can be obtained immediately:
Proposition 2. - (i)
- (ii)
- (iii)
is a strictly decreasing function for constant for and strictly increasing for
Proof. (i) and (ii) are immediate. For (iii), the result follows by observing that the sign of the first derivative of the hazard rate function in (
9) with respect to
x is the opposite to the sign of
. □
Furthermore, is increasing in and in Thus, the GMOE distribution is positively ordered with respect to according to the hazard rate ordering, and analogously, with respect to
In contrast with the ordinary families of gamma and Weibull distributions, observe that and that at the origin the hazard rate varies continuously with the parameters. Moreover, for the GMOE distribution, , is bounded and continuous in the parameters.
Finally, the residual life distribution of the random variable
X—distributed as a GMOE distribution with the parameters
and
—provided there is no failure prior to time
has the survival function
where
Thus, the residual life distribution of a random variable
X distributed as
at time
t is another GMOE distribution with the third parameter depending upon time
Henceforth, from (
12) the mean residual life function, i.e., the mean of the residual life distribution, is given by
It is then easy to see that
and
3.3. The Mode
From Remarks 1 and 2 in
Section 2, we now focus on the values of
and
The GMOE distribution can present its unique mode either at
or at
Let us define the function
such that
where
and
Now, to determine whether there exists a positive mode we need merely decide whether
:
or equivalently,
Assuming
, we define the auxiliary function as
Hence, in order to find the mode of GMOE distribution we need only decide whether The solution to this question depends on the range of values for .
- (Case a)
If , for any , and therefore the mode of distribution is reached at
- (Case b)
If
implies one of the following two cases. On the one hand,
which is contradictory, and on the other hand,
that is,
However, for
, the inequality
never holds. In summary, we conclude that the mode is reached at
in this case.
- (Case c)
If , the condition reduces to , or equivalently .
- (Case d)
Finally, if
,
implies
Notice that, for any
,
so we conclude that, in this case,
if and only if
3.4. Order Statistics
Let
be a random sample of size
n from the GMOE distribution in (
8). Then, the density of the
jth order statistics
for
is given by
where
In particular, the sample distributions of the minimum
and maximum
are easily obtained by (
22) replacing
j by 1 and
respectively.
4. Estimation
In this section, we estimate the unknown parameters of the GMOE distribution. Let
be a sample of size
n from the GMOE distribution in (
8). The log-likelihood function for the parameters
is expressed as
where
By differentiating with respect to
and
and then equating to zero, we obtain the normal equations needed to estiate the maximum likelihood.
These non–linear equations do not have a closed expression, but require numerical methods, available in standard software such as Mathematica.
The pdf of the GMOE distribution in (
8) satisfies all the regularity conditions, and thus from the usual, large sample approximation, the MLE
treated as being approximately multivariate normal with a mean vector
and variance–covariance matrix
and where the elements are provided by the inverse Fisher information matrix, the expected values of the second order derivatives are as shown in
Appendix A.
4.1. Simulation Study
In this section, we evaluate the performance of the MLEs and Bayesian estimators using Monte Carlo simulation, for certain sample sizes and parameter values. The simulation study is repeated
times with sample sizes
Table 1 shows the results obtained for different parameter combinations, together with the estimated bias and root mean squared error (RMSE) for each estimated parameter given a simulated sample of size
n, using the common expressions
Table 1 shows that the parameter estimators perform very badly, mainly due to the nonlinearity and instability of the solutions to Equations (23)–(25), even for large values of
n. The above three likelihood equations are very complicated, and the Newton–Raphson method is a gradient procedure whose stability depends on the selection of the initial solutions. It is not easy to set up good initial solutions to these three equations. An alternative procedure to obtain stable MLE consists of developing a non-informative Bayesian estimation approach. Doing so, we employ the MCMC method to generate samples from the posterior distributions of the parameters
and
from independent, uniform vague priors and then compute the corresponding Bayes estimators using the common squared errors loss function. From
Table 2 it is clear that MCMC samples can be used to estimate the parameters in GMOE distributions and that this method obtains better results than solving the normal equations directly by maximum likelihood. A simple code implemented using
OpenBUGS is given in
Appendix B. The summary statistics shown in
Table 2 are based on
simulations with 50,000 iterations following a burn-in stage of 5000 iterations.
6. Extensions of the GMO Scheme
In this Section, we show some general properties of the
scheme applied to any absolutely continuous distribution. Consider a pair of absolutely continuous distributions, denoted by
and
, for
, their respective cdfs, survival and pdfs’ functions. We assume that each
depends on its parameter
. We then define the survival function of the
with respect to
as the function
The corresponding cdf is then given by
and the corresponding pdf, by
We require that
for all
x. Clearly, in the case
, this condition is always met. On the other hand, when
, the required condition reduces to