Abstract
Acceptance of any new approach by the organizations depends upon the users’ needs. Currently, reducing the cost and time invested in maintenance is a major challenge for the practitioners. Moreover, symmetrical and optimal maintenance is the need of the hour and it can be achieved by increasing the durability of software. Many attributes of the quality may affect the durability of the software and identification of durability attributes is a crucial task at the early stage of software development. Thus, it is a problem that contains multi-criteria within it. With the help of quantitative estimation, software durability may be assessed symmetrically and increased. In this row, the authors of this article have attempted to posit an effective technique to assess the durability of software. Based on empirical data through research, the presenters of this article suggest that fuzzy-based symmetrical method of Analytic Network Process (ANP) and Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) would be an accurate methodology for assessing the durability of software. For determining the efficacy of this assessment, the researchers took six alternative software of a University. The results, as presented in this paper, would serve as guidelines for the practitioners who aim at achieving the preferred software durability.
1. Introduction
Software development is quite a complex process that involves high cost investments in stipulated timelines. Hence, the software developers have the formidable task of designing software that is not only user-centric but also durable. For over a decade now, the longevity of software has become a critical context for all developers. Evaluating and looking after software durability factors such as reliability amidst the phases of development is considered to be a noteworthy approach to achieve durable software [1]. Software durability is not built in a day; rather, it is a development strategy that focuses on crafting durable software. A technical report published for Software-as-a-Service (SaaS), an operations and a management Company, states that more than 73% of companies want to upgrade their technology till 2020 [2].
The same issue of maintenance was discussed in Cisco’s Global Cloud Index in the years 2013–2018. It was observed that 59% of cloud workflows will be delivered by SaaS till the end of 2020. Organizations spend lots of time and money to improve the life span of software [3]. These reports show the need for long lasting software in this era. Development of a new concept of software durability was proposed by the experts Kelty C. and Erickson S. in 2015 [4]. According to them, software-durability is termed as enhancing the life of software for a specific period to get the services as per the user’s requirements. Also, practitioners know that the market value of software depends upon its durability [4]. After a time period, this property of software decreases and its ability to work for a long time deteriorates. Hence, software services depend upon the timeliness of software.
For assessing and improving software durability, Kumar R. et al., proposed a novel concept of durability in software engineering [5]. According to him, software durability has four major factors including trustworthiness, dependability, human-trust, and usability. Furthermore, the integration of software and durability helps in getting long term services in software. In this row, authors of the present research are also trying to evaluate software durability of different alternatives, quantitatively. Software durability estimation can be done through attributes of durability and quality [6]. Additionally, assessment is a decision compelled with different attributes of it, therefore, software durability estimation is considered as a Multiple Criteria Decision Making (MCDM) problem. MCDM methods are eventually popular for assessing a decision with multiple criteria [7].
There are so many MCDM methods to resolve such kind of choice for building problems [7]. However, durability assessment is a crucial task. In this paper, the authors have used the Fuzzy-based Analytic Network Process (ANP) and Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) [8]. Further, many practitioners are using Fuzzy AHP-TOPSIS for assessment [9]. However, ANP is yet another widely employed method of the Analytic Hierarchy Process (AHP) practiced in MCDM problem [9]. AHP is based on hierarchy structure while the ANP is based on network structure. Both of these methods use arrangement of pair-wise comparisons to measure the weights of the criteria and to put the alternatives in the rank. In the AHP method, every attribute is independent of the other and created in a hierarchy, same as with the alternative. While in many real time cases, alternatives and attributes both depend on each other [9]. ANP does favor this approach and creates dependency. Hence, ANP can be used for such real time cases. Many practitioners have been using this method to solve their problems with the help of Fuzzy ANP.
Bijoyeta Roy et al. adopted MCDM approach of Fuzzy ANP-TOPSIS for software project selection [10]. This method helped in project decisions and ranked the alternatives in the priority-wise order to select the best among available options. Madjid Tavana et al. adopted Fuzzy ANP-TOPSIS in e-governance willingness for assessing a single attribute such as community [11]. Baozhu Li et al. adopted Fuzzy ANP methodology to evaluate the factors of computer security [12]. From the literature reviewed in this concern, we found that the Fuzzy-based symmetrical ANP-TOPSIS method is appropriate for assessing the critical criteria. For a more conclusive analysis on the same, we have also tried to evaluate the software durability through Fuzzy ANP-TOPSIS in this paper.
The rest of the paper is organized as follows: In Section 2, the paper describes the basics of software durability. Section 3 defines the methodology. With the help of Fuzzy ANP-TOPSIS, software durability is evaluated in Section 4. Comparisons of the results and sensitivity analysis have been enlisted in Section 5 of the paper, respectively. Finally, discussion and conclusions are given in Section 6.
2. Materials and Methods
2.1. Software Durability
Quality is a noteworthy element of software that tends to improve durability. Software quality can be evaluated using software durability. Hence, it becomes important for improvement of quality. Software quality development is not a one-time structure process; it is based on the maintenance of different aspects which include the adaptive and reuse engineering. Analysis of service life of the software relating to quality is the key point [13]. Considerable efforts for ensuring less maintenance are not done in the beginning of development. This creates problems for durable software and to mitigate them more maintenance process is followed. This further decreases the durability of software. Before buying any software, the user expects it to be durable and wants to invest in software that would give consistent services [5,13]. These expectations and the end users’ satisfaction leads to the optimal maintenance process, which further leads to software durability. Software durability is described as the service life of software with optimal maintenance.
An expert of both maintenance and durability, J. J Cusick talks in his book about problems in maintenance and durability [14]. The author states that there is a need to put more emphasis on issues related to durability and optimal maintenance. According to Cusick, the term software durability is somehow related to software serviceability, and it has been pointed out that achieving durability may enhance the serviceability of the software. Software durability is defined, “as the service of a software when it is working efficiently and effectively till the end user’s satisfaction or up to his/her expected duration” [5,14]. Thus, it appears that the priority is not just the software; it is elementally the durability of the software that should be the nodal focus. Software durability or longevity is directly or by implication associated with the administration life of the product. This discussion leads to the fact that durability is directly or indirectly involved in the progress of software and vice-versa.
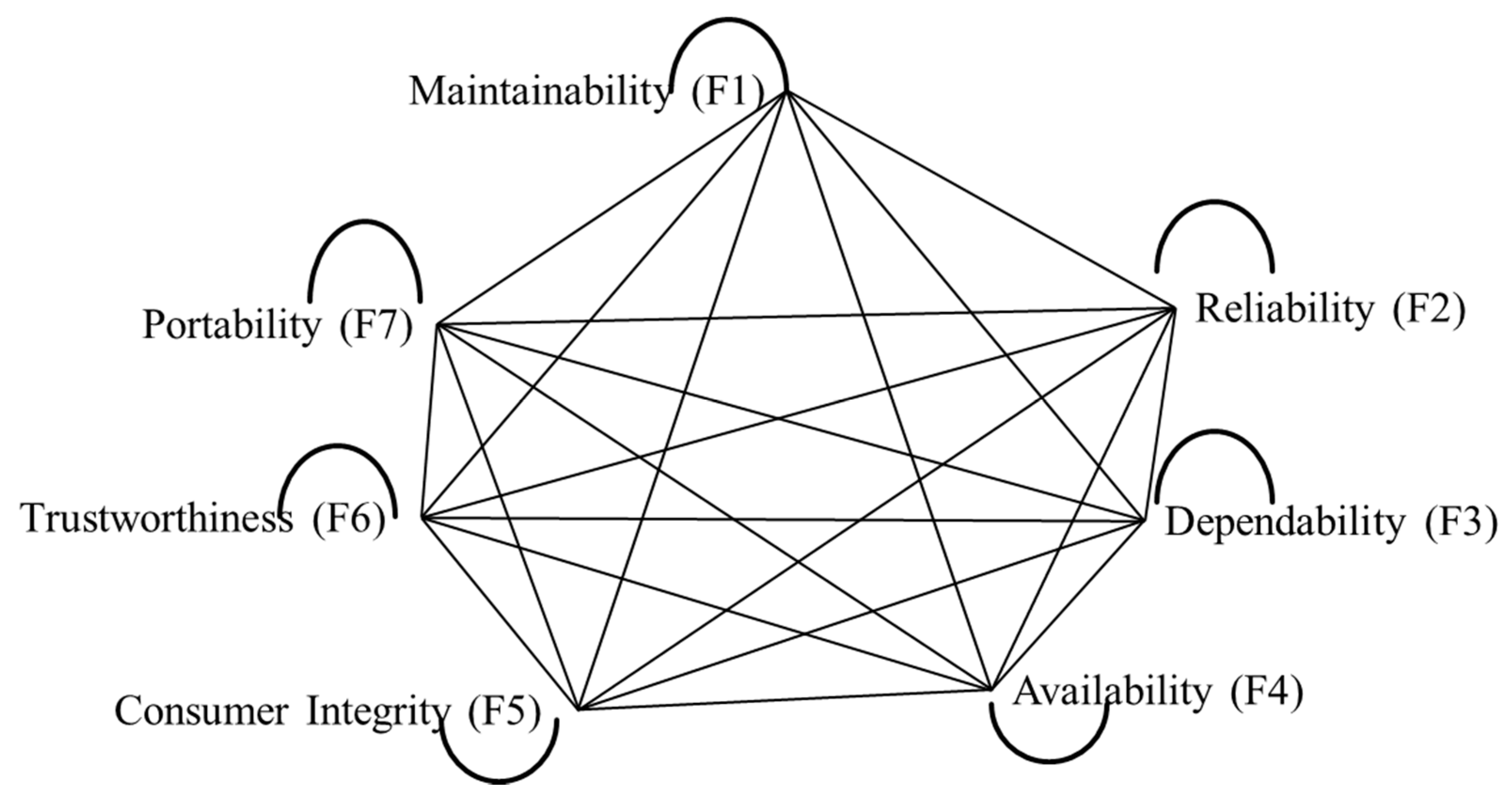
Defining a relationship between software’s characteristics and durability is a critical process. Some of the key attributes of software directly or indirectly help in achieving optimal maintenance. Durability is one of these attributes. Durability can also be called the longevity of software services [4,13]. The software durability is an important issue especially in the context of educational and banking sectors, etc. There are so many attributes of software and durability that are related to each other including trustworthiness, reliability, maintainability, portability, availability, dependability, consumer integrity, and usability [5,13]. The relationship between the attributes is shown in Figure 1.
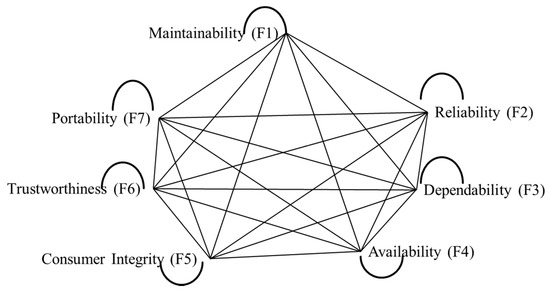
Figure 1.
Network Structure of Software Durability Attributes.
With the help of Figure 1, quality can be enhanced by bringing durability to it. Further, classification and identification of software durability attributes helps in assessing and improving durability during software development. The assessment process involves not only quantifying attributes of durability that contribute towards quality but also in identifying the most crucial attributes among them. Attributes of software durability are defined as:
Maintainability (F1) is the parameter concerned with how the system in use can be restored after a failure [15,16].
Reliability (F2) is defined as the capacity of software to continuously achieve what it is made for, according to its conditions [17].
Dependability (F3) is defined as the ability to distribute service for a long time [18].
Availability (F4) means the probability that a system is working for a given time, which further means the amount of time a software is actually operating [19].
Consumer Integrity (F5) is defined as managing the trustworthiness and accuracy of integrity of the user for expected duration in the life cycle of software [20].
Trustworthiness (F6) is the assurance that the software will perform as expected [21].
Portability (F7) is the ability of software to be easily carried or moved, which means easily maintainable [22].
In a nutshell, identifying, prioritizing, and evaluating the factors are a very critical process. Without it, the practitioners may not optimize the maintenance issues of a profitable and successful software product. To optimize maintenance issues, software durability plays a key role. Further, software durability and its attributes are always ambiguous and have multiple meanings; their description is often linguistic and vague. Moreover, it is recognized that an expert’s judgment is always imprecise. The usage of the fuzzy logic is recommended to model the uncertainties of experts’ preferences [19].
2.2. Fuzzy ANP-TOPSIS Method
After evaluating the problem of software durability assessment, it is found that this is a decision-making problem that has multiple criteria in the form of software durability attributes. Thus, in technical terms, software durability assessment relates to a multiple criteria decision-making problem. There are multiple methods to solve the problem of decision making [7]. MCDM method is also concerned with helping decision makers when they are confused with the same type of criteria [5]. The MCDM approach is very suitable to take two or more conflicting problems side by side. This work is using the Fuzzy ANP-TOPSIS for assessing the software durability. Further, ANP is in the form of a network, hence the relationship within each factor can be seen in this. The TOPSIS method results of the analysis in several research endeavours show that quality evaluation indicators positively affect the consequences of the assessment. Therefore, the choice of the particular attribute is very significant [19]. Thus, in this paper, we have used a fuzzy-based hybrid method of TOPSIS and ANP [7]. The step-by-step procedure for evaluating weightage and ranking through Fuzzy ANP-TOPSIS is specified as follows:
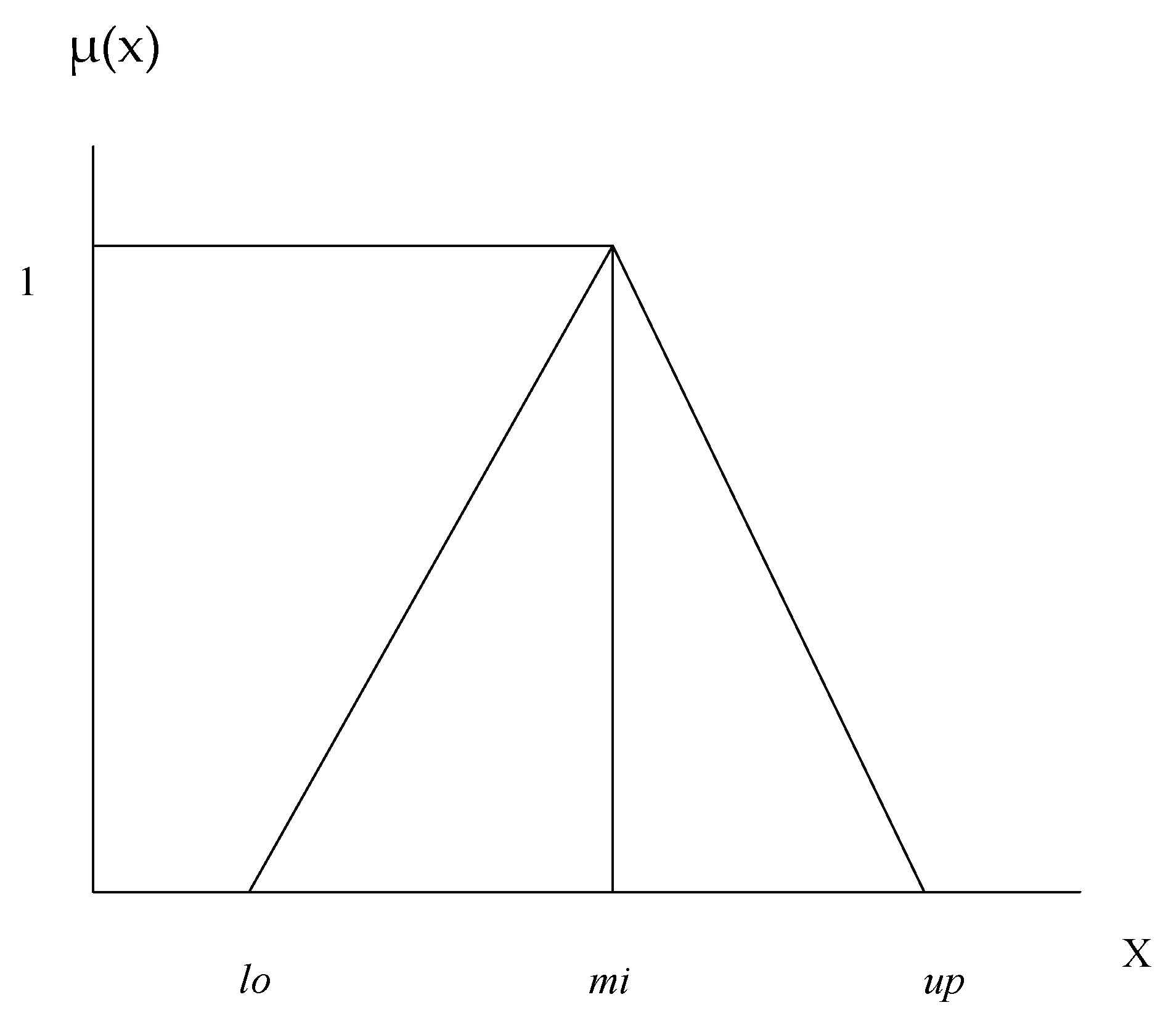
Step1: Defining Membership Function: There are multiple types of membership functions such as Gaussian, Trapezoidal, Triangular Fuzzy Numbers (TFN), etc., [18]. This research, in particular, is using the TFN as the membership functions and it lies between 0 and 1 [19]. Triangular Fuzzy Number can be well-defined as (lo, mi, up), where lo, mi, and up (lo ≤ mi ≤ up) are parameters indicating the smallest, middle value, and major value in the TFN, respectively. After taking the linguistic values, the authors have converted them into crisp numbers and Triangular Fuzzy Number (TFN). In addition, a fuzzy number O on g is called TFN, if its membership functions is given in Equations (1) and (2) as shown in Figure 2.
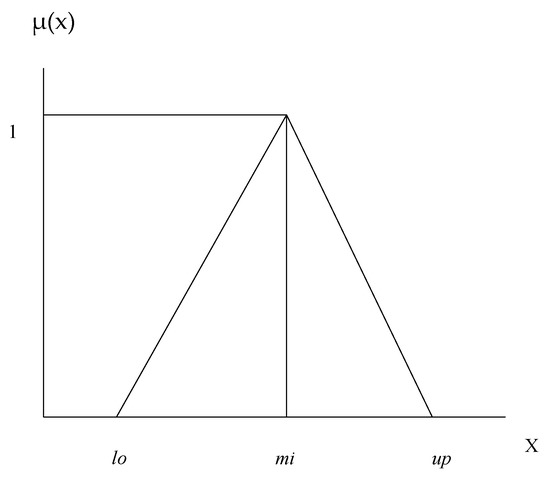
Figure 2.
Triangular Fuzzy Number.
Firstly, the opinions for every set of attributes of software durability and data related to this have been taken from 50 academicians and industry professionals who had rich experience in software maintenance and its service-oriented approach. For collating their perspectives, the experts were invited in a virtual meeting environment and were informed about the attributes with respect to different groups as well as the linguistic values through the scale. With the help of the collected data, authors accumulated a network structure for assessing the weights of software durability attributes. Experts of software development gave the responses by assigning scores to the attributes affecting each other in a measurable way according to scale, which is shown in Table 1 [20].

Table 1.
Linguistic terms and the corresponding TFNs.
The Equations (3)–(6) are used in converting the numeric values into Triangular Fuzzy Number (TFN) [20] and denoted as (loij, miij, upij) where, loij is lower value, miij is middle value, and upij is uppermost level values. Further, TFN [ηij] is established as the following:
where
and
In the above equations, Jijk shows the responses given by the experts d in comparative ways. Also, i and j represent a pair of attributes being judged by experts or practitioners. Value ηij i.e., TFN is calculated based on the geometric mean of the practitioner’s opinions. Further, Equations (7)–(9) help to aggregate the TFN values. Consider two TFNs, O1 and O2, O1 = (lo1, mi1, up1) and O2 = (lo2, mi2, up2). The fuzzy rules of operations on them are:
Step 2: Prepare the pair-wise comparison matrix by using the responses received from the decision makers. The calculation of the Consistency Index (CI) is done by using the formula in Equation (10) as follows:
where CI: Consistency Index and Q: is the number of compared elements, and λmax is the obtained eigenvalue.
The calculation of the Consistency Ratio (CR) is done by using a random index as given below:
where RI = random index (CI of the randomly generated pair-wise comparison matrix). Random index is derived from Saaty [9].
Step 3: After the construction of the comparison matrix, defuzzification is performed to produce a quantifiable value based on the calculated TFN values. The defuzzification method adopted in this work has been derived from [12] as formulated in Equations (12)–(14), which is commonly referred to as the alpha cut method.
where 0 ≤ α ≤ 1 and 0 ≤ β ≤ 1
Such that,
α and β in these equations are used for preferences of experts. These two values vary between 0 and 1.
Step 4: Next step is the formation of the super-matrix which is the result of the priority vector from the paired comparisons between groups including goal, criteria, sub-criteria, and alternatives.
Step 5: Determining the TOPSIS needs performance ranking in every alternative option over every normalized factor. The formula for this is as follows:
where is the performance ranking, and is the normalized factor with i = 1, 2, … m; and j = 1,2, …… n.
Next step is calculation of the Normalized Weighted Decision Matrix
where is the weight associated with the factor with i = 1, 2, … m and j = 1, 2, … n.
Step 6: Calculate the positive ideal solution R+ matrix and negative ideal solution R− matrix
where is Max sij if j is an advantage factor and Max sij if j is a cost factor; is Min sij if j is an advantage factor and Min sij if j is a cost factor.
Step 7: Next step is identifying the gap between the values of each option with the positive ideal solution matrix and negative ideal solution matrix:
Positive ideal solution:
Negative ideal solution:
where is the distance to the negative ideal solution for i option, and is the distance to the negative ideal solution.
Calculating the preference value for every alternative (gi).
where i = 1, 2, 3, … m
The abovementioned steps are to be followed to assess software durability using Fuzzy ANP TOPSIS method with different alternatives. The next section performs a case study and gives the numerical assessment to achieve software durability.
3. Data Analysis and Results
Generally, qualitative estimation is suitable for estimating software durability. It is difficult to evaluate the software durability quantitatively. At present, in order to gain profit from the market and fulfill the needs of maintenance-free software, the software durability plays an important role. To maximize software durability, the role of maintenance is crucially important. The challenge is to discover “what works today must be related to optimal maintenance and should improve the life span of software services” from both the practical and the theoretical point of views. Unfortunately, few attempts have been made for evaluating the software durability and balancing their trade-offs in meeting the desired software durability level. However, many practitioners are now trying to assess the life span of software or web applications [5,6,7]. Moreover, software durability factors also play a noteworthy role in the development process of software. Hence, the authors of this paper proposition a possible method for the assessment of software durability and recommend the Fuzzy ANP-TOPSIS. The assessment is as follows:
Firstly, the authors identified and categorized the durability factors that affect the software service life span. These factors have already been discussed in the previous sections. For assembling the data to estimate the software durability, this paper has taken the opinions of 50 experts who hail from academia as well as industry. This input aims to estimate the sustainable-security of web applications through the inputs of experts. With the help of Equations (1)–(11), triangular fuzzy numbers are evaluated. Table 2 shows the aggregated triangular fuzzy pair-wise comparison matrix. For defuzzification process, we used alpha-cut method that is shown in Equations (12)–(14). Table 3 shows the defuzzified pair-wise comparison matrix. Further, to evaluate the supermatrix, lower matrix and overall results, methods have been adopted [10]. Final weights and priority of the software durability are shown in Table 4.

Table 2.
Pair-Wise Comparison Matrix.

Table 3.
Defuzzification by using Alpha-Cut Method.

Table 4.
Global Weights of Software Durability Attributes.
This unit attempts to evaluate and estimate software durability through the subjective and objective assessment with a real-time example of a University’s software. Here, six successive versions of Web applications for Babasaheb Bhimrao Ambedkar University (A Central University), Lucknow, India, including A1, A2, A3 A4, A5, and A6 for projects have been taken to estimate the software durability. With the help of Equation (15), triangular fuzzy numbers are evaluated. Table 5 shows the subjective cognition results. With the help of Equations (16) and (17), Table 6 and Table 7 show the normalized and weighted normalized fuzzy-decision matrix, respectively. Finally, Table 8 shows the weighted normalized fuzzy-decision matrix. Closeness coefficients to the aspired level show in Table 8, with the help of Equations (18)–(20).

Table 5.
Subjective cognition results of evaluators in linguistic terms.

Table 6.
The normalized fuzzy-decision matrix.

Table 7.
The weighted normalized fuzzy-decision matrix.

Table 8.
Closeness coefficients to the aspired level among the different alternatives.
defines the Satisfaction degree in the i-th alternative. Table 8 shows the overall gap degree as rated between good and very good. Hence, the durability of software with respect to different alternatives is in good condition according to the case study.
Thus, it can be concluded from the above results that application of Fuzzy ANP TOPSIS for software durability in the case study of web applications for Babasaheb Bhimrao Ambedkar University (A Central University), Lucknow, India, is compatible and gives precise results. The closeness coefficients show that durability of Alternative 2 is the highest among the six alternatives.
4. Sensitivity Analysis
For validating the results obtained by the projected technique in this research article, the authors of this study conducted a sensitivity analysis [21]. Sensitivity analysis provides clarity in the derived results and validates the calculated results through numeric calculation. Authors have conducted the sensitivity analysis on calculated weights. In the proposed study, six alternatives are taken by the authors in hierarchy so the sensitivity analysis will also be performed on six alternatives. Table 9 illustrates the results of sensitivity analysis.

Table 9.
Sensitivity Analysis.
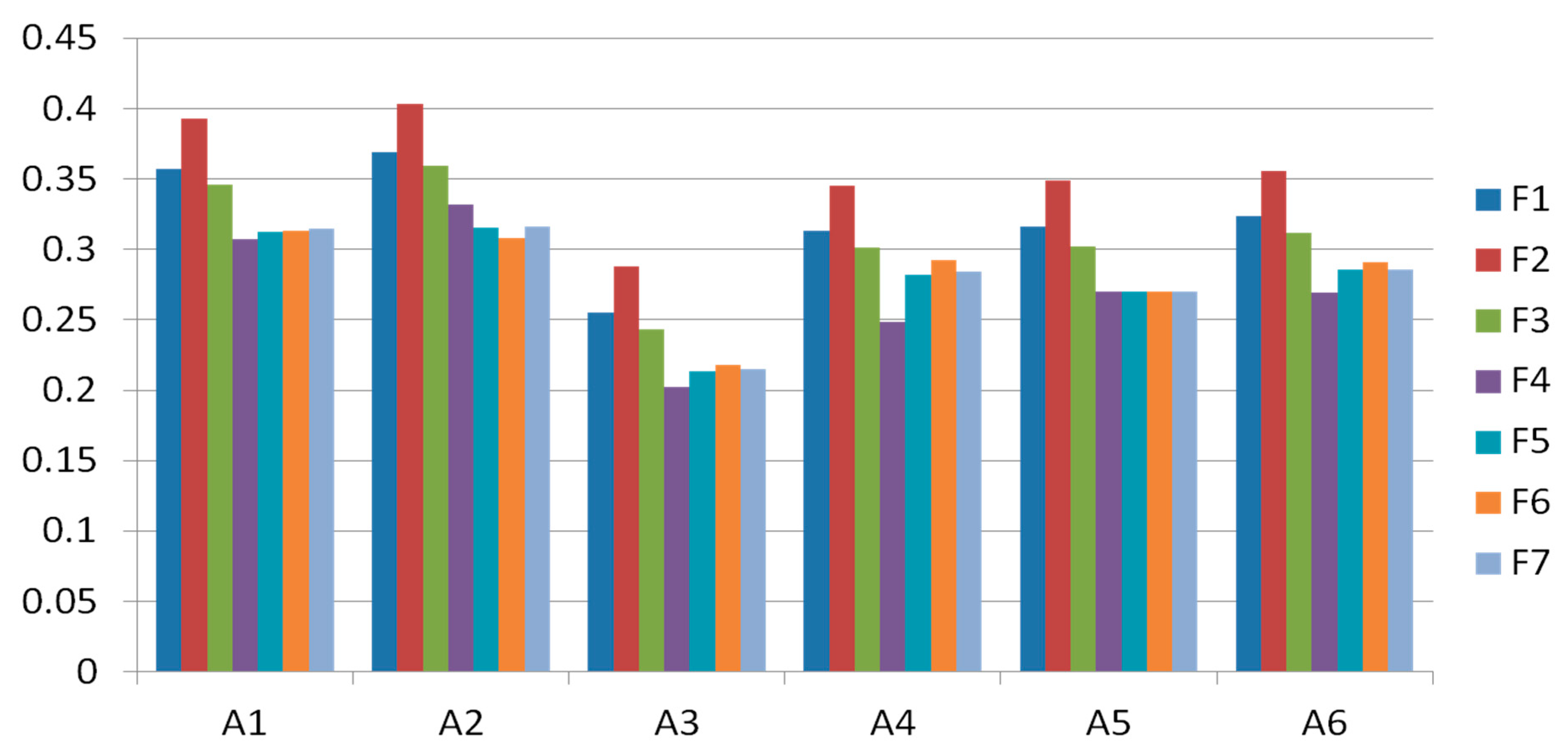
Through Table 10 and Figure 3, it is clearly evident that factor 2 has the highest value in all the factors. The first row of Table 10 and Figure 3 show the original weights of factors. Through the calculated results of sensitivity analysis, the authors can say that factor still has the same highest value in all the alternatives. This type of result portrays that the ratings of the alternatives are sensitive to weights.

Table 10.
Comparison through classical ANP-TOPSIS technique.
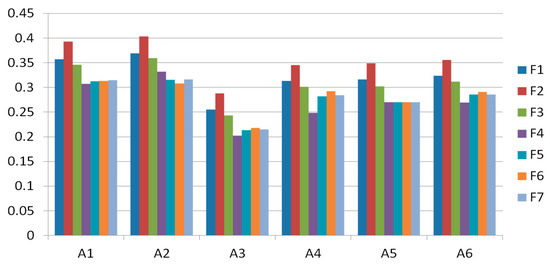
Figure 3.
Graphical representation of sensitivity analysis.
5. Comparisons between Obtained Results and Previous Work
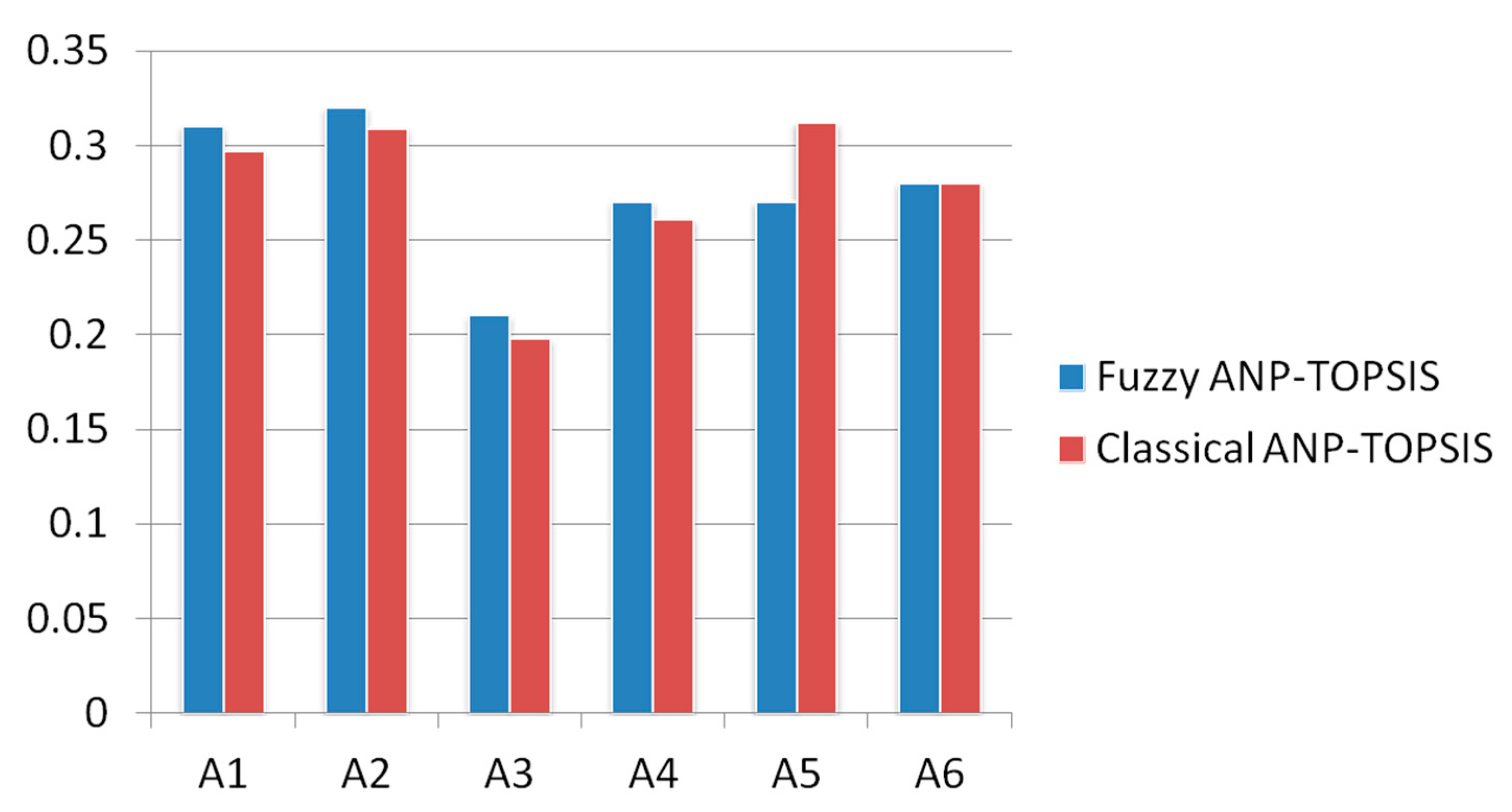
Variety in analysis techniques can be a conclusive means to establish whether the analyzed result and projected technique is better or not. Authors of this study have compared the results of the classical ANP-TOPSIS methodology [16] with the results of fuzzy ANP-TOPSIS technique to gauge the affectivity of the proposed methodology. The result obtained through the Classical ANP-TOPSIS technique is the same as the result achieved through fuzzy ANP-TOPSIS techniques. The only difference is in the case of fuzzification and defuzzification process. In fuzzy ANP-TOPSIS methodology, the numbers are later converted into the fuzzy numbers for fuzzification and defuzzification process. In the classical ANP-TOPSIS, the process uses original values for evaluation. Table 10 and Figure 4 describe the comparison through tabular and graphical view.
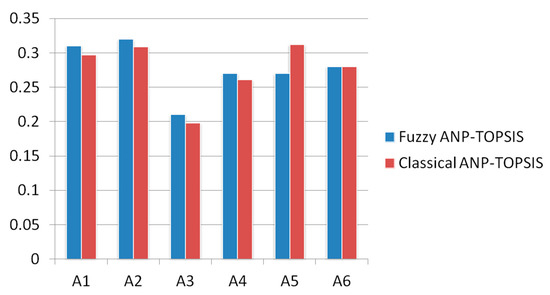
Figure 4.
Graphical representation of comparison.
From the results of Table 10 it is evident that the results obtained by fuzzy ANP TOPSIS are more efficient than the results obtained by using classical ANP TOPSIS. This is because of the usage of fuzzy environment with the hybridization of ANP and TOPSIS. Therefore, employing the hybrid method of Fuzzy ANP TOPSIS is more efficacious than the classical approach.
Several research endeavors have defined durability of software. Furthermore, some of the research initiatives have also evaluated security-durability from different perspectives [5,6,16]. However, there is no single research on software durability assessment, quantitatively. In 2016, V. Bartlett et al. addressed the relationship between durability and reliability with respect to the design experience of the user [22]. According to Bartlett, reliability and durability are also critical for the longer service life of the user-friendly applications. In addition, in 2016, R. Kumar et al. defined the durability challenges in software engineering. These studies classified the durability attributes theoretically. In 2015, Kelty C. et al. explained the role of software in computer prices and how long-lasting software affects the cost of computers [4]. They indicated that the software design process also needs to be changed for better user experience. In a similar context, in 1994, Thomas R. discussed that a long life cycle of software is required to increase user satisfaction [23]. He also addressed the fact that due to high-maintenance costs and time involved, practitioners compromise on quality design during software development.
6. Conclusions
Designing an efficient, user friendly, cost-effective, and durable software that requires minimum investments in maintenance would be an ideal package for any software developing organization. Ironically, though companies want maintenance free software, they often overlook the most crucial aspect which is the thorough and accurate estimation of the software’s durability. This forces the developers to adapt quick fix techniques at times, which subsequently makes the maintenance harder. It is a challenge to estimate the durability of software before its deployment. The main cause of software failure is the focus on less maintainability rather than improving durability. To enhance the working life/ service life of software for better understanding of maintenance issues, the practitioners must focus on the software design and its durability.
The knowledge gained from the above study would be instrumental in the following:
The assessment of software durability is helpful in economizing on both the time and cost incurred in software maintenance after its deployment.
This work will help the developers to think of more avenues to increase the durability of software with its assessment.
Assessment has been done with different alternatives in this study, and it was found that trustworthiness is the highest priority attribute. Hence, it is conclusively stated that trustworthiness should be given the utmost focus for improving the durability of software.
This research proposes a novel idea of Fuzzy ANP-TOPSIS for software durability evaluation. According to different studies, 75% of the overall cost for project development is spent only on maintenance. Increasing the life-span of software will significantly reduce the investment done on maintenance, which is the demand of this era.
Author Contributions
S.A.K. and M.A. contributed to the motivation, the interpretation of the method effects and the results. A.A. proposed minor suggestions. R.K. and R.A.K. provided the concept, prepared the draft versions, performed the evaluation and extracted the conclusions. A.A. and R.A.K. supervised the study. All authors have read and agreed to the published version of the manuscript.
Funding
College of Computer and Information Sciences, Prince Sultan University, Saudi Arabia.
Acknowledgments
Authors are grateful to the College of Computer and Information Sciences, Prince Sultan University for providing the funds to undertake this research study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tekinerdoğan, B.; Sözer, H.; Aksit, M. Software architecture reliability analysis using failure scenarios. J. Syst. Softw. 2008, 81, 558–575. [Google Scholar] [CrossRef]
- Bøegh, J. A New Standard for Quality Requirements. IEEE Softw. 2008, 25, 57–63. [Google Scholar] [CrossRef]
- Barnett, T. Cisco Global Cloud Index 2015–2020. Available online: https://www.cisco.com/c/dam/m/en_us/service-provider/ciscoknowledgenetwork/files/622_11_15-16-Cisco_GCI_CKN_2015-2020_AMER_EMEAR_NOV2016.pdf (accessed on 15 January 2020).
- Kelty, C.; Erickson, S. The Durability of Software; Meson Press: Lüneburg, Germany, 2015; Volume 1, pp. 1–13. [Google Scholar]
- Agrawal, A.; Zarour, M.; Alenezi, M.; Kumar, R.; Khan, R.A. Security durability assessment through fuzzy analytic hierarchy process. Peer J. Comput. Sci. 2019, 5, e215. [Google Scholar] [CrossRef]
- Kumar, R.; Khan, S.A.; Khan, R.A. Revisiting Software Security: Durability Perspective. Int. J. Hybrid Inf. Technol. 2015, 8, 311–322. [Google Scholar] [CrossRef]
- Triantaphyllou, E.; Shu, B.; Sanchez, S.N.; Ray, T. Multi-criteria decision making: an operations research approach. Encycl. Electr. Electron. Eng. 1998, 15, 175–186. [Google Scholar]
- Ertuğrul, I.; Karakaşoğlu, N. Comparison of fuzzy AHP and fuzzy TOPSIS methods for facility location selection. Int. J. Adv. Manuf. Technol. 2007, 39, 783–795. [Google Scholar] [CrossRef]
- Saaty, T.L. Analytic network process. Encycl. Oper. Res. Manag. Sci. 2001, 1, 28–35. [Google Scholar] [CrossRef]
- Bijoyeta, R.; Santanu, K.M. An Integrated Fuzzy ANP and TOPSIS Methodology for Software Selection under MCDM Perspective. Int. J. Innov. Res. Comput. Commun. Eng. 2018, 6, 492–501. [Google Scholar]
- Tavana, M.; Zandi, F.; Katehakis, M.N. A hybrid fuzzy group ANP–TOPSIS framework for assessment of e-government readiness from a CiRM perspective. Inf. Manag. 2013, 50, 383–397. [Google Scholar] [CrossRef]
- Li, B.Z.; Bi, R. The Application of Fuzzy-ANP in Evaluation Index System of Computer Security. Key Eng. Mater. 2010, 439, 754–759. [Google Scholar] [CrossRef]
- Kumar, R.; Khan, S.A.; Khan, R.A. Durability challenges in software engineering. Cross. J. Def. Softw. Eng. 2016, 29–31. [Google Scholar]
- Cusick, J.J. Durable Ideas in Software Engineering: Concepts, Methods and Approaches from my Virtual Toolbox; Bentham Science Publishers: Sharjah, UAE, 2013; Available online: https://www.amazon.com/Durable-Ideas-Software-Engineering-Approaches-ebook/dp/B00E7TCBEI (accessed on 15 January 2020).
- Available online: https://www.igi-global.com/dictionary/markovian-reliability-in-multiple-agv-system/25011 (accessed on 15 January 2020).
- Kumar, R.; Zarour, M.; Alenezi, M.; Agrawal, A.; Khan, R.A. Measuring Security Durability of Software through Fuzzy-Based Decision-Making Process. Int. J. Comput. Intell. Syst 2019, 12, 627–642. [Google Scholar] [CrossRef]
- Avizienis, A.; Laprie, J.C.; Randell, B. Fundamental Concepts of Dependability; University of Newcastle upon Tyne: Newcastle, UK, 2001; pp. 7–12. [Google Scholar]
- Available online: https://www.sebokwiki.org/wiki/Reliability,_Availability,_and_Maintainability (accessed on 15 January 2020).
- Wang, C.-N.; Van Thanh, N.; Su, C.-C. The Study of a Multicriteria Decision Making Model for Wave Power Plant Location Selection in Vietnam. Processes 2019, 7, 650. [Google Scholar] [CrossRef]
- Kahraman, C. Fuzzy Multi-Criteria Decision Making: Theory and Applications With Recent Developments; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 16. [Google Scholar]
- Gupta, H.; Razavi, S. Challenges and Future Outlook of Sensitivity Analysis. In Sensitivity Analysis in Earth Observation Modelling; Elsevier BV: Amsterdam, The Netherlands, 2017; pp. 397–415. [Google Scholar]
- Bartlett, E.V.; Simpson, S. Durability and Reliability, Alternative Approaches to Assessment of Component Performance over Time. Available online: https://www.irbnet.de/daten/iconda/CIB8616.pdf (accessed on 18 February 2020).
- Thomas, R. Durable, Low Cost Educational Software. In Computer Assisted Learning: Selected Contributions from the Cal’93 Symposium; Pergamon Press: Elmsford, NY, USA, 1994; pp. 65–72. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).