Thermogravitational Convection of Hybrid Nanofluid in a Porous Chamber with a Central Heat-Conducting Body
Abstract
:1. Introduction
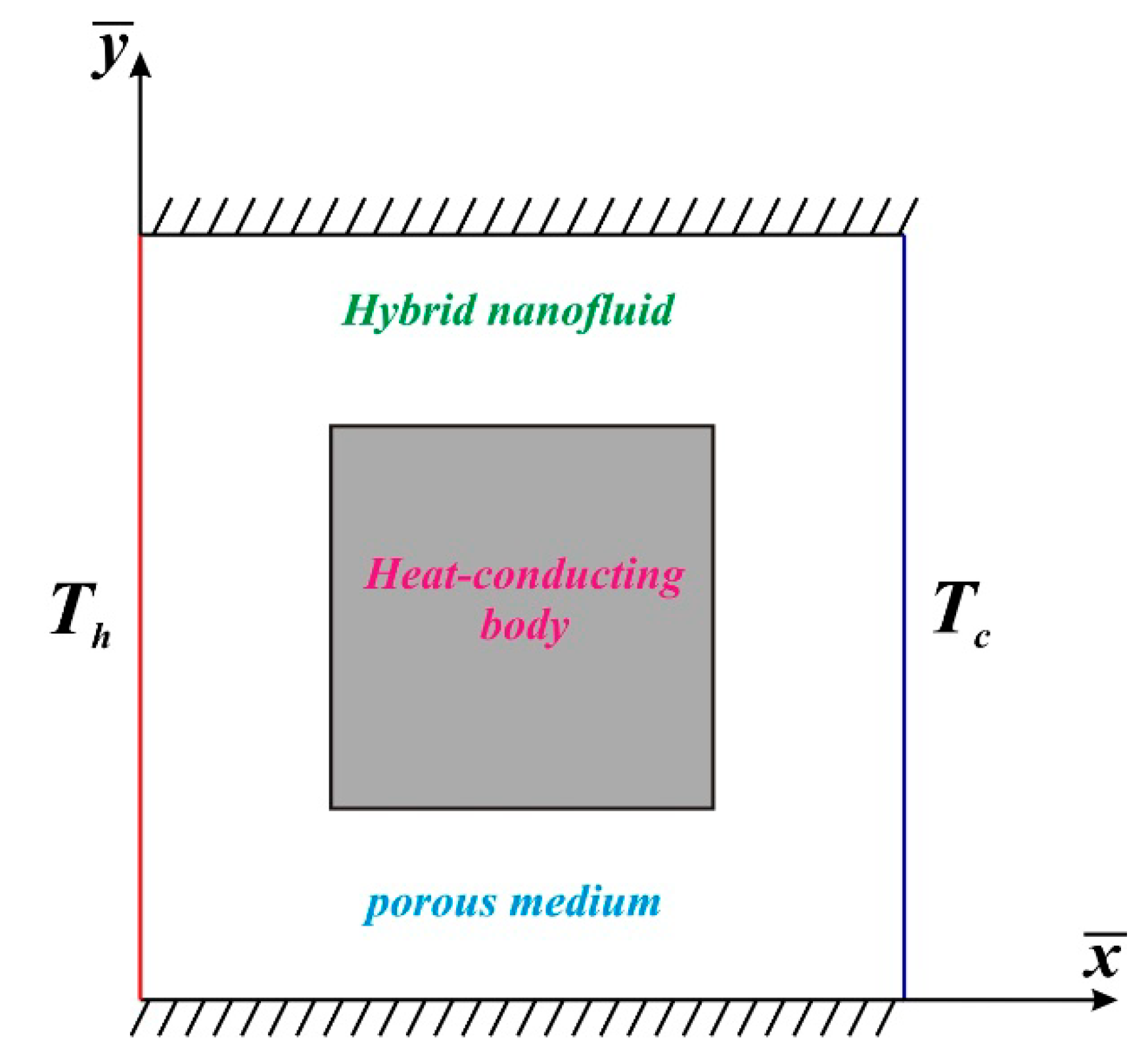
2. Control Equations and Conditions
- hybrid nanosuspension density,
- hybrid nanofluid buoyancy coefficient
- hybrid nanofluid heat capacitance
- hybrid nanofluid thermal conductivity
- hybrid nanofluid viscosity
- porous medium thermal conductivity saturated with hybrid nanofluid
- and porous medium heat capacity ratio
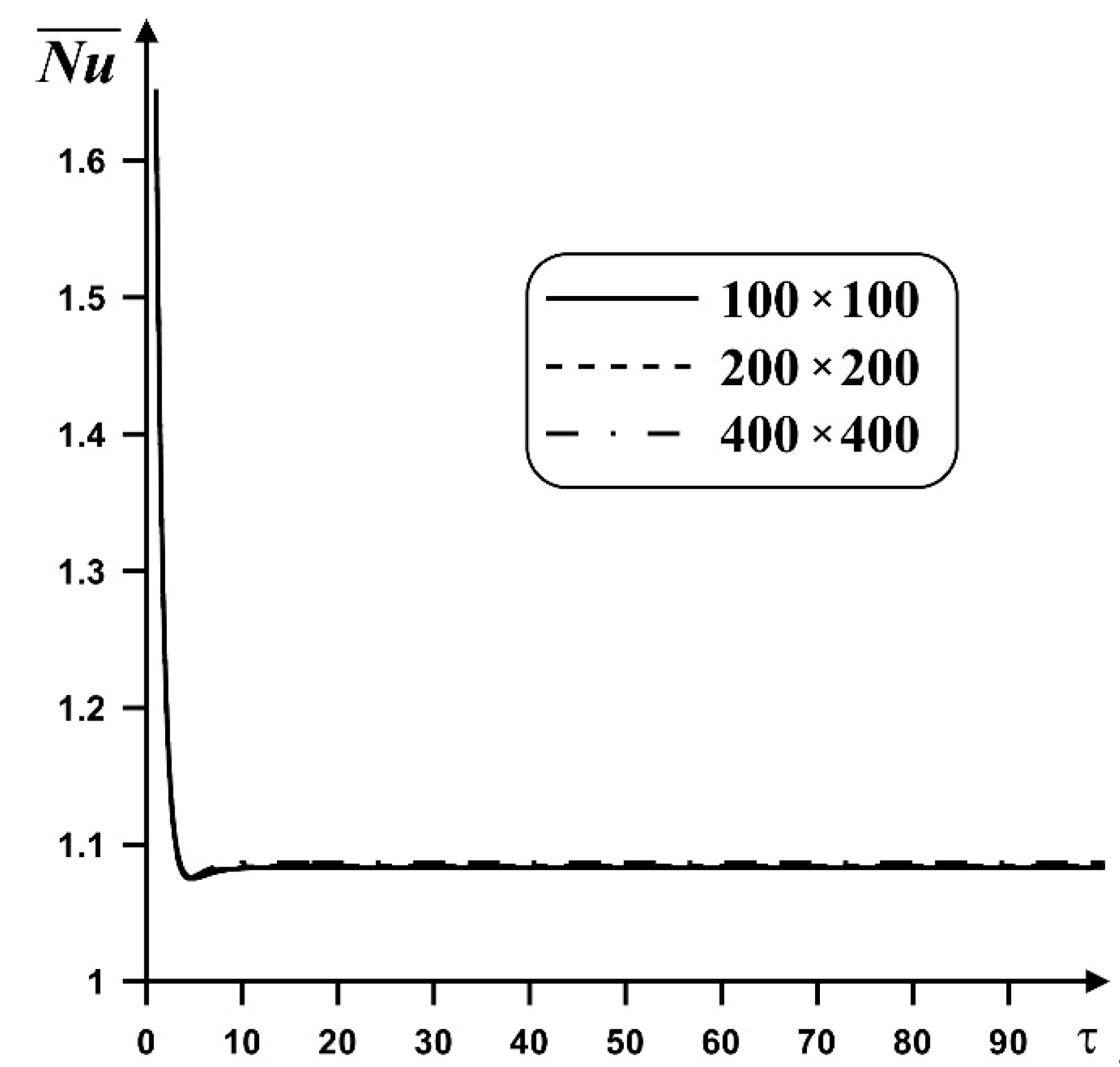
3. Computational Technique and Validation
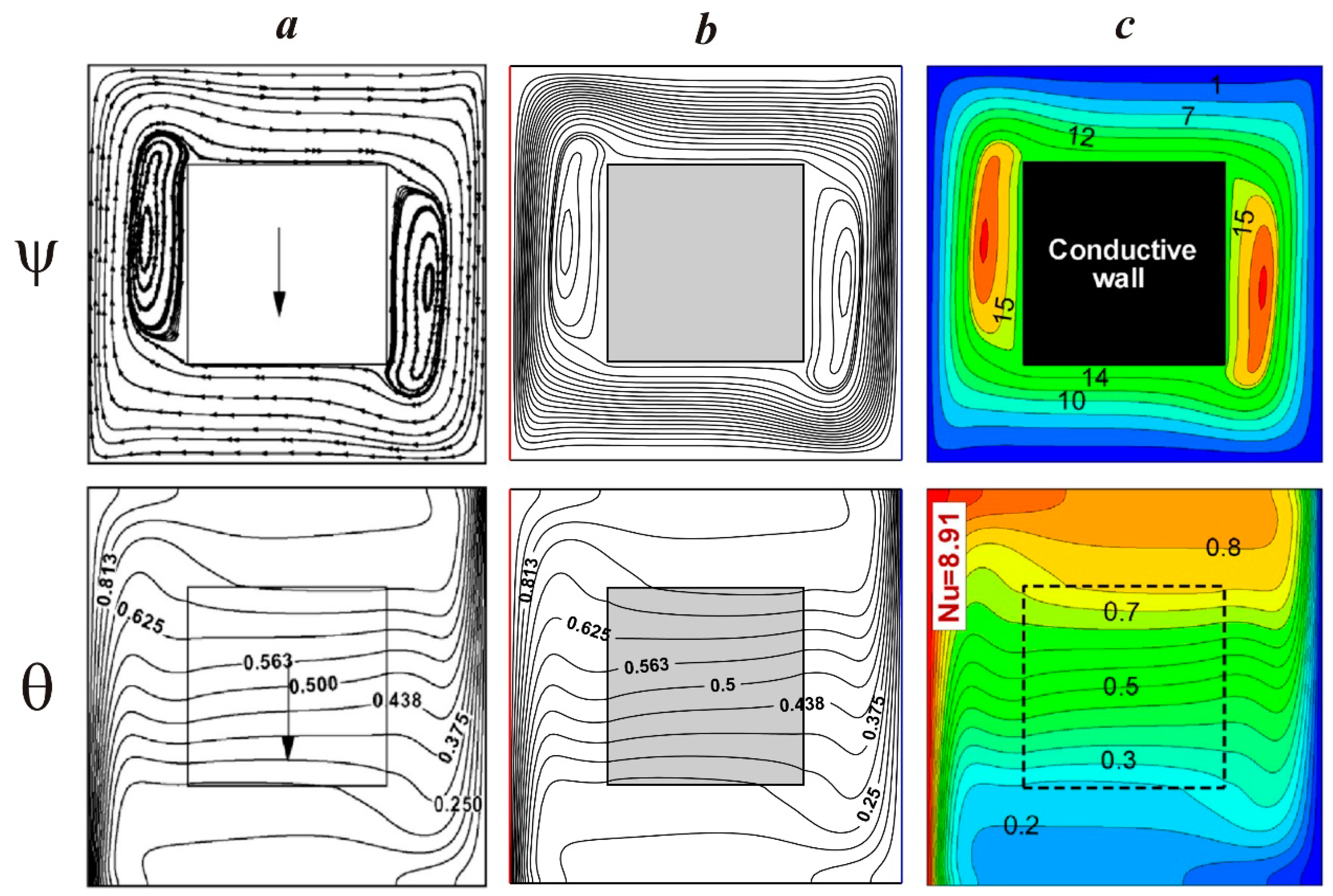
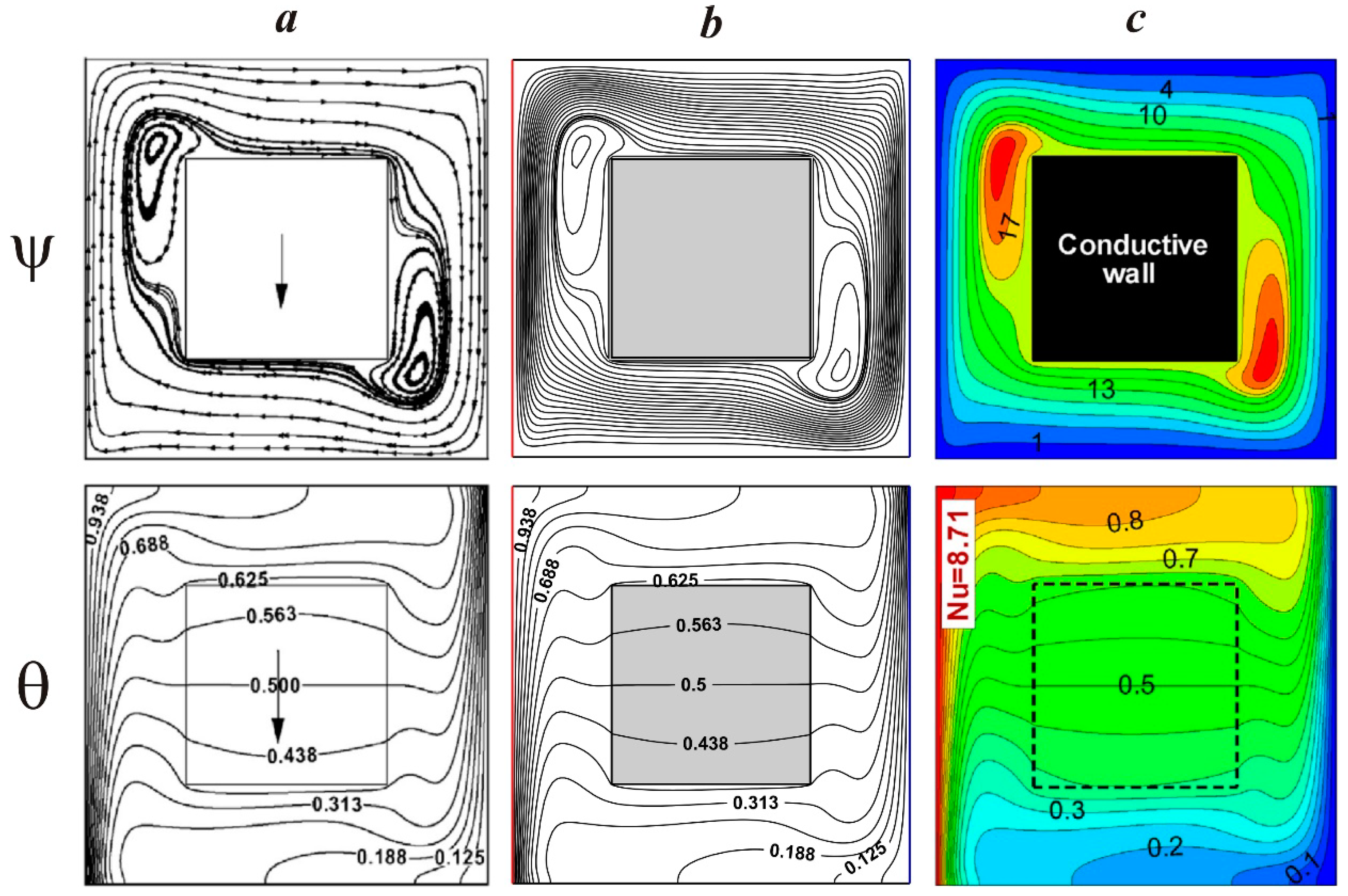
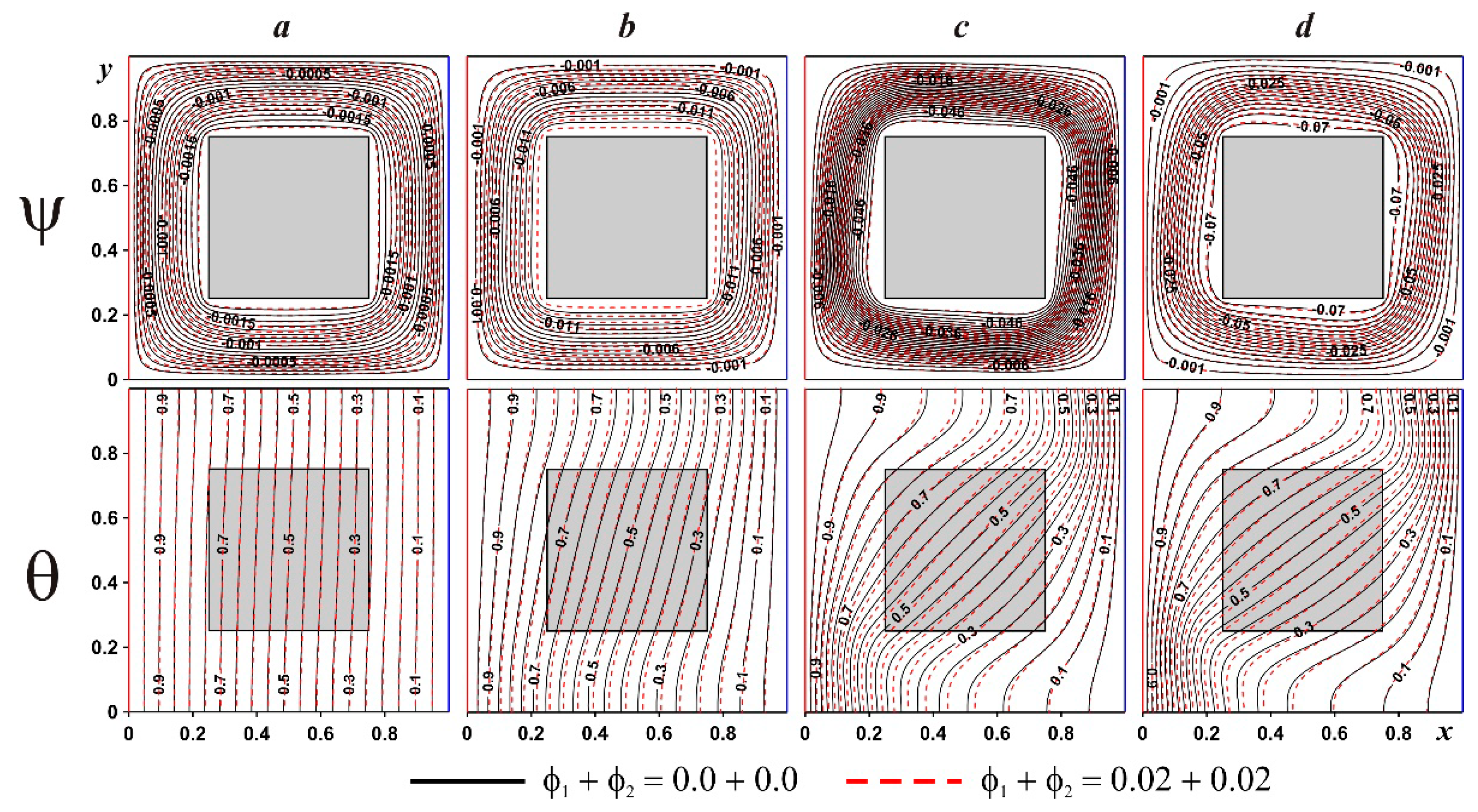
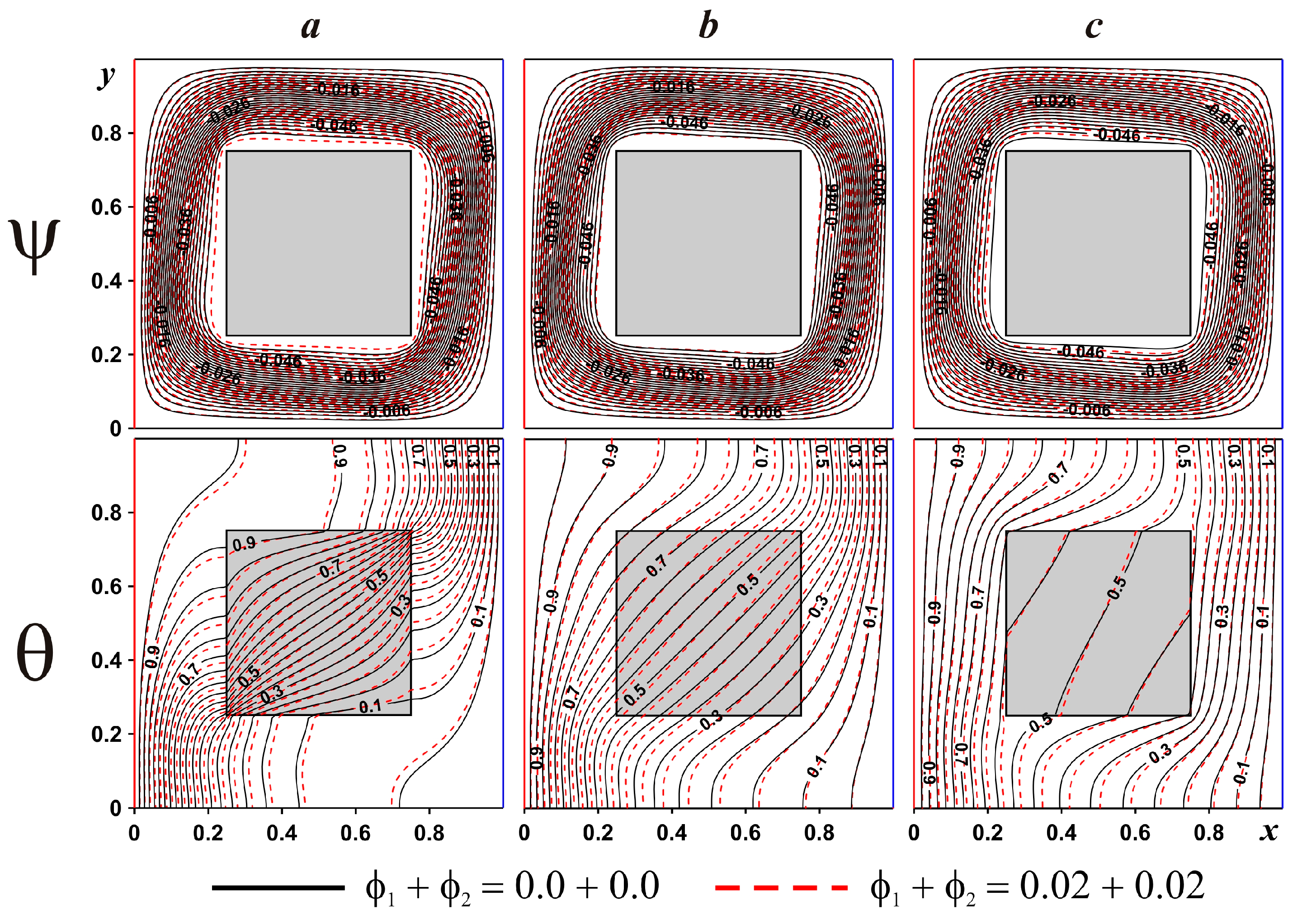
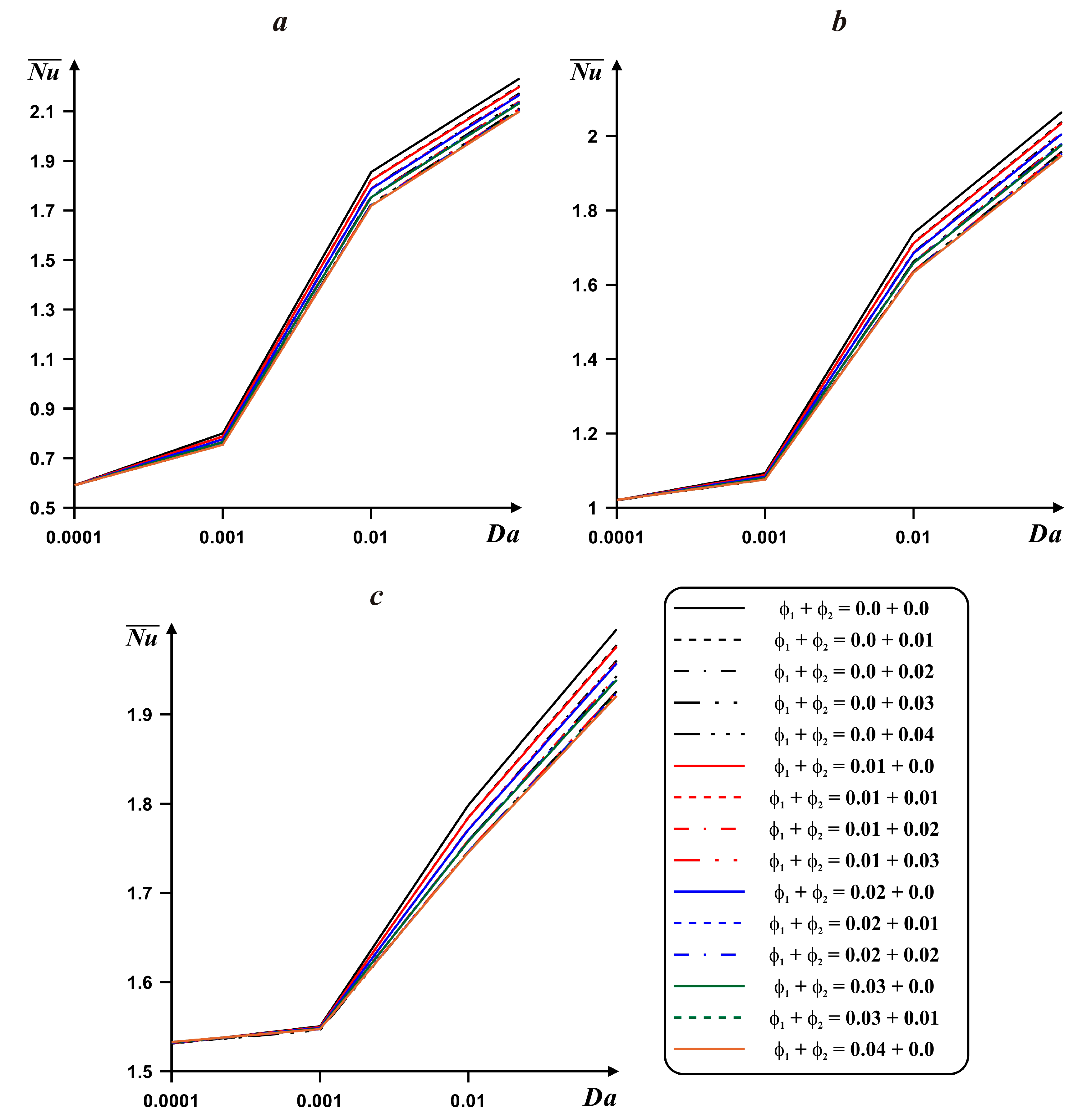
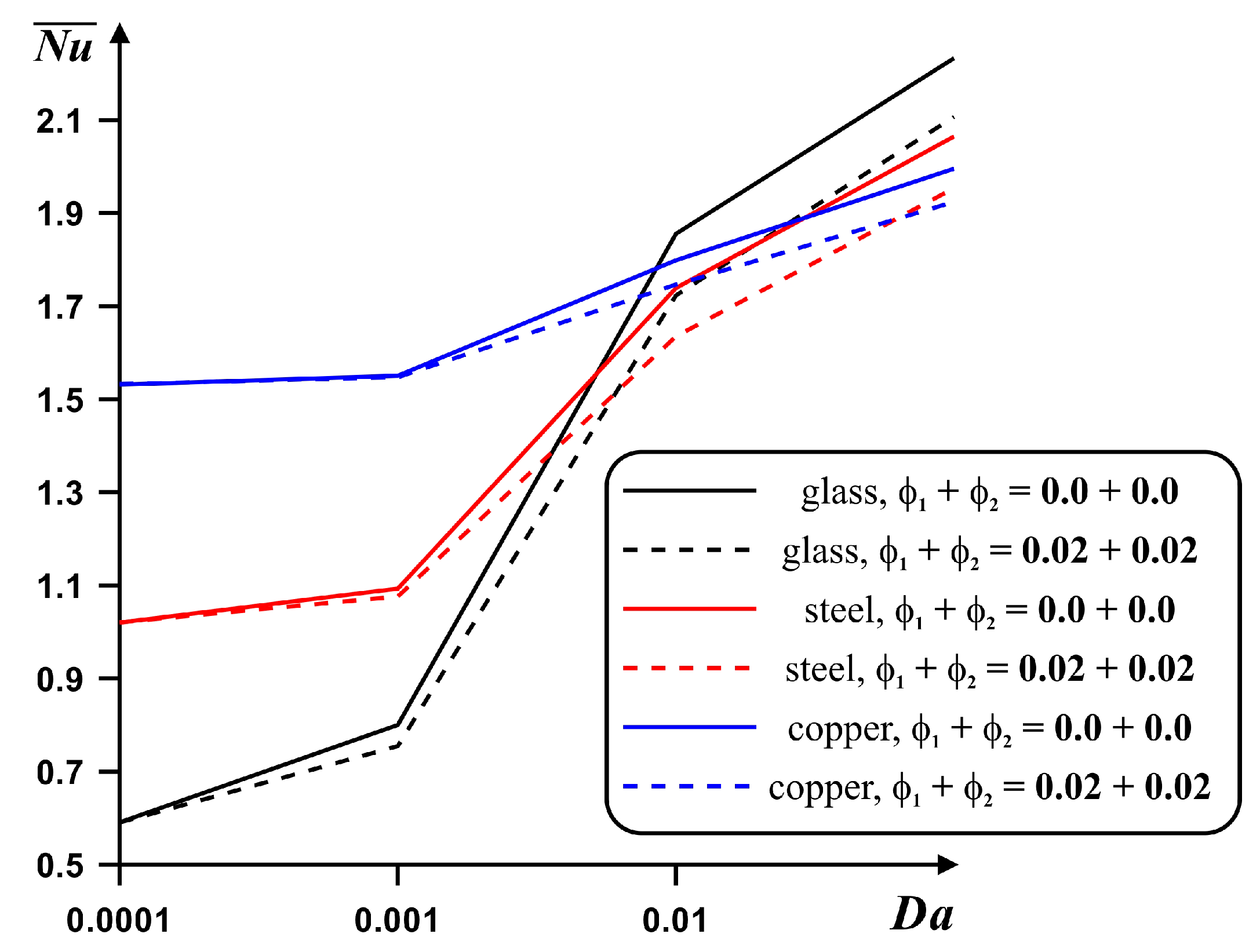
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Izadi, S.; Armaghani, T.; Ghasemiasl, R.; Chamkha, A.J.; Molana, M. A comprehensive review on mixed convection of nanofluids in various shapes of enclosures. Powder Technol. 2019, 343, 880–907. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the 1995 ASME International Mechanical Engineering Congress and Exposition, FED 231/MD, San Francisco, CA, USA, 12–17 November 1955; Volume 6, pp. 99–105. [Google Scholar]
- Das, S.K.; Choi, S.U.S.; Yu, W.; Pradeep, Y. Nanofluids: Science and Technology; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Minkowycz, W.J.; Sparrow, E.M.; Abraham, J.P. Nanoparticle Heat Transfer and Fluid Flow; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Shenoy, A.; Sheremet, M.; Pop, I. Convective Flow and Heat Transfer from Wavy Surfaces: Viscous Fluids, Porous Media and Nanofluids; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media, 5th ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Ambreen, T.; Kim, M.-H. Influence of particle size on the effective thermal conductivity of nanofluids: A critical review. Appl. Energy 2020, 264, 114684. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Hassan Kamyab, M.; Valadkhani, M. Application of nanofluids and fluids in photovoltaic thermal system: An updated review. Sol. Energy 2020, 199, 796–818. [Google Scholar] [CrossRef]
- Pandya, N.S.; Shah, H.; Molana, M.; Tiwari, A.K. Heat transfer enhancement with nanofluids in plate heat exchangers: A comprehensive review. Eur. J. Mech./B Fluids 2020, 81, 173–190. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ghazvini, M.; Sadeghzadeh, M.; Nazari, M.A.; Ghalandari, M. Utilization of hybrid nanofluids in solar energy applications: A review. Nano-Struct. Nano-Objects 2019, 20, 100386. [Google Scholar] [CrossRef]
- Pordanjani, A.H.; Aghakhani, S.; Afrand, M.; Mahmoudi, B.; Mahian, O.; Wongwises, S. An updated review on application of nanofluids in heat exchangers for saving energy. Energy Convers. Manag. 2019, 198, 111886. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estelle, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Siavashi, M.; Taylor, R.A.; Niazmand, H.; et al. Recent advances in modeling and simulation of nanofluid flows—Part I: Fundamentals and theory. Phys. Rep. 2019, 790, 1–48. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estelle, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Taylor, R.A.; Abu-Nada, E.; Rashidi, S.; et al. Recent advances in modeling and simulation of nanofluid flows—Part II: Applications. Phys. Rep. 2019, 791, 1–59. [Google Scholar] [CrossRef]
- Keshteli, A.N.; Sheikholeslami, M. Nanoparticle enhanced PCM applications for intensification of thermal performance in building: A review. J. Mol. Liq. 2019, 274, 516–533. [Google Scholar] [CrossRef]
- Groşan, T.; Sheremet, M.A.; Pop, I. Heat transfer enhancement in cavities filled with nanofluids. In Advances Heat Transfer Fluids: From Numerical to Experimental Techniques; Minea, A.A., Ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 267–284. [Google Scholar]
- Sajid, M.U.; Ali, H.M. Recent advances in application of nanofluids in heat transfer devices: A critical review. Renew. Sustain. Energy Rev. 2019, 103, 556–592. [Google Scholar] [CrossRef]
- Ranga Babu, J.A.; Kiran Kumar, K.; Srinivasa Rao, S. State-of-art review on hybrid nanofluids. Renew. Sustain. Energy Rev. 2017, 77, 551–565. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Hybrid nanofluids for heat transfer applications—A state of the art review. Int. J. Heat Mass Transf. 2018, 125, 82–103. [Google Scholar] [CrossRef]
- Huminic, G.; Huminic, A. Entropy generation of nanofluid and hybrid nanofluid flow in thermal systems: A review. J. Mol. Liq. 2020, 302, 112533. [Google Scholar] [CrossRef]
- Salman, S.; Abu Talib, A.R.; Saadon, S.; Hameed Sultan, M.T. Hybrid nanofluid flow and heat transfer over backward and forward steps: A review. Powder Technol. 2020, 363, 448–472. [Google Scholar] [CrossRef]
- Devi, S.U.; Devi, S.A. Numerical investigation of three-dimensional hybrid Cu–Al2O3/water nanofluid flow over a stretching sheet with effecting Lorentz force subject to Newtonian heating. Can. J. Phys. 2016, 94, 490–496. [Google Scholar] [CrossRef]
- Devi, S.U.; Devi, S.A. Heat transfer enhancement of Cu–Al2O3/water hybrid nanofluid flow over a stretching sheet. J. Niger. Math. Soc. 2017, 36, 419–433. [Google Scholar]
- Sarkar, J.; Ghosh, P.; Adil, A. A review on hybrid nanofluids: Recent research, development and applications. Renew. Sustain. Energ. Rev. 2015, 43, 164–177. [Google Scholar] [CrossRef]
- Akilu, S.; Sharma, K.V.; Baheta, A.T.; Mamat, R. A review of thermophysical properties of water based composite nanofluids. Renew. Sustain. Energ. Rev. 2016, 66, 654–678. [Google Scholar] [CrossRef] [Green Version]
- Sidik, N.A.; Adamu, I.M.; Jamil, M.M.; Kefayati, G.H.; Mamat, R.; Najafi, G. Recent progress on hybrid nanofluids in heat transfer applications: A comprehensive review. Int. Commun. Heat Mass Transf. 2016, 78, 68–79. [Google Scholar] [CrossRef]
- Sundar, L.S.; Sharma, K.V.; Singh, M.K.; Sousa, A.C. Hybrid nanofluids preparation, thermal properties, heat transfer and friction factor—A review. Renew. Sustain. Energ. Rev. 2017, 68, 185–198. [Google Scholar] [CrossRef]
- Hayat, T.; Nadeem, S. Heat transfer enhancement with Ag–CuO/water hybrid nanofluid. Results Phys. 2017, 7, 2317–2324. [Google Scholar] [CrossRef]
- Yousefi, M.; Dinarvand, S.; Yazdi, M.E.; Pop, I. Stagnation-point flow of an aqueous titania-copper hybrid nanofluid toward a wavy cylinder. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 1716–1735. [Google Scholar] [CrossRef]
- Sajid, M.U.; Ali, H.M. Thermal conductivity of hybrid nanofluids: A critical review. Int. J. Heat Mass Transf. 2018, 126, 211–234. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Miroshnichenko, I.V.; Sheremet, M.A. Numerical analysis of unsteady conjugate natural convection of hybrid water-based nanofluid in a semicircular cavity. J. Therm. Sci. Eng. Appl. 2017, 9, 041004. [Google Scholar] [CrossRef]
- Izadi, M.; Mohebbi, R.; Karimi, D.; Sheremet, M.A. Numerical simulation of natural convection heat transfer inside a ┴ shaped cavity filled by a MWCNT-Fe3O4/water hybrid nanofluids using LBM. Chem. Eng. Process. Process Intensif. 2018, 125, 56–66. [Google Scholar] [CrossRef]
- Izadi, M.; Oztop, H.F.; Sheremet, M.A.; Mehryan, S.A.M.; Abu-Hamdeh, N. Coupled FHD-MHD free convection of a hybrid nanoliquid in an inversed T-shaped enclosure occupied by partitioned porous media. Numer. Heat Transf. A 2019, 76, 479–498. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Synthesis of Al2O3–Cu/water hybrid nanofluids using two step method and its thermo physical properties. Colloid. Surf. A-Phys. Eng. Asp. 2011, 388, 41–48. [Google Scholar] [CrossRef]
- Suresh, S.; Venkitaraj, K.P.; Selvakumar, P.; Chandrasekar, M. Effect of Al2O3–Cu /water hybrid nanofluid in heat transfer. Exp. Therm. Fluid Sci. 2012, 38, 54–60. [Google Scholar] [CrossRef]
- Soltani, O.; Akbari, M. Effects of temperature and particles concentration on the dynamic viscosity of MgO-MWCNT/ethylene glycol hybrid nanofluid: Experimental study. Phys. E Low Dimens. Syst. Nanostruct. 2016, 84, 564–570. [Google Scholar] [CrossRef]
- Leong, K.Y.; Ahmad, K.K.; Ong, H.C.; Ghazali, M.J.; Baharum, A. Synthesis and thermal conductivity characteristic of hybrid nanofluids–a review. Renew. Sustain. Energ. Rev. 2017, 75, 868–878. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Unsteady flow and heat transfer past a stretching/shrinking sheet in a hybrid nanofluid. Int. J. Heat Mass Transf. 2019, 136, 288–290. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Flow and heat transfer along a permeable stretching/shrinking curved surface in a hybrid nanofluid. Phys. Scr. 2019, 94, 105219. [Google Scholar] [CrossRef]
- Waini, I.; Ishak, A.; Pop, I. Hybrid nanofluid flow and heat transfer over a nonlinear permeable stretching/shrinking surface. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3110–3127. [Google Scholar] [CrossRef]
- Aly, E.; Pop, I. MHD flow and heat transfer over a permeable stretching/shrinking sheet in a hybrid nanofluid with a convective boundary condition. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3012–3038. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Sheremet, M.A.; Mehryan, S.A.M.; Kashkooli, F.M.; Pop, I. Local thermal non-equilibrium analysis of conjugate free convection within a porous enclosure occupied with Ag-MgO hybrid nanofluid. J. Therm. Anal. Calorim. 2019, 135, 1381–1398. [Google Scholar] [CrossRef]
- Pop, I.; Sheremet, M.A.; Grosan, T. Thermal convection of nanoliquid in a double-connected chamber. Nanomaterials 2020, 10, 588. [Google Scholar] [CrossRef] [Green Version]
- Sivaraj, C.; Sheremet, M.A. MHD natural convection in an inclined square porous cavity with a heat conducting solid block. J. Magn. Magn. Mater. 2017, 426, 351–360. [Google Scholar] [CrossRef]
- Sheremet, M.A.; Pop, I.; Oztop, H.F.; Abu-Hamdeh, N. Natural convection of nanofluid inside a wavy cavity with a non-uniform heating: Entropy generation analysis. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 958–980. [Google Scholar] [CrossRef]
- Astanina, M.S.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. MHD natural convection and entropy generation of ferrofluid in an open trapezoidal cavity partially filled with a porous medium. Int. J. Mech. Sci. 2018, 136, 493–502. [Google Scholar] [CrossRef]
- Shulepova, E.V.; Sheremet, M.A.; Oztop, H.F.; Abu-Hamdeh, N. Mixed convection of Al2O3–H2O nanoliquid in a square chamber with complicated fin. Int. J. Mech. Sci. 2020, 165, 105192. [Google Scholar] [CrossRef]
- Das, M.K.; Reddy, S.K. Conjugate natural convection heat transfer in an inclined square cavity containing a conducting block. Int. J. Heat Mass Transf. 2006, 49, 4987–5000. [Google Scholar]
- Garoosi, F.; Rashidi, M.M. Two phase flow simulation of conjugate natural convection of the nanofluid in a partitioned heat exchanger containing several conducting obstacles. Int. J. Mech. Sci. 2017, 130, 282–306. [Google Scholar] [CrossRef] [Green Version]

| Physical Properties | Host Fluid (Water) | Al2O3 | SiO2 | Aluminum (Solid Matrix) | Central Block Material | ||
|---|---|---|---|---|---|---|---|
| Glass | Steel | Copper | |||||
| cp (J·kg−1·K−1) | 4179 | 765 | 703 | 880 | 750 | 460 | 380 |
| ρ (kg·m−3) | 997.1 | 3970 | 2200 | 2700 | 2600 | 7800 | 8960 |
| λ (W·m−1·K−1) | 0.613 | 40 | 1.2 | 211 | 0.65 | 46 | 385 |
| β × 10−5 (K−1) | 21.0 | 0.85 | 6.0 | – | – | – | – |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
A. Sheremet, M.; Cimpean, D.S.; Pop, I. Thermogravitational Convection of Hybrid Nanofluid in a Porous Chamber with a Central Heat-Conducting Body. Symmetry 2020, 12, 593. https://doi.org/10.3390/sym12040593
A. Sheremet M, Cimpean DS, Pop I. Thermogravitational Convection of Hybrid Nanofluid in a Porous Chamber with a Central Heat-Conducting Body. Symmetry. 2020; 12(4):593. https://doi.org/10.3390/sym12040593
Chicago/Turabian StyleA. Sheremet, Mikhail, Dalia Sabina Cimpean, and Ioan Pop. 2020. "Thermogravitational Convection of Hybrid Nanofluid in a Porous Chamber with a Central Heat-Conducting Body" Symmetry 12, no. 4: 593. https://doi.org/10.3390/sym12040593
APA StyleA. Sheremet, M., Cimpean, D. S., & Pop, I. (2020). Thermogravitational Convection of Hybrid Nanofluid in a Porous Chamber with a Central Heat-Conducting Body. Symmetry, 12(4), 593. https://doi.org/10.3390/sym12040593





