The Linguistic Interval-Valued Intuitionistic Fuzzy Aggregation Operators Based on Extended Hamacher T-Norm and S-Norm and Their Application

Abstract

Linguistic interval-valued intuitionistic fuzzy sets, as an extension of interval-valued intuitionistic fuzzy sets, have strong practical value in the management of complex uncertainty system with qualitative evaluation information. This study focuses on the development of several linguistic interval-valued intuitionistic fuzzy Hamacher (LIVIFH) aggregation operators based on the extended Hamacher t-norm and s-norm. First, the extended Hamacher t-norm and s-norm, which are applicable to linguistic information environment, are applied to define the linguistic interval-valued intuitionistic fuzzy Hamacher operational laws. Second, based on the proposed operational laws, this study defines the linguistic interval-valued intuitionistic fuzzy Hamacher weighted average (LIVIFHWA) operator and the linguistic interval-valued intuitionistic fuzzy Hamacher weighted geometric (LIVIFHWG) operator, and then investigates their properties. Furthermore, the degeneracy and monotonicity of the proposed operators with respect to the adjustable parameter are explored. Finally, a multiple attribute group decision-making (MAGDM) approach is developed based on the proposed LIVIFH aggregation operators, and then this approach is applied to a supplier selection problem. Parameter analysis indicates that the adjustable parameter in the proposed LIVIFH aggregation operators could reflect the attitudes of decision makers. The LIVIFHWA operator would be more appropriate to optimistic decision makers, and the LIVIFHWG operator to pessimistic decision makers. In addition, as the adjustable parameter increasing, both attitudes tend to be neutral. The proposed method is also compared with two other approaches to show its feasibility and efficiency.

1. Introduction

Linguistic multi-attribute group decision-making (LMAGDM) is an important branch in decision theory. When making qualitative evaluations for alternative-to-attribute objects in the decision-making process, experts get used to use linguistic variables [1], such as “Reject”, “Major revision”, “Minor revision”, and “Accept”, rather than numerical scales. Ordered qualitative scales generated by linguistic variable are common in social sciences, engineering, computer sciences, and other fields. Along with the development of fuzzy information processing technology, many extensions based on the concept of linguistic variable have been introduced in recent years, such as 2-tuple fuzzy linguistic representation model [2], virtual linguistic model [3], proportional 2-tuple linguistic variable [4], etc. These extended concepts and models support the construction of normative description, operation and aggregation of linguistic evaluation information, and improve the efficiency of solving LMAGDM problems. Furthermore, as the LMAGDM problems are getting complicated, in order to facilitate the integration of linguistic evaluation information provided by group experts, scholars have extended statistical methods such as probability theory, possibility theory, and proportional concepts to linguistic variables based on hesitant fuzzy sets [5], and proposed various corresponding distribution linguistic term sets (DLTSs) [6,7,8,9,10,11]. Decision-makers can apply these DLTSs based on the characteristics of MAGDM problems and linguistic evaluation information from experts. The DLTSs show its wide applicability in the fields of medical treatment [12,13], product evaluation [14,15], engineering construction [16], and public emergency [17,18,19].

It is worth noting that the above-mentioned DLTSs focus on the qualitative representation of membership degree, and do not pay attention to the non-membership degree that can feedback experts’ negation. In order to comprehensively consider the advantages of membership and non-membership in characterizing experts’ psychological characteristics, scholars extended the concept of intuitionistic fuzzy sets (IFSs) [20] to linguistic information environment and proposed linguistic intuitionistic fuzzy sets (LIFSs) [21,22]. LIFSs could qualitatively represent membership or non-membership through linguistic variables. When dealing with LMAGDM problems, linguistic aggregation operator is usually the key technique to fuse the evaluation information of multiple experts. In order to deal with the LMAGDM problem with attribute association, based on the Power average (PA), Bonferroni mean (BM) and Heronian mean (HM), the linguistic intuitionistic PA, BM and HM operators [23,24,25,26] are developed. Some aggregation operators that can capture and reflect and interrelationships among aggregated arguments are intensively studied, which include the linguistic intuitionistic Hamy and Shapley fuzzy operator [27,28]. They enrich the linguistic intuitionistic fuzzy set theory and its decision-making method. However, in some complex LMAGDM problems, it is difficult for experts to provide accurate linguistic terms, instead, it is not uncommon to represent preference through interval-valued linguistic numbers [29]. Therefore, some scholars [30,31] put forward the concept of linguistic interval-valued intuitionistic fuzzy sets (LIVIFSs), so that experts can use interval-valued linguistic terms to express the membership degree and non-membership degree of alternatives under evaluation attributes. Some algebraic operational laws [30,31] are defined to construct the interval-valued linguistic intuitionistic fuzzy aggregation operators. A rank method is developed to distinguish between different interval-valued linguistic intuitionistic fuzzy numbers (LIVIFNs) by proposing the score and accuracy functions [30,31].

In developing various linguistic term sets such as hesitant fuzzy linguistic term sets (HFLTSs), LIFSs, and DLTSs, the basic operations play a critical role, and LIVIFSs is no exception. However, few studies have been conducted with regard to the operations for LIVIFSs [30,31], especially for the generalized operations. In fact, based on the Hamacher t-norm and s-norm [32], several generalized operations on various types of extended fuzzy sets have been developed, such as intuitionistic fuzzy Hamacher operations [33], hesitant fuzzy Hamacher operations [34], and Pythagorean fuzzy Hamacher operations [35]. Two main characteristics of Hamacher t-norm and s-norm are that: (i) decision-makers (DMs) can obtain various types of t-norm and s-norm by selecting different parameter values. In the cases of $\gamma \to 1$ and $\gamma \to 2$, for example, the Hamacher t-norm(s-norm) will reduce to the Algebraic t-norm(s-norm) and Einstein t-norm(s-norm), respectively, and (ii) the Hamacher t-norm and s-norm would decrease and increase respectively with the increasing of parameter $\gamma$. When solving group decision-making problems, these properties will provide a new perspective for the analysis of expert behavior. What needs to be mentioned is that, based on the traditional t-norm and s-norm, literature [36] proposed extended t-norm and s-norm that are suitable for LMAGDM environment, and constructed a serial of generalized operations and aggregation operators of linguistic term sets.

Inspired by their research, based on the Hamacher operational laws, to the current study develops the linguistic interval-valued intuitionistic fuzzy Hamacher weighted average (LIVIFHWA) and interval-valued intuitionistic fuzzy Hamacher weighted geometric (LIVIFHWG) operators, which will be used to fuse the evaluation information of multiple experts. Then, the relationships between the proposed linguistic interval-valued intuitionistic fuzzy Hamacher (LIVIFH) aggregation operators and their corresponding adjustable parameters will be explored, focused on the degeneracy and monotonicity properties. Finally, based on the proposed LIVIFH aggregation operators, a MAGDM approach is developed to deal with the problems with LIVIFNs, and the practical meaning of the adjustable parameters is illustrated accordingly through a numerical example.

The rest of the paper is structured as follows. Some preliminaries of LIVIFSs and extended Hamacher t-norm(s-norm) are provided in Section 2. In Section 3, the linguistic interval-valued intuitionistic fuzzy Hamacher operations and operator are proposed, and their special cases and desire properties are explored. Furthermore, in Section 4, this study proposes a LIVIF MAGDM approach for solving the LMAGDM problems, and applies this method to select a platform supplier for a large corporation. Finally, Section 5 concludes this paper.

2. Preliminaries

This section introduces primarily the definitions of LIVIFSs as well as their operational laws. Some concepts of the extended Hamacher t-norm and s-norm are also introduced.

Definition 1.

[1] Let$S=\left\{s_{\theta }|\theta =0,1,\cdots ,t\right\}$be a finite and totally ordered linguistic term set, and$t$is a positive integer and$s_{\theta }$is the possible value of linguistic variable. We call$S$as a discrete linguistic set if$S$satisfies: (i) if$\theta >\delta$, then$s_{\theta }>s_{\delta }$; (ii) there exists negation function$neg$, so that $neg\left(s_{\theta }\right)=s_{t-\theta }$.

For ease of calculation, literature [37] extended the discrete linguistic set into continuous linguistic set $\overline{S}=\left\{s_{\theta }|\theta \in \left[0,t\right]\right\}$, and $\overline{S}$ also satisfied the aforementioned conditions.

Generalization of interval-valued intuitionistic fuzzy set and linguistic term set leads to the concept of a linguistic interval-valued intuitionistic fuzzy set, which provides the more freedom to the decision-makers [31].

Definition 2.

[30,31] Let$X$be a fixed set and$S_{[0,t]}$ be a continuous linguistic set. Then a linguistic interval-valued intuitionistic fuzzy set $A$ associated with $X$ can be written as

$$A=\left\{\left(x,s_{{\mu }_{A\left(x\right)}},s_{{\nu }_{A\left(x\right)}}\right)|x\in X\right\},$$

where $s_{{\mu }_{A\left(x\right)}}=\left[s_{{\mu }_{A\left(x\right)}^L},s_{{\mu }_{A\left(x\right)}^U}\right]\subseteq \left[s_0,s_t\right]$ and $s_{{\nu }_{A\left(x\right)}}=\left[s_{{\nu }_{A\left(x\right)}^L},s_{{\nu }_{A\left(x\right)}^U}\right]\subseteq \left[s_0,s_t\right]$are the membership degree and non-membership degree, respectively, and ${\mu }_A^U+{\nu }_A^U\le t$. $s_{{\pi }_A}=[s_{{\pi }_A^L},s_{{\pi }_A^U}]=\left[s_{t-{\mu }_A^U-{\nu }_A^U},s_{t-{\mu }_A^L-{\nu }_A^L}\right]$ is the hesitant degree of $A$.

For convenience, we call $\alpha =\left(\left[s_{{\mu }_A^L},s_{{\mu }_A^U}\right],\left[s_{{\nu }_A^L},s_{{\nu }_A^U}\right]\right)$ as linguistic interval-valued intuitionistic fuzzy number (LIVIFN) and simply express it as $\alpha =\left(\left[s_a,s_b\right],\left[s_c,s_d\right]\right)$, where $\left[s_a,s_b\right]\subseteq \left[s_0,s_t\right]$ and $\left[s_c,s_d\right]\subseteq \left[s_0,s_t\right]$, and $b+d\le t$,$s_a,s_b,s_c,s_d\in S_{\left[0,t\right]}$.

Definition 3.

[31] Let${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)\left(i=1,2\right)$ be two LIVIFNs, then

(1) 

if$a_1=a_2,b_1=b_2,c_1=c_2,d_1=d_2$, then ${\alpha }_1={\alpha }_2$;

(2) 

if$a_1\le a_2,b_1\le b_2,c_1\ge c_2,d_1\ge d_2$, then ${\alpha }_1\le {\alpha }_2$;

(3) 

the negation of${\alpha }_1$is defined as ${\alpha }_1^c=\left(\left[s_{c_1},s_{d_1}\right],\left[s_{a_1},s_{b_1}\right]\right)$.

To compare the LIVIFNs, the score function and accuracy function are defined as follows.

Definition 4.

[31] Let$\alpha =\left(\left[s_a,s_b\right],\left[s_c,s_d\right]\right)$be a LIVIFN, then the score function and accuracy function of$\alpha$are defined as$S\left(\alpha \right)=s_{\left(2t+a-c+b-d\right)/4}$and $H\left(\alpha \right)=s_{\left(a+b+c+d\right)/2}$, respectively.

Let${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)\left(i=1,2\right)$be two LIVIFNs, then the rank method based on score function and accuracy function are defined as follows:

(1) 

if$S\left({\alpha }_1\right)<S\left({\alpha }_2\right)$, then ${\alpha }_1<{\alpha }_2$;

(2) 

if $S\left({\alpha }_1\right)=S\left({\alpha }_2\right)$, $H\left({\alpha }_1\right)<H\left({\alpha }_2\right)$, then ${\alpha }_1<{\alpha }_2$.

Next, we introduce the existing operational laws and weighted aggregation operators for LIVIFNs.

Definition 5.

[30,31] Let${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)\left(i=1,2\right)$be two LIVIFNs, and parameter$\lambda >0$, then some operational laws of${\alpha }_i\left(i=1,2\right)$1are defined as follows:

(1) 

${\alpha }_1\oplus {\alpha }_2=\left(\left[s_{a_1+a_2-\frac{a_1{a}_2}{t}},s_{b_1+b_2-\frac{b_1{b}_2}{t}}\right],\left[s_{\frac{c_1{c}_2}{t}},s_{\frac{d_1{d}_2}{t}}\right]\right)$;

(2) 

${\alpha }_1\otimes {\alpha }_2=\left(\left[s_{\frac{a_1{a}_2}{t}},s_{\frac{b_1{b}_2}{t}}\right],\left[s_{c_1+c_2-\frac{c_1{c}_2}{t}},s_{d_1+d_2-\frac{d_1{d}_2}{t}}\right]\right)$;

(3) 

$\lambda {\alpha }_1=\left(\left[s_{t\left(1-{\left(1-\frac{a_1}{t}\right)}^{\lambda }\right)},s_{t\left(1-{\left(1-\frac{b_1}{t}\right)}^{\lambda }\right)}\right],\left[s_{t{\left(\frac{c_1}{t}\right)}^{\lambda }},s_{t{\left(\frac{d_1}{t}\right)}^{\lambda }}\right]\right)$;

(4) 

${\alpha }_1^{\lambda }=\left(\left[s_{t{\left(\frac{a_1}{t}\right)}^{\lambda }},s_{t{\left(\frac{b_1}{t}\right)}^{\lambda }}\right],\left[s_{t\left(1-{\left(1-\frac{c_1}{t}\right)}^{\lambda }\right)},s_{t\left(1-{\left(1-\frac{d_1}{t}\right)}^{\lambda }\right)}\right]\right)$.

Definition 6.

[31] Let${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)$,$i=1,2,\dots ,n$, be a collection of LIVIFNs, then

(1) 

the linguistic interval-valued intuitionistic fuzzy weighted average (LIVIFWA) operator is a mapping $LIVAIFWA:{\mathsf{\Omega }}^n\to \mathsf{\Omega }$ given by

$$LIVIFWA\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)=\underset{i=1}{\overset{n}{\oplus }}{\omega }_i{\alpha }_i=\left(\left[s_{t-{\displaystyle {\prod }_{i=1}^n{\left(t-a_i\right)}^{{\omega }_i}}},s_{t-{\displaystyle {\prod }_{i=1}^n{\left(t-b_i\right)}^{{\omega }_i}}}\right],\left[s_{{\displaystyle {\prod }_{i=1}^n{c}_i^{{\omega }_i}}},s_{{\displaystyle {\prod }_{i=1}^n{c}_i^{{\omega }_i}}}\right]\right).$$

(2) 

the linguistic interval-valued intuitionistic fuzzy weighted geometric (LIVIFWG) operator is a mapping$LIVAIFWG:{\mathsf{\Omega }}^n\to \mathsf{\Omega }$given by

$$LIVIFWG\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)=\underset{i=1}{\overset{n}{\otimes }}{\alpha }_i{}^{{\omega }_i}=\left(\left[s_{{\displaystyle {\prod }_{i=1}^n{a}_i^{{\omega }_i}}},s_{{\displaystyle {\prod }_{i=1}^n{b}_i^{{\omega }_i}}}\right],\left[s_{t-{\displaystyle {\prod }_{i=1}^n{\left(t-c_i\right)}^{{\omega }_i}}},s_{t-{\displaystyle {\prod }_{i=1}^n{\left(t-d_i\right)}^{{\omega }_i}}}\right]\right),$$

where$\omega ={\left({\omega }_1,{\omega }_2,\dots ,{\omega }_n\right)}^T$is the weight vector, and ${\omega }_i>0,{\displaystyle \sum _{i=1}^n{\omega }_i}=1$.

Extended Hamacher T-Norm and S-Norm

Next, we require some related concepts of Hamacher t-norm and s-norm, which are the core theoretical tools for constructing linguistic interval-valued intuitionistic fuzzy Hamahcer laws and aggregation operators. Then, we analyse the relationship between Hamacher t-norm(s-norm) and extended Hamacher t-norm(s-norm) based on the negative function.

Definition 7.

A function$N_E:\left[0,t\right]\to \left[0,t\right]$is called an extended negation function if it satisfies the following conditions: (1)$N_E:\left[0,t\right]\to \left[0,t\right]$is continuous; (2)$N_E\left(0\right)=t,N_E\left(t\right)=0$; (3) if$x>y$, then$N_E\left(x\right)<N_E\left(y\right)$; (4) $N_E\left(N_E\left(x\right)\right)=x$.

Definition 8.

Given an extended negation function $N_E$,

(1) 

if$f_E:{\left[0,t\right]}^n\to \left[0,t\right]$satisfies: (1)$f_E\left(0,\cdots ,0\right)=0$,$f_E\left(t,\cdots ,t\right)=t$; (2)$x_i\le y_i$,$f_E\left(x_1,x_2,\cdots ,x_n\right)\le f_E\left(y_1,y_2,\cdots ,y_n\right)$,$i=1,2,\dots ,n$, then$f_E$is called an extended aggregation function.

(2) 

if$f_E^d$satisfies$f_E^d\left(x_1,x_2,\cdots ,x_n\right)=N_E\left(f_E\left(N_E\left(x_1\right),N_E\left(x_2\right),\cdots ,N_E\left(x_n\right)\right)\right)$, then$f_E$and$f_E^d$are dual aggregation function with$N_E$.

Definition 9.

A mapping$T^{\ast }:{\left[0,t\right]}^2\to \left[0,t\right]$is called an extended triangular norm (t-norm) if it satisfies the following conditions:

(1) 

Commutativity:$T^{\ast }\left(a,b\right)=T^{\ast }\left(b,a\right)$;

(2) 

Associativity:$T^{\ast }\left(T^{\ast }\left(a,b\right),c\right)=T^{\ast }\left(a,T^{\ast }\left(b,c\right)\right)$;

(3) 

Monotonicity:$a\le c,b\le d\Rightarrow T^{\ast }\left(a,b\right)\le T^{\ast }\left(c,d\right)$;

(4) 

Neutral element:$T^{\ast }\left(t,a\right)=a$.

Definition 10.

A mapping$S^{\ast }:{\left[0,t\right]}^2\to \left[0,t\right]$is called an extended t-conorm (s-norm) if it satisfies the following conditions:

(1) 

Commutativity:$S^{\ast }\left(a,b\right)=S^{\ast }\left(b,a\right)$;

(2) 

Associativity:$S^{\ast }\left(S^{\ast }\left(a,b\right),c\right)=S^{\ast }\left(a,S^{\ast }\left(b,c\right)\right)$;

(3) 

Monotonicity:$a\le c,b\le d\Rightarrow S^{\ast }\left(a,b\right)\le S^{\ast }\left(c,d\right)$;

(4) 

Neutral element:$S^{\ast }\left(0,a\right)=a$.

Definition 11.

Given an extended t-norm and s-norm$T^{\ast }$and$S^{\ast }$, then$T^{\ast }$and$S^{\ast }$are dual with respect to function$N_E$if and only if

$$S^{\ast }\left(x,y\right)=N_E\left(T^{\ast }\left(N_E\left(x\right),N_E\left(y\right)\right)\right),T^{\ast }\left(x,y\right)=N_E\left(S^{\ast }\left(N_E\left(x\right),N_E\left(y\right)\right)\right).$$

Remark 1.

When$t=1$, some degenerate properties of above functions is provided: (1) extended negative function$N_E$reduce to the traditional negative function [38]$N:\left[0,1\right]\to \left[0,1\right]$; (2) extended aggregation function$f_E$reduce to the aggregation function in unit interval [38]; (3) extended t-norm and s-norm reduce to the traditional t-norm and s-norm [38].

On the basis of Hamacher t-norm and s-norm, the research [32] proposed the extended Hamacher t-norm and s-norm.

Definition 12.

A mapping$T_{E-H}:{\left[0,t\right]}^2\to \left[0,t\right]$is called an extended Hamacher t-norm if it satisfies:

$$T_{E-H}\left(x,y\right)={\phi }_{E-H}^{-1}\left({\phi }_{E-H}\left(x\right)+{\phi }_{E-H}\left(y\right)\right)=\frac{txy}{t^2\gamma +\left(1-\gamma \right)\left(tx+ty-xy\right)},$$

where the parameter$\gamma \in \left(0,\infty \right)$.${\phi }_{E-H}$is the generator of$T_{E-H}$and${\phi }_{E-H}\left(x\right)=\log \frac{t\gamma +\left(1-\gamma \right)x}{x},\gamma >0$.${\phi }_{E-H}^{-1}$is the pseudo inverse function of${\phi }_{E-H}$,and${\phi }_{E-H}^{-1}\left(x\right)=\sup \left\{z\in \left[0,t\right]|{\phi }_{E-H}\left(z\right)>x\right\}$.

Definition 13.

A mapping$S_{E-H}:{\left[0,t\right]}^2\to \left[0,t\right]$is called an extended Hamacher s-norm if it satisfies:

$$S_{E-H}\left(x,y\right)={\varphi }_{E-H}^{-1}\left({\varphi }_{E-H}\left(x\right)+{\varphi }_{E-H}\left(y\right)\right)=t\frac{tx+ty-\left(2-\gamma \right)xy}{t^2-\left(1-\gamma \right)xy},$$

where the parameter$\gamma \in \left(0,\infty \right)$.${\varphi }_{E-H}\left(x\right)$is the generator of$S_{E-H}$, and

$${\varphi }_{E-H}\left(x\right)={\phi }_{E-H}\left(N_E\left(x\right)\right)=\log \frac{t\gamma +\left(1-\gamma \right)\left(t-x\right)}{t-x},$$

where$N_E$is negation function and$N_E\left(x\right)=t-x$.

Theorem 1.

Let$T_{E-H}$and$S_{E-H}$be a pair of dual extended Hamacher t-norm and s-norm, then

(1) 

$S_{E-H}\left(x,y\right)=N_E\left(T_{E-H}\left(N_E\left(x\right),N_E\left(y\right)\right)\right)$;

(2) 

$T_{E-H}\left(x,y\right)=N_E\left(S_{E-H}\left(N_E\left(x\right),N_E\left(y\right)\right)\right)$

According to Theorem 1, $T_{E-H}$ and $S_{E-H}$ are dual with respect to $N_E$.

3. Linguistic Interval-Valued Intuitionistic Fuzzy Hamacher Aggregation Operators

3.1. Linguistic Interval-Valued Intuitionistic Fuzzy Hamacher Operational Laws

In the theoretical study of fuzzy sets, t-norm and s-norm are generally used to construct operational laws, while laws are further used to construct aggregation operators, which are progressive layer by layer. Next, we will use the extended Hamacher t-norm and s-norm to construct the Hamacher operational laws.

Definition 14.

Let${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)\left(i=1,2\right)$be two LIVIFNs,$\lambda >0$, then linguistic interval-valued intuitionistic fuzzy Hamacher operational laws is defined as following:

(1) 

${\alpha }_1{\oplus }_{E-H}{\alpha }_2=\left(\left[s_{S_{E-H}\left(a_1,a_2\right)},s_{S_{E-H}\left(b_1,b_2\right)}\right],\left[s_{T_{E-H}\left(c_1,c_2\right)},s_{T_{E-H}\left(d_1,d_2\right)}\right]\right)$;

(2) 

${\alpha }_1{\otimes }_{E-H}{\alpha }_2=\left(\left[s_{T_{E-H}\left(a_1,a_2\right)},s_{T_{E-H}\left(b_1,b_2\right)}\right],\left[s_{S_{E-H}\left(c_1,c_2\right)},s_{S_{E-H}\left(d_1,d_2\right)}\right]\right)$;

(3) 

$\lambda {\alpha }_1=\left(\left[s_{H_A\left(a_1\right)},s_{H_A\left(b_1\right)}\right],\left[s_{H_B\left(c_1\right)},s_{H_B\left(d_1\right)}\right]\right)$;

(4) 

${\alpha }_1{}^{\lambda }=\left(\left[s_{H_B\left(a_1\right)},s_{H_B\left(b_1\right)}\right],\left[s_{H_A\left(c_1\right)},s_{H_A\left(d_1\right)}\right]\right)$.

where${\phi }_{E-H}$and${\varphi }_{E-H}$are generators of$T_{E-H}$and$S_{E-H}$. Function$H_A$and$H_B$satisfy:

$$H_A\left(x\right)={\varphi }_{E-H}^{-1}\left(\lambda {\varphi }_{E-H}\left(x\right)\right),H_B\left(x\right)={\phi }_{E-H}^{-1}\left(\lambda {\phi }_{E-H}\left(x\right)\right).$$

Theorem 2.

The operator laws in definition 14 is closed.

Proof. 

Need to prove that ${\alpha }_1{\oplus }_{E-H}{\alpha }_2$ and $\lambda {\alpha }_1$ are LIVIFNs. Since ${\alpha }_i$ are LIVIFNs, then $b_i\le t-d_i=N_E\left(d_i\right),i=1,2$.

(1) To prove ${\alpha }_1{\oplus }_{E-H}{\alpha }_2$ is closed is equivalent to prove that $S_{E-H}\left(b_1,b_2\right)+T_{E-H}\left(d_1,d_2\right)\le t$. Since $S_{E-H}$ is monotonicity, and $S_{E-H}\left(x,y\right)=N_E\left(T_{E-H}\left(N_E\left(x\right),N_E\left(y\right)\right)\right)$, then

$S_{E-H}\left(b_1,b_2\right)\le S_{E-H}\left(N_E\left(d_1\right),N_E\left(d_2\right)\right)=N_E\left(T_{E-H}\left(N_E\left(N_E\left(d_1\right)\right),N_E\left(N_E\left(d_2\right)\right)\right)\right)=N_E\left(T_{E-H}\left(d_1,d_2\right)\right)$,

Therefore,

$S_{E-H}\left(b_1,b_2\right)+T_{E-H}\left(d_1,d_2\right)\le N_E\left(T_{E-H}\left(d_1,d_2\right)\right)+T_{E-H}\left(d_1,d_2\right)=t$.

Thus, ${\alpha }_1{\oplus }_{E-H}{\alpha }_2$ is also a LIVIFN.

(2) To prove $\lambda {\alpha }_1$ is closed is equivalent to prove that $H_A\left(b_1\right)+H_B\left(d_1\right)\le t$. Since $\varphi$ is monotonicity, and ${\varphi }_{E-H}={\phi }_{E-H}\circ N_E$, then

${\varphi }_{E-H}^{-1}\left(\lambda {\varphi }_{E-H}\left(b_1\right)\right)\le {\varphi }_{E-H}^{-1}\left(\lambda {\varphi }_{E-H}\left(N_E\left(d_1\right)\right)\right)=N_E\left({\phi }_{E-H}^{-1}\left(\lambda {\phi }_{E-H}\left(N_E\left(N_E\left(d_1\right)\right)\right)\right)\right)=N_E\left({\phi }_{E-H}^{-1}\left(\lambda {\phi }_{E-H}\left(d_1\right)\right)\right)$

Therefore,

${\varphi }_{E-H}^{-1}\left(\lambda {\varphi }_{E-H}\left(b_1\right)\right)+{\phi }_{E-H}^{-1}\left(\lambda {\phi }_{E-H}\left(d_1\right)\right)\le N_E\left({\phi }_{E-H}^{-1}\left(\lambda {\phi }_{E-H}\left(d_1\right)\right)\right)+{\phi }_{E-H}^{-1}\left(\lambda {\phi }_{E-H}\left(d_1\right)\right)\le t$,

Thus, $\lambda {\alpha }_1$ is also a LIVIFN.

Similarly, ${\alpha }_1{\otimes }_{E-H}{\alpha }_2$ and ${\alpha }_1{}^{\lambda }$ is also closed. □

Moreover, some relations of the operational laws can be summarized as follows:

Theorem 3.

Let${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)\left(i=1,2\right)$be two LIVIFNs, and$k,k_1,k_2>0$, then

(1) 

${\alpha }_1{\oplus }_{E-H}{\alpha }_2={\alpha }_2{\oplus }_{E-H}{\alpha }_1$;

(2) 

${\alpha }_1{\otimes }_{E-H}{\alpha }_2={\alpha }_2{\otimes }_{E-H}{\alpha }_1$;

(3) 

$k{\alpha }_1{\oplus }_{E-H}k{\alpha }_2=k\left({\alpha }_1{\oplus }_{E-H}{\alpha }_2\right)$;

(4) 

${\alpha }_1{}^k{\otimes }_{E-H}{\alpha }_2{}^k={\left({\alpha }_1{\otimes }_{E-H}{\alpha }_2\right)}^k$;

(5) 

$k_1{\alpha }_1{\oplus }_{E-H}{k}_2{\alpha }_1=\left(k_1+k_2\right){\alpha }_1$;

(6) 

${\alpha }_1{}^{k_1}{\otimes }_{E-H}{\alpha }_1{}^{k_2}={\alpha }_1{}^{k_1+k_2}$.

3.2. Linguistic Interval-Valued Intuitionistic Fuzzy Hamacher Aggregation Operators

Aggregation operators are one of the most powerful tools in the fuzzy multi-attribute decision-making (MADM) problems, in which fusing fuzzy information from various sources is required. In this subsection, the proposed Hamacher operational laws are used to construct two LIVIFH operators, namely, the linguistic interval-valued intuitionistic fuzzy Hamacher weighted average (LIVIFHWA) operator and the linguistic interval-valued intuitionistic fuzzy Hamacher weighted geometric (LIVIFHWG) operator.

3.2.1. LIVIFHWA Operator and LIVIFHWG Operator

Definition 15.

Let${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)$$\left(i=1,2,\dots ,n\right)$be a collection of LIVIFNs,$\omega ={\left({\omega }_1,{\omega }_2,\dots ,{\omega }_n\right)}^T$is the weight vector, and${\omega }_t>0,{\displaystyle \sum _{i=1}^n{\omega }_t}=1$. Then the linguistic interval-valued intuitionistic fuzzy Hamacher weighted average (LIVIFHWA) operator is mapping$LIVIFHWA:{\mathsf{\Omega }}^n\to \mathsf{\Omega }$, which satisfies

$$LIVIFHWA\left({\alpha }_1,{\alpha }_2\dots {\alpha }_n\right)=\underset{i=1}{\overset{n}{\oplus }}{\omega }_i{\alpha }_i.$$

Theorem 4.

Let${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)$$\left(i=1,\dots ,n\right)$be a collection of LIVIFNs, then

$$LIVIFHWA\left({\alpha }_1,{\alpha }_2\dots {\alpha }_n\right)=\left(\left[s_{{\varphi }_{E-H}^{-1}\left({\displaystyle \sum _{i=1}^n{\omega }_i{\varphi }_{E-H}\left(a_i\right)}\right)},s_{{\varphi }_{E-H}^{-1}\left({\displaystyle \sum _{i=1}^n{\omega }_i{\varphi }_{E-H}\left(b_i\right)}\right)}\right],\left[s_{{\phi }_{E-H}^{-1}\left({\displaystyle \sum _{i=1}^n{\omega }_i{\phi }_{E-H}\left(c_i\right)}\right)},s_{{\phi }_{E-H}^{-1}\left({\displaystyle \sum _{i=1}^n{\omega }_i{\phi }_{E-H}\left(d_i\right)}\right)}\right]\right).$$

Proof. 

This is easy to prove according to induction.  □

Definition 16.

Let${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)$$\left(i=1,2,\dots ,n\right)$be a collection of LIVIFNs,$\omega ={\left({\omega }_1,{\omega }_2,\dots ,{\omega }_n\right)}^T$is the weight vector, and${\omega }_t>0,{\displaystyle \sum _{i=1}^n{\omega }_t}=1$. Then the linguistic interval-valued intuitionistic fuzzy Hamacher weighted geometric (LIVIFHWG) operator is mapping$LIVIFHWG:{\mathsf{\Omega }}^n\to \mathsf{\Omega }$, which satisfies

$$LIVIFHWG\left({\alpha }_1,{\alpha }_2\dots {\alpha }_n\right)=\underset{i=1}{\overset{n}{\otimes }}{\alpha }_i{}^{{\omega }_i}.$$

Theorem 5.

Let${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)\left(i=1,2,\dots ,n\right)$be a collection of LIVIFNs, then

$$LIVIFHWG\left({\alpha }_1,{\alpha }_2\dots {\alpha }_n\right)=\left(\left[s_{{\phi }_{E-H}^{-1}\left({\displaystyle \sum _{i=1}^n{\omega }_i{\phi }_{E-H}\left(a_i\right)}\right)},s_{{\phi }_{E-H}^{-1}\left({\displaystyle \sum _{i=1}^n{\omega }_i{\phi }_{E-H}\left(b_i\right)}\right)}\right],\left[s_{{\varphi }_{E-H}^{-1}\left({\displaystyle \sum _{i=1}^n{\omega }_i{\varphi }_{E-H}\left(c_i\right)}\right)},s_{{\varphi }_{E-H}^{-1}\left({\displaystyle \sum _{i=1}^n{\omega }_i{\varphi }_{E-H}\left(d_i\right)}\right)}\right]\right).$$

3.2.2. Some Properties of Two LIVIFH Operators

Before discussing the concrete forms and related properties of the proposed LIVIFH operators, we first construct a pair of dual Hamacher functions.

Definition 17.

Let${\phi }_{E-H}$and${\varphi }_{E-H}$be the generator of extended Hamacher t-norm$T_{E-H}$and s-norm$S_{E-H}$respectively, then

(1) A Hamacher aggregation function$H_{\gamma }:{\left[0,t\right]}^n\to \left[0,t\right]$is defined as

$$H_{\gamma }\left(x_1,x_2,\dots ,x_n\right)={\phi }_{E-H}^{-1}\left({\displaystyle \sum _{i=1}^n{\omega }_i{\phi }_{E-H}\left(x_i\right)}\right)=\frac{t\gamma {\displaystyle {\prod }_{i=1}^n{x}_i{}^{{\omega }_i}}}{{\displaystyle {\prod }_{i=1}^n{\left(t\gamma +\left(1-\gamma \right)x_i\right)}^{{\omega }_i}}+\left(\gamma -1\right){\displaystyle {\prod }_{i=1}^n{x}_i{}^{{\omega }_i}}}.$$

(2) A dual Hamacher aggregation function$H_{\gamma }^d:{\left[0,t\right]}^n\to \left[0,t\right]$is defined as

$$H_{\gamma }^d\left(x_1,x_2,\dots ,x_n\right)={\varphi }_{E-H}^{-1}\left({\displaystyle \sum _{i=1}^n{\omega }_i{\varphi }_{E-H}\left(x_i\right)}\right)=\frac{t{\displaystyle {\prod }_{i=1}^n{\left(t+\left(\gamma -1\right)x_i\right)}^{{\omega }_i}}-t{\displaystyle {\prod }_{i=1}^n{\left(t-x_i\right)}^{{\omega }_i}}}{{\displaystyle {\prod }_{i=1}^n{\left(t+\left(\gamma -1\right)x_i\right)}^{{\omega }_i}}+\left(\gamma -1\right){\displaystyle {\prod }_{i=1}^n{\left(t-x_i\right)}^{{\omega }_i}}}.$$

Now, a desirable property of above dual Hamacher functions is investigated in detail.

Theorem 6.

Given two aggregation operators defined in Definition 17, then

(1)$H_{\gamma }\left(x_1,x_2,\dots ,x_n\right)=N_E\left(H_{\gamma }^d\left(N_E\left(x_1\right),N_E\left(x_2\right),\dots ,N_E\left(x_n\right)\right)\right)$;

(2)$H_{\gamma }^d\left(x_1,x_2,\dots ,x_n\right)=N_E\left(H_{\gamma }\left(N_E\left(x_1\right),N_E\left(x_2\right),\dots ,N_E\left(x_n\right)\right)\right)$.

Proof. 

Only (1) is proved here, it is similar for (2). Since ${\phi }_{E-H}={\varphi }_{E-H}\circ N_E$, ${\phi }_{E-H}^{-1}=N_E\circ {\varphi }_{E-H}^{-1}$,

$$\begin{array}{l}{H}_{\gamma }\left(x_1,x_2,\dots ,x_n\right)={\phi }_{E-H}^{-1}\left({\displaystyle \sum _{i=1}^n{\omega }_i{\phi }_{E-H}\left(x_i\right)}\right)\\ =N_E\left({\varphi }_{E-H}^{-1}\left({\displaystyle \sum _{i=1}^n{\omega }_i{\varphi }_{E-H}\left(N_E\left(x_i\right)\right)}\right)\right)=\left(H_{\gamma }^d\left(N_E\left(x_1\right),N_E\left(x_2\right),\dots ,N_E\left(x_n\right)\right)\right).\end{array}$$

Thus, $H_{\gamma }\left(x_1,x_2,\dots ,x_n\right)=N_E\left(H_{\gamma }^d\left(N_E\left(x_1\right),N_E\left(x_2\right),\dots ,N_E\left(x_n\right)\right)\right)$.  □

The following theorem reveal that the closed relations between the above dual aggregation functions and the LIVIFH operators.

Corollary 1.

Let${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)$$\left(i=1,2,\dots ,n\right)$be a collection of LIVIFNs, then

(1)$LIVIFHWA\left({\alpha }_1,{\alpha }_2, \cdots ,{\alpha }_n\right)=\left(\left[s_{H_{\gamma }^d\left(a_1,a_2,\cdots ,a_n\right)},s_{H_{\gamma }^d\left(b_1,b_2,\cdots ,b_n\right)}\right],\left[s_{H_{\gamma }\left(c_1,c_2,\cdots ,c_n\right)},s_{H_{\gamma }\left(d_1,d_2,\cdots ,d_n\right)}\right]\right)$;

(2)$LIVIFHWG\left({\alpha }_1,{\alpha }_2, \cdots ,{\alpha }_n\right)=\left(\left[s_{H_{\gamma }\left(a_1,a_2,\cdots ,a_n\right)},s_{H_{\gamma }\left(b_1,b_2,\cdots ,b_n\right)}\right],\left[s_{H_{\gamma }^d\left(c_1,c_2,\cdots ,c_n\right)},s_{H_{\gamma }^d\left(d_1,d_2,\cdots ,d_n\right)}\right]\right)$.

Besides, some other basic properties of the LIVIFH operators are also studied.

Theorem 7.

Let${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)$$\left(i=1,2,\dots ,n\right)$be a collection of LIVIFNs, then

(1) The LIVIFHWA operator and LIVIFHWG operator are closed.

(2) If${\alpha }_i=\alpha =\left(\left[s_a,s_b\right],\left[s_c,s_d\right]\right)$,$i=1,2\dots n$, then

$$LIVIFHWA\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)=LIVIFHWG\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)=\alpha .$$

(3) Let${\beta }_i=\left(\left[s_{e_i},s_{f_i}\right],\left[s_{g_i},s_{h_i}\right]\right)$$\left(i=1,2,\dots ,n\right)$be a collection of LIVIFNs, and$a_i\le e_i,b_i\le f_i,c_i\ge g_i,d_i\ge h_i$, then

$$LIVIFHWA\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)\le LIVIFHWA\left({\beta }_1,{\beta }_2,\dots ,{\beta }_n\right),$$

$$LIVIFHWG\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)\le LIVIFHWG\left({\beta }_1,{\beta }_2,\dots ,{\beta }_n\right).$$

Proof. 

As ${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)\left(i=1,2,\dots ,n\right)$ is a collection of LIVIFNs, then

$$b_i+d_i\le t\Rightarrow b_i\le t-d_i=N_E\left(d_i\right),i=1,2,\dots ,n.$$

(1) According to Inference 1, operator LIVIFHWA is closed is equivalent to $H_{\gamma }^d\left(b_1,b_2,\cdots ,b_n\right)+H_{\gamma }\left(d_1,d_2,\cdots ,d_n\right)\le t$. Then according to the monotonicity of $H_{\gamma }$ and Theorem 6(2), we have

$$\begin{array}{cc}\hfill H_{\gamma }^d\left(b_1,b_2,\cdots ,b_n\right)+H_{\gamma }\left(d_1,d_2,\cdots ,d_n\right)& \le H_{\gamma }^d\left(N_E\left(d_1\right),N_E\left(d_2\right),\cdots ,N_E\left(d_n\right)\right)+H_{\gamma }\left(d_1,d_2,\cdots ,d_n\right)\hfill \\ & =N_E\left(H_{\gamma }\left(d_1,d_2,\cdots ,d_n\right)\right)+H_{\gamma }\left(d_1,d_2,\cdots ,d_n\right)=t .\hfill \end{array}$$

Thus, the LIVIFHWA operator is closed. Similarly, the LIVIFHWG operator is also closed.

(2) This is easy to prove according to idempotency.

(3) According the monotonicity of aggregation function $H_{\gamma }$ and $H_{\gamma }^d$,

$$\begin{array}{l}{H}_{\gamma }^d\left(a_1,a_2,\cdots ,a_n\right)\le H_{\gamma }^d\left(e_1,e_2,\cdots ,e_n\right),H_{\gamma }^d\left(b_1,b_2,\cdots ,b_n\right)\le H_{\gamma }^d\left(f_1,f_2,\cdots ,f_n\right)\\ H_{\gamma }\left(c_1,c_2,\cdots ,c_n\right)\ge H_{\gamma }\left(g_1,g_2,\cdots ,g_n\right),H_{\gamma }\left(d_1,d_2,\cdots ,d_n\right)\ge H_{\gamma }\left(h_1,h_2,\cdots ,h_n\right)\end{array}$$

 □

Case 1. If $a_i=e_i,b_i=f_i,c_i=g_i,d_i=h_i$ hold for each $i=1,2,\dots ,n$, i.e., ${\alpha }_i={\beta }_i=\left(\left[s_{e_i},s_{f_i}\right],\left[s_{g_i},s_{h_i}\right]\right)$, then

$$LIVIFHWA\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)=LIVIFHWA\left({\beta }_1,{\beta }_2,\dots ,{\beta }_n\right).$$

Case 2. If there exists $i_0\in \left\{1,2,\dots ,n\right\}$ that does not satisfy $\left\{a_{i_0}=e_{i_0},b_{i_0}=f_{i_0},c_{i_0}=g_{i_0},d_{i_0}=h_{i_0}\right\}$, assume that $a_{i_0}<e_{i_0}$, then $H_{\gamma }^d\left(a_1,a_2,\cdots ,a_n\right)<H_{\gamma }^d\left(e_1,e_2,\cdots ,e_n\right)$.

According score function,

$$S\left(LIVIFHWA\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)\right)<S\left(LIVIFHWA\left({\beta }_1,{\beta }_2,\dots ,{\beta }_n\right)\right),$$

therefore,

$$LIVIFHWA\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)\le LIVIFHWA\left({\beta }_1,{\beta }_2,\dots ,{\beta }_n\right).$$

Similarly, we can prove that

$$LIVIFHWG\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)\le LIVIFHWG\left({\beta }_1,{\beta }_2,\dots ,{\beta }_n\right).$$

Theorem 8.

Let${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)$$\left(i=1,2,\dots ,n\right)$be a collection of LIVIFNs, then

(1)$LIVIFHWA\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)={\left(LIVIFHWG\left({\alpha }_1^c,{\alpha }_2^c,\cdots ,{\alpha }_n^c\right)\right)}^c$;

(2)$LIVIFHWG\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)={\left(LIVIFHWA\left({\alpha }_1^c,{\alpha }_2^c,\cdots ,{\alpha }_n^c\right)\right)}^c$.

Proof. 

According Inference 1,

$$\begin{array}{l}{\left(LIVIFHWG\left({\alpha }_1^c,{\alpha }_2^c,\cdots ,{\alpha }_n^c\right)\right)}^c\\ ={\left(\left[s_{H_{\gamma }\left(c_1,c_2,\cdots ,c_n\right)},s_{H_{\gamma }\left(d_1,d_2,\cdots ,d_n\right)}\right],\left[s_{H_{\gamma }^d\left(a_1,a_2,\cdots ,a_n\right)},s_{H_{\gamma }^d\left(a_1,a_2,\cdots ,a_n\right)}\right]\right)}^c=LIVIFHWA\left({\alpha }_1,{\alpha }_2, \cdots ,{\alpha }_n\right).\end{array}$$

Similarly,

$$LIVIFHWG\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)={\left(LIVIFHWA\left({\alpha }_1^c,{\alpha }_2^c,\cdots ,{\alpha }_n^c\right)\right)}^c.$$

 □

3.3. Relationship between Operator and Parameter

In this subsection, we will discuss the relationship between two kinds of operators and their related parameters, including the degeneracy and the monotonicity of operators with regard to parameters.

3.3.1. Limiting Cases of LIVIFH Operators

Before moving forward to the investigation of degeneracy of the LIVIFHWA and LIVIFHWG operators, we study the limiting cases of the dual Hamacher functions with adjustable parameters.

Lemma 1.

Let$H_{\gamma }$and$H_{\gamma }^d$be functions defined in Definition 17, then

(1) 

$\underset{\gamma \to 0}{\lim }{H}_{\gamma }\left(x_1,x_2,\dots ,x_n\right)=1/\left({\displaystyle {\sum }_{i=1}^n{\omega }_i}/x_i\right)$;

(2) 

$\underset{\gamma \to 0}{\lim }{H}_{\gamma }^d\left(x_1,x_2\dots x_n\right)=t-\frac{1}{{\displaystyle \sum _{i=1}^n{\omega }_i/\left(t-x_i\right)}}$;

(3) 

$\underset{\gamma \to 1}{\lim }{H}_{\gamma }\left(x_1,x_2\dots x_n\right)={\displaystyle {\prod }_{i=1}^n{x}_i{}^{{\omega }_i}}$;

(4) 

$\underset{\gamma \to 1}{\lim }{H}_{\gamma }^d\left(x_1,x_2\dots x_n\right)=t-{\displaystyle {\prod }_{i=1}^n{\left(t-x_i\right)}^{{\omega }_i}}$;

(5) 

$\underset{\gamma \to 2}{\lim }{H}_{\gamma }\left(x_1,x_2\dots x_n\right)=\frac{2t{\displaystyle {\prod }_{i=1}^n{x}_i{}^{{\omega }_i}}}{{\displaystyle {\prod }_{i=1}^n{\left(2t-x_i\right)}^{{\omega }_i}}+{\displaystyle {\prod }_{i=1}^n{x}_i{}^{{\omega }_i}}}$;

(6) 

$\underset{\gamma \to 2}{\lim }{H}_{\gamma }^d\left(x_1,x_2\dots x_n\right)=t-\frac{2t{\displaystyle {\prod }_{i=1}^n{\left(t-x_i\right)}^{{\omega }_i}}}{{\displaystyle {\prod }_{i=1}^n{\left(t+x_i\right)}^{{\omega }_i}}+{\displaystyle {\prod }_{i=1}^n{\left(t-x_i\right)}^{{\omega }_i}}}$;

(7) 

$\underset{\gamma \to \infty }{\lim }{H}_{\gamma }\left(x_1,x_2\dots x_n\right)=\frac{t{\displaystyle {\prod }_{i=1}^n{x}_i^{{\omega }_i}}}{{\displaystyle {\prod }_{i=1}^n{\left(t-x_i\right)}^{{\omega }_i}}+{\displaystyle {\prod }_{i=1}^n{x}_i^{{\omega }_i}}}$;

(8) 

$\underset{\gamma \to \infty }{\lim }{H}_{\gamma }^d\left(x_1,x_2\dots x_n\right)=\frac{t{\displaystyle {\prod }_{i=1}^n{x}_i^{{\omega }_i}}}{{\displaystyle {\prod }_{i=1}^n{\left(t-x_i\right)}^{{\omega }_i}}+{\displaystyle {\prod }_{i=1}^n{x}_i^{{\omega }_i}}}$.

Proof. 

We only proved (1), (2), (7) and (8) here.

(1)

According to Definition 17 and L’Hospital’s rule,

$$\underset{\gamma \to 0}{\lim }{H}_{\gamma }\left(x_1,x_2\dots x_n\right)=\underset{\gamma \to 0}{\lim }\frac{t}{\left({\displaystyle \sum _{i=1}^n\frac{{\omega }_i\left(t/x_i-1\right)}{t\gamma /x_i+\left(1-\gamma \right)}}\right)\times {\displaystyle {\prod }_{i=1}^n{\left(t\gamma /x_i+\left(1-\gamma \right)\right)}^{{\omega }_i}}+1} =\underset{\gamma \to 0}{\lim }\frac{t}{{\displaystyle \sum _{i=1}^n{\omega }_i\left(t/x_i-1\right)}+1}=\frac{1}{{\displaystyle \sum _{i=1}^n{\omega }_i/x_i}}.$$

(2)

According to Theorem 6,

$$\underset{\gamma \to 0}{\lim }{H}_{\gamma }^d\left(x_1,x_2\dots x_n\right)=t-\underset{\gamma \to 0}{\lim }{H}_{\gamma }\left(N_E\left(x_1\right),N_E\left(x_2\right),\dots ,N_E\left(x_n\right)\right)=t-\frac{1}{{\displaystyle \sum _{i=1}^n{\omega }_i/\left(t-x_i\right)}}.$$

(3)

According to Definition 17,

$$\underset{\gamma \to \infty }{\lim }{H}_{\gamma }\left(x_1,x_2\dots x_n\right)=\underset{\gamma \to \infty }{\lim }\frac{t}{{\displaystyle {\prod }_{i=1}^n{\left(t/x_i+1/\gamma -1\right)}^{{\omega }_i}}+1-1/\gamma }=\frac{t{\displaystyle {\prod }_{i=1}^n{x}_i^{{\omega }_i}}}{{\displaystyle {\prod }_{i=1}^n{\left(t-x_i\right)}^{{\omega }_i}}+{\displaystyle {\prod }_{i=1}^n{x}_i^{{\omega }_i}}}.$$

(4)

According to Definition 17,

$$\underset{\gamma \to \infty }{\lim }{H}_{\gamma }^d\left(x_1,x_2\dots x_n\right)=t-\underset{\gamma \to \infty }{\lim }{H}_{\gamma }\left(N_E\left(x_1\right),N_E\left(x_2\right),\dots ,N_E\left(x_n\right)\right)=\frac{t{\displaystyle {\prod }_{i=1}^n{x}_i^{{\omega }_i}}}{{\displaystyle {\prod }_{i=1}^n{\left(t-x_i\right)}^{{\omega }_i}}+{\displaystyle {\prod }_{i=1}^n{x}_i^{{\omega }_i}}}.$$

 □

Remark 2.

In the following, the limit function of$H_{\gamma }$,$\underset{\gamma \to k}{\lim }{H}_{\gamma }$, will be denoted as$H_{\gamma }{}_{\to k}$, the limit function of$H_{\gamma }^d$,$\underset{\gamma \to k}{\lim }{H}_{\gamma }^d$, will be denoted as$H_{\gamma \to k}^d$,$k\in \left[0,\infty \right]$.

Based on the above analysis and the internal relationship between dual Hamacher functions and operators, the relationship between operators and parameters are analyzed below.

Theorem 9.

Let${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)$$\left(i=1,2,\dots ,n\right)$be a collection of LIVIFNs, then

(1) 

When$\gamma \to 0$, the LIVIFHWA operator degenerates into the Harmonic weighted average (LIVIFHarWA) operator:

$$\underset{\gamma \to 0}{\lim }LIVIFHWA\left({\alpha }_1,{\alpha }_2, \cdots ,{\alpha }_n\right)=\left(\left[s_{H_{{\gamma }_{\to 0}}^d\left(a_1,a_2,\cdots ,a_n\right)},s_{H_{{\gamma }_{\to 0}}^d\left(b_1,b_2,\cdots ,b_n\right)}\right],\left[s_{H_{{\gamma }_{\to 0}}\left(c_1,c_2,\cdots ,c_n\right)},s_{H_{{\gamma }_{\to 0}}\left(d_1,d_2,\cdots ,d_n\right)}\right]\right).$$

(2) 

When$\gamma \to 0$, the LIVIFHWG operator degenerates into the Harmonic weighted geometric (LIVIFHarWG) operator:

$$\underset{\gamma \to 0}{\lim }LIVIFHWG\left({\alpha }_1,{\alpha }_2, \cdots ,{\alpha }_n\right)=\left(\left[s_{H_{\gamma \to 0}\left(a_1,a_2,\cdots ,a_n\right)},s_{H_{\gamma \to 0}\left(b_1,b_2,\cdots ,b_n\right)}\right],\left[s_{H_{\gamma \to 0}^d\left(c_1,c_2,\cdots ,c_n\right)},s_{H_{\gamma \to 0}^d\left(d_1,d_2,\cdots ,d_n\right)}\right]\right).$$

(3) 

When$\gamma \to 1$, the LIVIFHWA operator degenerates into the Algebraic weighted average (LIVIFAWA) operator:

$$\underset{\gamma \to 1}{\lim }LIVIFHWA\left({\alpha }_1,{\alpha }_2, \cdots ,{\alpha }_n\right)=\left(\left[s_{H_{{\gamma }_{\to 1}}^d\left(a_1,a_2,\cdots ,a_n\right)},s_{H_{{\gamma }_{\to 1}}^d\left(b_1,b_2,\cdots ,b_n\right)}\right],\left[s_{H_{{\gamma }_{\to 1}}\left(c_1,c_2,\cdots ,c_n\right)},s_{H_{{\gamma }_{\to 1}}\left(d_1,d_2,\cdots ,d_n\right)}\right]\right).$$

(4) 

When$\gamma \to 1$, the LIVIFHWG operator degenerates into the Algebraic weighted geometric (LIVIFAWG) operator:

$$\underset{\gamma \to 1}{\lim }LIVIFHWG\left({\alpha }_1,{\alpha }_2, \cdots ,{\alpha }_n\right)=\left(\left[s_{H_{\gamma \to 1}\left(a_1,a_2,\cdots ,a_n\right)},s_{H_{\gamma \to 1}\left(b_1,b_2,\cdots ,b_n\right)}\right],\left[s_{H_{\gamma \to 1}^d\left(c_1,c_2,\cdots ,c_n\right)},s_{H_{\gamma \to 1}^d\left(d_1,d_2,\cdots ,d_n\right)}\right]\right).$$

(5) 

When$\gamma \to 2$, the LIVIFHWA operator degenerates into the Einstein weighted average (LIVIFEWA) operator:

$$\underset{\gamma \to 2}{\lim }LIVIFHWA\left({\alpha }_1,{\alpha }_2, \cdots ,{\alpha }_n\right)=\left(\left[s_{H_{{\gamma }_{\to 2}}^d\left(a_1,a_2,\cdots ,a_n\right)},s_{H_{{\gamma }_{\to 2}}^d\left(b_1,b_2,\cdots ,b_n\right)}\right],\left[s_{H_{{\gamma }_{\to 2}}\left(c_1,c_2,\cdots ,c_n\right)},s_{H_{{\gamma }_{\to 2}}\left(d_1,d_2,\cdots ,d_n\right)}\right]\right).$$

(6) 

When$\gamma \to 2$, the LIVIFHWG operator degenerates into the Einstein weighted geometric (LIVIFEWG) operator:

$$\underset{\gamma \to 2}{\lim }LIVIFHWG\left({\alpha }_1,{\alpha }_2, \cdots ,{\alpha }_n\right)=\left(\left[s_{H_{\gamma \to 2}\left(a_1,a_2,\cdots ,a_n\right)},s_{H_{\gamma \to 2}\left(b_1,b_2,\cdots ,b_n\right)}\right],\left[s_{H_{\gamma \to 2}^d\left(c_1,c_2,\cdots ,c_n\right)},s_{H_{\gamma \to 2}^d\left(d_1,d_2,\cdots ,d_n\right)}\right]\right).$$

(7) 

When$\gamma \to \infty$, the LIVIFHWA operator degenerates into the Symmetric weighted average (LIVIFSWA) operator:

$$\underset{\gamma \to \infty }{\lim }LIVIFHWA\left({\alpha }_1,{\alpha }_2, \cdots ,{\alpha }_n\right)=\left(\left[s_{H_{{\gamma }_{\to \infty }}^d\left(a_1,a_2,\cdots ,a_n\right)},s_{H_{{\gamma }_{\to \infty }}^d\left(b_1,b_2,\cdots ,b_n\right)}\right],\left[s_{H_{{\gamma }_{\to \infty }}\left(c_1,c_2,\cdots ,c_n\right)},s_{H_{{\gamma }_{\to \infty }}\left(d_1,d_2,\cdots ,d_n\right)}\right]\right).$$

(8) 

When$\gamma \to \infty$, the LIVIFHWG operator degenerates into the Symmetric weighted geometric (LIVIFSWG) operator:

$$\underset{\gamma \to \infty }{\lim }LIVIFHWG\left({\alpha }_1,{\alpha }_2, \cdots ,{\alpha }_n\right)=\left(\left[s_{H_{{\gamma }_{\to \infty }}\left(a_1,a_2,\cdots ,a_n\right)},s_{H_{{\gamma }_{\to \infty }}\left(b_1,b_2,\cdots ,b_n\right)}\right],\left[s_{H_{{\gamma }_{\to \infty }}^d\left(c_1,c_2,\cdots ,c_n\right)},s_{H_{{\gamma }_{\to \infty }}^d\left(d_1,d_2,\cdots ,d_n\right)}\right]\right).$$

3.3.2. Monotonicity of Operators with Respect to Their Parameters

The degeneracy of the operator with respect to parameters is mainly based on the perspective of the discrete value of the parameter. Below we analyze the relationship between the operator and the parameter from the perspective of the continuous value of the parameter. First, the monotonicity of dual Hamacher functions with respect to their parameters are discussed.

Lemma 2.

$H_{\gamma }$decreases with increasing parameter$\gamma$, while$H_{\gamma }^d$increases with increasing parameter$\gamma$.

Proof. 

(1) Since $H_{\gamma }\left(x_1,x_2\dots x_n\right)=\frac{t}{{\displaystyle {\prod }_{i=1}^n{\left(t/x_i+1/\gamma -1\right)}^{{\omega }_i}}+1-1/\gamma }$, then the derivation of $H_{\gamma }\left(x_1,x_2\dots x_n\right)$ regarding $\gamma$ would be

$$\begin{array}{l}\frac{\partial H_{\gamma }}{\partial \gamma }=\frac{t}{{\left({\displaystyle {\prod }_{i=1}^n{\left(t/x_i+1/\gamma -1\right)}^{{\omega }_i}}+1-1/\gamma \right)}^2}\times \frac{1}{{\gamma }^2}\left(\left({\displaystyle {\sum }_{i=1}^n\frac{{\omega }_i}{t/x_i+1/\gamma -1}}\right)\times {\displaystyle {\prod }_{i=1}^n{\left(t/x_i+1/\gamma -1\right)}^{{\omega }_i}}-1\right)\\ \ge \frac{t}{{\left({\displaystyle {\prod }_{i=1}^n{\left(t/x_i+1/\gamma -1\right)}^{{\omega }_i}}+1-1/\gamma \right)}^2}\times \frac{1}{{\gamma }^2}\left({\displaystyle {\prod }_{i=1}^n{\left(\frac{1}{t/x_i+1/\gamma -1}\right)}^{{\omega }_i}}\times {\displaystyle {\prod }_{i=1}^n{\left(t/x_i+1/\gamma -1\right)}^{{\omega }_i}}-1\right)=0.\end{array}$$

Thus, $\frac{\partial H_{\gamma }}{\partial \gamma }\ge 0$, $H_{\gamma }$ increases with increasing parameter $\gamma$.

(2) According to Theorem 6,

$$H_{\gamma }^d\left(x_1,x_2,\dots ,x_n\right)=N_E\left(H_{\gamma }\left(N_E\left(x_1\right),N_E\left(x_2\right),\dots ,N_E\left(x_n\right)\right)\right)=t-H_{\gamma }\left(t-x_1,t-x_2,\dots ,t-x_n\right).$$

 □

According to (1), $H_{\gamma }\left(t-x_1,t-x_2,\dots ,t-x_n\right)$ increases with increasing parameter $\gamma$, then $H_{\gamma }^d$ decreases with increasing parameter $\gamma$.

Next, the monotonicity of operators with respect to their parameters are analyzed below.

Theorem 10.

Let${\alpha }_i=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)$$\left(i=1,2,\dots ,n\right)$be a collection of LIVIFNs, then,

(1) 

The LIVIFHWA operator decreases with increasing parameter$\gamma$;

(2) 

The LIVIFHWG operator increases with increasing parameter$\gamma$.

Proof. 

According to Theorem 6 and the definition of score function,

$$S\left(LIVIFHWA\left({\alpha }_1,{\alpha }_2, \cdots ,{\alpha }_n\right)\right)=s_{\left(2t+H_{\gamma }^d\left(a_1,a_2,\cdots ,a_n\right)+H_{\gamma }^d\left(b_1,b_2,\cdots ,b_n\right)-H_{\gamma }\left(c_1,c_2,\cdots ,c_n\right)-H_{\gamma }\left(d_1,d_2,\cdots ,d_n\right)\right)/4};$$

$$S\left(LIVIFHWG\left({\alpha }_1,{\alpha }_2, \cdots ,{\alpha }_n\right)\right)=s_{\left(2t+H_{\gamma }\left(a_1,a_2,\cdots ,a_n\right)+H_{\gamma }\left(b_1,b_2,\cdots ,b_n\right)-H_{\gamma }^d\left(c_1,c_2,\cdots ,c_n\right)-H_{\gamma }^d\left(d_1,d_2,\cdots ,d_n\right)\right)/4}.$$

Then according to Lemma 2,

$$\left(2t+H_{\gamma }^d\left(a_1,a_2,\cdots ,a_n\right)+H_{\gamma }^d\left(b_1,b_2,\cdots ,b_n\right)-H_{\gamma }\left(c_1,c_2,\cdots ,c_n\right)-H_{\gamma }\left(d_1,d_2,\cdots ,d_n\right)\right)/4$$

is strictly monotone decreasing regarding $\gamma$.

$$\left(2t+H_{\gamma }\left(a_1,a_2,\cdots ,a_n\right)+H_{\gamma }\left(b_1,b_2,\cdots ,b_n\right)-H_{\gamma }^d\left(c_1,c_2,\cdots ,c_n\right)-H_{\gamma }^d\left(d_1,d_2,\cdots ,d_n\right)\right)/4$$

is strictly monotone increasing regarding $\gamma$. Therefore, the LIVIFHWA operator decreases with increasing parameter $\gamma$, and the LIVIFHWG operator increases with increasing parameter $\gamma$.  □

4. Multiple Attributes Decision-Making Approach Based on the LIVIFH Operators and Its Application

In this section, the proposed linguistic interval-valued intuitionistic fuzzy Hamacher operators were applied for solving the supplier selection problem.

4.1. Supplier Selection Problem

The supplier selection problem is a typical MADM problem. Decision makers need to evaluate suppliers based on a set of evaluation indicators, and then select the best supplier for cooperation. With the rapid development of economy and the increasing complexity of society, the knowledge and experience from various fields become essential in this decision-making process. To improve the reliability and rationality of the decision, a comprehensive evaluation of suppliers through an expert group is necessary. Therefore, the supplier selection problem is gradually transformed into a MAGDM problem. The supplier selection MAGDM problem generally consists of four parts: supplier alternatives, group of experts, evaluation attributes, and decision-making information matrixes. For convenience, the symbols of some sets and variables associated with the supplier selection problem will be expressed uniformly as follows.

(1)

Supplier alternatives: Let $X=\left\{x_1,x_2,\cdots ,x_m\right\}$ be the set of $m$ supplier alternatives, where $x_i$ denotes the $i$th supplier alternative, $i=1,2,\cdots ,m$. The best supplier will be selected from the set of alternatives.

(2)

Evaluation attributes: $C=\left\{c_1,c_2,\cdots ,c_n\right\}$ is the set of $n$ attributes for the supplier alternatives, where $c_j$ is the $j$ th attribute, $j=1,2,\cdots ,n$.

(3)

Group of experts: Let $E=\left\{e_1,e_2,\cdots ,e_t\right\}$ be the $t$ experts from different research areas, where $e_k$ is the $k$th expert,$k=1,2,\cdots ,t$. $\lambda =\left\{{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_t\right\}$ is the weight vector of experts, where ${\lambda }_k$ is the weight of the expert $e_k$, and satisfies ${\displaystyle {\sum }_{k=1}^t{\lambda }_t=1}$ and $0\le {\lambda }_k\le 1$ for $k=1,2,\cdots ,t$. The decision maker aims to coordinate the insights of different experts and select the best one out of $m$ supplier alternatives measured on $n$ attributes.

(4)

Decision-making information matrixes: The experts are requested to express their preferences by using LIVIFNs generated by a discrete linguistic set $S=\left\{s_{\theta }|\theta =1,2,\cdots ,t\right\}$, which described in Definition 1. For an alternative $x_i$ with respect to an attribute $c_j$, an expert $e_k$ provides his/her assessments by using LIVIFNs ${\tilde{\alpha }}_{ij}^k=\left(\left[s_{a_{ij}^k},s_{b_{ij}^k}\right],\left[s_{c_{ij}^k},s_{d_{ij}^k}\right]\right)$. By collecting each attribute’s evaluation information from expert $e_k$, the decision-making information matrix $D_k={\left({\tilde{\alpha }}_{ij}^k\right)}_{m\times n}$ is obtained. $S_{\left[0,h\right]}$ is continuous virtual linguistic term set with respect to $S=\left\{s_{\theta }|\theta =1,2,\cdots ,t\right\}$, and $\left[s_{a_{ij}^k},s_{b_{ij}^k}\right]\subseteq S_{\left[0,h\right]}$,$\left[s_{c_{ij}^k},s_{d_{ij}^k}\right]\subseteq S_{\left[0,h\right]}$, $i=1,2,\cdots ,m$, $j=1,2,\cdots ,n$, $k=1,2,\cdots ,t$.

4.2. Decision-Making Method for Solving Supplier Selection Problem

Based on the proposed aggregation operators, the LIVIF MAGDM method is constructed as the following:

Step 1. Obtain decision-making matrix by collecting assessment information from experts.

$$D_k={\left({\tilde{\alpha }}_{ij}^k\right)}_{m\times n}={\left(\left(\left[s_{a_{ij}^k},s_{b_{ij}^k}\right],\left[s_{c_{ij}^k},s_{d_{ij}^k}\right]\right)\right)}_{m\times n}\left(k=1,2,\cdots ,t\right).$$

Step 2. Aggregate the individual evaluation matrix $D_k\left(k=1,2,\cdots ,t\right)$ into a collective evaluation matrix $D={\left({\tilde{\alpha }}_{ij}\right)}_{m\times n}$ by using the LIVIFHWA operator or the LIVIFHWG operator.

$${\tilde{\alpha }}_{ij}=LIVIFHWA\left({\tilde{\alpha }}_{ij}^1,{\tilde{\alpha }}_{ij}^2,\dots ,{\tilde{\alpha }}_{ij}^t\right)\mathrm{or}{\tilde{\alpha }}_{ij}=LIVIFHWG\left({\tilde{\alpha }}_{ij}^1,{\tilde{\alpha }}_{ij}^2,\dots ,{\tilde{\alpha }}_{ij}^t\right)$$

Step 3. Aggregate the attribute values $\left({\tilde{\alpha }}_{i1},{\tilde{\alpha }}_{i2},\cdots ,{\tilde{\alpha }}_{in}\right)$ with respect to alternative $x_i$ in matrix $D={\left({\tilde{\alpha }}_{ij}\right)}_{m\times n}$ by using the LIVIFHWA operator or the LIVIFHWG operator, and obtain the comprehensive evaluation values ${\tilde{\alpha }}_i\left(i=1,2,\cdots ,m\right)$:

$${\tilde{\alpha }}_i=LIVIFHWA\left({\alpha }_{i1},{\alpha }_{i2},\dots ,{\alpha }_{in}\right)\mathrm{or}{\tilde{\alpha }}_i=LIVIFHWG\left({\alpha }_{i1},{\alpha }_{i2},\dots ,{\alpha }_{in}\right).$$

Step 4. Rank the comprehensive evaluation values ${\tilde{\alpha }}_i\left(i=1,2,\cdots ,m\right)$ based on the score function

$${\tilde{\alpha }}_{\sigma \left(m\right)}\prec {\tilde{\alpha }}_{\sigma \left(m-1\right)}\prec \cdots \prec {\tilde{\alpha }}_{\sigma \left(2\right)}\prec {\tilde{\alpha }}_{\sigma \left(1\right)}.$$

Step 5. According to the rank of ${\tilde{\alpha }}_i\left(i=1,2,\cdots ,m\right)$, obtain the rank of alternatives:

$$A_{\sigma \left(m\right)}\prec A_{\sigma \left(m-1\right)}\prec \cdots \prec A_{\sigma \left(2\right)}\prec A_{\sigma \left(1\right)}.$$

4.3. Case Study

In this section, an example was provided to illustrate how the proposed LIVIF MAGDM method was working in practice. Then a parametric analysis was performed to verify the rationality of the relevant Theorems, and to show that the proposed operators had the ability to reflect the decision attitude characteristics. Finally, the proposed LIVIF MAGDM method was compared with the existing two approaches that could deal with the MADM problem involving LIVIFSs.

4.3.1. Illustrative Example

Assume that a large corporation needs to build a data platform. There are four alternative platform suppliers $X=\left\{x_1,x_2,x_3,x_4\right\}$, and the large corporation consults three experts $E=\left\{e_1,e_2,e_3\right\}$ to select the most suitable one, and assume the weight vector for evaluation experts is $\lambda ={\left(0.5,0.3,0.2\right)}^T$. The four platform suppliers are assessed based on four evaluation attributes [39]: Quality $c_1$, “Rationality of Price $c_2$, After Sales Performance $c_3$, Delivery Time Performance $c_4$, with the corresponding weight vector being $w={\left(0.2,0.3,0.2,0.3\right)}^T$. Based on the given linguistic term set

$$S=\left\{\begin{array}{l}\mathrm{extremely}\mathrm{poor}\left(s_0\right),\mathrm{very}\mathrm{poor}\left(s_1\right),\mathrm{poor}\left(s_2\right),\mathrm{slightly}\mathrm{poor}\left(s_3\right),\mathrm{fair}\left(s_4\right),\\ \mathrm{slightly}\mathrm{good}\left(s_5\right),\mathrm{good}\left(s_6\right),\mathrm{very}\mathrm{good}\left(s_7\right),\mathrm{extremely}\mathrm{good}\left(s_8\right)\end{array}\right\},$$

experts use the LIVIFNs to provide their evaluation information matrix $D_k={\left({\tilde{\alpha }}_{ij}^k\right)}_{4\times 4}$, where ${\tilde{\alpha }}_{ij}^k=\left(\left[s_{a_{ij}^k},s_{b_{ij}^k}\right],\left[s_{c_{ij}^k},s_{d_{ij}^k}\right]\right)$ is an LIVIFN. The proposed MAGDM method in Section 4.2 is applied to fuse different experts’ opinions to get the final decision.

Step 1. Collect the evaluation information from expert group, the decision matrix $D_k={\left({\tilde{\alpha }}_{ij}^k\right)}_{4\times 4}\left(k=1,2,3\right)$ for experts are shown in

Table 1. Evaluation matrixes of experts.

Expert	Alternative	Attribute
		${\mathit{c}}_1$	${\mathit{c}}_{\mathbf{2}}$	${\mathit{c}}_{\mathbf{3}}$	${\mathit{c}}_{\mathbf{4}}$
$e_1$	$x_1$	$\left(\left[s_5,s_6\right],\left[s_1,s_2\right]\right)$	$\left(\left[s_4,s_6\right],\left[s_1,s_1\right]\right)$	$\left(\left[s_4,s_5\right],\left[s_2,s_3\right]\right)$	$\left(\left[s_6,s_7\right],\left[s_1,s_1\right]\right)$
	$x_2$	$\left(\left[s_3,s_5\right],\left[s_2,s_3\right]\right)$	$\left(\left[s_5,s_6\right],\left[s_1,s_2\right]\right)$	$\left(\left[s_2,s_4\right],\left[s_3,s_4\right]\right)$	$\left(\left[s_3,s_4\right],\left[s_2,s_3\right]\right)$
	$x_3$	$\left(\left[s_5,s_6\right],\left[s_1,s_2\right]\right)$	$\left(\left[s_5,s_6\right],\left[s_1,s_2\right]\right)$	$\left(\left[s_3,s_5\right],\left[s_2,s_3\right]\right)$	$\left(\left[s_3,s_5\right],\left[s_1,s_3\right]\right)$
	$x_4$	$\left(\left[s_4,s_5\right],\left[s_2,s_3\right]\right)$	$\left(\left[s_1,s_3\right],\left[s_3,s_4\right]\right)$	$\left(\left[s_3,s_5\right],\left[s_1,s_3\right]\right)$	$\left(\left[s_6,s_7\right],\left[s_1,s_1\right]\right)$
$e_2$	$x_1$	$\left(\left[s_2,s_4\right],\left[s_1,s_3\right]\right)$	$\left(\left[s_4,s_5\right],\left[s_1,s_2\right]\right)$	$\left(\left[s_4,s_5\right],\left[s_1,s_3\right]\right)$	$\left(\left[s_3,s_6\right],\left[s_1,s_2\right]\right)$
	$x_2$	$\left(\left[s_3,s_5\right],\left[s_1,s_3\right]\right)$	$\left(\left[s_1,s_2\right],\left[s_1,s_4\right]\right)$	$\left(\left[s_2,s_3\right],\left[s_3,s_4\right]\right)$	$\left(\left[s_3,s_5\right],\left[s_1,s_3\right]\right)$
	$x_3$	$\left(\left[s_3,s_4\right],\left[s_1,s_2\right]\right)$	$\left(\left[s_3,s_6\right],\left[s_1,s_2\right]\right)$	$\left(\left[s_2,s_5\right],\left[s_2,s_3\right]\right)$	$\left(\left[s_3,s_4\right],\left[s_2,s_3\right]\right)$
	$x_4$	$\left(\left[s_4,s_5\right],\left[s_1,s_2\right]\right)$	$\left(\left[s_3,s_3\right],\left[s_3,s_5\right]\right)$	$\left(\left[s_3,s_3\right],\left[s_2,s_3\right]\right)$	$\left(\left[s_4,s_6\right],\left[s_1,s_1\right]\right)$
$e_3$	$x_1$	$\left(\left[s_2,s_4\right],\left[s_1,s_2\right]\right)$	$\left(\left[s_2,s_3\right],\left[s_1,s_4\right]\right)$	$\left(\left[s_3,s_5\right],\left[s_2,s_3\right]\right)$	$\left(\left[s_5,s_7\right],\left[s_1,s_1\right]\right)$
	$x_2$	$\left(\left[s_1,s_4\right],\left[s_2,s_3\right]\right)$	$\left(\left[s_4,s_5\right],\left[s_1,s_2\right]\right)$	$\left(\left[s_2,s_4\right],\left[s_1,s_3\right]\right)$	$\left(\left[s_3,s_4\right],\left[s_2,s_4\right]\right)$
	$x_3$	$\left(\left[s_2,s_3\right],\left[s_1,s_5\right]\right)$	$\left(\left[s_3,s_5\right],\left[s_1,s_2\right]\right)$	$\left(\left[s_3,s_5\right],\left[s_1,s_3\right]\right)$	$\left(\left[s_3,s_5\right],\left[s_2,s_3\right]\right)$
	$x_4$	$\left(\left[s_3,s_4\right],\left[s_2,s_3\right]\right)$	$\left(\left[s_1,s_2\right],\left[s_3,s_4\right]\right)$	$\left(\left[s_3,s_5\right],\left[s_1,s_2\right]\right)$	$\left(\left[s_5,s_6\right],\left[s_1,s_1\right]\right)$

.

Step 2. Aggregate individual evaluation matrix $D_k={\left({\tilde{\alpha }}_{ij}^k\right)}_{4\times 4}\left(k=1,2,3\right)$ into a comprehensive matrix $D={\left({\tilde{\alpha }}_{ij}\right)}_{4\times 4}$ by using the LIVIFHWA operator (set $\gamma =8$).

$${\tilde{\alpha }}_{ij}=LIVIFHWA\left({\tilde{\alpha }}_{ij}^1,{\tilde{\alpha }}_{ij}^2,{\tilde{\alpha }}_{ij}^3\right)=\left(\left[s_{a_{ij}},s_{b_{ij}}\right],\left[s_{c_{ij}},s_{d_{ij}}\right]\right)$$

and where

$$\begin{array}{l}{a}_{ij}=\frac{t{\displaystyle {\prod }_{k=1}^3{\left(t+\left(\gamma -1\right)a_{ij}^k\right)}^{{\lambda }_k}}-t{\displaystyle {\prod }_{k=1}^3{\left(t-a_{ij}^k\right)}^{{\lambda }_k}}}{{\displaystyle {\prod }_{k=1}^3{\left(t+\left(\gamma -1\right)a_{ij}^k\right)}^{{\lambda }_k}}+\left(\gamma -1\right){\displaystyle {\prod }_{k=1}^3{\left(t-a_{ij}^k\right)}^{{\lambda }_k}}},b_{ij}=\frac{t{\displaystyle {\prod }_{k=1}^3{\left(t+\left(\gamma -1\right)b_{ij}^k\right)}^{{\lambda }_k}}-t{\displaystyle {\prod }_{k=1}^3{\left(t-b_{ij}^k\right)}^{{\lambda }_k}}}{{\displaystyle {\prod }_{k=1}^3{\left(t+\left(\gamma -1\right)b_{ij}^k\right)}^{{\lambda }_k}}+\left(\gamma -1\right){\displaystyle {\prod }_{k=1}^3{\left(t-b_{ij}^k\right)}^{{\lambda }_k}}}\\ c_{ij}=\frac{t\gamma {\displaystyle {\prod }_{k=1}^3{\left(c_{ij}^k\right)}^{{\lambda }_k}}}{{\displaystyle {\prod }_{k=1}^3{\left(t\gamma +\left(1-\gamma \right)c_{ij}^k\right)}^{{\lambda }_k}}+\left(\gamma -1\right){\displaystyle {\prod }_{k=1}^3{\left(c_{ij}^k\right)}^{{\lambda }_k}}},d_{ij}=\frac{t\gamma {\displaystyle {\prod }_{k=1}^3{\left(c_{ij}^k\right)}^{{\lambda }_k}}}{{\displaystyle {\prod }_{k=1}^3{\left(t\gamma +\left(1-\gamma \right)c_{ij}^k\right)}^{{\lambda }_k}}+\left(\gamma -1\right){\displaystyle {\prod }_{k=1}^3{\left(c_{ij}^k\right)}^{{\lambda }_k}}}\end{array}$$

Step 3. Aggregate the line element $\left({\tilde{\alpha }}_{i1},{\tilde{\alpha }}_{i2},\cdots ,{\tilde{\alpha }}_{i4}\right)$ of alternative $x_i$ in matrix $D={\left({\tilde{\alpha }}_{ij}\right)}_{4\times 4}$ through the LIVIFHWA operator,

$${\tilde{\alpha }}_i=LIVIFHWA\left({\alpha }_{i1},{\alpha }_{i2},\dots ,{\alpha }_{in}\right)=\left(\left[s_{a_i},s_{b_i}\right],\left[s_{c_i},s_{d_i}\right]\right)$$

where

$$\begin{array}{l}{a}_i=\frac{t{\displaystyle {\prod }_{j=1}^4{\left(t+\left(\gamma -1\right)a_{ij}\right)}^{w_j}}-t{\displaystyle {\prod }_{j=1}^4{\left(t-a_{ij}\right)}^{w_j}}}{{\displaystyle {\prod }_{j=1}^4{\left(t+\left(\gamma -1\right)a_{ij}\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle {\prod }_{j=1}^4{\left(t-a_{ij}\right)}^{w_j}}},b_i=\frac{t{\displaystyle {\prod }_{j=1}^4{\left(t+\left(\gamma -1\right)b_{ij}\right)}^{w_j}}-t{\displaystyle {\prod }_{j=1}^4{\left(t-b_{ij}\right)}^{w_j}}}{{\displaystyle {\prod }_{j=1}^4{\left(t+\left(\gamma -1\right)b_{ij}\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle {\prod }_{j=1}^4{\left(t-b_{ij}\right)}^{w_j}}}\\ c_{ij}=\frac{t\gamma {\displaystyle {\prod }_{j=1}^4{\left(c_{ij}\right)}^{w_j}}}{{\displaystyle {\prod }_{j=1}^4{\left(t\gamma +\left(1-\gamma \right)c_{ij}\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle {\prod }_{j=1}^4{\left(c_{ij}\right)}^{w_j}}},d_{ij}=\frac{t\gamma {\displaystyle {\prod }_{j=1}^4{\left(d_{ij}\right)}^{w_j}}}{{\displaystyle {\prod }_{j=1}^4{\left(t\gamma +\left(1-\gamma \right)d_{ij}\right)}^{w_j}}+\left(\gamma -1\right){\displaystyle {\prod }_{j=1}^4{\left(d_{ij}\right)}^{w_j}}}\end{array}$$

and then obtain ${\tilde{\alpha }}_i\left(i=1,2,3,4\right)$:

$$\begin{array}{l}{\tilde{\alpha }}_1=\left(\left[s_{4.0486},s_{5.7189}\right],\left[s_{1.1069},s_{1.8554}\right]\right),{\tilde{\alpha }}_2=\left(\left[s_{2.9005},s_{4.4388}\right],\left[s_{1.5480},s_{3.0783}\right]\right),\\ {\tilde{\alpha }}_3=\left(\left[s_{3.4272},s_{5.1715}\right],\left[s_{1.2501},s_{2.5705}\right]\right),{\tilde{\alpha }}_4=\left(\left[s_{3.4543},s_{4.5970}\right],\left[s_{1.6382},s_{2.4285}\right]\right).\end{array}$$

Step 4. Calculate the score function value $S\left({\tilde{\alpha }}_i\right)$ for each collective evaluation value ${\tilde{\alpha }}_i\left(i=1,2,3,4\right)$

$$S\left({\tilde{\alpha }}_1\right)=5.7103,S\left({\tilde{\alpha }}_2\right)=4.6782,S\left({\tilde{\alpha }}_3\right)=5.1945,S\left({\tilde{\alpha }}_4\right)=4.9962$$

Therefore, ${\tilde{\alpha }}_2\prec {\tilde{\alpha }}_4\prec {\tilde{\alpha }}_3\prec {\tilde{\alpha }}_1$ according the score function value.

Step 5. According to the comprehensive evaluation rank, obtain the alternatives rank $x_2\prec x_4\prec x_3\prec x_1$, and the optimal alternative $x_1$.

$$D=\left(\begin{array}{cccc}\left(\left[s_{3.5501},s_{5.1010}\right],\left[s_{1.0000},s_{2.2713}\right]\right)& \left(\left[s_{3.6052},s_{5.2058}\right],\left[s_{1.0000},s_{1.6860}\right]\right)& \left(\left[s_{3.8039},s_{5.0000}\right],\left[s_{1.6389},s_{3.000}\right]\right)& \left(\left[s_{5.0320},s_{6.7588}\right],\left[s_{1.0000},s_{1.2412}\right]\right)\\ \left(\left[s_{2.5774},s_{4.8112}\right],\left[s_{1.6389},s_{3.0000}\right]\right)& \left(\left[s_{3.6231},s_{4.7721}\right],\left[s_{1.0000},s_{2.5123}\right]\right)& \left(\left[s_{2.0000},s_{3.7048}\right],\left[s_{2.4652},s_{3.4833}\right]\right)& \left(\left[s_{3.0000},s_{4.3135}\right],\left[s_{1.6389},s_{3.4833}\right]\right)\\ \left(\left[s_{3.8481},s_{4.9313}\right],\left[s_{1.6389},s_{2.4805}\right]\right)& \left(\left[s_{4.0436},s_{5.8219}\right],\left[s_{1.0000},s_{2.0000}\right]\right)& \left(\left[s_{2.6963},s_{5.0000}\right],\left[s_{1.7531},s_{3.0000}\right]\right)& \left(\left[s_{3.0000},s_{4.7145}\right],\left[s_{1.4286},s_{3.0000}\right]\right)\\ \left(\left[s_{3.8039},s_{4.8112}\right],\left[s_{1.6389},s_{2.6718}\right]\right)& \left(\left[s_{1.5592},s_{2.7974}\right],\left[s_{1.0000},s_{4.2952}\right]\right)& \left(\left[s_{3.0000},s_{4.4408}\right],\left[s_{1.2412},s_{2.7786}\right]\right)& \left(\left[s_{5.2795},s_{6.0000}\right],\left[s_{1.0000},s_{1.0000}\right]\right)\end{array}\right).$$

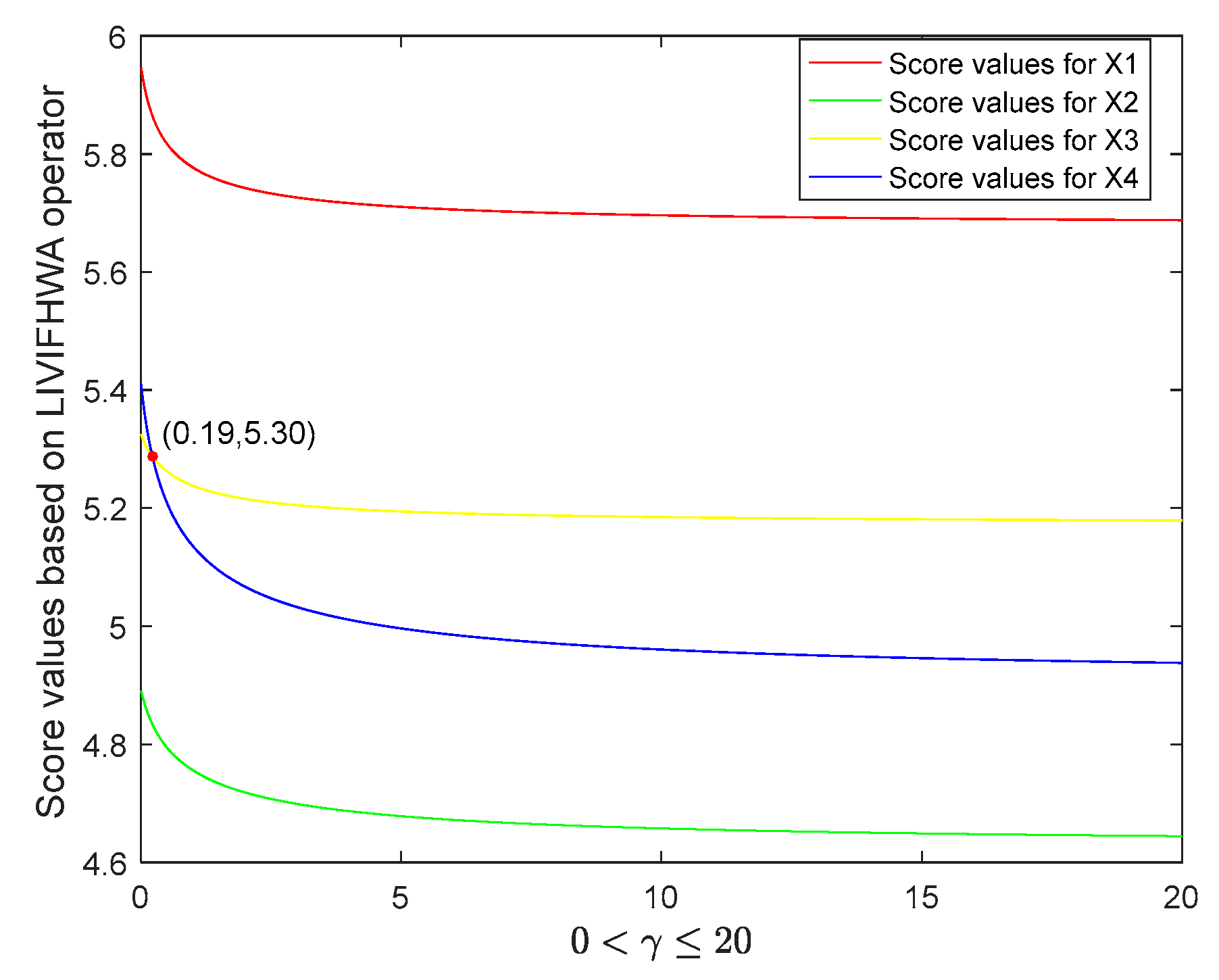
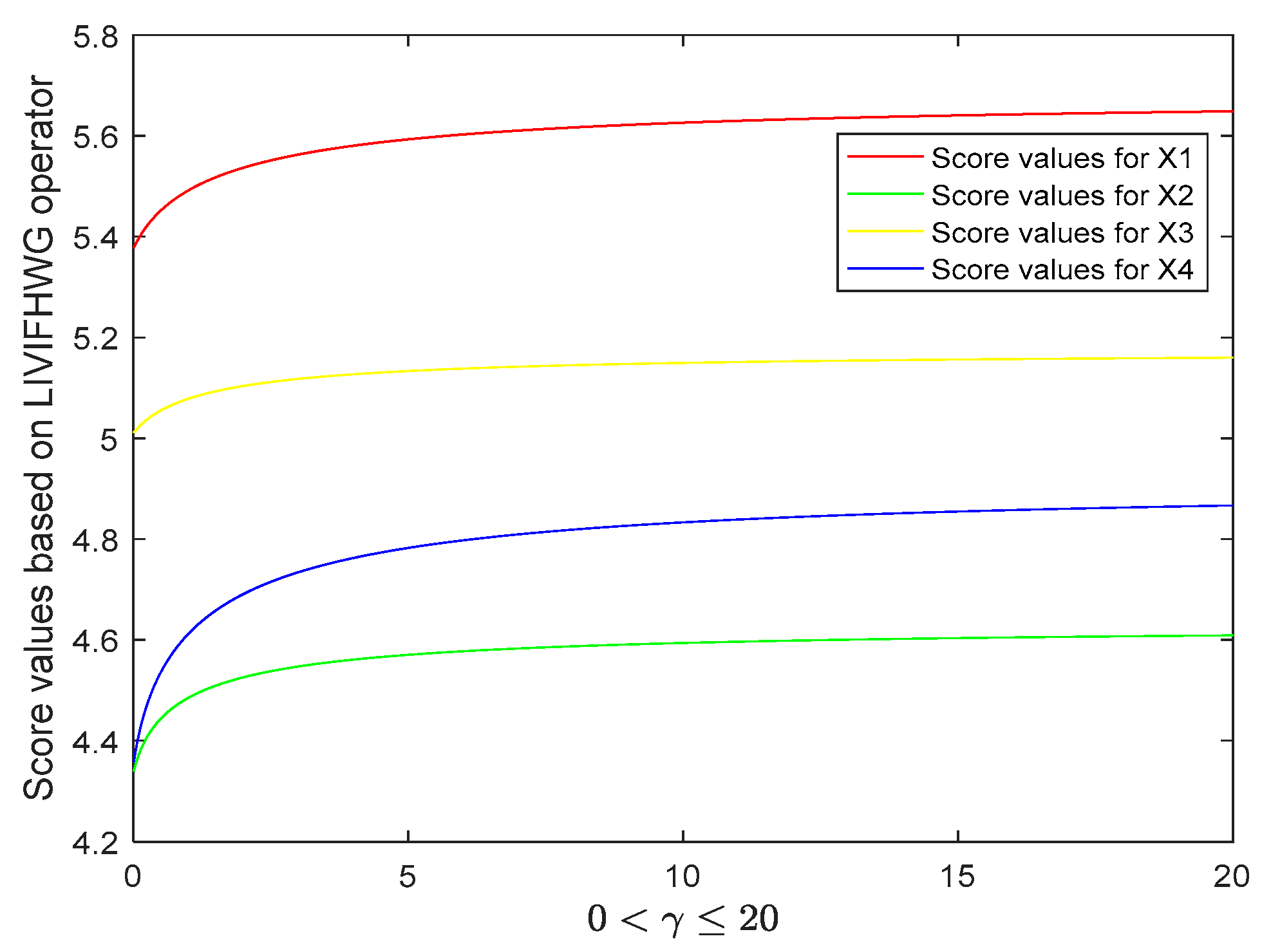
4.3.2. Parameter Analysis

In the multi-attribute decision-making process, compared with traditional quantitative representations, the qualitative linguistic term representations can sometimes better reflect the experts’ preferences on the alternatives. Therefore, based on the example provided, we illustrated this property through parameter analysis.

To investigate to what extent the change of parameter $\gamma$ can influence the MAGDM results, we calculated and compared different results as the parameter varying within a given range ($0<\gamma \le 20$). Use the LIVIFHWA operator and the LIVIFHWG operator to obtain the score values of four alternatives, as shown in Figure 1 and Figure 2, respectively. For convenience, denote the comprehensive evaluation value based on the LIVIFHWA operator as ${\tilde{\alpha }}_i^{LIVIFHWA}\left(i=1,2,3,4\right)$, and denote the comprehensive evaluation value based on the LIVIFHWG operator as ${\tilde{\alpha }}_i^{LIVIFHWG}\left(i=1,2,3,4\right)$.

Case 1. Figure 1 shows the score values of four alternatives based on the LIVIFHWA operator.

(1)

$S\left({\tilde{\alpha }}_i^{LIVIFHWA}\right)\left(i=1,2,3,4\right)$ decreased with increasing parameter. This is consistent with the Theorem 10 (1);

(2)

When $0<\gamma \le 0.19$, the rank of alternatives was $x_2\prec x_3\prec x_4\prec x_1$; when $0.19<\gamma \le 20$, the rank of alternatives was $x_2\prec x_4\prec x_3\prec x_1$, which means the rank of alternatives $x_3$ and $x_4$ switched. This is because the decreasing in score value of $x_4$ was relatively smaller compared with that of $x_3$. Alternative $x_1$ was always the optimal alternative.

Case 2. Figure 2 shows the score values of alternatives based on LIVIFHWG operator.

(1)

$S\left({\tilde{\alpha }}_i^{LIVIFHWG}\right)\left(i=1,2,3,4\right)$ increased with increasing parameter $\gamma$. This is consistent with the Theorem 10 (2);

(2)

The rank of alternative was always $x_2\prec x_4\prec x_3\prec x_1$.

Case 3. Furthermore, we also explored the relationships between the two general operators (LIVIFHWA/LIVIFHWG) and the other three special aggregation operators (LIVIFHarWA, LIVIFHarWG, and LIVIFSWA), their score values are depicted in Figure 3 and Figure 4 when parameter $0<\gamma \le 20$.

(1)

The difference between score values of LIVIFHWA operator and LIVIFHarWA operator $S\left({\tilde{\alpha }}_i^{LIVIFHarWA}\right)-S\left({\tilde{\alpha }}_i^{LIVIFHWA}\right)$ increased with increasing parameter, while the difference between score values of LIVIFHWA operator and the LIVIFSWA operator $S\left({\tilde{\alpha }}_i^{LIVIFHWA}\right)-S\left({\tilde{\alpha }}_i^{LIVIFSWA}\right)$ decreased.

(2)

The difference between score values of LIVIFHWG operator and LIVIFHarWG operator $S\left({\tilde{\alpha }}_i^{LIVIFHWG}\right)-S\left({\tilde{\alpha }}_i^{LIVIFHarWG}\right)$ increased with increasing parameter, while the difference between score values of LIVIFHWG operator and LIVIFSWA operator $S\left({\tilde{\alpha }}_i^{LIVIFSWA}\right)-S\left({\tilde{\alpha }}_i^{LIVIFHWG}\right)$ decreased.

To summarize, the relationships between the score values of these five operators were:

$$S\left({\tilde{\alpha }}_i^{LIVIFHarWG}\right)<S\left({\tilde{\alpha }}_i^{LIVIFHWG}\right)<S\left({\tilde{\alpha }}_i^{LIVIFSWA}\right)<S\left({\tilde{\alpha }}_i^{LIVIFHWA}\right)<S\left({\tilde{\alpha }}_i^{LIVIFHarWA}\right).$$

Based on the above analysis, the aggregation value of the LIVIFHWA operator was always greater than the value of the LIVIFHWG operator. As the increasing of parameter $\gamma$, their difference became smaller and reduced towards 0 when the parameter tended to infinity. Therefore, the LIVIFHWA operator would be more appropriate to optimistic decision makers. The bigger of the parameter $\gamma$ represents the lower of the optimistic level. When the parameter approaches infinity, the decision maker’s attitude tended to be neutral. In contrast, the LIVIFHWG operator would be more appropriate to pessimistic decision makers. The bigger of the parameter $\gamma$ represents the lower of the pessimistic level. When the parameter approaches infinity, the decision maker’s attitude tended to be neutral.

4.3.3. Comparative Analysis

For the MADM problem involving LIVIFSs, there are only two existing approaches available [30,31]. Therefore, in this section we made a straightforward comparison between our result and the results based on these two approaches.

(1) Comparison with the decision-making method in reference [30].

Liu and Qin [30] proposed the weighted interval-valued linguistic intuitionistic fuzzy Maclaurin symmetric mean (WIVLIFMSM) operator, and applied the WIVLIFMSM operator to solve the MADM problems with LIVIFSs.

First, based on the case study in Section 4.3.1, the operators in this paper were compared with the WIVLIFMSM operator in [30]. Since the WIVLIFMSM operator is only applicable for MADM, not for MAGDM, our approach was used to obtain the comprehensive matrix $D={\left({\tilde{\alpha }}_{ij}\right)}_{4\times 4}$ (step 1 and step 2). Then, assuming that its parameter $x=2$, we applied the WIVLIFMSM operator to solve the comprehensive matrix $D={\left({\tilde{\alpha }}_{ij}\right)}_{4\times 4}$. For more details regarding this operator and method, we encourage readers to consult [30].

Step 1–2. Same as in Section 4.3.1.

Step 3. Use the WIVLIFMSM operator to produce the comprehensive evaluation values ${\tilde{\alpha }}_i\left(i=1,2,3,4\right)$:

$$\begin{array}{l}{\tilde{\alpha }}_1=\left(\left[s_{4.3937},s_{5.9737}\right],\left[s_{1.0850},s_{1.6729}\right]\right),{\tilde{\alpha }}_2=\left(\left[s_{3.1849},s_{4.6624}\right],\left[s_{1.4358},s_{2.9647}\right]\right),\\ {\tilde{\alpha }}_3=\left(\left[s_{3.6273},s_{5.2896}\right],\left[s_{1.2042},s_{2.4482}\right]\right),{\tilde{\alpha }}_4=\left(\left[s_{3.9852},s_{4.9203}\right],\left[s_{1.4839},s_{2.0359}\right]\right).\end{array}$$

Step 4. Calculate the score function value $S\left({\tilde{\alpha }}_i\right)$ of collective evaluation value ${\tilde{\alpha }}_i\left(i=1,2,3,4\right)$

$$S\left({\tilde{\alpha }}_1\right)=5.9024,S\left({\tilde{\alpha }}_2\right)=4.8617,S\left({\tilde{\alpha }}_3\right)=5.3061,S\left({\tilde{\alpha }}_4\right)=5.3464$$

Therefore, ${\tilde{\alpha }}_2\prec {\tilde{\alpha }}_3\prec {\tilde{\alpha }}_4\prec {\tilde{\alpha }}_1$ according the score function value.

Step 5. According to the comprehensive evaluation rank, obtain the alternatives rank $x_2\prec x_3\prec x_4\prec x_1$, and the optimal alternative $x_1$.

The decision results by using the WIVLIFMSM operator was the same as that of the LIVIFHWA operator in this paper under the limit of $0<\gamma \le 0.19$.

Second, based on the inner structure of operators, a comparative analysis was carried out between the WIVLIFMSM operator and the LIVIFHWA operator in this paper.

According to the Theorem 6 in [30], the WIVLIFMSM operator was decreasing when the parameter $x$ increased, $x=1,2,\cdots ,n$. While from theorem 10(1) in Section 3.3.2 of the current study, the LIVIFHWA operator also decreased with increasing parameter $\gamma$, and the parameter $\gamma$ was continuous. Moreover, regarding the degeneracy, some special cases of the WIVLIFMSM operator was analyzed with respected to the parameter $x$ in [30]. For example, when $x=1$, the WIVLIFMSM operator degenerated into the LIVIFAWA operator [30]. Interestingly, according to theorem 9(3), the LIVIFHWA operator in this paper could also degenerate into the LIVIFAWA operator when $\gamma \to 1$.

The above comparative analysis indicates that the operators proposed in the current study had the same properties as those in [30]. In addition, the decision-making method in this paper could deal with MAGDM problems.

(2) Comparison with decision-making method in reference [31].

In [31], the LIVAIFWA operator and LIVAIFWG operator are developed to solve the MAGDM problems with LIVIFSs. In fact, according to Theorem 9(3) and (5), when $\gamma \to 1$, the LIVIFHWA operator and the LIVIFHWA operator in this paper reduced to the LIVAIFWA operator and LIVAIFWG operator in [31], respectively. Thus, when applying the LIVAIFWA operator and LIVAIFWG operator to solve the MAGDM problem in the Section 4.3, we could obtain the same decision results as the LIVIFHWA operator ($0.19<\gamma \le 20$) and the LIVIFHWG operator $0<\gamma \le 20$: $x_2\prec x_4\prec x_3\prec x_1$.

In comparison to the WIVLIFMSM and the LIVAIFWA/LIVAIFWG operators, the proposed LIVIFH aggregation operators could be concluded with the following merits.

(1)

The adjustable parameter could reflect the DM’s attitude.

The parameter analysis has manifested that the LIVIFH aggregation operators were capable of reflecting the DM’s preferences by determining the appropriate values of the adjustable parameter $\gamma$.

(2)

The expansion of the domain for evaluation.

The WIVLIFMSM operator could deal with MADM problems with LIVIF inputs, but not MAGDM problems. While the LIVAIFWA/LIVAIFWG operators are capable of dealing with MAGDM problems with LIVIF inputs, but they were merely degenerate cases of the proposed LIVIFHWA and LIVIFHWG operators when the adjustable parameter $\gamma \to 1$.

5. Conclusions

Linguistic interval-valued intuitionistic fuzzy set is proposed in [30,31] by combining the concepts of linguistic variable and the interval-valued intuitionistic fuzzy set. Its prominent properties are that that (i) represent the preference like the linguistic variable does and (ii) consider both membership and non-membership information. The Hamacher t-norm and s-norm are popular in defining operations and aggregation operators of various fuzzy sets because of their advantages on parameter degeneracy and monotonicity. With these considerations, the extended Hamacher t-norm and s-norm were used to the LIVIF environment in this paper.

In this study, we applied the extended Hamacher t-norm and s-norm to define the linguistic interval-valued intuitionistic fuzzy Hamacher operations. We revealed that the operations for LIVIFNs in reference [31] were a special case of generalized operation in this paper. Some basic properties of this generalized operations, such as its closeness and exchangeability, were discussed. Then, we constructed the LIVIFHWA and LIVIFHWG operators on the basis of the developed Hamacher operations, and investigated their instrumental properties. Several limiting cases of the LIVIFHWA and LIVIFHWG operators have been explored with regard to the introduced adjustable parameter. Based on the LIVIFHWA (or LIVIFHWAG) operator, we developed a new decision-making technique for the classical LMAGDM problem, and verified its applicability and feasibility through an example of supplier selection problem. Furthermore, the parameter analysis illustrated the adjustable parameter’s capability to reflect the DM’s attitudes, and the comparative analysis showed the superiority of the proposed LIVIFHWA and LIVIFHWG operators over the previous techniques.