Time-Varying Delayed H? Control Problem for Nonlinear Systems: A Finite Time Study Using Quadratic Convex Approach
Abstract
:1. Introduction
- I.
- We consider some new Lyapunov-Krasovskii functional which has not been considered yet in stability analysis of finite-time control. The new Lyapunov-Krasovskii functional includes some integral terms of the form which the integrands are polynomial multiplied by and one may estimate an upper bound of the integral by employing some techniques from [22,25], the matrix based quadratic convex approach, the use of a tighter bounding technique and useful integral inequality such as Wirtinger inequality.
- II.
- Lyapunov-Krasovskii with the matrix based quadratic convex approach is introduced to formulate finite-time stability criteria and performance level where the time-varying delay satisfies Moreover, the restriction of upper bound derivative is not necessary restricted less than 1 compared with [20]
- III.
- Two numerical examples are given to demonstrate the effectiveness of theoretical result.
2. Problem Statement
3. Preliminaries
- (i)
- The zero solution of the closed-loop system, where ,is finite-time bounded.
- (ii)
- Under zero-initial condition the output satisfies
- (i)
- (ii)
- (iii)
- .
4. Main Results
5. Numerical Examples
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Park, P.; Lee, W.I.; Lee, S.Y. Auxiliary function-based integral inequalities for quadratic functions and there applications to time delay systems. J. Frankl. Inst. 2015, 352, 1378–1396. [Google Scholar] [CrossRef]
- Bao, H.; Cao, J. Stochastic global exponential stability for neutral-type impulsive neural networks with mixed time-delays and Markovian jumping parameters. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 3786–3791. [Google Scholar] [CrossRef]
- Emharuethai, C.; Niamsup, P. H∞ control problem for linear time-varying systems with time-varying delay. Adv. Differ. Equations Control. Process. 2009, 4, 7–27. [Google Scholar]
- Emharuethai, C.; Niamsup, P. Robust H∞ control of linear systems with interval non-differentiable time-varying delay. In Proceedings of the 2012 10th World Congress on Intelligent Control and Automation (WCICA), Beijing, China, 6–8 July 2012; pp. 1507–1512. [Google Scholar]
- Tuan, L.A.; Nam, P.T.; Phat, V.N. New H∞ controller Design for neural networks with interval time-varying delays in State and Observation. Neural Process Lett. 2013, 37, 235–249. [Google Scholar] [CrossRef]
- Huang, H.; Huang, T.; Chen, X. Further Result on Guaranteed H∞ performance state estimation of delayed static neural networks. IEEE Trans. Neu. Net. Lear. Syst. 2015, 26, 1335–1341. [Google Scholar]
- Thanh, N.T.; Phat, V.N. H∞ control for nonlinear systems with interval non-differentiable time-varying delays. Eur. J. Control. 2013, 19, 190–198. [Google Scholar] [CrossRef]
- Dorato, P. Short time stability in linear time-varying systems. Proc. IRT Int. Conv. Rec. 1961, 4, 83–87. [Google Scholar]
- Amato, F.; Ariola, M.; Dorato, P. Finite-time control of linear systems subject to parametric uncertainties and disturbances. Automatica 2001, 37, 1459–1463. [Google Scholar] [CrossRef]
- Meng, Q.; Shen, Y. Finite-time H∞ control for continuous system with norm-bounded disturbance. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1043–1049. [Google Scholar] [CrossRef]
- Niamsup, P.; Phat, V.N. Robust Finite-time H∞ control of linear time-varying delay systems with bounded control via Riccati Equations. Int. J. Autom. Comput. 2018, 15, 355–363. [Google Scholar] [CrossRef]
- Niamsup, P.; Ratchagit, K.; Phat, V.N. Novel criteria for finite-time stbilization ans guaranteed cost control of delay systems delayed neural networks. Neurocomputing 2015, 160, 281–286. [Google Scholar] [CrossRef]
- Raul, C.R.; Radu, E.P.; Radu, C.D. Second order intelligent proportional-integral fuzzy control of twin rotor aerodynamic systems. Procedia Comput. Sci. 2018, 139, 372–380. [Google Scholar]
- Zhang, H.; Liu, X.; Ji, H.; Hou, Z.; Fan, L. Multi-Agent-Based Data-Driven Distributed Adaptive Cooperative Control in Urban Traffic Signal Timing. Energies 2019, 12, 1402. [Google Scholar] [CrossRef] [Green Version]
- Li, K.; Boonto, S.; Nuchkrua, T. On-line Self Tuning of Contouring Control for High Accuracy Robot Manipulators under Various Operations. Int. J. Control Autom. Syst. 2020. [Google Scholar] [CrossRef]
- Ma, P.; Liu, X.; Qin, L.; Wu, G. Finite-time event-triggered H∞ control for switched systems with time-varying delay. Neurocomputing 2016, 207, 828–842. [Google Scholar] [CrossRef]
- Xiang, Z.R.; Sun, Y.N.; Mahmoud, M.S. Robust finite-time H∞ control for a class of uncertain switched neutral systems. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1766–1778. [Google Scholar] [CrossRef]
- Jun Jun, H.; He, X.Z.; Xiang, Y.K. Delay-dependent non-fragile H∞ control for linear systems with interval time-varying dela. Int. J. Autom. Comput. 2015, 12, 109–116. [Google Scholar]
- Hao, L.; Peng, S.; Hamid, R.K.; Mohammed, C. Finite-time and stabilisation for a class of nonlinear systems with time-varying delay. Int. J. Syst. Sci. 2016, 6, 1433–1444. [Google Scholar]
- Stojanovic, S.B. Further improvement in delay-dependent finite-time stability criteria for uncertain continuous-time system with time varying delays. IET Control. Theory Appl. 2016, 10, 926–938. [Google Scholar] [CrossRef]
- Raja, R.; Zhu, Q.; Samidurai, R.; Senthilraj, S.; Hu, W. Improved results on delay-dependent H∞ control for uncertain systems with time-varying delays. Circuits Syst. Signal Process. 2017, 36, 1836–1859. [Google Scholar] [CrossRef]
- Seuret, A.; Gouaisbaut, F. Wirtinger-based integral inequality: Application to time-delay systems. Automatica 2013, 49, 2860–2866. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.H. Note on stability of linear systems with time-varying delays. Automatica 2011, 47, 2118–2121. [Google Scholar] [CrossRef]
- Park, P.G.; Ko, J.W.; Jeong, C. Reciprocally convex approach to stability of systems with time-varying delays. Automatica 2011, 47, 235–238. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L. A new stability criterion using a matrix-based quadratic convex approach. IET Control. Theory Appl. 2014, 8, 1054–1061. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L. Global asymptotic stability analysis for delayed neural networks using a matrix-based quadratic convex approach. Neural Netw. 2014, 54, 57–69. [Google Scholar] [CrossRef]
- Zhang, X.M.; Han, Q.L. Noval delays-derivative-dependent stability criteria using new bounding techniques. Int. J. Robust Nonlinear Control. 2013, 23, 1419–1432. [Google Scholar] [CrossRef]
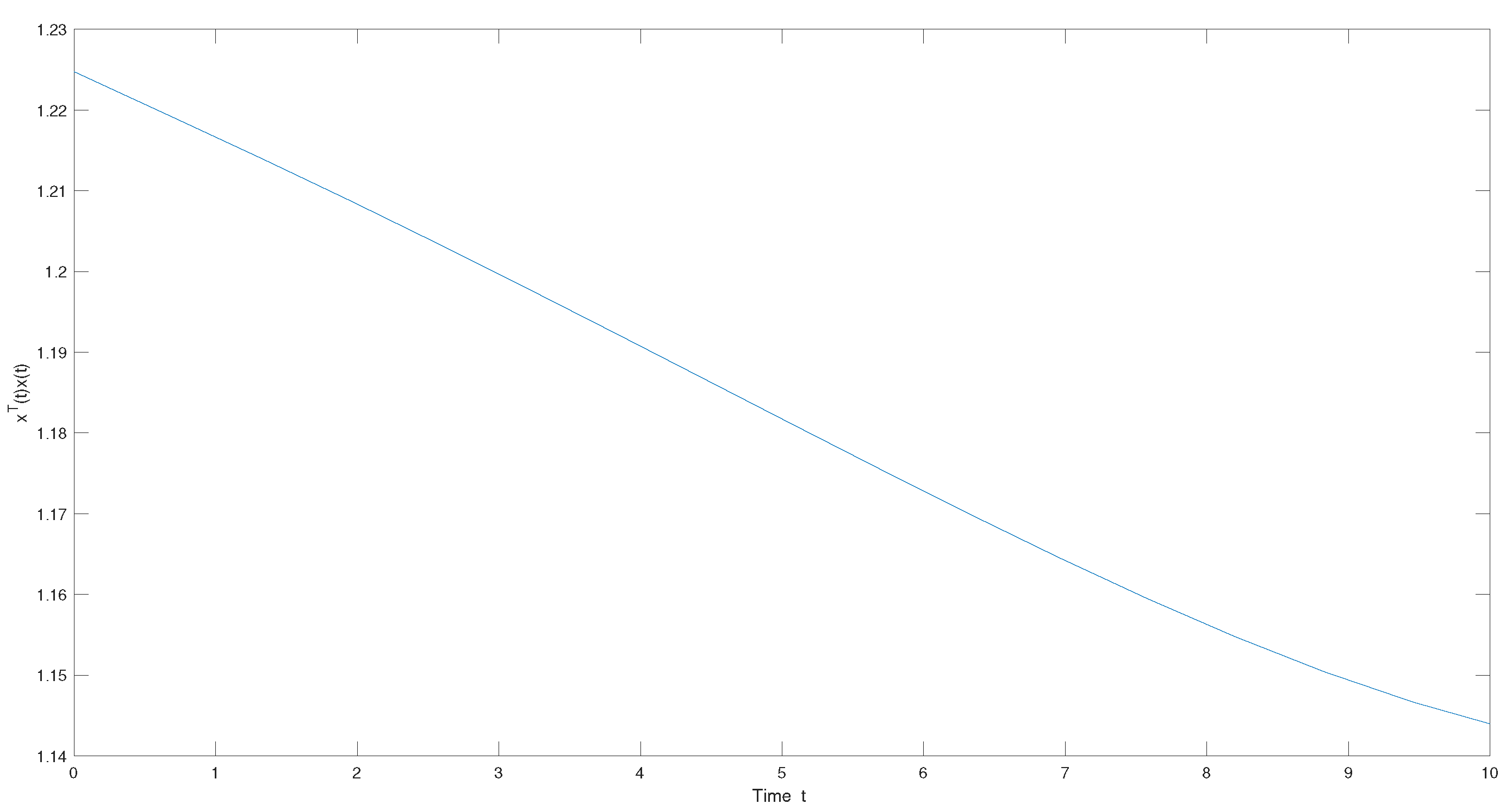
| Method | |||
| By Theorem 1 | 0.1 | 0.3 | 0.2377 |
| 0.1 | 0.5 | 0.2474 | |
| Method | |||
| By Theorem 1 | 0.1 | 0.3 | 0.8991 |
| 0.1 | 0.5 | 0.9643 |
| Method | |||
| By Theorem 1 | 0.1 | 0.5 | 0.2487 |
| T | 2 | 4 | 6 | 8 | 10 |
|---|---|---|---|---|---|
| By Theorem 1 | 5.5527 | 6.2606 | 7.0589 | 7.9589 | 8.9736 |
| Stojanovic [20] | NF | NF | NF | NF | NF |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emharuethai, C.; Niamsup, P.; Ramachandran, R.; Weera, W. Time-Varying Delayed H? Control Problem for Nonlinear Systems: A Finite Time Study Using Quadratic Convex Approach. Symmetry 2020, 12, 713. https://doi.org/10.3390/sym12050713
Emharuethai C, Niamsup P, Ramachandran R, Weera W. Time-Varying Delayed H? Control Problem for Nonlinear Systems: A Finite Time Study Using Quadratic Convex Approach. Symmetry. 2020; 12(5):713. https://doi.org/10.3390/sym12050713
Chicago/Turabian StyleEmharuethai, Chanikan, Piyapong Niamsup, Raja Ramachandran, and Wajaree Weera. 2020. "Time-Varying Delayed H? Control Problem for Nonlinear Systems: A Finite Time Study Using Quadratic Convex Approach" Symmetry 12, no. 5: 713. https://doi.org/10.3390/sym12050713
APA StyleEmharuethai, C., Niamsup, P., Ramachandran, R., & Weera, W. (2020). Time-Varying Delayed H? Control Problem for Nonlinear Systems: A Finite Time Study Using Quadratic Convex Approach. Symmetry, 12(5), 713. https://doi.org/10.3390/sym12050713





