Integration of AHP and GTMA to Make a Reliable Decision in Complex Decision-Making Problems: Application of the Logistics Provider Selection Problem as a Case Study
Abstract
:1. Introduction
2. Literature Review
2.1. Literature Review on the Selection of LPs Using AHP
2.2. Literature Review on the Selection of LPs Using ANP
2.3. Literature Review on the Use of GTMA in General
3. The Integration of AHP and GTMA Method (AH-GTMA) to Solve Complex Decision-Making Problems
3.1. Definition of the Alternatives, Attributes/Criteria, Clusters, and the Network Structure
3.2. Normalization of Positive and Negative Alternatives’ Attributes
3.3. Definition of the Relative Importance of Alternatives within the Clusters, Using the AHP Method
3.4. Digraph Definition, Permanent Computation, and Final Rank of the Alternatives
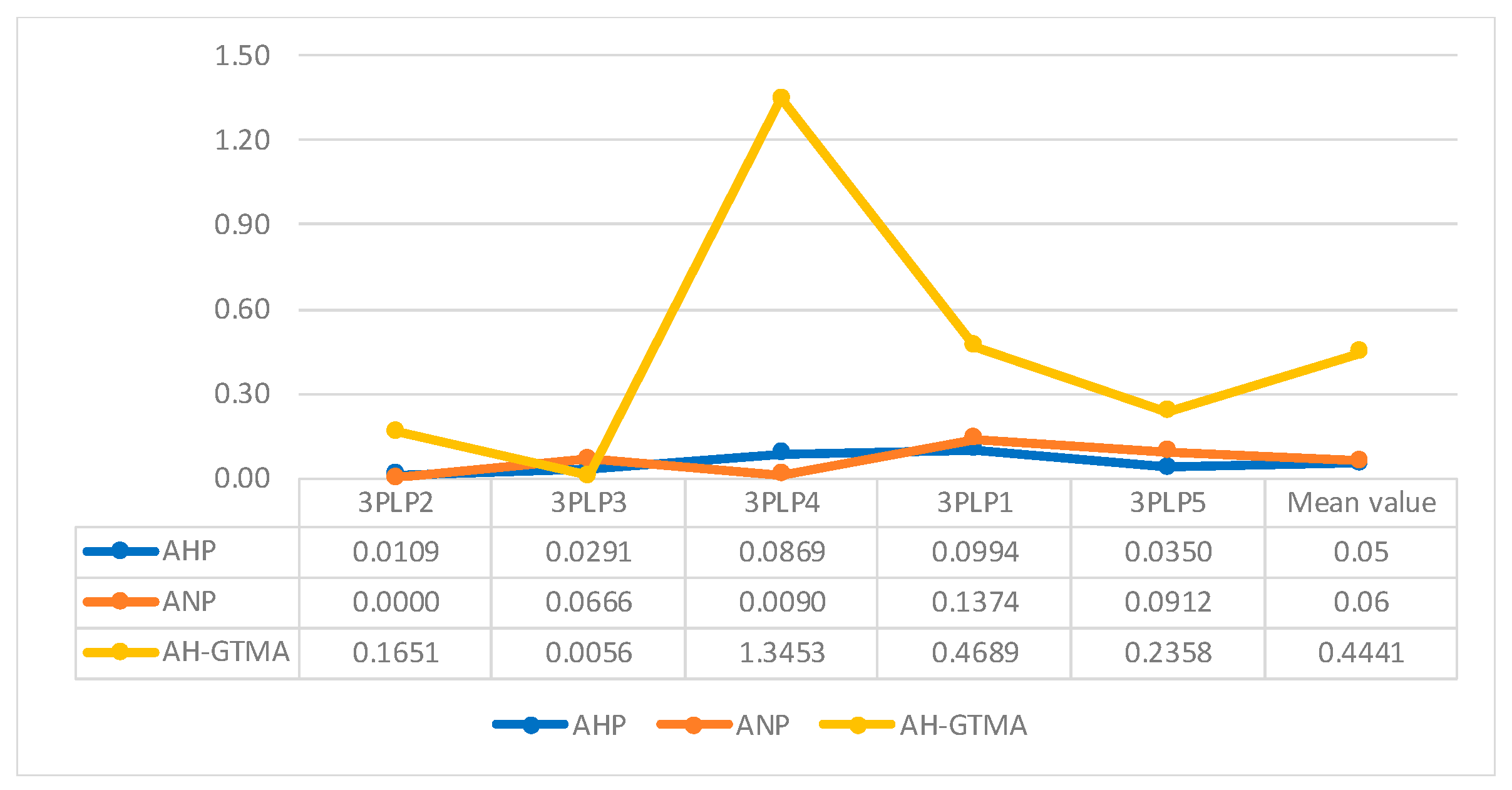
3.5. Evaluation of the Pairwise Comparisons Number among the AHP, ANP, and the AH-GTMA Method
4. Numerical Example
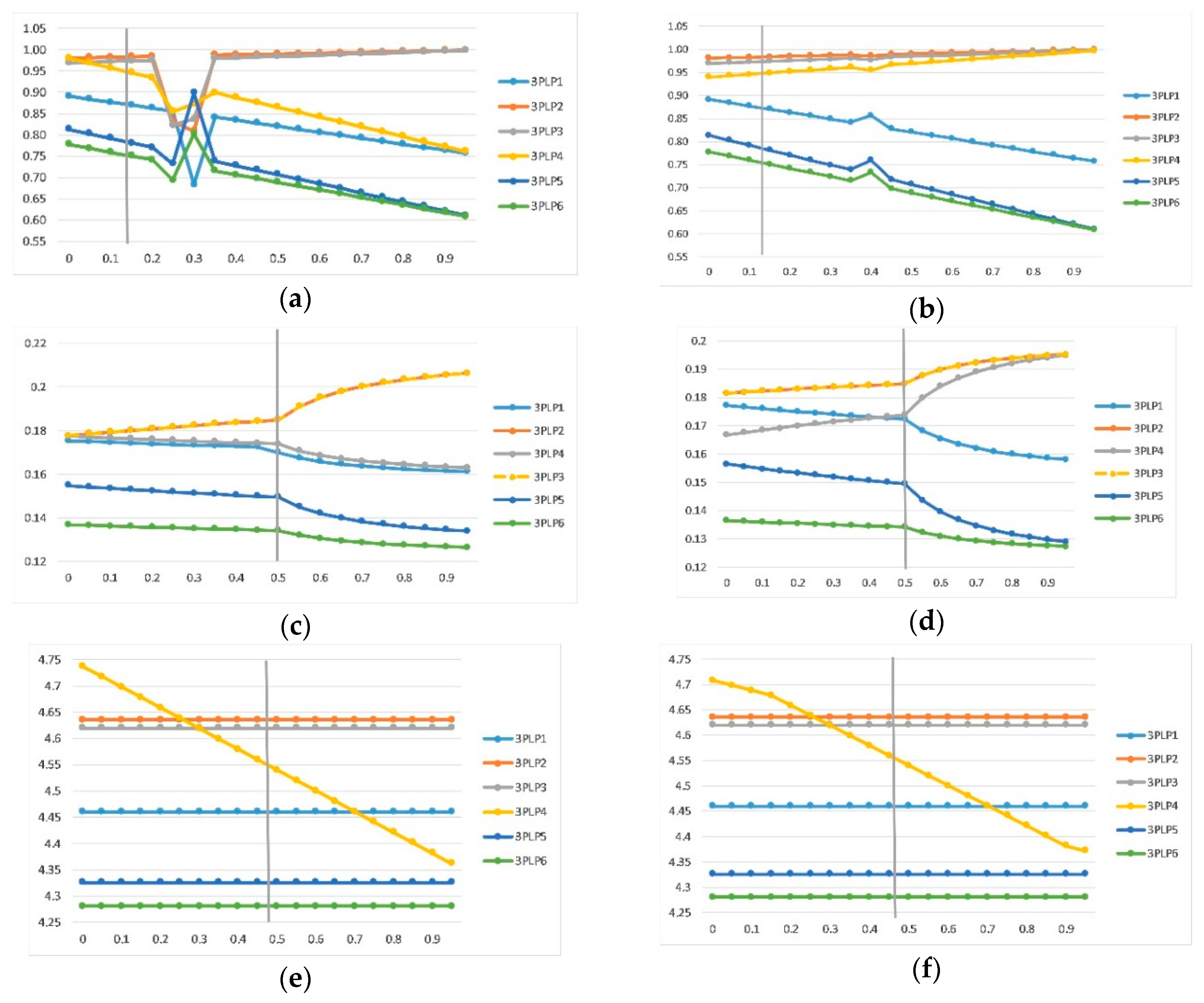
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rao, R.V. Decision Making in the Manufacturing Environment: Using Graph Theory and Fuzzy Multiple Attribute Decision Making Methods; Springer: London, UK, 2007. [Google Scholar]
- Saaty, R.W. The analytic hierarchy process—What it is and how it is used. Math. Model. 1987, 9, 161–176. [Google Scholar] [CrossRef] [Green Version]
- Paramasivam, V.; Senthil, V.; Rajam Ramasamy, N. Decision making in equipment selection: An integrated approach with digraph and matrix approach, AHP and ANP. Int. J. Adv. Manuf. Technol. 2011, 54, 1233–1244. [Google Scholar] [CrossRef]
- Saaty, T.; Vargas, L. The Analytic Network Process; Springer US: Boston, MA, USA, 2006; pp. 1–26. [Google Scholar] [CrossRef]
- Kabir, G.; Sumi, R.S. Integrating fuzzy Delphi with graph theory and matrix methods for evaluation of hazardous industrial waste transportation firm. Int. J. Logist. Econ. Glob. 2012, 4, 221–237. [Google Scholar] [CrossRef]
- Bajec, P.; Tuljak-Suban, D. A Framework for Detecting the Proper Multi-Criteria Decision-Making Method Taking into Account the Characteristics of Third-Party Logistics, the Requirements of Managers, and the Type of Input Data. In Application of Decision Science in Business and Management; Márquez, F.P.G., Ed.; IntechOpen: Rijeka, Croatia, 2019. [Google Scholar] [CrossRef] [Green Version]
- Xiu, G.; Chen, X. The third party logistics supplier selection and evaluation. J. Softw. 2012, 7, 1783–1790. [Google Scholar] [CrossRef] [Green Version]
- Mohammaditabar, D.; Teimoury, E. Integrated freight Transportation carrier selection and network flow assignment: Methodology and case study. J. Appl. Sci. 2008, 8, 2928–2938. [Google Scholar] [CrossRef]
- Lehmusvaara, A.; Tuominen, M.; KORPELA, J. An integrated approach for truck carrier selection. Int. J. Logist. Res. Appl. 1999, 2, 5–20. [Google Scholar] [CrossRef]
- Ji, G. Market-motivated value systems, reverse logistics and the evaluation model for the third party reverse logistics providers. Int. Logist. Trade 2006, 4, 53–92. [Google Scholar] [CrossRef]
- Tavana, M.; Zareinejad, M.; Di Caprio, D.; Kaviani, M.A. An integrated intuitionistic fuzzy AHP and SWOT method for outsourcing reverse logistics. Appl. Soft Comput. 2016, 40, 544–557. [Google Scholar] [CrossRef]
- Ecer, F. Third-party logistics (3PLs) provider selection via Fuzzy AHP and EDAS integrated model. Technol. Econ. Dev. Econ. 2018, 24, 615–634. [Google Scholar] [CrossRef]
- Ho, W.; He, T.; Lee, C.K.M.; Emrouznejad, A. Strategic logistics outsourcing: An integrated QFD and fuzzy AHP approach. Expert Syst. Appl. 2012, 39, 10841–10850. [Google Scholar] [CrossRef]
- Prakash, C.; Barua, M. A combined MCDM approach for evaluation and selection of third-party reverse logistics partner for Indian electronics industry. Sustain. Prod. Consum. 2016, 7, 66–78. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Göçer, F.; Karabulut, Y. A new group decision making approach with IF AHP and IF VIKOR for selecting hazardous waste carriers. Measurement 2019, 134, 66–82. [Google Scholar] [CrossRef]
- Shan, L. Research on logistics service providers selection based on AHP and VIKOR. In Intelligent Computing and Information Science; Springer: New York, NY, USA, 2011; pp. 93–98. [Google Scholar]
- Hasan, K.; Albayrakoglu, M.M. Selecting a third-party logistics provider for an autmomtive company: An analytic hierarchy process model. In Proceedings of the International Symposium on the Analytic Hierarchy Process, Viña Del Mar, Chile, 3–6 August 2007. [Google Scholar]
- Soh, S. A decision model for evaluating third-party logistics providers using fuzzy analytic hierarchy process. Afr. J. Bus. Manag. 2010, 4, 339–349. [Google Scholar]
- Gürcan, Ö.F.; Yazıcı, İ.; Beyca, Ö.F.; Arslan, Ç.Y.; Eldemir, F. Third Party Logistics (3PL) Provider Selection with AHP Application. Procedia Soc. Behav. Sci. 2016, 235, 226–234. [Google Scholar] [CrossRef]
- Daim, T.U.; Udbye, A.; Balasubramanian, A. Use of analytic hierarchy process (AHP) for selection of 3PL providers. J. Manuf. Technol. Manag. 2012, 24, 28–51. [Google Scholar] [CrossRef]
- Teker, S.Ç. The Implementation of Analytic Hierarchy Process In Pharmaceutical Industry For Selection Process Of 3rd Party Logistics Service Provider. Öneri Dergisi 2017, 12, 107–124. [Google Scholar]
- Garg, K.; Agarwal, V.; Jha, P. Transportation Decision Making Through Logistics Outsourcing and 3PL Selection in an Integrated Closed-Loop Supply Chain. In Proceedings of the Fourth International Conference on Soft Computing for Problem Solving, Silchar, Assam, India, 27–29 December 2014; pp. 473–485. [Google Scholar]
- Göl, H.; Çatay, B. Third-party logistics provider selection: Insights from a Turkish automotive company. Supply Chain Manag. Int. J. 2007, 12, 379–384. [Google Scholar] [CrossRef]
- Sardana, G.; Thatchenkery, T.; Vijayvargiya, A.; Dey, A. An analytical approach for selection of a logistics provider. Manag. Decis. 2010, 48, 403–418. [Google Scholar]
- Niestrój, K. The Conformity Assessment of Lead Logistics Provider and Third Party Logistics Preferences Using Analytic Hierarchy Process Method (AHP). J. Econ. Manag. Univ. Econ. Katow. 2013, 2013, 61–74. [Google Scholar]
- Chiang, Z.; Tzeng, G.-H. A Third Party Logistics Provider for the Best Selection in Fuzzy Dynamic Decision Environments. Int. J. Fuzzy Syst. 2009, 11, 9. [Google Scholar]
- Çakir, E.; Tozan, H.; Vayvay, O. A method for selecting third party logistic service provider using fuzzy AHP. J. Naval Sci. Eng. 2009, 5, 38–54. [Google Scholar]
- Nitin Kumar, S.; Atul Kumar, S.; Anoop Kumar, S. Fuzzy-AHP: A Boon in 3PL Decision Making Process. In Theoretical and Practical Advancements for Fuzzy System Integration; Li, D.-F., Ed.; IGI Global: Hershey, PA, USA, 2017; pp. 97–125. [Google Scholar] [CrossRef]
- Ramírez-Flórez, G.; Tabares-Urrea, N.; Osorio-Gómez, J.C. Fuzzy AHP for 3PL supplier’s performance evaluation considering risk. Facultad de Ingeniería 2017, 26, 165–172. [Google Scholar]
- Efendigil, T.; Önüt, S.; Kongar, E. A holistic approach for selecting a third-party reverse logistics provider in the presence of vagueness. Comput. Ind. Eng. 2008, 54, 269–287. [Google Scholar] [CrossRef]
- Kabir, G. Third party logistic service provider selection using fuzzy AHP and TOPSIS method. Int. J. Qual. Res. 2012, 6, 71–79. [Google Scholar]
- Rajesh, R.; Pugazhendhi, S.; Muralidharan, C.; Ganesh, K. Development of a composite model for selection of third party logistics service provider. Int. J. Electron. Cust. Relatsh. Manag. 2009, 3, 375–401. [Google Scholar] [CrossRef]
- Singh, R.K.; Gunasekaran, A.; Kumar, P. Third party logistics (3PL) selection for cold chain management: A fuzzy AHP and fuzzy TOPSIS approach. Ann. Oper. Res. 2018, 267, 531–553. [Google Scholar] [CrossRef]
- Xiuqing, Y.; Lina, Z. Study on Selection of 3pl service providers based on improved AHP and TOPSIS method. J. Henan Univ. Sci. Technol. 2013, 3, 127–129. [Google Scholar]
- Perçin, S. Evaluation of third-party logistics (3PL) providers by using a two-phase AHP and TOPSIS methodology. Benchmarking Int. J. 2009, 16, 588–604. [Google Scholar] [CrossRef]
- Kumar, P. An integrated model of AHP and TOPSIS for 3PL evaluation. Asia Pac. Bus. Rev. 2008, 4, 14–21. [Google Scholar] [CrossRef]
- Akman, G.; Baynal, K. Logistics Service Provider Selection through an Integrated Fuzzy Multicriteria Decision Making Approach. J. Ind. Eng. 2014, 2014, 794918. [Google Scholar] [CrossRef] [Green Version]
- Kishore, P.; Padmanabhan, G. An Integrated Approach of Fuzzy AHP and Fuzzy TOPSIS to Select Logistics Service Provider. J. Manuf. Sci. Prod. 2016, 6, 51–59. [Google Scholar] [CrossRef]
- Bianchini, A. 3PL provider selection by AHP and TOPSIS methodology. Benchmarking Int. J. 2018, 25, 235–252. [Google Scholar] [CrossRef]
- Singh, R.; Shankar, R.; Kumar, P.; Singh, R.K. A fuzzy AHP and TOPSIS methodology to evaluate 3PL in a supply chain. J. Model. Manag. 2012, 7, 287–303. [Google Scholar]
- Bansal, A.; Kumar, P. 3PL selection using hybrid model of AHP-PROMETHEE. Int. J. Serv. Oper. Manag. 2013, 14, 373–397. [Google Scholar] [CrossRef]
- Gupta, R.; Sachdeva, A.; Bhardwaj, A. Selection of logistic service provider using fuzzy PROMETHEE for a cement industry. J. Manuf. Technol. Manag. 2012, 23, 899–921. [Google Scholar] [CrossRef]
- Jung, H. Evaluation of Third Party Logistics Providers Considering Social Sustainability. Sustainability 2017, 9, 777. [Google Scholar] [CrossRef] [Green Version]
- Yilmaz, O.; Endüstri, B.Y.; Güneri, A.F.; Gülsün, B.; Özgürler, Ş. A solution to customer selection problem in logistics using the Analytic Network Process (ANP). In Proceedings of the Trends in the Development of Machinery and Associated Technology, TMT Mediteranean Cruise, Venice, Italy, 11–18 September 2010. [Google Scholar]
- Fadavi, A.; Khanghah, A.S.; Asli, M.N. A Hybrid Model for Supplier Selection in Outsourcing: Evidence from Shima Film Company in Iran. Res. J. Appl. Sci. Eng. Technol. 2013, 5, 3298–3305. [Google Scholar] [CrossRef]
- Cooper, O.; Tadikamalla, P.; Shang, J. Selection of a Third-Party Logistics Provider: Capturing the Interaction and Influence of Performance Metrics with the Analytical Network Process. J. Multi Criteria Decis. Anal. 2012, 19, 115–128. [Google Scholar] [CrossRef]
- Janssen, L.; Claus, T.; Sauer, J. Literature review of deteriorating inventory models by key topics from 2012 to 2015. Int. J. Prod. Econ. 2016, 182, 86–112. [Google Scholar] [CrossRef] [Green Version]
- Liou, J.J.H.; Chuang, Y.-T. Developing a hybrid multi-criteria model for selection of outsourcing providers. Expert Syst. Appl. 2010, 37, 3755–3761. [Google Scholar] [CrossRef]
- Hsu, C.-C.; Liou, J.J.H.; Chuang, Y.-C. Integrating DANP and modified grey relation theory for the selection of an outsourcing provider. Expert Syst. Appl. 2013, 40, 2297–2304. [Google Scholar] [CrossRef]
- Wong, J.-T. DSS for 3PL provider selection in global supply chain: Combining the multi-objective optimization model with experts’ opinions. J. Intell. Manuf. 2012, 23, 599–614. [Google Scholar] [CrossRef]
- Thakkar, J.; Deshmukh, S.; Gupta, A.; Shankar, R. Selection of third-party logistics (3PL): A hybrid approach using interpretive structural modeling (ISM) and analytic network process (ANP). Supply Chain Forum Int. J. 2005, 6, 32–46. [Google Scholar] [CrossRef]
- Zareinejad, M.; Javanmard, H. Evaluation and selection of a third-party reverse logistics provider using ANP and IFG-MCDM methodology. Life Sci. J. 2013, 10, 350–355. [Google Scholar]
- Senturk, S.; Erginel, N.; Binici, Y. Interval Type-2 Fuzzy Analytic Network Process for Modelling a Third-party Logistics (3PL) Company. J. Mult. Valued Logic Soft Comput. 2017, 28, 311–333. [Google Scholar]
- Tavana, M.; Zareinejad, M.; Santos-Arteaga, F.J.; Kaviani, M.A. A conceptual analytic network model for evaluating and selecting third-party reverse logistics providers. Int. J. Adv. Manuf. Technol. 2016, 86, 1705–1721. [Google Scholar] [CrossRef]
- Esra Aytaç, A.; Egül, A.T. Integration of DEMATEL, ANP and DEA methods for third party logistics providers’ selection. Manag. Sci. Lett. 2016, 6, 325–340. [Google Scholar] [CrossRef]
- Raut, R.; Kharat, M.; Kamble, S.; Kumar, C.S. Sustainable evaluation and selection of potential third-party logistics (3PL) providers: An integrated MCDM approach. Benchmarking Int. J. 2018, 25, 76–97. [Google Scholar] [CrossRef]
- Muduli, K.; Govindan, K.; Barve, A.; Geng, Y. Barriers to green supply chain management in Indian mining industries: A graph theoretic approach. J. Clean. Prod. 2013, 47, 335–344. [Google Scholar] [CrossRef]
- Agrawal, S.; Singh, R.K.; Murtaza, Q. Disposition decisions in reverse logistics: Graph theory and matrix approach. J. Clean. Prod. 2016, 137, 93–104. [Google Scholar] [CrossRef]
- Mohaghar, A.; Kashef, M.; Khanmohammadi, E. A novel technique to solve the supplier selection problems: Combination of decision making trial & evaluation laboratory, graph theory and matrix approach methods. Int. J. Ind. Eng. 2014, 25, 103–113. [Google Scholar]
- Athawale, V.M.; Mukherjee, P.; Chakraborty, S. Supplier Selection Using Multi-Criteria Decision-Making Methods. IUP J. Oper. Manag. 2009, 8, 831–851. [Google Scholar]
- Malik, S.; Kumari, A.; Agrawal, S. Selection of Locations of Collection Centers for Reverse Logistics Using GTMA. Mater. Today Proc. 2015, 2, 2538–2547. [Google Scholar] [CrossRef]
- Zhuang, Z.-Y.; Lin, C.-C.; Chen, C.-Y.; Su, C.-R. Rank-Based Comparative Research Flow Benchmarking the Effectiveness of AHP–GTMA on Aiding Decisions of Shredder Selection by Reference to AHP–TOPSIS. Appl. Sci. 2018, 8, 1974. [Google Scholar] [CrossRef] [Green Version]
- Safari, H.; Faghih, A.; Fathi, M.R. Integration of graph theory and matrix approach with fuzzy AHP for equipment selection. J. Ind. Eng. Manag. (JIEM) 2013, 6, 477–494. [Google Scholar]
- Chaghooshi, A.J.; Safari, H.; Fathi, M.R. Integration of fuzzy AHP and fuzzy GTMA for location selection of gas pressure reducing stations: A case study. J. Manag. Res 2012, 4, 152–169. [Google Scholar]
- Singh, D.; Rao, R. A hybrid multiple attribute decision making method for solving problems of industrial environment. Int. J. Ind. Eng. Comput. 2011, 2, 631–644. [Google Scholar] [CrossRef]
- Mu, E.; Pereyra-Rojas, M. Practical Decision Making: An Introduction to the Analytic Hierarchy Process (AHP) Using Super Decisions V2; Springer: Pittsburg, PA, USA, 2017. [Google Scholar]
- Brunelli, M. Introduction to the Analytic Hierarchy Process; Springer International Publishing: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Saaty, T.L. Decision Making for Leaders: The Analytic Hierarchy Process for Decisions in a Complex World; RWS Publications: Pittsburgh, PA, USA, 1990. [Google Scholar]
- Lanjewar, P.B.; Rao, R.V.; Kale, A.V. Assessment of alternative fuels for transportation using a hybrid graph theory and analytic hierarchy process method. Fuel 2015, 154, 9–16. [Google Scholar] [CrossRef]
- Saaty, T.L. Axiomatic Foundation of the Analytic Hierarchy Process. Manag. Sci. 1986, 32, 841–855. [Google Scholar] [CrossRef]
- Tuljak-Suban, D.; Bajec, P. The Influence of Defuzzification Methods to Decision Support Systems Based on Fuzzy AHP with Scattered Comparison Matrix: Application to 3PLP Selection as a Case Study. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2018, 26, 475–491. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision Making with Dependence and Feedback: The Analytic Network Process: The Organization and Prioritization of Complexity; Rws Publications: Pittsburgh, PA, USA, 2001. [Google Scholar]
- Kordi, M. Comparison of Fuzzy and Crisp Analytic Hierarchy Process (AHP) Methods for Spatial Multicriteria Decision Analysis in GIS; University of Gävle: Gävle, Sweden, 2008. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Geetha, N.K.; Sekar, P. Graph Theory Matrix Approach–A Qualitative Decision Making Tool. Mater. Today Proc. 2017, 4, 7741–7749. [Google Scholar] [CrossRef]
- Beineke, L.W.; Wilson, R.J.; Cameron, P.J. Topics in Algebraic Graph Theory; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Jurkat, W.B.; Ryser, H.J. Matrix factorizations of determinants and permanents. J. Algebra 1966, 3, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Tung, Y.A. Time complexity and consistency issues in using the AHP for making group decisions. J. Multi Criteria Decis. Anal. 1998, 7, 144–154. [Google Scholar] [CrossRef]
- Kadoić, N.; Divjak, B.; Begičević Ređep, N. Integrating the DEMATEL with the analytic network process for effective decision-making. Cent. Eur. J. Oper. Res. 2018. [Google Scholar] [CrossRef]
- Han, Q.; Li, W.; Song, Y.; Zhang, T.; Wang, R. A New Method for MAGDM Based on Improved TOPSIS and a Novel Pythagorean Fuzzy Soft Entropy. Symmetry 2019, 11, 905. [Google Scholar] [CrossRef] [Green Version]

| Relative Importance Definition | aij | aji = 1 − aij |
|---|---|---|
| Two attributes are equally important | 0.5 | 0.5 |
| One attribute is slightly more important than the other | 0.6 | 0.4 |
| One attribute is strongly more important than the other | 0.7 | 0.3 |
| One attribute is very strongly more important than the other | 0.8 | 0.2 |
| One attribute is extremely more important than the other | 0.9 | 0.1 |
| One attribute is exceptionally more important than the other | 1.0 | 0.0 |
| Cluster Level | Criteria Level |
|---|---|
| K1—costs | C11—cost of warehousing |
| C12—costs of inventory management | |
| C13—additional service costs | |
| K2—services | C21—opening hours |
| C22—order size and configuration flexibility | |
| C23—possibility to change order details | |
| C24—shipment errors (quality, quantity and place) | |
| C25—product variety | |
| C26—ability to provide added value services | |
| C27—response time | |
| C28—possibility for temperature control, humidity | |
| C29—historical on-time delivery and deviations | |
| K3—information technology (IT) | C31—transfer of data in real time |
| C32—use of technology (RFID/barcode) | |
| K4—infrastructure and suprastructure | C41—separation of storage areas |
| C42—handling equipment (electric, gas, diesel) | |
| C43—number and characteristics of docks | |
| C44—distance to highway connection | |
| K5—human resources | C51—worker satisfaction |
| C52—types and quality of communication | |
| C53—personal relationships with key customers | |
| K6—risk management | C61—willingness to assume risk |
| C62—data security |
| 3PLP Evaluation | 3PLP Normalized Evaluation | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3PLP1 | 3PLP2 | 3PLP3 | 3PLP4 | 3PLP5 | 3PLP6 | 3PLP1 | 3PLP2 | 3PLP3 | 3PLP4 | 3PLP5 | 3PLP6 | |
| C11 | 4 | 3 | 3 | 4 | 5 | 5 | 0.75 | 1 | 1 | 0.75 | 0.6 | 0.6 |
| C12 | 4 | 3 | 3 | 3 | 5 | 5 | 0.75 | 1 | 1 | 1 | 0.6 | 0.6 |
| C13 | 4 | 3 | 3 | 3 | 5 | 5 | 0.75 | 1 | 1 | 1 | 0.6 | 0.6 |
| C21 | 4 | 4 | 4 | 4 | 4 | 4 | 1 | 1 | 1 | 1 | 1 | 1 |
| C22 | 4 | 5 | 5 | 5 | 4 | 3 | 0.8 | 1 | 1 | 1 | 0.8 | 0.6 |
| C23 | 4 | 5 | 5 | 5 | 3 | 3 | 0.8 | 1 | 1 | 1 | 0.6 | 0.6 |
| C24 | 4 | 4 | 4 | 4 | 3 | 4 | 0.75 | 0.75 | 0.75 | 0.75 | 1 | 0.75 |
| C25 | 5 | 5 | 5 | 5 | 5 | 3 | 1 | 1 | 1 | 1 | 1 | 0.6 |
| C26 | 5 | 5 | 5 | 5 | 5 | 5 | 1 | 1 | 1 | 1 | 1 | 1 |
| C27 | 4 | 5 | 5 | 5 | 4 | 4 | 1 | 0.8 | 0.8 | 0.8 | 1 | 1 |
| C28 | 5 | 5 | 5 | 5 | 5 | 5 | 1 | 1 | 1 | 1 | 1 | 1 |
| C29 | 4 | 4 | 4 | 4 | 4 | 4 | 1 | 1 | 1 | 1 | 1 | 1 |
| C31 | 4 | 5 | 5 | 5 | 4 | 3 | 0.8 | 1 | 1 | 1 | 0.8 | 0.6 |
| C32 | 5 | 5 | 5 | 5 | 5 | 5 | 1 | 1 | 1 | 1 | 1 | 1 |
| C41 | 4 | 5 | 5 | 5 | 4 | 4 | 0.8 | 1 | 1 | 1 | 0.8 | 0.8 |
| C42 | 5 | 5 | 5 | 5 | 3 | 3 | 1 | 1 | 1 | 1 | 0.6 | 0.6 |
| C43 | 3 | 4 | 4 | 4 | 3 | 3 | 0.75 | 1 | 1 | 1 | 0.75 | 0.75 |
| C44 | 4 | 4 | 4 | 4 | 4 | 4 | 1 | 1 | 1 | 1 | 1 | 1 |
| C51 | 4 | 4 | 4 | 4 | 3 | 3 | 1 | 1 | 1 | 1 | 0.75 | 0.75 |
| C52 | 3 | 4 | 4 | 4 | 3 | 3 | 0.75 | 1 | 1 | 1 | 0.75 | 0.75 |
| C53 | 4 | 4 | 3 | 4 | 4 | 4 | 1 | 1 | 0.75 | 1 | 1 | 1 |
| C61 | 2 | 5 | 5 | 5 | 2 | 2 | 0.4 | 1 | 1 | 1 | 0.4 | 0.4 |
| C62 | 4 | 4 | 4 | 4 | 4 | 4 | 1 | 1 | 1 | 1 | 1 | 1 |
| Cluster Level Weights (CR = 0.0145) | Criteria Level Weights | Final Level Weights | Consistency Check | ||
|---|---|---|---|---|---|
| K1 | 0.3189 | C11 | 0.4444 | 0.1417 | |
| C12 | 0.4444 | 0.1417 | |||
| C13 | 0.1111 | 0.0354 | |||
| K2 | 0.2125 | C21 | 0.1705 | 0.0362 | |
| C22 | 0.0337 | 0.0072 | |||
| C23 | 0.0337 | 0.0072 | |||
| C24 | 0.1705 | 0.0362 | |||
| C25 | 0.1705 | 0.0362 | |||
| C26 | 0.0905 | 0.0192 | |||
| C27 | 0.1705 | 0.0362 | |||
| C28 | 0.0210 | 0.0045 | |||
| C29 | 0.1392 | 0.0296 | |||
| K3 | 0.0905 | C31 | 0.3333 | 0.0302 | |
| C32 | 0.6667 | 0.0603 | |||
| K4 | 0.1973 | C41 | 0.0883 | 0.0174 | |
| C42 | 0.4824 | 0.0952 | |||
| C43 | 0.2718 | 0.0536 | |||
| C44 | 0.1575 | 0.0311 | |||
| K5 | 0.0904 | C51 | 0.4286 | 0.0387 | |
| C52 | 0.1429 | 0.0129 | |||
| C53 | 0.4286 | 0.0387 | |||
| K6 | 0.0904 | C61 | 0.2000 | 0.0181 | |
| C62 | 0.8000 | 0.0723 | |||
| Name | Normalized by Cluster | Limiting |
|---|---|---|
| 3PLP5 | 0.1495 | 0.8085 |
| 3PLP4 | 0.1739 | 0.9403 |
| 3PLP6 | 0.1343 | 0.7259 |
| 3PLP1 | 0.1724 | 0.9321 |
| 3PLP3 | 0.185 | 1 |
| 3PLP2 | 0.185 | 1 |
| 0.6 | 0.7 | 0.6 | 0.7 | 0.7 | ||
| 0.4 | 0.6 | 0.5 | 0.7 | 0.7 | ||
| 0.3 | 0.4 | 0.3 | 0.5 | 0.5 | ||
| 0.4 | 0.5 | 0.7 | 0.6 | 0.6 | ||
| 0.3 | 0.3 | 0.5 | 0.4 | 0.5 | ||
| 0.3 | 0.3 | 0.5 | 0.4 | 0.5 |
| PAI | Rank | |
|---|---|---|
| 3PLP1 | 4.4594 | 4 |
| 3PLP2 | 4.6356 | 1 |
| 3PLP3 | 4.6197 | 2 |
| 3PLP4 | 4.5796 | 3 |
| 3PLP5 | 4.3259 | 5 |
| 3PLP6 | 4.2808 | 6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuljak-Suban, D.; Bajec, P. Integration of AHP and GTMA to Make a Reliable Decision in Complex Decision-Making Problems: Application of the Logistics Provider Selection Problem as a Case Study. Symmetry 2020, 12, 766. https://doi.org/10.3390/sym12050766
Tuljak-Suban D, Bajec P. Integration of AHP and GTMA to Make a Reliable Decision in Complex Decision-Making Problems: Application of the Logistics Provider Selection Problem as a Case Study. Symmetry. 2020; 12(5):766. https://doi.org/10.3390/sym12050766
Chicago/Turabian StyleTuljak-Suban, Danijela, and Patricija Bajec. 2020. "Integration of AHP and GTMA to Make a Reliable Decision in Complex Decision-Making Problems: Application of the Logistics Provider Selection Problem as a Case Study" Symmetry 12, no. 5: 766. https://doi.org/10.3390/sym12050766
APA StyleTuljak-Suban, D., & Bajec, P. (2020). Integration of AHP and GTMA to Make a Reliable Decision in Complex Decision-Making Problems: Application of the Logistics Provider Selection Problem as a Case Study. Symmetry, 12(5), 766. https://doi.org/10.3390/sym12050766






