2.1. The Modified Wilson Loop for Coopers Pairs
In quantum mechanics, the orbital of an electron in graphene is modeled as a wavefunction which gives the probability of finding the electron in the momentum space k and of a sphere in Fermi sea. In the Ginzburg-Landau (GL) theory, we use in 4-spheres for a superstatistics of couplings in the Chern-Simons 3-forms between the Cooper pairs and a graviphoton. The wavefunction separates into the left and right supersymmetry in the upper half plane of the complex plane. The left symmetry of the orbital is modeled by the Hilbert transform with three hidden layers of instantaneous frequency. The right supersymmetry is an imaginary part and it is hidden.
Let
be a superspace of the Chern-Simons (CS) manifold D-brane of a graphene wormhole. The cohomology theory of superspace is adopted for measuring the invariant property of equilibrium state of the coupling between Cooper pairs and graviphoton. The Bose-Einstein condensation, at equilibrium of electron vibrations in the graphene lattice, induces a superstatistic with a superdistribution of cocycles of Cooper pairs in
. Here
is an equivalent homotopy path of cocycles in the equivalent value of an order parameter for a superconductor. In GL theory of phase transitions, the order parameter to change normal state to superconductivity state is a condensed wave function of the Cooper pairs. The fourth order wave function is analogue to a new type of Chern-Simons current with
. It might be also a new type of superstatistics of Bose-Einstein condensation in supercurrent condensation state in the fourth dimension induced by the integration of 3-forms over three new types of modified Wilson loops with coupling behavior of the Cooper pairs
(see
Figure 1). By the interaction of two mathematical hybrid objects, the so called Wilson loop
and the Chern-Simons current
, we can relax the gauge theory definition and redefine new mathematical objects for more flexible and suitable study of phase transition in the superconductor.
The quantum foam model in graphene wormhole is a moduli state space model similar to quantum dots, an array of Josephson junction. Inside the Josephson junction there exists a supercurrent tunneling effect across the wormhole from the left to the right supersymmetry. The model of Cooper pairs tunneling across Josephson junctions involves three forms of coupling between three Lie algebras. The first form is induced by the coherent state of coupling between a photon with a graviton. The second and third fields are the Cooper pairs of electrons in graphene wormhole with quantum foam condensation states. The superconductivity state of Coopers pairs is related to ribbon graph of loop gravity algorithm with Wilson loop of graviphoton over the link between their edge of free electron spinor field in Cooper pairs. The spinor network and the quantum holonomy can be implemented by the Ising algorithm of quantum machine learning [
39] to find the order parameters in the wormhole structure. We assume that, in the superconductor state of the wormhole, the state is coherent and the energy of states cannot be lost with respect to changing the gauge field in the Chern-Simons current. When we change free energy, the superconductor magnetic flux will not change up to some threshold. We quantize free energy of Cooper pairs in the wormhole by using the moduli state space model of the Chern-Simons forms
,
,
.
In gauge theory, is a gauge field that can be realized as a Wilson loop. Traditionally, we represent an electric field or an electromagnetic field with the field strength , that is, a Yang-Mills field. In the Chern-Simons theory, is represented by a general field for any fields to be unified. In this paper, we use for the field of electron attributes to be learned within the supersymmetric support Dirac network. These attributes are induced by three types of molecular orbitals of carbon lattice in the graphene wormwhole.
Definition 1. Let A be a connection along spinor field of the Cooper pairs. Let be a coupling between two connection fields, one is from hexagonal carbon ring of graphene as an edge A of spinor network, the other is from localized electrons around bonding of carbon atoms. We use the wedge product of three bonds and denote it as the Chern-Simons 3-forms .
In the molecular orbital of the graphene with repeated
N carbon atoms, the trajectory of an electron is visualized by an energy band. We alternatively use a new methodology to visualize the energy band by using a partition function over the free energy. The orbital is induced by the supersymmetry of group operations on the principle bundle of the connection. The trajectory of the free electron can be a knot state of modified Wilson loop with the spin invariant. The connection of spinor field gives a parallel transport of the free electron along hexagonal carbon atoms in the equilibrium state of the superconductor (see
Figure 1).
Let be the Kolmogorov space of time series data of the Cooper pairs trajectory. The loop is coming from the chosen point on the momentum space of the free electron with the equivalent class of fundamental group .
Definition 2. Let A be a connection of Cooper pairs. We define the equilibrium state of Cooper pairs with partition function with the chosen action of the system equal to one form of the third connection in carbon lattice .
Definition 3. The canonical form of the Chern-Simons supercurrent in a graphene wormhole is an equilibrium state of parallel transport of Cooper pairs along the 3-form of connections over 3 carbon rings of 6 carbon atoms per rings with canonical state k of partition function. The formula is At the equilibrium of parallel transport, the current is a conserved free energy for moving Cooper pairs so that we have the change of path integral to differential form over cohomology
. It is
. We approximate
so we have
with
as a partition function of states of Cooper pairs trajectory as modified Wilson loop in the framework of electrons as a co-differential map of co-chain complex. We have
if we consider a space trajectory of the Cooper pairs
over carbon lattice
. It is a complex spanned by the cell as the edge of ribbon graph
with the connection
A for each edge. In each cell complex, we have a partition function
as the equilibrium state for coherent superconductivity states of the Cooper pairs with an exact sequence of infinite cohomology
.
We define the kernel function as the partition function with Lie derivative in the form of exponential. So we have a general form of the supercurrent by
with
Definition 4. A cohomology of free energy in graphene wormhole is composed by a chain of carbon lattice complex with three types of connections , , of the gauge fields for an electron.
In this model, the first cohomology group is a ribbon graph of spinor network. We assume that the supercurrent is the Chern-Simons current over holonomy of the Cooper pairs along ribbon graph of carbon lattice. The connection
is a modified Wilson loop from our definition above. The behavior of electron parallel transport can be expressed by the coupling between these connection gauge fields. The attribute
is also having some extra-property asthe behavior of supersymmetric Dirac neuron network in our new model of quantum machine learning. We have an expectation of the attribute as a group action with fixed points of the gauge group in the mirror symmetry gauge group action along the ribbon graph of carbon lattice, that is
2.2. Geometry of the Cooper Pairs
The decomposition of the Cooper pairs, while tunneling through Josephson junction in a wormhole, switches the spin orbital of Cooper pairs electrons from the left chiral supersymmetry to the right chiral supersymmetry in the superconductor junction of child manifold through a normal junction of the Chern-Simons manifold. The mechanism of phase shift in the tunneling produces a graviphoton by inducing the Chern-Simons supercurrent in the fifth dimensional extension of the fourth dimensional model of double graphene sheet. We assume that energy is conserved over extradimensions in the form of exact sequence of cohomology of free energy. The Cooper pairs tunnel from fourth dimension to fifth dimension by using the differential operator over the chain complex of the superspace. The distortion of fifth dimension produces a gravitational curvature as the graviphoton mass produces two electrons in the Cooper pairs separated, each other, inside the graphene wormhole. This mechanism is analogue of the quantum entanglement state in quantum information theory with warping state as entanglement states of the Cooper pairs. The supercurrent is produced by changing the phase of the Cooper pairs from child1 manifold to child2 manifold with starting superconductivity as the supercurrent. Our theoretical study is based on the superspace of two sheets of graphene in -dimensional model with where is a left child manifold of graphene sheet with the left chiral supersymmetry and is a right child manifold of graphene sheet with the right chiral supersymmetry and the extradimension is a dual superspace of graphene with real ground field as fifth dimension.
In this section, we relax some properties as curvature, connection, Yang-Mill field and Dirac operator by adding new properties to definitions of modified Dirac operator and supersymmetric support Dirac network just for the purpose to study specific property of the Chern-Simons current in the superspace of extradimensions.
We consider the connections , , between two molecules of graphene in the wormhole as a simple example of two child manifolds , with single bond link between them as the Chern-Simons manifold. We can use this model to extend to more carbon molecules in child manifold and add some extra carbon molecules to the Chern-Simons manifold in next steps by using optimization along the spinor network. A graphene molecule is hexagonal without defect. The other molecule is pentagonal with one defect. The Chern-Simons-bridge connects bonds of carbon atoms and induces closed surfaces with curvature and graviphotons as the connection of electrons. These electrons move freely around free energy close surface for N combination of hexagonal and pentagonal carbon molecular lattice of graphene.
Let homotopy path over manifold of pentagon
be a homotopy from deformed crystal lattice distance between pointed space of time series data as a ground gauge field without excitation
of free electron in bonds of pentagons along the path
. Giving a projection map
, we take a covariant functor to the trajectory of Cooper pairs free electrons in the wormhole with curvature of topological defect in child manifold
by
so we have
in which a cohomology group is induced by using kernel map from a conservation of free energy in the fifth dimension. We define the Hamiltonian of the global system by using the differential map in the chain sequence with moduli state space of kernel and image map in
and turn an arrow from covariant functor to contravariant functor in order to produce a gauge field of deformed curvature of spinor field as induced gravitomagnetic field with graviphoton mass as source from
Bending the covalent bond from hexagonal to pentagonal, we have
Consider now the other side of the D-brane with induced operator and anti-D-brane with a trajectory of free Cooper pairs with electronic spin in Kolmogorov space as ground state of with covering space . Consider the homotopy path of the Hopf fibration from with group action of spinor field of graviphoton in mirror symmetry for quantum tunneling . Taking a covariant functor as above, we get a cohomolgy group.
The tunneling in the wormhole induces a graviphoton over the Hopf fibration and violates the CPT invariance because of the electron warping across the tunnelling. Let us now compute the hidden 8 states of the graviphoton with spin 1. The states of graviphoton can be interpreted as qubit state over the Hopf fibration .
We define three cohomology sequences, a sequence of free electrons , an external magnetic supercurrent field of photons and a qubit memory holding states of graviphotons . The coupling between these cohomology sequences induces an chiral state from left hand to right hand by deformed curvature of spacetime in the wormhole with changing cohomolgy connections.
Physical interpretation of a monopole or an instanton in the graphene crystal is equivalent to the quantum tunneling in the semiclassical scale of wormhole connected by a single group of graphene molecules from different sides of Einstein-Rosen bridge as child1 and child2 manifolds. The Chern-Simons manifold is equivalent to the length of group of graphene crystal as a single coupling constant.
Let a general solution, induced by the trajectory of 3-orbitals between the coupling of Cooper pairs and graviphotons, be written in the general form of coupling between three cosines with unknown frequencies and amplitudes of energy states, that is
The first term is induced by the tensor correlation between the graviphoton and others, the second and third terms are equivalent in the construction. A mirror symmetry to
can be written in the form
Let
be a partition function as a boundary volume 3-forms
over the superspace of graphene wormhole. We explicitly approximate the current to the boundary in
by
Let
be a superspace of child1 and
be a superspace of child2. The Chern-Simons bridge is denoted by a moduli state space
which can twist to
by using a supersymmetric Wilson loop operator inside the wormhole. We define a superconductor junction in the graphene wormhole by the spectral sequence of sheave cohomology over a section of graphene vector field in the wormhole. Let
(
D—D-brane,
—anti-D-brane) be a pointed space of starting states of Cooper pairs from the layer of D-brane
In order to link the D-brane
and the anti-D-brane
, one needs a supersymmetry to warp between sheets without loosing time. In order to do that one needs to define a BV-cohomology [
40] for the superspace of graphene wormhole
.
The chain complex of carbon atoms in graphene lattice is denoted by
. Let
be a BV-cohomolgy model for the superspace of graphene wormhole defined by warping between twistors of 2 sheets in the Chern-Simons manifold with Cooper pairs production of graviphotons. The stable orbital is defined as
We take a contravariant
, functor of the ground base-space
X, in the commutative diagram
We have the image of differential map by the homotopy class
with the image map from the fifth dimension to the fourth dimension defined as
. The image modulo kernel map is defining the coupling of graviphoton in the fourth dimension with homotopy equivalent to
(a moduli based space of Hopf fibration
) as the space of graviphotons. In a fourth dimensional model of a graphene wormhole, we define a superspace of Cooper pairs orbital as
Definition 5. Let be a free electron orbital of a separated free electron around a lattice of carbon atoms in the graphene with homotopy equivalent to unit sphere of the Cooper pairs with spin orbital , . For the other part of the Cooper pairs, is a free electron orbital of separated free electrons around a lattice of carbon atoms in the graphene with homotopy equivalent to unit sphere of Cooper pairs with spin orbital , . An orbital of Cooper pairs is ; it is the Hopf fibration .
Definition 6. Let a Josephson effect for the Cooper pairs be defined by the connection between Cooper pairs wave function and graviphotons in the extradimension warp between fourth dimension and fifth dimension. We denote the connection from the free electrons to the wall of space border in fifth dimension by . We define an instantaneous phase shift from a superconductor junction to another superconductor junction by a curvature in an amount of warped time in . The Josephson equation can be transformed to the equation over the curvature of fifth dimension by .
We define the Chern-Simons current in a 5-dimensional model and in an 11-dimensional model by the application of free electron transport in the graphene wormhole. Let
be a curvature of electron trajectory homotopy path with the spin in parallel and anti-parallel direction with respect to its momentum. Let
be the distance between atoms in the graphene with defects inducing the curvature. The fifth dimensional model is denoted by the Hopf fibration. We use a metric on the Ricci flat cone superspace
where
,
are the Cooper pairs orbitals in Hopf fibration which are self dual between D-brane and anti-D-brane of graphene child manifold
. The curvature
deforms the superspace in the wormhole between the connection in D-brane
a and anti-D-brane
b. We define a current in 5-dimensions
, by gluing four unit spheres
by disjoining the sum
. Let
be a Kolmogorov space of free electrons in the wormhole. We use homotopy path
for the projection from extra-dimensions to 4-dimensional D-branes. We have the Hopf fibration
acting on a fibre of tangent space
to orbit based space in
. The current metric in the wormhole is defined over
as a stable pointed space embedded in 11-dimensional manifold. It is contractible to the Chern-Simons child manifold over
, a principle bundle orbit of Cooper pairs with self-dual two form over
. Lie algebras can be defined by the Chern-Simons 3-forms connecting two child manifolds as the Einstein-Rosen bridge in the superconductor grahene wormhole.
The Chern-Simons current is an axial correlation and projection from 5-dimensional model of D-brane into 4 dimensions by using 3-forms. These forms are the main tool for the measurement of induced changing volume of interaction flux of gravitational field with magnetic field in 3-vector fields with their induced dual fields in AdS -Yang-Mill fields. The superspace of graphene is composed by a tensor product of 3-forms in 4-dimensional model of the Chern-Simons form glued up into the superspace with modulo . We can use the Chern-Simons 3-current to measure the interaction between two D-branes in the graphene as a metric of Lie algebras 3-forms of imaginary map modulo kernel projection map in the cohomology theory.
Definition 7. Let be a Kolmogorov space of trajectory of a pair with Hopf fibration of free electrons in the wormhole. The superspace with dimension of graphene wormhole is defined by the homotopy class deformed in a double plane (one time deformed in D-brane and one time in anti-D-brane simultaneously) with moduli space of the Chern-Simons 3-formsThe elementary form is similar to the modified Nahm equation of the coupling between 3-Lie algebras in 11-dimensional model with string in the superspace with a projection to the i-dimension. In 3-dimensions, we have a moduli superspace of the graphene between three string couplings with the curvature of graviphotons in three bonds of deformed hexagon of graphene wormhole. It isfor , . Let
be an integral of the momentum of Cooper pairs, let
be the Chern-Simons current. We define the moduli superspace of free energy in the wormhole by a quantization of the coupling between the momentum of Cooper pairs and the induced Chern-Simons current from the graviphoton
. We have
where the Proca equation for the full canonical momentum of the Cooper pairs, including gravitational fields, is given by
Let the orbital of graviphoton be belonging to the tangent of manifold one form with Lie algebra as tangent of the graviphoton manifold . The Cooper pairs in the left chiral state are and . The right chiral state of the Cooper pairs in mirror symmetry is denoted by and in dual one form over the manifold of the Cooper pairs. We glue three orbitals as coherent states in the Chern-Simons 3-forms over . The trace invariant is measured by the Hermitian product over the tangent of supermanifold. We denote, as Chern-Simons current, the density of superconductor states in graphene wormhole . It is a group action of Hopf fibration over the tangent space of Calabi-Yau orbifold in a quantum foam model for the superconductor. We will compute the integral for finding the optimal Chern-Simons current in the superconductor state with the radius of the wormhole in the next section.
Consider a 4-dimension space with the curvature
. The volume form in the Chern-Simons graphene wormhole with the free energy of coupling between the graviphoton and Cooper electron pairs can be written as an equation with boundary conditions, that is,
where
(
) is a connection over the fibration. The moduli term signifies quantum states with the warping of an electron around a graviphoton. The confinement produces a gluon exchange since it is possible to transform the above equation with the energy state as
where
and
is the 2-dual basis span over lattice of graphene D-brane in 2-dimensions, basis
, basis
.
The process is a quantum foam model of confinement similar to the gluon exchange of a quark and an antiquark producing a knot in the modified Wilson loop of a graviphoton.
2.3. The Supersymmetric Support Dirac Network
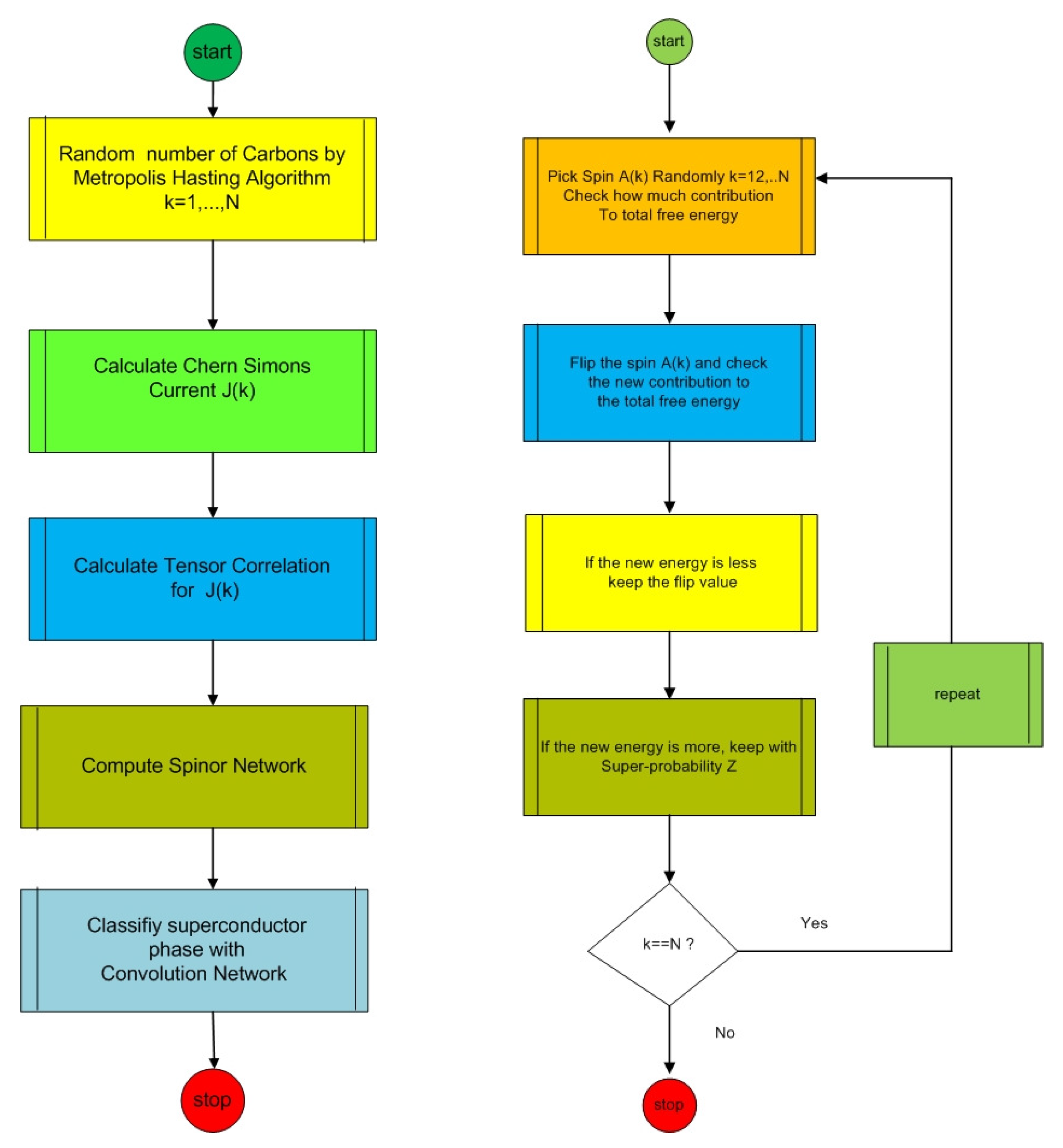
A supersymmetric support Dirac network (SSDN) is a support spinor network. It presents some extraproperties of the attachment of a modified Dirac operator for each edge with a capacity of the Chern-Simons current in the form of modified curvature keeping in each three node types. They represent three types of molecular orbital of graphene carbon atom with a holonomy of spin connection. It is a network of couplings between the Cooper pairs and graviphotons in superconductivity states with underlying superspace of ribbon graph model of induced supersymmetric support Dirac machine. The SSDN algorithm is the extended algorithm of a quantum machine learning of the Ising model for phase transition [
41] by using convolutional neural network. Let curvature
be a capacity over a ribbon graph node. The Hamiltonian operator is defined over the ribbon graph with maximum flow of the holonomy of connection algorithm along the closed loops in the ribbon graph. We use the definition of a modified Wilson loop over spinor network which is equivalent to the loop of trajectory of Cooper pairs in the graphene carbon lattice atoms with pentagonal defect inside a wormhole structure. The annihilation and creation operators around vertices along the loop are defined with modified Dirac operator for warping D-brane of Cooper pairs. In the equilibrium state of a starting superconductor with a spinor network, we have an optimization of total curvatures along the modified Wilson loop with total curvature in superconductor state of the system equals to zero
The holonomy operotor of
is defined by a flow of quantum flux in the form of a connection
along the edge of the ribbon graph. We define SSDN for graphene wormhole, composed by the three types of modified Dirac operators for measuring the Chern-Simons current flow over supersymmetric spinor network. For the left and right supersymmetry of the Cooper pairs, it is
and
and, for the graviphoton, it is
. We have three types of nodes with the total number of carbon atoms
N. The first type is a superconductor child1 node
with
as
n chain of the Cooper pairs in the ribbon graph node. The second type is a superconductor child2 node
with
as
n chain of the Cooper pairs in the ribbon graph node. The third type of node is a normal state of Josephson junction with the chain of tunnel Cooper pairs as
. The spinor network of ribbon graph for lattice structure is shown in
Figure 2.
Definition 8. A modified Dirac operator for the left chiral fermion is defined by turning the mirror symmetry of D-brane to anti-D-brane with reversed time scale . Let be an imaginary number representing the hidden time scale in the extradimension perpendicular with D-brane A modified Dirac operator for the right chiral fermion is defined by turning the mirror symmetry of anti-D-brane to D-brane with time scale The supersymmetric Dirac operator is an operator where we have a coupling of annihilation and creation Dirac field in D-brane and anti-D-brane in the wormhole Chern-Simons manifold
. The coupling can be considered a warping state of the Cooper pairs over supersymmetry next carbon atom bonding in the symmetric group action of modified Wilson loop of
,
,
(
Figure 3). The mechanism is an entangled state at the end point of trajectory of Cooper pairs loop space in time series data of Kolmogorov space. We can explain it by the quantum confinement of the interaction between D-brane and anti-D-brane of the Cooper pairs (
Figure 4)
The operator can react with a vertex of spinor network in the sense of a quantum form of holonomy with the connection
producing a change of curvature deformed from fifth dimension into the supercurrent in fourth dimension in analogy with the electron-graviphoton interaction, that is,
We define three types of vertices, , , , with superspace parameters as the capacity to hold inside the node. Let and and .
Definition 9. We define supersymmetric the spinor network Dirac operator along N nodes of carbon atoms in the system of graphene wormhole as with predefined wave function with − for the left and + for the right configuration parameters as a new order parameter where , , is the connection of the Cooper pair and graviphoton in the wormhole. is a supercurrent and is the free energy of the graviphoton in the hidden fifth dimension.
Let
be a ribbon graph of a spin network with involution map
i. The vertex is defined by the accumulation of free energy of supersymmetric Dirac operator from the left and right supersymmetry wave function of the Cooper pairs free electrons. The edge is a supersymmetric Dirac operator
when the network is in a nonequilibrium of forbidden transition state in superconductor state, we have
We define three types of coupling between the Cooper pairs and graviphoton by using the supersymmetric wave function with underlying ghost field with parity modulo excitation state. The ghost field is the right symmetry in child1 manifold and the antighost field is defined by the orbital of Coopers pairs in child2 manifold with the left symmetry. For Cooper pairs in the normal junction of the coupling between graviphoton, we denote it as . The modified Dirac operator in the superspace is defined by the induced normal field to the superfield, so we can split the Dirac operator into the left and right supersymmetric Dirac operator , with three types of supercurrent as the eigenvalues of the annihilation and creation of a supersymmetric Dirac operator.