First-Principles Calculations of High-Pressure Physical Properties of Ti_0.5Ta_0.5 Alloy

Abstract

In this paper, an in-depth theoretical study on some physical properties of Ti_0.5Ta_0.5 alloy with systematic symmetry under high pressure is conducted via first-principles calculations, and relevant physical parameters are calculated. The results demonstrate that the calculated parameters, including lattice parameter, elastic constants, and elastic moduli, fit well with available theoretical and experimental data when the Ti_0.5Ta_0.5 alloy is under $T=0$ and $P=0$, indicating that the theoretical analysis method can effectively predict the physical properties of the Ti_0.5Ta_0.5 alloy. The microstructure and macroscopic physical properties of the alloy cannot be destroyed as the applied pressure ranges from 0 to 50GPa, but the phase transition of crystal structure may occur in the Ti_0.5Ta_0.5 alloy if the applied pressure continues to increase according to the TDOS curves and charge density diagram. The value of Young’s and shear modulus is maximized at $P=25\mathrm{GPa}$. The anisotropy factors $A_{\left(100\right)\left[001\right]}$ and $A_{\left(110\right)\left[001\right]}$ are equal to 1, suggesting the Ti_0.5Ta_0.5 alloy is an isotropic material at 28 GPa, and the metallic bond is strengthened under high pressure. The present results provide helpful insights into the physical properties of Ti_0.5Ta_0.5 alloy.

1. Introduction

Ti alloys have many outstanding properties, including high strength, low density, corrosion resistance, thermostability, and superior biocompatibility, and thus are extensively applied into aerospace, marine, chemical, and biological fields [1,2,3,4,5]. Among them, it has been found that TiTa alloy is one of the best biomaterials since it is cheaper than pure Ta and more corrosion-resistant than pure Ti; hence, it has attracted more and more attention [6,7,8]. Zhou et al. [9] found that TiTa alloys showed different microstructures with respect to various Ta contents, such as the ${\alpha }^{\prime }$ phase of lamellar HCP structure under 20% Ta contents, the ${\alpha }^{″}$ phase of needle-like orthorhombic structure between 30%–50% Ta contents, the $\beta +{\alpha }^{″}$ phase of metastable structure for Ta contents of 60%, along with a single metastable $\beta$ phase beyond Ta contents of 60%. Yin et al. [10] found that in Ti-28 Ta at % alloy, the cooling rate had a remarkable impact on the percentage of martensitic phase ${\alpha }^{″}$ and metastable phase $\beta$, and ${\alpha }^{″}$ phases tended to be induced at grain boundaries. Via the powder metallurgy method, Dercz et al. [11] evaluated the possibilities of synthesis of porous Ti-50Ta alloys; the microstructure and porosity of Ti-50 Ta alloys were greatly affected by the sintering time, and the corrosion resistance of sintered Ti-50 Ta alloys was better than that of pure Ti or Ta. Sing et al. [12] reported that TiTa alloy was composed of $\beta$ phase with the help of its rapid solidification and stabilizing effect, and the strength was higher with respect to pure Ti and Ti6Al4V. Behera et al. [13] measured the enthalpy change of Ti-xTa alloys at the temperatures ranging 463 to 1257 K, and then clearly revealed that the enthalpy came mainly from the contributions of two parts: (i) one part from untransformed $\alpha$ and coexisting $\beta$ phases, (ii) another part from the diffusional phase transformation from $\alpha$ phase to $\beta$ phase. Furthermore, plenty of studies on TiTa alloys were also carried out by others [14,15,16,17].

On the basis of the above studies, plenty of physical properties of Ti_0.5Ta_0.5 alloy were revealed through theory and experiment, as far as we know, but high-pressure physical properties in Ti_0.5Ta_0.5 alloy have not been studied yet, such as the structural, mechanical, and electronic properties. Therefore, the aim of this paper is to apply the first-principles calculations to investigate the high-pressure physical properties in Ti_0.5Ta_0.5 alloy in the frame of density functional theory (DFT), and related physical parameters are computed to reveal the relationships between these parameters and applied pressure acting on Ti_0.5Ta_0.5 alloy. In this paper, the main framework is listed below: In Section 2, the theoretical methodology and design parameters are introduced in detail. In Section 3, the calculated parameters of Ti_0.5Ta_0.5 alloy are presented and discussed. Finally, a brief summary is provided in Section 4.

2. Theoretical Methodology

In this work, all DFT energy calculations are carried out via the Cambridge Serial Total Energy Package Program [18,19,20]. Herein, we adopt the generalized-gradient approximation (GGA) within the Perdew–Burke–Ernzerhof (PBE) as the exchange-correlation functional for calculations [21]. The pseudopotential is described by Vanderbilt-type ultrasoft pseudopotentials (USPP) to decide the interatomic interactions, which is determined by the shell electrons, namely, the valence electrons [22]. The valence electrons of Ti and Ta elements are 4s²3d² and 6s²5d³, respectively. To ensure the convergence accuracy of the electronic calculations of the Ti_0.5Ta_0.5 alloy, the k-mesh in the Brillouin zone is set as 13 × 13 × 13, and the cutoff energy is optimized as 400 eV. The energy convergence criterion in the self-consistent calculation is optimized for 1.0 × 10^-6 eV/atom. For Ti_0.5Ta_0.5 alloy, it has the space group of Im-3m, and Figure 1 displays the crystal structure. The algorithm of Broyden–Fletcher–Goldfarb–Shanno (BFGS) [23] is selected for optimizing the geometric configuration of the alloy in the pressure range of -10 to 50 GPa. Meanwhile, the Hellmann–Feyman force of each atom is accurate to 0.01 eV/Å.

Figure 1. The crystal structure of Ti_0.5Ta_0.5 alloy.

3. Analysis and Discussions

3.1. Structure and Stability

In the light of the set parameters, the adequate structural optimization of the unit cell is first performed to get the theoretical E–V data, herein, E denotes total energy and V indicates the volume of the unit cell, and we fit the E–V data to determine the equilibrium crystal structure of Ti_0.5Ta_0.5 alloy according to the Birch–Murnaghan equation of state, as depicted in Figure 2, in which the volume range is set to 0.9–1.1 V₀, and each unit cell is optimized sufficiently. From the variation curve, the total energy gets the minimum value ($E_t=-19.401\mathrm{eV}$) when the volume is $V_0=34.660{\mathsf{\AA }}^3$, which shows that the crystal structure reaches the most stable state when these physical parameters are taken, and then the theoretical prediction of corresponding lattice constant is obtained by derivation, namely, $a_0=3.260\mathsf{\AA }$, where $V_0$ and $a_0$ represents the primitive cell volume and equilibrium lattice constant under $T=0$ and $P=0$, respectively. Meanwhile, Table 1 lists the comparative results of the calculated lattice constant $a_0$ versus other data for Ti_0.5Ta_0.5 alloy, and it fits well with these available data, indicating the validity of the theoretical analysis method.

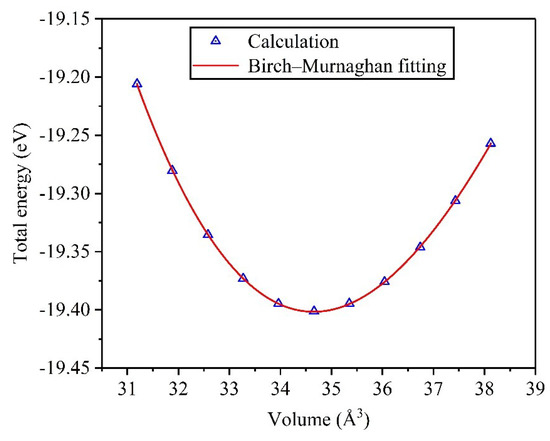
Figure 2. E–V fitting curve in Ti_0.5Ta_0.5 alloy.

Table 1. Comparisons of lattice constant with experimental and theoretical data for Ti_0.5Ta_0.5 alloy.

Ti0.5Ta0.5 Alloy	Present	Experimental Data	Theoretical Data
Lattice constant a0 (Å)	3.260	3.295 [11], 3.286 [14]	3.278 [24], 3.274 [25]

A series of structural optimizations are performed on the crystal structure of the Ti_0.5Ta_0.5 alloy under different applied pressures to get the corresponding volumes and equilibrium lattice constants, which are used to investigate the impacts of applied pressure on the unit cell volume and lattice constant. Subsequently, the dependencies of dimensionless ratios $V/V_0$ and $a/a_0$ on the applied pressure are obtained in the range of −10 to 50 GPa, where the negative pressure denotes the tension, as shown in Figure 3. From the variation curves, it can be found that the two ratios decrease when applied pressure increases and the descent speed for $V/V_0$ is significantly faster compared to $a/a_0$, suggesting that applying pressure can greatly reduce interatomic distance, and then strengthen electron interactions between adjacent atoms in the Ti_0.5Ta_0.5 alloy.

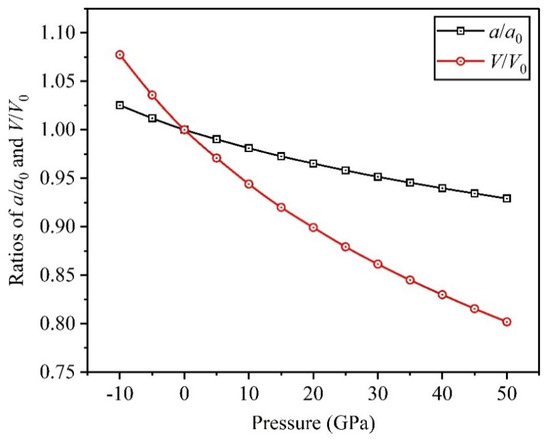
Figure 3. Dependencies of dimensionless ratios $V/V_0$ and $a/a_0$ on applied pressure in Ti_0.5Ta_0.5 alloy.

As we all know, elastic constants are the important physical parameters in influencing mechanical properties for anisotropic materials, and they are often used for assessing structural stability of crystalline materials and obtain relevant physical quantities, such as elastic moduli, anisotropy factors, Poisson’s ratio, and so on, thereby determining the deformation resistance of materials. For cubic structures, these three elastic constants $C_{11}$, $C_{12}$, and $C_{44}$ are usually used for estimating their structural stability, and they must satisfy the corresponding stability criterion, namely, $C_{11}>0$, $C_{44}>0$, $C_{11}-C_{12}>0$, and $C_{11}+2C_{12}>0$ [26]. Through calculation, the theoretical predictions for them are presented, and Table 2 lists the theoretical calculation results for comparisons with other theoretical data at $T=0$ and $P=0$, indicating that they agree well with other theoretical results [24,25].

Table 2. Comparisons of three elastic constants with available theoretical data in Ti_0.5Ta_0.5 alloy.

Ti0.5Ta0.5 Alloy	Present	Theoretical Data
$C_{11}$ (GPa)	180.34	163.40 [24], 181.80 [25]
$C_{12}$ (GPa)	142.16	132.80 [24], 138.86 [25]
$C_{44}$ (GPa)	30.14	39.00 [24], 45.18 [25]

At the same time, Figure 4 demonstrates the variation curves of elastic constants $C_{ij}$ in Ti_0.5Ta_0.5 alloy under the applied pressure ranging 0 to 50 GPa. Results display that $C_{11}$ and $C_{12}$ have the same trend that the values of theoretical predictions increase monotonously with the increase of applied pressure, and the elastic constant $C_{44}$ increases slowly and then decreases gradually, where the increase of elastic constants indicates that the deformation resistance of Ti_0.5Ta_0.5 alloy becomes stronger. Meanwhile, the calculated values of $C_{ij}$ always satisfy the stability criterion of crystal structure in the range of applied pressure, suggesting that the high-pressure mechanical stability of Ti_0.5Ta_0.5 alloy cannot be destroyed.

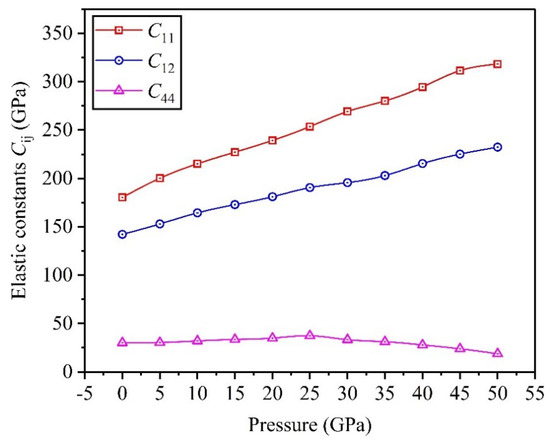
Figure 4. Dependencies of elastic constants $C_{ij}$ on applied pressure in Ti_0.5Ta_0.5 alloy.

3.2. Mechanical Properties

Ti alloys have outstanding mechanical performances, such as high strength, wear resistance, and nontoxicity, and they are extensively used in modern industries, which are closely connected with the material modulus against deformation, such as Young’s modulus E, shear modulus G, and bulk modulus B [27]. Herein, the elastic moduli of materials with cubic crystal can be obtained through elastic constants $C_{ij}$ according to the research work of Iotova et al. [28], and the specific expressions are $B=\left(C_{11}+C_{12}\right)/3$, $G=\left(G_V+G_R\right)/2$, and $E=9BG/\left(3B+G\right)$, in which $G_V=\left(C_{11}-C_{12}+C_{44}\right)/5$ represents the Voigt modulus of shear resistance, and $G_R=5C_{44}\left(C_{11}-C_{12}\right)/\left[4C_{44}+3\left(C_{11}-C_{12}\right)\right]$ denotes the Reuss modulus of shear resistance.

Through calculation, the theoretical predictions of elastic moduli are obtained, and Figure 5 depicts the corresponding variation curves for the Ti_0.5Ta_0.5 alloy under the applied pressure in the range of 0 to 50 GPa. Obviously, bulk modulus B increases gradually as applied pressure increases, which indicates that high pressure for Ti_0.5Ta_0.5 alloy can enhance its resistance to volume change. E and G first increase and then decrease gradually, and both of them get the maximum values at P = 25 GPa, which indicates that increasing pressure can improve the resistances to elastic and shear deformations between 0 and 25 GPa, but decline their resistances beyond 25 GPa. Furthermore, we compare the theoretical predictions of elastic moduli with available theoretical and experimental data for Ti_0.5Ta_0.5 alloy under $T=0$ and $P=0$, and Table 3 shows that the calculated data of this work are well consistent with the research results of others [7,12,25].

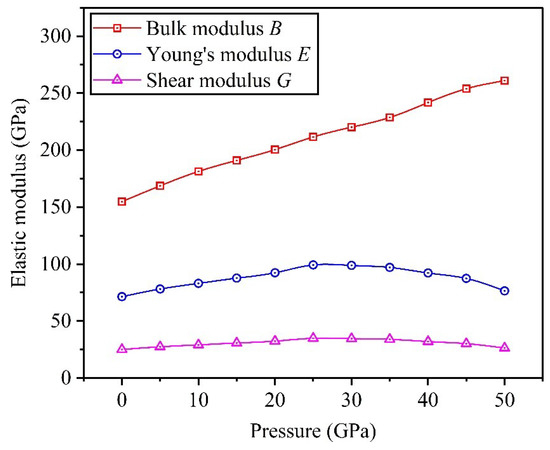
Figure 5. Dependencies of elastic moduli on applied pressure in Ti_0.5Ta_0.5 alloy.

Table 3. Comparisons of the current elastic moduli with other data in Ti_0.5Ta_0.5 alloy (unit: GPa).

Ti0.5Ta0.5 Alloy	Present	Theoretical Data	Experimental Data
Bulk modulus B	154.89	153.18 [25]
Young’s modulus E	71.44	93.71 [25]	69.00 [7], 71.73 [12]
Shear modulus G	25.10	33.51 [25]

Researches show that putting pressure on materials will affect the ductile-brittle transition of crystal structure, thereby influencing the mechanical properties of materials [29,30]. Pugh proposed a significant conclusion that the brittleness or ductility of materials depends on the modulus ratio $B/G$ [27], and $B/G>1.75$ denotes the ductility, and $B/G<1.75$ indicates the brittleness. In light of the calculated elastic moduli, Figure 6 depicts the changing curve of the modulus ratio $B/G$ under pressure changing from 0 to 50 GPa. The result shows $B/G>1.75$ at any pressure, suggesting that the Ti_0.5Ta_0.5 alloy has good ductility. Additionally, there is a critical pressure P = 25 GPa; namely, the ductility of Ti_0.5Ta_0.5 alloy is almost invariable at the pressure between 0 and 25 GPa, whereas the ductility of the alloy significantly increases when the applied pressure further increases.

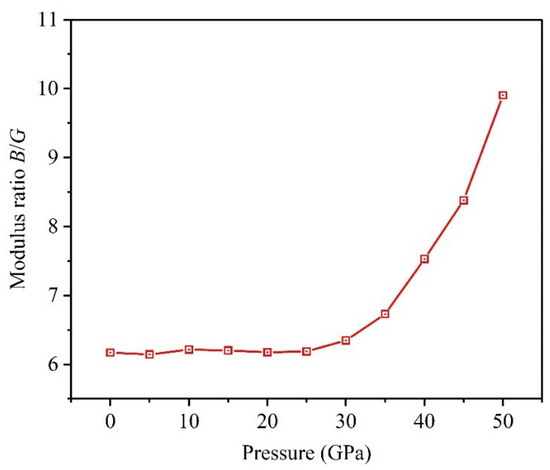
Figure 6. Dependencies of modulus ratio $B/G$ on applied pressure in Ti_0.5Ta_0.5 alloy.

3.3. Anisotropy

In crystalline materials, the elastic anisotropy of crystal structure influences the mechanical properties of materials. At present, researchers usually use the anisotropy factor A to investigate this physical characterize, and materials with $A=1$ are isotropic, otherwise anisotropic [31,32]. In 1986, the impacts of elastic anisotropy on mechanical properties of materials had been thoroughly studied by Yoo [33], he found an interesting phenomenon that a large A can enhance the tangential force to drive the cross slip of screw dislocations, and then proposed a significant model, namely, the cross-slip and pinning model. Herein, $A_{\left(100\right)\left[001\right]}$ and $A_{\left(110\right)\left[001\right]}$ denote the elastic anisotropy in the (100)[001] and (110)[001] directions, and the calculation formulas are $A_{\left(100\right)\left[001\right]}=2C_{44}/\left(C_{11}-C_{12}\right)$ and $A_{\left(110\right)\left[001\right]}=C_{44}\left(C_{11}+2C_{12}+C^{\prime }\right)/\left(C_{11}{C}^{\prime }-C_{12}^2\right)$, in which $C^{\prime }=C_{44}+\left(C_{11}+C_{12}\right)/2$ [34,35]. Through calculation, Figure 7 plots the variation curves of anisotropy factors of Ti_0.5Ta_0.5 alloy under applied pressure. The values of two anisotropy factors are equal to 1 when the applied pressure is about 28 GPa, indicating that the Ti_0.5Ta_0.5 alloy is an isotropic material at 28 GPa. In the light of the trend of variation curves, the elastic anisotropy of Ti_0.5Ta_0.5 alloy decreases with increasing pressure between 0 and 28 GPa, but increases under applied pressure ranging from 28 to 50 GPa, thereby the tangential force decreases first and then increases in promoting the cross slip of screw dislocations.

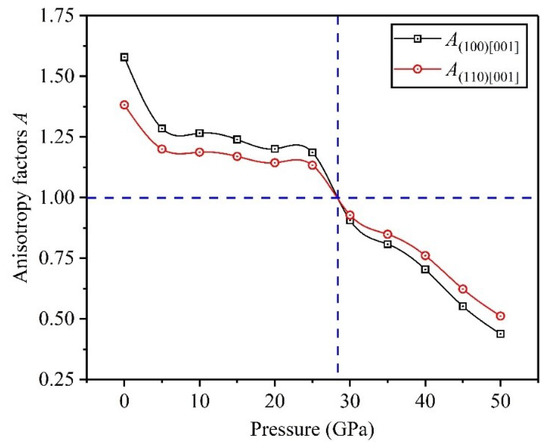
Figure 7. Dependencies of anisotropy factors on applied pressure in Ti_0.5Ta_0.5 alloy.

Poisson’s ratio $\sigma$ is a significant physical parameter that can be used to determine the plasticity of materials; thus, we investigate the change of Poisson’s ratio $\sigma$ of Ti_0.5Ta_0.5 alloy under the applied pressure in this paper. For Poisson’s ratio $\sigma$, the value changes from −1 to 0.5, and a large value indicates good plasticity. Reed et al. [36] put forward an important conclusion that $\sigma =0.25$ and $\sigma =0.5$ were the smallest and largest bounds for central-force solids, respectively. Additionally, Fu et al. [35] found that the magnitude of $\sigma$ was used for defining the sort of interatomic bonding. In this paper, Poisson’s ratios ${\sigma }_{\left[001\right]}$ and ${\sigma }_{\left[111\right]}$ in the [001] and [111] crystallographic directions are calculated according to the theoretical predictions of elastic constants $C_{ij}$, and the calculation formulas are ${\sigma }_{\left[001\right]}=C_{12}/\left(C_{11}+C_{12}\right)$ and ${\sigma }_{\left[111\right]}=\left(C_{11}+2C_{12}-2C_{44}\right)/2\left(C_{11}+2C_{12}+C_{44}\right)$ [37]. Figure 8 plots the changing curves of Poisson’s ratios with respect to applied pressure in Ti_0.5Ta_0.5 alloy. The values of ${\sigma }_{\left[001\right]}=0.441$ and ${\sigma }_{\left[111\right]}=0.409$ reveal that the central forces in the [001] and [111] crystallographic directions make a greater contribution to the interatomic bonding for the Ti_0.5Ta_0.5 alloy in essence. Clearly, Poisson’s ratio ${\sigma }_{\left[001\right]}$ monotonously decreases with the increase of applied pressure, while Poisson’s ratio ${\sigma }_{\left[111\right]}$ is reversed and gradually approaches the value of upper bound 0.5, which shows that the high pressure can strengthen the interatomic bonding, thereby improving the plasticity of Ti_0.5Ta_0.5 alloy in the [111] crystallographic direction.

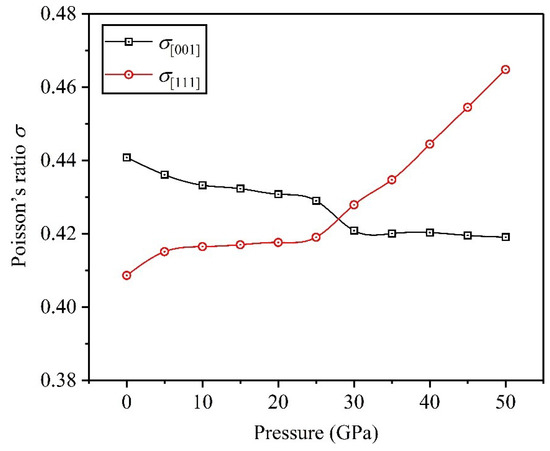
Figure 8. Dependencies of Poisson’s ratios on applied pressure in Ti_0.5Ta_0.5 alloy.

Furthermore, we calculate the other moduli of Ti_0.5Ta_0.5 alloy, including $G_{\left(100\right)\left[010\right]}$, $G_{\left(110\right)\left[1\overline{1}0\right]}$, and $E_{<100>}$, to further study the related mechanical performances, where $G_{\left(100\right)\left[010\right]}$ represents the shear modulus in the $\left(100\right)\left[010\right]$ direction, and $G_{\left(110\right)\left[1\overline{1}0\right]}$ indicates the one in the $\left(110\right)\left[1\overline{1}0\right]$ direction, respectively, and $E_{<100>}$ denotes Young’s modulus along the $<100>$ direction. These parameters can also be obtained by elastic constants $C_{ij}$, and the calculation formulas are $G_{\left(100\right)\left[010\right]}=C_{44}$, $G_{\left(110\right)\left[1\overline{1}0\right]}=\left(C_{11}-C_{12}\right)/2$, and $E_{<100>}=\left(C_{11}-C_{12}+C_{11}{C}_{12}-C_{12}^2\right)/\left(C_{11}+C_{12}\right)$ [32,38], and Figure 9a draws the variation curves of material moduli under applied pressure ranging from 0 to 50 GPa. It shows that the total varying trends of $G_{\left(110\right)\left[1\overline{1}0\right]}$ and $E_{<100>}$ increase gradually as the applied pressure increases, although $E_{<100>}$ decreases slightly at 50 GPa, indicating that high pressure strengthens the resistances to shear and elastic deformations of Ti_0.5Ta_0.5 alloy in the $\left(110\right)\left[1\overline{1}0\right]$ and $<100>$ crystallographic directions. Different from $G_{\left(110\right)\left[1\overline{1}0\right]}$ and $E_{<100>}$, shear modulus $G_{\left(100\right)\left[010\right]}$ initially increases and then decreases when applied pressure increases, and reaches the maximum value at 25 GPa, which shows that the Ti_0.5Ta_0.5 alloy has the strongest shear resistance along the $\left(100\right)\left[010\right]$ direction under P = 25 GPa, while the shear deformation resistance of the alloy will decline if the pressure continues to increase.

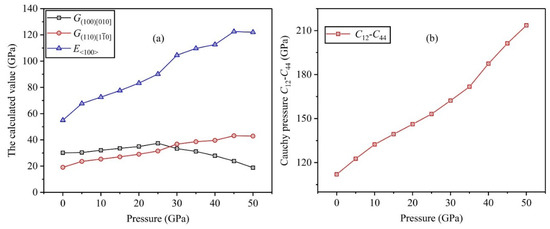
Figure 9. Dependencies of calculated moduli (a) and Cauchy pressure (b) on applied pressure in Ti_0.5Ta_0.5 alloy.

Meanwhile, another important physical parameter, Cauchy pressure $C_{12}-C_{44}$, is calculated for evaluating the bonding characteristics from the atomic level under high pressure. Herein, the positive value of Cauchy pressure stands for the metallic characteristics of atomic bonding, indicating that there is a uniform electron gas near the spherical atom, which is composed of electrons without directionality and regionality. However, the atomic bonding exhibits the directional characteristic as the Cauchy pressure is negative, and a large value denotes the strong directional characteristic of atomic bonding [32,39]. According to elastic constants $C_{ij}$, Figure 9b shows the changing curve of $C_{12}-C_{44}$ versus different pressure in Ti_0.5Ta_0.5 alloy. It is noted from the curve that the value of $C_{12}-C_{44}$ is positive at any pressures, and quickly increases for the Ti_0.5Ta_0.5 alloy between 0 and 50 GPa, suggesting that the metallic bond is the main bonding form of Ti_0.5Ta_0.5 alloy, and the metallic bond can be strengthened in the case of high pressure.

3.4. Electronic Properties

The valence electrons determine the bonding form between atoms, thereby influencing the microstructure and macroscopic physical properties of the crystal. Therefore, the electronic structures are given and discussed to study the structural stability of Ti_0.5Ta_0.5 alloy under applied pressure in this paper. Figure 10 exhibits the changing curves of the partial density of states (PDOS) and the total density of states (TDOS) at P = 0 GPa, where the red dash line stands for the Fermi level ($E_{\mathrm{F}}=0\mathrm{eV}$). For the TDOS curve, it can be found that the value is not zero at $E_{\mathrm{F}}=0\mathrm{eV}$, suggesting that the Ti_0.5Ta_0.5 alloy exhibits the metallicity, which verifies the conclusion in Figure 9b. For PDOS curves, they show that the Ti-3d and Ta-5d states have the greatest effect on DOS at 0 eV, while the effects of the Ti-4s and Ta-6s states on DOS are almost negligible.

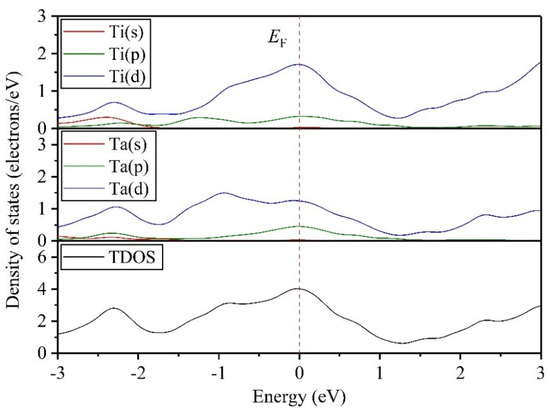
Figure 10. Changing curves of the partial density of states (PDOS) and the total density of states (TDOS) for Ti_0.5Ta_0.5 alloy at 0 GPa.

Meanwhile, Figure 11 describes the changing curves of TDOS versus pressures of 0, 15, 25, 35, and 50 GPa. From these changing curves, the results show that energy of the valence-band maximum increases as applied pressure increases, while the one of the conduction-band bottoms was reversed, indicating that high pressure decreases the band gap between the conduction band and valence band, and the outer electrons tend to easily transfer from the valence-band maximum to the conduction-band bottom. Hence, high pressure may destroy the structural stability of Ti_0.5Ta_0.5 alloy, which affects the microstructure and macroscopic physical properties of Ti_0.5Ta_0.5 alloy. At the same time, according to the results of Figure 4, it can be found that the value of elastic constant $C_{44}$ may become negative as the applied pressure increases further, which indicates that the Ti_0.5Ta_0.5 alloy may produce the structural phase transition under higher pressure, and the analysis result is consistent with the previous conclusion in Figure 11.

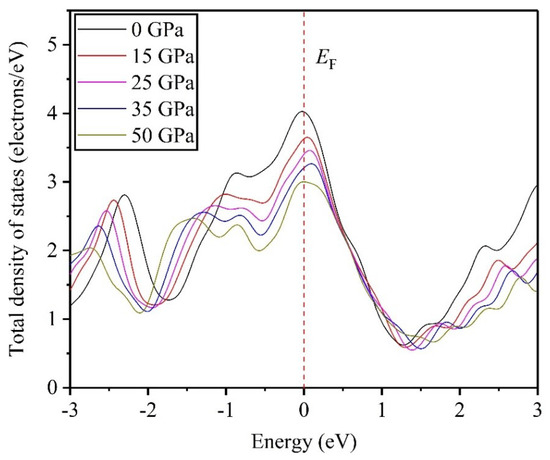
Figure 11. Changing curves of TDOS for Ti_0.5Ta_0.5 alloy under different pressures.

Finally, the charge density diagrams of isosurface contours versus various pressures are presented to understand the local chemical bonding in the Ti_0.5Ta_0.5 alloy, as shown in Figure 12, where the isosurface levels are set to 0.0425 $r_0^{-3}$ ($r_0$ is the Bohr radius). With increasing applied pressure, the local chemical bonding between Ti and Ta atoms gradually increases, implying that the high pressure can enhance the electron interaction between the two atoms, thereby increasing the local chemical bonding between them, and the change increases as applied pressure increases. However, the strong interactions between two atoms may destroy the stability of the crystal structure. Therefore, the structural phase transition may occur in the Ti_0.5Ta_0.5 alloy under higher pressure beyond 50 GPa, which coincides with the result in Figure 11.

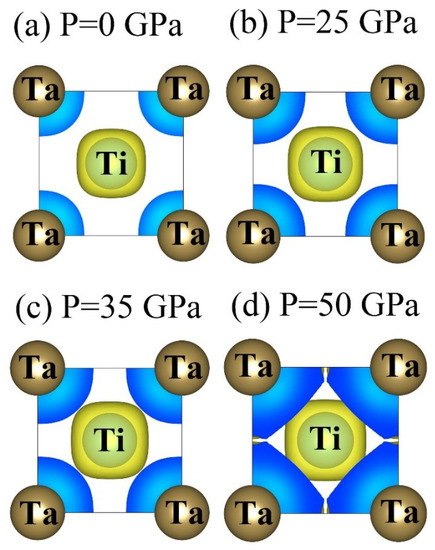
Figure 12. Charge density diagrams of isosurface contours versus various pressures in Ti_0.5Ta_0.5 alloy.

4. Conclusions

In conclusion, DFT calculations are implemented to study the influences of applied pressure on the relevant physical parameters of Ti_0.5Ta_0.5 alloy, including structural, mechanical, and electronic properties. Results reveal that the calculated data for equilibrium lattice parameter, elastic constants, elastic moduli are consistent with the research results of others for Ti_0.5Ta_0.5 alloy under $T=0$ and $P=0$. $C_{11}$ and $C_{12}$ increase monotonously as applied pressure increases, but $C_{44}$ increases slowly and then decreases gradually. The applied pressure cannot destroy the mechanical stability of Ti_0.5Ta_0.5 alloy because the stability criterion is always satisfied in the range of 0–50GPa. Bulk modulus B gradually increases with increasing applied pressure, but E and G reach the maximum values at P = 25 GPa, suggesting that high pressure increases the resistance to volume deformation, and the resistances to elastic and shear deformation are maximized under P = 25 GPa in Ti_0.5Ta_0.5 alloy. $B/G$ indicates that the ductility of the alloy significantly increases as applied pressure increases further when P > 25 GPa. The Ti_0.5Ta_0.5 alloy is an isotropic material when the applied pressure is 28 GPa because the values of anisotropy factors $A_{\left(100\right)\left[001\right]}$ and $A_{\left(110\right)\left[001\right]}$ are equal to 1. The major atomic bonding in Ti_0.5Ta_0.5 alloy is characterized by a metallic bond, and high pressure can enhance the metallic bond. The TDOS curves and the isosurface contours of charge density indicate that the structural phase transition may occur in the Ti_0.5Ta_0.5 alloy if the applied pressure increases further. The present results are valuable for the application of Ti_0.5Ta_0.5 alloy under high pressure in the future, such as the wide applications in aerospace, marine, chemical, and biological fields under high pressure.