Abstract
Digital image watermarking aims to protect the information in an image without significantly affecting visual quality. In this paper, a new image watermarking technique has been proposed that uses Gaussian filters and first-order partial differential matrix to extort the edge surface of a host image. This paper influence on the edge surface curvelet coefficients as human eyes are not equally sensitive to a smooth and an edged surface. To preserve the quality of the artwork and to increase the resistance against attacks, the author utilizes the edge surface area of an image, coarse levels of curvelet transform, and strength parameters. The selection of host coefficients are conforming to the human visual system (HVS) is the uniqueness of the research. The exploitation of the Gaussian filters and first-order partial differential coarse curvelet coefficients and the watermark strength parameter offers robustness against image processing attacks. The standard visual quality perception of HVS evaluation metrics are used to measure the superiority of the presented work.
1. Introduction
In this contemporary world of digital media and e-commerce, most businesses secure their online content with the use of algorithmic copyrights, product patents, and business logos. In the same context there is a dire need for robust security procedures and to ensure reliable quality and availability. The proliferation of digitized image, video, and audio create the need for protection of copyright and enforcement of intellectual property right. The patent and copyright issues in the digital media are reported in the Digital Millennium Copyright Act (DMCA) [1]. DMCA acts as a catalyst to further advance the current state of the art technology. Many methods are available for protecting digital media such as cryptography, steganography, digital signature, and digital watermarking [2]. Cryptography provides little protection against data piracy and also confronts the reproduction of images [3]. Among them, digital watermarking is a better solution for image authentication and forgery prevention which modify an original image by hiding secret information [4,5]. Digital watermarking is a combination of two processes:
Process 1: Embedding in which information (i.e., author and buyer data) is embedded into a test image.
Process 2: Extraction in which watermark is extracted from the watermarked image as the test image [6].
The Watermark embedding algorithm falls into two categories. The first category embeds the watermark in the spatial-domain by directly changing the pixel intensity of a base image, yet watermark is not robust against image processing attacks [7,8,9]. Another category embeds the watermark and analyzes images in the frequency domain by changing and enchasing frequencies of the cover image. Frequency domain in watermarking is common, which includes Discrete Cosine Transform (DCT) [10,11,12,13], Digital Wavelet Transform (DWT) [14,15,16,17], and Curvelet Transform (CT) [18,19,20,21]. To make the watermark more invisible, DC coefficients of DCT transforms are often used to hide the watermark [22]. The magnitude of DC coefficients has larger values than AC coefficients so that more invisibility will be added to the watermark. DCT coefficients of an image are modified by using BCH coding to hide the watermark [23,24,25,26,27].
To obtain the optimum imperceptibility of the watermarking technique, information is inserted in the neighbor of DCT coefficients using Just Noticeable Difference (JND) of HVS. To optimize the quality of the watermarked image, and LWT-SVD technique was proposed that employs ant colony objective function [28,29,30,31,32,33,34,35,36,37]. The combination of SVD, DWT, and Firefly algorithm was proposed to find the optimized watermarking. Some authors applied the benefits of curvelet transform for watermarking in [23,37,38]. To improve the robustness against compression, a technique embed watermark was given in the curvelet domain. It is drawn out from the literature that there is a possibility of improving the robustness and the invisibility of watermarking by using the different transforms and embedding methods for better results.
To attain the improved tradeoff between invisibility and robustness, the combined properties of visual masking effects of human eyes and curvelet transform are utilized. It comes from the fact that eyes are also less sensitive to the edge surface of the image rather than the smoothing part [39,40].
Curvelet transform has been introduced to overwhelm the restrictions of Continuous Wavelet Transform (CWT) [24]. Image processing operations require wavelet transforms to represent images in more adequately. However, wavelet transform is not suitable to characterize the objects covering randomly sloping of corners as edge and boundaries as a curve. Images are amalgamating of corners as edge and boundaries as curve; thus, requiring a transform that depicts edges and curves efficiently. Curvelet transform has the property of represents line singularity because it has orientation, scaling, and direction parameter. The 1st generation curvelet transform was developed by [25,26]. The need for finer image analysis is the reason to develop advancement in curvelet transform. The speed of 1st generation curvelet transform is very slow so that in 2006, a new modified curvelet transform was introduced by [27,28]. This modified curvelet transform obeying the parabolic scaling law i.e., [20,21,22] to represent the anisotropic elements. This curvelet transform adds more parameters like orientation and directional.
A family of dilated and translated functions for signal analysis there use one mother wavelet . Each signal can be exclusively denoted in equation given below:
where = wavelet coefficients.
In frequency domain polar coordinates are represents as functions , and . The below equation shows the stretched curvelets in polar coordinates. Corresponds to the translation of - periodic rotation , and two window function and .
Objective of the paper is:
To propose a new image watermarking algorithm that uses Gaussian filters and first-order partial differential matrix to extort the edge surface of a host image. Embedding of the watermark may affect the quality of the visual quality of the original work or image. Therefore, the embedding procedure should make the watermark more perceptible so it will not disturb the quality of the original image. As well as at the receiving end, the extracted watermark should be similar to the embedded one and be robust against image processing attacks. So, evaluation of the quality of embedded watermark image and extracted watermark different performance metrics were used. These metrics evaluated or compared the visual quality of the original, embedded, and extracted images.
We utilized coarse levels of curvelet transform and watermark strength parameters to be employed to improve the invisibility and robustness. The exploitation of the edged surface offered robustness against filtering, rotation, Gaussian noise, histogram equalization, and cropping. Performance metric of Peak-Signal to Noise-Ratio (PSNR), Normalized Correlation (NC), Bit-Error-Rate (BER), and Structure Similarity Index Measure (SSIM) [29,30] were used to measure the superiority of presented work. It was compared against other existing techniques to emphasize the invisibility and robustness of achieved results.
2. Proposed Algorithm
In this section, the proposed method has been explained and the process for embedded and extraction of images has defined and explained.
2.1. Watermark Embedding
Let the host image (I) of size and the binary logotype image as a watermark image. The edge surface area gives higher imperceptibility to the watermark. Thus, to investigate the edge surface area, firstly we found the zero-crossing points by convoluting the original image with the Gaussian filter. Then, we calculated the Slope (M) and Direction (R) of edges by using first-order partial differential in the X image as below (as per Equation (3)),
where P = first order partial differential matrix (P), and is angular and define
Each edge is redefined by applying the slope and direction where each edge of the host image is redefined. Now, the host image with refined edges of the new image is called as the texture image (B) by generating the edge surface in the original image. We divide the original image and edge surface image into a non-overlapped n*n blocks to identify the edge surface blocks in the original image. We calculated the edge points in the contexture image by selecting a threshold (Th). The blocks having numbers of edge points more than Th were discovered as an edge surface area of an image. The blocks were extracted from the original image and identified as the edge surface in the contexture image. Then, we combined the extracted blocks to make a p*p size image, which was called an edge surface image used as the embedding domain of watermark.
To decompose the edge surface image T, the discrete curvelet transform was applied. Then, the edge surface image T was decomposed into Coarse, Detail, and Fine which are the levels of curvelet transform. It was appropriate to hide information into the Coarse level (Q) of the curvelet domain because it provides more invisibility. We transformed the logo image W into a 1-D pixel array . The curvelet coefficients Coarse (C) was modified as below (as per Equation (4)).
where α is the watermark strength factor. The value of α was calculated from pixel intensities of the original image as follows (as per Equation (5)),
where is the average intensity of original image. where , is the average of selected embedding domain of edge surface image. The modified curvelet coefficients—Coarse are contained in the watermark. Now, inverse curvelet transform was applied to the modified curvelet coefficients-Coarse to convert the image into the time domain. Then, the revised blocks were rearranged into their exact places. This transformed image is called a watermarked image .
2.2. Watermark Extraction
From the watermarked image T and the edge surface image were obtained from the logotype watermarked image T. To identify the edge surface area of images, threshold Th was used and treated as a key. We extracted the blocks from the watermarked image that were identified as the edge surface in the contexture image. These edge surface areas were then combined to make the edge surface images . Then, FDCT was applied to the edge surface images T and to convert them into the frequency domain. Next, the embedding domains were selected. Let the coarse levels (Q) and () be the selected domains from the original image (T) and edge surface image () respectively. The strength parameter (α) is the second key that was used in the receiving end to extract the embedded information. The value of α was obtained in the embedding procedure. Equation (6) was used to extract the watermark from the watermarked image.
The identified watermark is arranged into a m*n dimensional pixel array = {; }. The extracted watermark is .
2.3. Algorithm
Input: Grayscale image I of M*N, and binary image W of m*n.
Output: Watermarked image.
Phase 1: Embedding
- (1)
- Read grayscale image I of M*N sizes as the original image.
- (2)
- Read binary image W of m*n sizes as a watermark image.
- (3)
- The following steps have been used to identify the edge surfaces of the original image.
- Apply the filtering operation to the original image to obtain a filtered image.
- Convolute the filtered image and Gaussian filter.
- Initialize the values and .
- Calculate the slope (M) using following equation:
- Calculate direction (R) of edges uses following equation
- (4)
- From step 3 edge surface areas have been identified, now combine these edge surface areas of the original image. This combined edge surface image is named as image B.
- (5)
- Divide the original image and edge surface image (B) into 8*8 size of the non-overlapped block. Now calculate the edge points of each edge surface 8*8 blocks. Set the threshold (th) of edge points.
- (6)
- To convert into frequency domain discrete curvelet transform on edge surface image (B). Now in the frequency domain, the coarse level (Q) has been selected to hide the watermark.
- (7)
- In this step, the 2-D watermark image (W) is converted into a 1-D pixel array W = . α was calculated as the watermark strength factor from the pixel intensities of the original image by using Equation (5).
- (8)
- Curvelet domain Coarse level (Q) coefficients were reformed by multiply the values of the watermark image W, watermark strength factor α, and coarse level (Q) coefficients.
- (9)
- Now, this reformed values of curvelet domain coarse level (Q) coefficients was transformed into the time domain by applying inverse curvelet transform. Then, the revised 8*8 edge surface blocks were rearranged into their exact places. This new time-domain image is called a watermarked image .
Phase 2: Extraction
- We read logotype watermarked image T, and obtained the edge surfaces form the watermarked image as discussed in step 3 and step 4 in phase 1. To identify the edge surface area of images, threshold Th was used and treated as a key.
- These edge surface areas were then combined to make the edge surface images from the watermarked image .
- Then, FDCT was applied to the edge surface images T and to convert them into the frequency domain.
- Now, the embedding domains—the coarse levels (Q) and ()—are the selected domains from the watermarked image (T) and edge surface image () respectively.
- The second key was the value of watermark strength factor α. The value α was obtained as discussed in step 7 in the phase 1 embedding procedure.
- Next we extracted the one by one bit of watermark form the coarse levels of watermarked image (T) and edge surface image () respectively using Equation (6).
- We then arranged the extracted bits into m*n dimensional pixel array, and read this as a 2-D image. The resulting image was an embedded logo-type watermark.
In this section, to protect the copy-write content the watermark was embedded or inserted into the original image by using the Gaussian filters, first-order partial differential, and the curvelet transform. Here the imperceptible concept of edge surface was utilized. It has already been discussed in the previous section that the course level and texture surface provide imperceptibility. So, the technique of making an embedded watermark invisible for a more robust at course level of curvelet was utilized. The quality extraction an of embedded watermark proves the originality of the original content. To show the superiority of the proposed algorithm visual quality embedded image extracted watermark was compared with the perception of HVS [30].
3. Results
In this section, we perform experiments on five 8-bit grayscale images, namely “Lena”, “cameraman”, “Men”, “boat”, and “Peppers” from the SIPI image database. As a watermark, a 64*64 binary logo image is used. The threshold Th was set as 15 to provide a balanced performance in invisibility and robustness. The word “Balanced performance” is an application of attaining suitable robustness holding acceptable invisibility of watermark. Figure 1 shows six original images along with the binary logo watermark. As for embedding phase 1 result, Figure 2 shows the watermarked images from the respective original image. The visual superiority and resemblance between the host images and logo based watermarked images are precisely extraordinary.

Figure 1.
The host images: (a) Lena, (b) Cameraman, (c) Men, (d) Boat, (e) Pepper, and (f) Original watermark image.

Figure 2.
The Watermarked images: (a) Lena, (b) Cameraman, (c) Men, (d) Boat, and (e) Pepper.
In this paper, the Peak-Signal to Noise-Ratio (PSNR), Normalized Correlation (NC), Bit Error Rate (BER), and Structure and Similarity Index Measure (SSIM) were used to estimate the grade of similarity between the host image and logo based watermark W and the extracted (as per Equations (7)–(9)) watermark .
where , the M and N denoted the row and column of the image . is the base /original image and is the disturbed image and is a xor operation. PSNR is the traditional error summation approach to evaluating the similarity, but it does not correlate toughly with the visual quality of the image. The “Structure Similarity Index Measure” (SSIM) [29] was calculated by modeling any image distortion as a combination of loss of correlation, luminance distortion, and contrast distortion. SSIM correlate with the visual quality perception of HVS [30]. The values of SSIM lie between 0 and 1. If two images are significantly undistinguishable, the value of SSIM is equal to 1. Zero value of SSIM indicates that there is no correlation between two images. SSIM is defined in the following steps (as per Equation (10)):
Table 1 shows the performance of the proposed technique in terms of PSNR, NC, BER, and SSIM of the watermarked image. The value of NC for each image is one and SSIM is near to 1. From the table, it is observed that the quality of the watermarked image does not degrade. The human eyes cannot distinguish between the original and watermarked images.

Table 1.
Performance of the proposed technique on watermarked images. Abbreviations: Peak-Signal to Noise-Ratio (PSNR), Normalized Correlation (NC), Bit-Error-Rate (BER), and Structure Similarity Index Measure (SSIM).
Logos extracted from the above-watermarked image are revealed in Figure 3. The PSNR values of the extracted watermark are above 47 dB in all images that prove the reliability of the proposed technique to extract the watermark having similar visual quality as the embedded watermark. It is also analyzed that the subjective and visual quality of extracted watermark is the same as of base image. Table 2 shows the performance of extracted/processed watermark from the watermarked image. The correlation of embedded and extracted watermark is shown by NC whose value is one in all extracted watermark images. The value of Structure Similarity Index Measure (SSIM) inspects losses of luminance and contrast of two images. The proposed algorithm gives the values of SSIM ≈ 1 that identify there is no visible difference even in the human visual system. The values of performance evaluation metrics demonstrate that the hiding capability of the proposed algorithm is good. Besides, the proposed algorithm also provides identical extracted watermark.

Figure 3.
Corresponding extracted watermark from Figure 2 from (a–e).

Table 2.
Performance of extracted watermark.
To estimate the strength of the projected technique, the numbers of image processing operations are considered. The performance of extracting watermark concerning different attacks and image processing operations is presented as:
- 1.
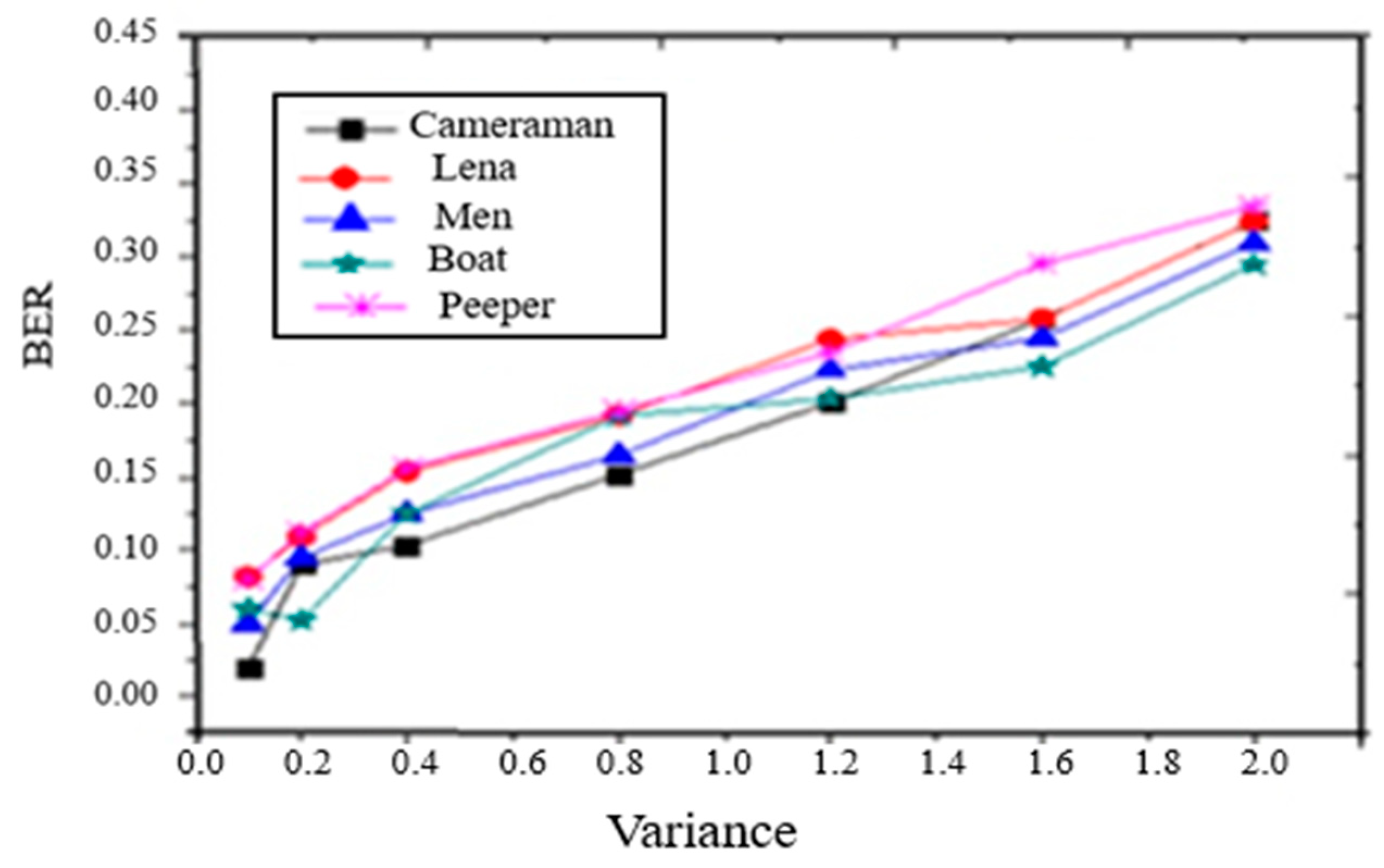
- Gaussian noise: The performance of the proposed watermarking technique is shown in Figure 4 where the watermarked images are tainted by Gaussian noise with the variance (V) set at {0.2, 0.4, 0.6, 0.8, and 1.0}. From the figure, it is observed that the robustness of the algorithm is high because the watermark is still able to detect even when the density of the noise is 1.0.
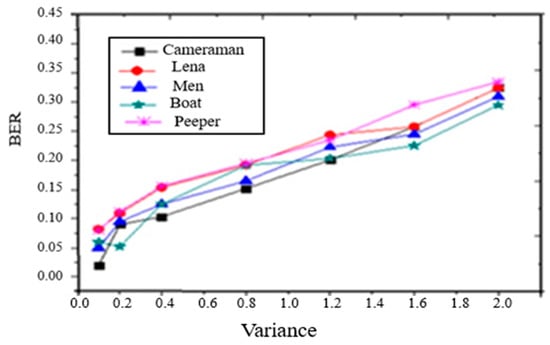 Figure 4. BER of extracted watermark under Gaussian noise.
Figure 4. BER of extracted watermark under Gaussian noise. - 2.
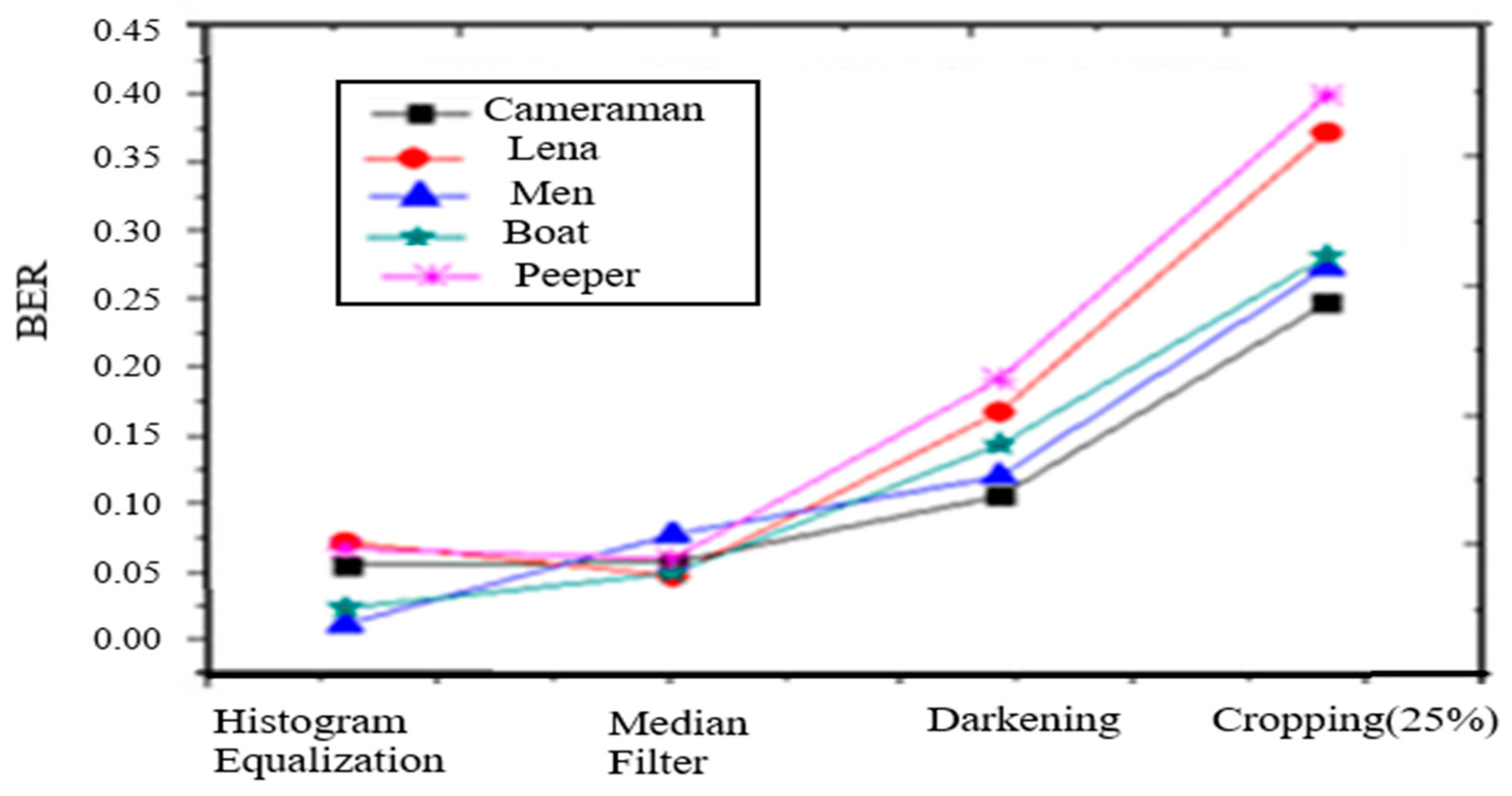
- Median Filtering: Filtering is the most important operation of image processing. 3*3 mask is applied to the watermarked images. Figure 5 shows the BER of the extracted watermark from 3*3 filtered images. The values of BER of the extracted watermark with embedded ones are negligible to prove the robustness of embedded information against filtering.
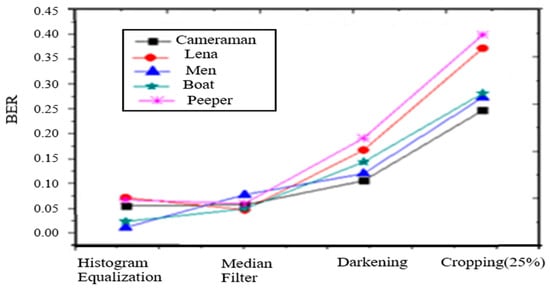 Figure 5. BER of extracted watermark under histogram equalization, median filtering, darkening, cropping operation.
Figure 5. BER of extracted watermark under histogram equalization, median filtering, darkening, cropping operation. - 3.
- Histogram equalization: Another important operation is histogram equalization which shows the robustness of the proposed algorithm. The watermark is extracted from the histogram equalized watermarked image. The values of BER of extracted and embedded watermarks are shown in Figure 5. The quality of extracted information from the histogram equalized watermarked image is comparable to the embedded one. The results of the proposed algorithm confirm the presence of an embedded watermark.
- 4.
- Cropping: The watermarked images are cropped 25% from the middle. Figure 5 also shows the BER of the extracted watermark from the cropped images.
- 5.
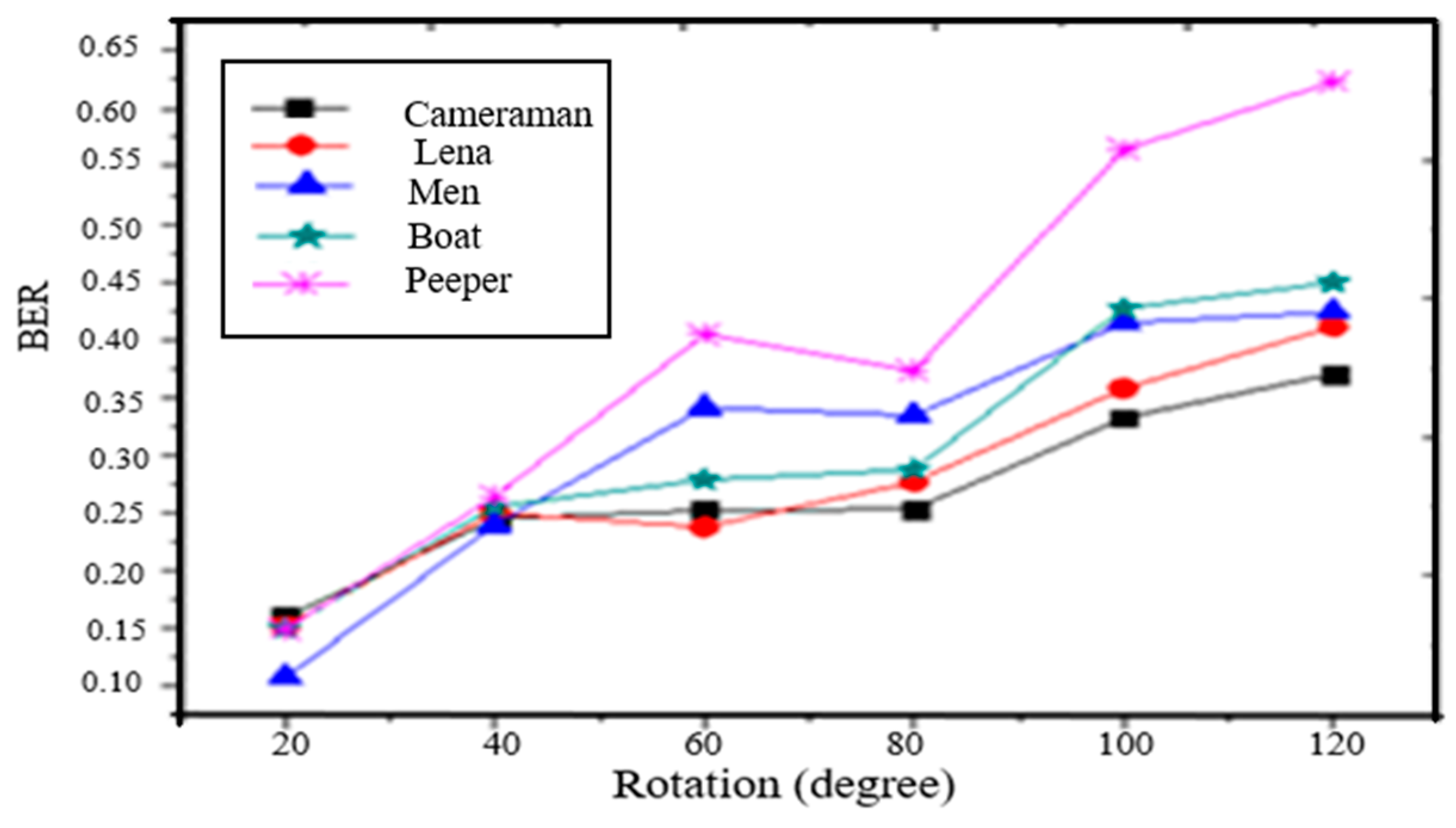
- Rotation: Rotation is another important image processing operation. The watermarked images are rotated by . The watermark can be detected even higher degrees of rotation. Figure 6 shows the BER of the extracted watermark image.
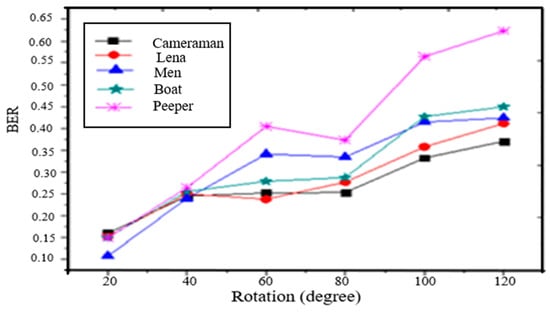 Figure 6. BER of extracted watermark under rotation.
Figure 6. BER of extracted watermark under rotation. - 6.
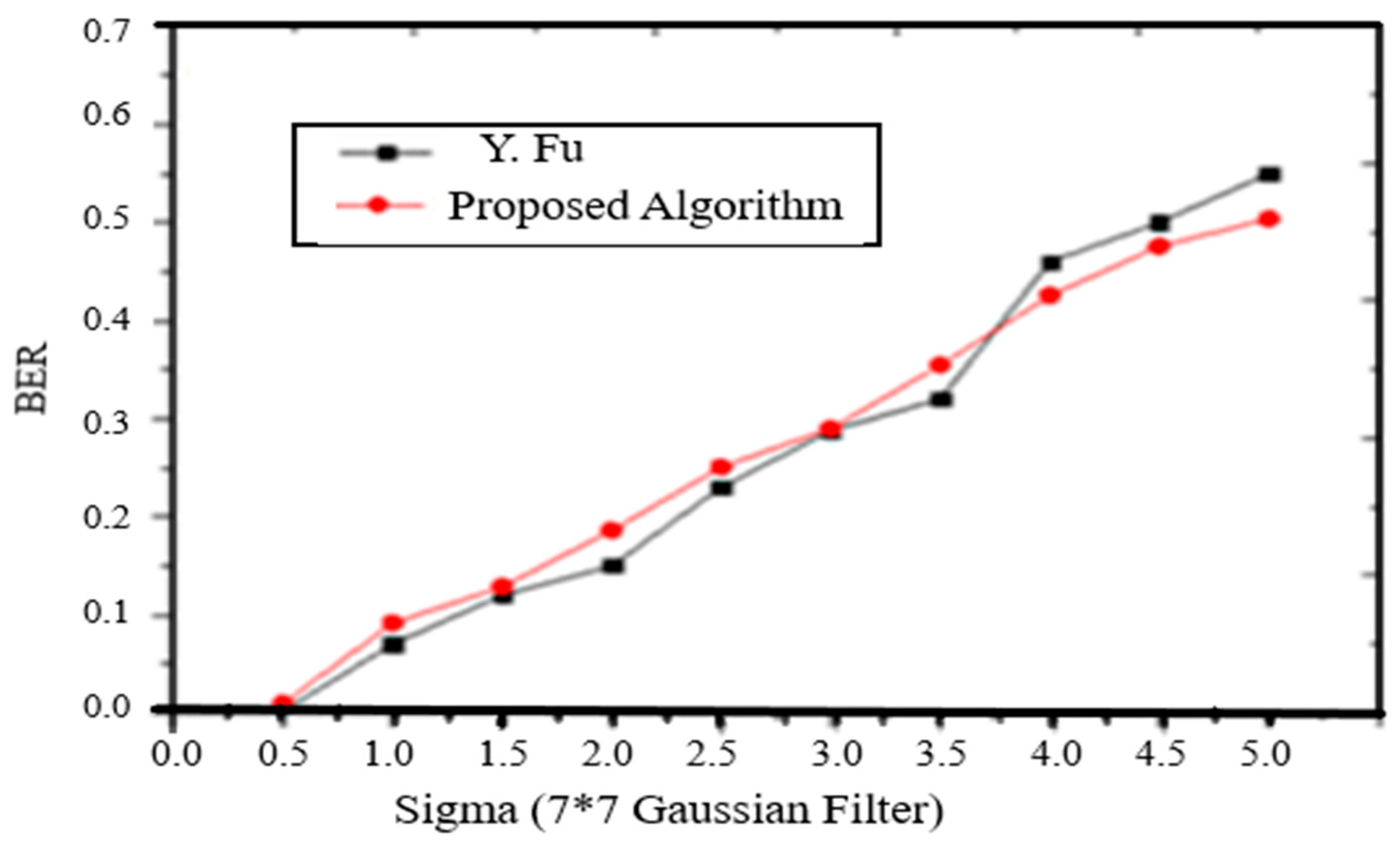
- Gaussian Filtering: To demonstrate the robustness of embedded watermark, the information is extracted from the Gaussian filtered watermarked image. The BER of the extracted watermark from that image is shown and compared with the method proposed in (Fu, 2013) (Figure 7).
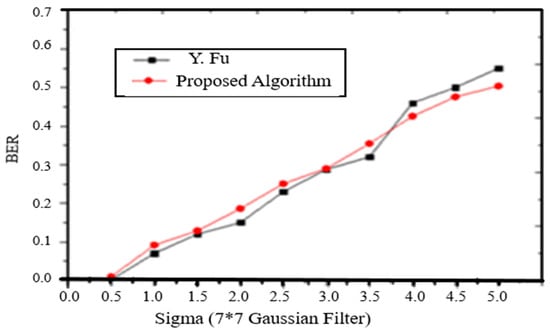 Figure 7. Comparison BER of extracted watermark with the Gaussian filtered [7*7] watermarked image.
Figure 7. Comparison BER of extracted watermark with the Gaussian filtered [7*7] watermarked image. - 7.
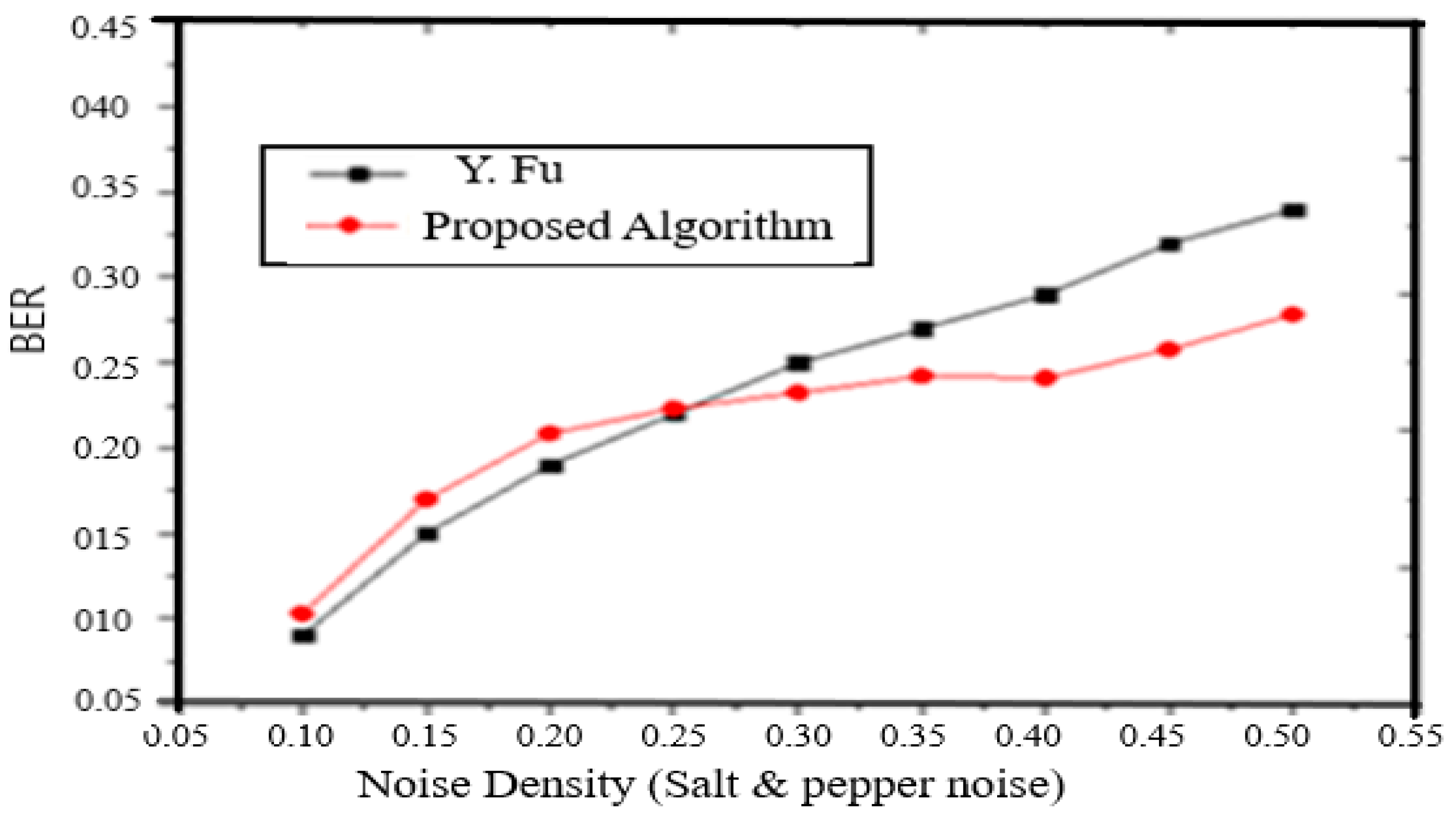
- Salt and pepper noise: Figure 8 shows the BER of the extracted/processed watermark from the watermarked image “Lena”, which is corrupted by the Salt and pepper noise with {0.05, 0.10 to 0.55} density. The results are also compared with those in (Fu, 2013).
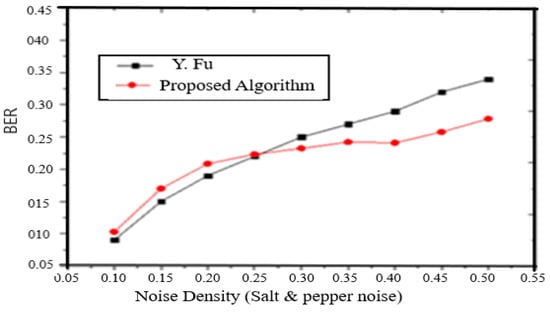 Figure 8. BER of extracted watermark from the salt and pepper noisy watermarked image.
Figure 8. BER of extracted watermark from the salt and pepper noisy watermarked image.
To accentuate the performance of the proposed technique, four dissimilar techniques based on different transforms and domains are compared. For the sake of easiness, these four techniques are named as DC-Spatial (Parekh, Bidani, and Santhi, 2018), DCT-IBCC (Das et al., 2014), MSF (Mishra et al., 2014), and LWT-SVD (Loukhaoukha et al., 2011). Table 3 lists statistics of measured PSNR, NC, and SSIM on six watermarked images. For the proposed technique, the average peak-signal to noise-ratio of the watermarked images is 54.663 dB. The peak-signal to noise-ratio can not only use as an indicator for visual-quality, but it is observed as a metric of implanting strength. The average PSNR shows the resemblance among the host images and watermarked images. As the average PSNR achieved by the MSF and DCT-IBCC algorithms is 53 dB, which can serve as the baseline when conducting performance calculation. The average PSNR values of LWT-SVD and DC-Spatial are 49.941 dB and 38.76 dB respectively. The average values of SSIM obtained from the proposed method, DCT-IBCC and DC-Spatial are 0.9902, 0.9836, and 0.9798 respectively. This shows the imperceptibility capability of the proposed algorithm. The average execution time per image for the watermarking techniques is shown in Table 4. The execution time of the proposed algorithm is lower as compared to other techniques listed in the table. The extraction of the edge surface and curvelet transforms takes a lesser amount of time compared to the DWT. Further, as an application of the work one can also calculate normalized absolute error as per [31].

Table 3.
Comparison of proposed method with existing techniques.

Table 4.
Average execution time per image (in second).
4. Discussion
The paper the watermarking technique in the curvelet domain by utilizing the textured surface of the original image has been presented. The visual superiority and resemblance between the host images and logo based watermarked images are precisely extraordinary. It means that the embedding of the watermark does not affect the originality of the artwork. To authenticate the original work the quality of extracted watermark is also important the above results show the comparison of extracted and embedded watermark using different metrics. Further, it presents the quality of extracted watermark and the robustness of the watermark. This technique provides good robustness and imperceptible when the original image is enriched with a good texture surface. But the technique is limited with the edge surface area. Imperceptibility is depending upon the textured surface. But the contour images or less edge surface images do not show promising results. As well as the algorithm is applied to the square size and gray-scale images. Further refinement in terms of future scope one can use the textures blocks in color images and contour images. As well as one can use other transforms like ridget, radon, and shearlet. The work can be incorporated with a genetic algorithm and machine learning that may be applied for the faulty images discard process. The genetic with seed as the initial threshold may be used for progressive improvement for the extraction process.
5. Conclusions
In this paper, an edge surface-based watermarking technique to conceal the binary logotype image into the curvelet domain of the 8-bit grayscale image was proposed. It identifies the edge surface n*n blocks by using the Gaussian filter, first-order partial differential, and a threshold. Further, it makes the edge surface image by using the blocks and embeds the watermark into the curvelet transform of the edge surface image. Edge surface curvelet coefficients have lower perceptible than the smooth surface coefficients of the image because human eyes are not equally sensitive to smooth an edged surface. To balance the invisibility and improve resistance ability against geometric and non-geometric attacks, the watermark strength parameter has been used. Experimental results supported the suitability of the edge surface-based watermarking technique for robustly hiding the watermark into an image. Comparative analysis among four existing techniques showed that the proposed method has imperceptibility and robustness against others with concerning to Watermark Embedding time 0.40716, Watermark Extraction time 0.2076, and Total time 0.61476.
Author Contributions
Conceptualization, M.M. and S.R.; Formal analysis, R.K. and L.M.G.; Funding acquisition, T.-h.K.; Investigation, S.R. and T.-h.K.; Methodology, M.M., R.K., I.K., A.V. and T.-h.K.; Project administration, I.K. and T.-h.K.; Resources, L.M.G.; Software, A.V. and L.M.G.; Supervision, A.V., L.M.G. and S.R.; Validation, A.V. and I.K.; Visualization, A.V. and L.M.G.; Writing – original draft, M.M., R.K., A.V., I.K. and L.M.G.; Writing – review & editing, S.R. and T.-h.K.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Congress, U.S. Digital millennium copyright act. Public Law 1998, 105, 112. [Google Scholar]
- Liu, Y.; Tang, S.; Liu, R.; Zhang, L.; Ma, Z. Secure and robust digital image watermarking scheme using logistic and RSA encryption. Expert Syst. Appl. 2018, 97, 95–105. [Google Scholar] [CrossRef]
- Gupta, R.; Mishra, A.; Jain, S. A semi-blind HVS based image watermarking scheme using elliptic curve cryptography. Multimed. Tools Appl. 2018, 77, 19235–19260. [Google Scholar] [CrossRef]
- Shih, F.Y. Digital Watermarking and Steganography: Fundamentals and Techniques; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Singh, A.K. Improved hybrid algorithm for robust and imperceptible multiple watermarking using digital images. Multimed. Tools Appl. 2017, 76, 8881–8900. [Google Scholar] [CrossRef]
- Abdelhakim, A.M.; Abdelhakim, M. A time-efficient optimization for robust image watermarking using machine learning. Expert Syst. Appl. 2018, 100, 197–210. [Google Scholar] [CrossRef]
- Anwar, M.I.; Singh, G. A Robust Digital Image Watermarking Algorithm using Ridgelet Transform. Int. J. Res. Eng. Soc. Sci. 2017, 7, 29–35. [Google Scholar]
- Parekh, M.; Bidani, S.; Santhi, V. Spatial Domain Blind Watermarking for Digital Images. In Progress in Computing, Analytics and Networking; Springer: Singapore, 2018; pp. 519–527. [Google Scholar]
- Su, Q.; Chen, B. Robust color image watermarking technique in the spatial domain. Soft Comput. 2018, 22, 91–106. [Google Scholar] [CrossRef]
- Das, C.; Panigrahi, S.; Sharma, V.K.; Mahapatra, K.K. A novel blind robust image watermarking in DCT domain using inter-block coefficient correlation. AEU-Int. J. Electron. Commun. 2014, 68, 244–253. [Google Scholar] [CrossRef]
- Fu, Y. Robust oblivious image watermarking scheme based on coefficient relation. Opt. Int. J. Light Electron Opt. 2013, 124, 517–521. [Google Scholar] [CrossRef]
- Singh, R.K.; Shaw, D.K.; Sahoo, J. A secure and robust block based DWT-SVD image watermarking approach. J. Inf. Optim. Sci. 2017, 38, 911–925. [Google Scholar] [CrossRef]
- Zear, A.; Singh, A.K.; Kumar, P. A proposed secure multiple watermarking technique based on DWT, DCT and SVD for application in medicine. Multimed. Tools Appl. 2018, 77, 4863–4882. [Google Scholar] [CrossRef]
- Lalani, S.; Doye, D.D. Discrete wavelet transform and a singular value decomposition technique for watermarking based on an adaptive fuzzy inference system. J. Inf. Process. Syst. 2017, 13, 340–347. [Google Scholar]
- Loukhaoukha, K.; Chouinard, J.Y.; Taieb, M.H. Optimal image watermarking algorithm based on LWT-SVD via multi-objective ant colony optimization. J. Inf. Hiding Multimed. Signal Process. 2011, 2, 303–319. [Google Scholar]
- Mishra, A.; Agarwal, C.; Sharma, A.; Bedi, P. Optimized gray-scale image watermarking using DWT–SVD and Firefly Algorithm. Expert Syst. Appl. 2014, 41, 7858–7867. [Google Scholar] [CrossRef]
- Yu, X.; Wang, C.; Zhou, X. Review on Semi-Fragile Watermarking Algorithms for Content Authentication of Digital Images. Future Internet 2017, 9, 56. [Google Scholar]
- Agilandeeswari, L.; Ganesan, K. RST invariant robust video watermarking algorithm using quaternion curvelet transform. Multimed. Tools Appl. 2018, 77, 25431–25474. [Google Scholar] [CrossRef]
- Kim, W.H.; Nam, S.H.; Lee, H.K. Blind curvelet watermarking method for high-quality images. Electron. Lett. 2017, 53, 1302–1304. [Google Scholar] [CrossRef]
- Sharma, S.G.; Raheja, L.R. Efficient Algorithms for Embedding Digital Watermark in Curvelet Domain. Ph.D. Thesis, Thapar University, Patiala, India, 2017. [Google Scholar]
- Tulapurkar, H.; Mohan, B.K.; Bharadi, V. Invisible watermarking algorithm for GIS data using Curvelet transform—Comparitive study with wavelet. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3389–3392. [Google Scholar]
- Moosazadeh, M.; Ekbatanifard, G. An improved robust image watermarking method using DCT and YCoCg-R color space. Opt. Int. J. Light Electron Opt. 2017, 140, 975–988. [Google Scholar] [CrossRef]
- Roy, R.; Ahmed, T.; Changder, S. Watermarking through image geometry change tracking. Vis. Inform. 2018, 2, 125–135. [Google Scholar] [CrossRef]
- Terrasse, G.; Nicolas, J.M.; Trouvé, E.; Drouet, E. Application of the Curvelet Transform for Clutter and Noise Removal in GPR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4280–4294. [Google Scholar] [CrossRef]
- Candes, E.J.; Donoho, D.L. Curvelets: A Surprisingly Effective Nonadaptive Representation for Objects with Edges; Stanford Univ Ca Dept of Statistics: Stanford, CA, USA; Vanderbilt University Press: Nashville, TN, USA, 2000. [Google Scholar]
- Candes, E.J.; Donoho, D.L. Curvelets, multiresolution representation, and scaling laws. In Proceedings of the Wavelet Applications in Signal and Image Processing VIII, San Diego, CA, USA, 4 December 2000; Volume 4119, pp. 1–13. [Google Scholar]
- Candes, E.; Demanet, L.; Donoho, D.; Ying, L. Fast discrete curvelet transforms. Multiscale Model. Simul. 2006, 5, 861–899. [Google Scholar] [CrossRef]
- Choi, M.; Kim, R.Y.; Kim, M.G. The curvelet transform for image fusion. Int. Soc. Photogramm. Remote Sens. ISPRS 2004, 35, 59–64. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Bianco, S.; Celona, L.; Napoletano, P.; Schettini, R. On the use of deep learning for blind image quality assessment. SignalImage Video Process. 2018, 12, 355–362. [Google Scholar] [CrossRef]
- Hemanth, D.J.; Umamaheswari, S.; Popescu, D.E.; Naaji, A. Application of Genetic Algorithm and Particle Swarm Optimization techniques for improved image steganography systems. Open Phys. 2016, 14, 452–462. [Google Scholar] [CrossRef]
- Verma, A.; Gakhar, A. Design and Development of Algorithm Using Chemical Cryptography. Procedia Comput. Sci. 2015, 58, 643–648. [Google Scholar] [CrossRef][Green Version]
- Chandramouli, R.; Memon, N. Analysis of LSB based image steganography techniques. In Proceedings of the 2001 International Conference on Image Processing (Cat. No.01CH37205), Thessaloniki, Greece, 7–10 October 2001; ISBN 0-7803-6725-1. [Google Scholar]
- Cachin, C. An information-theoretic model for steganography. In Proceedings of the 2nd Information Hiding Workshop, Portland, OR, USA, 14–17 April 1998; Springer-Verlag: Berlin/Heidelberg, Germany, 1998; Volume 1525, pp. 306–318. [Google Scholar]
- Mittal, M.; Verma, A.; Kaur, I.; Kaur, B.; Sharma, M.; Goyal, L.M.; Roy, S.; Kim, T. An Efficient Edge Detection Approach to Provide Better Edge Connectivity for Image Analysis. IEEE Access 2019, 7, 33240–33255. [Google Scholar] [CrossRef]
- Sene, I.; Ciss, A.A.; Niang, O. I2PA: An Efficient ABC for IoT. Cryptography 2019, 3, 16. [Google Scholar] [CrossRef]
- Ching, S.L.P.; Yunos, F. Effect of Self-Invertible Matrix on Cipher Hexagraphic Polyfunction. Cryptography 2019, 3, 15. [Google Scholar] [CrossRef]
- Helleseth, T.; Preneel, B. Special issue on recent trends in cryptography. Cryptogr. Commun. 2018, 10, 1–3. [Google Scholar] [CrossRef]
- Mittal, A.; Kumar, D.; Mital, M.; Saba, T.; Abunadi, I.; Rehman, A.; Roy, S. Detecting Pneumonia using Convolutions and Dynamic Capsule Routing for Chest X-ray Images. Sensors 2020, 20, 1068. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Yue, Q.; Wu, Y.; Kong, X. Complete weight enumerators of a class of two-weight linear codes. Cryptogr. Commun. 2019, 11, 609. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).