Solute Transport in the Element of Fractured Porous Medium with an Inhomogeneous Porous Block

Abstract

In this paper, the problem of solute transport in a fractured-porous medium taking into account the non-equilibrium adsorption kinetic is studied. The solute transport in fractured-porous medium consisting of two fractures and a porous block between them located in a symmetric form is considered. The problem is then solved numerically by using the finite difference method. Based on the numerical results, the solute concentration and adsorption fields in the fractures and porous blocks are shown in graphical form. The effect of adsorption on the solute transport in a fractured-porous medium is then analyzed. In the case of different parameters in two zones, asymmetric distribution of the solute concentration and adsorption is obtained. The nonlinear kinetics of adsorption leads to an increase in the adsorption effects, conversely slowing down the rate of the distribution of concentration of the solute in the fluid.

1. Introduction

The problem of solute transport and the fluid flow in porous [1,2,3] and fractured-porous media (FPM) [4,5,6] in recent years has received great attention. This is due to various applications where the processes of solute transport and fluid flow in the FPM are the basis of industrial, pilot industrial works on the utilization of various wastes in underground reservoirs [7,8] and the intensification of oil production by water flooding with various dissolved substances into reservoirs with fractured porous collectors [9]. One of the rational ways to analyze these processes is to compile and study the hydrodynamic models of the process.

A large number of works [10,11,12] are devoted to the problems of hydrodynamic modeling of the processes of solute transport in porous media. However, the issues of solute transport in FPM have been studied relatively less. It should be noted that one of the pioneer works was done in [13,14,15], where an approach was taken to compile and analyze the hydrodynamic models of the solute transport in FPM. In the aforementioned works, the process of solute transport in FPM is described by a combination of convective-diffusion transport, which is dominant in fractures, and diffusion transport, which is dominant in porous blocks.

The problem of the transport of pollutants in porous, fractured media has attracted considerable attention by many authors, especially in the case of radioactive waste disposal in underground storage facilities [16,17,18]. Using the Laplace transform method [19], a number of solutions to the equations for the migration of radionuclides in fractures, as well as in surrounding porous media, were obtained. Most models suggest that radionuclides are transported through fractures mainly due to advection and dispersion, while they move into the surrounding porous matrix due to molecular diffusion. It is now generally accepted that fractures can play an important role in the transport of contamination in the groundwater system, because the permeability of the fractured system is often much greater than the permeability of the porous matrix. For such a transport case, the authors of [20,21,22] obtained analytical stationary state solutions for various boundary conditions. Complete solution of transport processes can be found in [23].

In many studies of groundwater flow in fractured media, it was believed that the effective permeability of the medium is dominated by fractures [24,25]. Although fractures are the main pathways for water flow and solute transport, diffusion in neighboring porous blocks can play a significant role in the overall solute transport through the medium. One-dimensional motion through a single fracture can be described generally by the Navier–Stokes equations for non-turbulent flows of a viscous incompressible fluid in the space between two parallel planes, neglecting the inertial terms.

In [26], an exact solution to the problem of solute transport in two vertical fractures and a porous block between them is presented. In fractures, convective transport and hydrodynamic dispersion are taken into account; however, in the porous block, only molecular diffusion is taken into account. On the common surface of the porous blocks and fractures, as well as inside the block, the substance is adsorbed.

The inhomogeneity of the porous medium can have a significant effect on the solute transport, both in porous and fractured-porous media. Numerous works have been performed to study the relationship between heterogeneity and the solute transport in such media [27,28,29]. The inhomogeneity of the porous block in terms of porosity and permeability leads to heterogeneity of the medium and in the sense of diffusion solute transport in it. In [30,31], the behavior of solute transport in inhomogeneous media was numerically studied with emphasis on the influence of permeability inhomogeneities. There are two main mechanisms that control the solute transport process—diffusion and advection. The dispersion effect promotes diffusion and mechanical mixing during the solute transport due to advection of the liquid. The effects of heterogeneity on the processes of solute transport were studied using various permeability distributions, which are characterized as continuous and discontinuous models [31]. For continuous distribution models, numerical simulations show that the tracer distribution is distorted by a local change in permeability, but the global distribution behavior still resembles a uniform distribution behavior.

The process of solute transport in a system of parallel fractures located in a porous matrix was studied in [32], which takes into account advection transport, molecular diffusion and mechanical dispersion in a fracture, molecular diffusion from fractures into the matrix, adsorption on the surface and inside the matrix, and radioactive decay of the substance. The migration of radionuclides in the FPM, where porous blocks were modeled as spheres with a certain radius, is considered in [33]. The resulting solution was compared with a similar solution obtained for a system of parallel fractures. A model of parallel fractures with equal openness and width was used to analyze the labeled solute transport in the FPM [34]. In the region of small times, a single-fracture model gives satisfactory results, since the solute does not penetrate deep into the matrix and the effect of a neighboring fracture is not felt. Diffusion is dominant in matrix with high porosity. In the case of adsorption transport, the micropores of the matrix act as large sinks due to the large adsorption surface.

In [35], a solution to the problem of solute transport in a fractured medium is presented, where the solute diffuses from the fractures into the porous matrix. The solute is inert and does not react with the matrix skeleton and the fracture. The equation in a fracture is the equation of convective (advective) diffusion in the one-dimensional case, and in porous blocks it is the one-dimensional diffusion type equation. An analytical solution to the problem used to interpret laboratory data obtained in [36].

In this paper, we study the solute transport in an element of the FPM, a porous block surrounded by two fractures, taking into account the layered inhomogeneity of the porous block and non-equilibrium adsorption of the solute using schematization [35,36,37]. For the fractures and the porous block, the equations of solute transport are written separately, taking into account the mass transfer between them. Adsorption of solute is considered nonlinearly non-equilibrium both in fractures and in porous block. Based on the numerical solutions of the problem, the concentration fields of the solute and adsorbed mass are obtained. The role of adsorption and heterogeneity of the porous block on the characteristics of solute transport is estimated.

2. Problem Formulation

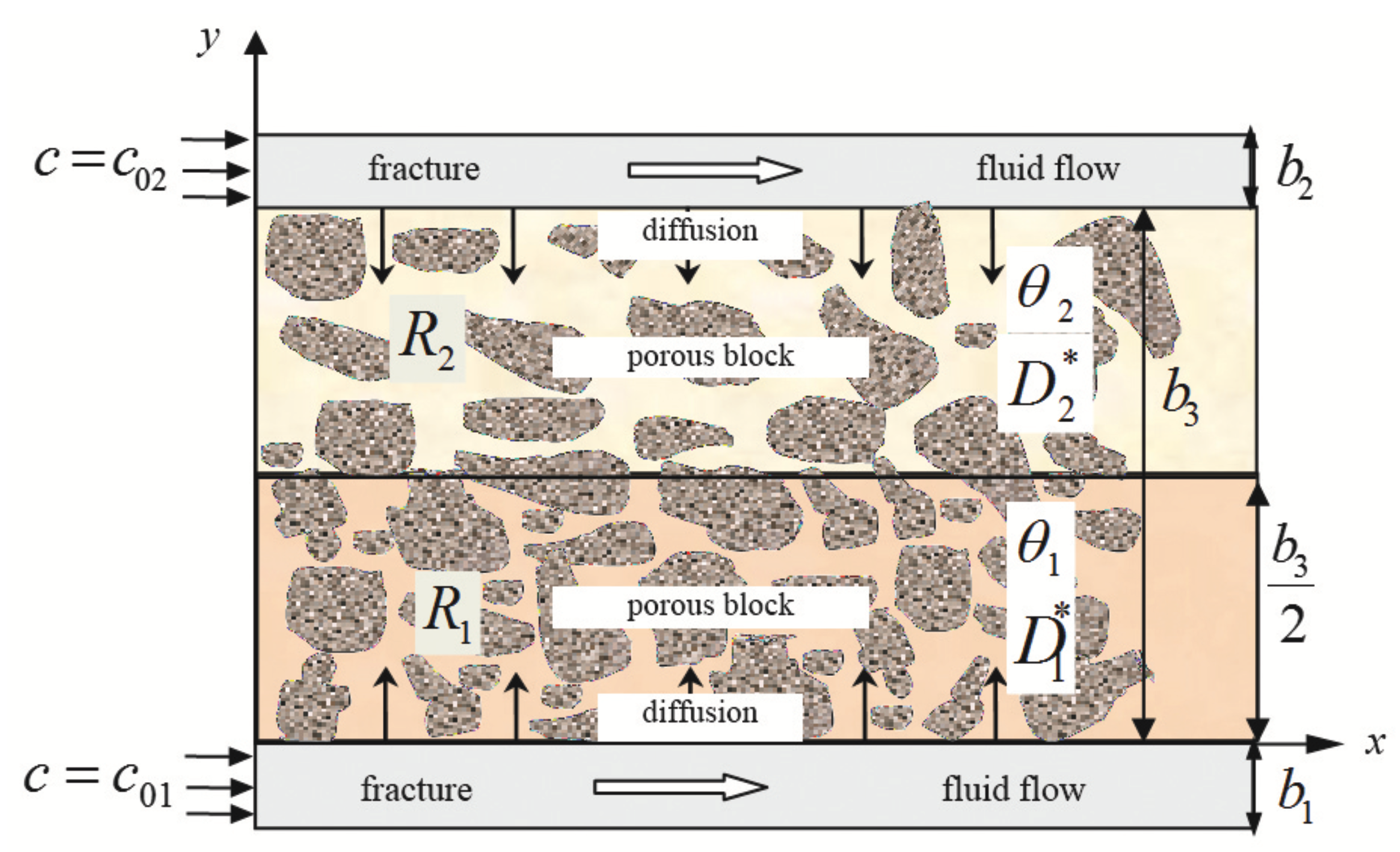
Consider a FPM element consisting of a porous block (matrix), which is surrounded by both sides with fractures (Figure 1). Fractures and porous block (and its parts $R_1\mathrm{and}{R}_2$) are considered one-dimensional and semi-infinite. The field of study of the problem consists of two parts: $R_1\left\{0\le t<\infty ,0\le x<\infty ,0\le y\le b_3/\phantom{b_{3}2}2\right\}$ with characteristics, ${\theta }_1$, $D_1^{*}$ and $R_2\left\{0\le t<\infty ,0\le x<\infty ,b_3/\phantom{b_{3}2}2\le y\le b_3\right\}$ with ${\theta }_2$, $D_2^{*}$, where ${\theta }_1$ and ${\theta }_2$ are the porosity coefficients in $R_1$ and $R_2$ (dimensionless quantities); $D_1^{*}$, $D_2^{*}$ (m${}^2$/s) are the coefficients of effective diffusion in the zones $R_1$ and $R_2$, respectively, which characterize diffusion properties of the parts of the porous block. In the porous block between the two fractures, diffusion mass transfer occurs in y direction.

The equations of convective-diffusive solute transport, taking into account the adsorption and mass transfer of the solute, are written separately for fractures and a porous block in the following form [38,39,40]:

$$b_1\left(\frac{\partial c_f}{\partial t}+{\rho }_1\frac{\partial s_f}{\partial t}+v_1\frac{\partial c_f}{\partial x}\right)=b_1{D}_{f1}^{*}\frac{{\partial }^2{c}_f}{\partial x^2}+{\theta }_1{D}_{{}_1}^{*}{\left.\frac{\partial c_f}{\partial y}\right|}_{y=o},$$

(1)

$$b_2\left(\frac{\partial c_f}{\partial t}+{\rho }_2\frac{\partial s_f}{\partial t}+v_2\frac{\partial c_f}{\partial x}\right)=b_2{D}_{f2}^{*}\frac{{\partial }^2{c}_f}{\partial x^2}-{\theta }_2{D}_2^{*}{\left.\frac{\partial c_f}{\partial y}\right|}_{y=b_3},$$

(2)

$$\frac{\partial c_m}{\partial t}+\frac{{\rho }_1}{{\theta }_1}\frac{\partial s_m}{\partial t}=D_1^{*}\frac{{\partial }^2{c}_m}{\partial y^2},0\le y\le \frac{b_3}{2},(x,y)\in R_1,$$

(3)

$$\frac{\partial c_m}{\partial t}+\frac{{\rho }_2}{{\theta }_2}\frac{\partial s_m}{\partial t}=D_2^{*}\frac{{\partial }^2{c}_m}{\partial y^2},\frac{b_3}{2}\le y\le b_3,(x,y)\in R_2,$$

(4)

where $c_m=c_m\left(t,x,y\right)$ is the concentration of the solute in the matrix, $c_f=c_f\left(t,x\right)$ is the concentration of the solute in the fractures (m${}^3$/m${}^3$); $s_m=s_m(t,x,y),s_f=s_f(t,x)$ are the concentration of adsorbed solute in the matrix and in the fractures, respectively (m${}^3$/kg); $D_{f1}^{*},D_{f2}^{*}$ are the convective diffusion coefficients in the first and second fractures (m${}^2$/s); $v_1,v_2$ are the fluid velocities in the first and second fractures (m/s); ${\rho }_1,{\rho }_2$ are the density of the medium in the $R_1$ and $R_2$ (kg/m${}^3)$; $b_1,b_2$ are the width of fractures (m); t is the time (s).

We use the following kinetic equations in equilibrium state corresponding to the Freundlich isotherms [41,42]

$$\frac{\partial s_f}{\partial t}={\alpha }_{f\left(n\right)}(k_{f\left(n\right)}{c}_f^N-s_f),$$

(5)

$$\frac{\partial s_m}{\partial t}={\alpha }_{m\left(n\right)}(k_{m\left(n\right)}{c}_m^N-s_m),$$

(6)

where $k_{f\left(n\right)},k_{m\left(n\right)}$ are the equilibrium constants of the Freundlich equation in the fracture and in the matrix (m${}^3$/kg; ${\alpha }_{f\left(n\right)},{\alpha }_{m\left(n\right)}$ are the adsorption rate coefficients characterizing the intensities of the adsorption processes in the fracture and in the matrix, respectively (s${}^{-1}$); N is constant ($0<N<1$); n is the index coefficient of the equations ($n=1$ for $R_1$, $n=2$ for $R_2$). From Equations (5) and (6) at $t\to \infty$, we obtain the equilibrium equations (Freundlich isotherm): $s_{f\left(n\right)}=k_{f\left(n\right)}{c}_f^N$ and $s_{m\left(n\right)}=k_{m\left(n\right)}{c}_m^N$. It is worth mentioning that, when $N=1$ at equilibrium state we obtain the linear law of adsorption isotherms (Henry Isotherm).

Let us assume that, at the initial moment the fractures and the porous block filled with pure fluid. At $t>0$, the fluid with a dissolved substance is fed into the fractures, for general case with different concentrations of $c_{01}$ and $c_{02}$, respectively. We assume that, for the time ranges used in this work, the concentration fields do not reach $x=\infty$. At the boundary of the porous block $y=\frac{b_3}{2}$, the concentration of the solute remains continuous. With this formulation, the initial and boundary conditions of the problem have the following form:

$$c_f\left(0,x\right)=c_m\left(0,x,y\right)=0,$$

(7)

$$c_f\left(t,0\right)=\left\{\begin{array}{c}{c}_{01},-b_1\le y\le 0,\hfill \\ c_{02},b_3\le y\le b_3+b_2,\hfill \end{array}\right.$$

(8)

$$c_f\left(t,\infty \right)=0,-b_1\le y\le 0,b_3\le y\le b_3+b_2,$$

(9)

$$c_f\left(t,x\right)=c_m\left(t,x,0\right),$$

(10)

$$c_f\left(t,x\right)=c_m\left(t,x,b_3\right),$$

(11)

$$c_m\left(t,x,\frac{b_3}{2}-0\right)=c_m\left(t,x,\frac{b_3}{2}+0\right),$$

(12)

$$D_1^{*}\frac{\partial c_m\left(t,x,\frac{b_3}{2}-0\right)}{\partial y}=D_2^{*}\frac{\partial c_m\left(t,x,\frac{b_3}{2}+0\right)}{\partial y},$$

(13)

$$s_f\left(0,x\right)=s_m\left(0,x,y\right)=0.$$

(14)

3. Numerical Solution Algorithm

The system of Equations (1)–(4) taking into account (5) and (6) under the conditions (7)–(14) is solved by using the finite difference method [43,44]. To do this, in the region $R_1\left\{0\le t<\infty ,0\le x<\infty ,0\le y\le \frac{b_3}{2}\right\}$ and $R_2\left\{0\le t<\infty ,0\le x<\infty ,\frac{b_3}{2}\le y\le b_3\right\}$, ($R_1\bigcup R_2$) we introduce a net ${\omega }_{h_1{h}_2\tau }={\omega }_{h_1{h}_2\tau }^{\left(1\right)}\bigcup {\omega }_{h_1{h}_2\tau }^{\left(2\right)}$, ${\omega }_{h_1{h}_2\tau }^{\left(1\right)}=$ $\{(t_k,x_i,y_j),t_k=\tau k,x_i=ih{}_1,y_j=jh{}_2,$ $k=\overline{0,K},i=0,1,\dots I,j=\overline{0,L},\tau =T/\phantom{TK}K,h_2=\frac{b_3}{J},L=\frac{J}{2}\}$, $\omega {}_{h{}_1{h}_2\tau }^{\left(2\right)}=\left\{\left(t_k,x_i,y_j\right),t_k=\tau k,x_i=ih{}_1,y_j=jh{}_2,k=\overline{0,K},i=0,1,\dots I,j=\overline{L,J},\tau =T/\phantom{TK}K,h_2=\frac{b_3}{J},L=\frac{J}{2}\right\}$, where $h_1$ is the grid step in the x direction, I is the number of grid intervals in x, $h_2$ is the grid step in the y direction, $\tau$ is the time step of the grid, K is the number of grid intervals by t, T is the maximum time during which the process is studied, L is the number of grid intervals by y in $R_1$, J is the total number of grid intervals of y in $R_1$ and $R_2$.

On this grid, Equations (1)–(4) are approximated as

$$\begin{gathered} \frac{c{f}_i^{k+1}-c{f}_i^k}{\tau }+{\rho }_1\frac{s{f}_i^{k+1}-s{f}_i^k}{\tau }+v_1\frac{c{f}_i^{k+1}-c{f}_{i-1}^{k+1}}{h_1}=D_{f1}^{*}\frac{c{f}_{i+1}^{k+1}-2c{f}_i^{k+1}+c{f}_{i-1}^{k+1}}{h_1^2}+ \\ \frac{{\theta }_1{D}_1^{*}}{b_1}\frac{c{m}_{i,1}^k-c{m}_{i,0}^k}{h_2},i=\overline{1,I-1},k=\overline{0,K-1},\mathrm{in}{\omega }_{h_1{h}_2\tau }^{\left(1\right)} \end{gathered}$$

(15)

$$\begin{gathered} \frac{c{f}_i^{k+1}-c{f}_i^k}{\tau }+{\rho }_2\frac{s{f}_i^{k+1}-s{f}_i^k}{\tau }+v_2\frac{c{f}_i^{k+1}-c{f}_{i-1}^{k+1}}{h_1}=D_{f2}^{*}\frac{c{f}_{i+1}^{k+1}-2c{f}_i^{k+1}+c{f}_{i-1}^{k+1}}{h_1^2}- \\ \frac{{\theta }_2{D}_2^{*}}{b_2}\frac{c{m}_{i,1}^k-c{m}_{i,0}^k}{h_2},i=\overline{1,I-1},k=\overline{0,K-1},\mathrm{in}{\omega }_{h_1{h}_2\tau }^{\left(2\right)} \end{gathered}$$

(16)

$$\begin{gathered} \frac{c{m}_{i,j}^{k+1}-c{m}_{i,j}^k}{\tau }+\frac{{\rho }_1}{{\theta }_1}\frac{s{m}_{i,j}^{k+1}-s{m}_{i,j}^k}{\tau }=D_1^{*}\frac{c{m}_{i,j+1}^{k+1}-2c{m}_{i,j}^{k+1}+c{m}_{i,j-1}^{k+1}}{h_2^2}, \\ i=\overline{0,I},j=\overline{1,L-1},k=\overline{0,K-1},\mathrm{in}{\omega }_{h_1{h}_2\tau }^{\left(1\right)} \end{gathered}$$

(17)

$$\begin{gathered} \frac{c{m}_{i,j}^{k+1}-c{m}_{i,j}^k}{\tau }+\frac{{\rho }_2}{{\theta }_2}\frac{s{m}_{i,j}^{k+1}-s{m}_{i,j}^k}{\tau }=D_2^{*}\frac{c{m}_{i,j+1}^{k+1}-2c{m}_{i,j}^{k+1}+c{m}_{i,j-1}^{k+1}}{h_2^2}, \\ i=\overline{0,I},j=\overline{L-1,J-1},k=\overline{0,K-1},\mathrm{in}{\omega }_{h_1{h}_2\tau }^{\left(2\right)} \end{gathered}$$

(18)

where $c{f}_i^k$, $c{m}_{i,j}^k$ are the net values of concentrations $c_f(t,x)$ and $c_m(t,x,y)$ at net points $\left(t_k,x_i\right)$ and $\left(t_k,x_i,y_j\right)$, respectively.

Equations (5) and (6) are approximated as follows

$$\frac{s{f}_i^{k+1}-s{f}_i^k}{\tau }={\alpha }_{f1}{k}_{f1}{\left(c{f}_i^k\right)}^N-{\alpha }_{f1}s{f}_i^{k+1},i=\overline{0,I},k=\overline{0,K-1},\mathrm{in}{\omega }_{h_1{h}_2\tau }^{\left(1\right)}$$

(19)

$$\frac{s{f}_i^{k+1}-s{f}_i^k}{\tau }={\alpha }_{f2}{k}_{f2}{\left(c{f}_i^k\right)}^N-{\alpha }_{f2}s{f}_i^{k+1},i=\overline{0,I},k=\overline{0,K-1},\mathrm{in}{\omega }_{h_1{h}_2\tau }^{\left(2\right)}$$

(20)

$$\frac{s{m}_{i,j}^{k+1}-s{m}_{i,j}^k}{\tau }={\alpha }_{m1}{k}_{m1}{\left(c{m}_{i,j}^k\right)}^N-{\alpha }_{m1}s{m}_{i,j}^{k+1},i=\overline{0,I},j=\overline{0,L},k=\overline{0,K-1},\mathrm{in}{\omega }_{h_1{h}_2\tau }^{\left(1\right)}$$

(21)

$$\frac{s{m}_{i,j}^{k+1}-s{m}_{i,j}^k}{\tau }={\alpha }_{m2}{k}_{m2}{\left(c{m}_{i,j}^k\right)}^N-{\alpha }_{m2}s{m}_{i,j}^{k+1},i=\overline{0,I},j=\overline{L,J},k=\overline{0,K-1},\mathrm{in}{\omega }_{h_1{h}_2\tau }^{\left(2\right)}$$

(22)

where $s{f}_i^k$, $s{m}_{i,j}^k$ are net values of concentrations $s_f(t,x)$ and $s_m(t,x,y)$ at net points $\left(t_k,x_i\right)$ and $\left(t_k,x_i,y_j\right)$, respectively.

The initial and boundary conditions are approximated as follows

$$c{f}_i^0=c{m}_{i,j}^0=0,in{\omega }_{h_1{h}_2\tau },$$

(23)

$$c{f}_0^{k+1}=c{m}_{0,j}^{k+1}=\left\{\begin{array}{c}{c}_{01},j=0\hfill \\ c_{02},j=J\hfill \end{array}\right.,$$

(24)

$$c{f}_I^{k+1}=0,$$

(25)

$$c{f}_i^k=c{m}_{i,0}^k,in{\omega }_{h_1{h}_2\tau }^{\left(1\right)},$$

(26)

$$c{f}_i^k=c{m}_{i,J}^k,in{\omega }_{h_1{h}_2\tau }^{\left(2\right)},$$

(27)

$$c{m}_{i,L-0}^{k+1}=c{m}_{i,L+0}^{k+1},$$

(28)

$$D_1^{*}\frac{c{m}_{i,L}^{k+1}-c{m}_{i,L-1}^{k+1}}{h_2}=D_2^{*}\frac{c{m}_{i,L+1}^{k+1}-c{m}_{i,L}^{k+1}}{h_2},$$

(29)

$$s{f}_i^0=s{m}_{i,j}^0=0,in{\omega }_{h_1{h}_2\tau },$$

(30)

where I is taken large enough so that the concentration profiles do not reach the selected conditional boundaries of the regions.

After approximation, Equations (15) and (17) are reduced to

$$A_{1}c{f}_{i-1}^{k+1}-B_{1}c{f}_i^{k+1}+C_{1}c{f}_{i+1}^{k+1}=-F_i^{\left(1\right)},i=\overline{1,I-1},k=\overline{0,K-1}$$

(31)

$$A_{2}c{m}_{i,j-1}^{k+1}-B_{2}c{m}_{i,j}^{k+1}+C_{2}c{m}_{i,j+1}^{k+1}=-F_{i,j}^{\left(2\right)},i=\overline{0,I},j=\overline{1,L-1},k=\overline{0,K-1}$$

(32)

where $A_1=\frac{D_{f1}^{*}}{h_1^2}+\frac{v_1}{h_1}$, $B_1=\frac{1}{\tau }+2\frac{D_{f1}^{*}}{h_1^2}+\frac{v_1}{h_1}$, $C_1=\frac{D_{f1}^{*}}{h_1^2}$, $A_2=\frac{\tau D_1^{*}}{h_2^2}$, $B_2=1+2\frac{\tau D_1^{*}}{h_2^2}$, $C_2=\frac{\tau D_1^{*}}{h_2^2}$,

$$F_i^{\left(1\right)}=\frac{1}{\tau }{c}_i^k+\frac{{\theta }_1{D}_1^{*}}{b_1{h}_2}\left(c{m}_{i,1}^k-c{m}_{i,0}^k\right)-\frac{{\rho }_1}{\tau }s{f}_i^{k+1}+\frac{{\rho }_1}{\tau }s{f}_i^k,F_{i,j}^{\left(2\right)}=c{m}_{ij}^k-\frac{{\rho }_1}{{\theta }_1}s{m}_{i,j}^{k+1}+\frac{{\rho }_1}{{\theta }_1}s{m}_{i,j}^k.$$

The Equations (16) and (18) are also reduced to

$$A_{3}c{f}_{i-1}^{k+1}-B_{3}c{f}_i^{k+1}+C_{3}c{f}_{i+1}^{k+1}=-F_i^{\left(3\right)},i=\overline{1,I-1},k=\overline{0,K-1},$$

(33)

$$A_{4}c{m}_{i,j-1}^{k+1}-B_{4}c{m}_{i,j}^{k+1}+C_{4}c{m}_{i,j+1}^{k+1}=-F_{i,j}^{\left(4\right)},i=\overline{0,I},j=\overline{L-1,J-1},k=\overline{0,K-1}$$

(34)

where, $A_3=\frac{D_{f2}^{*}}{h_1^2}+\frac{v_2}{h_1}$, $B_3=\frac{1}{\tau }+2\frac{D_{f2}^{*}}{h_1^2}+\frac{v_2}{h_1}$, $C_3=\frac{D_{f2}^{*}}{h_1^2}$, $A_4=\frac{\tau D_4^{*}}{h_2^2}$, $B_4=1+2\frac{\tau D_2^{*}}{h_2^2}$, $C_4=\frac{\tau D_2^{*}}{h_2^2}$,

$$F_i^{\left(3\right)}=\frac{1}{\tau }{c}_i^k-\frac{{\theta }_2{D}_2^{*}}{b_2{h}_2}\left(c{m}_{i,J}^k-c{m}_{i,J-1}^k\right)-\frac{{\rho }_2}{\tau }s{f}_i^{k+1}+\frac{{\rho }_2}{\tau }s{f}_i^k,F_{i,j}^{\left(4\right)}=c{m}_{ij}^k-\frac{{\rho }_2}{{\theta }_2}s{m}_{i,j}^{k+1}+\frac{{\rho }_2}{{\theta }_2}s{m}_{i,j}^k.$$

Similarly, after approximation, Equations (19)–(22) are respectively reduced to

$$s{f}_i^{k+1}=P_1{k}_{f1}{\left(c{f}_i^k\right)}^N+E_{1}s{f}_i^k,i=\overline{0,I},k=\overline{0,K-1},$$

(35)

$$s{f}_i^{k+1}=P_3{k}_{f2}{\left(c{f}_i^k\right)}^N+E_{3}s{f}_i^k,i=\overline{0,I},k=\overline{0,K-1},$$

(36)

$$s{m}_{i,j}^{k+1}=P_2{k}_{m1}{\left(c{m}_{i,j}^k\right)}^N+E_{2}s{m}_{i,j}^k,i=\overline{0,I},j=\overline{0,L}k=\overline{0,K-1},$$

(37)

$$s{m}_{i,j}^{k+1}=P_4{k}_{m2}{\left(c{m}_{i,j}^k\right)}^N+E_{4}s{m}_{i,j}^k,i=\overline{0,I},j=\overline{L,J},k=\overline{0,K-1},$$

(38)

where $P_1=\frac{\tau {\alpha }_{f1}}{1+\tau {\alpha }_{f1}}$, $E_1=\frac{1}{1+\tau {\alpha }_{f1}}$, $P_2=\frac{\tau {\alpha }_{m1}}{1+\tau {\alpha }_{m1}}$, $E_2=\frac{1}{1+\tau {\alpha }_{m1}}$, $P_3=\frac{\tau {\alpha }_{f2}}{1+\tau {\alpha }_{f2}}$, $E_3=\frac{1}{1+\tau {\alpha }_{f2}}$, $P_4=\frac{\tau {\alpha }_{m2}}{1+\tau {\alpha }_{m2}}$, $E_4=\frac{1}{1+\tau {\alpha }_{m2}}$.

The systems of Equations (31) and (32) are solved by the sweep method in the i and j directions, respectively [44,45]. We use the following relations

$$c{f}_i^{k+1}={\alpha }_{i+1}^{\left(1\right)}+{\beta }_{i+1}^{\left(1\right)}c{f}_{i+1}^{k+1},i=\overline{0,I-1},k=\overline{0,K-1},$$

(39)

$$c{m}_{ij}^{k+1}={\alpha }_{j+1}^{\left(2\right)}+{\beta }_{j+1}^{\left(2\right)}c{m}_{i,j+1}^{k+1},i=\overline{0,I},j=\overline{0,L-1},k=\overline{0,K-1}$$

(40)

where ${\alpha }_{i+1}^{\left(1\right)},{\beta }_{i+1}^{\left(1\right)},{\alpha }_{j+1}^{\left(2\right)},{\beta }_{j+1}^{\left(2\right)}$ are indeterminate coefficients.

To solve (33) and (34), the sweep method in the i and j directions is also used, respectively. For this, we use the following relations

$$c{f}_i^{k+1}={\alpha }_{i+1}^{\left(3\right)}+{\beta }_{i+1}^{\left(3\right)}c{f}_{i+1}^{k+1},i=\overline{0,I-1},k=\overline{0,K-1},$$

(41)

$$c{m}_{ij}^{k+1}={\alpha }_{j-1}^{\left(4\right)}+{\beta }_{j-1}^{\left(4\right)}c{m}_{i,j-1}^{k+1},i=\overline{0,I},j=\overline{J,L+1},k=\overline{0,K-1}$$

(42)

where ${\alpha }_{i+1}^{\left(3\right)},{\beta }_{i+1}^{\left(3\right)},{\alpha }_{j+1}^{\left(4\right)},{\beta }_{j+1}^{\left(4\right)}$ are indeterminate coefficients.

When using (39) from (31), we obtain the following recurrence formulas for determining the coefficients ${\alpha }_{i+1}^{\left(1\right)},{\beta }_{i+1}^{\left(1\right)}$

$${\alpha }_{i+1}^{\left(1\right)}=\frac{F_i^{\left(1\right)}+A_1\times {\alpha }_i^{\left(1\right)}}{B_1-A_1\times {\beta }_i^{\left(1\right)}},{\beta }_{i+1}^{\left(1\right)}=\frac{C_1}{B_1-A_1\times {\beta }_i^{\left(1\right)}},i=\overline{1,I-1}$$

(43)

Similarly, we obtain the following recurrence formulas for other sweep coefficients in (40)–(42)

$${\alpha }_{j+1}^{\left(2\right)}=\frac{F_{i,j}^{\left(2\right)}+A_2\times {\alpha }_j^{\left(2\right)}}{B_2-A_2\times {\beta }_j^{\left(2\right)}},{\beta }_{j+1}^{\left(2\right)}=\frac{C_2}{B_2-A_2\times {\beta }_j^{\left(2\right)}},i=\overline{0,I},j=\overline{1,L-1}$$

(44)

$${\alpha }_{i+1}^{\left(3\right)}=\frac{F_i^{\left(3\right)}+A_3\times {\alpha }_i^{\left(3\right)}}{B_3-A_3\times {\beta }_i^{\left(3\right)}},{\beta }_{i+1}^{\left(3\right)}=\frac{C_3}{B_3-A_3\times {\beta }_i^{\left(3\right)}},i=\overline{1,I-1}$$

(45)

$${\alpha }_{j-1}^{\left(4\right)}=\frac{F_{i,j}^{\left(4\right)}+C_4\times {\alpha }_j^{\left(4\right)}}{B_4-C_4\times {\beta }_j^{\left(4\right)}},{\beta }_{j-1}^{\left(4\right)}=\frac{A_4}{B_4-C_4\times {\beta }_j^{\left(4\right)}},i=\overline{0,I},j=\overline{J,L+1}$$

(46)

Starting values of coefficients ${\alpha }_{i+1}^{\left(1\right)},{\beta }_{i+1}^{\left(1\right)}$ and ${\alpha }_{i+1}^{\left(3\right)},{\beta }_{i+1}^{\left(3\right)}$ are determined based on the condition (24): ${\alpha }_1^{\left(1\right)}=c_{01},{\beta }_1^{\left(1\right)}=0,$ ${\alpha }_1^{\left(3\right)}=c_{02},{\beta }_1^{\left(3\right)}=0.$ Starting values of ${\alpha }_{j+1}^{\left(2\right)},{\beta }_{j+1}^{\left(2\right)}$ and ${\alpha }_{j-1}^{\left(4\right)},{\beta }_{j-1}^{\left(4\right)}$ are determined based on the conditions (26) and (27): ${\alpha }_1^{\left(2\right)}=c{f}_i^{k+1},{\beta }_1^{\left(2\right)}=0,$ ${\alpha }_{J-1}^{\left(4\right)}=c{f}_i^{k+1},{\beta }_1^{\left(4\right)}=0.$

According to recurrent formulas (44) and (46) we determine the values of ${\alpha }_{j+1}^{\left(2\right)},{\beta }_{j+1}^{\left(2\right)}$($j=\overline{1,L-1}$) and ${\alpha }_{j-1}^{\left(4\right)},{\beta }_{j-1}^{\left(4\right)}$($j=\overline{J-1,L+1}$). From condition (29), we find $c{m}_{i,L}^{k+1}$ in following form

$$c{m}_{i,L}^{k+1}=\frac{{\alpha }_L^{\left(2\right)}+\gamma {\alpha }_L^{\left(4\right)}}{1+\gamma -{\beta }_L^{\left(2\right)}-\gamma {\beta }_L^{\left(4\right)}},i=\overline{0,I},$$

(47)

where $\gamma =\frac{D_2^{*}}{D_1^{*}}$. From Equations (35)–(38), we find $s{f}_i^{k+1}$ and $s{m}_{i,j}^{k+1}$ in the zones $R_1$ and $R_2$, respectively.

We note, that sufficient stability conditions to apply Thomas’ algorithm to Equations (31)–(34) are satisfied.

Knowing the concentration field, we can determine the relative current flow rate of the solute through the common boundary of the fracture and the porous block in the zones $R_1$ and $R_2$

$$Q_1=-{\theta }_1{D}_1^{*}{\left.\frac{\partial c_m}{\partial y}\right|}_{y=0},Q_2=-{\theta }_2{D}_2^{*}{\left.\frac{\partial c_m}{\partial y}\right|}_{y=b_3},$$

(48)

and in the net approximation

$$Q_{1,i}^{k+1}=-{\theta }_1{D}_1^{*}\frac{c{m}_{i,1}^{k+1}-c{m}_{i,0}^{k+1}}{h_2},Q_{2,i}^{k+1}={\theta }_2{D}_2^{*}\frac{c{m}_{i,J}^{k+1}-c{m}_{i,J-1}^{k+1}}{h_2}.$$

(49)

The total relative flow rates across the common boundaries ($y=0$ and $y=b_3$) are defined as

$$Q_{1,2tot}={\int }_0^{\infty }{Q}_{1,2}dx,$$

(50)

and the relative summary flow rates as:

$$Q_{1,2sum}={\int }_0^t{\int }_0^{\infty }{Q}_{1,2}dxdt.$$

(51)

Integrals (50), (51) are calculated numerically based on numerical values of $Q_i^{k+1}$. In this case, the discretization of the integration region is carried out in accordance with the introduced grid.

4. Results and Discussion

The presented problem is numerically solved using the finite difference method. Some calculation results are shown in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 for various model parameters. The following values of parameters are used: $D_1^{*}=D_2^{*}=1\times {10}^{-6}{\mathrm{m}}^2/\mathrm{s}$, $v_1=v_2=5\times {10}^{-4}\mathrm{m}/\mathrm{s}$, $c_{01}=c_{02}=0.01{\mathrm{m}}^3/{\mathrm{m}}^3$, ${\rho }_1={\rho }_2=2500{\mathrm{kg}/\mathrm{m}}^3$, $b_1=b_2=4\times {10}^{-4}\mathrm{m}$, $b_3=m1$, ${\theta }_1={\theta }_2=0.2$ [35,36,37]. We used the following mesh parameters $h_1=h_2=0.1,\tau =1$.

Figure 2 shows surfaces $c_m/c_0$ and $s_m$ for linear kinetic adsorption (in the equilibrium case, the corresponding Henry isotherm) with the same characteristics of fractures and porous block. In Figure 3, the same surfaces given for nonlinear kinetic adsorption (in equilibrium case, corresponding to the Freundlich isotherm) of the solute. Comparing the data presented, it can be seen that the surfaces of the distribution of concentration and adsorption of the solute from the two fractures are symmetric, therefore, the relative current solute flow rate $Q_i,i=1,2$ from the first ($i=1$ in the zone $R_1$) and second ($i=2$ in the zone $R_2$) fractures in the porous block will be the same. This conclusions are similar with the results obtained by Grisak and Pickens [35].

Figure 4 and Figure 5 show the distribution fields of the concentration of the solute and the adsorption field in the medium for two cases of nonequilibrium adsorption. In this case, it was posed that in the region $R_2$ solute transport without taking into account adsorption, as well as in the $R_1$ zone, the calculation results are presented with an increase in the adsorption coefficient $k_{f1}=k_{m1}=k$ and ${\alpha }_{f1}={\alpha }_{m1}=\alpha$. As can be seen from these figures, that changing the values of parameters $k_{f1}$, $k_{m1}$ from $k_{f1}=k_{m1}=3\times {10}^{-5}{\mathrm{m}}^3/\mathrm{kg}$ to $k_{f1}=k_{m1}=3\times {10}^{-4}{\mathrm{m}}^3/\mathrm{kg}$, ${\alpha }_{f1}$, ${\alpha }_{m1}$ from ${\alpha }_{f1}={\alpha }_{m1}=4\times {10}^{-5}{\mathrm{s}}^{-1}$, to ${\alpha }_{f1}={\alpha }_{m1}=4\times {10}^{-4}{\mathrm{s}}^{-1}$, and N from $N=0.88$ to $N=0.83$ (increasing the adsorption effect), leads to a reduction in the distribution of the concentration field in the zone $R_1$ (Figure 4). The maximum values at $t=6000s$ for non-equilibrium adsorption corresponding at equilibrium conditions to the Freundlich isotherm are greater than for the Henry isotherms (Figure 5a,b).

The dynamics of the relative solute flow rate from the first ($Q_1$) and second ($Q_2$) fractures into the porous block for two cases of kinetic adsorption is shown in Figure 6. With an increase in adsorption, the distribution zone $Q_1$ decreases at small x, then the opposite tendency is observed. An increase in adsorption in the zone $R_1$ leads to an increase in the total and summary solute flow rate in the zone $R_1$ (Figure 7 and Figure 8).

As can be seen from Figure 7, both cases of linear and nonlinear adsorption kinetics, a non-monotonic kinetics of the total relative flow rate of the solute from the fractures to the porous block are obtained. Such non-monotonicity is characterized by the fact that in the initial stages of the transport process in a zone close to the input section of the medium, which is in the initial sections of the medium, relatively large concentration gradients are formed. As the solute transport continues, the porous block begins to saturated with the solute and concentration gradients begin to decrease. This leads to non-monotonic dynamics of the relative flow rate. Such non-monotonicity is observed at local time scales. In the summary relative solute flow rates non-monotonicity is not observed, since they represent an integral temporal characteristic (Figure 8). The lack of non-monotonicity in $Q_{1sum}$, $Q_{2sum}$ can also been explained by the fact that the solute mass transfer through the boundaries of fractures and the porous block over the entire length of the boundaries, for all times occurs in one direction–from fractures to the porous block.

5. Conclusions

The problem of solute transport in a FPM element, consisting of two fractures and a porous block between them, with the effect of the non-equilibrium kinetic adsorption of the solute on the transfer characteristics is considered. Based on numerical calculations, it was found that the adsorption in the $R_1$ zone leads to a decrease in the concentration field in the zone.

In this study, two cases of non-equilibrium adsorption are analyzed and its effect on the solute transport in the element are shown. For different effective diffusion coefficients in the porous block, an asymmetric distributions of the concentration and adsorption of the solute are obtained.

It is found that the layered inhomogeneity of the porous block leads to an asymmetric distribution of the concentration and adsorbed solute mass fields. The nonlinear kinetics of adsorption, ceteris paribus, leads to increase the adsorption effects. Thus, it slows down the rate of the distribution and the concentration of the solute in the fluid. A non-monotonic dependence is found for the current and total relative solute flow rates through the common boundary of the fractures and the porous block. Total relative solute flow rates sharply increases in small values of time, then over time it decreases slowly. This is explained by the formation of large concentration gradients in the initial sections of the medium in the initial stages of the process and their subsequent decrease. Non-monotonicity is not observed for the summary relative flow rate.

Thus, this approach together with the schematization of the porous block as a layered inhomogeneous medium by diffusion properties allows a qualitative and quantitative analysis of transport processes in inhomogeneous FPMs.