Simple Solutions of Lattice Sums for Electric Fields Due to Infinitely Many Parallel Line Charges
Abstract
:1. Introduction
2. Investigation Method
3. Results
3.1. Considered Cases
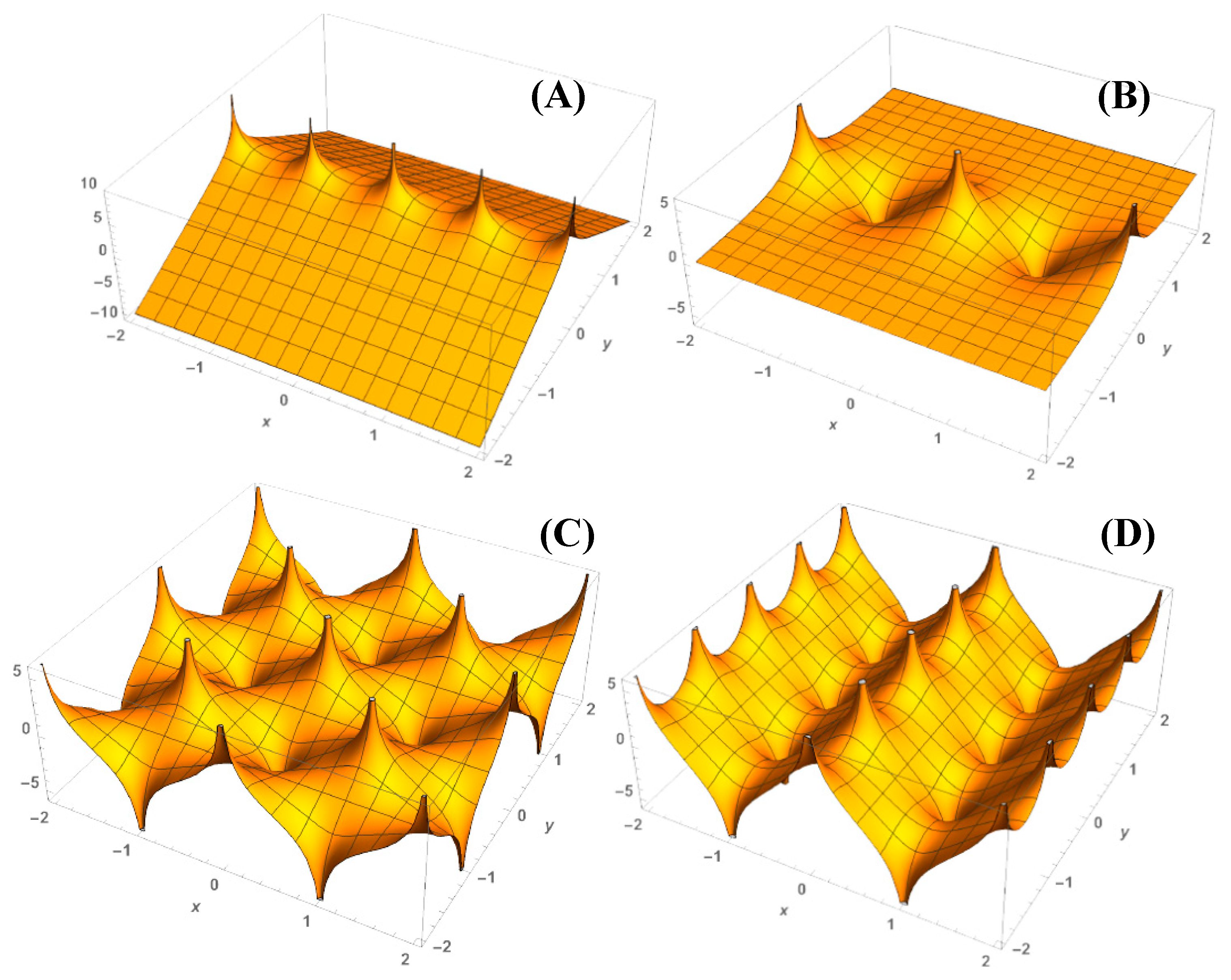
- Case A: “+” at ; co-ordinates [ vary, fixed at 0, only “+”]
- Case B: “+”/”−“ at even/odd ; co-ordinates [ vary, fixed at 0, “+”/”−“ if even/odd]
- Case C: “+”/”−“ at even/odd ; co-ordinates [ and vary, “+”/”−“ if even/odd]
- Case D: “+”/”−“ at even/odd ; co-ordinates [ and vary, “+”/”−“ if even/odd]
3.2. Electric-Field Components as Sum Formulas
3.3. Electric Potentials as Sum Formulas
3.4. Closed-Form Expressions
4. Discussion
4.1. Comparisons to Earlier Works
4.2. Duality Aspect and Corollary Findings Related to Gauss’s Constant
4.3. Potential Applications and Extension to Asymmetric Planar Arrangements
5. Summary and Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Borwein, J.M.; Glasser, M.L.; McPhedran, R.C.; Wan, J.G.; Zucker, I.J. Lattice sums then and now. In Encyclopedia of Mathematics and Its Applications; Cambridge University Press: Cambridge, UK, 2013; ISBN 978-1-107-03990-2. [Google Scholar]
- McDonald, K.T. Notes on Electrostatic Wire Grids (Published 2003). International Note. Available online: http://www.hep.princeton.edu/~mcdonald/examples/grids.pdf (accessed on 1 June 2020).
- Weertman, J. Dislocation Based Fracture Mechanics; World Scientific Publishing Company: Singapore, 1996; ISBN 978-9-813-10497-6. [Google Scholar]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series and Products, 7th ed.; Academic Press, Elsevier Inc.: Cambridge, MA, USA, 2007; ISBN 978-0-12-373637-6. [Google Scholar]
- Hansen, E.R.A. A Table of Series and Products; Prentice-Hall: Upper Saddle River, NJ, USA, 1975; ISBN 978-0-13-881935-5. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series; Gordon and Breach Science Publishers: New York, NY, USA, 1986–1992; Volumes 1–3. [Google Scholar]
- Markushevich, A.I. The Remarkable Sine Functions; American Elsevier Publishing Company: Amsterdam, The Netherlands, 1966. [Google Scholar]
- Eberhard, Z. Oxford Users’ Guide to Mathematics; Oxford University Press: Oxford, UK, 2004; ISBN 978-0-198-50763-5. [Google Scholar]
- Young, R.M. Excursions in Calculus: An Interplay of the Continuous and the Discrete; Cambridge University Press: Cambridge, UK, 1992; Volume 13, ISBN 978-0-883-85317-7. [Google Scholar]
- Lemniscate Functions. E.D. Solomontsev (Originator), Encyclopedia of Mathematics. Available online: http://encyclopediaofmath.org/index.php?title=Lemniscate_functions&oldid=17903 (accessed on 27 May 2020).
- A Collection of Infinite Products and Series (Andreas Dieckmann). Available online: http://www-elsa.physik.uni-bonn.de/~dieckman/InfProd/InfProd.html (accessed on 16 May 2020).
- The Online Encyclopedia of Integer Sequences (N. J. A. Sloane). Available online: https://oeis.org (accessed on 16 May 2020).
- Boyd, J.P. New series for the cosine lemniscate function and the polynomialization of the lemniscate integral. J. Comput. Appl. Math. 2011, 235, 1941–1955. [Google Scholar] [CrossRef] [Green Version]
- Wolfram Research, Inc. Mathematica, Version 12.1; Wolfram Research, Inc.: Champaign, IL, USA, 2020.
- Purcell, E.M. Electricity and Magnetism (Berkeley Physics Course, Vol.2); McGraw-Hill: New York, NY, USA, 1966; ISBN 978-0-070-04908-6. [Google Scholar]
- Table of Integrals (Andreas Dieckmann). Available online: http://www-elsa.physik.uni-bonn.de/~dieckman (accessed on 29 May 2020).
- Lu, C.; McDonald, K. The Electric Potential of Particle Detectors with Rectangular Cross-Section (Published 2002). Available online: http://puhep1.princeton.edu/~mcdonald/examples/iarocci.pdf (accessed on 1 June 2020).
- Orjubin, G. Closed-form expressions of the electrostatic potential close to a grid placed between two plates. J. Electrost. 2017, 87, 195–202. [Google Scholar] [CrossRef]
- Tomitani, T. Analysis of potential distribution in a gaseous counter of rectangular cross-section. Nucl. Instr. Methods 1972, 100, 179–191. [Google Scholar] [CrossRef]
- Cooperman, P. A theory for space-charge-limited currents with application to electrical precipitation. AIEE Trans. 1960, 79, 47–50. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vigren, E.; Dieckmann, A. Simple Solutions of Lattice Sums for Electric Fields Due to Infinitely Many Parallel Line Charges. Symmetry 2020, 12, 1040. https://doi.org/10.3390/sym12061040
Vigren E, Dieckmann A. Simple Solutions of Lattice Sums for Electric Fields Due to Infinitely Many Parallel Line Charges. Symmetry. 2020; 12(6):1040. https://doi.org/10.3390/sym12061040
Chicago/Turabian StyleVigren, Erik, and Andreas Dieckmann. 2020. "Simple Solutions of Lattice Sums for Electric Fields Due to Infinitely Many Parallel Line Charges" Symmetry 12, no. 6: 1040. https://doi.org/10.3390/sym12061040
APA StyleVigren, E., & Dieckmann, A. (2020). Simple Solutions of Lattice Sums for Electric Fields Due to Infinitely Many Parallel Line Charges. Symmetry, 12(6), 1040. https://doi.org/10.3390/sym12061040




