Approximating the Distribution of the Product of Two Normally Distributed Random Variables
Abstract
:1. Introduction
2. Product of Two Normal Random Variables
- Mean: .
- Variance: .
- Coefficient of variation: .
- Coefficient of skewness: .
- Excess of kurtosis:
- Skewness/kurtosis ratio:
- (i)
- First factor : its minimum value is one, which is reached at , while its maximum value is and reached at . Afterwards, the first factor ranges between .
- (ii)
- Second factor : its minimum value is and reached when , while its maximum is 16 at . Thus, the second factor ranges between .
- (iii)
- Third factor : its minimum value is three and reached at , while its maximum value is 120 at . Hence, the denominator of this skewness/kurtosis ratio is in the range .
3. The Extended Skew-Normal Distribution
- Mean: ;
- Variance: .
- Mean:
- Variance:
- Coefficient of variation:
- Coefficient of skewness:
- Excess of kurtosis:
- Skewness/kurtosis ratio:
4. Approximation for the Product Distribution with ESN Distributions
- As non-linear equations are generated, suitable numerical methods are required.
- As the solution obtained can be sensitive to the initial point, different points can be tested to avoid the stop at an inadequate point.
- Values of the coefficient of skewness and the excess of kurtosis are not always reached.
- A known distribution is employed and its PDF for any value of the product can be calculated with no need of numerical integrals.
- Inference using the ESN distribution is available.
5. Conclusions and Future Research
- (i)
- An approximation was proposed for the distribution of the product of two normally distributed random variables while using the extended skew-normal distribution.
- (ii)
- The moment generating function for the product of two normally distributed variables was considered as a function of the inverse coefficients of variation of both variables and of the corresponding correlation. From this moment generating function, the mean, variance, skewness, and kurtosis of this product were calculated.
- (iii)
- The probability density function of an extended skew-normal distribution is known and, using its cumulants, expressions for the mean, variance, skewness, and kurtosis were calculated. Skewness and kurtosis depended only on two parameters, while the mean and variance are functions of the four parameters of the extended skew-normal distribution.
- (iv)
- A numerical evaluation of the proposed approach was considered, which showed its potential for applications.
- (v)
- A graphical comparison of the proposed approach with other two approaches proposed in the recent literature on the topic was carried out showing the superiority of our approach.
- (i)
- The approximation to the distribution of the product of two normally distributed variables, while using the extended skew-normal distribution, showed some problems when the inverse coefficients of variation both are in the range . For this range, the adequate values of skewness and kurtosis cannot be reached and, thus, the approximation does not work well there. Some further research should be conducted in this line in order to improve our approach.
- (ii)
- (iii)
- (iv)
- If there are two random samples, the first one from the distribution of the product of two normally distributed random variables, and the second one from the fitted extended skew-normal distribution, and then some non-parametric tests can be used to compare them. Moreover, a sophisticated approach, as, for example, bootstrapping, can be applied in this context.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Craig, C.C. On the frequency of the function xy. Ann. Math. Stat. 1936, 7, 1–15. [Google Scholar] [CrossRef]
- Haldane, J.B.S. Moments of the distributions of powers and products of normal variates. Biometrika 1942, 32, 226–242. [Google Scholar] [CrossRef]
- Aroian, L.A. The probability function of the product of two normally distributed variables. Ann. Math. Stat. 1947, 18, 265–271. [Google Scholar] [CrossRef]
- Aroian, L.A.; Taneja, V.S.; Cornwell, L.W. Mathematical forms of the distribution of the product of two normal variables. Commun. Stat. Theory Methodol. 1978, 7, 165–172. [Google Scholar] [CrossRef]
- Rohatgi, V.K. An Introduction to Probability Theory Mathematical Studies; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Meeker, W.Q.; Odeh, R.D.; Cornwell, L.W.; Aroian, L.A.; Kennedy, W.J. Selected Tables in Mathematical Statistics: The Product of Two Normally Distributed Random Variables; American Mathematical Society: Providence, RI, USA, 1981. [Google Scholar]
- Cui, G.; Yu, X.; Iommelli, S.; Kong, L. Exact distribution for the product of two correlated Gaussian random variables. IEEE Signal Process. Lett. 2016, 23, 1662–1666. [Google Scholar] [CrossRef]
- Glen, A.G.; Lemmis, L.M.; Drew, J.H. Computing the distribution of the product of two continuous random variables. Comput. Stat. Data Anal. 2004, 44, 451–464. [Google Scholar] [CrossRef] [Green Version]
- Nadarajah, S.; Pogány, T.K. On the distribution of the product of correlated normal random variables. Comptes Research de la Academie Sciences Paris Serie I 2016, 354, 201–204. [Google Scholar] [CrossRef]
- Seijas-Macías, A.; Oliveira, A. An approach to distribution of the product of two normal variables. Discuss. Math. Probab. Stat. 2012, 32, 87–99. [Google Scholar]
- Ware, R.; Lad, F. Approximating the Distribution for Sums of Products of Normal Variables; Technical Report; The University of Queensland: Brisbane, Australia, 2003. [Google Scholar]
- Gaunt, R.E. On Stein’s method for products of normal random variables and zero bias couplings. Bernoulli 2017, 23, 3311–3345. [Google Scholar] [CrossRef] [Green Version]
- Gaunt, R.E. Products of normal, beta and gamma random variables: Stein operators and distributional theory. Braz. J. Probab. Stat. 2018, 32, 437–466. [Google Scholar] [CrossRef] [Green Version]
- Gaunt, R.E. A note on the distribution of the product of zero mean correlated normal random variables. Stat. Neerl. 2019, 73, 176–179. [Google Scholar] [CrossRef] [Green Version]
- Gaunt, R.E. Stein’s Method and the Distribution of the Product of Zero Mean Correlated Normal Random Variables. Commun. Stati. Theory Methods 2020. [Google Scholar] [CrossRef] [Green Version]
- Berberan-Santos, M.N. Expressing a probability density function in terms of another PDF: A generalized Gram-Charlier expansion. J. Math. Chem. 2006, 42, 585–594. [Google Scholar] [CrossRef]
- Wishart, J.; Bartlett, M.S. The distribution of second order moment statistics in a normal system. Math. Proc. Camb. Philos. Soc. 1932, 28, 455–459. [Google Scholar] [CrossRef]
- Springer, M.D.; Thompson, W.E. The distribution of products of beta, gamma and Gaussian random variables. SIAM J. Appl. Math. 1970, 18, 721–737. [Google Scholar] [CrossRef]
- Azzalini, A. A class of distributions which includes the normal ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Gómez-Déniz, E.; Iriarte, Y.A.; Calderin-Ojeda, E.; Gómez, H.W. Modified power-symmetric distribution. Symmetry 2019, 11, 1410. [Google Scholar] [CrossRef] [Green Version]
- Arnold, B.C.; Gómez, H.W.; Varela, H.; Vidal, I. Univariate and bivariate models related to the generalized epsilon-skew-Cauchy distribution. Symmetry 2019, 11, 794. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Mao, G.; Leiva, V.; Liu, S.; Tapia, A. Diagnostic analytics for an autoregressive model under the skew-normal distribution. Mathematics 2020, 8, 693. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Gómez, H.W.; Quintana, F. A new class of skew-normal distributions. Commun. Stat. Theory Methods 2004, 33, 1465–1480. [Google Scholar] [CrossRef]
- Arrué, J.; Arellano, R.; Gómez, H.W.; Leiva, V. On a new type of Birnbaum-Saunders models and its inference and application to fatigue data. J. Appl. Stat. 2020. [Google Scholar] [CrossRef]
- Azzalini, A. The Skew-Normal and Related Families; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Canale, A. Statistical aspects of the scalar extended skew-normal distribution. Metron 2011, 69, 279–295. [Google Scholar] [CrossRef]
- Capitanio, A.; Azzalini, A.; Stanghellini, E. Graphical models for skew-normal variates. Scand. J. Stat. 2003, 30, 129–144. [Google Scholar] [CrossRef]
- Oliveira, A.; Oliveira, T.; Seijas-Macías, A. Skewness into the product of two normally distributed variables and the risk consequences. Revstat 2016, 14, 119–138. [Google Scholar]
- Oliveira, A.; Oliveira, T.; Seijas-Macías, A. Evaluation of kurtosis into the product of two normally distributed variables. In AIP Conference Proceedings; AIP Publishing: College Park, MD, USA, 2016; Volume 1738, p. 470002. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Azzalini, A. Package ‘sn’. 2017. Available online: http://azzalini.stat.unipd.it/SN/sn-manual.pdf (accessed on 21 July 2020).
- Varadhan, R. Package ‘bb’. 2018. Available online: https://cran.r-project.org/web/packages/BB/BB.pdf (accessed on 21 July 2020).
- Bourguignon, M.; Leao, J.; Leiva, V.; Santos-Neto, M. The transmuted Birnbaum-Saunders distribution. Revstat 2017, 15, 601–628. [Google Scholar]
- Santos-Neto, M.; Cysneiros, F.J.A.; Leiva, V.; Barros, M. On a reparameterized Birnbaum-Saunders distribution and its moments, estimation and applications. Revstat 2014, 12, 247–272. [Google Scholar]
- Ventura, M.; Saulo, H.; Leiva, V.; Monsueto, S. Log-symmetric regression models: Information criteria, application to movie business and industry data with economic implications. Appl. Stoch. Models Bus. Ind. 2019, 35, 963–977. [Google Scholar] [CrossRef]
- Rojas, F.; Leiva, V.; Wanke, P.; Lillo, C.; Pascual, J. Modeling lot-size with time-dependent demand based on stochastic programming and case study of drug supply in Chile. PLoS ONE 2019, 14, e0212768. [Google Scholar] [CrossRef] [Green Version]
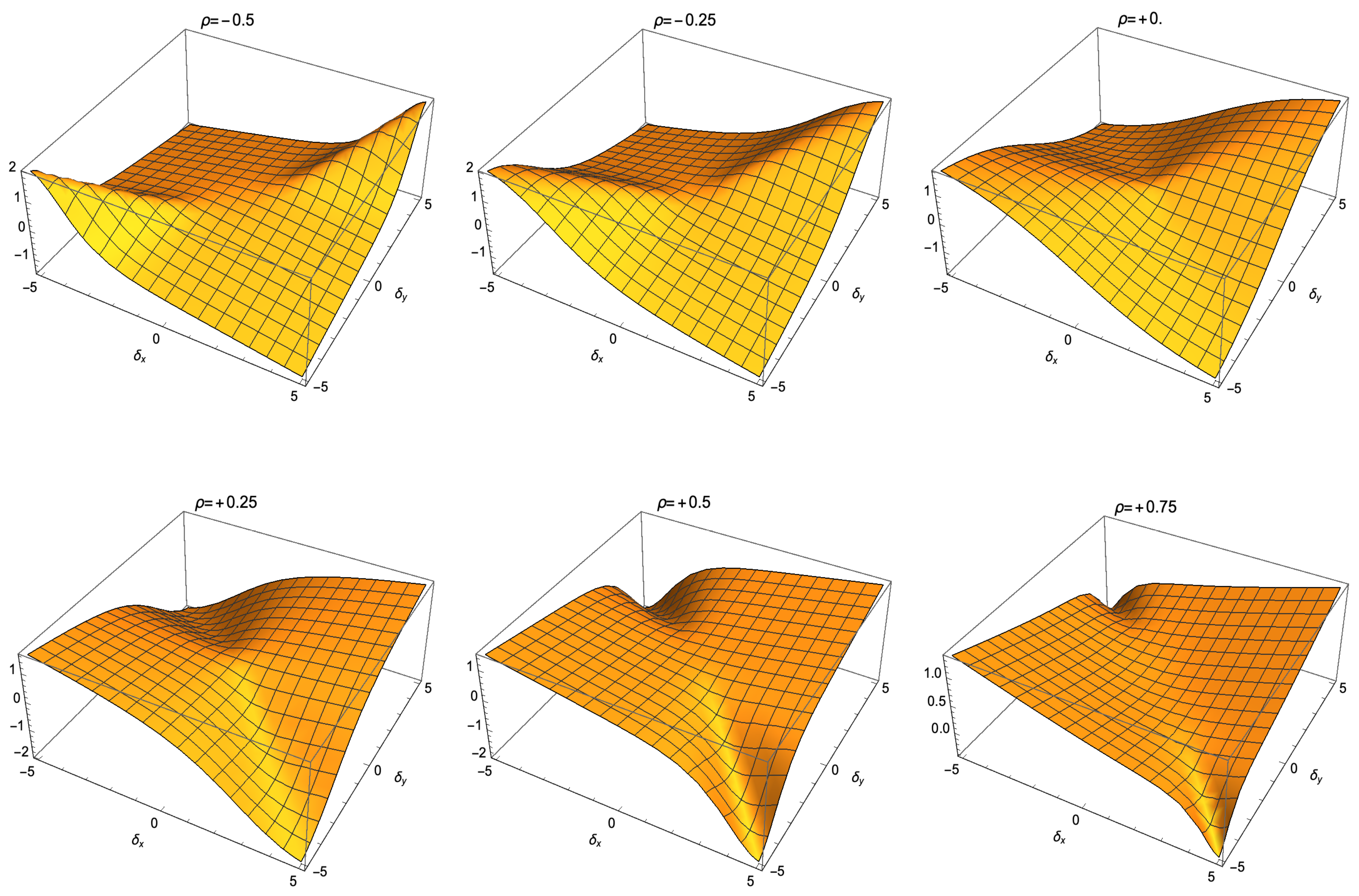
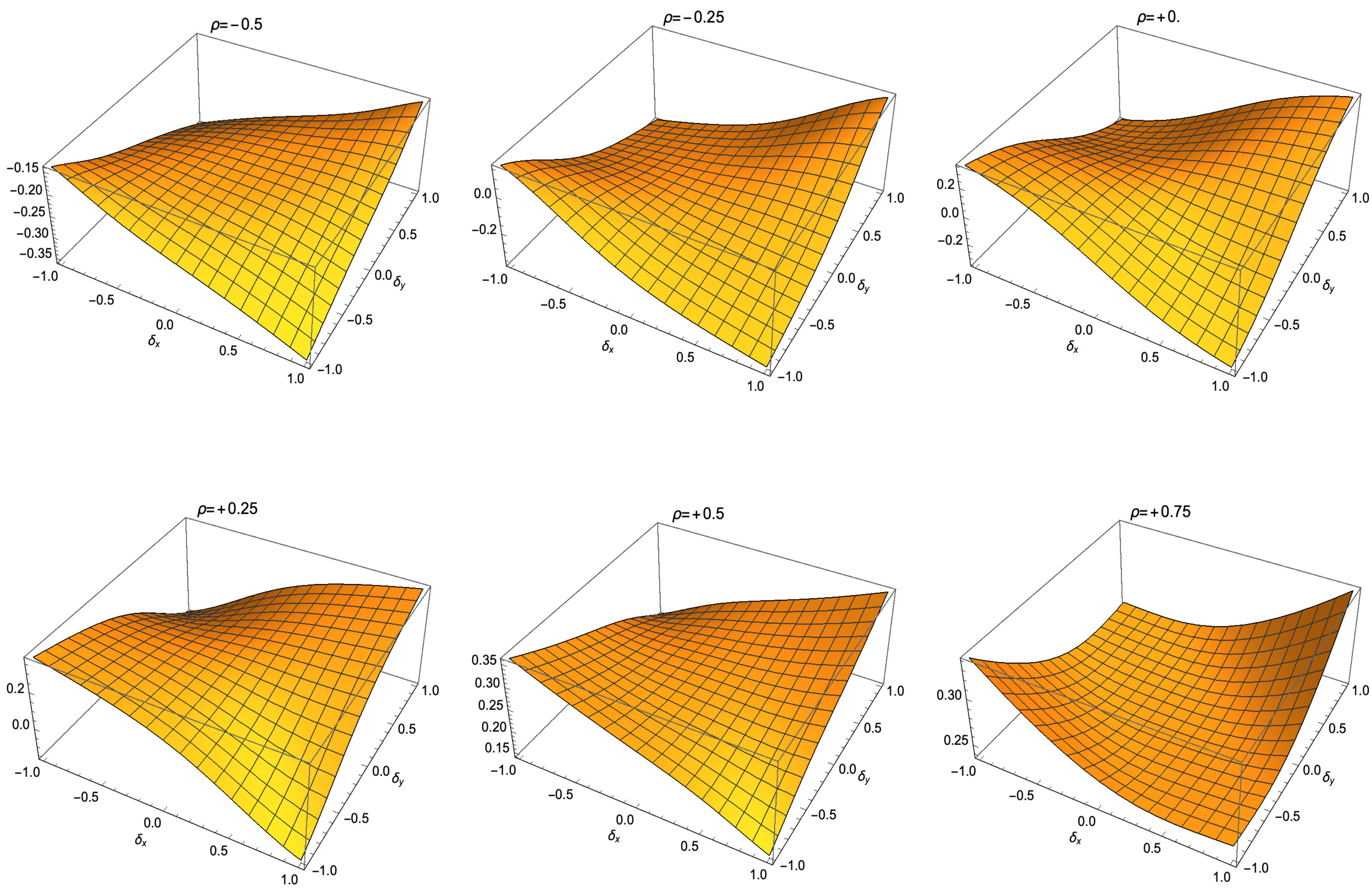





| Product | Mean | Variance | Skewness | Kurtosis |
|---|---|---|---|---|
| Theoretical value | 2.500 | 27.0000 | 2.3338 | 9.25995 |
| Simulated value | 2.499 | 26.9927 | 2.3337 | 9.40562 |
| Approximate value | 2.500 | 27.0000 | 1.9855 | 9.26592 |
| Theoretical value | 0.5500 | 1.650 | 1.06679 | 1.5634 |
| Simulated value | 0.5499 | 1.649 | 1.06684 | 1.5645 |
| Approximate value | 0.5500 | 1.650 | 1.06677 | 1.5634 |
| Theoretical value | 0.7000 | 1.4400 | 1.18981 | 2.479685 |
| Simulated value | 0.6999 | 1.4396 | 1.18956 | 2.479581 |
| Approximate value | 0.7000 | 1.4400 | 1.18981 | 2.479685 |
| Theoretical Value | Approximated Value | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Variance | Skewness | Kurtosis | Mean | Variance | Skewness | Kurtosis | |||
| 1.1 | 4.0 | 2.2188 | 4.4268 | 0.8043 | 1.0415 | 2.2188 | 4.4268 | 0.8043 | 1.0415 | |
| 1.3 | 2.0 | 2.3750 | 5.4531 | 1.3445 | 2.5612 | 2.3750 | 5.4531 | 1.3445 | 2.5612 | |
| 1.6 | 1.3 | 2.4688 | 6.7861 | 1.5038 | 3.1815 | 2.4688 | 6.7861 | 1.5038 | 3.1815 | |
| 2.0 | 1.0 | 2.5000 | 8.2500 | 1.4032 | 2.9146 | 2.5000 | 8.2500 | 1.4032 | 2.9146 | |
| 2.7 | 0.8 | 2.4688 | 9.7861 | 1.1440 | 2.1081 | 2.4688 | 9.7861 | 1.1440 | 2.1081 | |
| 4.0 | 0.7 | 2.3750 | 11.4531 | 0.7900 | 1.1209 | 2.3750 | 11.4531 | 0.7900 | 1.1209 | |
| 8.0 | 0.6 | 2.2188 | 13.4268 | 0.3924 | 0.3139 | 2.2188 | 13.4268 | 0.3923 | 0.3139 | |
| 4.0 | 1.1 | 1.7813 | 2.6768 | −0.3993 | 1.0253 | 1.7813 | 2.6768 | −0.4075 | 1.0254 | |
| 2.0 | 1.3 | 1.6250 | 2.4531 | −0.0641 | 1.7198 | 1.6250 | 2.4531 | −0.0640 | 1.7196 | |
| 1.3 | 1.6 | 1.5313 | 3.0361 | −0.0410 | 1.9499 | 1.5313 | 3.0361 | −0.0412 | 1.9527 | |
| 1.0 | 2.0 | 1.5000 | 4.2500 | −0.3709 | 2.3460 | 1.5000 | 4.2500 | −0.3709 | 2.3460 | |
| 0.8 | 2.7 | 1.5313 | 6.0361 | −0.5836 | 2.0131 | 1.5313 | 6.0361 | −0.5853 | 2.0139 | |
| 0.7 | 4.0 | 1.6250 | 8.4531 | −0.5593 | 1.1367 | 1.6250 | 8.4531 | −0.5593 | 1.1367 | |
| 0.6 | 8.0 | 1.7813 | 11.6768 | −0.3399 | 0.3192 | 1.7813 | 11.6770 | −0.3399 | 0.3290 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seijas-Macías, A.; Oliveira, A.; Oliveira, T.A.; Leiva, V. Approximating the Distribution of the Product of Two Normally Distributed Random Variables. Symmetry 2020, 12, 1201. https://doi.org/10.3390/sym12081201
Seijas-Macías A, Oliveira A, Oliveira TA, Leiva V. Approximating the Distribution of the Product of Two Normally Distributed Random Variables. Symmetry. 2020; 12(8):1201. https://doi.org/10.3390/sym12081201
Chicago/Turabian StyleSeijas-Macías, Antonio, Amílcar Oliveira, Teresa A. Oliveira, and Víctor Leiva. 2020. "Approximating the Distribution of the Product of Two Normally Distributed Random Variables" Symmetry 12, no. 8: 1201. https://doi.org/10.3390/sym12081201
APA StyleSeijas-Macías, A., Oliveira, A., Oliveira, T. A., & Leiva, V. (2020). Approximating the Distribution of the Product of Two Normally Distributed Random Variables. Symmetry, 12(8), 1201. https://doi.org/10.3390/sym12081201







