Fuzzy Random Chance-Constrained Programming Model for the Vehicle Routing Problem of Hazardous Materials Transportation
Abstract
:1. Introduction
2. Literature Review
2.1. Literature on Risk Assessment
2.2. Literature on Hazardous Materials Transportation Related to Uncertain Theory
2.3. Research Gap
3. Preliminaries
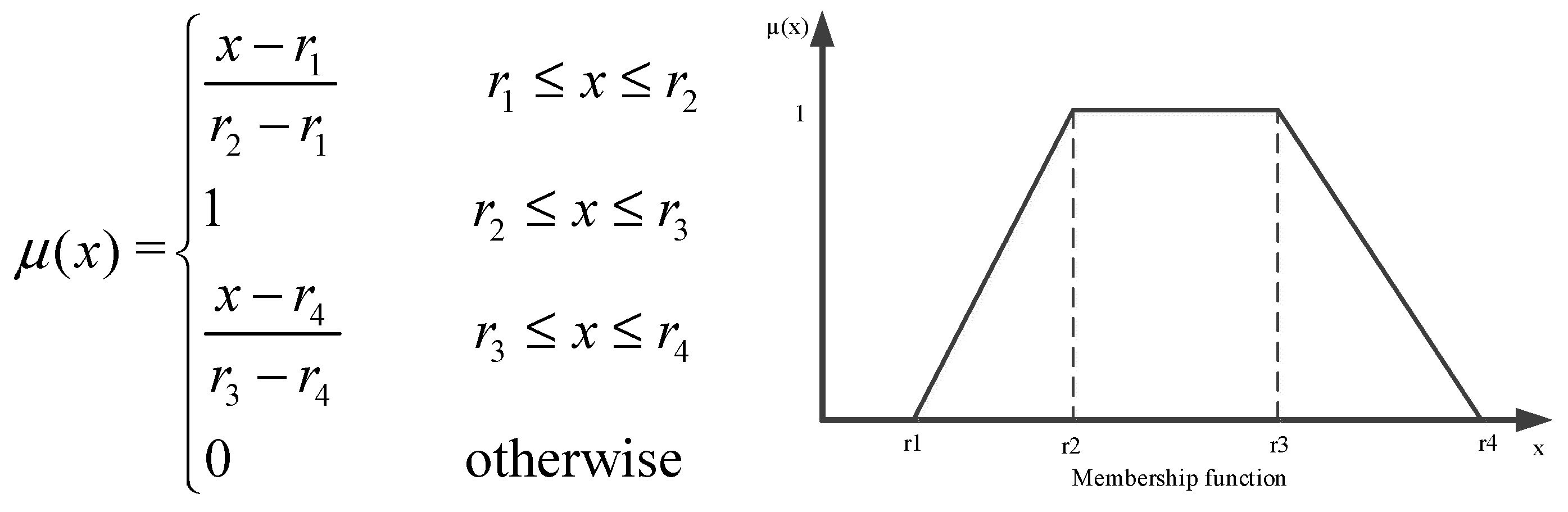
3.1. Fuzzy Theory
- (i)
- Pos {∅} = 0, Pos {Θ} = 1 and,
- (ii)
- Pos {∪kAk} = sup k Pos(Ak) for any arbitrary collection {Ak} in
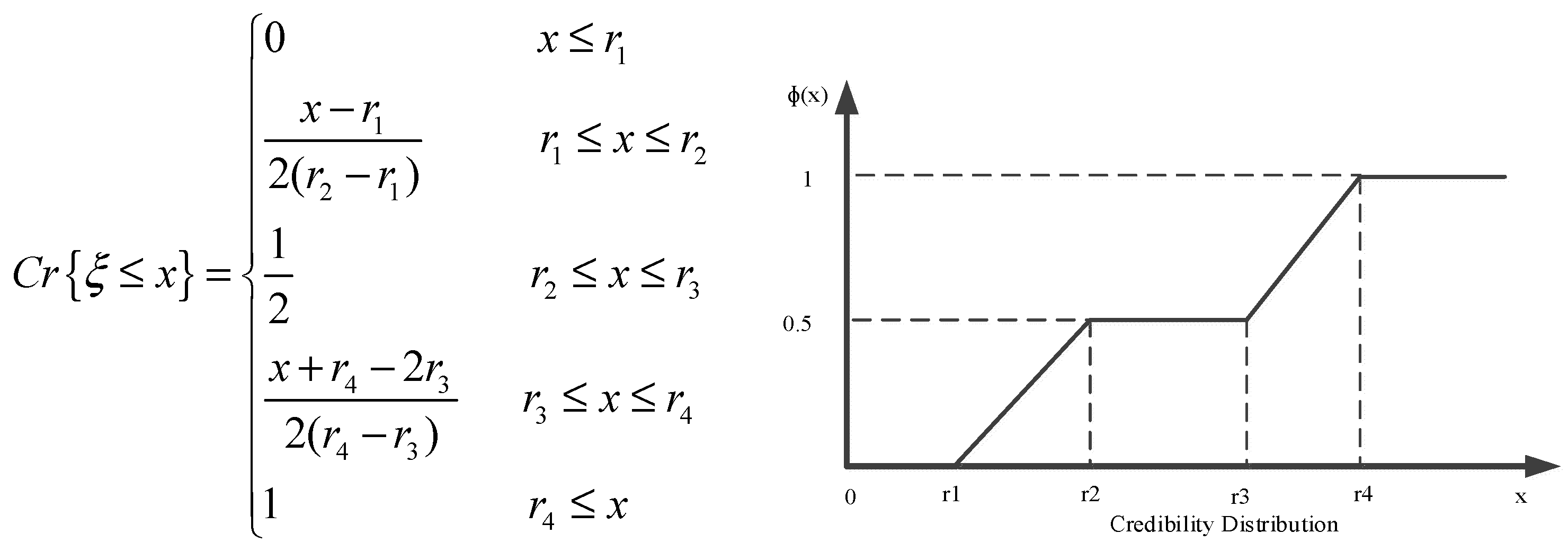
3.2. Fuzzy Random Theory
3.3. Chance-Constrained-Programming Model
4. Vehicle Routing Model Formulation
- (i)
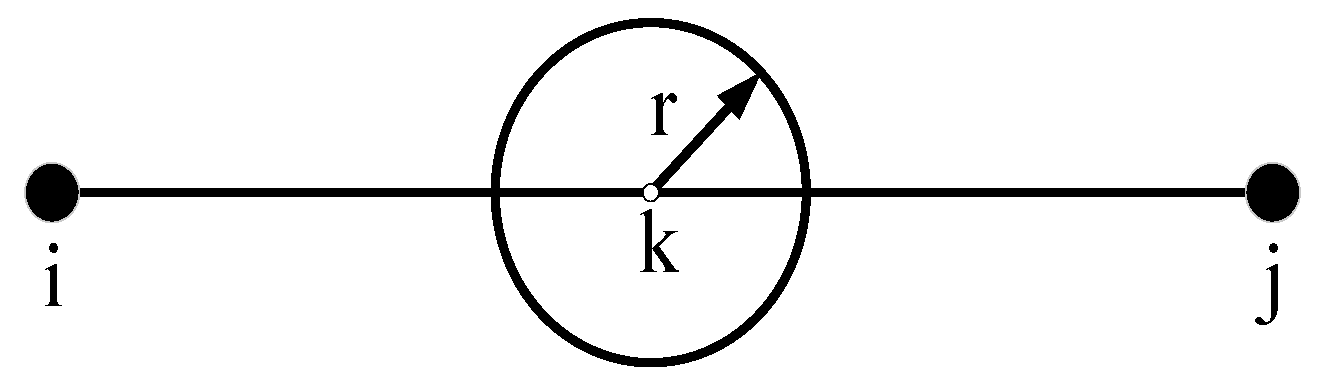
- Risk assessment: Due to a series of environmental and human factors, the occurrence of hazardous materials accident is a random event, and the exact consequence of hazardous materials accident was difficult to estimate in advance. Due to the lack of sufficient data, uncertain theory had to be used to solve this intractable problem.
- (ii)
- Cost calculation: This involved determining different components of total cost, especially green cost, and the biggest difference in this study was considering the distance and speed as uncertain factors from a conventional model.
- (iii)
- Vehicle routing assignment: This required arranging sequence serving a set of customers assigned to a vehicle under uncertain environment.
- The transportation network only has one depot but a set of customers; meanwhile, all vehicles are the same type;
- The number of vehicle fleet is decided by the depot; each vehicle has a physical limitation, i.e., capacity, meaning the sum upload amount of all customers shared a path that cannot exceed it;
- A customer must be served and visited once and only once, and transportation time can meet all customer’s time window limit;
- A vehicle routing scheduling must be a loop circle, beginning from the depot and ending at the same depot;
- A vehicle can visit an uncertain number of customers only if it is within capacity limitation, if not, the vehicle routing scheduling must be abandoned;
- The length of arc and population density along the arc are assumed to be fuzzy variables, this work uses triangle fuzzy variables to describe them;
- The hazmat accident probability is in a random format, similarly, the speed of the vehicle is adjustable, which is also a random variable.
- The customer demands, including time and amount are known, at least, one day earlier.
4.1. Model I-Vehicle Routing Model for Risk Reduction
4.2. Model II-Vehicle Routing Model for Cost Reduction
4.3. Model III-Vehicle Routing Model for Risk and Cost Minimization
4.4. Model Constraints
5. Solution Methodology
5.1. Fuzzy Random Simulation Algorithm
- Step 1.
- Initialize a small real number ε > 0.
- Step 2.
- Randomly generate vectors with membership degrees for all .
- Step 3.
- Calculate the minimum and maximum values and .
- Step 4.
- Set .
- Step 5.
- If , set . Otherwise, set .
- Step 6.
- If , go to Step 4.
- Step 7.
- Return as an approximation of the -pessimistic value.
- Step 1.
- Generate ω1, ω2, … ωN, from space Ω according to the probability measure .
- Step 2.
- Find the smallest values such that for by fuzzy simulation, respectively.
- Step 3.
- Set value, which equals to the integer part of .
- Step 4.
- Return the th largest element in .
5.2. Fuzzy Random Simulation Based Genetic Algorithm
5.2.1. Initialization Operation
5.2.2. Evaluation Function
5.2.3. Selection Operation
5.2.4. Crossover Operation
5.2.5. Mutation Operation
- Step 1.
- Set . Initialize relative parameters, such as population size, maximum generation, crossover probability, mutation probability, and so on.
- Step 2.
- Randomly generate feasible chromosomes to be the initial population.
- Step 3.
- According to the models used, calculate the objective values for all chromosomes to obtain evaluation values by fuzzy random simulation.
- Step 4.
- After performing selection, crossover, and mutation operations, update all chromosomes.
- Step 5.
- If i = max_gen, the simulation must be terminated, then choose the best chromosome as the ultimate solution. Otherwise, set and return to Step 3.
6. Case Study
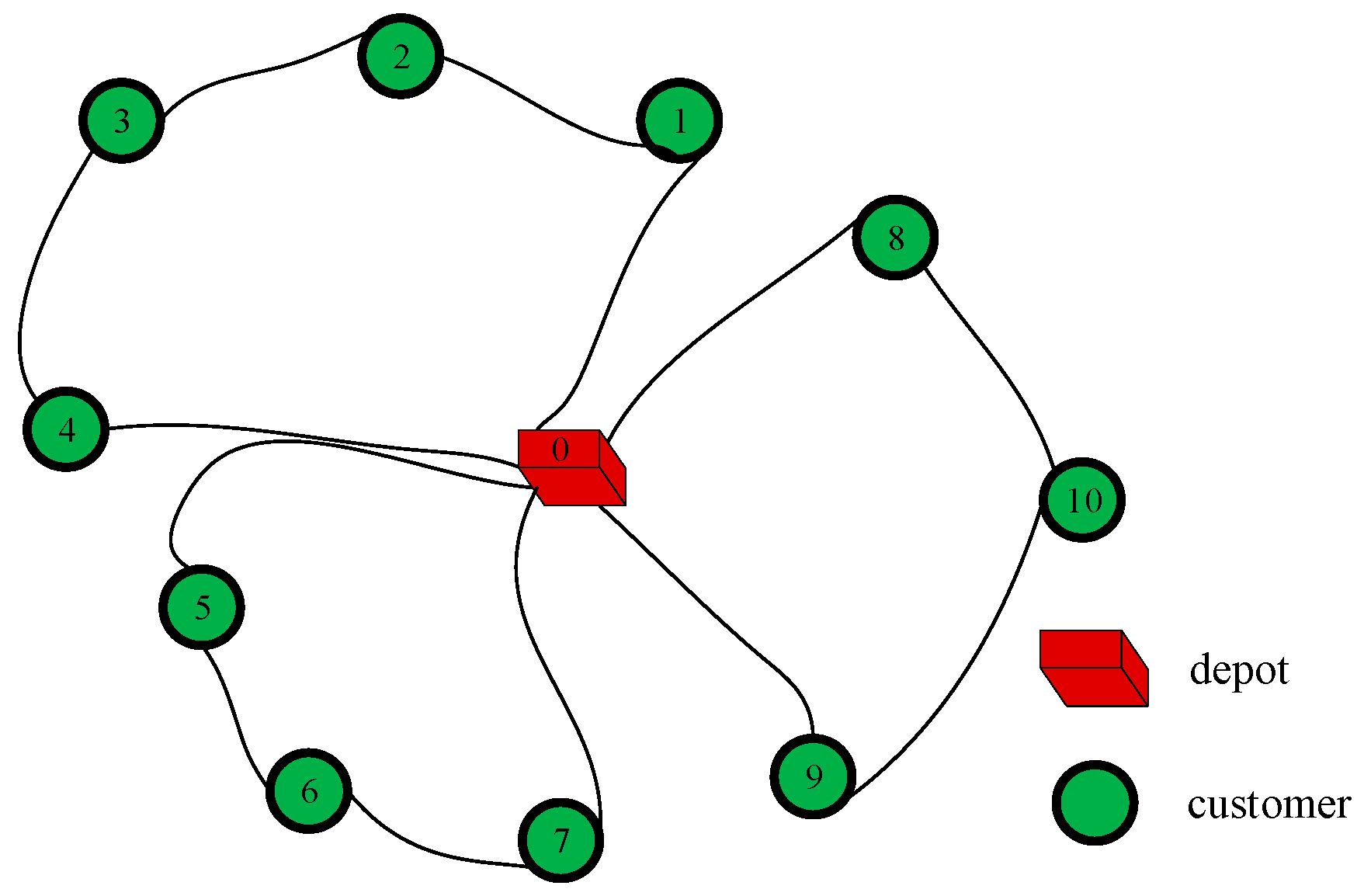
6.1. Case 1: Small Case
- Vehicle 1: 0-5-2-1-7-8-4-0
- Vehicle 2: 0-9-0
- Vehicle 3: 0-10-3-6-0
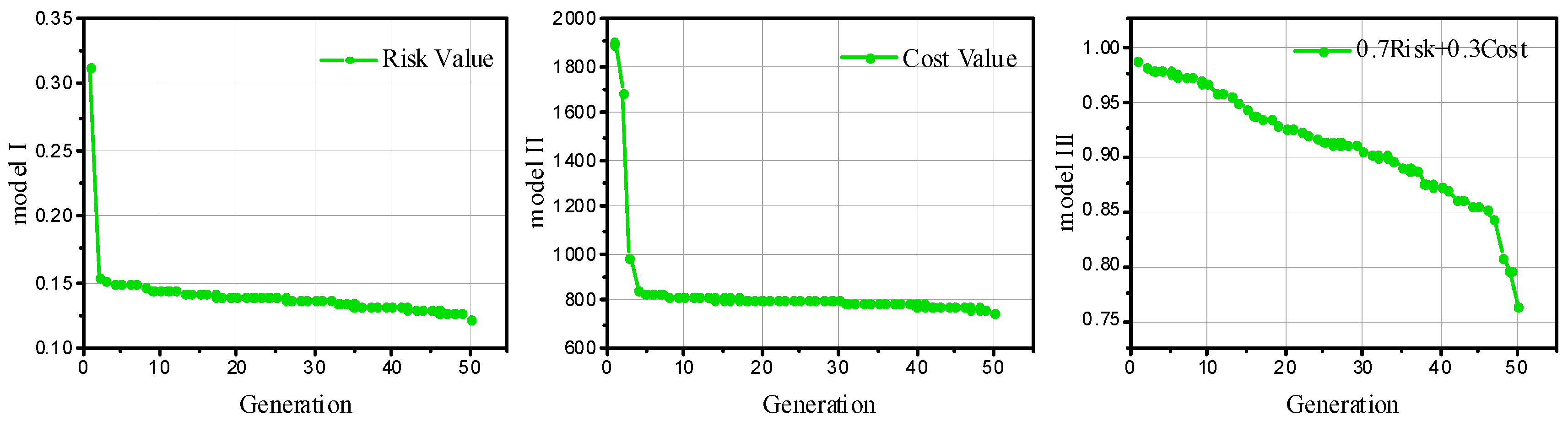
6.2. Case 2: Practical Case
7. Conclusions
- (1)
- The VRP models using uncertain theory were established by taking risk, cost, risk and cost, as the objective function for hazmat transportation, respectively. According to the risk assessment model, VRP models must be extended to chance-constrained. Different chance level has different solutions for the decision-maker, this can respond to changes in vehicle routing arrangements in time, when an accident occurs.
- (2)
- In order to attain feasible solution for the models proposed by this paper, a hybrid intelligence algorithm integrating the fuzzy random algorithm and GA algorithm was designed. It included mass of simulation calculation; however, two numerical cases showed that the models were efficient, and the hybrid intelligent algorithm was steady, convergent for a small-size, and a middle-size problem.
Author Contributions
Funding
Conflicts of Interest
References
- Zografos, K.G.; Androutsopoulos, K.N. Solving the bicriterion routing and scheduling problem for hazardous materials distribution. Transp. Res. Part C Emerg. Technol. 2010, 18, 713–726. [Google Scholar]
- Barma, P.S.; Dutta, J.; Mukherjee, A. A 2-opt guided discrete antlion optimization algorithm for multi-depot vehicle problem. Decis. Mak. Appl. Manag. Eng. 2019, 2, 112–125. [Google Scholar]
- Roy, A.; Manna, A.; Malty, S. A novel memetic genetic algorithm for solving traveling salesman problem based on multi-parent crossover technique. Decis. Mak. Appl. Manag. Eng. 2019, 2, 100–111. [Google Scholar] [CrossRef]
- Cam, O.N.; Sezen, H.K. The formulation of a linear programming model for the vehicle routing problem in order to minimize idle time. Decis. Making Appl. Manag. Eng. 2020, 3, 22–29. [Google Scholar]
- Holeczek, N. Hazardous materials truck transportation problems: A classification and state of the art literature review. Transp. Res. Part D Transp. Environ. 2019, 69, 305–328. [Google Scholar] [CrossRef]
- Erkut, E.; Ingolfsson, A. Catastrophe avoidance models for hazardous materials route planning. Transp. Sci. 2000, 34, 165–179. [Google Scholar] [CrossRef]
- Erkut, E.; Ingolfsson, A. Transport risk models for hazardous materials: Revisited. Oper. Res. Lett. 2005, 33, 81–89. [Google Scholar] [CrossRef]
- Erkut, E.; Verter, V. A framework for hazardous materials transport risk assessment. Risk Anal. 1995, 15, 589–601. [Google Scholar] [CrossRef]
- Jia, H.; Zhang, L.; Lou, X.; Cao, H. A fuzzy-stochastic constraint programming model for hazmat road transportation considering terrorism attacking. Syst. Eng. Proc. 2011, 1, 130–136. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Leung, Y. Multi-objective route planning for dangerous goods using compromise programming. J. Geogr. Syst. 2011, 13, 249–271. [Google Scholar] [CrossRef]
- Wei, M.Y.; Yu, L.; Li, X. Credibilistic Location-Routing Model for Hazardous Materials Transportation. Int. J. Intell. Syst. 2015, 30, 23–39. [Google Scholar] [CrossRef]
- Cordeiro, F.G.; Bezerra, B.S.; Peixoto, A.S.P.; Ramos, R.A.R. Methodological aspects for modeling the environmental risk of transporting hazardous materials by road. Transp. Res. Part D Transp. Environ. 2016, 44, 105–121. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Demir, E.; Bektaş, T.; Laporte, G. A review of recent research on green road freight transportation. Eur. J. Oper. Res. 2014, 237, 775–793. [Google Scholar] [CrossRef] [Green Version]
- Lam, C.Y.; Cruz, A.M. Risk analysis for consumer-level utility gas and liquefied petroleum gas incidents using probabilistic network modeling: A case study of gas incidents in Japan. Reliab. Eng. Syst. Saf. 2019, 185, 198–212. [Google Scholar] [CrossRef]
- Jabir, E.; Panicker, V.V.; Sridharan, R. Design and development of a hybrid ant colony-variable neighbourhood search algorithm for a multi-depot green vehicle routing problem. Transp. Res. Part D Transp. Environ. 2017, 57, 422–457. [Google Scholar] [CrossRef]
- Bula, G.A.; Afsar, H.M.; Gonzalez, F.A.; Prodhon, C.; Velasco, N. Bi-objective vehicle routing problem for hazardous materials transportation. J. Clean. Prod. 2019, 206, 976–986. [Google Scholar] [CrossRef]
- Poku-Boansi, M.; Tornyeviadzi, P.; Adarkwa, K.K. Next to suffer: Population exposure risk to hazardous material transportation in Ghana. J. Transp. Health 2018, 10, 203–212. [Google Scholar] [CrossRef]
- Ghaderi, A.; Burdett, R.L. An integrated location and routing approach for transporting hazardous materials in a bi-modal transportation network. Transp. Res. Part E Logist. Transp. Rev. 2019, 127, 49–65. [Google Scholar] [CrossRef]
- Qu, H.; Xu, J.; Wang, S.; Xu, Q. Dynamic Routing Optimization for Chemical Hazardous Material Transportation under Uncertainties. Ind. Eng. Chem. Res. 2018, 57, 10500–10517. [Google Scholar] [CrossRef]
- Ghaleh, S.; Omidvari, M.; Nassiri, P.; Momeni, M.; Lavasani, S.M.M. Pattern of safety risk assessment in road fleet transportation of hazardous materials (oil materials). Saf. Sci. 2019, 116, 1–12. [Google Scholar] [CrossRef]
- Deng, Y.; Chen, Y.; Zhang, Y.; Mahadevan, S. Short communication: Fuzzy Dijkstra algorithm for shortest path problem under uncertain environment. Appl. Soft Comput. 2012, 12, 1231–1237. [Google Scholar] [CrossRef]
- Zero, L.; Bersani, C.; Paolucci, M.; Sacile, R. Two new approaches for the bi-objective shortest path with a fuzzy objective applied to HAZMAT transportation. J. Hazard. Mater. 2019, 375, 96–106. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Zhai, X.; Li, Y.; Feng, B.; Wang, Z.; Zhang, M. Multi-objective optimization operation considering environment benefits and economy based on ant colony optimization for isolated micro-grids. Energy Procedia 2016, 104, e26. [Google Scholar] [CrossRef]
- Moon, S.; Rosenblum, F.; Tan, Y.H.; Nesset, J.; Waters, K.E.; Finch, J.A. Examination of the United Nations self-heating test for sulphides. Can. Metall. Q. 2019, 58, 438–444. [Google Scholar] [CrossRef]
- Hu, H.; Li, J.; Li, X. A credibilistic goal programming model for inventory routing problem with hazardous materials. Soft Comput. 2018, 22, 5803–5816. [Google Scholar] [CrossRef]
- Du, J.M.; Lia, X.; Yua, L.; Danb, R.; Zhoua, J. Multi-depot vehicle routing problem for hazardous materials transportation: A fuzzy bilevel programming. Inf. Sci. 2017, 399, 201–218. [Google Scholar] [CrossRef]
- Du, J.M.; Yu, L.; Li, X. Fuzzy multi-objective chance-constrained programming model for hazardous materials transportation. Int. J. Gen. Syst. 2016, 45, 286–310. [Google Scholar] [CrossRef]
- Ma, C.; Li, Y.; He, R.; Wu, F.; Qi, B.; Ye, Q. Route optimisation models and algorithms for hazardous materials transportation under different environments. Int. J. Bio Inspired Comput. 2013, 5, 252–265. [Google Scholar]
- Wei, M.Y.; Li, X.; Yu, L. Time-dependent fuzzy random location-scheduling programming for hazardous materials transportation. Transp. Res. Part C Emerg. Technol. 2015, 57, 146–165. [Google Scholar]
- Ghaffari-Nasab, N.; Ahari, S.G.; Ghazanfari, M. A hybrid simulated annealing based heuristic for solving the location-routing problem with fuzzy demands. Sci. Iran. 2013, 20, 919–930. [Google Scholar]
- Xu, J.; Yan, F.; Li, S. Vehicle routing optimization with soft time windows in a fuzzy random environment. Transp. Res. Part E Logist. Transp. Rev. 2011, 47, 1075–1091. [Google Scholar] [CrossRef]
- Hassan-Pour, H.A.; Mosadegh-Khah, M.; Tavakkoli-Moghaddam, R. Solving a multi-objective multi-depot stochastic location-routing problem by a hybrid simulated annealing algorithm. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2009, 223, 1045–1054. [Google Scholar] [CrossRef]
- Ji, X.; Iwamura, K.; Shao, Z. New models for shortest path problem with fuzzy arc lengths. Appl. Math. Model. 2007, 31, 259–269. [Google Scholar] [CrossRef]
- Hua, H.; Libc, X.; Zhang, Y.; Shang, C.; Zhang, S. Multi-objective location-routing model for hazardous material logistics with traffic restriction constraint in inter-city roads. Comput. Ind. Eng. 2019, 128, 861–876. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, L.; Cao, N.; Yang, L.; Chen, M. Vehicle routing optimum model of hazardous materials transportation under fuzzy environment. J. Intell. Fuzzy Syst. 2016, 31, 3067–3074. [Google Scholar] [CrossRef]
- Contreras, I.; Cordeau, J.F.; Laporte, G. Stochastic uncapacitated hub location. Eur. J. Oper. Res. 2011, 212, 518–528. [Google Scholar] [CrossRef]
- Mohammadi, M.; Jolai, F.; Tavakkoli-Moghaddam, R. Solving a new stochastic multi-mode p-hub covering location problem considering risk by a novel multi-objective algorithm. Appl. Math. Model. 2013, 37, 10053–10073. [Google Scholar] [CrossRef]
- Samanlioglu, F. A multi-objective mathematical model for the industrial hazardous waste location-routing problem. Eur. J. Oper. Res. 2013, 226, 332–340. [Google Scholar] [CrossRef]
- Tas, D.; Dellaert, N.; van Woensel, T.; de Kok, T. Vehicle routing problem with stochastic travel times including soft time windows and service costs. Comput. Oper. Res. 2013, 40, 214–224. [Google Scholar] [CrossRef] [Green Version]
- Bertazzi, L.; Bosco, A.; Guerriero, F.; Lagana, D. A stochastic inventory routing problem with stock-out. Transp. Res. Part C Emerg. Technol. 2013, 27, 89–107. [Google Scholar] [CrossRef]
- Zheng, Y.; Liu, B. Fuzzy vehicle routing model with credibility measure and its hybrid intelligent algorithm. Appl. Math. Comput. 2006, 176, 673–683. [Google Scholar] [CrossRef]
- Meng, Q.; Lee, D.H.; Cheu, R.L. Multiobjective vehicle routing and scheduling problem with time window constraints in hazardous material transportation. J. Transp. Eng. 2005, 131, 699–707. [Google Scholar] [CrossRef]
- Zhou, Z.; Chu, F.; Che, A.; Zhou, M. Constraint and fuzzy logic-based optimization of hazardous material transportation via lane reservation. IEEE Trans. Intell. Transp. Syst. 2013, 14, 847–857. [Google Scholar] [CrossRef]
- La, Z. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar]
- Li, X.; Liu, B. A sufficient and necessary condition for credibility measures. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2006, 15, 43–52. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1978, 1, 3–28. [Google Scholar] [CrossRef]
- Liu, B. Uncertain Theory: An Introduction to Its Axiomatic Foundations; Springer: Berlin, Germany, 2004. [Google Scholar]
- Liu, B. Toward Fuzzy Optimization without Mathematical Ambiguity. Fuzzy Optim. Decis. Mak. 2002, 1, 43–63. [Google Scholar] [CrossRef]
- Liu, B.; Liu, Y.K. Expected value of fuzzy variable and fuzzy expected value models. IEEE Trans. Fuzzy Syst. 2002, 10, 445–450. [Google Scholar]
- Liu, B.; Liu, B. Theory and Practice of Uncertain Programming; Springer: Berlin, Germany, 2009. [Google Scholar]
- Liu, Y.K.; Liu, B. Fuzzy Random Variables: A Scalar Expected Value Operator. Fuzzy Optim. Decis. Mak. 2003, 2, 143–160. [Google Scholar] [CrossRef]
- Bektas, T.; Laporte, G. The Pollution-Routing Problem. Transp. Res. Part B Methodol. 2011, 45, 1232–1250. [Google Scholar] [CrossRef]
- Liu, B.; Iwamura, K. Chance constrained programming with fuzzy parameters. Fuzzy Sets Syst. 1998, 94, 227–237. [Google Scholar] [CrossRef]
- Liu, B.D. Fuzzy random chance-constrained programming. IEEE Trans. Fuzzy Syst. 2001, 9, 713–720. [Google Scholar]





| No | Author | Stochastic | Fuzzy | Fuzzy Stochastic | Green | R | LR | VRP |
|---|---|---|---|---|---|---|---|---|
| 1 | Jabir [16] | √ | √ | √ | ||||
| 2 | Ghaderia [19] | √ | ||||||
| 3 | Qu [20] | √ | ||||||
| 4 | Deng [22] | √ | ||||||
| 5 | Du [28] | √ | √ | |||||
| 6 | Wei [11] | √ | √ | |||||
| 7 | Wei [30] | √ | √ | |||||
| 8 | Ghaffari [31] | √ | √ | |||||
| 9 | Xu [32] | √ | √ | |||||
| 10 | Hassan-Pour [33] | √ | √ | |||||
| 11 | Ji [34] | √ | √ | |||||
| 12 | Hu [35] | √ | √ | |||||
| 13 | Wang [36] | √ | √ | |||||
| 14 | Contreras [37] | √ | √ | |||||
| 15 | Mohammadi [38] | √ | √ | |||||
| 16 | Samanlioglu [39] | √ | √ | |||||
| 17 | Tas [40] | √ | √ | |||||
| 18 | Bertazzi [41] | √ | √ | |||||
| 19 | Zheng [42] | √ | √ | |||||
| 20 | Meng [43] | √ | √ | |||||
| 21 | Zhou [44] | √ | √ | |||||
| 22 | Present work | √ | √ | √ |
| Set: | |
|---|---|
| N = (A,V) | Transportation network |
| Node set, node 0 denotes single depot | |
| A0 = A/{0} | A set of customers waiting for delivery. |
| A collection of arcs that have been connected between customers. | |
| A collection of vehicles of the same type available in a depot. | |
| Indices: | |
| Customer index | |
| Depot index | |
| Vehicle index | |
| Parameter: | |
| Demand of customer | |
| Capacity of the vehicle. | |
| Vehicle weight (empty weight). | |
| Fixed cost for a vehicle. | |
| Variable vehicle operating cost per unit distance. | |
| CO2 emission cost per unit weight of vehicle per unit | |
| λij | Affected area of the accident on arc . |
| Fuzzy parameters: | |
| Length of arc . | |
| Average population density along arc . | |
| Random parameters: | |
| Probability of accident occurring on arc . | |
| Speed of vehicle traveling across arc . | |
| Decision variables: | |
| it takes value 1 if arc uses vehicle to travel, it takes value 0, otherwise. | |
| it takes value 1 if customer uses vehicle to travel, it takes value 0, otherwise. |
| Parameter | Meaning | Value |
|---|---|---|
| M | Total quality | 5 t |
| Road angle of arc | ||
| Acceleration | ||
| Gravitational constant | ||
| Drag resistance coefficient | ||
| Rolling resistance coefficient | ||
| Air density | 1.2041 kg/m2 | |
| S | Surface area of vehicle | 5 m2 |
| Fuel price | 7 RMB/L | |
| ηc | Fuel conversion factor | |
| carbon tax | ||
| Fuel efficiency |
| Arc | Length | Population Density | Pr | Speed | Area |
|---|---|---|---|---|---|
| (km) | (pop/km2) | (×10−5) | (km/h) | (km2) | |
| (0,1) | (70,90) | (80,83,87) | N(1,9) | U(40,60) | 24 |
| (0,2) | (100,120) | (185,189,205) | N(1,4) | U(40,60) | 32 |
| (0,3) | (90,110) | (200,210,235) | N(2,9) | U(40,60) | 18 |
| (0,4) | (75,90) | (70,72,75) | N(2,16) | U(40,60) | 27 |
| (0,5) | (150,180) | (140,145,160) | N(3,9) | U(40,60) | 56 |
| (0,6) | (200,230) | (65,70,72) | N(1,1) | U(40,60) | 60 |
| (0,7) | (40,60) | (260,270,278) | N(1,4) | U(40,60) | 19 |
| (0,8) | (120,140) | (262,268,270) | N(4,9) | U(40,60) | 45 |
| (0,9) | (220,250) | (205,210,220) | N(1,9) | U(40,60) | 52 |
| (0,10) | (120,140) | (150,160,165) | N(1,6) | U(40,60) | 38 |
| (1,2) | (100,150) | (78,81,85) | N(1,5) | U(40,60) | 29 |
| (1,3) | (220,300) | (65,72,88) | N(2,9) | U(40,60) | 41 |
| (1,4) | (150,330) | (210,220,235) | N(3,16) | U(40,60) | 37 |
| (1,5) | (210,300) | (270,278,298) | N(1,2) | U(40,60) | 87 |
| (1,6) | (180,260) | (68,70,72) | N(2,2) | U(40,60) | 34 |
| (1,7) | (110,350) | (130,135,140) | N(2,4) | U(40,60) | 15.5 |
| (1,8) | (180,280) | (160,170,180) | N(3,9) | U(40,60) | 21.5 |
| (1,9) | (160,300) | (300,310,322) | N(3,1) | U(40,60) | 40 |
| (1,10) | (220,300) | (96,100,105) | N(3,2) | U(40,60) | 31 |
| (2,3) | (115,135) | (100,105,115) | N(3,4) | U(40,60) | 17 |
| (2,4) | (290,340) | (102,110,124) | N(1,16) | U(40,60) | 29 |
| (2,5) | (260,300) | (165,175,186) | N(2,16) | U(40,60) | 47 |
| (2,6) | (180,240) | (320,336,361) | N(2,9) | U(40,60) | 16 |
| (2,7) | (260,380) | (280,295,315) | N(3,5) | U(40,60) | 25 |
| (2,8) | (220,235) | (90,95,100) | N(4,9) | U(40,60) | 82 |
| (2,9) | (220,380) | (200,205,220) | N(4,1) | U(40,60) | 54 |
| (2,10) | (300,360) | (55,60,62) | N(4,2) | U(40,60) | 26 |
| (3,4) | (180,380) | (170,175,186) | N(4,3) | U(40,60) | 54 |
| (3,5) | (120,280) | (215,222,236) | N(4,4) | U(40,60) | 61 |
| (3,6) | (200,260) | (105,108,116) | N(5,9) | U(40,60) | 57 |
| (3,7) | (210,290) | (195,203,215) | N(5,1) | U(40,60) | 38 |
| (3,8) | (160,390) | (155,162,176) | N(5,2) | U(40,60) | 28 |
| (3,9) | (280,360) | (195,202,215) | N(5,4) | U(40,60) | 37 |
| (3,10) | (160,420) | (66,68,72) | N(5,6) | U(40,60) | 26 |
| (4,5) | (220,270) | (305,315,340) | N(5,16) | U(40,60) | 45 |
| (4,6) | (260,350) | (345,350,370) | N(6,9) | U(40,60) | 32 |
| (4,7) | (120,210) | (210,215,230) | N(6,1) | U(40,60) | 17.5 |
| (4,8) | (180,240) | (75,78,82) | N(6,2) | U(40,60) | 47.2 |
| (4,9) | (240,350) | (55,60,64) | N(6,3) | U(40,60) | 35 |
| (4,10) | (220,310) | (320,354,376) | N(6,4) | U(40,60) | 43 |
| (5,6) | (190,285) | (310,322,340) | N(6,1) | U(40,60) | 34 |
| (5,7) | (180,320) | (280,290,312) | N(6,4) | U(40,60) | 28 |
| (5,8) | (320,420) | (260,285,320) | N(6,2) | U(40,60) | 34 |
| (5,9) | (250,360) | (115,119,128) | N(1,1) | U(40,60) | 64 |
| (5,10) | (170,250) | (175,180,192) | N(1,2) | U(40,60) | 35 |
| (6,7) | (220,290) | (260,275,292) | N(1,3) | U(40,60) | 29 |
| (6,8) | (270,365) | (220,231,245) | N(1,4) | U(40,60) | 75 |
| (6,9) | (320,390) | (293,300,321) | N(2,9) | U(40,60) | 61 |
| (6,10) | (305,375) | (215,223,236) | N(2,1) | U(40,60) | 84 |
| (7,8) | (260,320) | (293,303,324) | N(2,3) | U(40,60) | 34 |
| (7,9) | (150,240) | (200,210,225) | N(2,4) | U(40,60) | 43 |
| (7,10) | (210,275) | (262,272,286) | N(2,5) | U(40,60) | 19 |
| (8,9) | (200,255) | (360,383,405) | N(3,9) | U(40,60) | 56 |
| (8,10) | (230,285) | (260,266,282) | N(3,4) | U(40,60) | 34 |
| (9,10) | (180,270) | (365,377,400) | N(3,1) | U(40,60) | 28 |
| Genetic Algorithm Parameters | Chance Level | Model I | ||||
|---|---|---|---|---|---|---|
| pop | Max_Gen | pc | Cr | Best Solution | Risk | Consume Time |
| pm | Pr | |||||
| 3 | 50 | 0.8 0.3 | 0.99 0.99 | 0-1-6-0 | 8.7891 | 1203.68 s |
| 0-2-9-5-4-8-10-0 | ||||||
| 0-7-3-0 | ||||||
| 30 | 50 | 0.8 0.3 | 0.99 0.99 | 0-5-2-1-7-8-4-0 | 7.3103 | 8197.9 s |
| 0-9-0 | ||||||
| 0-10-3-6-0 | ||||||
| 100 | 50 | 0.8 0.3 | 0.99 0.99 | 0-5-3-10-8-4-0 | 6.6191 | 24,294.5 s |
| 0-7-9-2-6-1-0 | ||||||
| Genetic Algorithm Parameters | Chance Level | Model II | ||||
|---|---|---|---|---|---|---|
| pop | Max gen | pc | Cr | Best Solution | Cost | Consume Time |
| pm | Pr | |||||
| 3 | 50 | 0.8 0.3 | 0.99 0.99 | 0-8-9-0 | 38,393.4 | 768.761 s |
| 0-10-7-4-3-1-6-0 | ||||||
| 0-5-2-0 | ||||||
| 30 | 50 | 0.8 0.3 | 0.99 0.99 | 0-1-7-8-3-2-1 | 34,542.4 | 2882.98 s |
| 0-4-5-10-9-0 | ||||||
| 0-6-0 | ||||||
| 100 | 50 | 0.8 0.3 | 0.99 0.99 | 0-1-6-0 | 30,799.8 | 9184.34 s |
| 0-2-9-5-4-8-10-0 | ||||||
| 0-7-3-0 | ||||||
| Genetic Algorithm Parameters | Chance Level | Model III | ||||
|---|---|---|---|---|---|---|
| pop | Max | pc | Cr | Best Solution | 0.7 Risk + 0.3 Cost | Consume Time |
| gen | pm | Pr | ||||
| 3 | 50 | 0.8 0.3 | 0.99 0.99 | 0-8-9-10-7-4-0 | 0.84532 | 768.761 s |
| 0-3-1-0 | ||||||
| 0-6-5-2-0 | ||||||
| 30 | 50 | 0.8 0.3 | 0.99 0.99 | 0-9-2-6-10-0 | 0.832983 | 4843.76 s |
| 0-8-0 | ||||||
| 0-7-3-5-1-4-0 | ||||||
| 100 | 50 | 0.8 0.3 | 0.99 0.99 | 0-1-6-0 | 0.792522 | 15824.5 s |
| 0-2-9-5-4-8-10-0 | ||||||
| 0-7-3-0 | ||||||
| Arc | Length | Population Density | Probability | Speed | Area |
|---|---|---|---|---|---|
| (km) | (pop per km2) | (× 10−5) | (km/h) | (km2) | |
| (0,1) | Inf | Inf | N(1,2) | U(40,60) | Inf |
| (0,2) | (10,15) | (15,20,38) | N((1,3) | U(40,60) | 2 |
| (0,3) | (15,20) | (20,30,40) | N(2,6) | U(40,60) | 5 |
| (0,4) | (30,40) | (20,33,44) | N(1,4) | U(40,60) | 6 |
| (0,5) | (15,30) | (22,35,50) | N(1,6) | U(40,60) | 3 |
| (0,6) | (10,12) | (18,20,32) | N(2,4) | U(40,60) | 1 |
| (0,7) | (8,15) | (26,28,29) | N(1,1) | U(40,60) | 3.5 |
| (0,8) | (18,24) | (20,25,30) | N(2,5) | U(40,60) | 4.8 |
| (0,9) | (10,13) | (15,20,28) | N(1,3) | U(40,60) | 1.6 |
| (0,10) | (10,18) | (15,20,24) | N(2,5) | U(40,60) | 1.7 |
| (0,11) | (8,12) | (20,26,27) | N(1,4) | U(40,60) | 2.1 |
| (0,12) | (5,10) | (10,16,30) | N(1,1) | U(40,60) | 2.3 |
| (0,13) | (6,14) | (30,32,35) | N(2,1) | U(40,60) | 2.6 |
| (0,14) | (7,16) | (22,28,40) | N(2,2) | U(40,60) | 3 |
| (0,15) | (8,15) | (12,20,26) | N(1,3) | U(40,60) | 2.9 |
| (1,2) | (40,42) | (50,60,70) | N(2,6) | U(40,60) | 14 |
| (1,3) | (60,62) | (60,70,85) | N(2,8) | U(40,60) | 22 |
| (1,4) | (20,25) | (32,38,40) | N(2,3) | U(40,60) | 7 |
| (1,5) | (20,30) | (28,29,36) | N(2,4) | U(40,60) | 7.5 |
| (1,6) | (25,28) | (40,42,50) | N(3,5) | U(40,60) | 8 |
| (1,7) | (15,18) | (20,24,30) | N(1,4) | U(40,60) | 3 |
| (1,8) | (8,12) | (20,25,30) | N(2,2) | U(40,60) | 2.6 |
| (1,9) | Inf | Inf | Inf | U(40,60) | Inf |
| (1,10) | (28,32) | (39,45,48) | N(2,5) | U(40,60) | 10 |
| (1,11) | (20,26) | (30,36,45) | N(2,6) | U(40,60) | 8.2 |
| (1,12) | Inf | Inf | Inf | U(40,60) | Inf |
| (1,13) | (80,90) | (100,102,110) | N(1,5) | U(40,60) | 20 |
| (1,14) | (70,80) | (80,82,88) | N(3,6) | U(40,60) | 15 |
| (1,15) | (30,35) | (40,42,48) | N(1,3) | U(40,60) | 12.5 |
| (2,3) | (20,25) | (30,38,40) | N(1,1) | U(40,60) | 10.2 |
| (2,4) | (40,50) | (42,45,48) | N(3,3) | U(40,60) | 14.5 |
| (2,5) | (60,70) | (66,68,70) | N(3,7) | U(40,60) | 18 |
| (2,6) | Inf | Inf | Inf | U(40,60) | Inf |
| (2,7) | Inf | Inf | Inf | U(40,60) | Inf |
| (2,8) | (50,55) | (65,70,78) | N(5,2) | U(40,60) | 22 |
| (2,9) | Inf | Inf | Inf | U(40,60) | Inf |
| (2,10) | (5,8) | (10,15,20) | N(1,2) | U(40,60) | 1.2 |
| (2,11) | (10,15) | (12,15,19) | N(2,2) | U(40,60) | 1.8 |
| (2,12) | (20,25) | (30,32,37) | N(2,3) | U(40,60) | 2.0 |
| (2,13) | (25,30) | (40,46,50) | N(2,4) | U(40,60) | 2.3 |
| (2,14) | Inf | Inf | Inf | U(40,60) | Inf |
| (2,15) | Inf | Inf | Inf | U(40,60) | Inf |
| (3,4) | (40,50) | (50,55,60) | N(3,2) | U(40,60) | 15 |
| (3,5) | (30,40) | (33,38,42) | N(3,5) | U(40,60) | 14.6 |
| (3,6) | (30,35) | (32,39,49) | N(2,5) | U(40,60) | 13.2 |
| (3,7) | (70,75) | (82,84,90) | N(5,8) | U(40,60) | 30 |
| (3,8) | (80,82) | (90,95,105) | N(4,9) | U(40,60) | 32 |
| (3,9) | Inf | Inf | Inf | U(40,60) | Inf |
| (3,10) | (60,70) | (65,70,80) | N(3,5) | U(40,60) | 23 |
| (3,11) | (40,50) | (50,62,82) | N(3,3) | U(40,60) | 24 |
| (3,12) | (40,42) | (50,62,72) | N(3,6) | U(40,60) | 26 |
| (3,13) | (35,40) | (42,50,53) | N(3,5) | U(40,60) | 25 |
| (3,14) | (15,22) | (32,38,42) | N(2,3) | U(40,60) | 10.2 |
| (3,15) | (25,30) | (30,40,42) | N(3,2) | U(40,60) | 20 |
| (4,5) | (15,20) | (20,25,36) | N(1,4) | U(40,60) | 16 |
| (4,6) | (30,40) | (42,55,65) | N(2,2) | U(40,60) | 25 |
| (4,7) | (10,15) | (20,26,34) | N(1,3) | U(40,60) | 6.5 |
| (4,8) | (15,25) | (20,28,35) | N(1,2) | U(40,60) | 7.2 |
| (4,9) | (5,8) | (10,20,32) | N(1,1) | U(40,60) | 2.5 |
| (4,10) | (50,80) | (65,72,88) | N(3,4) | U(40,60) | 19 |
| (4,11) | (60,62) | (80,82,86) | N(4,5) | U(40,60) | 28 |
| (4,12) | (50,55) | (62,68,72) | N(2,4) | U(40,60) | 24 |
| (4,13) | (40,50) | (44,48,52) | N(1,6) | U(40,60) | 20 |
| (4,14) | (15,20) | (20,25,30) | N(2,2) | U(40,60) | 13 |
| (4,15) | (4,15) | (10,20,32) | N(1,1) | U(40,60) | 2.2 |
| (5,6) | (8,12) | (15,20,25) | N(1,2) | U(40,60) | 4.5 |
| (5,7) | (12,15) | (20,23,27) | N(1,3) | U(40,60) | 7.2 |
| (5,8) | (13,20) | (20,30,40) | N(1,3) | U(40,60) | 7.5 |
| (5,9) | Inf | Inf | Inf | U(40,60) | Inf |
| (5,10) | (60,70) | (80,90,96) | N(2,5) | U(40,60) | 26 |
| (5,11) | (70,72) | (82,88,90) | N(2,6) | U(40,60) | 32 |
| (5,12) | Inf | Inf | Inf | U(40,60) | Inf |
| (5,13) | (30,50) | (36,44,54) | N(2,3) | U(40,60) | 15 |
| (5,14) | (8,10) | (20,22,28) | N(1,3) | U(40,60) | 4.2 |
| (5,15) | (5,12) | (12,18,28) | N(1,2) | U(40,60) | 2.4 |
| (6,7) | (5,8) | (13,18,28) | N(1,1) | U(40,60) | 2.2 |
| (6,8) | (8,12) | (20,32,40) | N(1,2) | U(40,60) | 4 |
| (6,9) | (8,12) | (20,32,40) | N(1,2) | U(40,60) | 4 |
| (6,10) | (8,12) | (20,32,40) | N(1,2) | U(40,60) | 4 |
| (6,11) | (10,15) | (25,30,38) | N(1,3) | U(40,60) | 4.2 |
| (6,12) | (12,15) | (25,32,42) | N(1,4) | U(40,60) | 4.4 |
| (6,13) | (15,18) | (20,30,40) | N(2,2) | U(40,60) | 4.8 |
| (6,14) | (16,20) | (22,30,32) | N(2,2) | U(40,60) | 5 |
| (6,15) | (8,10) | (15,20,22) | N(1,3) | U(40,60) | 3 |
| (7,8) | (5,7) | (12,20,22) | N(1,1) | U(40,60) | 1.9 |
| (7,9) | (8,12) | (18,24,35) | N(1,2) | U(40,60) | 2.8 |
| (7,10) | (10,14) | (25,30,33) | N(1,3) | U(40,60) | 4.3 |
| (7,11) | (15,20) | (22,28,32) | N(2,1) | U(40,60) | 4.5 |
| (7,12) | (16,22) | (23,29,35) | N(2,2) | U(40,60) | 4.6 |
| (7,13) | (20,22) | (30,36,40) | N(2,3) | U(40,60) | 4.8 |
| (7,14) | (20,30) | (30,36,45) | N(2,3) | U(40,60) | 5.6 |
| (7,15) | (10,12) | (17,22,25) | N(1,1) | U(40,60) | 3.8 |
| (8,9) | (10,12) | (17,22,25) | N(1,1) | U(40,60) | 3.8 |
| (8,10) | (9,12) | (10,15,16) | N(1,2) | U(40,60) | 3.6 |
| (8,11) | (15,25) | (12,16,23) | N(2,1) | U(40,60) | 5.2 |
| (8,12) | (15,25) | (12,16,23) | N(2,1) | U(40,60) | 5.2 |
| (8,13) | (15,30) | (12,18,28) | N(2,3) | U(40,60) | 5.6 |
| (8,14) | (35,40) | (50,55,62) | N(2,3) | U(40,60) | 28 |
| (8,15) | (10,12) | (20,22,25) | N(1,1) | U(40,60) | 4.8 |
| (9,10) | (8,12) | (15,20,25) | N(1,1) | U(40,60) | 2.2 |
| (9,11) | (12,15) | (20,28,30) | N(1,2) | U(40,60) | 3.3 |
| (9,12) | (15,18) | (25,30,32) | N(1,2) | U(40,60) | 3.3 |
| (9,13) | (15,20) | (25,30,36) | N(1,2) | U(40,60) | 3.0 |
| (9,14) | (10,12) | (20,22,25) | N(1,1) | U(40,60) | 2.6 |
| (9,15) | (4,8) | (10,20,30) | N(0,1) | U(40,60) | 1 |
| (10,11) | (4,6) | (10,20,26) | N(0,1) | U(40,60) | 0.9 |
| (10,12) | (8,10) | (10,26,32) | N(1,3) | U(40,60) | 2.0 |
| (10,13) | (10,15) | (18,28,36) | N(1,2) | U(40,60) | 3.2 |
| (10,14) | (18,20) | (20,30,40) | N(2,1) | U(40,60) | 3.1 |
| (10,15) | (10,12) | (18,28,32) | N(2,1) | U(40,60) | 2.6 |
| (11,12) | (5,8) | (15,20,25) | N(1,1) | U(40,60) | 0.8 |
| (11,13) | (8,10) | (18,22,28) | N(1,2) | U(40,60) | 1.1 |
| (11,14) | (15,18) | (20,32,38) | N(1,3) | U(40,60) | 3.3 |
| (11,15) | (12,14) | (20,24,28) | N(2,3) | U(40,60) | 2.8 |
| (12,13) | (6,8) | (10,16,22) | N(1,1) | U(40,60) | 0.6 |
| (12,14) | (10,15) | (20,28,32)) | N(1,2) | U(40,60) | 2.7 |
| (12,15) | (12,18) | (18,26,31) | N(2,1) | U(40,60) | 2.8 |
| (13,14) | (12,14) | (16,20,26) | N(2,1) | U(40,60) | 2.8 |
| (13,15) | (20,25) | (30,32,38) | N(3,1) | U(40,60) | 5.2 |
| (14,15) | (10,12) | (18,22,26) | N(2,2) | U(40,60) | 2.0 |
| Genetic Algorithm Parameters | Chance Level | Model I | ||||
|---|---|---|---|---|---|---|
| pop | Max_gen | pc | Cr | Best Solution | Risk | Consume Time |
| pm | Pr | |||||
| 3 | 50 | 0.8 0.3 | 0.99 0.99 | 0-12-13-15-0 | 0.571448 | 296.519 s |
| 0-10-6-4-5-1-2-11-14-9-8-0 | ||||||
| 0-7-3-0 | ||||||
| 30 | 50 | 0.8 0.3 | 0.99 0.99 | 0-4-14-5-13-0 | 0.372853 | 2051.57 s |
| 0-10-1-2-6-0 | ||||||
| 0-7-9-8-11-15-12-2-0 | ||||||
| 100 | 50 | 0.8 0.3 | 0.99 0.99 | 0-8-6-11-0 | 0.129406 | 7010.85 s |
| 0-10-1-2-13-12-9-15-3-0 | ||||||
| 0-14-7-0 | ||||||
| Genetic Algorithm Parameters | Chance Level | Model II | ||||
|---|---|---|---|---|---|---|
| pop | Max_gen | pc | Cr | Best Solution | Cost | Consume Time |
| pm | Pr | |||||
| 3 | 50 | 0.8 0.3 | 0.99 0.99 | 0-12-13-15-0 | 3658.17 | 579.293 s |
| 0-10-6-4-5-1-2-11-14-9-8-0 | ||||||
| 0-7-3-0 | ||||||
| 30 | 50 | 0.8 0.3 | 0.99 0.99 | 0-8-6-0 | 834.382 | 3972.98 s |
| 0-11-10-1-2-0 | ||||||
| 0-13-12-9-15-3-5-4-14-7-0 | ||||||
| 100 | 50 | 0.8 0.3 | 0.99 0.99 | 0-8-6-0 | 820.419 | 15,353.4 s |
| 0-11-10-1-2-0 | ||||||
| 0-13-12-9-15-3-5-4-14-7-0 | ||||||
| Genetic Algorithm Parameters | Chance Level | Model III | ||||
|---|---|---|---|---|---|---|
| pop | Max_gen | pc | Cr | Best Solution | 0.7Risk + 0.3 Cost | Consume Time |
| pm | Pr | |||||
| 3 | 50 | 0.8 0.3 | 0.99 0.99 | 0-1-9-3-0 | 0.982762 | 901.49 s |
| 0-13-8-6-14-12-11-5-2-15-7-0 | ||||||
| 0-10-4-0 | ||||||
| 30 | 50 | 0.8 0.3 | 0.99 0.99 | 0-12-15-3-14-13-0 | 0.803568 | 6395.4 s |
| 0-10-0 | ||||||
| 0-4-11-8-2-5-9-1-6-7-0 | ||||||
| 100 | 50 | 0.8 0.3 | 0.99 0.99 | 0-9-14-0 | 0.778511 | 20,173 s |
| 0-12-5-6-8-1-10-0 | ||||||
| 0-4-3-11-7-15-2-13-0 | ||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Cao, N. Fuzzy Random Chance-Constrained Programming Model for the Vehicle Routing Problem of Hazardous Materials Transportation. Symmetry 2020, 12, 1208. https://doi.org/10.3390/sym12081208
Zhao L, Cao N. Fuzzy Random Chance-Constrained Programming Model for the Vehicle Routing Problem of Hazardous Materials Transportation. Symmetry. 2020; 12(8):1208. https://doi.org/10.3390/sym12081208
Chicago/Turabian StyleZhao, Liying, and Ningbo Cao. 2020. "Fuzzy Random Chance-Constrained Programming Model for the Vehicle Routing Problem of Hazardous Materials Transportation" Symmetry 12, no. 8: 1208. https://doi.org/10.3390/sym12081208
APA StyleZhao, L., & Cao, N. (2020). Fuzzy Random Chance-Constrained Programming Model for the Vehicle Routing Problem of Hazardous Materials Transportation. Symmetry, 12(8), 1208. https://doi.org/10.3390/sym12081208





