Topological Symmetry Transition between Toroidal and Klein Bottle Graphenic Systems †
Abstract
:1. Introduction
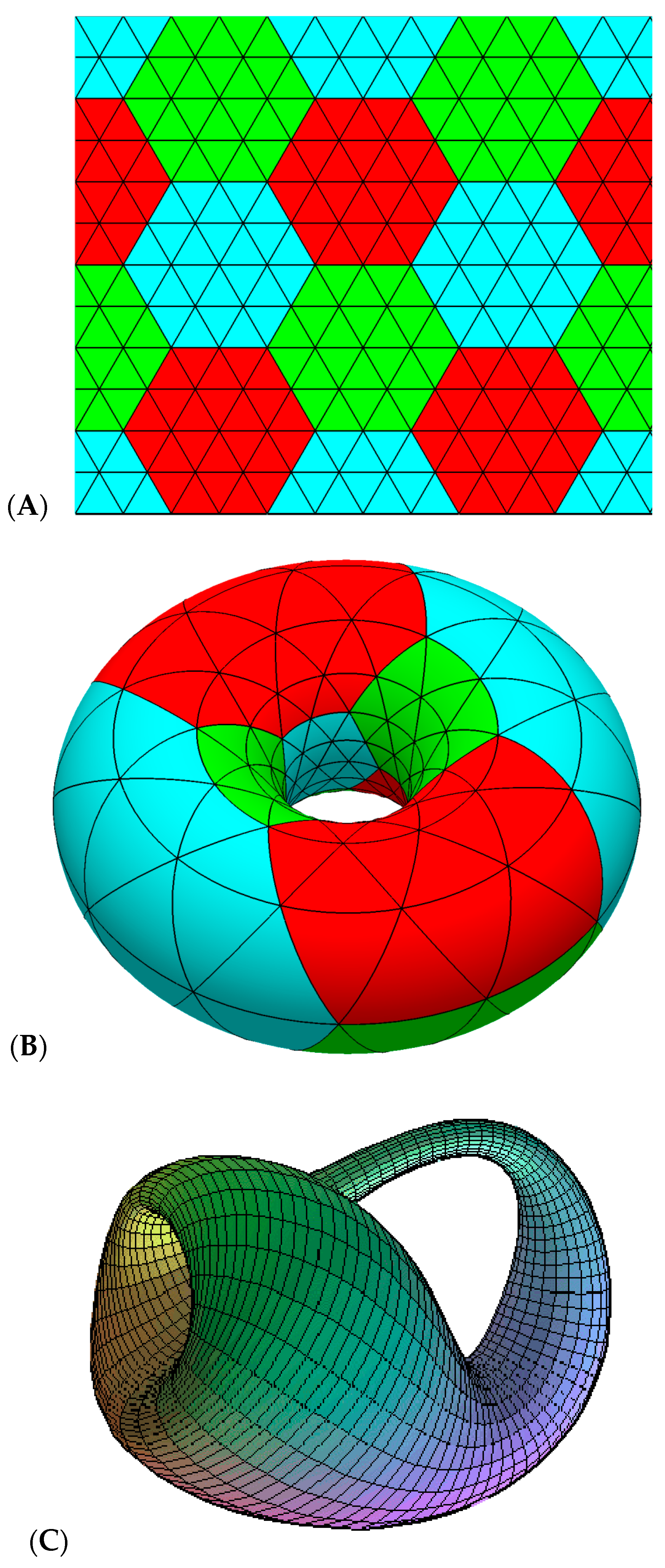
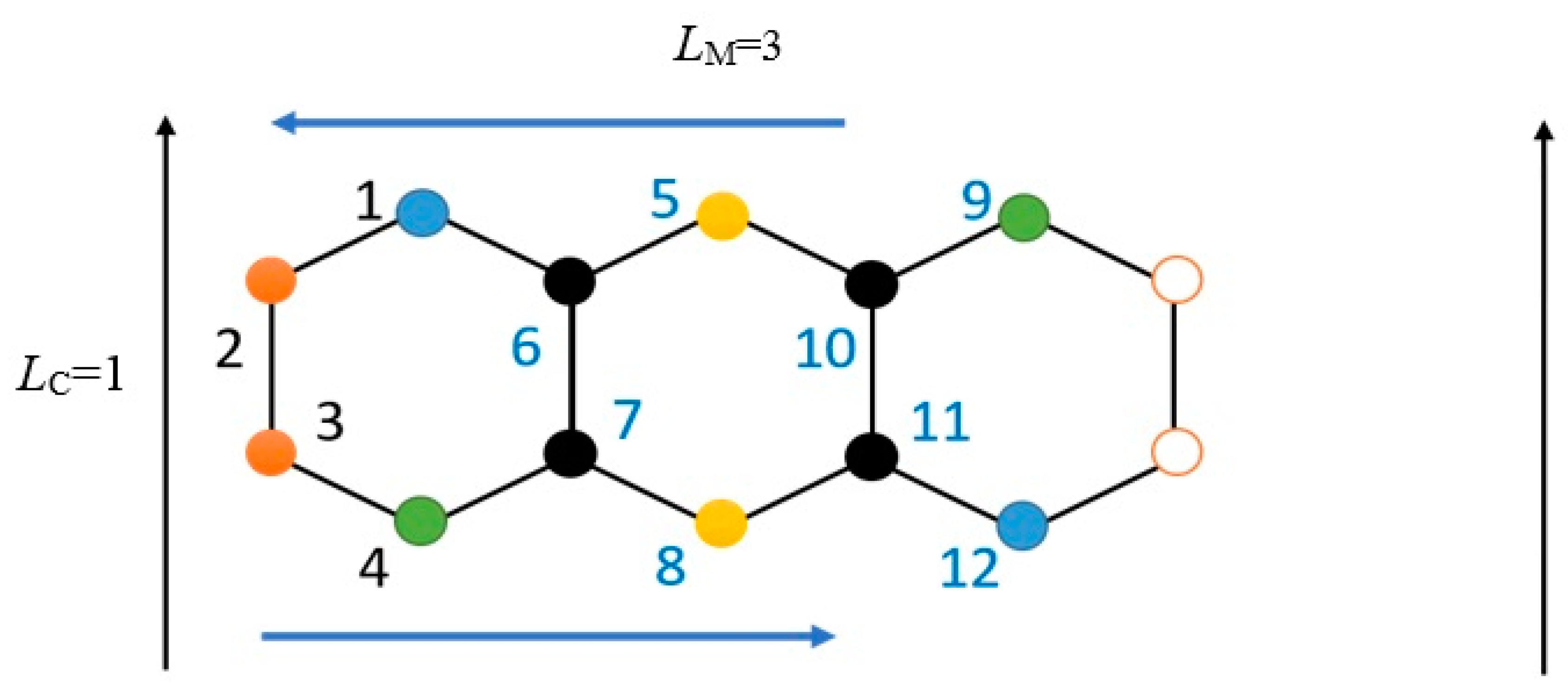
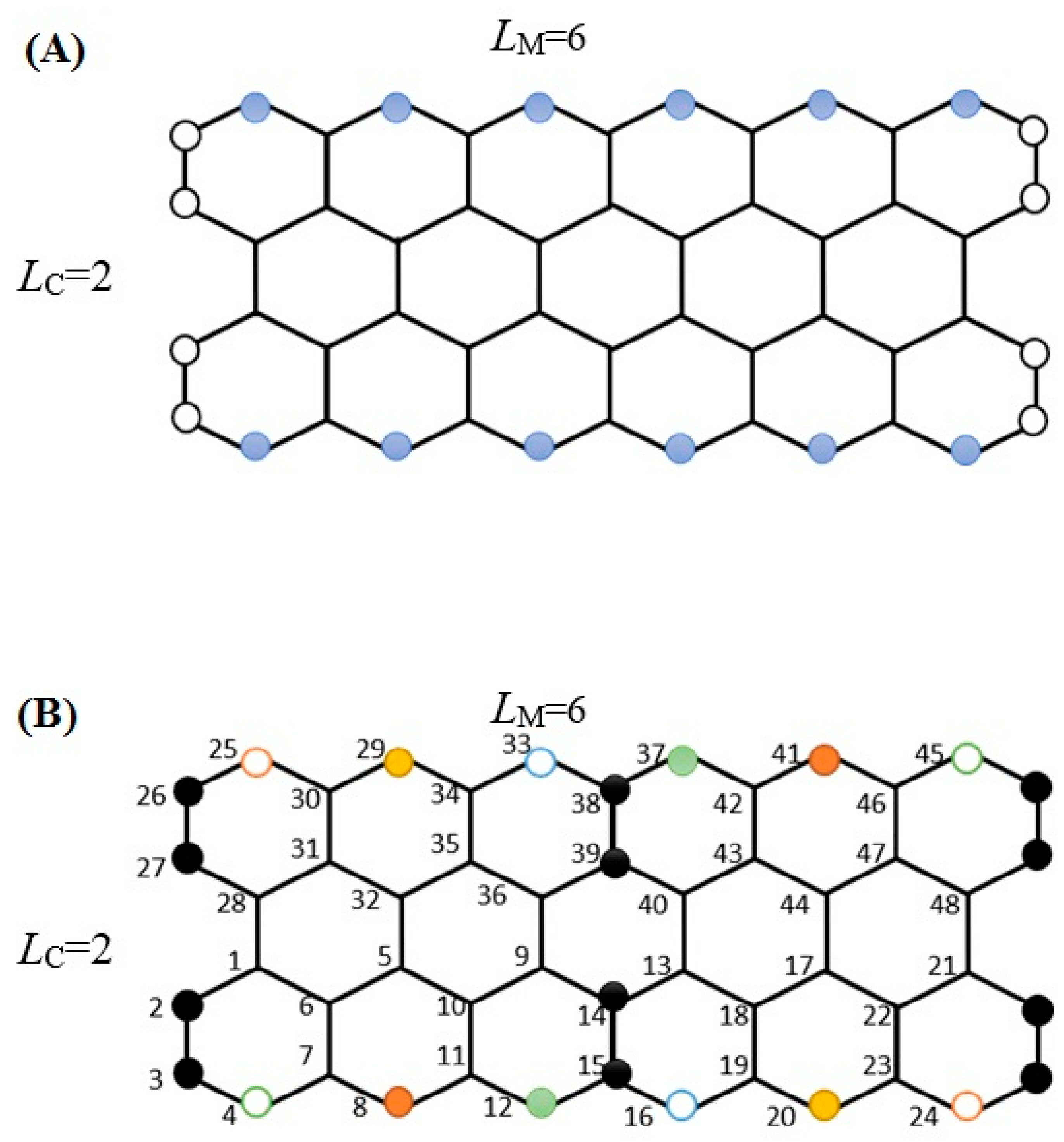
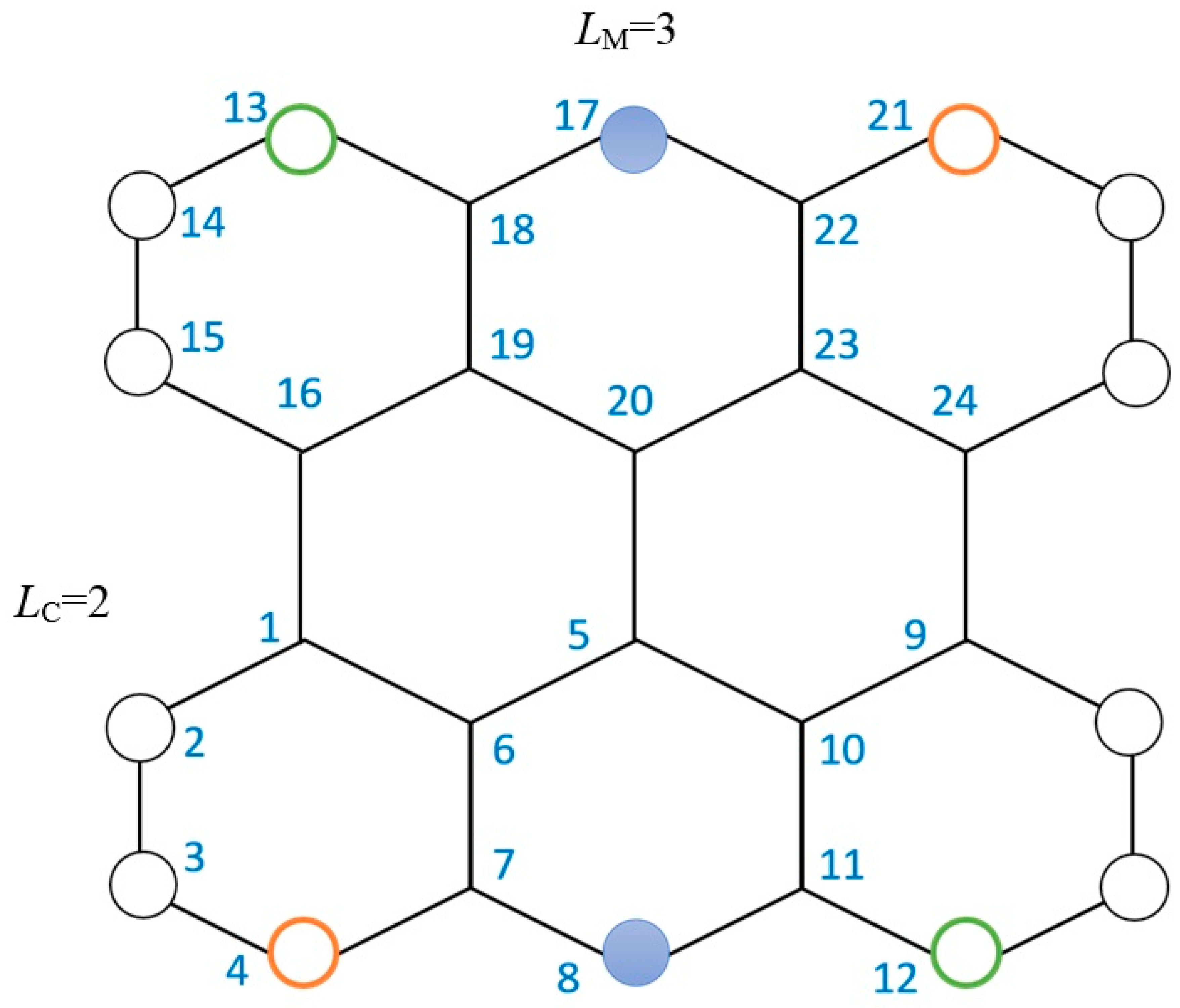
2. Method: Topological Invariants for Polyhex Graphs
3. Results: Topological Similarities between Toroidal and Klein Bottle Polyhexes
- ➢
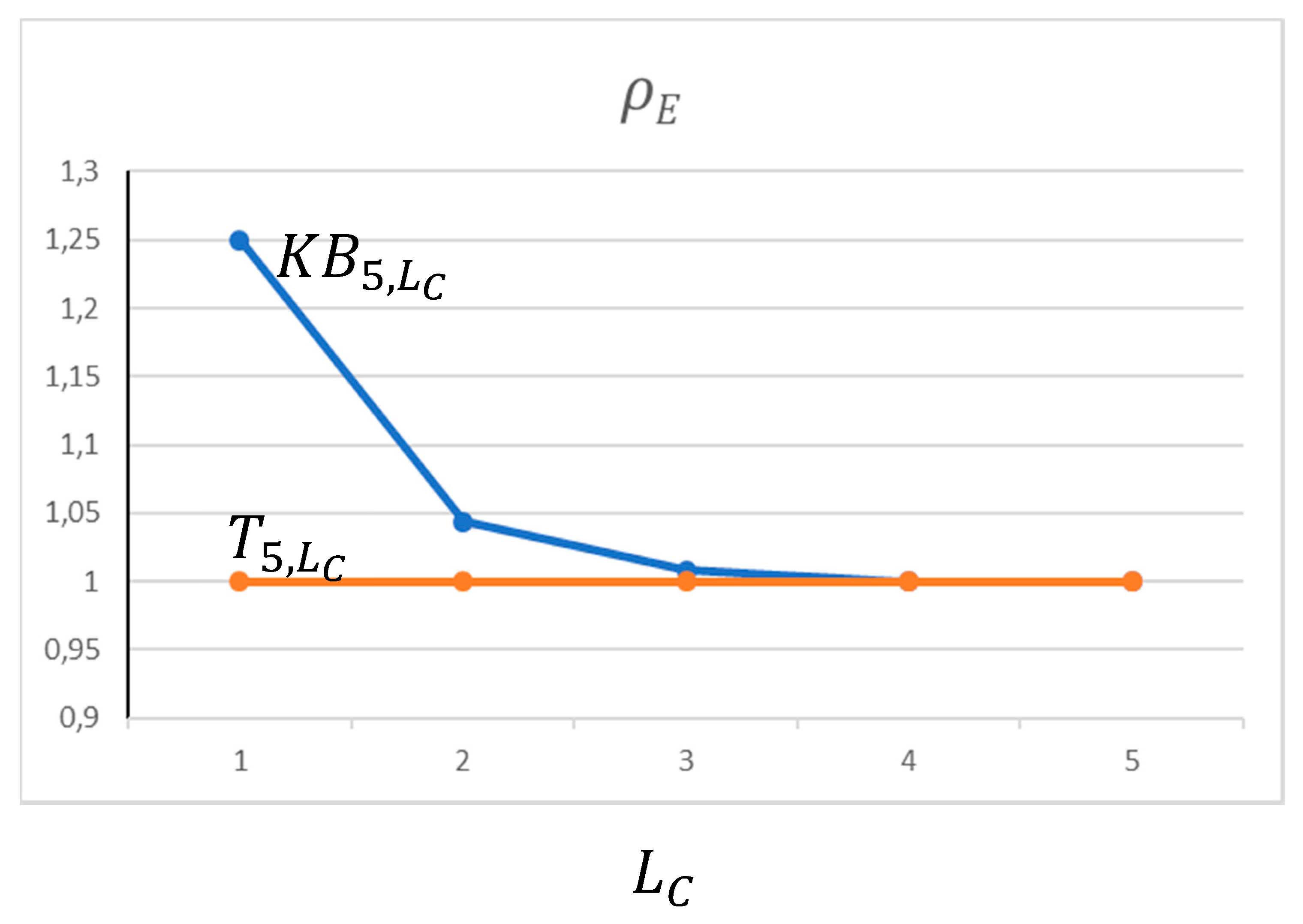
- LC < ŁC: in this region, the eccentricity shrinkage of Equation (4b) holds and the Klein bottle is therefore more compact than the toroidal graphenic structure with equal size. The Wiener indices (2) of the Klein bottles are lower than those of the tori; see Table 3.
- ➢
- LC ≥ ŁC: in this region, the conjectured topological similarity of Equation (5a) holds and the Klein bottle thus becomes topologically equivalent to the isomeric toroidal polyhex sharing the same values of W and ; see Figure 5.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. On Topological and Quantum Coverings of Nano-Space

References
- Weeks, J.R. The Shape of Space; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Weisstein, E.W. “Klein Bottle”. From MathWorld—A Wolfram Web Resource. Available online: http://mathworld.wolfram.com/KleinBottle.html (accessed on 8 May 2020).
- Ferréol, R.; Mandonnet, J. 2017, Klein surface, MathCurve.com. Available online: https://www.mathcurve.com/surfaces.gb/klein/klein.shtml (accessed on 3 March 2020).
- Ferréol, R.; Mandonnet, J. 2017, Genus of a Surface, MathCurve.com. Available online: https://www.mathcurve.com/surfaces.gb/genre/genre.shtml (accessed on 3 March 2020).
- Li, P.; Zhang, Z. Continuous-time quantum walks on nonorientable surfaces: Analytical solutions for Möbius strips and Klein bottles. J. Phys. A Math. Theor. 2012, 45, 285301. [Google Scholar] [CrossRef]
- Haruo, H. How to design non-Kekulé polyhex graphs? Croat. Chem. Acta 1986, 59, 583–590. [Google Scholar]
- Kirby, E.C. Remarks upon recognising genus and possible shapes of chemical cages in the form of Polyhedra, Tori and Klein bottles. Croat. Chem. Acta CCACAA 1995, 68, 269–282. [Google Scholar]
- Deza, M.; Fowler, P.W.; Rassat, A.; Rogers, K.M. Fullerenes as tilings of surfaces. J. Chem. Inf. Comput. Sci. 2000, 40, 550–558. [Google Scholar] [CrossRef]
- Freiberger, M. Introducing the Klein bottle. Plus Magazine. 6 January 2015. Available online: https://plus.maths.org/content/introducing-klein-bottle (accessed on 15 June 2020).
- Ori, O.; Putz, M.V. Isomeric formation of 5| 8| 5 defects in graphenic systems. Fuller. Nanotub. Carbon Nanostructures 2014, 22, 887–900. [Google Scholar] [CrossRef]
- Ori, O.; Cataldo, F.; Putz, M.V. Topological anisotropy of Stone-Wales waves in graphenic fragments. Int. J. Mol. Sci. 2011, 12, 7934–7949. [Google Scholar] [CrossRef]
- Ori, O.; Putz, M.V. Topological evolution of the 5| 8| 5 defect in graphene. New Front. Chem. 2018, 27, 105–113. [Google Scholar]
- Putz, M.V.; Ori, O.; Diudea, M.V. Bondonic electronic properties of 2D graphenic lattices with structural defects. In Graphene Science Handbook, Electrical and Optical Properties; CRC Press (Taylor & Francis Group): Boca Raton, FL, USA, 2016; Volume 3, pp. 55–80. [Google Scholar]
- Ori, O.; Putz, M.V.; Gutman, I.; Schwerdtfeger, P. Generalized Stone-Wales transformations for fullerene graphs derived from Berge’s switching theorem. Ante Graovac Life Work. Math. Chem. Monogr. 2014, 16, 259–272. [Google Scholar]
- Balasubramanian, K. Integration of graph theory and quantum chemistry for structure-activity relationships. SAR QSAR Environ. Res. 1994, 2, 59–77. [Google Scholar] [CrossRef]
- Randić, M. Quantum chemical justification for Clar’s valence structures. In Reviews of Modern Quantum Chemistry. A Celebration of the Contributions of the Robert G. Parr; Sen, K.D., Ed.; World Scientific: Singapore, 2002; Volume I, pp. 204–239. [Google Scholar]
- Cataldo, F.; Ori, O.; Graovac, A. Graphene topological modifications. Int. J. Chem. Model. 2011, 3, 45. [Google Scholar]
- Cataldo, F.; Ori, O.; Iglesias-Groth, S. Topological lattice descriptors of graphene sheets with fullerene-like nanostructures. Mol. Simul. 2010, 36, 341–353. [Google Scholar] [CrossRef]
- Koorepazan-Moftakhar, F.; Ashrafi, A.R.; Ori, O.; Putz, M.V. Topological efficiency of fullerene. J. Comput. Theor. Nanosci. 2015, 12, 971–975. [Google Scholar] [CrossRef]
- Deza, M.M.; (At the 15th International Conference Computational and Mathematical Methods in Science and Engineering, Cadiz, Spain, 6–10 July 2015). Private Communication, 2015.
- Sabirov, D.S.; Ori, O.; László, I. Isomers of the C84 fullerene: A theoretical consideration within energetic, structural, and topological approaches. Fuller. Nanotub. Carbon Nanostructures 2018, 26, 100–110. [Google Scholar] [CrossRef]
- Dobrynin, A.A.; Ori, O.; Putz, M.V.; Vesnin, A.Y. Generalized topological efficiency–case study with C84 fullerene. Fuller. Nanotub. Carbon Nanostructures 2020, 28, 545–550. [Google Scholar] [CrossRef]
- Putz, M.V.; De Corato, M.; Benedek, G.; Sedlar, J.; Graovac, A.; Ori, O. Topological invariants of Moebius-like graphenic nanostructures. In Topological Modelling of Nanostructures and Extended Systems; Ashrafi, A.R., Cataldo, F., Iranmanesh, A., Ori, O., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 229–244. [Google Scholar]
- Putz, M.V. The bondons: The quantum particles of the chemical bond. Int. J. Mol. Sci. 2010, 11, 4227–4256. [Google Scholar] [CrossRef]
- Putz, M.V.; Ori, O. Bondonic characterization of extended nanosystems: Application to graphene’s nanoribbons. Chem. Phys. Lett. 2012, 548, 95–100. [Google Scholar] [CrossRef]
- Putz, M.V.; Ori, O. Bondonic effects in Group-IV honeycomb nanoribbons with Stone-Wales topological defects. Molecules 2014, 19, 4157–4188. [Google Scholar] [CrossRef] [Green Version]
- Putz, M.V.; Ori, O. Predicting bondons by Goldstone mechanism with chemical topological indices. Int. J. Quantum Chem. 2015, 115, 137–143. [Google Scholar] [CrossRef]
- Kirby, E.C. Recent Work on Toroidal and Other Exotic Fullerenes Structures. In From Chemical Topology to Three-Dimensional Geometry; Balaban, A.T., Ed.; Kluwer Academic Publishers: New York, NY, USA, 2002; pp. 263–296. [Google Scholar]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef] [Green Version]
- Everett, H. ‘Relative State’ formulation of quantum mechanics. Rev. Mod. Phys. 1957, 29, 454–462. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, S.; Allori, V.; Tumulka, R.; Zanghi, N. Many-worlds and Schrödinger’s first quantum theory. Br. J. Philos. Sci. 2011, 62, 1–27. [Google Scholar]
- Norsen, T. Foundations of Quantum Mechanics. An Exploration of the Physical Meaning of Quantum Theory; Springer International Publishing AG 2017: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Wolfram, S. Finally We May Have a Path to the Fundamental Theory of Physics…and It’s Beautiful. Stephen Wolfram’s Writings. 2020. Available online: https://writings.stephenwolfram.com/2020/04/finally-we-may-have-a-path-to-the-fundamental-theory-of-physics-and-its-beautiful/ (accessed on 8 May 2020).
- Kroto, H.W.; Heath, J.R.; Obrien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Terrones, M.; Terrones, H.; Banhart, F.; Charlier, J.-C.; Ajayan, P.M. Coalescence of single-walled carbon nanotubes. Science 2000, 288, 1226–1229. [Google Scholar] [CrossRef]
- Umemoto, K.; Saito, S.; Berber, S.; Tománek, D. Carbon foam: Spanning the phase space between graphite and diamond. Phys. Rev. B 2001, 64, 193409. [Google Scholar] [CrossRef] [Green Version]
- Banhart, F. The formation of a connection between carbon nanotubes in an electron beam. Nano Lett. 2001, 1, 329–332. [Google Scholar] [CrossRef]
- Collins, P.C.; Arnold, M.S.; Avouris, P. Engineering carbon nanotubes and nanotube circuits using electrical breakdown. Science 2001, 292, 706–709. [Google Scholar] [CrossRef]
- Borwein, J.; Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002; p. 1050. [Google Scholar]
- Ori, O.; D’Mello, M. A topological study of the structure of the C76 fullerene. Chem Phys. Lett. 1992, 197, 49–54. [Google Scholar] [CrossRef]
- Ori, O.; D’Mello, M. Analysis of the structure of the C78 fullerene: A topological approach. Appl. Phys. A 1993, 56, 35–39. [Google Scholar] [CrossRef]
- Schwerdtfeger, P.; Wirz, L.N.; Avery, J. The topology of fullerenes. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 96–145. [Google Scholar] [CrossRef] [PubMed]
- Kirby, E.C.; Mallion, R.B.; Pollak, P. Toroidal polyhexes. J. Chem. Soc. Faraday Trans. 1993, 89, 1945–1953. [Google Scholar] [CrossRef]
- Klein, D.J. Elemental benzenoids. J. Chem. Inf. Comput. Sci. 1994, 34, 453–459. [Google Scholar] [CrossRef]
- Ceulemans, A.; Chibotaru, L.F.; Bovin, S.A.; Fowler, P.W. The electronic structure of polyhex carbon tori. J. Chem. Phys. 2000, 112, 4271–4278. [Google Scholar] [CrossRef] [Green Version]
- Diudea, M.V.; (Covering Nanostructures, Faculty of Chemistry and Chemical Engineering, “Babes-Bolyai” University, 400084 Cluj, Romania). Personal Communication, 2016.
- Reiter, K.; Weigend, F.; Wirz, L.N.; Dimitrova, M.; Sundholm, D. Magnetically induced current densities in toroidal carbon nanotubes. J. Phys. Chem. C 2019, 123, 15354–15365. [Google Scholar] [CrossRef] [Green Version]
- King, R.B. Chemical Applications of topology and group theory. 29. Low density polymeric carbon allotropes based on negative curvature structures. J. Phys. Chem. 1996, 100, 15096–15104. [Google Scholar] [CrossRef]
- King, R.B. Novel highly symmetrical trivalent graphs which lead to negative curvature carbon and boron nitride chemical structures. Disc. Math. 2002, 244, 203–210. [Google Scholar] [CrossRef] [Green Version]
- Jos, L. Topology Movies. Mathematical Imagery. Available online: http://www.josleys.com/galleries.php?catid=13 (accessed on 15 June 2020).
- Bohm, D. Wholeness and the Implicate Order; Routledge; Kegan: London, UK, 2002. [Google Scholar]
- Rapoport, D.L. Surmounting the cartesian with philosophy, physics, logic, cybernetics and geometry: Self-reference, torsion, the Klein bottle, the time operator, multivalued logics and quantum mechanics. Found. Phys. 2011, 41, 33–76. [Google Scholar] [CrossRef]
- Rapoport, D.L. Surmounting the cartesian cut: Klein bottle logophysics, the Dirac algebra & the genetic code. Neuroquantoloy 2011, 9, 862–881. [Google Scholar]
- Boeyens, J.C.A. New Theories for Chemistry; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Rapoport, D.L. Torsion fields, the extended photon, quantum jumps, the Klein bottle, multivalued logic, the time operator, chronomes, perception, semiosis, neurology and cognition. In Focus in Quantum Mechanics; Hathaway, D., Randolph, E., Eds.; Nova Science: New York, NY, USA, 2011. [Google Scholar]
- Stern, A. Quantum Theoretic Machines; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Rapoport, D.L. Klein bottle logophysics: A unified principle for non-linear systems, cosmology, geophysics, biology, biomechanics and perception. J. Phys. Conf. Ser. 2013, 437, 012024. [Google Scholar] [CrossRef]
- Horwitz, L.P.; Biedenharn, L.C. Quaternion quantum mechanics: Second quantization and gauge fields. Ann. Phys. 1984, 157, 432–488. [Google Scholar] [CrossRef]
- Adler, S.L. Quaternionic Quantum Mechanics and Quantum Fields; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Hardy, L. Quantum Theory From Five Reasonable Axioms, 4th ed.Cornell University Archive: New York, NY, USA, 2001. [Google Scholar]
- Renes, J.M.; Blume-Kohout, R.; Scott, A.J.; Caves, C.M. Symmetric informationally complete quantum measurements. J. Math. Phys. 2004, 45, 2171–2180. [Google Scholar] [CrossRef]
- Masanes, L.; Mueller, M.P. A derivation of quantum theory from physical requirements. New J. Phys. 2001, 13, 063001. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement Sharing in Real-Vector-Space Quantum Theory. Found. Phys. 2012, 42, 19–28. [Google Scholar] [CrossRef] [Green Version]
- Clegg, B. Gravitational Waves. How Einstein’s Spacetime Ripples Reveal the Secrets of the Universe; Icon Books Ltd.: London, UK, 2018. [Google Scholar]
- Sparrow, G. What Shape Is Space? A Primer for the 21st Century; Thames & Hudson Ltd.: London, UK, 2018. [Google Scholar]
- González-Díaz, P.; Alonso-Serrano, A. Observing other universe through ringholes and Klein bottle holes. Phys. Rev. D 2011, 84, 023008. [Google Scholar] [CrossRef] [Green Version]
| W = 4504; = 98/91 = 1.0769 | |||
| V | {} | ||
| (8) v5 v8 v17 v20 v29 v32 v41 v44 | 3 6 9 12 11 5 1 | 7 | 91 |
| (16) v6 v7 v10 v11 v18 v19 v22 v23 v30 v31 v34 v35 v42 v43 v46 v47 | 3 6 9 11 11 6 1 | 7 | 92 |
| (16) v1 v4 v9 v12 v13 v16 v21 v24 v25 v28 v33 v36 v37 v40 v45 v48 | 3 6 9 10 9 7 3 | 7 | 95 |
| (8) v2 v3 v14 v15 v26 v27 v38 v39 | 3 6 9 9 8 7 4 1 | 8 | 98 |
| W = 4704; = 1 | |||
| (48) v1, v2, …, v47, v48 | 3 6 9 9 8 7 4 1 | 8 | 98 |
| = | ||
|---|---|---|
| 1 | 3,4 = 3 | 4 |
| 2 | 7,8= 7 | 8 |
| 3 | 10,11,12= 10 | 12 |
| 4 | 13,14,15,16= 13 | 16 |
| 5 | 17,18,19,20= 17 | 20 |
| 6 | 20,21,22,23,24= 20 | 24 |
| 7 | 23,24,25,26,27,28= 23 | 28 |
| 8 | 27,28,29,30,31,32= 27 | 32 |
| 9 | 30,31,32,33,34,35,36= 30 | 36 |
| 10 | 33,34,35,36,37,38,39,40= 33 | 40 |
| LM = 5, ŁC = 4; for LC ≥ ŁC, the two polyhexes are equivalent. | ||||
| LC | {}= min{} | KB | T | |
| 1 | 4,5,6= 4 | 528 | 6 | 600 |
| 2 | 6,7= 6 | 2800 | 7 | 2880 |
| 3 | 7,8= 7 | 7632 | 8 | 7680 |
| 4 | 9= 9 | 16,000 | 9 | 16,000 |
| 5 | 10= 10 | 29,000 | 10 | 29,000 |
| 6 | 12= 12 | 48,000 | 12 | 48,000 |
| 7 | 14= 14 | 74,200 | 14 | 74,200 |
| 8 | 16= 16 | 108,800 | 16 | 108,800 |
| 9 | 18= 18 | 153,000 | 18 | 153,000 |
| 10 | 20= 20 | 208,000 | 20 | 208,000 |
| 15 | 30= 30 | 687,000 | 30 | 687,000 |
| 20 | 40= 40 | 1,616,000 | 40 | 1,616,000 |
| 25 | 50= 50 | 3,145,000 | 50 | 3,145,000 |
| LM = 6, ŁC = 5; for LC ≥ ŁC, the two polyhexes are equivalent. | ||||
| LC | {}= min{} | KB | T | |
| 1 | 4,5,6,7= 4 | 860 | 7 | 1008 |
| 2 | 7,8= 7 | 4504 | 8 | 4704 |
| 3 | 8,9= 8 | 12,084 | 9 | 12,240 |
| 4 | 9,10= 9 | 24,880 | 10 | 24,960 |
| 5 | 11= 11 | 44,400 | 11 | 44,400 |
| 6 | 12= 12 | 72,288 | 12 | 72,288 |
| 7 | 14= 14 | 110,544 | 14 | 110,544 |
| 8 | 16= 16 | 160,896 | 16 | 160,896 |
| 9 | 18= 18 | 225,072 | 18 | 225,072 |
| 10 | 20= 20 | 304,800 | 20 | 304,800 |
| 15 | 30= 30 | 997,200 | 30 | 997,200 |
| 20 | 40= 40 | 2,337,600 | 40 | 2,337,600 |
| 25 | 50= 50 | 4,542,000 | 50 | 4,542,000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Putz, M.V.; Ori, O. Topological Symmetry Transition between Toroidal and Klein Bottle Graphenic Systems. Symmetry 2020, 12, 1233. https://doi.org/10.3390/sym12081233
Putz MV, Ori O. Topological Symmetry Transition between Toroidal and Klein Bottle Graphenic Systems. Symmetry. 2020; 12(8):1233. https://doi.org/10.3390/sym12081233
Chicago/Turabian StylePutz, Mihai V., and Ottorino Ori. 2020. "Topological Symmetry Transition between Toroidal and Klein Bottle Graphenic Systems" Symmetry 12, no. 8: 1233. https://doi.org/10.3390/sym12081233






