A Generalization of Binomial Exponential-2 Distribution: Copula, Properties and Applications

Abstract

In this paper, we propose a new three-parameter lifetime distribution for modeling symmetric real-life data sets. A simple-type Copula-based construction is presented to derive many bivariate- and multivariate-type distributions. The failure rate function of the new model can be “monotonically asymmetric increasing”, “increasing-constant”, “monotonically asymmetric decreasing” and “upside-down-constant” shaped. We investigate some of mathematical symmetric/asymmetric properties such as the ordinary moments, moment generating function, conditional moment, residual life and reversed residual functions. Bonferroni and Lorenz curves and mean deviations are discussed. The maximum likelihood method is used to estimate the model parameters. Finally, we illustrate the importance of the new model by the study of real data applications to show the flexibility and potentiality of the new model. The kernel density estimation and box plots are used for exploring the symmetry of the used data.

1. Introduction

The monotonicity asymmetric failure (hazard) rate function (HRF) of a certain lifetime probabilistic distribution has an important role in modeling real lifetime data. Distributions with the “monotonicity increasing” failure rate (MIFR) function have useful real applications in “pricing” and “supply” chain contracting problems. The MIFR property is a well-known and useful concept in “dynamic programming”, “reliability theory” and other areas of applied probability and statistics (see [1,2]). The paper [3] introduced a new two-parameter lifetime model with MIFR named the binomial-exponential-2 (BE2) model, which is constructed as a model of a random sum (RSm) of independent exponential random variables (RVs) when the sample size has a “zero truncated binomial” distribution. The BE2 distribution can be used as an alternative to the Weibull (W), gamma (Gam), exponentiated exponential (EE), and weighted exponential (WhE) distributions in real life applications.

The survival function (SF) of the binomial exponential-2 (BE2) distribution is given by

$${\overline{G}}_{BE2}\left(y\right)=\left(1+\frac{\theta \alpha y}{2-\theta }\right)e^{-\alpha y}{|}_{y>0}^{\left(0\le \theta \le 1\right)},$$

(1)

where $\alpha >0$ is a scale parameter, $G_{BE2}\left(y\right)=1-{\overline{G}}_{BE2}\left(y\right)$ is the cumulative distribution function (CDF) of the BE2 model and $\theta$ is a shape parameter. It is easy to show that the SF in (1) is increasing in $0\le \theta \le$1 where $e^{-\alpha y}\le {\overline{G}}_{BE2}\left(y\right)\le \left(\alpha y+1\right)e^{-\alpha y}$1 (see [2]). The probability density function (PDF) corresponding to (1) is

$$g_{BE2}\left(y\right)=\left[1+\frac{\theta }{2-\theta }\left(\alpha y-1\right)\right]\alpha e^{-\alpha y},$$

(2)

which can be expressed as

$$g_{BE2}\left(y\right)=\frac{\alpha }{2-\theta }\left[2\left(1-\theta \right)+\alpha y \theta \right]e^{-\alpha y}.$$

(3)

Since $\frac{{\partial }^2}{\partial y^2}$ is negative, the $log\left[g_{BE2}\left(y\right)\right]$ is “concave” for all $\alpha$ and $0\le \theta \le$ 1. As a result, $g_{BE2}\left(y\right)$ is “log-concave” and “unimodal”. Additionally, the PDF (2) can be written as

$$g_{BE2}\left(y\right)={\pi }_{\left(\theta \right)}\alpha e^{-\alpha y}+{\overline{\pi }}_{\left(\theta \right)}{\alpha }^{2}y{e}^{-\alpha y},$$

where

$$\begin{gathered} {\pi }_{\left(\theta \right)}=\frac{2}{2-\theta }\left(1-\theta \right)\mathrm{and}{\overline{\pi }}_{\left(\theta \right)}=1-{\pi }_{\left(\theta \right)}. \\ {\pi }_{\left(\theta \right)}=\frac{2}{2-\theta }\left(1-\theta \right)\mathrm{and}{\overline{\pi }}_{\left(\theta \right)}=1-{\pi }_{\left(\theta \right)}. \end{gathered}$$

The BE2 model is a mixture of the standard exponential (with parameter $\alpha$) model and standard gamma model (with shape parameter $2$ and scale parameter $\alpha$); when $\theta =0$, we get the standard exponential model, and when $\theta =1$, the BE2 model reduces to the Gam model. In the last few decades, many new G families of continuous distributions have been developed. One of the most famous ones is called the new type II half-logistic (TIIHL-G) family (see [4]). According to [4], the CDF of the TIIHL-G family of distributions is given by

$$F_{\lambda ,\underset{\_}{\Psi }}\left(y\right)=\frac{2G_{\underset{\_}{\Psi }}{\left(y\right)}^{\lambda }}{1+G_{\underset{\_}{\Psi }}{\left(y\right)}^{\lambda }},$$

(4)

where $G_{\underset{\_}{\Psi }}\left(y\right)$ is the baseline CDF depending on a parameter vector $\underset{\_}{\Psi }$ and $\lambda >0$ is an additional shape parameter. For each baseline $G_{\underset{\_}{\Psi }}\left(y\right)$, we can generate a new TIIHL model using (4). The corresponding PDF to (4) is given by

$$f_{\lambda ,\underset{\_}{\Psi }}\left(y\right)=2\lambda \frac{g_{\underset{\_}{\Psi }}\left(y\right)G_{\underset{\_}{\Psi }}{\left(y\right)}^{\lambda -1}}{{\left[1+G_{\underset{\_}{\Psi }}{\left(y\right)}^{\lambda }\right]}^2},$$

(5)

where $g_{\underset{\_}{\Psi }}\left(y\right)=d{G}_{\underset{\_}{\Psi }}\left(y\right)/dx$ is the baseline PDF. Equation (5) will be most tractable when $G_{\underset{\_}{\Psi }}\left(y\right)$ and $g_{\underset{\_}{\Psi }}\left(y\right)$ have simple expressions. The survival function, the failure (hazard) rate function and the quantile function are ${\overline{F}}_{\lambda ,\underset{\_}{\Psi }}\left(y\right)=\frac{1-G_{\underset{\_}{\Psi }}{\left(y\right)}^{\lambda }}{1+G_{\underset{\_}{\Psi }}{\left(y\right)}^{\lambda }},h_{\lambda ,\underset{\_}{\Psi }}\left(y\right)=\frac{2\lambda g_{\underset{\_}{\Psi }}\left(y\right)G_{\underset{\_}{\Psi }}{\left(y\right)}^{\lambda -1}}{1-G_{\underset{\_}{\Psi }}{\left(y\right)}^{2\lambda }},$ and $Q\left(u\right)=G^{-1}\sqrt[\lambda ]{\frac{u}{2-u}}.$ Equations (4) and (5) are used for generating the new model.

2. The New Model and Its Motivation

In this section, we introduce the three-parameter type II half-logistic binomial exponential 2 (TIIHLBE2) distribution. Substituting from (1) into (4), the CDF of the TIIHLBE2 (or expanded BE2 “EBE” for short) model can be expressed as

$$F_{\lambda ,\alpha ,\theta }\left(y\right)=\frac{2{\left[1-\left(1+\frac{\theta \alpha y}{2-\theta }\right)e^{-\alpha y}\right]}^{\lambda }}{1+{\left[1-\left(1+\frac{\theta \alpha y}{2-\theta }\right)e^{-\alpha y}\right]}^{\lambda }},$$

(6)

The corresponding PDF is given by

$$f_{\lambda ,\alpha ,\theta }\left(y\right)=\frac{2\lambda \alpha e^{-\alpha y}\left(1+\frac{\left(\alpha y-1\right)\theta }{2-\theta }\right){\left[1-\left(1+\frac{\theta \alpha y}{2-\theta }\right)e^{-\alpha y}\right]}^{\lambda -1}}{{\left\{1+{\left[1-\left(1+\frac{\theta \alpha y}{2-\theta }\right)e^{-\alpha y}\right]}^{\lambda }\right\}}^2}.$$

(7)

Here and henceforth, an RV $Y$ having PDF (7) is denoted by $Y\sim$ EBE $\left(\lambda ,\alpha ,\theta \right)$. For the EBE distribution, the HRF can be derived as

$$h_{\lambda ,\alpha ,\theta }\left(y\right)=\frac{2\lambda \alpha e^{-\alpha y}\left(1+\frac{\left(\alpha y-1\right)\theta }{2-\theta }\right)}{\left[1-\left(1+\frac{\theta \alpha y}{2-\theta }\right)e^{-\alpha y}\right]\left\{1+{\left[1-\left(1+\frac{\theta \alpha y}{2-\theta }\right)e^{-\alpha y}\right]}^{\lambda }\right\}}.$$

(8)

Figure 1 presents some plots of the PDF of the EBE model for some different values of the parameters $\lambda ,\alpha$ and $\theta$. We note that the new PDF can be “right skewed” with different shapes of “skewness” and “kurtosis”.

Figure 2 gives the plots of the HRF of the EBE distribution. We note that the new HRF can be “increasing”, “increasing-constant”, “decreasing” and “upside-down-constant” shaped. Thus, the new model may be useful in modeling different shapes of real data.

3. Copula under the EBE Model

3.1. Bivariate EBE (BivEBE) Type via Renyi’s Entropy

Following [5], the joint CDF (JCDF) of the “Renyi’s entropy Copula” can be expressed as

$C\left(\mathbf{𝓊},v\right)=y_2\mathbf{𝓊}+y_{1}v-y_1{y}_2$; then, the associated BivEBE will be $\mathbf{𝓗}\left(t_1,t_2\right)=\mathbf{𝓗}\left(F_{{\underset{\_}{V}}_1}\left(y_1\right),F_{{\underset{\_}{V}}_2}\left(y_2\right)\right)$ where ${\underset{\_}{V}}_1$ and ${\underset{\_}{V}}_2$ are the parameter vectors for $F_{{\underset{\_}{V}}_1}\left(y_1\right)$ and $F_{{\underset{\_}{V}}_2}\left(y_2\right)$, respectively.

3.2. BivEBE Type Using “Farlie-Gumbel-Morgenstern” (FGM) Copula

Consider the JCDF of the FGM family, where ${\mathbf{𝓗}}_{\Delta }\left(\mathbf{𝓊},v\right)=uv\left(1+\Delta \overline{\mathbf{𝓊}}\overline{v}\right)|\Delta \in \left[-1,1\right].$ The marginal functions are $\mathbf{𝓊}=F_1\left(y_1\right)\in \left[0,1\right]$ and $v=F_2\left(y_2\right)\in \left[0,1\right]$. The unknown parameter $\Delta$ is a dependence parameter, and for every $\mathbf{𝓊},v\in \left[0,1\right]$, ${\mathbf{𝓗}}_{\Delta }\left(\mathbf{𝓊},0\right)=C_{\Delta }\left(0,v\right)=0$, which is the “grounded minimum” property, and ${\mathbf{𝓗}}_{\Delta }\left(\mathbf{𝓊},1\right)=u$ and ${\mathbf{𝓗}}_{\Delta }\left(1,v\right)=v$, which is “grounded maximum” property. $\overline{\mathbf{𝓊}}={\overline{\mathbf{𝓊}}}_{{\underset{\_}{V}}_1}=1-F_{{\underset{\_}{V}}_1}\left(y_1\right)$ and $\overline{v}={\overline{v}}_{{\underset{\_}{V}}_2}=1-F_{{\underset{\_}{V}}_2}\left(y_2\right)$ are then set.

Then, $F\left(y_1,y_2\right)=\mathbf{𝓗}(F_{{\underset{\_}{V}}_1}\left(y_1\right),F_{{\underset{\_}{V}}_2}\left(y_2\right).$ The joint PDF can be derived from

$$h_{\Delta }\left(\mathbf{𝓊},v\right)=\Delta {\mathbf{𝓊}}^{\ast }{v}^{\ast }+1{|}_{\left({\mathbf{𝓊}}^{\ast }=1-2\mathbf{𝓊}\mathrm{and}{v}^{\ast }=1-2v\right)}$$

or from

$$f\left(y_1,y_2\right)=h\left(F_{{\underset{\_}{V}}_1}\left(y_1\right),F_{{\underset{\_}{V}}_2}\left(y_2\right)\right)f_{{\underset{\_}{V}}_1}\left(y_1\right)f_{{\underset{\_}{V}}_2}\left(y_2\right).$$

For more details, see [6,7,8,9,10,11,12].

3.3. BivEBE Type via “Modified FGM” (MFGM) Copula

The modified JCDF of the bivariate FGM copula can be expressed as

$${\mathbf{𝓗}}_{\Delta }\left(\mathbf{𝓊},w\right)=\mathbf{𝓊}v+\Delta \widetilde{O\left(\mathbf{𝓊}\right)}\widetilde{\mathsf{\phi }\left(w\right)},$$

where $\widetilde{O\left(\mathbf{𝓊}\right)}=\mathbf{𝓊}\overline{O\left(\mathbf{𝓊}\right)}$ and $\widetilde{\mathsf{\phi }\left(w\right)}=w\widetilde{\mathsf{\phi }\left(w\right)}$, where $O\left(\mathbf{𝓊}\right)$ and $\mathsf{\phi }\left(w\right)$ are two absolutely continuous functions on $\left(0,1\right)$ where $O\left(0\right)=O\left(1\right)=\mathsf{\phi }\left(0\right)=\mathsf{\phi }\left(1\right)=0.$ Let

$$\begin{gathered} \alpha =inf\left\{\frac{\partial }{\partial \mathbf{𝓊}}\widetilde{O\left(\mathbf{𝓊}\right)}:{\mathrm{C}}_1\right\}<0,\beta =sup\left\{\frac{\partial }{\partial \mathbf{𝓊}}\widetilde{O\left(\mathbf{𝓊}\right)}:{\mathrm{C}}_1\right\}<0, \\ \xi =inf\left\{\frac{\partial }{\partial w}\widetilde{\mathsf{\phi }\left(w\right)}:{\mathrm{C}}_2\right\}>0,\eta =sup\left\{\frac{\partial }{\partial w}\widetilde{\mathsf{\phi }\left(w\right)}:{\mathrm{C}}_2\right\}>0. \end{gathered}$$

Then,

$$min\left(\beta \alpha ,\eta \xi \right)\ge 1,$$

where

$$\begin{gathered} O\left(\mathbf{𝓊}\right)+\mathbf{𝓊}\frac{\partial }{\partial \mathbf{𝓊}}O\left(\mathbf{𝓊}\right)=\frac{\partial }{\partial \mathbf{𝓊}}\widetilde{O\left(\mathbf{𝓊}\right)}, \\ {\mathrm{C}}_1=\left\{\mathbf{𝓊}\in \left(0,1\right)\hspace{0.17em}\hspace{0.17em}:\hspace{0.17em}\hspace{0.17em}\frac{\partial }{\partial \mathbf{𝓊}}\widetilde{O\left(\mathbf{𝓊}\right)}\mathrm{exists}\right\}, \end{gathered}$$

and

$${\mathrm{C}}_2=\left\{w\in \left(0,1\right)\hspace{0.17em}\hspace{0.17em}:\hspace{0.17em}\hspace{0.17em}\frac{\partial }{\partial w}\widetilde{\mathsf{\phi }\left(w\right)}\mathrm{exists}\right\}.$$

3.3.1. BivEBE-FGM (Type-I) Model

The BivEBE-FGM (Type-I) model can be derived directly using

$${\mathbf{𝓗}}_{\Delta }\left(\mathbf{𝓊},w\right)=\Delta \widetilde{O\left(\mathbf{𝓊}\right)}\widetilde{\mathsf{\phi }\left(w\right)}+\mathbf{𝓊}v,$$

3.3.2. BivEBE-FGM (Type-II) Model

Consider $O\left(\mathbf{𝓊}\right)$ and $\mathsf{\phi }\left(w\right)$ that satisfy all the conditions stated earlier where

$$O\left(\mathbf{𝓊}\right){|}_{\left({\Delta }_1>0\right)}={\mathbf{𝓊}}^{{\Delta }_1}{\left(1-\mathbf{𝓊}\right)}^{1-{\Delta }_1}\mathrm{and}\mathsf{\phi }\left(w\right){|}_{\left({\Delta }_2>0\right)}=v^{{\Delta }_2}{\left(1-w\right)}^{1-{\Delta }_2}.$$

The corresponding BivEBE-FGM (Type-II) copula can be derived from

$$C_{\Delta ,{\Delta }_1,{\Delta }_2}\left(\mathbf{𝓊},w\right)=uw\left[1+\Delta {\mathbf{𝓊}}^{{\Delta }_1}{w}^{{\Delta }_2}{\left(1-\mathbf{𝓊}\right)}^{1-{\Delta }_1}{\left(1-w\right)}^{1-{\Delta }_2}\right].$$

3.3.3. BivEBE-FGM (Type-III) Model

Consider $O\left(\mathbf{𝓊}\right)$ and $\mathsf{\phi }\left(w\right)$ that satisfy all the conditions stated earlier where

$$O\left(\mathbf{𝓊}\right)=\mathbf{𝓊}\left[log\left(1+\overline{\mathbf{𝓊}}\right)\right]\mathrm{and}\mathsf{\phi }\left(w\right)=w\left[log\left(1+\overline{w}\right)\right].$$

In this case, one can also derive a closed form expression for the associated CDF of the BivEBE-FGM (Type-III).

3.3.4. BivEBE-FGM (Type-IV) Model

The JCDF of the BivEBE-FGM (Type-IV) model can be derived from

$$\mathbf{𝓗}\left(\mathbf{𝓊},w\right)=\mathbf{𝓊}{F}^{-1}\left(w\right)+w{F}^{-1}\left(\mathbf{𝓊}\right)-F^{-1}\left(\mathbf{𝓊}\right)F^{-1}\left(w\right).$$

3.4. BivEBE Type via Clayton Copula

The Clayton Copula can be considered as

$$\mathbf{𝓗}\left({\mathbf{𝓊}}_1,{\mathbf{𝓊}}_2\right)={\left({\mathbf{𝓊}}_1^{-\Delta }+{\mathbf{𝓊}}_2^{-\Delta }-1\right)}^{-\frac{1}{\Delta }}{|}_{\Delta \in \left[0,\infty \right]}.$$

Let $T\sim$ EBE $\left({\underset{\_}{V}}_1\right)$ and $W\sim$ EBE $\left({\underset{\_}{V}}_2\right)$. Set ${\mathbf{𝓊}}_1=\mathbf{𝓊}\left(t\right)=F_{{\underset{\_}{V}}_1}\left(t\right){|}_{{\underset{\_}{V}}_1>0}$ and ${\mathbf{𝓊}}_2=\mathbf{𝓊}\left(w\right)=F_{{\underset{\_}{V}}_1}\left(w\right){|}_{{\underset{\_}{V}}_2>0}.$ Then, the BivEBE-type distribution can be derived from $F\left(t,w\right)=\mathbf{𝓗}\left(F_{{\underset{\_}{V}}_1}\left(t\right),F_{{\underset{\_}{V}}_2}\left(w\right)\right).$ A straightforward $n$-dimensional extension from the above will be $\mathbf{𝓗}\left({\mathbf{𝓊}}_i\right)={\left[1-n+\sum _{i=1}^n{\mathbf{𝓊}}_i^{-\Delta }\right]}^{-\frac{1}{\Delta }}$. Many other useful details can be found in [13,14,15,16,17,18,19,20,21,22].

4. Properties

4.1. Expansions and Quantile Function (QF)

Consider the series representation

$${\left(\frac{{\omega }_1}{{\omega }_2}+1\right)}^{-{\omega }_3}={\displaystyle \sum }_{i=0}^{\infty }{\left(-\frac{{\omega }_1}{{\omega }_2}\right)}^i\left(\begin{array}{c}{\omega }_3+i-1\\ i\end{array}\right){|}_{\left(|\frac{{\omega }_1}{{\omega }_2}|\langle 1{\mathrm{and}\mathsf{\omega }}_3\rangle 0\right)};$$

(9)

expanding ${\left\{1+{\left[1-\left(1+\frac{\theta \alpha y}{2-\theta }\right)e^{-\alpha y}\right]}^{\lambda }\right\}}^{-2}$, we can write (7) as

$$f\left(y\right)=2\lambda \alpha {\displaystyle \sum }_{i=0}^{\infty }{(-1)}^i \left(i+1\right)e^{-\alpha y}\left(1+\frac{\left(\alpha y-1\right)\theta }{2-\theta }\right){\left[1-\left(1+\frac{\theta \alpha y}{2-\theta }\right)e^{-\alpha y}\right]}^{\lambda \left(i+1\right)-1}.$$

(10)

Then, consider the power series expansion

$${\left(1-\frac{{\omega }_1}{{\omega }_2}\right)}^{{\omega }_3-1}={\displaystyle \sum }_{j=0}^{\infty }{\left(-\frac{{\omega }_1}{{\omega }_2}\right)}^j\left(\begin{array}{c}{\omega }_3-1\\ j\end{array}\right){|}_{\left(|\frac{{\omega }_1}{{\omega }_2}|\langle 1\mathrm{and}{\omega }_3\rangle 0\right)};$$

(11)

using (11) in Equation (10), and after some algebra, the PDF of EBE can be written as

$$f\left(y\right)=2\lambda \alpha {\displaystyle \sum }_{i,j=0}^{\infty }{(-1)}^i\left(i+1\right)\left(\begin{array}{c}\lambda \left(i+1\right)-1\\ j\end{array}\right)\left(1+\frac{\left(\alpha y-1\right)\theta }{2-\theta }\right){\left(1+\frac{\theta \alpha y}{2-\theta }\right)}^j{e}^{-\alpha \left(1+j\right)y},$$

Then, we have

$${\left(1+\frac{\theta \alpha y}{2-\theta }\right)}^j={\displaystyle \sum }_{\kappa =0}^{\infty }\left(\begin{array}{c}j\\ \kappa \end{array}\right){\left(\frac{\theta \alpha }{2-\theta }\right)}^{\kappa }{y}^{\kappa } ;$$

therefore, the PDF of the EBE model becomes

$$f\left(y\right)={\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa } {\Pi }_{\theta ,\alpha }^{j,\kappa }\left(y\right),$$

where

$$C_{\kappa }=2\lambda {\displaystyle \sum }_{i,j=0}^{\infty }{\alpha }^{1+\kappa } {(-1)}^i\left(i+1\right)\left(\begin{array}{c}\lambda \left(i+1\right)-1\\ j\end{array}\right)\left(\begin{array}{c}j\\ \kappa \end{array}\right)\frac{{\theta }^{\kappa }}{{\left(2-\theta \right)}^{1+\kappa }},$$

and

$${\Pi }_{\theta ,\alpha }^{j,\kappa }\left(y\right)=\left[2\left(1-\theta \right)y^{\kappa }+\theta \alpha y^{\kappa +1}\right]e^{-\alpha \left(1+j\right)y}.$$

The QF of the EBE model is given by the real solution of the following equation:

$$\left(1+\frac{\theta \alpha y_q}{2-\theta }\right)e^{-\alpha y_p}+{\left(\frac{q}{2-q}\right)}^{\frac{1}{\lambda }}=1,$$

(12)

where the above equation has no closed form solution in $y_q$, so we have to use a numerical technique.

4.2. Moments

Theorem 1.

If$Y\sim$EBE$\left(\lambda ,\alpha ,\theta \right),$then the$r^{th}$moment of$Y$is given by

$${\mu }_r^{\prime }\left(y\right)={\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa }^r\Gamma \left(r+\kappa +1\right),$$

(13)

where

$$C_{\kappa }^r=C_{\kappa }\frac{2\alpha \left(1+j\right)\left(1-\theta \right)+\theta \alpha \left(r+\kappa +1\right)}{{\left[\alpha \left(1+j\right)\right]}^{r+\kappa +2}}.$$

Proof. 

Let $Y$ be an RV following the EBE distribution. The $r^{th}$ ordinary moment can be obtained using the well-known formula

$${\mu }_r^{\prime }\left(y\right)={{\displaystyle \int }}_0^{\infty }f\left(y\right)y^{r}dy={\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa }^{} {{\displaystyle \int }}_0^{\infty }{y}^r{\Pi }_{\theta ,\alpha }^{j,\kappa }\left(y\right)dy,$$

then

$${\mu }_r^{\prime }\left(y\right)={\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa }^{} {{\displaystyle \int }}_0^{\infty }\left[2\left(1-\theta \right)y^{r+\kappa }+\theta \alpha y^{r+\kappa +1}\right]e^{-\alpha \left(1+j\right)y}dy.$$

Setting $x=\alpha \left(1+j\right)y$, after some algebra, we obtain

$${\mu }_r^{\prime }\left(y\right)={\displaystyle \sum }_{\kappa =0}^j{C}_{\kappa }^r\Gamma \left(r+\kappa +1\right).$$

(14)

If we set $r=1$, we obtain the mean of the EBE distribution. Variance, skewness and kurtosis measures can be easily derived from the well-known relationships. Three-dimensional plots of the skewness and kurtosis of the EBE model are presented in Figure 3 and Figure 4. □

These plots indicate that both measures depend very much on the shape parameter $\theta .$ The first four moments and the skewness and kurtosis of the EBE distribution for different values of parameters are represented in

Table 1. Moments, skewness and kurtosis of the EBE model.

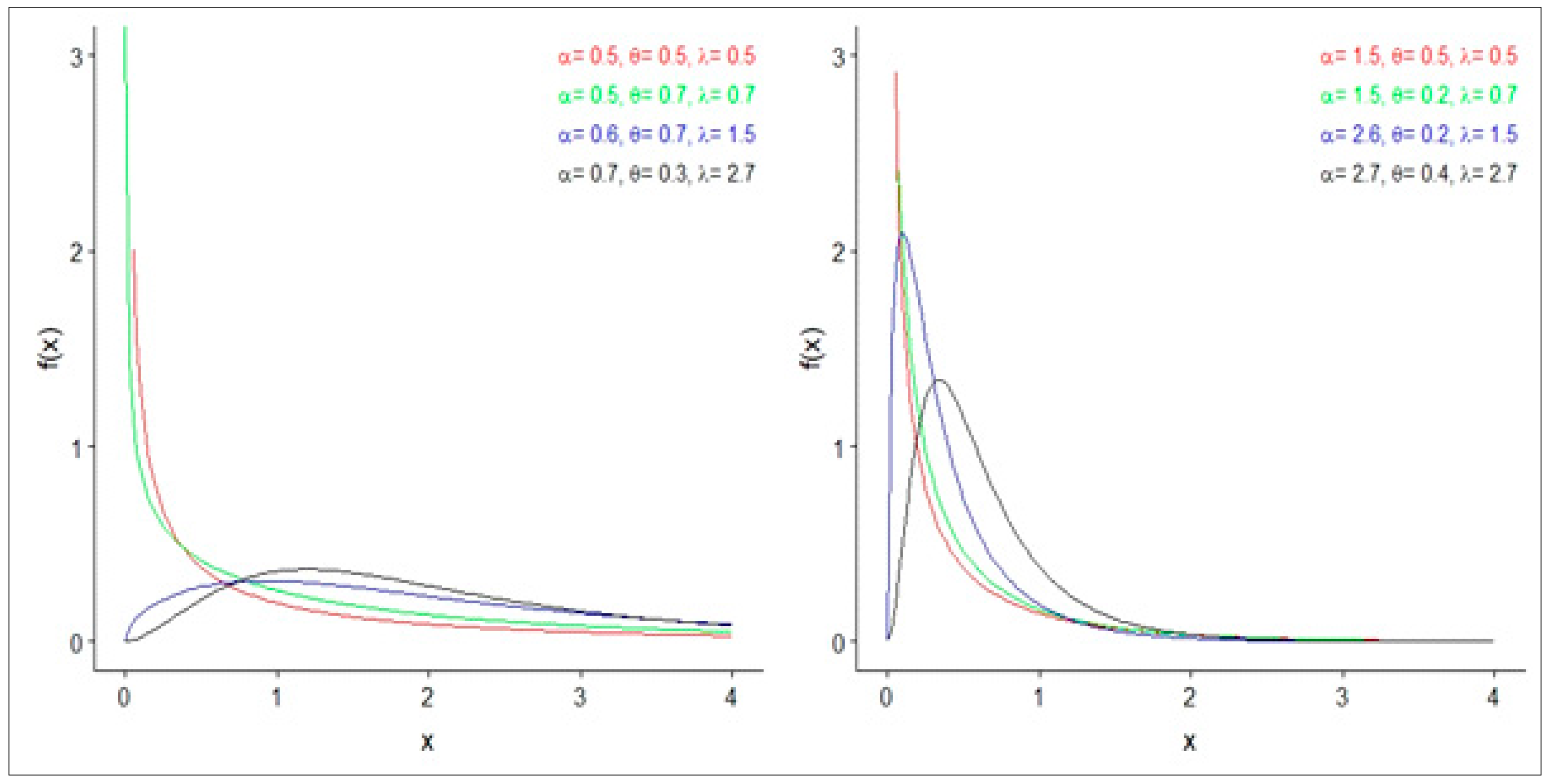
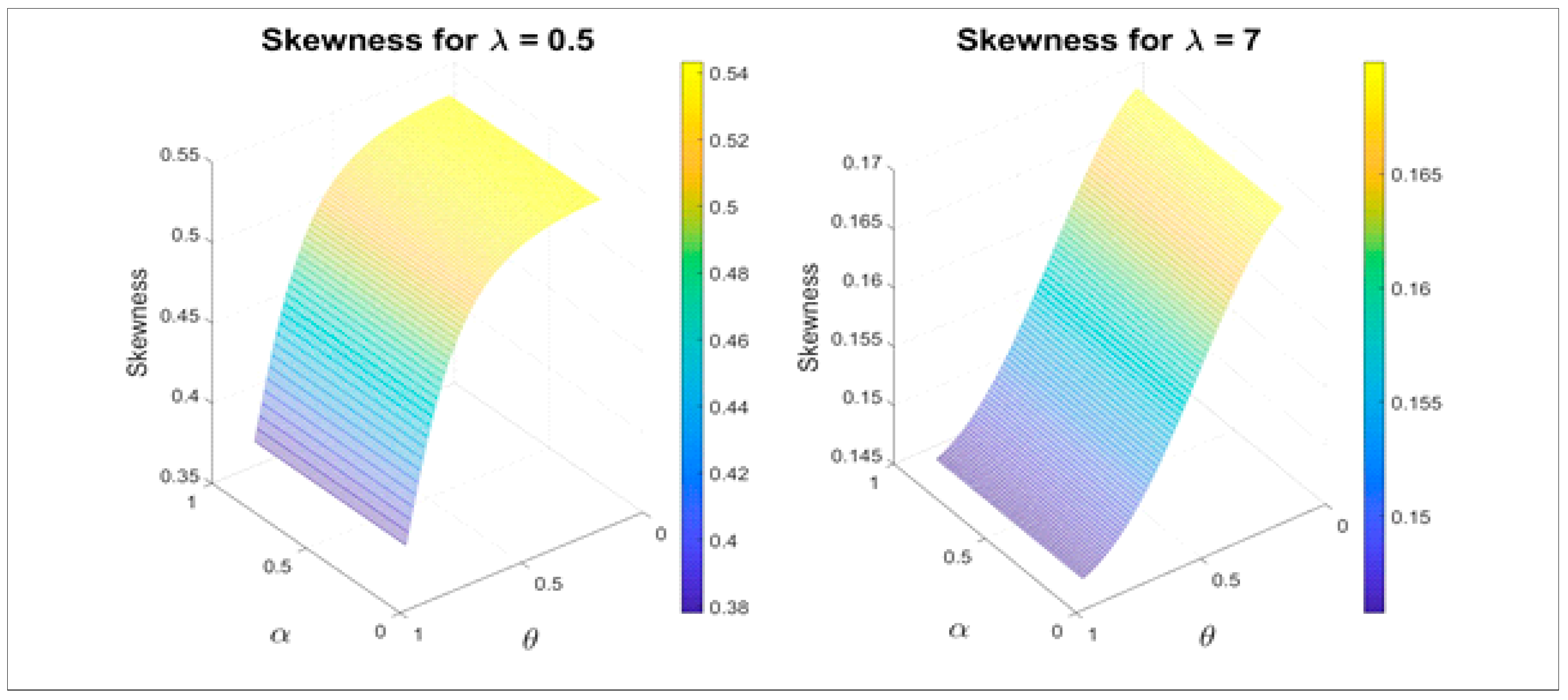
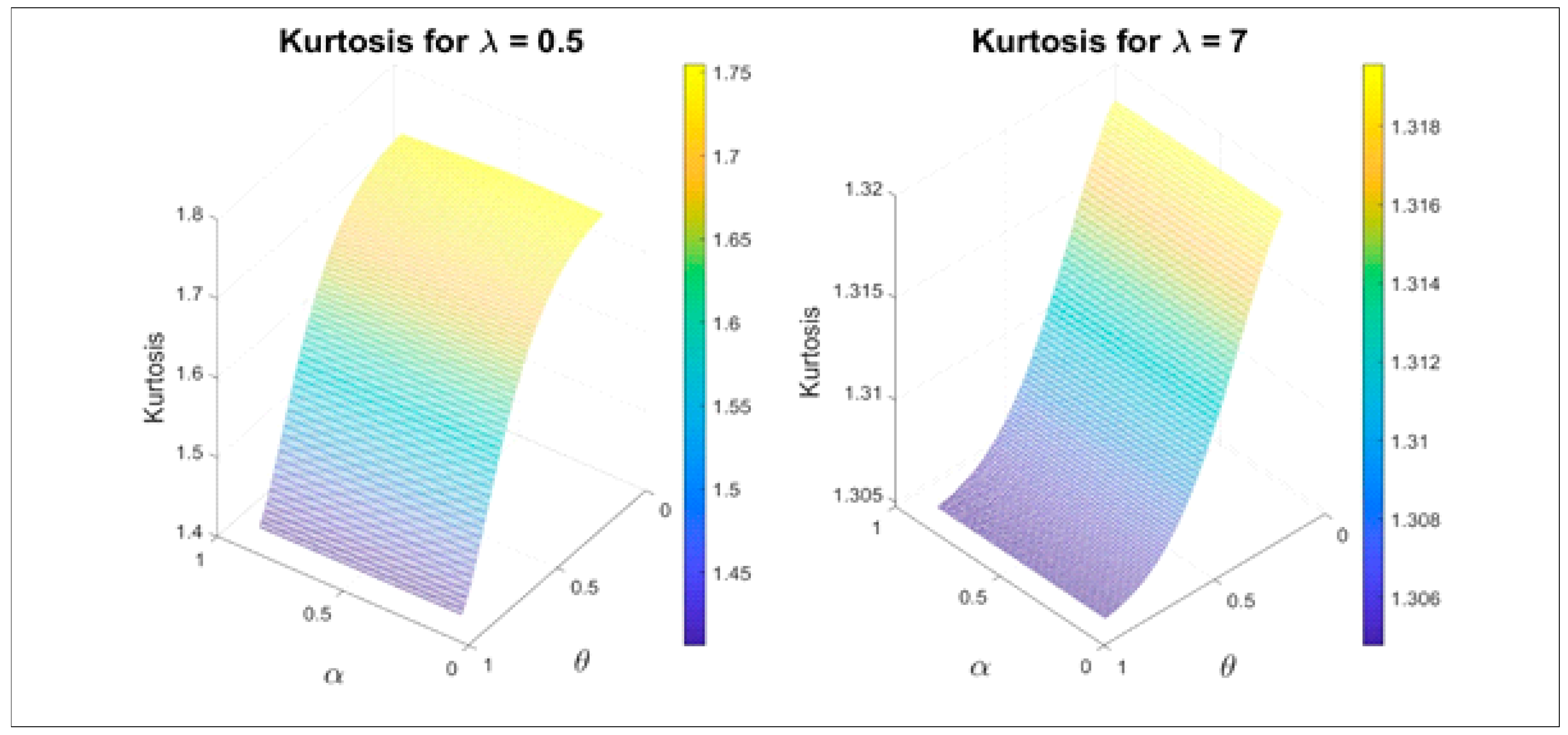
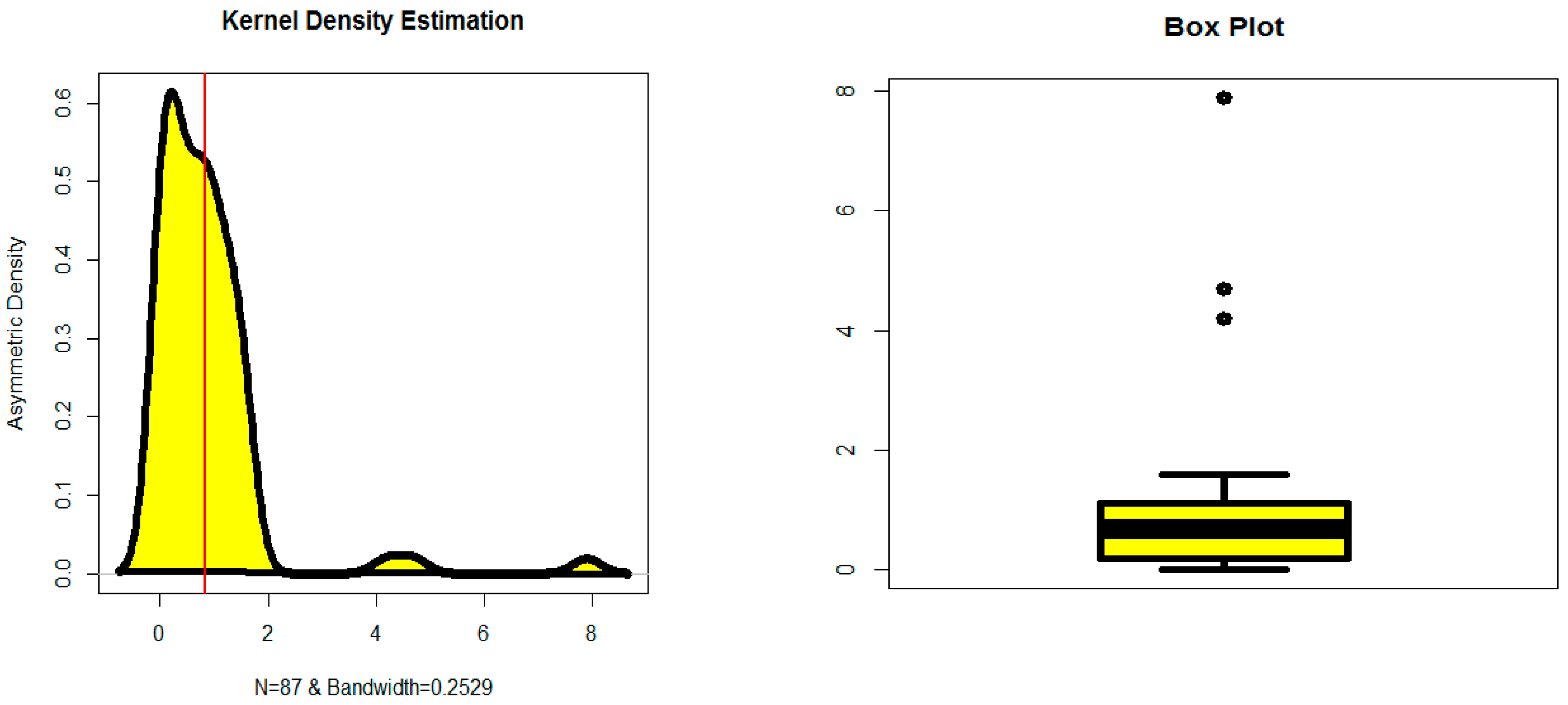
α	θ	λ	μ1′	μ2′	μ3′	μ4′	Skewness	Kurtosis
0.5	0.5	0.5	1.066	3.009	16.07	149.755	2.752	12.349
0.5	0.7	0.7	1.660	4.313	23.29	277.509	2.189	9.1470
0.6	0.7	1.5	2.414	4.008	14.47	125.278	1.669	6.8000
0.7	0.3	2.7	2.273	2.749	8.148	60.4810	1.627	6.6450
1.5	0.5	0.5	0.243	0.316	0.545	1.58900	2.753	12.231
1.5	0.2	0.7	0.381	0.294	0.458	1.26900	2.539	11.139
2.6	0.2	1.5	0.404	0.149	0.121	0.23300	1.929	8.0020
2.7	0.4	2.7	0.626	0.195	0.153	0.32500	1.571	6.3250

.

Theorem 2.

The moment generating function$M_{\mathrm{Y}}\left(\mathsf{\tau }\right)$of the EBE is given by

$$M_Y\left(\tau \right)={\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa }^{\left(r,\tau \right)}\Gamma \left(\kappa +1\right),$$

where

$$C_{\kappa }^{\left(r,\tau \right)}=C_{\kappa }\frac{2\left(1-\theta \right)\left(\alpha \left(1+j\right)-\tau \right)+\theta \alpha \left(\kappa +1\right)}{{\left[\alpha \left(1+j\right)\right]}^{\kappa +2}}.$$

Proof. 

Starting with

$$M_Y\left(\tau \right)=E\left(e^{\tau Y}\right)={{\displaystyle \int }}_0^{\infty }{e}^{\tau Y}f\left(y\right)dy,$$

then

$$M_Y\left(\tau \right)={\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa } {{\displaystyle \int }}_0^{\infty }\left[2\left(1-\theta \right)y^{\kappa +1}+\theta \alpha y^{\kappa +2}\right]e^{-\left[\alpha \left(1+j\right)-\tau \right]y}dy,$$

finally, we get

$$M_Y\left(\tau \right)={\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa }^{\left(r,\tau \right)}\Gamma \left(\kappa +1\right).$$

In the same way, the characteristic function of the EBE distribution becomes

$${\varphi }_Y\left(\tau \right)=M_Y\left(i\tau \right)$$

where $i=\sqrt{-1}$ is the unit imaginary number. □

4.3. Incomplete Moments

The $s^{th}$ lower and upper incomplete moments of $Y$ are defined by

$${\upsilon }_{s,Y}\left(\tau \right)=E\left(Y^s\hspace{0.17em}{|}_{\left(Y<\tau \right)}\right)={{\displaystyle \int }}_0^{\tau }{y}^{s}f\left(y\right)dy,$$

and

$$v_{s,Y}\left(\tau \right)=E\left(Y^s\hspace{0.17em}{|}_{\left(Y>\tau \right)}\right)={{\displaystyle \int }}_{\tau }^{\infty }{y}^{s}f\left(y\right)dy,$$

respectively, for any real $s>0.$ The $s^{th}$ lower incomplete moment of the EBE distribution is

$$v_{s,Y}\left(\tau \right)={{\displaystyle \int }}_0^{\tau }{y}^{s}f\left(y\right)dy={\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa } {{\displaystyle \int }}_0^{\tau }\left[2\left(1-\theta \right)y^{s+\kappa }+\theta \alpha y^{s+\kappa +1}\right]e^{-\alpha \left(1+j\right)y}dy,$$

then

$$v_{s,Y}\left(\tau \right)={\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa }\left[c_{\left(s,j\right)}^{\left(1\right)}\gamma \left(s+\kappa +1,\alpha \left(1+j\right)\tau \right)+c_{\left(s,j\right)}^{\left(2\right)}\gamma \left(s+\kappa +2,\alpha \left(1+j\right)\tau \right)\right],$$

(15)

where $c_{\left(\Delta ,j\right)}^{\left(1\right)}=2\left(1-\theta \right)\frac{1}{{\left[\alpha \left(1+j\right)\right]}^{\Delta +\kappa +1}},c_{\left(\Delta ,j\right)}^{\left(2\right)}=\theta \alpha \frac{1}{{\left[\alpha \left(1+j\right)\right]}^{\Delta +\kappa +2}}$ and $\gamma \left(s,\tau \right)={\int }_0^{\tau }{y}^{s-1}{e}^{-y}dy$ is the lower incomplete gamma function. Similarly, the $s_{th}$ upper incomplete moment of the EBE distribution is

$${\eta }_s\left(\tau \right)={{\displaystyle \int }}_{\tau }^{\infty }{y}^{s}f\left(y\right)dy={\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa } {{\displaystyle \int }}_{\tau }^{\infty }\left[2\left(1-\theta \right)y^{s+\kappa }+\theta \alpha y^{s+\kappa +1}\right]e^{-\alpha \left(1+j\right)y}dy,$$

then

$${\eta }_s\left(\tau \right)={\sum }_{\kappa =0}^{\infty }{C}_{\kappa }\left[c_{\left(s,j\right)}^{\left(1\right)}\zeta \left(s+\kappa +1,\alpha \left(1+j\right)\tau \right)+c_{\left(s,j\right)}^{\left(2\right)}\zeta \left(s+\kappa +2,\alpha \left(1+j\right)\tau \right)\right],$$

(16)

where

$$\zeta \left(s,\tau \right)={{\displaystyle \int }}_{\tau }^{\infty }{e}^{-y}{y}^{s-1}dy,$$

is the upper incomplete gamma function.

4.4. Mean Deviation and Bonferroni and Lorenz Curve

The mean deviations about the mean $\mu =E\left(Y\right)$ and the mean deviations about the median $M$ can be written as

$${\delta }_1\left(y\right)=2\left[\mu F\left(\mu \right)-\varpi \left(\mu \right)\right]={{\displaystyle \int }}_0^{\infty }f\left(y\right)\hspace{0.17em}\left|\hspace{0.17em}y-\mu \hspace{0.17em}\right|\hspace{0.17em}dy,$$

and

$${\delta }_2\left(y\right)=\mu -2\varpi \left(M\right)={{\displaystyle \int }}_0^{\infty }f\left(y\right)\hspace{0.17em}\left|\hspace{0.17em}y-M\hspace{0.17em}\right|\hspace{0.17em}dy,$$

respectively, where

$$\varpi \left(d\right)={{\displaystyle \int }}_0^{d}y f\left(y\right)dy={\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa }\left[c_{\left(1,j\right)}^{\left(1\right)}\gamma \left(\kappa +2,\alpha \left(1+j\right)d\right)+c_{\left(1,j\right)}^{\left(2\right)}\gamma \left(\kappa +3,\alpha \left(1+j\right)d\right)\right].$$

(17)

The Lorenz curve for a positive RV $Y$ is defined as

$$L\left(p\right)=\frac{1}{\mu }{{\displaystyle \int }}_0^{h}y\left(f\right)dy=\frac{\varpi \left(h\right)}{\mu }=\frac{1}{\mu }{\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa }\left[c_{\left(1,j\right)}^{\left(1\right)}\gamma \left(\kappa +2,\alpha \left(1+j\right)h\right)+c_{\left(1,j\right)}^{\left(2\right)}\gamma \left(\kappa +3,\alpha \left(1+j\right)h\right)\right],$$

where $h$ $=$ $G^{-1}\left(p\right)$. Additionally, the Bonferroni curve is defined by

$$B\left(p\right)=\frac{1}{\mu p}{{\displaystyle \int }}_0^{h}y\left(f\right)dy=\frac{\varpi \left(h\right)}{\mu p}=\frac{1}{\mu p}{\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa }\left[c_{\left(1,j\right)}^{\left(1\right)}\gamma \left(\kappa +2,\alpha \left(1+j\right)h\right)+c_{\left(1,j\right)}^{\left(2\right)}\gamma \left(\kappa +3,\alpha \left(1+j\right)h\right)\right],$$

4.5. Residual Life and Reversed Residual Life Functions

The $r_{\tau h}$ moment of the residual life via the general formula is given by

$$\begin{array}{c}{\mu }_{r,Y}\left(\tau \right)=E(\left(Y-\tau {)}^r\hspace{0.17em}{|}_{\left(Y>\tau \right)}\right)=\frac{1}{\overline{F}\left(\tau \right)}{{\displaystyle \int }}_{\tau }^{\infty }f\left(y\right){(y-\tau )}^{r}dy{|}_{\left(r\ge 1\right)}\\ =\frac{1}{\overline{F}\left(\tau \right)}{\displaystyle {\displaystyle \sum }_{\kappa =0}^{\infty }}{C}_{\kappa }{\displaystyle {\displaystyle \sum }_{h=0}^r}\left(\begin{array}{c}r\\ h\end{array}\right){(-1)}^{r-h}{\tau }^{r-i}{{\displaystyle \int }}_{\tau }^{\infty }\left[2\left(1-\theta \right)y^{r+\kappa }+\theta \alpha y^{r+\kappa +1}\right]e^{-\alpha \left(1+j\right)y}dy,\end{array}$$

then

$${\mu }_{r,Y}\left(\tau \right)=\frac{1}{\overline{F}\left(\tau \right)}{\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa }{\displaystyle \sum }_{h=0}^r{(-1)}^{r-h}\left(\begin{array}{c}r\\ h\end{array}\right){\tau }^{r-i}\left[c_{\left(r,j\right)}^{\left(1\right)}\zeta \left(r+\kappa +1,\alpha \left(1+j\right)\tau \right)+c_{\left(r,j\right)}^{\left(2\right)}\zeta \left(r+\kappa +2,\alpha \left(1+j\right)\tau \right)\right].$$

The mean residual life (MRL) of the EBE distribution is given by

$${\mu }_{1,Y}\left(\tau \right)=\frac{1}{\overline{F}\left(\tau \right)}{\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa }\left[c_{\left(1,j\right)}^{\left(1\right)}\zeta \left(\kappa +2,\alpha \left(1+j\right)\tau \right)+c_{\left(1,j\right)}^{\left(2\right)}\zeta \left(\kappa +3,\alpha \left(1+j\right)\tau \right)\right]-\tau$$

The $rth$ order moment of the reversed residual life can be obtained by the well-known formula

$$m_{r,Y}\left(\tau \right)=E(\left(\tau -y{)}^r\hspace{0.17em}{|}_{\left(Y\le \tau \right)}\right)=\frac{1}{F\left(\tau \right)}{{\displaystyle \int }}_0^{\tau }f\left(y\right){(\tau -y)}^{r}dy{|}_{\left(r\ge 1\right)}.$$

Applying the binomial expansion of ${(\tau -y)}^r$ and substituting $f_{\lambda ,\alpha ,\theta }\left(y\right)$ given by (7) into the above formula gives

$$m_{r,Y}\left(\tau \right)=\frac{1}{F\left(\tau \right)}{\displaystyle \sum }_{h=0}^r{\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa }\left(\begin{array}{c}r\\ h\end{array}\right){(-1)}^{r-h}{\tau }^{r-i}{{\displaystyle \int }}_0^{\tau }\left[2\left(1-\theta \right)y^{r+\kappa }+\theta \alpha y^{r+\kappa +1}\right]e^{-\alpha \left(1+j\right)y}dy,$$

then

$$\begin{array}{c}{m}_{r,Y}\left(\tau \right)=\frac{1}{F\left(\tau \right)}{\displaystyle {\displaystyle \sum }_{\kappa =0}^{\infty }}{C}_{\kappa }{\displaystyle {\displaystyle \sum }_{h=0}^r}\left(\begin{array}{c}r\\ h\end{array}\right){(-1)}^{r-h}{\tau }^{r-i}\\ \times \left[c_{\left(r,j\right)}^{\left(1\right)}\gamma \left(r+\kappa +1,\alpha \left(1+j\right)\tau \right)+c_{\left(r,j\right)}^{\left(2\right)}\gamma \left(r+\kappa +2,\alpha \left(1+j\right)\tau \right)\right],\end{array}$$

where

$$\gamma \left(s,p\right)={{\displaystyle \int }}_0^p{w}^{s-1}{e}^{-w}dw,$$

is the lower incomplete gamma function. The mean waiting time of the EBE distribution is given by

$$m_1\left(\tau \right)=\tau -\frac{1}{F\left(\tau \right)}{\displaystyle \sum }_{\kappa =0}^{\infty }{C}_{\kappa }\left[c_{\left(1,j\right)}^{\left(1\right)}\gamma \left(\kappa +2,\alpha \left(1+j\right)\tau \right)+c_{\left(1,j\right)}^{\left(1\right)}\gamma \left(\kappa +3,\alpha \left(1+j\right)\tau \right)\right].$$

Using $m_{1,Y}\left(\tau \right)$ and $m_{2,Y}\left(\tau \right)$, one can obtain the “variance” and the “coefficient of variation” of the reversed residual life of the EBE distribution.

5. Estimation and Inference

Let $Y_1,Y_2,\dots ,Y_n$ be a random sample of size $n$ from EBE $\left(\underset{\_}{\psi }\right)$. The log likelihood function for the vector of parameters $\lambda ,\alpha$ and $\theta$ can be written as

$$\begin{array}{c}logL=nlog(2\lambda )+nlog\alpha -nlog(2-2\theta )-\alpha {\displaystyle {\displaystyle \sum }_{i=1}^n}{y}_i\\ +\left(\lambda -1\right){\displaystyle \sum }_{i=1}^{n}log\left(1-m_i{s}_i\right)-2{\displaystyle \sum }_{i=1}^{n}log\left[1+{\left(1-m_i{s}_i\right)}^{\lambda }\right],\end{array}$$

(18)

where $m_i=1+\frac{\theta \alpha y_i}{2-\theta }$ and $s_i=e^{-\alpha y_i}.$ The associated score function is given by

$$U_n\left(\underset{\_}{\psi }\right)={\left[\frac{\partial logL}{\partial \lambda },\frac{\partial logL}{\partial \alpha },\frac{\partial logL}{\partial \theta }\right]}^T.$$

The $logL$ in (18) can be maximized by solving the nonlinear likelihood equations obtained by differentiating (18). The components of the score vector are given by

$$U_{\lambda }=\frac{\partial log L}{\partial \lambda }=\frac{n}{\lambda }+{\displaystyle \sum }_{i=1}^{n}log\left(1-m_i{s}_i\right)-2{\displaystyle \sum }_{i=1}^n\frac{{\left(1-m_i{s}_i\right)}^{\lambda }log\left(1-m_i{s}_i\right)}{1+{\left(1-m_i{s}_i\right)}^{\lambda }},$$

$$\begin{array}{c}{U}_{\alpha }=\frac{\partial logL}{\partial \alpha }=\frac{n}{\alpha }-{\displaystyle \sum _{i=1}^n}{y}_i+\left(\lambda -1\right){\displaystyle \sum _{i=1}^n}\frac{s_i\left[\alpha m_i+\frac{\theta y_i}{2-\theta }\right]}{1-m_i{s}_i}\\ -2\lambda {\displaystyle \sum _{i=1}^n}\frac{s_i{\left[1-m_i{s}_i\right]}^{\lambda -1}\left(\alpha m_i+\frac{\theta y_i}{2-\theta }\right)}{1+{\left(1-m_i{s}_i\right)}^{\lambda }}\end{array}$$

and

$$\begin{array}{c}{U}_{\theta }=\frac{\partial logL}{\partial \theta }=\frac{n}{1-\theta }-2\left(\lambda -1\right){\displaystyle \sum _{i=1}^n}\frac{\frac{\alpha }{{\left(2-\theta \right)}^2}y{s}_i}{1-m_i{s}_i}+\left(\lambda -1\right){\displaystyle \sum _{i=1}^n}\frac{\alpha log(y_i)y_i^{-\beta }{e}^{-\alpha y_i^{-\beta }}}{1-e^{-\alpha y_i^{-\beta }}}\\ -4\lambda {\displaystyle \sum _{i=1}^n}\frac{\frac{\alpha y{s}_i}{{\left(2-\theta \right)}^2}{\left(1-m_i{s}_i\right)}^{\lambda -1}}{1+{\left(1-m_i{s}_i\right)}^{\lambda }}\end{array}$$

6. Simulation

The “inverse transform algorithm” is used to generate random data from the EBE distribution. We generated samples of sizes $n=50,100,200,500$ and $1000$, and the simulations were repeated $N=1000$ times from the EBE model for some parameter values.

Table 2. Mean square errors (MSEs) for n = 50, 100, 200, 500 and 1000.

n		λ	α	θ	MSEs
50		0.5	0.5	0.5	0.11892, 0.23647, 0.06169
100					0.08304, 0.17158, 0.04192
200					0.05794, 0.12764, 0.02949
500					0.03636, 0.08476, 0.01866
1000					0.02595, 0.06105, 0.01325
50		0.5	0.7	0.7	0.08813, 0.17030, 0.08578
100					0.06136, 0.11879, 0.05894
200					0.04320, 0.08131, 0.04139
500					0.02764, 0.04874, 0.02616
1000					0.01964, 0.03346, 0.01856
50		0.6	0.7	1.5	0.06866, 0.12976, 0.18044
100					0.04885, 0.08743, 0.12657
200					0.03427, 0.06270, 0.08909
500					0.02180, 0.03709, 0.05538
1000					0.01550, 0.02515, 0.03903
50		0.7	0.3	2.7	0.07211, 0.13178, 0.29484
100					0.05105, 0.09550, 0.20625
200					0.03537, 0.07094, 0.14854
500					0.02227, 0.04645, 0.09524
1000					0.01545, 0.03457, 0.06935
50		0.5	0.5	0.5	0.11892, 0.23647, 0.06169
100					0.08304, 0.17158, 0.04192
200					0.05794, 0.12764, 0.02949
500					0.03636, 0.08476, 0.01866
1000					0.02595, 0.06105, 0.01325

and

Table 3. Biases for n = 50, 100, 200, 500 and 1000.

n		λ	α	θ	MSEs
50		0.5	0.5	0.5	0.18356, 0.31326, 0.06034
100					0.14037, 0.29166, 0.02491
200					0.10718, 0.27047, 0.00952
500					0.07427, 0.22547, 0.00392
1000					0.05854, 0.18297, 0.00431
50		0.5	0.7	0.7	0.13103, 0.32039, 0.16804
100					0.09571, 0.29243, 0.12804
200					0.07617, 0.25160, 0.11495
500					0.05278, 0.17909, 0.10177
1000					0.03559, 0.11151, 0.09647
50		0.6	0.7	1.5	0.11728, 0.32816, 1.12796
100					0.09252, 0.29394, 1.03834
200					0.07715, 0.27919, 0.98811
500					0.05480, 0.21775, 0.91763
1000					0.03922, 0.17326, 0.88793
50		0.7	0.3	2.7	0.16086, 0.36788, 2.90744
100					0.13715, 0.35482, 2.70484
200					0.10661,0.32348, 2.66995
500					0.08491, 0.27404, 2.64048
1000					0.07009, 0.22686, 2.72810
50		0.5	0.5	0.5	0.18356, 0.31326, 0.06034
100					0.14037, 0.29166, 0.02491
200					0.10718, 0.27047, 0.00952
500					0.07427, 0.22547, 0.00392
1000					0.05854, 0.18297, 0.00431

give the mean square errors (MSEs) and the biases, respectively. The average values of estimates (AVs), estimated average length (EAL) and the coverage probability (CP) are listed in

Table 4. Average values (AVs) for n = 50, 100, 200, 500 and 1000.

n		λ	α	θ	MSEs
50		0.5	0.5	0.5	0.55465, 0.50616, 0.52281
100					0.53818, 0.51109, 0.50207
200					0.52237, 0.48520, 0.49930
500					0.50325, 0.47041, 0.49911
1000					0.49813, 0.46471, 0.50127
50		0.5	0.7	0.7	0.50550, 0.58874, 0.72531
100					0.49190, 0.60765, 0.70470
200					0.48878, 0.63157, 0.69991
500					0.49378, 0.66331, 0.69945
1000					0.49624, 0.67996, 0.70161
50		0.6	0.7	1.5	0.57701, 0.58491, 1.52331
100					0.58530, 0.61671, 1.51090
200					0.57826, 0.61435, 1.50499
500					0.58310, 0.65758, 1.47994
1000					0.58988, 0.68285, 1.47548
50		0.7	0.3	2.7	0.74776, 0.45747, 2.49293
100					0.74369, 0.44427, 2.46686
200					0.72548, 0.39578, 2.51294
500					0.71662, 0.36901, 2.54710
1000					0.70309, 0.31662, 2.62308
50		0.5	0.5	0.5	0.55465, 0.50616, 0.52281
100					0.53818, 0.51109, 0.50207
200					0.52237, 0.48520, 0.49930
500					0.50325, 0.47041, 0.49911
1000					0.49813, 0.46471, 0.50127

,

Table 5. Estimated average lengths (EALs) for n = 50, 100, 200, 500 and 1000.

n		λ	α	θ	MSEs
50		0.5	0.5	0.5	0.46616, 0.92696, 0.24180
100					0.32550, 0.67258, 0.16431
200					0.22713, 0.50034, 0.11560
500					0.14251, 0.33226, 0.07314
1000					0.10172, 0.23930, 0.05195
50		0.5	0.7	0.7	0.34545, 0.66757, 0.33625
100					0.24054, 0.46565, 0.23104
200					0.16935, 0.31873, 0.16226
500					0.10834, 0.19105, 0.10255
1000					0.07700, 0.13116, 0.07274
50		0.6	0.7	1.5	0.26914, 0.50864, 0.70733
100					0.19150, 0.34271, 0.49614
200					0.13434, 0.24579, 0.34924
500					0.08545, 0.14539, 0.21710
1000					0.06077, 0.09860, 0.15300
50		0.7	0.3	2.7	0.28268, 0.51657, 1.15574
100					0.20011, 0.37434, 0.80847
200					0.13865, 0.27809, 0.58226
500					0.08730, 0.18209, 0.37332
1000					0.06055, 0.13552, 0.27184
50		0.5	0.5	0.5	0.46616, 0.92696, 0.24180
100					0.32550, 0.67258, 0.16431
200					0.22713, 0.50034, 0.11560
500					0.14251, 0.33226, 0.07314
1000					0.10172, 0.23930, 0.05195

and

Table 6. Coverage probabilities (CPs) for n = 50, 100, 200, 500 and 1000.

n		λ	α	θ	MSEs
50		0.5	0.5	0.5	0.82686, 0.71564, 0.79176
100					0.76642, 0.65414, 0.75986
200					0.69834, 0.57143, 0.79418
500					0.66517, 0.51762, 0.82334
1000					0.57302, 0.51648, 0.81022
50		0.5	0.7	0.7	0.81610, 0.73529, 0.76823
100					0.78664, 0.58513, 0.72796
200					0.73695, 0.52505, 0.62213
500					0.72222, 0.47172, 0.60909
1000					0.74675, 0.49449, 0.61361
50		0.6	0.7	1.5	0.73690, 0.54738, 0.00000
100					0.70523, 0.40712, 0.00000
200					0.65622, 0.34796, 0.00000
500					00.6434, 0.28687, 0.00000
1000					0.65265, 0.25726, 0.00000
50		0.7	0.3	2.7	0.63454, 0.50188, 0.00000
100					0.51110, 0.28606, 0.00000
200					0.42228, 0.23378, 0.00000
500					0.31797, 0.22104, 0.00000
1000					0.29115, 0.20381, 0.00000
50		0.5	0.5	0.5	0.82686, 0.71564, 0.79176
100					0.76642, 0.65414, 0.75986
200					0.69834, 0.57143, 0.79418
500					0.66517, 0.51762, 0.82334
1000					0.57302, 0.51648, 0.81022

, respectively. From Table 2, we note that the AVs of estimates approach the initial values as $n\to \infty$, the MSEs for each parameter decrease to zero as $n\to \infty$, and the coverage lengths for each parameter decrease to zero as $n\to \infty .$ From Table 3, we note that the biases for each parameter are generally positive and decrease to zero as $n\to \infty$, and the coverage probabilities for each parameter approach the nominal level as $n\to \infty .$

7. Modeling Stress-Rupture Life of Kevlar 49/Epoxy Strands Data

In this section, we illustrate the performance of the EBE distribution as compared to some alternative distributions using a real data application. The goodness-of-fit (GOF) statistics for this distribution are compared with other competitive distributions, and the maximum likelihood estimations (MLEs) of the distribution parameters are determined numerically. We compare the fits of the EBE distribution with the Burr type X (Burr X) distribution, Burr type XII (Burr XII) distribution, beta log logistic Weibull distribution (BLLW), beta Weibull log logistic (BWLL) and beta log logistic, beta linear failure rate geometric (BLFRG), exponentiated linear failure rate geometric (ELFRG), beta Rayleigh (BR), and beta Weibull geometric distributions (BWG) (see [23]). In order to compare the distributions, we consider the measures of GOF including the Akaike Information Criterion (C$\left[1\right]$), Bayesian Information Criterion (C$\left[2\right]$), Consistent Akaike Information Criterion (C$\left[4\right]$) and Hannan–Quinn Information Criterion (C$\left[3\right]$) statistics.

The following real data set represents the stress-rupture life of Kevlar 49/epoxy strands that are subjected to constant sustained pressure at the 90% stress level until all have failed that were provided by [24], given as 0.01, 0.08, 0.09, 0.09, 0.10, 0.02, 0.02, 0.03, 0.03, 0.04, 0.05, 0.43, 0.52, 0.54, 0.56, 0.60, 0.60, 1.00, 0.06, 1.34, 0.10, 1.45, 1.50, 1.51, 0.63, 0.72,0.99, 1.52, 1.53, 1.54, 1.54, 1.55, 1.58, 4.20, 4.69, 7.89, 0.07, 0.07, 0.36, 0.38, 0.40, 0.65, 0.67, 0.68, 0.79, 0.80, 0.80, 0.83, 0.72, 0.42, 0.12, 0.13, 0.18, 0.19, 0.20, 0.23, 0.24, 1.01, 1.02, 1.03, 0.72, 0.73, 0.79, 0.85, 0.90, 0.92, 0.95, 1.05, 0.11, 0.24, 0.29, 0.34, 0.35, 1.10, 1.10, 1.11, 1.15, 1.18, 1.20, 1.29, 1.31, 0.11, 0.01, 0.02, 1.40, 1.43 and 1.33.

Table 7. The MLE for all the models corresponds to the failure times data set.

Model	Estimates
Burr X	a
	0.462891
Burr XII	a	b
	1.14571	1.94994
ELLG	a	b
	1.211659	0.570392
BLLG	a	b	c
	0.581650	1.091929	1.295956
EBE	α	θ	λ
	0.803609	0.001	0.999053
BLLGW	a	b	c	α	β
	6.468097	5.07658	0.22372	0.24463	0.93981
BWLLG	a	b	c	α	β
	0.70773	0.15311	1.45779	5.74192	0.72356

gives the MLE for all the models corresponds to the failure times data set.

Table 8. Statistics for failure times of Kevlar data set.

Model	−2 logL	$\mathbf{C}\left[1\right]$	$\mathbf{C}\left[2\right]$	$\mathbf{C}\left[3\right]$	$\mathbf{C}\left[4\right]$
EBE	143.3996	149.4100	152.3784	152.3784	149.6087
Burr XII	145.4801	149.4801	154.4119	152.4660	149.6229
BLLGW	204.0771	214.0771	227.1527	219.3705	214.7087
BWLLG	204.8205	214.8205	227.8961	220.1139	215.4521
Burr X	285.8730	287.8730	290.3389	288.8659	287.9200
ELLG	587.6830	591.6830	596.9133	593.8004	591.8055
BLLG	462.1078	468.1078	175.9531	471.2838	468.3552

shows the statistics for the failure times of the Kevlar data set. Figure 5 gives the kernel density estimation and box plot for exploring the symmetry of the stress-rupture life data. Figure 6 provides the fitted PDF in the left panel and fitted CDF in the right panel.

Based on Table 8, it is clear that the EBE distribution provides the best fit to these data, with −2logL = 143.3996, C$\left[1\right]$ = 149.41, C$\left[4\right]$ = 149.6887, C$\left[2\right]$ = 152.3784 and C$\left[3\right]$ = 152.3784. Thus, it is concluded that this model can be a better model than other competitive lifetime models for explaining the data set. Based on Figure 6, we note that the EBE distribution gives adequate fits. Many symmetric and near symmetric real-life data sets can be modeled using the new EBE model and found in [25,26,27,28,29,30,31,32,33,34,35,36]. For other right heavy tailed real data sets see [37,38,39,40,41,42,43,44,45]. As a future work we will consider “bivariate” and “multivariate” extensions of the EBE distribution. In particular with the “copula-based construction” method, “trivariate reduction” etc.

8. Conclusions

A new three-parameter lifetime distribution is proposed and studied. A simple-type Copula-based construction is presented to derive many bivariate- and multivariate-type distributions. We investigated some of mathematical properties such as the ordinary moments, moment generating function and conditional moment. Bonferroni and Lorenz curves and mean deviations are discussed. Residual life and reversed residual functions are also obtained. Some bivariate- and multivariate-type extensions are proposed. The maximum likelihood method is used to estimate the model parameters. Finally, we illustrate the importance of the new model by studying real data applications to show the flexibility and potentiality of the new model.