Large Deflection Analysis of Axially Symmetric Deformation of Prestressed Circular Membranes under Uniform Lateral Loads
Abstract
:1. Introduction
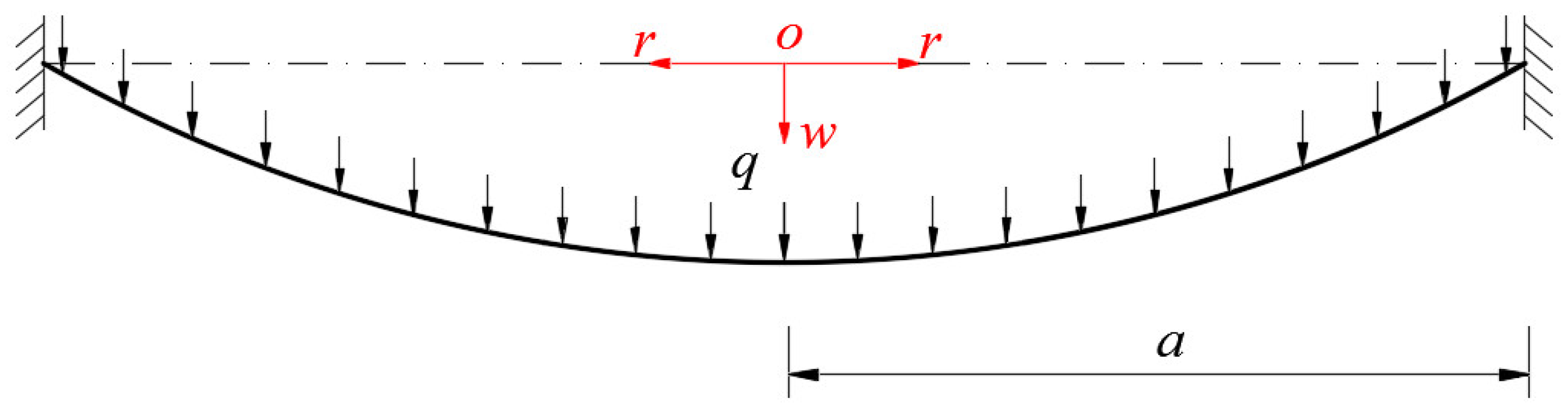
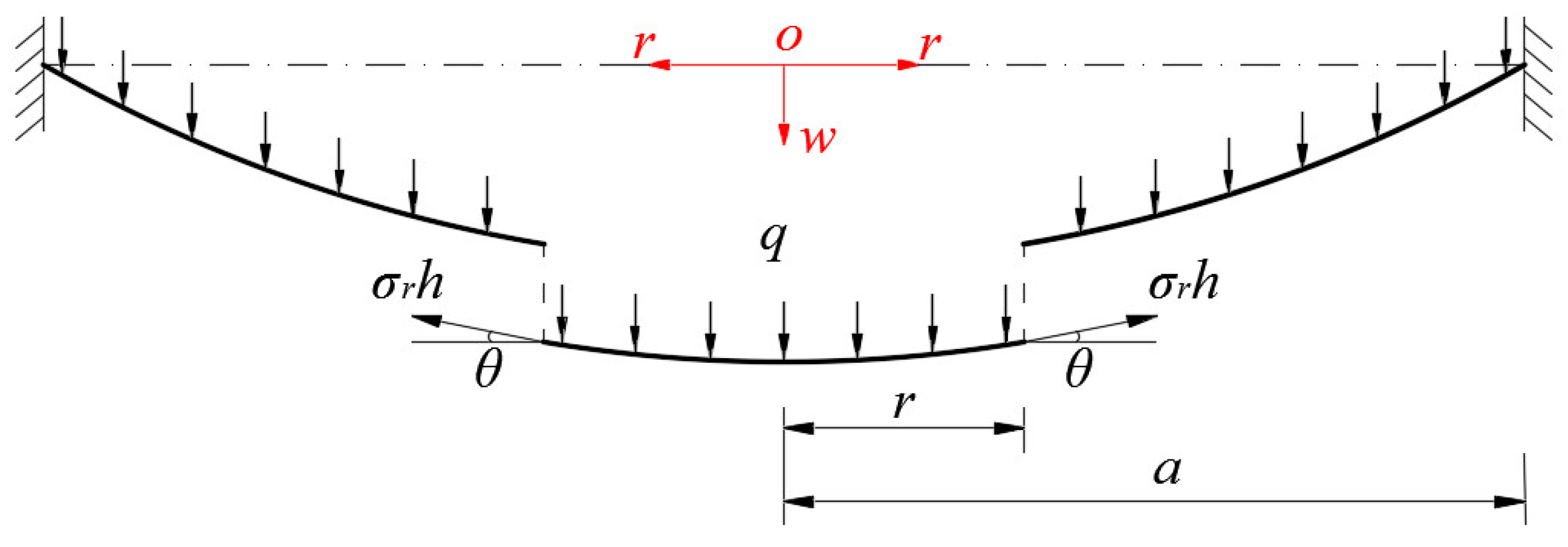
2. Membrane Equations and Closed-Form Solution
2.1. Reformulation of the Generalized Föppl–Hencky Membrane Problem
2.2. Power Series Solution
3. Results and Discussions
3.1. Regression of the Solution Presented in Second Section
3.2. Comparison with Existing Solutions
3.3. Convergence of the Power Series Solution Obtained in Second Section
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Radius of the circular membrane | |
| Thickness of the circular membrane | |
| Young’s modulus of elasticity | |
| Poisson’s ratio | |
| Uniformly distributed transverse loads | |
| Radial coordinate | |
| Circumferential coordinate | |
| Transverse coordinate and transverse displacement of the deflected membrane | |
| Radial displacement of the deflected membrane | |
| Radial plane displacement | |
| Radial stress | |
| Circumferential stress | |
| Radial strain | |
| Circumferential strain | |
| Initial stress | |
| Initial strain | |
| Slope angle of the deflected membrane | |
| Pi (ratio of circumference to diameter) | |
| Dimensionless loads | |
| Dimensionless transverse displacement | |
| Dimensionless radial stress | |
| Dimensionless circumferential stress | |
| Dimensionless initial stress | |
| Dimensionless radial coordinate | |
| Coefficients of the power-series for | |
| Coefficients of the power-series for |
Appendix A
Appendix B
References
- Le, N.T.; Wang, J.-W.; Wang, C.-C.; Nguyen, T.N. Automatic defect inspection for coated eyeglass based on symmetrized energy analysis of color channels. Symmetry 2019, 11, 1518. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Wang, R.; Tian, H.; Wang, Y.; Qi, D. Research on the gradual process of the metallization structures and mechanical properties of wood veneer. Symmetry 2018, 10, 550. [Google Scholar] [CrossRef] [Green Version]
- Rehman, A.; Salleh, Z.; Gul, T.; Zaheer, Z. The impact of viscous dissipation on the thin film unsteady flow of GO-EG/GO-W nanofluids. Mathematics 2019, 7, 653. [Google Scholar] [CrossRef] [Green Version]
- Barba, P.D.; Fattorusso, L.; Versaci, M. A 2D non-linear second-order differential model for electrostatic circular membrane MEMS devices: A result of existence and uniqueness. Mathematics 2019, 7, 1193. [Google Scholar] [CrossRef] [Green Version]
- Hencky, H. On the stress state in circular plates with vanishing bending stiffness. Z. Für Math. Und Phys. 1915, 63, 311–317. (In German) [Google Scholar]
- Fernando, M.; Kinloch, A.J. Use of the inverted-blister test to study the adhesion of photopolymers. Int. J. Adhes. Adhes. 1990, 10, 69–76. [Google Scholar] [CrossRef]
- Jensen, H.M.; Thouless, M.D. Effects of residual-stresses in the blister test. Int. J. Solids Struct. 1993, 30, 779–795. [Google Scholar] [CrossRef]
- Lai, Y.H.; Dillard, D.A. A study of the fracture efficiency parameter of blister tests for films and coatings. J. Adhes. Sci. Technol. 1994, 8, 663–678. [Google Scholar] [CrossRef]
- Wan, K.T.; Guo, S.; Dillard, D.A. A theoretical and numerical study of a thin clamped circular film under an external load in the presence of a tensile residual stress. Thin Solid Film. 2003, 425, 150–162. [Google Scholar] [CrossRef]
- Sun, Z.; Wan, K.T.; Dillard, D.A. A theoretical and numerical study of thin film delamination using the pull-off test. Int. J. Solids Struct. 2004, 41, 717–730. [Google Scholar] [CrossRef]
- Guo, S.; Wan, K.T.; Dillard, D.A. A bending-to-stretching analysis of the blister test in the presence of tensile residual stress. Int. J. Solids Struct. 2005, 42, 2771–2784. [Google Scholar] [CrossRef]
- Fichter, W.B. Some solutions for the large deflections of uniformly loaded circular membranes. NASA Technical Paper No. 3658 1997. [Google Scholar]
- Jenkins, C.H.; Faisal, S.M. Thermal load effects on precision membranes. J. Spacecr. Rocket. 2001, 38, 207–211. [Google Scholar] [CrossRef]
- Williams, J.G. Energy release rates for the peeling of flexible membranes and the analysis of blister tests. Int. J. Fract. 1997, 87, 265–288. [Google Scholar] [CrossRef]
- Noyan, I.C.; Cohen, J.B. Residual Stress Measurement by Diffraction and Interpretation; Springer: New York, NY, USA, 1987. [Google Scholar]
- Malhotra, S.G.; Rek, Z.U.; Yalisove, S.M.; Bilello, J.C. Strain gradients and normal stresses in textured Mo thin films. J. Vac. Sci. Technol. A Vac. Surf. Film. 1997, 15, 345–352. [Google Scholar] [CrossRef]
- Tao, J.; Lee, L.H.; Bilello, J.C. Non-destructive evaluation of residual stresses in thin films via x-ray diffraction topography methods. J. Electron. Mater. 1991, 20, 819–825. [Google Scholar] [CrossRef]
- Geisz, J.F.; Kuech, T.F.; Lagally, M.G.; Cardone, F.; Potemski, R.M. Film stress of sputtered W/C multilayers and strain relaxation upon annealing. J. Appl. Phys. 1994, 75, 1530–1533. [Google Scholar] [CrossRef]
- Maden, M.A.; Jagota, A.; Mazur, S.; Farris, R.J. Vibrational technique for stress measurement in films: I, Ideal membrane behavior. J. Am. Ceram. Soc. 1994, 77, 625–635. [Google Scholar] [CrossRef]
- Tong, Q.K.; Maden, M.A.; Jagota, A.; Farris, R.J. Vibrational technique for stress measurement in films: II, Extensions and complicating effects. J. Am. Ceram. Soc. 1994, 77, 636–648. [Google Scholar] [CrossRef]
- Dannenberg, H. Measurement of adhesion by a blister method. J. Appl. Polym. Sci. 1961, 5, 125–134. [Google Scholar] [CrossRef]
- Williams, M.L. Relation of continuum mechanics to adhesive fracture. J. Adhes. 1972, 4, 307–332. [Google Scholar] [CrossRef]
- Beams, J.W. Mechnical properties of thin films of gold and silver. In Structure and Properties of Thin Films; proceedings; Neugebauer, C.A., Ed.; Wiley: New York, NY, USA, 1959. [Google Scholar]
- Zheng, D.; Xu, Y.; Tsai, Y.P.; Tu, K.N.; Patterson, P.; Zhao, B.; Liu, Q.Z.; Brongo, M. Mechanical property measurement of thin polymeric-low dielectric-constant films using bulge testing method. Appl. Phys. Lett. 2000, 76, 2008–2010. [Google Scholar] [CrossRef]
- Xu, D.; Liechti, K.M. Bulge testing transparent thin films with moiré deflectometry. Exp. Mech. 2010, 50, 217–225. [Google Scholar] [CrossRef]
- Sun, J.Y.; Hu, J.L.; Zheng, Z.L.; He, X.T.; Geng, H.H. A practical method for simultaneous determination of Poisson’s ratio and Young’s modulus of elasticity of thin films. J. Mech. Sci. Technol. 2011, 25, 3165–3171. [Google Scholar] [CrossRef]
- Sun, J.Y.; Qian, S.H.; Li, Y.M.; He, X.T.; Zheng, Z.L. Theoretical study of adhesion energy measurement for film/substrate interface using pressurized blister test: Energy release rate. Measurement 2013, 46, 2278–2287. [Google Scholar] [CrossRef]
- Xu, D.; Liechti, K.M. Analytical and experimental study of a circular membrane in Hertzian contact with a rigid substrate. Int. J. Solids Struct. 2010, 47, 207–214. [Google Scholar] [CrossRef] [Green Version]
- Chien, W.Z. Asymptotic behavior of a thin clamped circular plate under uniform normal pressure at very large deflection. Sci. Rep. Natl. Tsinghua Univ. 1948, 5, 193–208. [Google Scholar]
- Alekseev, S.A. Elastic circular membranes under the uniformly distributed loads. Eng. Corpus. 1953, 14, 196–198. (In Russian) [Google Scholar]
- Chien, W.Z.; Wang, Z.Z.; Xu, Y.G.; Chen, S.L. The symmetrical deformation of circular membrane under the action of uniformly distributed loads in its portion. Appl. Math. Mech. (Engl. Ed.) 1981, 2, 653–668. [Google Scholar]
- Chien, W.Z.; Chen, S.L. The solution of large deflection problem of thin circular plate by the method of composite expansion. Appl. Math. Mech. (Engl. Ed.) 1985, 6, 103–118. [Google Scholar]
- Arthurs, A.M.; Clegg, J. On the solution of a boundary value problem for the nonlinear Föppl-Hencky equation. Z. Angew. Math. Mech. 1994, 74, 281–284. [Google Scholar] [CrossRef]
- Plaut, R.H. Linearly elastic annular and circular membranes under radial, transverse, and torsional loading. Part I: Large unwrinkled axisymmetric deformations. Acta Mech. 2009, 202, 79–99. [Google Scholar] [CrossRef]
- Lian, Y.S.; He, X.T.; Liu, G.H.; Sun, J.Y.; Zheng, Z.L. Application of perturbation idea to well-known Hencky problem: A perturbation solution without small-rotation-angle assumption. Mech. Res. Commun. 2017, 83, 32–46. [Google Scholar] [CrossRef]
- Sun, J.Y.; Rong, Y.; He, X.T.; Gao, X.W.; Zheng, Z.L. Power series solution of circular membrane under uniformly distributed loads: Investigation into Hencky transformation. Struct. Eng. Mech. 2013, 45, 631–641. [Google Scholar] [CrossRef]
- Yang, Z.X.; Sun, J.Y.; Ran, G.M.; He, X.T. A new solution to Föppl-Hencky membrane equation. J. Mech. 2017, 33, N7–N11. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Yang, Z.X.; He, X.T.; Zheng, Z.L. Closed-form solution of well-known Hencky problem without small-rotation-angle assumption. Z. Angew. Math. Mech. 2016, 96, 1434–1441. [Google Scholar] [CrossRef]
- Lian, Y.S.; Sun, J.Y.; Zhao, Z.H.; He, X.T.; Zheng, Z.L. A revisit of the boundary value problem for Föppl–Hencky membranes: Improvement of geometric equations. Mathematics 2020, 8, 631. [Google Scholar] [CrossRef] [Green Version]
- Ku, C.L. On the large deflection of elastic circular membrane with initial tension under uniformly distributed load. Chin. J. Phys. 1956, 12, 319–338. (In Chinese) [Google Scholar]
- He, X.T.; Wu, J.L.; Zheng, Z.L.; Chen, S.L. Axisymmetrical deformation of prestressed circular membrane under uniformly distributed loads. J. Chongqing Univ. 2010, 33, 109–112. (In Chinese) [Google Scholar]
- Sun, J.Y.; Lian, Y.S.; Li, Y.M.; He, X.T.; Zheng, Z.L. Closed-form solution of elastic circular membrane with initial stress under uniformly-distributed loads: Extended Hencky solution. Z. Angew. Math. Mech. 2015, 95, 1335–1341. [Google Scholar] [CrossRef]
- Yang, Z.X.; Sun, J.Y.; Li, K.; Lian, Y.S.; He, X.T.; Zheng, Z.L. Theoretical study on synchronous characterization of surface and interfacial mechanical properties of thin-film/substrate systems with residual stress based on pressure blister test technique. Polymers 2018, 10, 49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lian, Y.S.; Sun, J.Y.; Dong, J.; Zheng, Z.L.; Yang, Z.X. Closed-form solution of axisymmetric deformation of prestressed Föppl-Hencky membrane under constrained deflecting. Struct. Eng. Mech. 2019, 69, 693–698. [Google Scholar]
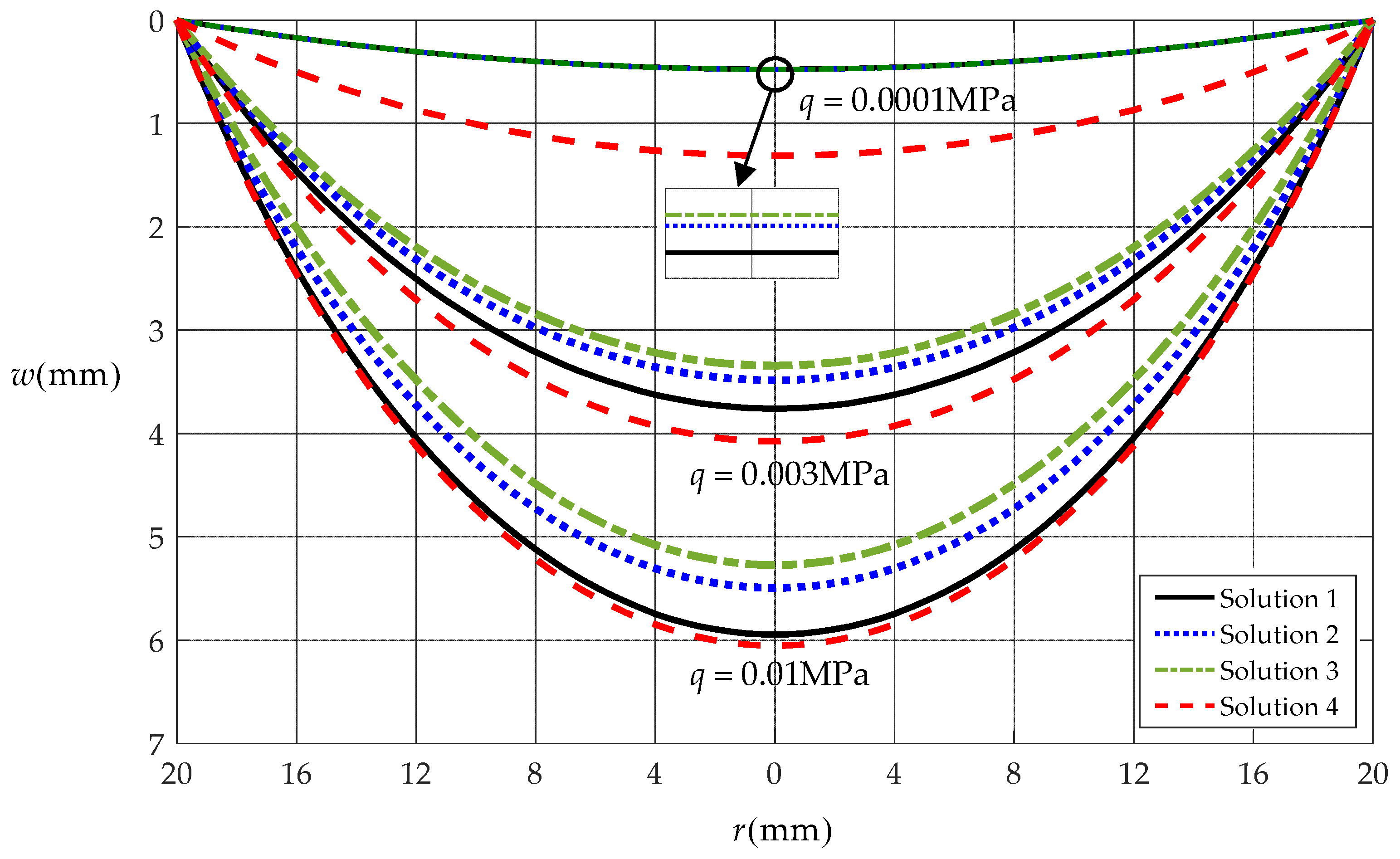
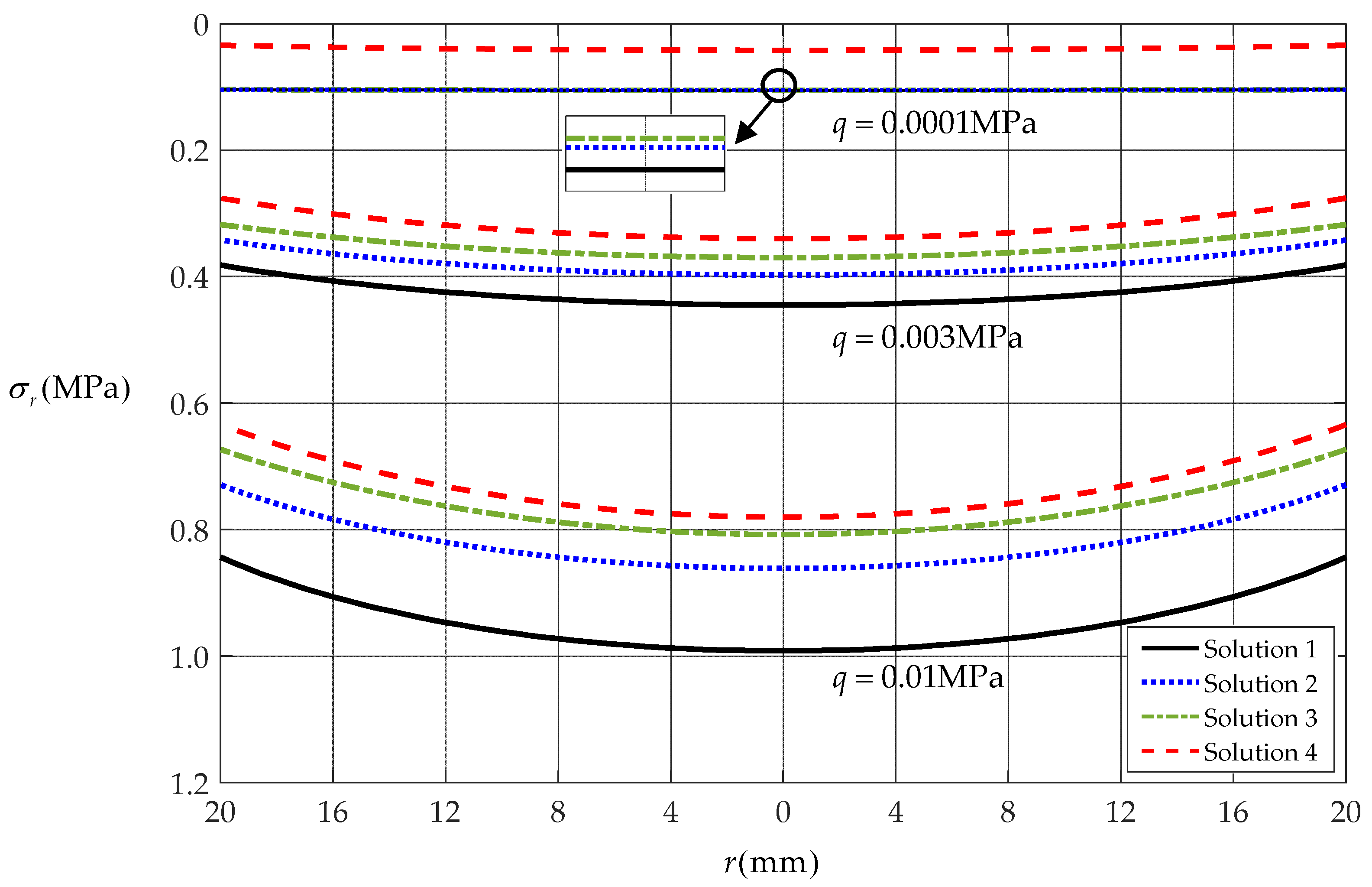
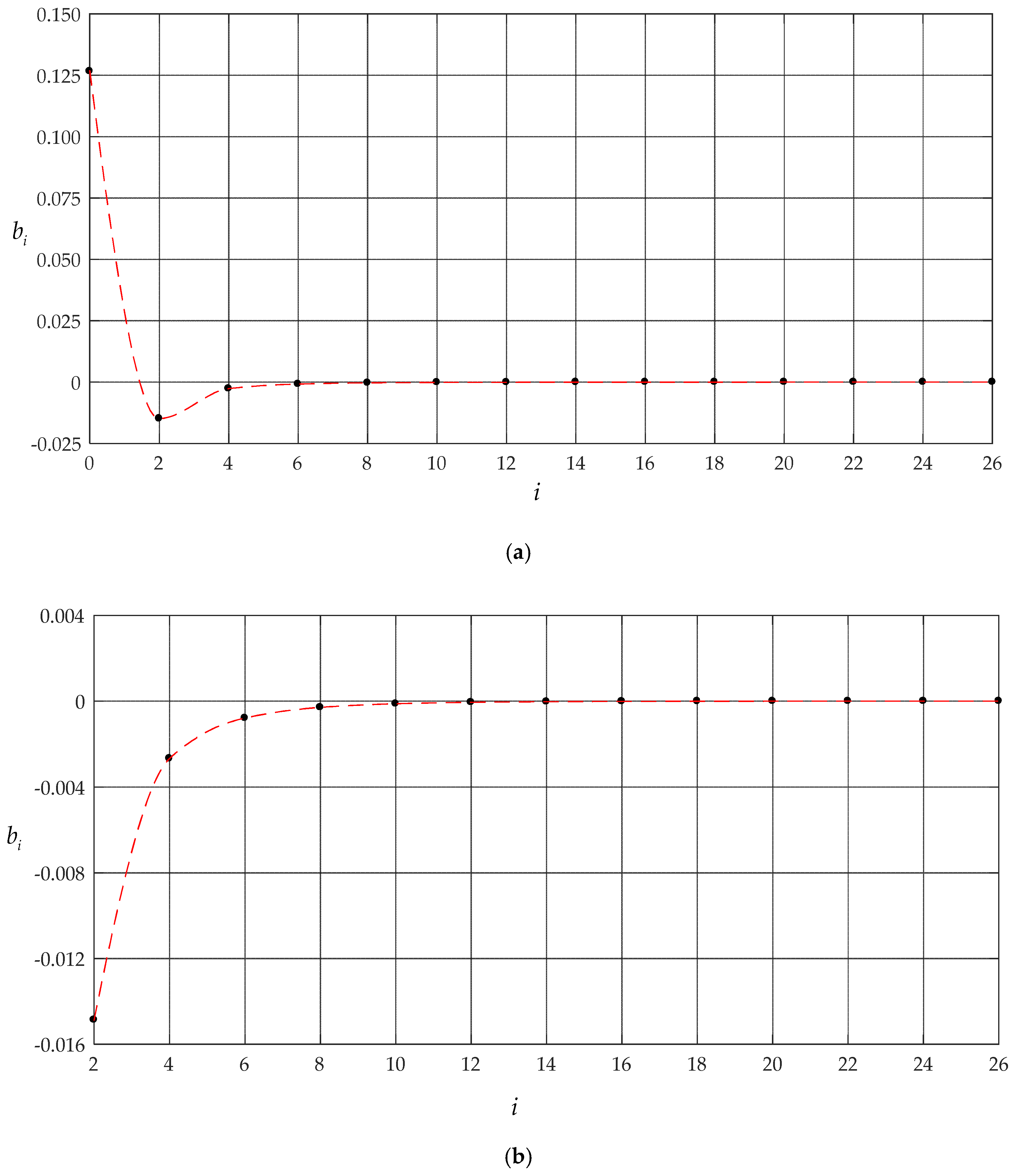
| Loads q [MPa] | Solution 1 | Solution 2 | Solution 3 | Solution 4 | |
|---|---|---|---|---|---|
| [mm] | 0.0001 | 0.47756 | 0.47743 | 0.47718 | 1.31183 |
| 0.003 | 3.69050 | 3.43552 | 3.34403 | 4.07615 | |
| 0.01 | 5.94663 | 5.49420 | 5.27261 | 6.05366 | |
| [MPa] | 0.0001 | 0.10536 | 0.10534 | 0.10534 | 0.04202 |
| 0.003 | 0.44479 | 0.39752 | 0.36977 | 0.33981 | |
| 0.01 | 0.99162 | 0.86134 | 0.80763 | 0.78009 |
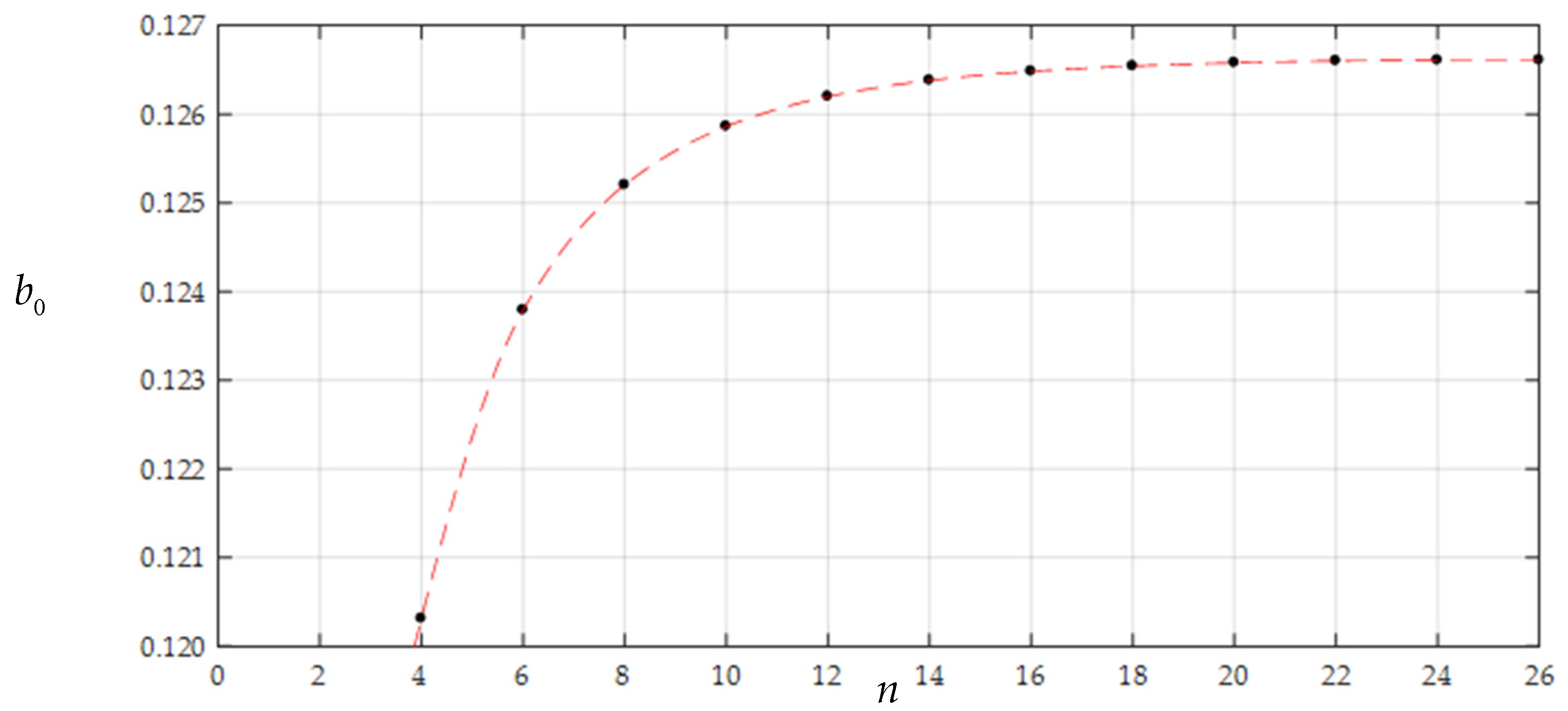
| n | b0 | b2 | b4 | b6 |
| 4 | 1.20311 × 10−1 | −1.65094 × 10−2 | −3.36329 × 10−3 | ― |
| 6 | 1.23788 × 10−1 | −1.55680 × 10−2 | −2.95482 × 10−3 | −9.30349 × 10−4 |
| 8 | 1.25201 × 10−1 | −1.52080 × 10−2 | −2.80646 × 10−3 | −8.58923 × 10−4 |
| 10 | 1.25861 × 10−1 | −1.50439 × 10−2 | −2.74022 × 10−3 | −8.27699 × 10−4 |
| 12 | 1.26198 × 10−1 | −1.49612 × 10−2 | −2.70718 × 10−3 | −8.12280 × 10−4 |
| 14 | 1.26380 × 10−1 | −1.49168 × 10−2 | −2.68953 × 10−3 | −8.04083 × 10−4 |
| 16 | 1.26483 × 10−1 | −1.48918 × 10−2 | −2.67964 × 10−3 | −7.99504 × 10−4 |
| 18 | 1.26541 × 10−1 | −1.48776 × 10−2 | −2.67400 × 10−3 | −7.96896 × 10−4 |
| 20 | 1.26579 × 10−1 | −1.48686 × 10−2 | −2.67044 × 10−3 | −7.95252 × 10−4 |
| 22 | 1.26600 × 10−1 | −1.48635 × 10−2 | −2.66844 × 10−3 | −7.94329 × 10−4 |
| 24 | 1.26607 × 10−1 | −1.48616 × 10−2 | −2.66770 × 10−3 | −7.93987 × 10−4 |
| 26 | 1.26609 × 10−1 | −1.48612 × 10−2 | −2.66754 × 10−3 | −7.93915 × 10−4 |
| n | b8 | b10 | b12 | b14 |
| 8 | −3.27991 × 10−4 | ― | ― | ― |
| 10 | −3.11944 × 10−4 | −1.33536 × 10−4 | ― | ― |
| 12 | −3.04098 × 10−4 | −1.29313 × 10−4 | −5.98144 × 10−5 | ― |
| 14 | −2.99948 × 10−4 | −1.27091 × 10−4 | −5.85763 × 10−5 | −2.86800 × 10−5 |
| 16 | −2.97637 × 10−4 | −1.25857 × 10−4 | −5.78906 × 10−5 | −2.82872 × 10−5 |
| 18 | −2.96323 × 10−4 | −1.25157 × 10−4 | −5.75019 × 10−5 | −2.80649 × 10−5 |
| 20 | −2.95495 × 10−4 | −1.24716 × 10−4 | −5.72576 × 10−5 | −2.79253 × 10−5 |
| 22 | −2.95030 × 10−4 | −1.24469 × 10−4 | −5.71206 × 10−5 | −2.78471 × 10−5 |
| 24 | −2.94858 × 10−4 | −1.24377 × 10−4 | −5.70698 × 10−5 | −2.78181 × 10−5 |
| 26 | −2.94822 × 10−4 | −1.24358 × 10−4 | −5.70592 × 10−5 | −2.78121 × 10−5 |
| n | b16 | b18 | b20 | b22 |
| 16 | −1.44729 × 10−5 | ― | ― | ― |
| 18 | −1.43427 × 10−5 | −7.60266 × 10−6 | ― | ― |
| 20 | −1.42610 × 10−5 | −7.55386 × 10−6 | −4.12285 × 10−6 | ― |
| 22 | −1.42152 × 10−5 | −7.52654 × 10−6 | −4.10626 × 10−6 | −2.29738 × 10−6 |
| 24 | −1.41983 × 10−5 | −7.51642 × 10−6 | −4.10013 × 10−6 | −2.29360 × 10−6 |
| 26 | −1.41947 × 10−5 | −7.51431 × 10−6 | −4.09884 × 10−6 | −2.29281 × 10−6 |
| n | b24 | b26 | ||
| 24 | −1.31103 × 10−6 | ― | ― | ― |
| 26 | −1.31054 × 10−6 | −7.63614 × 10−7 | ― | ― |
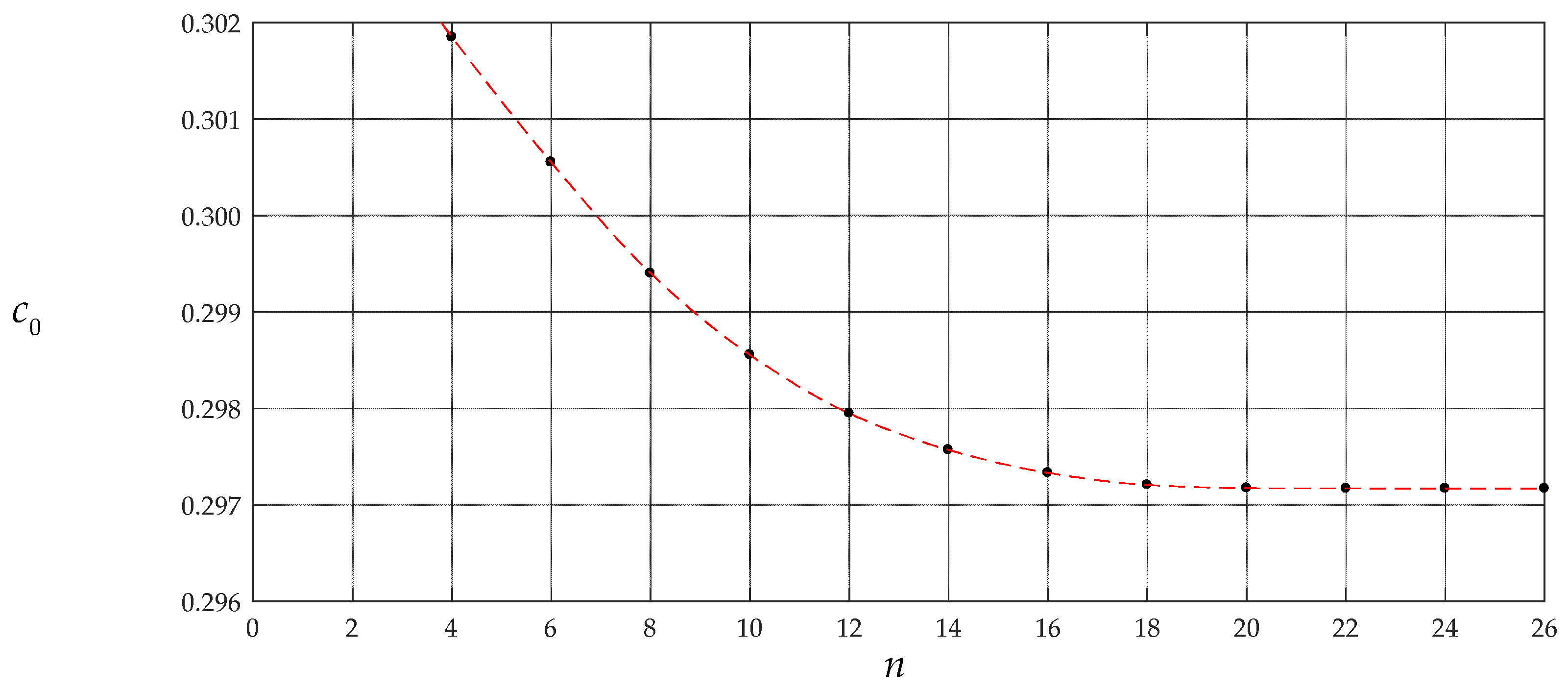
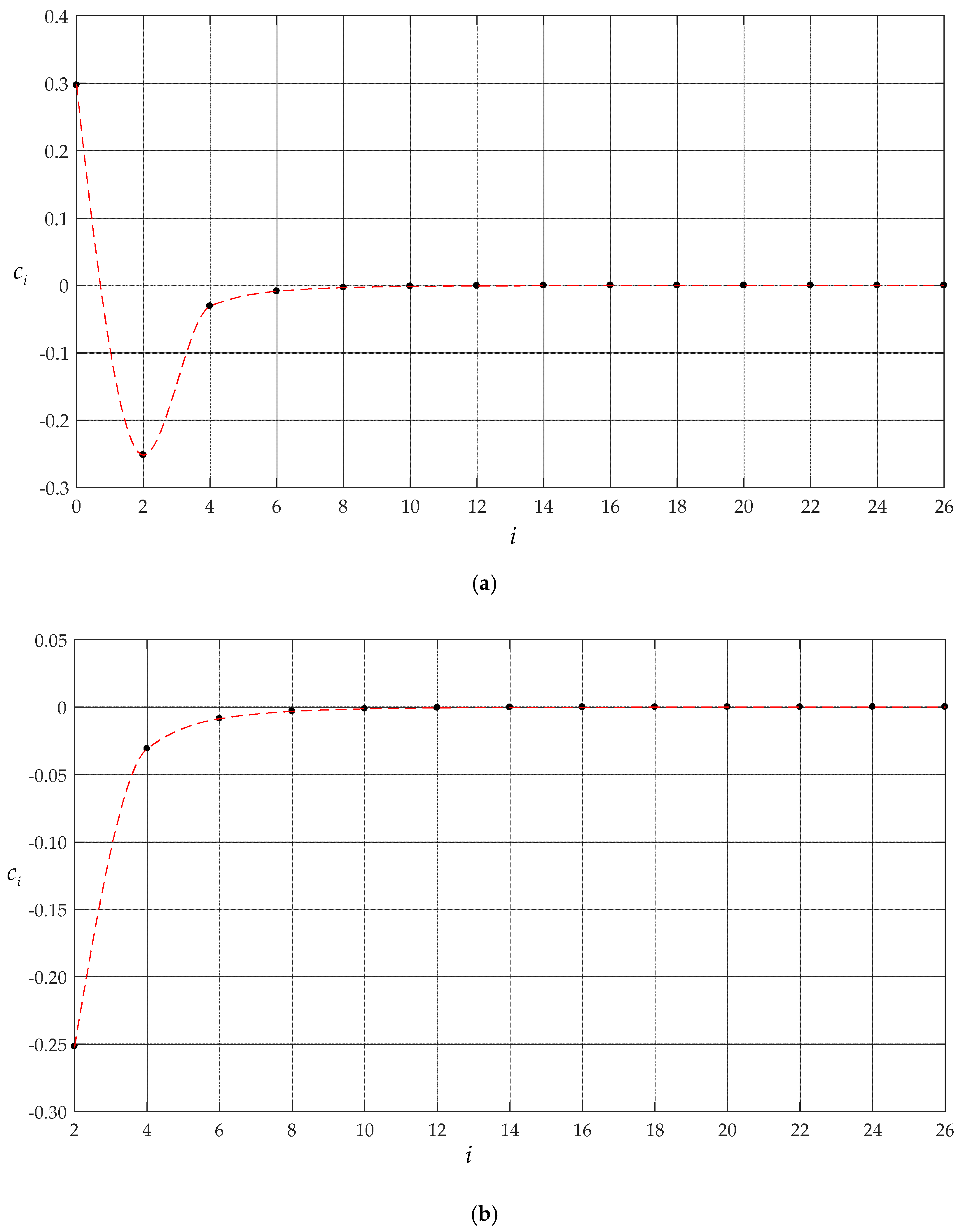
| n | c0 | c2 | c4 | c6 |
| 4 | 3.01849 × 10−1 | −2.65045 × 10−1 | −3.68042 × 10−2 | ― |
| 6 | 3.00567 × 10−1 | −2.575995 × 10−1 | −3.32919 × 10−2 | −9.97580 × 10−3 |
| 8 | 2.99505 × 10−1 | −2.546935 × 10−1 | −3.19904 × 10−2 | −9.31291 × 10−3 |
| 10 | 2.98554 × 10−1 | −2.53357 × 10−1 | −3.14045 × 10−2 | −9.02080 × 10−3 |
| 12 | 2.97949 × 10−1 | −2.52681 × 10−1 | −3.11111 × 10−2 | −8.87599 × 10−3 |
| 14 | 2.97569 × 10−1 | −2.52317 × 10−1 | −3.09540 × 10−2 | −8.79885 × 10−3 |
| 16 | 2.97332 × 10−1 | −2.52112 × 10−1 | −3.08659 × 10−2 | −8.75572 × 10−3 |
| 18 | 2.97207 × 10−1 | −2.51995 × 10−1 | −3.08156 × 10−2 | −8.73114 × 10−3 |
| 20 | 2.97173 × 10−1 | −2.51921 × 10−1 | −3.07839 × 10−2 | −8.71564 × 10−3 |
| 22 | 2.97171 × 10−1 | −2.51879 × 10−1 | −3.07661 × 10−2 | −8.70693 × 10−3 |
| 24 | 2.97171 × 10−1 | −2.51864 × 10−1 | −3.07594 × 10−2 | −8.70370 × 10−3 |
| 26 | 2.97171 × 10−1 | −2.51861 × 10−1 | −3.07581 × 10−2 | −8.70303 × 10−3 |
| n | c8 | c10 | c12 | c14 |
| 8 | −3.47991 × 10−3 | ― | ― | ― |
| 10 | −3.35337 × 10−3 | −1.41877 × 10−3 | ― | ― |
| 12 | −3.27724 × 10−3 | −1.37720 × 10−3 | −6.26249 × 10−4 | ― |
| 14 | −3.23690 × 10−3 | −1.35529 × 10−3 | −6.14040 × 10−4 | −2.93518 × 10−4 |
| 16 | −3.21441 × 10−3 | −1.34310 × 10−3 | −6.07272 × 10−4 | −2.89687 × 10−4 |
| 18 | −3.20161 × 10−3 | −1.33618 × 10−3 | −6.03433 × 10−4 | −2.87518 × 10−4 |
| 20 | −3.19355 × 10−3 | −1.33183 × 10−3 | −6.01020 × 10−4 | −2.86156 × 10−4 |
| 22 | −3.18902 × 10−3 | −1.32938 × 10−3 | −5.99666 × 10−4 | −2.85392 × 10−4 |
| 24 | −3.18734 × 10−3 | −1.32848 × 10−3 | −5.99164 × 10−4 | −2.85109 × 10−4 |
| 26 | −3.18699 × 10−3 | −1.32829 × 10−3 | −5.99059 × 10−4 | −2.85050 × 10−4 |
| n | c16 | c18 | c20 | c22 |
| 16 | −1.43691 × 10−4 | ― | ― | ― |
| 18 | −1.42448 × 10−4 | −7.27170 × 10−5 | ― | ― |
| 20 | −1.41668 × 10−4 | −7.22652 × 10−5 | −3.77500 × 10−5 | ― |
| 22 | −1.41231 × 10−4 | −7.20122 × 10−5 | −3.76022 × 10−5 | −2.00212 × 10−5 |
| 24 | −1.41069 × 10−4 | −7.19185 × 10−5 | −3.75475 × 10−5 | −1.99890 × 10−5 |
| 26 | −1.41035 × 10−4 | −7.18989 × 10−5 | −3.75361 × 10−5 | −1.99822 × 10−5 |
| n | c24 | c26 | ||
| 24 | −1.08172 × 10−5 | ― | ― | ― |
| 26 | −1.08132 × 10−5 | −5.93435 × 10−6 | ― | ― |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Sun, J.-Y.; Zhao, Z.-H.; He, X.-T. Large Deflection Analysis of Axially Symmetric Deformation of Prestressed Circular Membranes under Uniform Lateral Loads. Symmetry 2020, 12, 1343. https://doi.org/10.3390/sym12081343
Li X, Sun J-Y, Zhao Z-H, He X-T. Large Deflection Analysis of Axially Symmetric Deformation of Prestressed Circular Membranes under Uniform Lateral Loads. Symmetry. 2020; 12(8):1343. https://doi.org/10.3390/sym12081343
Chicago/Turabian StyleLi, Xue, Jun-Yi Sun, Zhi-Hang Zhao, and Xiao-Ting He. 2020. "Large Deflection Analysis of Axially Symmetric Deformation of Prestressed Circular Membranes under Uniform Lateral Loads" Symmetry 12, no. 8: 1343. https://doi.org/10.3390/sym12081343
APA StyleLi, X., Sun, J.-Y., Zhao, Z.-H., & He, X.-T. (2020). Large Deflection Analysis of Axially Symmetric Deformation of Prestressed Circular Membranes under Uniform Lateral Loads. Symmetry, 12(8), 1343. https://doi.org/10.3390/sym12081343





