1. Introduction
A brain computer interface (BCI) provides direct communication between the brain and an external device that translates neuronal signals into user commands without the use of the peripheral nerve and muscle pathways. Many research groups have created electroencephalography (EEG)-based BCIs that offer sufficient time resolution, usability, and are associated with lower brain surgery risks [
1,
2,
3,
4] for medical and industrial applications. The analysis of EEG signals induced by motor imagery (MI), i.e., the imagery of body-part movements, has received considerable attention because of its widespread application in motor tasks, such as wheelchairs and mouse cursor controls [
1]. Although many data-driven approaches have been developed to automatically design BCIs, low signal-to-noise ratios of EEG signals and the highly complex connectivity of the human brain make the decoding of the user’s intention difficult.
The EEG signal possesses task-specific features in the spectral and spatial domains during the MI task [
5]. The spectral features are extracted by a spectral filter with a specific frequency band. The spectral-filtered signals are spatially transformed by a spatial filter. The spatially transformed signals are expected to be maximally discriminative between the two MI classes. Therefore, the identification of spectral and spatial filters constitutes the main BCI design issue.
In the spectral domain, task-related changes in the EEG band power induced by MI tasks, commonly referred to as event-related desynchronization (ERD) or event-related synchronization (ERS), have attracted attention in the analysis of EEG signals. A power decrease in the
µ-rhythm (8–14 Hz), and a power increase in the
β-rhythm (14–30 Hz) of the motor and somatosensory cortices, respectively, indicate ERD and ERS during the execution of MI tasks. Therefore, the selection of frequency bands that possess discriminative power among different MI tasks is the key issue of the BCI design. However, ERD/ERS patterns vary greatly across subjects and even across trials [
6]. This makes the selection of frequency bands difficult. The spectral filter is often either manually selected based on visual inspection or is usually designed for broadband frequency operations, including both
µ- and
β-rhythms [
6,
7,
8,
9]. Several research studies have attempted to determine the optimal frequency bands and spatial patterns related to ERD/ERS using the techniques of signal processing and pattern recognition [
7,
10]. However, these approaches cannot find the optimal frequency bands in a general analytic manner.
For spatial filter optimization, machine learning has been considered as the main tool because of the increasing development of computational hardware and statistical learning theory [
7]. A common spatial pattern (CSP) algorithm, a data-driven method, has been extensively used in the design of spatial filters for two-class MI problems [
6,
11]. This CSP identifies the spatial filter and an optimal projection direction that maximizes the variance of the data conditioned on one class. Simultaneously, the CSP minimizes the variance of the data conditioned on the other class. Raw EEG signals are then projected to this direction which makes MI classification easier. However, the CSP is highly sensitive to the spectral filter and the EEG signal. Improper spectral filters or misleading EEG signals may lead to degraded BCI performances [
7,
10,
12]. Therefore, simultaneously optimizing spectral and spatial filters is desirable in most EEG-based BCIs.
A CSP augments spatial signals with time-delayed signals, thus resulting in double channels [
13]. However, the first-order, finite impulse response, filter optimization approach, restricts the adaptability of this method. Accordingly, the time-delay parameter must be tuned by experience. The adaptability of this work was extended by introducing arbitrary order finite impulse response filters that allow the extraction of spectral features with a higher degree for the CSP [
14]. However, the filter coefficients were strongly correlated with the initial parameters.
Numerous iterative procedures have been proposed to jointly optimize both the spectral and spatial filters. One approach uses a convex optimization to automatically learn feature extraction, selection, and combine them in the spectral and spatial domains [
15]. An iterative spatiospectral pattern learning approach was proposed to learn spatial filters based on the optimized spectral filters and the classifier in the preceding iteration [
16].
Numerous research groups developed a bank of bandpass filters to extract spectral features in various frequency bands. Filter-bank CSP (FBCSP) has been considered as the most computationally efficient algorithm that divides a broadband frequency range into small nonoverlapping frequency bands with fixed bandwidths. FBCSP then independently employs an individual CSP module to each individual frequency band to extract spatial features from EEG signals. A feature set possessing discriminative power was selected by a maximal mutual information criterion [
17]. Conversely, a coefficient decimation method was developed to select a subject-specific CSP discriminative filter bank [
18]. However, these methods determine optimal filters for unimodal multivariate normal distributions only. An optimal spatiospectral filter network further optimizes the spatiospectral filters by estimating the mutual information between the features and the class labels, and can thus be applied to complex data structures [
19].
The frequency bands of the filter bank usually cover the
µ- and
β-rhythms, and the spatial filter was optimized in each frequency band which led to improved classification accuracy [
17,
20]. However, these methods need to predefine the frequency bands according to the neurophysiological knowledge [
18,
19]. A Bayesian spatiospectral filter optimization (BSSFO) was proposed to simultaneously design spectral and spatial filters without predefined frequency bands [
21]. Nevertheless, the features extracted from EEG signals contaminated by noise and artifacts may not be related to the motor imagery tasks, and may thus lead to inaccurate learning of spectral and spatial patterns.
The EEG signals are easily contaminated by background noise and eye-blink artifacts which lead to low signal-to-noise ratios. Conversely, the EEG signals may be contaminated by improper motor imagery wherein the subjects do not perform the imagery tasks properly, or performed the wrong mental tasks. Data-driven BCI classifiers were sensitive to these noisy and atypical observations (contaminated trials). The performance of BCI was degraded when the contaminated trials participated in classifier training. Therefore, eliminating the contaminated trials is desired during classifier training to achieve reliable MI classification. The contaminated trials induced by muscle and eye-blinks can either be removed by independent component analysis (ICA), or rejected by threshold methods [
22]. However, ICA requires a visual inspection to select the artificial components that make the implementation of an automatic BCI system nearly impossible. In addition, both the ICA and threshold methods cannot detect the noise caused by improper imagery.
A relevant dimensionality estimation-based method was proposed [
23] to detect contaminated trials caused by improper motor imagery. Wang et al. proposed a trial pruning method that used a Gaussian mixture model and a genetic algorithm to eliminate the trials contaminated by artifacts and improper imagery [
12]. These approaches extracted features with predefined frequency bands along with CSP. Therefore, the trial pruning method may be improved further when the spectral and spatial patterns can be automatically learnt without predefined frequency bands.
This study aims to tackle the challenges associated with the design of filter banks without predefined frequency bands and with contaminated trials for the EEG-based BCIs. This study proposes Parzen Windows-based spatiospectral patterns with trial pruning (PWSPTP) to achieve the research goal. The main contributions of the present study are summarized as follows:
A particle-based approximation technique was developed to iteratively construct a filter band and detect potential contamination trials. The spectral and spatial features were learnt as the contaminated trials were eliminated during classifier training that led to improved MI classification accuracy;
The discriminative power of a feature and the contamination level of a trial were simultaneously estimated by the difference of the class conditional probability density function (pdf) instead of using mutual information. The class conditional pdf was estimated by the Parzen window density estimator;
The importance weight (particle weight) of each feature was estimated by analysis of variance (ANOVA) F-tests with the use of the class conditional pdf that can be simply implemented.
The remaining parts of this study are organized as follows:
Section 2 illustrates the proposed PWSPTP and provides a better understanding of the relationship between PWSPTP and other methods, including similarities and differences.
Section 3 demonstrates the performance of the PWSPTP for MI classification. Finally,
Section 4 summarizes the present study.
2. Parzen Windows-Based Spatiospectral Patterns with Trial Pruning
This study aimed to design an EEG-based BCI that could automatically eliminate the contaminated trials during classifier training, and to simultaneously learn the spectral and spatial patterns without predefined frequency bands and negative effects of the contaminated trials. Inspired by a particle-based approximation technique, this study constructs a filter bank with overlapping frequency bands. The discriminative power of each frequency band is estimated by the Parzen window density estimator. Compared with BSSFO, the present study measured the discriminative power of the frequency bands based on the difference of the class conditional
pdf of two MI classes instead of using the mutual information. Furthermore, the particle weight was estimated by analysis of variance (ANOVA) F-tests instead of mutual information. Conversely, inspired by the trial pruning method proposed by [
12], the present study eliminated the contaminated trials during classifier training. The trials potentially contaminated by artifacts and improper imagery are detected by the class conditional
pdf. This study combines the merits of the particle-based approximation technique and trial pruning method to simultaneously measure the discriminative power of the frequency band and eliminate the contaminated trials. This innovation overcame the limitation of the trial pruning method that adopted fixed nonoverlapping frequency bands and overcame the negative effects of the contaminated trials when learning the spectral and spatial patterns.
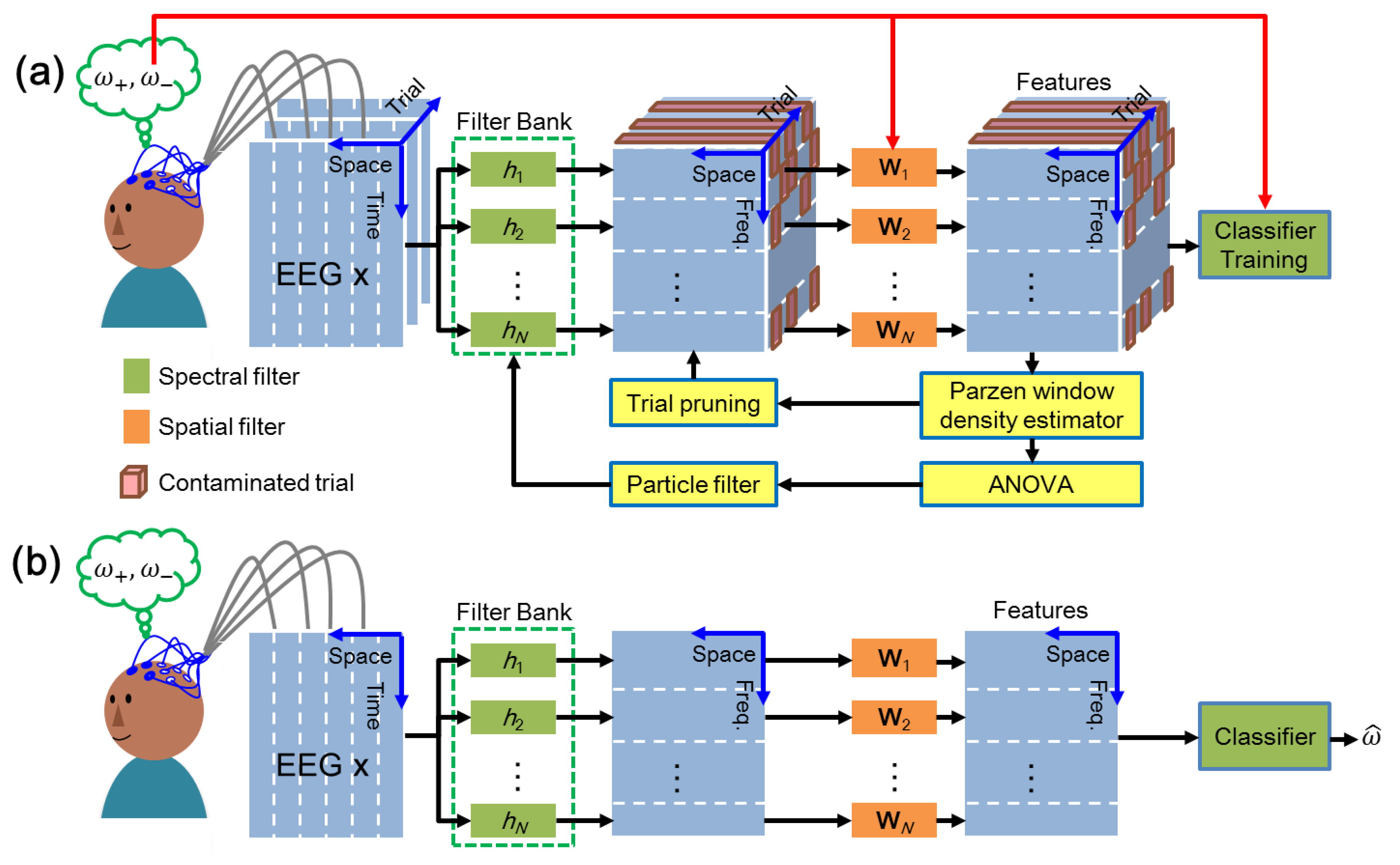
PWSPTP mainly consisted of three parts: (a) estimation of the discriminative power of the feature, (b) estimation of the contamination level of a trial, and (c) composition of a filter bank without contaminated trials.
Figure 1 shows the plot of the PWSPTP. In the training phase, a set of EEG signals corresponding to two MI classes were processed by a set of spectral filters (filter bank) and spatial filters (CSP). The discriminative power of spatiospectral features and contamination level of a trial were quantified by a Parzen window density estimator. A filter bank was constructed by the particle filter whose particle weight was estimated by an ANOVA F-test. A spectrally weighted classifier was trained according to the learnt spectral and spatial features without contaminated trials. In the testing phase, the classifier made an MI prediction based on the features extracted by the learnt spatiospectral filters.
2.1. Spatiospectral Filter Optimization
Consider a single-EEG trial of a MI task, where τ denotes the number of electrode channels. This study considered a binary classification problem whose class label ω was positive (+) or negative (−), e.g., left- or right-hand motor imagery. The features of x are usually extracted by the following three steps:
- (1)
spectral filtering: ;
- (2)
spatial filtering: ;
- (3)
feature extraction: ;
where h represents the spectral filter, represents the spatial filter, represents the spectrally filtered EEG, represents the spatially filtered signal, and represents the variance function. Each spectral filter is specified by the start and the end of the frequency band, whereby . The goal was to find a set of spectral filters whose features could be correctly discriminated between two MI tasks. The function of the random variable defines the probability of the spatially filtered signal and its correct classification between the two MI tasks. Given K trials of EEGs and their corresponding class labels , , a posterior pdf was defined as . As the spectrally filtered EEG , spatially filtered signal , and the feature were computed deterministically, could be directly obtained by a posterior pdf .
Inspired by the particle-based approximation [
21], a weighted particle-set
was generated to approximate
, where
denotes the importance weight of the particle,
N denotes the number of particles,
denotes a particle (a single-frequency band), and
denotes a set of noisy trial marks with
. Each particle represents a frequency band of a spectral filter and its corresponding noisy trial mark. An individual CSP module was independently performed based on the features that correspond to one spectral filter to obtain
[
8]. The features
were extracted by these spectral filters (particles) and their corresponding spatial filters. The importance weight of each particle
was computed by a class conditional
pdf (detailed in
Section 2.2). The noisy trial mark
was updated by the class conditional
pdf as well (detailed in
Section 2.3). For the next sampling iteration, a new set of particles was generated by an effective prior
, as defined in the previous iteration. A particle
was randomly chosen from
by roulette wheel selection with the use of
. In other words, the chance for the selection of
was proportional to
. A detailed description of roulette wheel selection could be found in [
24]. The chosen
was copied as the new particle
for the next iteration. If
has been chosen multiple times, a diffusion method was applied to avoid identical copies of the particle and was implemented by adding noise to the particle as follows,
where
is a Gaussian noise with a zero mean and a unit variance. This ensured that the particle with a large discriminative power could be reserved and was prevented from converging to a local optimum [
25]. Once a set of new particles
was obtained, the new particles replaced old particles
. Iterative sampling of the particle around the current particle with the importance weight helped the particles converge to
. The resulted particles constructed a weighted filter bank whose spectral filter bandwidths may be different from those of other particles and may overlap each other. This overcame the limitation of the predefinition of the frequency bands according to accumulated neurophysiological knowledge [
17,
19].
2.2. Importance Weight Update Rule for Particles
The importance weight of each particle was updated based on the evaluation of the discriminative power of the features. Compared with the BSSFO [
21], the discriminative power of a feature was estimated based on the difference of the class conditional
pdf instead of mutual information. Furthermore, the class conditional
pdf was also adopted to measure the contamination level of a trial.
Inspired from the F-score for feature selection [
26], ANOVA [
27] in conjunction with class conditional
pdf was used to measure the discriminative power of a feature (particle). It has been known that the trials with low signal-to-noise ratios and the trials contaminated by improper motor imagery may reduce the discriminative power of a feature. The trials with low signal-to-noise ratios possessed low class conditional probabilities. The trials contaminated by improper motor imagery possessed higher class conditional probability for the improper class than the class assigned in the MI task. Therefore, a difference of the class conditional
pdf for the trial of the class
was defined as
while that for the trial of the class
was defined as
The discriminative power of a feature was large when
was large, and vice versa. Furthermore,
was small for the trial contaminated by noise and artifacts. Thus, this value could be adopted to detect contaminated trials as well (detailed in
Section 2.2). The class conditional
pdf was determined using a Parzen window density estimator [
28,
29] as follows:
where
where
,
denotes the number of trials belonging to class
c,
denotes the width of the window function,
denotes a covariance matrix, and
r denotes the dimension of the feature. Note that a multivariate Gaussian window function
was adopted.
The importance weight of each particle
was defined as follows,
where
represents a set of trials that are not marked as noisy trials. In other words, the importance weight was calculated exclusively for noisy trials to ensure the discriminative power of a feature (particle) could be carefully measured without the effect of noisy trials. The numerator denotes the discrimination between two MI classes, while the denominator denotes the discrimination within each MI class based on the use of the difference of the class conditional
pdf.
2.3. Trial Pruning Process
Trial pruning aimed to prune trials contaminated by noise, artifacts, and improper motor imagery in the training data. The contamination level of the trial was measured by the class conditional
pdf that was also adopted in the importance weight-update rule of the particles. The trial contaminated by noise and artifacts were identified as a type-1 noisy trial and had low
for either the
or
classes, and led to small sums
. Therefore, the sum of the class conditional
pdf was used as a type-1 noisy indicator and was defined as follows,
Conversely, the trials contaminated by improper motor imagery were identified as type-2 noisy trials. These trials had lower values than when the assigned class label was , and vice versa. This led to negative or values. Therefore, the difference of the class conditional pdf, , was used as a type-2 noisy indicator, while it was also used to update the importance weight of each particle.
Once the contamination level of each trial has been measured,
was sorted in order as follows,
where
and
denote the sorted indices of the trials in classes
and
, respectively, and
and
denote the numbers of trials in classes
and
, respectively. The first
and
noisy trial marks of
were set to zero for classes
and
, where
denote a predefined percentage of the type 1 noisy trials and
represent the “flooring” operation. In other words, type-1 noisy trials are detected as follows,
For type-2 noisy trials,
and
were sorted according to the following order,
where
and
denote the sorted indices of the trials in classes
and
, respectively. The first
and
noisy trial marks of
were set to zero for classes
and
, respectively, where
denotes a predefined percentage of the type-2 noisy trials. In other words, type-2 noisy trials were detected as follows,
Note that the spatiospectral filter (corresponding to one particle) may filter out the noise that leads to a high
value. Therefore, the noisy trials in one particle may be different from those in another particle. These contaminated trials were iteratively pruned when the CSP was executed at the instant at which the importance weight of the particle was updated. The impact of the contaminated trials could then be reduced during the design of the filters and classifier in the training phase. As a result, a set of spectral and spatial filters could be iteratively constructed by simultaneously estimating the discriminative power of the features and contamination levels of the trials. The overall algorithm of the proposed PWSPTP is summarized in
Figure 2.
2.4. Mixture of Expert Classifiers
It has been determined that a mixture of expert classifiers could improve the classification accuracy [
30]. The present study linearly combined multiple classifiers to predict the MI class. Each classifier
played the role of one expert and was trained by the features extracted from one spectral filter with bandwidth
and one spatial filter
. The mixing coefficient of
was the importance weight
. A support vector machine (SVM) that possessed a strong classification performance [
31] was used as the classifier. Note that these classifiers were trained after the spectral and spatial filters were optimized by the PWSPTP and the contaminated trials were removed during the training process. The output of the mixture of expert models was
2.5. Performance Evaluation
To demonstrate the efficiency of discriminative feature extraction of the PWSPTP, this study considered the evaluation protocol of paired binary classification, i.e., left- versus right hand, left hand versus foot, left hand versus tongue, right hand versus foot, right hand versus tongue, and foot versus tongue. This protocol evaluated the discriminative power of the features extracted by the learnt frequency bands when the contaminated trials were eliminated during the training process.
The classification accuracy of the evaluation protocol was the percentage of correctly classified trials. All experiments were conducted with MATLAB (Version R2019a, MathWorks, Natick, MA, USA), with an Intel (R) Core (TM) i7-6900K central processing unit (CPU) @3.2 GHz, a 64 GB random access memory (RAM), and the Microsoft Windows 10 operating system.