Mathematical Modeling of Autoimmune Diseases
Abstract
1. Introduction
2. Description of the Mathematical Model of a General Autoimmune Disease
- Target cells are denoted by the subscript 1.
- Damaged cells are denoted by the subscript 2.
- Effector immune cells are denoted by the subscript 3. For brevity, hereafter they are mentioned as immune cells.
- Viral particles are denoted by the subscript 4.
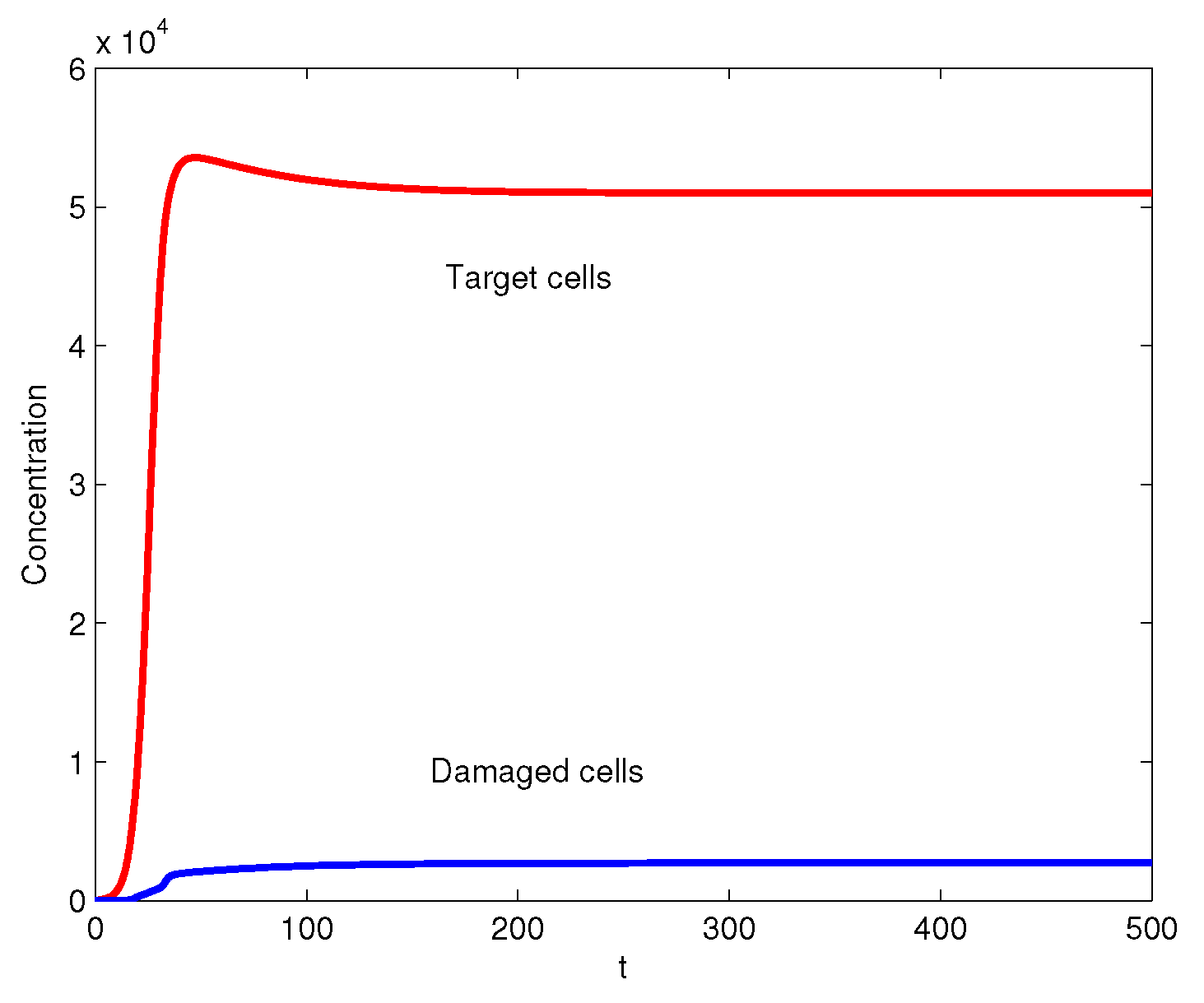
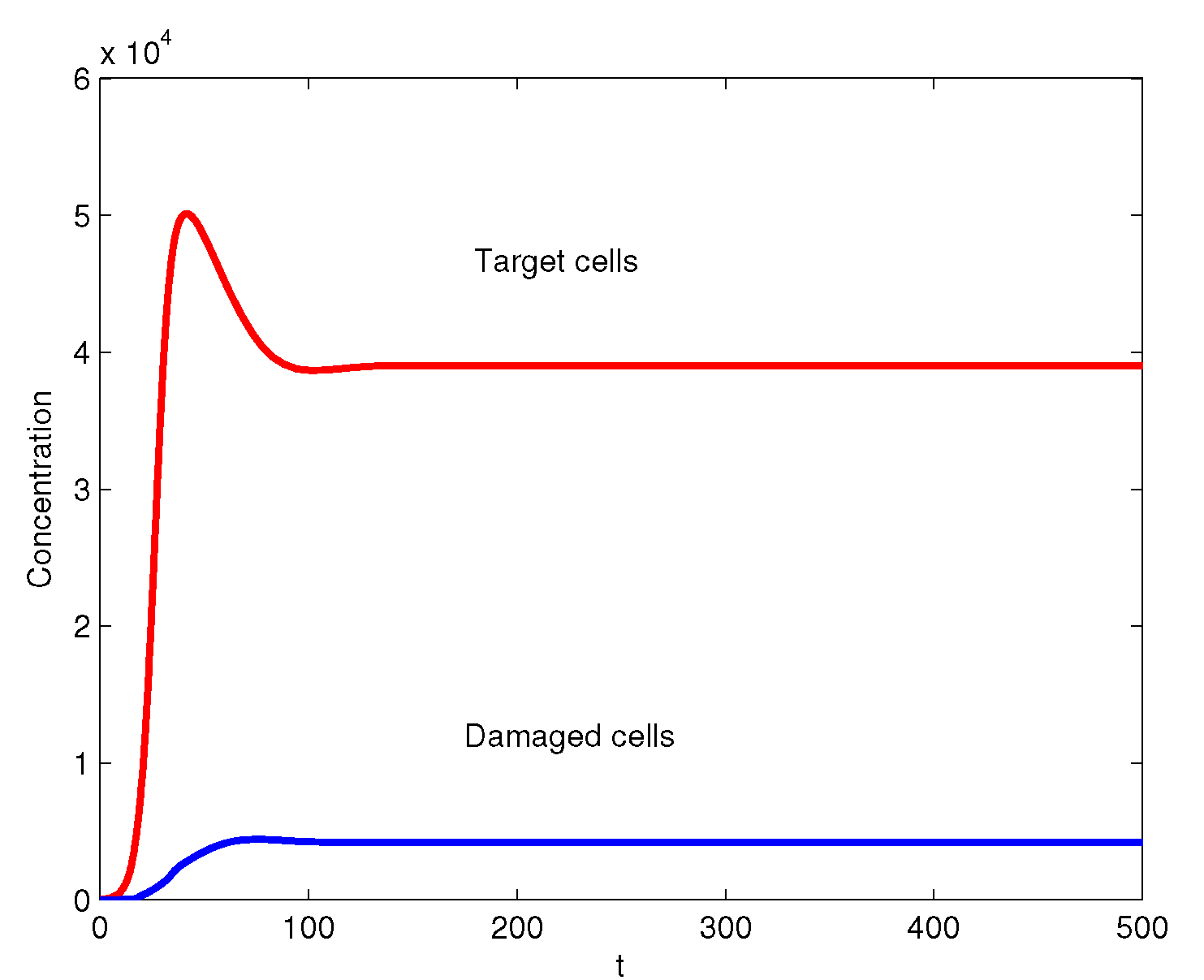
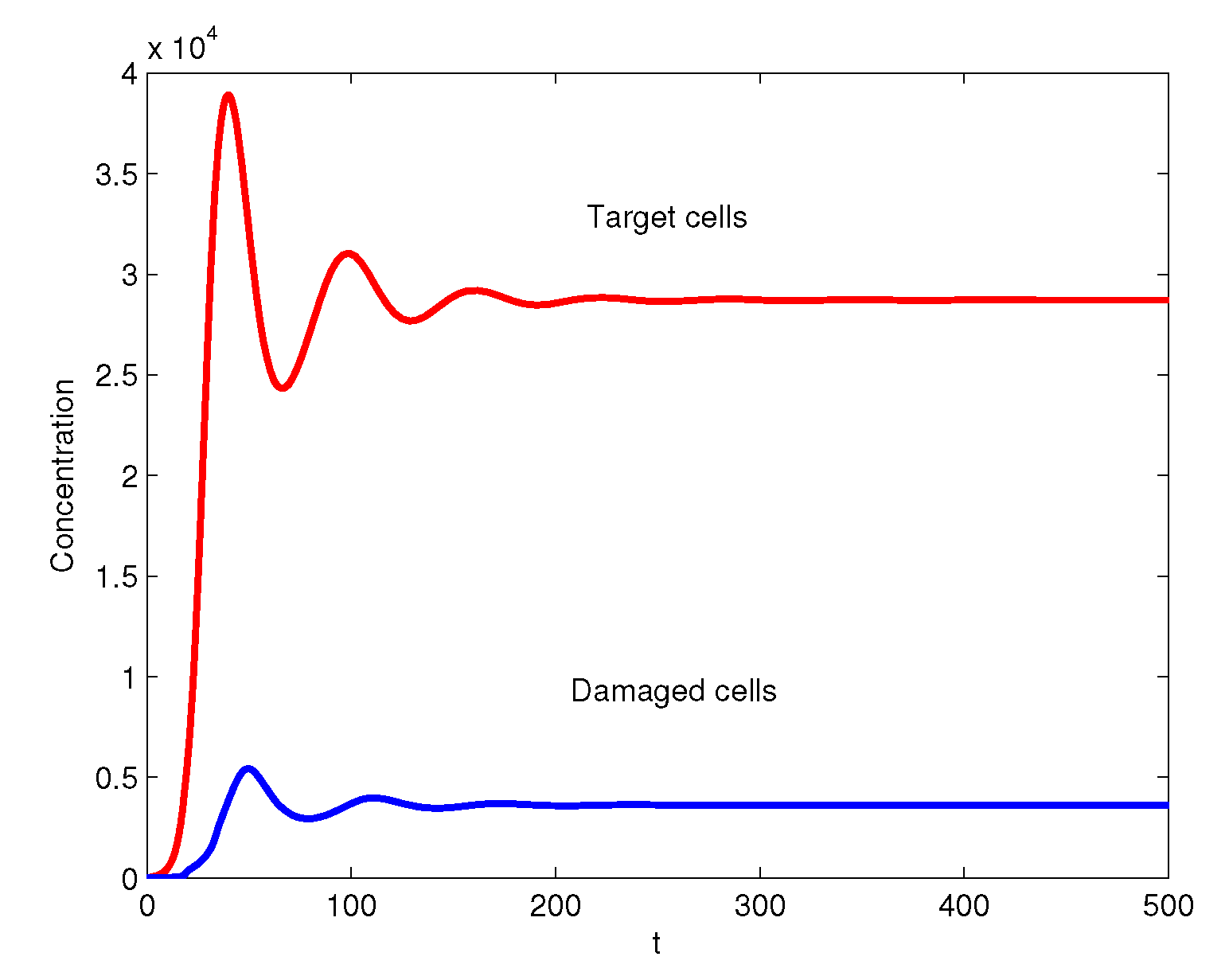
3. Numerical Simulations
4. Conclusions
Funding
Conflicts of Interest
References
- Bianca, C.; Bellomo, N. Towards a Mathematical Theory of Multiscale Complex Biological Systems; World Scientific: Singapore, 2011. [Google Scholar]
- Janeway, C.; Travers, P.; Walport, M.; Shlomchik, M. Immunobiology: The Immune System in Health and Disease; Garland: New York, NY, USA, 2006. [Google Scholar]
- Bellomo, N.; Brezzi, F. Challenges in active particles methods: Theory and applications. Math. Model. Methods Appl. Sci. 2018, 28, 1627–1633. [Google Scholar] [CrossRef]
- Bellomo, N.; Brezzi, F. Towards a multiscale vision of active particles. Math. Model. Methods Appl. Sci. 2019, 29, 581–588. [Google Scholar] [CrossRef]
- Bianca, C. Thermostatted kinetic equations as models for complex systems in physics and life sciences. Phys. Life Rev. 2012, 9, 359–399. [Google Scholar] [CrossRef]
- Bianca, C. Modeling complex systems by functional subsystems representation and thermostatted-KTAP methods. Appl. Math. Inf. Sci. 2012, 6, 495–499. [Google Scholar]
- Bianca, C.; Mogno, C. A thermostatted kinetic theory model for event-driven pedestrian dynamics. Eur. Phys. J. Plus 2018, 133, 213. [Google Scholar] [CrossRef]
- Degond, P.; Pareschi, L.; Russo, G. (Eds.) Modeling and Computational Methods for Kinetic Equations; Springer Science + Bussiness Media: New York, NY, USA, 2004; pp. 219–258. [Google Scholar]
- Elaiw, A.; Al-Turki, Y.; Alghamdi, M. A critical analysis of behavioural crowd dynamics—From a modelling strategy to kinetic theory methods. Symmetry 2019, 11, 851. [Google Scholar] [CrossRef]
- Vojdani, A. A potential link between environmental triggers and autoimmunity. Autoimmune Dis. 2013, 2013, 437231. [Google Scholar] [CrossRef]
- Ceccarelli, F.; Agmon-Levin, N.; Perricone, C. Genetic factors of autoimmune diseases 2017. J. Immunol. Res. 2017, 2017, 1–2. [Google Scholar] [CrossRef] [PubMed]
- Campbell, A.W. Autoimmunity and the Gut. Autoimmune Dis. 2014, 2014, 152428. [Google Scholar] [CrossRef] [PubMed]
- Lebwohl, B.; Ludvigsson, J.F.; Green, P.H.R. Celiac disease and non-celiac gluten sensitivity. Autoimmune Dis. 2015, 351, 4347. [Google Scholar] [CrossRef] [PubMed]
- Syage, J.; Kelly, C.; Dickason, M.; Ramirez, A.C.; Leon, F.; Dominguez, R.; Sealey-Voyksner, J. Determination of gluten consumption in celiac disease patients on agluten-free diet. Am. J. Clin. Nutr. 2018, 107, 201–207. [Google Scholar] [CrossRef] [PubMed]
- Davies, T.F. Infection and autoimmune thyroid disease. J. Clin. Endocrinol. Metab. 2008, 93, 674–676. [Google Scholar] [CrossRef] [PubMed]
- Kivity, S.; Agmon-Levin, N.; Blank, M.; Shoenfeld, Y. Infections and autoimmunity: Friends or foes? Trends Immunol. 2009, 30, 409–414. [Google Scholar] [CrossRef]
- Lidar, M.; Lipschitz, N.; Agmon-Levin, N.; Langevitz, P.; Barzilai, O.; Ram, M.; Porat-Katz, B.S.; Bizzaro, N.; Damoiseaux, J.; Tervaert, J.W.C.; et al. Infectious serologies and autoantibodies in hepatitis C and autoimmune disease-associated mixed cryoglobulinemia. Clin. Rev. Allergy Immunol. 2012, 42, 238–246. [Google Scholar] [CrossRef] [PubMed]
- Martinelli, M.; Agmon-Levin, N.; Amital, H.; Shoenfeld, Y. Infections and autoimmune diseases: An interplay of pathogenic and protective links. In Infection and Autoimmunity; Shoenfeld, Y., Agmon-Levin, N., Rose, N., Eds.; Academic Press: San Diego, CA, USA, 2015; pp. 13–23. [Google Scholar]
- Corthay, A. How do Regulatory T Cells Work? Scand. J. Immunol. 2009, 70, 326–336. [Google Scholar] [CrossRef] [PubMed]
- von Herrath, M.G.; Oldstone, M.B.A. Virus-induced autoimmune disease. Cur. Opt. Immunol. 1996, 8, 878–885. [Google Scholar] [CrossRef]
- Fujinami, R.S. Viruses and autoimmune disease-two sides of the same coin? TRENDS Microbiol. 2001, 9, 377–381. [Google Scholar] [CrossRef]
- Kolev, M. Mathematical Analysis of an Autoimmune Diseases Model: Kinetic Approach. Mathematics 2019, 7, 1024. [Google Scholar] [CrossRef]
- Nikolova, I. On stochastic models in biology and medicine. Asian-Eur. J. Math. 2020, 13, 2050168. [Google Scholar] [CrossRef]
- Sojka, D.K.; Huang, Y.H.; Fowell, D.J. Mechanisms of regulatory T-cell suppression—A diverse arsenal for a moving target. Immunology 2008, 124, 13–22. [Google Scholar] [CrossRef]
- Tang, Q.; Bluestone, J.A. The Foxp3+ regulatory T cell: A jack of all trades, master of regulation. Nat. Immun. 2008, 9, 239–244. [Google Scholar] [CrossRef] [PubMed]
- Shampine, L.F.; Reichelt, M.W. The Matlab ODE suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolev, M. Mathematical Modeling of Autoimmune Diseases. Symmetry 2020, 12, 1457. https://doi.org/10.3390/sym12091457
Kolev M. Mathematical Modeling of Autoimmune Diseases. Symmetry. 2020; 12(9):1457. https://doi.org/10.3390/sym12091457
Chicago/Turabian StyleKolev, Mikhail. 2020. "Mathematical Modeling of Autoimmune Diseases" Symmetry 12, no. 9: 1457. https://doi.org/10.3390/sym12091457
APA StyleKolev, M. (2020). Mathematical Modeling of Autoimmune Diseases. Symmetry, 12(9), 1457. https://doi.org/10.3390/sym12091457




