A New Parametric Life Family of Distributions: Properties, Copula and Modeling Failure and Service Times

Abstract

A new family of probability distributions is defined and applied for modeling symmetric real-life datasets. Some new bivariate type G families using Farlie–Gumbel–Morgenstern copula, modified Farlie–Gumbel–Morgenstern copula, Clayton copula and Renyi’s entropy copula are derived. Moreover, some of its statistical properties are presented and studied. Next, the maximum likelihood estimation method is used. A graphical assessment based on biases and mean squared errors is introduced. Based on this assessment, the maximum likelihood method performs well and can be used for estimating the model parameters. Finally, two symmetric real-life applications to illustrate the importance and flexibility of the new family are proposed. The symmetricity of the real data is proved nonparametrically using the kernel density estimation method.

1. Introduction and Genesis

Statistical probability distributions are an important tool in modeling the characteristics of real-life datasets such as “symmetric” or “right” or “left” skewness, “symmetric/asymmetric bi-modality” or “multi-modality” in different applied sciences such as reliability, medicine, engineering and finance, among others. The well-known distributions such as Burr X, normal, Burr XII, Weibull, beta, gamma, Kumaraswamy and Lindley are widely used because of their simple forms and identifiability of their properties. However, in the last few decades, statisticians have focused on the more complex and flexible distributions to increase the modeling ability of these models via adding one or more shape parameters. The well-known family of distributions can be cited as follows: the Marshall–Olkin-G (MO-G) family [1], the beta-G (B-G) family [2], the Kumaraswamy-G (K-G) family [3], the Burr X-G (BX-G) family [4], the Burr XII-G (BXII-G) family [5] and a new Weibull class of distributions [6], among others.

Consider a baseline cumulative distribution function (CDF) $G_{\underset{\_}{\delta }}\left(x\right)$ and probability density function (PDF) $g_{\underset{\_}{\delta }}\left(x\right)$ with a parameter vector $\underset{\_}{\delta }$ where $\underset{\_}{\delta }=\left({\underset{\_}{\delta }}_k\right)=\left({\delta }_1,{\delta }_2,\dots \right).$ Then due to [4], the CDF BX-G family of distributions is defined by

$$H_{\lambda ,\underset{\_}{\delta }}\left(x\right)={\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(x\right)\right]\right\}}^{\lambda }{|}_{\lambda \in R^{+} \mathrm{and} x\in \mathrm{R}}$$

(1)

where $O_{\underset{\_}{\delta }}^2\left(x\right)={\left(\frac{G_{\underset{\_}{\delta }}\left(x\right)}{1-G_{\underset{\_}{\delta }}\left(x\right)}\right)}^2.$ Note that the BX-G family of distributions can be called as the exponentiated Rayleigh-G (ER-G) family of distributions. For $\lambda =1,$ the BX-G family of distributions reduces to the Rayleigh-G (R-G) family. In this paper, we define and study a new family of stochastic models by adding two extra shape parameters in (1) to provide more flexibility to the newly generated family. Based on the Kumaraswamy-G (Kw-G) family pioneered by [3], we define a new G family so called the Kumaraswamy Burr X-G (KBX-G) family and give a comprehensive description of some of its mathematical properties. We hope that this model will attract wider applications in engineering, insurance, reliability and other areas of research. For an arbitrary baseline CDF $G_{\underset{\_}{\delta }}\left(x\right)$, [3] defined the K-G family by the CDF given by $F_{\alpha ,\theta ,\underset{\_}{\delta }}\left(x\right)=1-{\left[1-G_{\underset{\_}{\delta }}^{\alpha }\left(x\right)\right]}^{\theta }$.

In this paper, we define and study a new family of probability distributions based on the Kumaraswamy and Burr X families. The new family is applied to failure and service times of real datasets which are symmetric real data. The symmetricity of the real data is proved nonparametrically using the kernel density estimation (KDE) method. For checking the data “normality”, the quantile–quantile (Q–Q) plot is sketched. On the other hand, concentrating on the Lomax model (as a base line model), the new family contains the “symmetric density” with many useful applied shapes. In applied section, the probability–probability (P–P) plot is presented.

The paper concentrates on the univariate version of the new family. On the other hand, some new bivariate type G families using “copula of Farlie–Gumbel–Morgenstern (FGM)”, modified copula of “Farlie–Gumbel–Morgenstern”, “the well-known Clayton copula” and “copula of Renyi’s entropy” are derived. The authors of [7] gave two major justifications as to why presenting new copulas are of interest to many statisticians. Following [3], the CDF of the KBX-G family can be expressed as

$$F_{\alpha ,\theta ,\lambda ,\underset{\_}{\delta }}\left(x\right)=1-{\left[1-H_{\lambda ,\underset{\_}{\delta }}^{\alpha }\left(x\right)\right]}^{\theta }{|}_{\alpha ,\theta ,\lambda \in R^{+} \mathrm{and} x\in \mathrm{R}}$$

(2)

For $\theta =1,$ the KBX-G reduces to the exponentiated Burr type X G (ExpBX-G) family. For $\lambda =1,$ the KBX-G reduces to the Kumaraswamy Rayleigh-G (KR-G) family. The PDF corresponding to (2) can be derived as

$$f_{\alpha ,\theta ,\lambda ,\underset{\_}{\delta }}\left(x\right)=\frac{2\alpha \theta \lambda g_{\underset{\_}{\delta }}\left(x\right)G_{\underset{\_}{\delta }}\left(x\right){\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(x\right)\right]\right\}}^{\lambda \left(\alpha +1\right)-1}}{{\overline{G}}_{\underset{\_}{\delta }}^3\left(x\right)\mathit{exp}\left[O_{\underset{\_}{\delta }}^2\left(x\right)\right]{\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(x\right)\right]\right\}}^{\alpha \lambda }\right)}^{1-\theta }}{|}_{\alpha ,\theta ,\lambda \in R^{+} \mathrm{and} x\in \mathrm{R}}.$$

(3)

The rest of the paper is outlined as follows: In Section 2, we derive a useful representation for the KBX-G density function. Five special models of this family are presented in Section 3 corresponding to the baseline exponential, Weibull, Rayleigh, Lomax and Burr XII distributions. We obtain in Section 4 some general mathematical properties of the proposed KBX-G family. In Section 5, simple-type copula using Farlie–Gumbel–Morgenstern (FGM) copula, modified FGM copula, Clayton copula and Renyi’s entropy are presented. Maximum likelihood estimation is defined in Section 6. Section 7 provides a graphical simulation study based on Kumaraswamy Burr X Lomax model. Section 8 provides two applications. Finally, concluding remarks are listed in Section 9.

2. Useful Expansions

Consider the binomial series given by

$${\left(1-\frac{{\zeta }_1}{{\zeta }_2}\right)}^{{\zeta }_3}={\displaystyle \sum }_{i=0}^{\infty }{\left(\frac{{\zeta }_1}{{\zeta }_2}\right)}^i\left(\begin{array}{c}{\zeta }_3\\ i\end{array}\right){(-1)}^i={\displaystyle \sum }_{i=0}^{\infty }{\left(\frac{{\zeta }_1}{{\zeta }_2}\right)}^i\frac{{(-1)}^j}{i!\Gamma \left(1+{\zeta }_3-i\right)}\Gamma \left(1+{\zeta }_3\right){|}_{{\zeta }_3>0,|\frac{{\zeta }_1}{{\zeta }_2}|<1},$$

(4)

Then, Equation (3) can be written as

$$f_{\alpha ,\theta ,\lambda ,\underset{\_}{\delta }}\left(x\right)=\frac{2\alpha \theta \lambda g_{\underset{\_}{\delta }}\left(x\right)}{{\overline{G}}_{\underset{\_}{\delta }}^3\left(x\right)\mathit{exp}\left[O_{\underset{\_}{\delta }}^2\left(x\right)\right]}{\displaystyle \sum }_{i=0}^{\infty }\frac{{(-1)}^i\left(\begin{array}{c}\theta -1\\ i\end{array}\right)G_{\underset{\_}{\delta }}\left(x\right)}{\underset{A\left(x\right)}{\underset{}{\underbrace{{\left[1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(x\right)\right]\right]}^{-\lambda \alpha \left(i+1\right)+1}}}}}$$

(5)

By expanding $A\left(x\right),$ we get

$$A\left(x\right)={\displaystyle \sum }_{h=0}^{\infty }{(-1)}^h\left(\begin{array}{c}\lambda \alpha \left(i+1\right)-1\\ h\end{array}\right)\mathit{exp}\left[-h{O}_{\underset{\_}{\delta }}^2\left(x\right)\right]$$

(6)

By merging (6) into (5) we have

$$f_{\alpha ,\theta ,\lambda ,\underset{\_}{\delta }}\left(x\right)=\frac{2\alpha \theta \lambda g_{\underset{\_}{\delta }}\left(x\right)G_{\underset{\_}{\delta }}\left(x\right)}{{\overline{G}}_{\underset{\_}{\delta }}^3\left(x\right)}{\displaystyle \sum }_{i,h=0}^{\infty }{(-1)}^{i+h}\frac{\left(\begin{array}{c}\theta -1\\ i\end{array}\right)\left(\begin{array}{c}\lambda \alpha \left(i+1\right)-1\\ h\end{array}\right)}{\underset{B\left(x\right)}{\underset{}{\underbrace{\mathit{exp}\left[\left(1+h\right)O_{\underset{\_}{\delta }}^2\left(x\right)\right]}}}}.$$

(7)

By expanding $B\left(x\right),$ we get

$$B\left(x\right)={\displaystyle \sum }_{j=0}^{\infty }\frac{O_{\underset{\_}{\delta }}^{2j}\left(x\right)}{j!}{(-1)}^j{(1+h)}^j.$$

(8)

Incorporating (8) into (7), we get

$$f_{\alpha ,\theta ,\lambda ,\underset{\_}{\delta }}\left(x\right)=2\alpha \theta \lambda g_{\underset{\_}{\delta }}\left(x\right){\displaystyle \sum }_{i,j,h=0}^{\infty }\frac{{(-1)}^{i+h+j}{(h+1)}^j\left(\begin{array}{c}\theta -1\\ i\end{array}\right)}{j!{\overline{G}}_{\underset{\_}{\delta }}{\left(x\right)}^{\left(2j+3\right)}{G}_{\underset{\_}{\delta }}{\left(x\right)}^{-2j-1}}\left(\begin{array}{c}\lambda \alpha \left(i+1\right)-1\\ h\end{array}\right).$$

(9)

Consider the generalized binomial expansion

$${\left(1-\frac{{\zeta }_1}{{\zeta }_2}\right)}^{-{\zeta }_3}={\displaystyle \sum }_{k=0}^{\infty }{\left(\frac{{\zeta }_1}{{\zeta }_2}\right)}^k\frac{\Gamma \left({\zeta }_3+k\right)}{k!\Gamma \left({\zeta }_3\right)}{|}_{{\zeta }_3>0,|\frac{{\zeta }_1}{{\zeta }_2}|<1}$$

(10)

Applying (10) to (9) gives

$$f_{\alpha ,\theta ,\lambda ,\underset{\_}{\delta }}\left(x\right)={\displaystyle \sum }_{k=0}^{\infty }{𝛻}_{j,k }\left(x\right){\pi }_{2j+k+2}\left(x\right),$$

(11)

where ${\pi }_{2j+k+2}\left(x\right)=\left(2j+k+2\right)g_{\underset{\_}{\delta }}\left(x\right)G_{\underset{\_}{\delta }}{(x)}^{2j+k+1}$ refers to the PDF of the exponentiated G (Exp-G) densities with power parameter $2j+k+2$ and

$${𝛻}_{j,k }=2\alpha \theta \lambda {\displaystyle \sum }_{i,h=0}^{\infty }\frac{{(-1)}^{i+h+j}{(h+1)}^j\Gamma \left(2j+3+k\right)}{j!k!\Gamma \left(2j+3\right)\left(2j+k+2\right)}\left(\begin{array}{c}\theta -1\\ i\end{array}\right)\left(\begin{array}{c}\lambda \alpha \left(i+1\right)-1\\ h\end{array}\right).$$

(12)

The CDF of the KBX-G family can be expressed as

$$F_{\alpha ,\theta ,\lambda ,\underset{\_}{\delta }}\left(x\right)={\displaystyle \sum }_{j,k=0}^{\infty }{𝛻}_{j,k }{\Pi }_{2j+k+2}\left(x\right),$$

(13)

where ${\Pi }_{2j+k+2}\left(x\right)=G_{\underset{\_}{\delta }}{(x)}^{2j+k+2}$ denotes the PDF of the exponentiated G (Exp-G) densities with power parameter $2j+k+2$.

3. Special Models

This section presents some special KBX models based on Exponential (E), Weibull (W), Rayleigh (R), Lomax (Lx) and Burr XII (BXII) distributions.

Table 1. New Sub Models Based on the New Kumaraswamy Burr X-G (KBX-G) Family.

No.	$\mathbf{Baseline} \mathbf{Model}$	${\mathit{O}}_{\underset{¯}{\mathit{\delta }}}^2\left(\mathit{x}\right)$	$\mathbf{The} \mathbf{New} \mathbf{Model}$	$\mathbf{Author}$
1	$\mathrm{Exponential} \left(E\right)$	${\left(e^{ax}-1\right)}^2$	$\mathrm{KBXE}$	$\mathrm{New}$
2	$\mathrm{Weibull} \left(W\right)$	${\left(e^{x^{\beta }}-1\right)}^2$	$\mathrm{KBXW}$	$\mathrm{New}$
3	$\mathrm{Rayleigh} \left(R\right)$	${\left(e^{x^2}-1\right)}^2$	$\mathrm{KBXR}$	$\mathrm{New}$
4	$\mathrm{Lomax} \left(\mathrm{Lx}\right)$	${\left[{\left(\frac{1}{a}x+1\right)}^b-1\right]}^2$	$\mathrm{KBXLx}$	$\mathrm{New}$
5	$\mathrm{Burr} \mathrm{XII} (\mathrm{BXII})$	${\left[{\left(x^a+1\right)}^b-1\right]}^2$	$\mathrm{KBXBXII}$	$\mathrm{New}$

below presents some new submodels based on the new KBX-G family. For the KBXLx, Figure 1 (right panel) and Figure 1 (left panel) give some plots of its PDF and the hazard rate function (HRF), respectively. Based on Figure 1 (right panel), the PDF of the KBX Lomax (KBXLx) can be “symmetric PDF” and “asymmetric right skewed PDF” with many useful shapes. Based on Figure 1 (left panel), the HRF of the KBXLx can be “decreasing–constant–increasing or U-shape HRF”, “decreasing HRF”, increasing HRF” and “J-HRF”.

4. Statistical Properties

4.1. Quantile Function

For the KBX quantile function, say $x=Q\left(u\right)$ can be derived via inverting (2) as

$$F^{-1}\left(u\right)=Q_G\left(u\right)=G^{-1}\left(\frac{-\frac{1}{2}{q}_{u^{•},\theta ,\alpha ,\lambda }}{1-\frac{1}{2}{q}_{u^{•},\theta ,\alpha ,\lambda }}\right){|}_{u^{•}=1-u},$$

where

$$q_{u^{•},\theta ,\alpha ,\lambda }=\mathit{log}\left[1-{\left(1-u^{•\frac{1}{\theta }}\right)}^{\frac{1}{\alpha \lambda }}\right]$$

4.2. Moments

Let $Z_{2j+k+2}$ be a nonnegative random variable which has the Exp-G with power parameter $2j+k+2$. The r$th$ moment of the KBX-G family can be obtained from (11) as

$${\mu }_r^{/}=E\left(X^r\right)={{\displaystyle \sum }}_{j,k=0}^{\infty }{\mathit{𝛻}}_{j,k } E\left(Z_{2j+k+2}^r\right),$$

where $E\left(Z_{\nu }^r\right)=\nu {{\displaystyle \int }}_{-\infty }^{\infty }{x}^r{g}_{\underset{\_}{\delta }}\left(x\right)G_{\underset{\_}{\delta }}{(x)}^{\nu -1},\nu >0$ can be calculated and analyzed numerically in terms of the baseline quantile function $Q_G\left(u\right)$, i.e., $Q_G\left(u\right)=G^{-1}\left(u\right)$ as

$$E\left(Z_{\nu }^r\right)=\nu {{\displaystyle \int }}_0^1{u}^{\nu -1}{Q}_G{(u)}^{r}du.$$

For the KBXLx model

$${\mu }_r^{/}={\displaystyle \sum }_{j,k=0}^{\infty }{\displaystyle \sum }_{w=0}^r{𝛻}_{j,k,w }^{\left(2j+k+2,r\right)}B\left(2j+k+2,\frac{w-r}{b}+1\right){|}_{b>r}.$$

where ${𝛻}_{j,k,w }^{\left(2j+k+2,r\right)}={𝛻}_{j,k }\left(2j+k+2\right)a^r{\left(-1\right)}^w\left(\begin{array}{c}r\\ w\end{array}\right)$ and $B\left(v_1,v_2\right)={{\displaystyle \int }}_0^1{u}^{v_1-1}{\left(1-u\right)}^{v_2-1}du$ is the complete beta function. Here, we introduce a formula for the moment generating function (MGF) as

$$M_X\left(t\right)=E\left(E^{tX}\right)={\displaystyle \sum }_{j,k=0}^{\infty }{𝛻}_{j,k } M_{2j+k+2}\left(t\right),$$

where $M_{2j+k+2}\left(t\right)$ is the moment generating function (MGF) of $Z_{2j+k+2}$. Consequently, we can easily determine $M_X\left(t\right)$ from the Exp-G MGF as

$$M_{\kappa }\left(t\right){|}_{\kappa >0}=\kappa {{\displaystyle \int }}_{-\infty }^{\infty }\mathit{exp}\left(tX\right)g_{\underset{\_}{\delta }}\left(x\right)G_{\underset{\_}{\delta }}{(x)}^{\kappa -1}=\kappa {{\displaystyle \int }}_0^1{u}^{\kappa -1}\mathit{exp}\left[t{Q}_G\left(u\right)\right]du$$

which can be calculated numerically from the baseline quantile function, i.e., $Q_G\left(u\right)=G^{-1}\left(u\right).$ Thus, for the KBXLx model we have

$$M_X\left(t\right)={{\displaystyle \sum }}_{j,k,r=0}^{\infty }{{\displaystyle \sum }}_{w=0}^r{𝛻}_{j,k,w }^{\left(2j+k+2,r\right)}\frac{t^r}{r!}B\left(2j+k+2,\frac{w-r}{b}+1\right){|}_{b>r}.$$

4.3. Conditional Moments

The s$th$ incomplete moments of $X$ defined by ${\Omega }_s\left(t\right)$ for any real $s>0$ can be expressed from (11) as

$${\Omega }_s\left(t\right)={{\displaystyle \int }}_{-\infty }^t{x}^{s}f\left(x\right)dx={\displaystyle \sum }_{j,k=0}^{\infty }{𝛻}_{j,k }{I}_{\left(-\infty ,t\right)}\left(x\right),$$

where $I_{\left(-\infty ,t\right)}\left(x\right)={{\displaystyle \int }}_{-\infty }^t{x}^s{\Omega }_{s,2j+k+2}\left(t\right)dx$ and ${\Omega }_{s,2j+k+2}\left(t\right)={{\displaystyle \int }}_0^{G\left(t\right)}{u}^{2j+k+1}{Q}_G{(u)}^{s}du$ and ${\Omega }_{s,2j+k+2}\left(t\right)$ can be evaluated numerically. For the KBXLx

$${\Omega }_s\left(t\right)={\displaystyle \sum }_{j,k=0}^{\infty }{\displaystyle \sum }_{w=0}^s{𝛻}_{j,k,w }^{\left(2j+k+2,s\right)}{B}_t\left(2j+k+2,\frac{w-s}{b}+1\right){|}_{b>r}.$$

where $B_y\left(v_1,v_2\right)={{\displaystyle \int }}_0^y{u}^{v_1-1}{\left(1-u\right)}^{v_2-1}du$ is the incomplete beta function.

4.4. Mean Deviation

The mean deviations of the mean $\mu =E\left(X\right)$ and the mean deviations of the median $Med$ are defined by

$$M_1\left(x\right)=E\hspace{0.17em}|\hspace{0.17em}X-{\mu }_1^{/}\hspace{0.17em}|=2{\mu }_1^{/}F\left({\mu }_1^{/}\right)-2{\Omega }_1\left({\mu }_1^{/}\right)$$

and

$$M_2\left(x\right)=E\hspace{0.17em}|\hspace{0.17em}X-Med\hspace{0.17em}|={\mu }_1^{/}-2{\Omega }_1\left(Med\right)$$

respectively, where ${\mu }_1^{/}=E\left(X\right),$ $Med=$ median $\left(X\right)=Q\left(\frac{1}{2}\right)$, and ${\Omega }_1\left(t\right)$ is the first complete moment given by ${\Omega }_s\left(t\right)$ with $s=1$.

5. Simple Type Copula

5.1. BvKBX Type via FGM Copula

Consider the joint CDF of the FGM family $C_{\pi }\left(u,v\right)=uv\left(1+\pi u^{•}{v}^{•}\right){|}_{u^{•}=1-u},$ where the marginal function $u=F_1$, $v=F_2$, $\pi \in \left(-1,1\right)$ is a dependence parameter and for every $u,v\in \left(0,1\right)$, $C_{\pi }\left(u,0\right)=C_{\pi }\left(0,v\right)=0$ which is “grounded minimum” and $u=C_{\pi }\left(u,1\right)$ and $v=C_{\pi }\left(1,v\right)$ which is “grounded maximum” (see [7,8,9,10,11,12]). Then, setting

$$u^{•}={\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(x_1\right)\right]\right\}}^{{\alpha }_1{\lambda }_1}\right)}^{{\theta }_1}{|}_{u\in \left[0,1\right]},$$

and

$$v^{•}={\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(x_2\right)\right]\right\}}^{{\alpha }_2{\lambda }_2}\right)}^{{\theta }_2}{|}_{v\in \left[0,1\right]},$$

we have

$$\begin{array}{c}C\left(F_1,F_2\right)=F\left(x_1,x_2\right)=\left[1-{\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(x_1\right)\right]\right\}}^{{\alpha }_1{\lambda }_1}\right)}^{{\theta }_1}\right]\\ \times \left[1-{\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(x_2\right)\right]\right\}}^{{\alpha }_2{\lambda }_2}\right)}^{{\theta }_2}\right]\\ \times \left\{1+\pi \left[\begin{array}{c}{\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(x_1\right)\right]\right\}}^{{\alpha }_1{\lambda }_1}\right)}^{{\theta }_1}\\ \times {\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(x_2\right)\right]\right\}}^{{\alpha }_2{\lambda }_2}\right)}^{{\theta }_2}\end{array}\right]\right\}.\end{array}$$

The joint PDF can then derived from $c_{\pi }\left(u,v\right)=1+\pi u^{*}{v}^{*}{|}_{\left(u^{*}=1-2u \mathrm{and} v^{*}=1-2v\right)}$ or from $f\left(x_1,x_2\right)=f_1{f}_{2}c\left(F_1,F_2\right).$

5.2. BvKBX Type via Modified FGM Copula

Consider the modified version of FGM copula defined as (see [11]) $C_{\pi }\left(u,v\right)=uv\left[1+\pi \vartheta \left(u\right)\omega \left(v\right)\right]{|}_{\pi \in \left(-1,1\right)}$ or $C_{\pi }\left(u,v\right)=uv+\pi {\vartheta }_u^{•}\hspace{0.17em}{\omega }_v^{•}{|}_{\pi \in \left(-1,1\right)}$ where ${\vartheta }_u^{•}=u\vartheta \left(u\right)$, and ${\omega }_v^{•}=v\omega \left(v\right)$. Where $\vartheta \left(u\right)$ and $\omega \left(v\right)$ are two functions on $\left(0,1\right)$ with the following conditions:

I The boundary condition:

$$\vartheta \left(0\right)=\vartheta \left(1\right)=\omega \left(0\right)=\omega \left(1\right)=0.$$

II Let

$${\tau }_1=\stackrel{\underset{}{}}{inf}\left\{{\vartheta }_u^{•}\hspace{0.17em}\hspace{0.17em}:\hspace{0.17em}\hspace{0.17em}\frac{\partial }{\partial u}{\vartheta }_u^{•}|K_1\right\}<0,$$

$${\tau }_2=\stackrel{\underset{}{}}{sup}\left\{{\vartheta }_u^{•}\hspace{0.17em}\hspace{0.17em}:\hspace{0.17em}\hspace{0.17em}\frac{\partial }{\partial u}{\vartheta }_u^{•}|K_1\right\}<0,$$

$${\xi }_1=\stackrel{\underset{}{}}{inf}\left\{{\omega }_v^{•}\hspace{0.17em}\hspace{0.17em}:\hspace{0.17em}\hspace{0.17em}\frac{\partial }{\partial v}{\omega }_v^{•}|K_2\right\}>0,$$

$${\xi }_2=\stackrel{\underset{}{}}{sup}\left\{{\omega }_v^{•}\hspace{0.17em}\hspace{0.17em}:\hspace{0.17em}\hspace{0.17em}\frac{\partial }{\partial v}{\omega }_v^{•}|K_2\right\}>0.$$

Then,

$$1\le \stackrel{\underset{}{}}{min}\left({\tau }_1{\tau }_2,{\xi }_1{\xi }_2\right)<\infty ,$$

where

$$\frac{\partial }{\partial u}{\vartheta }_u^{•}=\vartheta \left(u\right)+u\frac{\partial }{\partial u}\vartheta \left(u\right),$$

$$K_1=\left\{u\hspace{0.17em}\hspace{0.17em}:\hspace{0.17em}\hspace{0.17em}u\in \left(0,1\right)|\frac{\partial }{\partial u}{\vartheta }_u^{•} \mathrm{exists}\right\},$$

and

$$K_2=\left\{v\hspace{0.17em}\hspace{0.17em}:\hspace{0.17em}\hspace{0.17em}v\in \left(0,1\right)|\frac{\partial }{\partial v}{\omega }_v^{•} \mathrm{exists}\right\}.$$

BvKBX-FGM (Type I) model

Consider $C_{\pi }\left(u,v\right)=uv+\pi {\vartheta }_u^{•}{\omega }_v^{•}{|}_{\pi \in \left(-1,1\right)}$, then we get

$$C_{\pi }\left(u,v\right)=\pi {\vartheta }_u^{•}{\omega }_v^{•} +\left\{\begin{array}{c}\left[1-{\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(u\right)\right]\right\}}^{{\alpha }_1{\lambda }_1}\right)}^{{\theta }_1}\right]\\ \times \left[1-{\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(v\right)\right]\right\}}^{{\alpha }_2{\lambda }_2}\right)}^{{\theta }_2}\right]\end{array}\right\},$$

where ${\vartheta }_u^{•}=u{\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(u\right)\right]\right\}}^{{\alpha }_1{\lambda }_1}\right)}^{{\theta }_1}$ and ${\omega }_v^{•}$$=v{\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(v\right)\right]\right\}}^{{\alpha }_2{\lambda }_2}\right)}^{{\theta }_2}.$

BvKBX-FGM (Type II) model

Let $\vartheta \left(u\right)$ and $\omega \left(v\right)$ be two functional forms to satisfy all the conditions stated earlier where

$$\vartheta {\left(u\right)}^{•}=u^{{\pi }_1}{\left(1-u\right)}^{1-{\pi }_1}{|}_{\left({\pi }_1>0\right)} \mathrm{and} \mathsf{\omega }{\left(v\right)}^{•}=v^{{\pi }_2}{\left(1-v\right)}^{1-{\pi }_2}{|}_{\left({\pi }_2>0\right)}.$$

The corresponding BvKBX-FGM (Type II) can be derived from

$$C_{\pi ,{\pi }_1,{\pi }_2}\left(u,v\right)=uv\left[1+\pi \vartheta {\left(u\right)}^{•}\omega {\left(v\right)}^{•}\right].$$

BvKBX-FGM (Type III) model

Consider the following functional form for both $\Theta \left(u\right)$ and $\mathsf{\phi }\left(v\right)$ which satisfy all the conditions stated earlier where

$$\Theta \left(u\right)=u\left[\mathit{log}\left(1+\overline{u}\right)\right]|\overline{u}=1-\mathrm{u} \mathrm{and} \mathsf{\phi }\left(v\right)=w\left[\mathit{log}\left(1+\overline{v}\right)\right]|\overline{v}=1-v.$$

In this case, one can also derive a closed form expression for the associated CDF of the BivKBX-FGM (Type III).

BvKBX-FGM (Type IV) model

According to [13], the CDF of the BvKBX-FGM (Type IV) model can be derived from

$$C_{\pi }\left(u,v\right)=u{F}^{-1}\left(v\right)+v{F}^{-1}\left(u\right)-F^{-1}\left(u\right)F^{-1}\left(v\right),$$

Then,

$$F^{-1}\left(u\right)=G^{-1}\left(\frac{-\frac{1}{2}{q}_{u^{•},{\theta }_1,{\alpha }_1,{\lambda }_1}}{1-\frac{1}{2}{q}_{u^{•},{\theta }_1,{\alpha }_1,{\lambda }_1}}\right),F^{-1}\left(v\right)=G^{-1}\left(\frac{-\frac{1}{2}{q}_{v^{•},{\theta }_2,{\alpha }_2,{\lambda }_2}}{1-\frac{1}{2}{q}_{v^{•},{\theta }_2,{\alpha }_2,{\lambda }_2}}\right),$$

where $q_{u^{•},{\theta }_1,{\alpha }_1,{\lambda }_1}=\mathit{log}\left[1-\sqrt[{\alpha }_1{\lambda }_1]{1-\sqrt[{\theta }_1]{u^{•}}}\right]$ and $q_{v^{•},{\theta }_2,{\alpha }_2,{\lambda }_2}=\mathit{log}\left[1-\sqrt[{\alpha }_2{\lambda }_2]{1-\sqrt[{\theta }_2]{v^{•}}}\right]$.

5.3. BvKBX Type via Clayton Copula

The Clayton copula can be considered as

$$C\left(v_1,v_2\right)={\left[{\left(1/v_1\right)}^{𝛻}+{\left(1/v_2\right)}^{𝛻}-1\right]}^{-\frac{1}{𝛻}}{|}_{𝛻\in \left[0,\infty \right]}.$$

Let us assume that $T\sim$ KBX $\left({\alpha }_1,{\theta }_1,{\lambda }_1,\underset{\_}{\delta }\right)$ and $W\sim$ KBX $\left({\alpha }_2,{\theta }_2,{\lambda }_2,\underset{\_}{\delta }\right)$. Then, setting

$$v_1=v\left(t\right)=\left[1-{\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(t\right)\right]\right\}}^{{\alpha }_1{\lambda }_1}\right)}^{{\theta }_1}\right],$$

and

$$v_2=v\left(w\right)=\left[1-{\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(w\right)\right]\right\}}^{{\alpha }_2{\lambda }_2}\right)}^{{\theta }_2}\right],$$

Then, the BvKBX type distribution can be derived as

$$C\left(v_1,v_2\right)=C\left(F\left(t\right),F\left(w\right)\right)={\left[\begin{array}{c}{\left(\left[1-{\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(t\right)\right]\right\}}^{{\alpha }_1{\lambda }_1}\right)}^{{\theta }_1}\right]\right)}^{-𝛻}\\ +{\left(\left[1-{\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(w\right)\right]\right\}}^{{\alpha }_2{\lambda }_2}\right)}^{{\theta }_2}\right]\right)}^{-𝛻}\\ -1\end{array}\right]}^{-\frac{1}{𝛻}}.$$

5.4. BvKBX Type via Renyi’s Entropy

Consider the theorem of [14] where

$$R\left(u,v\right)=x_{2}u+x_{1}v-x_1{x}_2,$$

then, the associated BvKBX will be

$$\begin{array}{c}R\left(u,v\right)=R\left(F\left(x_1\right),F\left(x_2\right)\right)=-x_1{x}_2\\ +x_2\left[1-{\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(x_1\right)\right]\right\}}^{{\alpha }_1{\lambda }_1}\right)}^{{\theta }_1}\right]\\ +x_1\left[1-{\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(x_2\right)\right]\right\}}^{{\alpha }_2{\lambda }_2}\right)}^{{\theta }_2}\right].\end{array}$$

By fixing $a$ and $b$ we then have a five-dimension parameter BvKBX-type distribution.

5.5. MvKBX Extention via Clayton Copula

The $m$-dimensional extension from the above will be

$$C\left(v_i\right)={\left[{\displaystyle \sum }_{i=1}^m{v}_i^{-𝛻}+1-m\right]}^{-\frac{1}{𝛻}}.$$

Then, the MvKBX extension can expressed as

$$C\left(\underset{\_}{X}\right)={\left({\displaystyle \sum }_{i=1}^m{\left\{\left[1-{\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(x_i\right)\right]\right\}}^{{\alpha }_i{\lambda }_i}\right)}^{{\theta }_i}\right]\right\}}^{-𝛻}+1-m\right)}^{-\frac{1}{𝛻}},$$

where $\underset{\_}{X}=x_1,x_2,\cdots ,x_m$.

6. Maximum Likelihood Estimation

Let $\underset{\_}{\psi }={(\alpha ,\theta ,\lambda ,\underset{\_}{\delta })}^T$ be the vector of parameters, then the log-likelihood function for $\underset{\_}{\psi }$ is given by

$$\begin{array}{c}{L}_n\left(\underset{\_}{\psi }\right)=n\mathit{log}\left(2\alpha \theta \lambda \right)+{\displaystyle {\displaystyle \sum }_{i=0}^n}\mathit{log}{g}_{\underset{\_}{\delta }}\left(x_i\right)+{\displaystyle {\displaystyle \sum }_{i=0}^n}\mathit{log}{G}_{\underset{\_}{\delta }}\left(x_i\right)-3{\displaystyle {\displaystyle \sum }_{i=0}^n}\mathit{log}{\overline{G}}_{\underset{\_}{\delta }}\left(x_i\right)\\ +\left[\lambda \left(\alpha +1\right)-1\right]{\displaystyle {\displaystyle \sum }_{i=0}^n}\mathit{log}\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(x_i\right)\right]\right\}-{\displaystyle {\displaystyle \sum }_{i=0}^n}{O}_{\underset{\_}{\delta }}^2\left(x_i\right)\\ +\left(\theta -1\right){\displaystyle {\displaystyle \sum }_{i=0}^n}\mathit{log}\left(1-{\left\{1-\mathit{exp}\left[-O_{\underset{\_}{\delta }}^2\left(x_i\right)\right]\right\}}^{\alpha \lambda }\right).\end{array}$$

The components of the score function $U_n\left(\underset{\_}{\psi }\right)=\left(U_n\left(\alpha \right),U_n\left(\theta \right),U_n\left(\lambda \right),U_n\left(\underset{\_}{\delta }\right)\right).$ Setting the nonlinear system of equations $U_n\left(\alpha \right),U_n\left(\theta \right),U_n\left(\lambda \right),U_n\left(\underset{\_}{\delta }\right)$ equal to zero and solving the equations simultaneously yields the maximum likelihood estimation (MLE) of $\underset{\_}{\psi }$, where these equations cannot be solved analytically; thus, we use any statistical software to solve these equations.

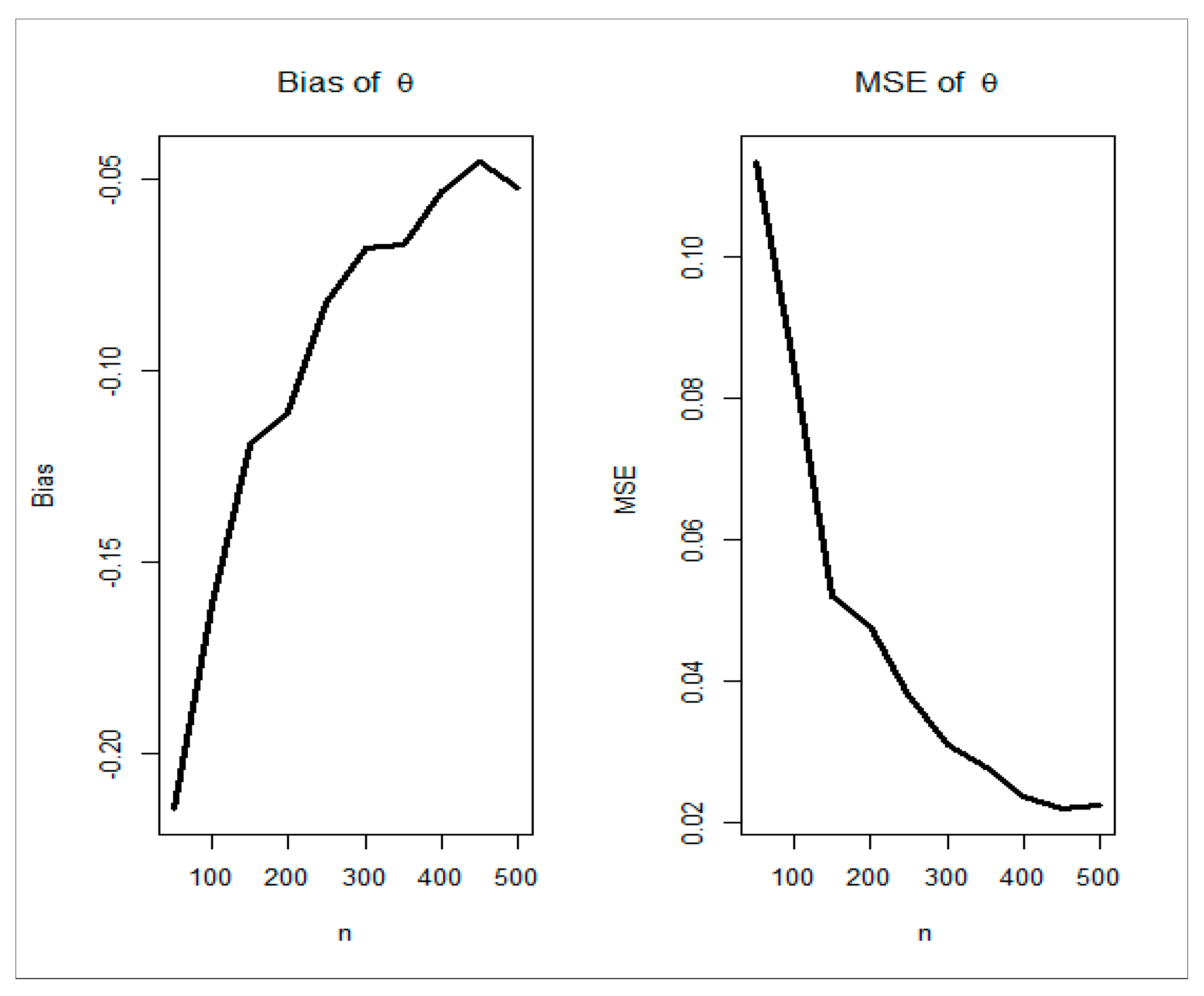
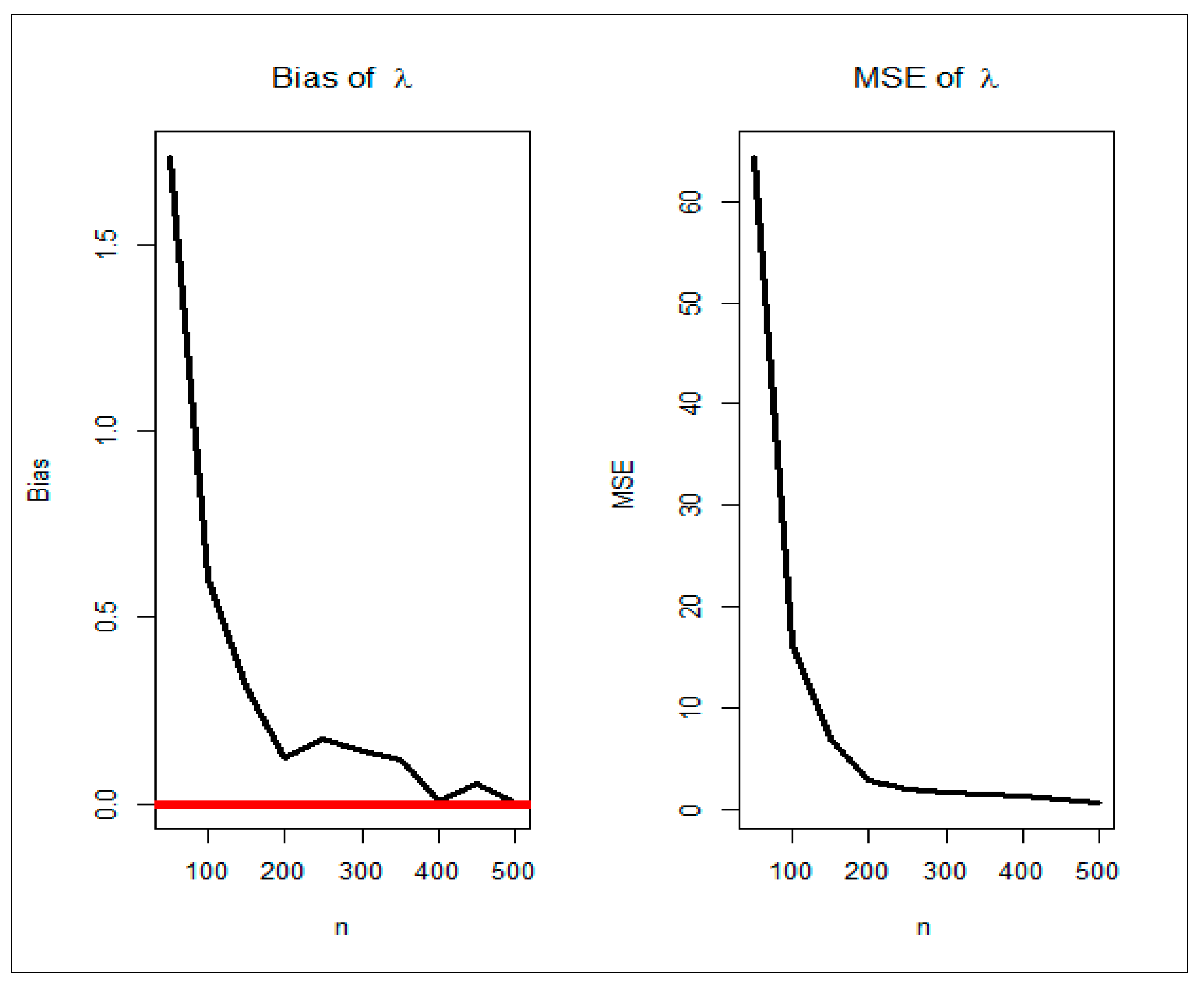
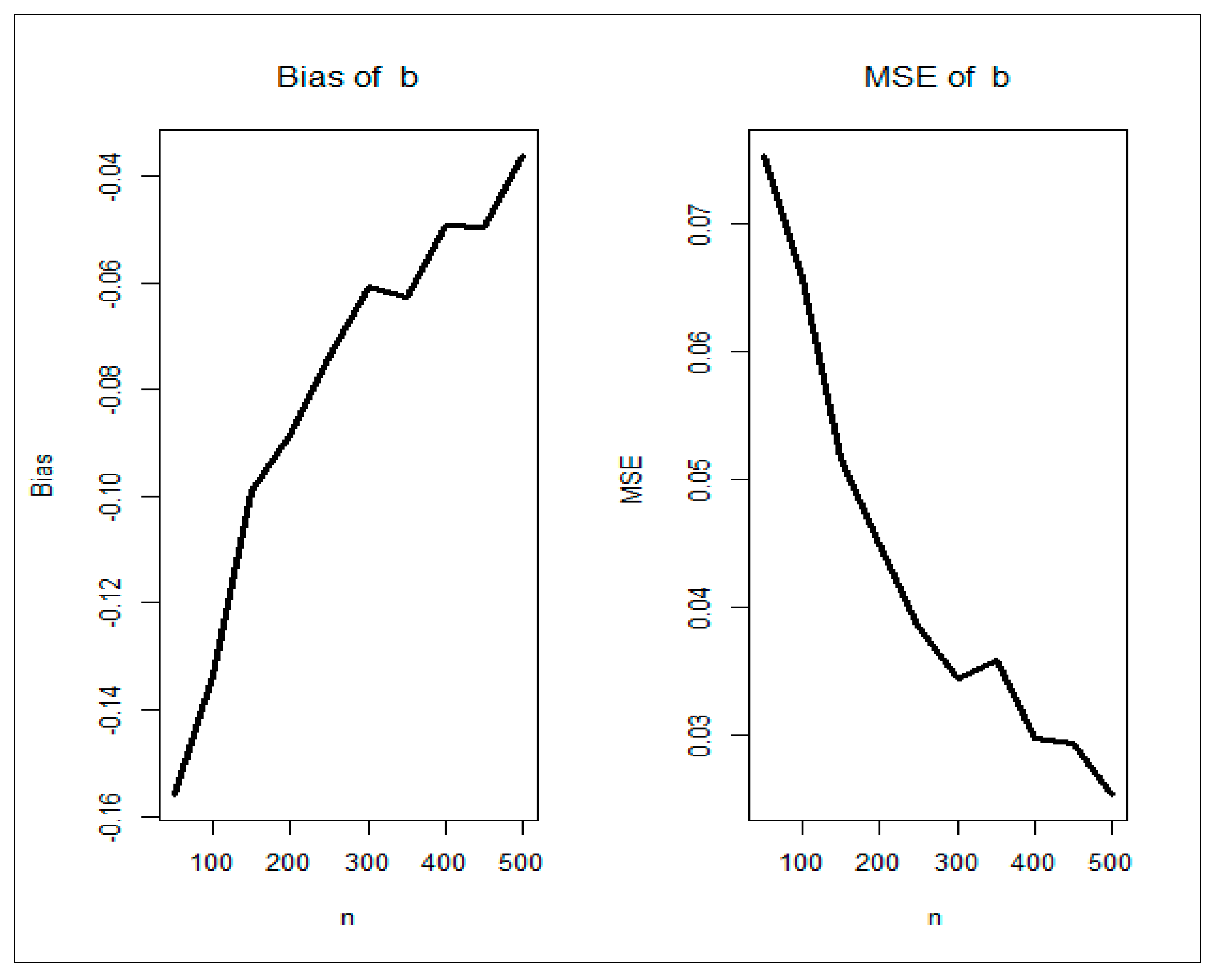
7. Simulations

To assess of the finite sample behavior of the MaxLEs under the KBXLx model, we will consider and apply the following algorithm:

1—Use

$$x_u=a\left\{{\left[1-\left(\frac{-\frac{1}{2}{q}_{u^{•},\theta ,\alpha ,\lambda }}{1-\frac{1}{2}{q}_{u^{•},\theta ,\alpha ,\lambda }}\right)\right]}^{-\frac{1}{b}}-1\right\}$$

to generate N = 1000 samples of size $n$ from the KBXLx distribution;

2—Compute the MaxLEs for the N = 1000 samples.

3—Compute the standard errors (StErs) of the MaxLEs for the N = 1000 samples.

4—Compute the biases $\left(B_h\right)$ and mean squared errors ($MSEs$) given for $h=\alpha ,\theta ,\lambda ,a,b$. We repeated these steps for $n=100,\dots ,500$ with $\alpha =\theta =\lambda =a=b=1$ so computing biases, mean squared errors $\left(MS{E}_h\right)$ for $\alpha ,\theta ,\lambda ,a,b$ and $n=100,\dots ,500$.

Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 (left panels) prove that the five biases decrease as $n\to \infty$. Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 (right panels) prove that the five MSEs decrease as $n\to \infty$. The red line in Figure 4 means that the bias reached zero. From Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 (left panels), the biases for each parameter decrease to zero as $n\to \infty$. From Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 (right panels), the MSEs decrease to zero as $n\to \infty$.

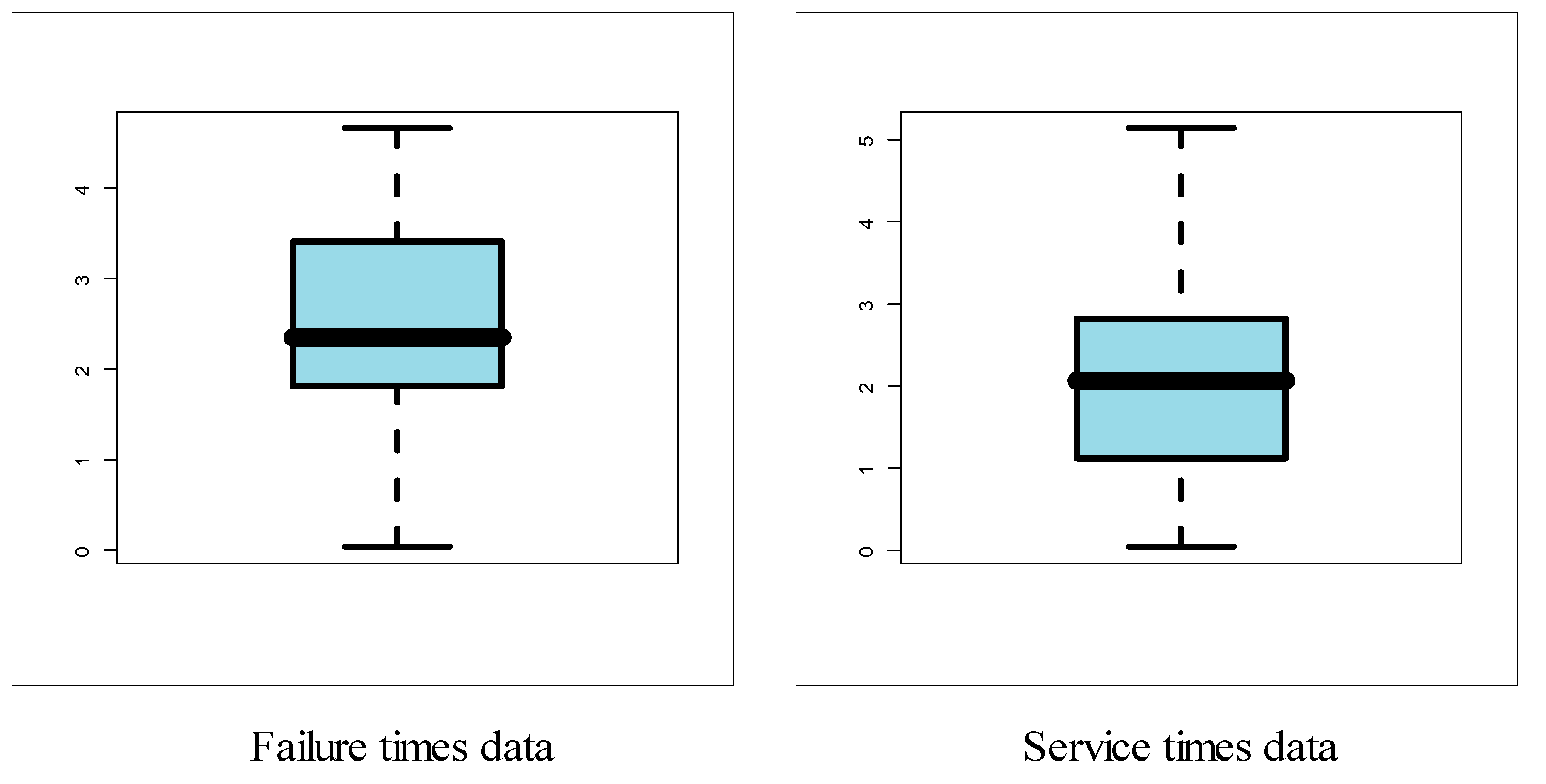
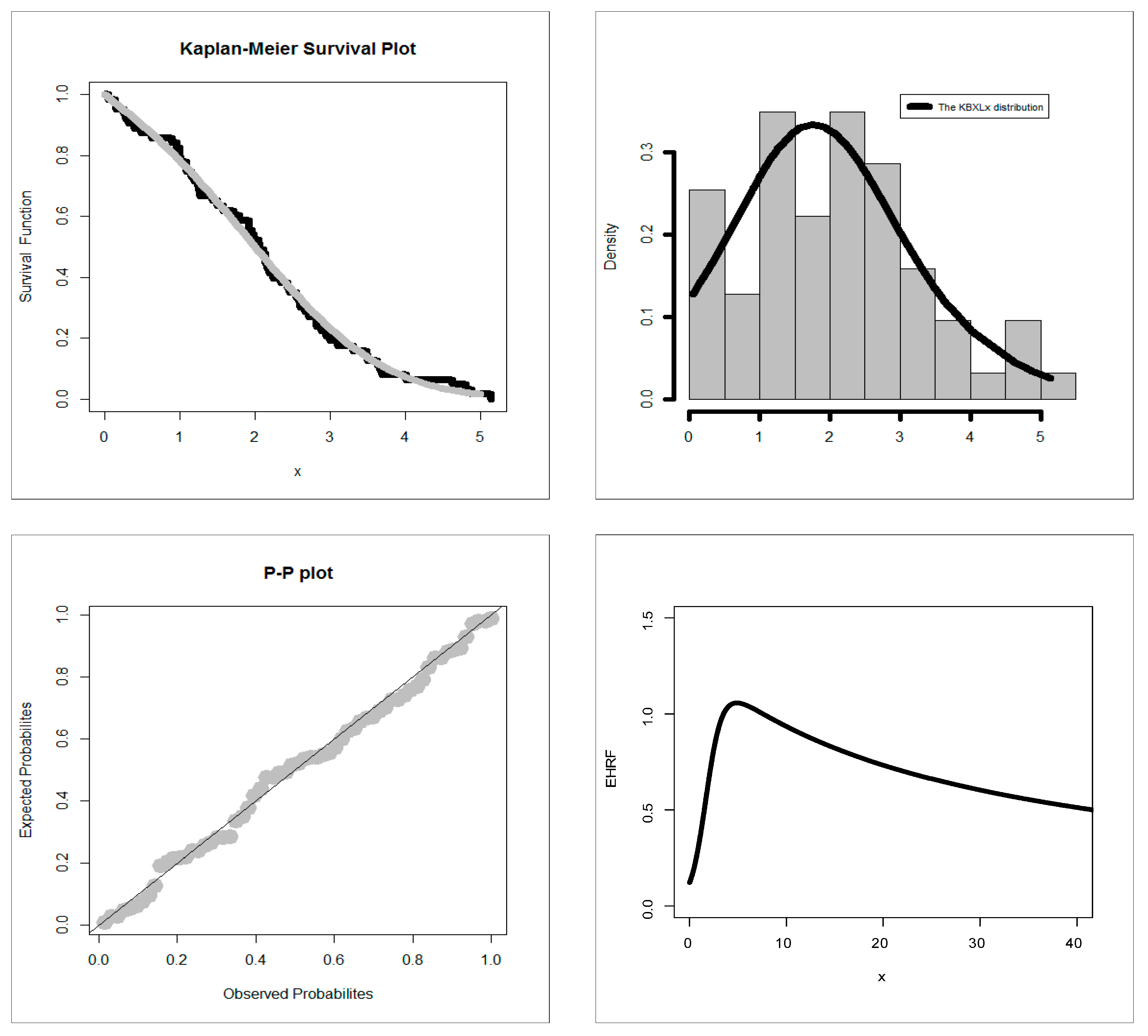
8. Applications and Comparing Models

In this section, we provide two real-life applications to illustrate the importance, potentiality and flexibility of the KBXLx model. We compare the fit of the KBXLx with some well-known competitive models (see

Table 2. The Competitive Model.

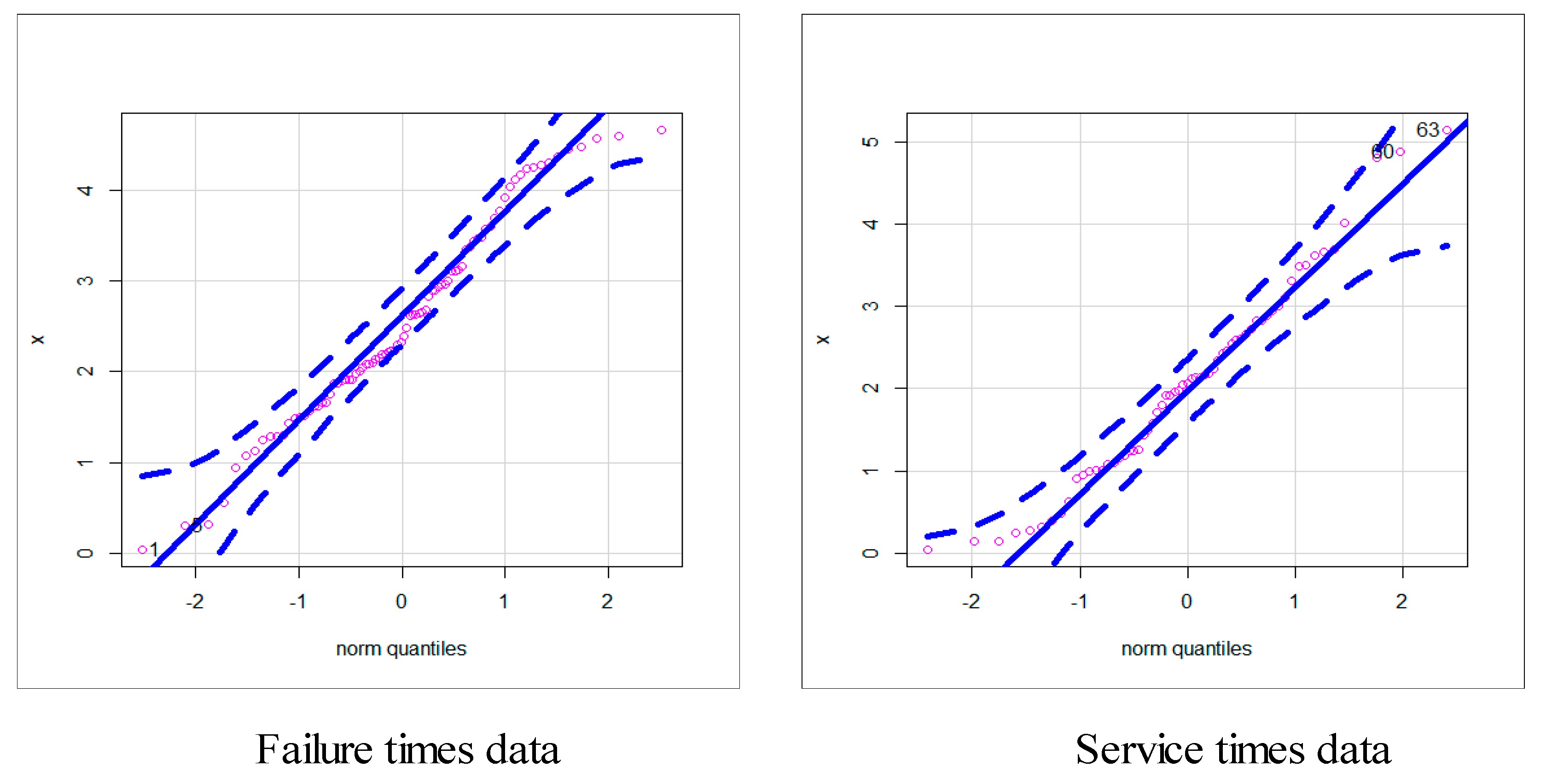
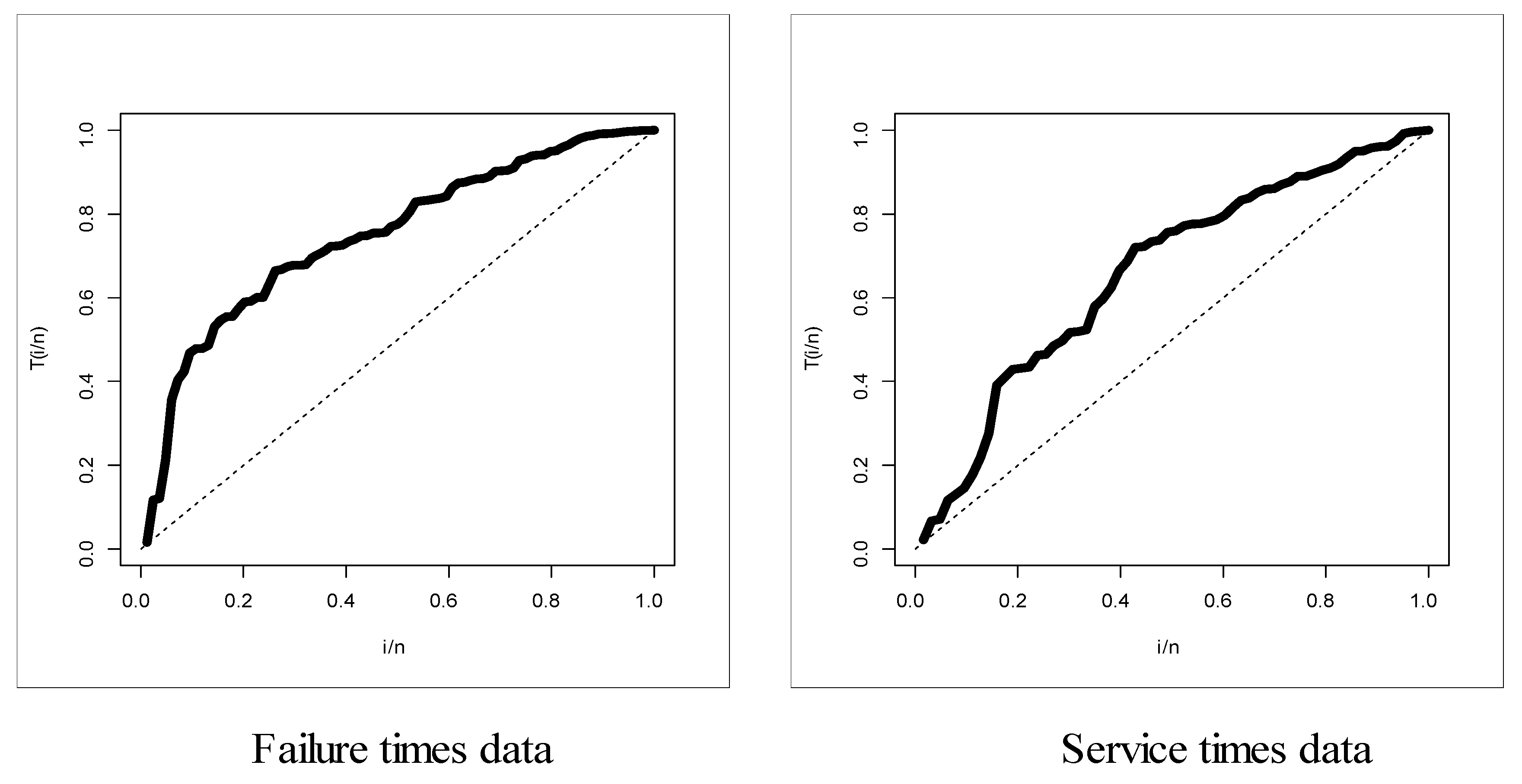
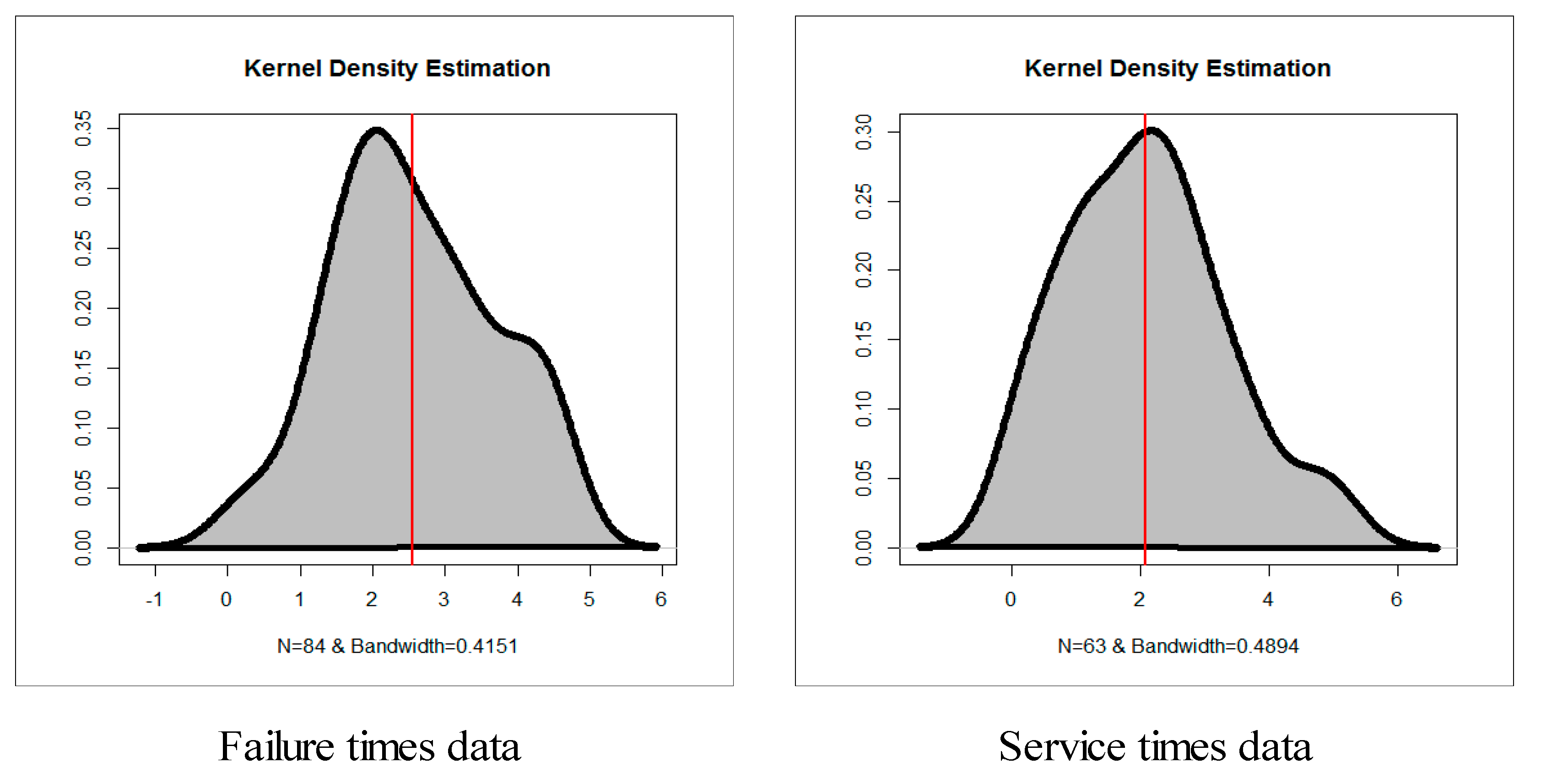
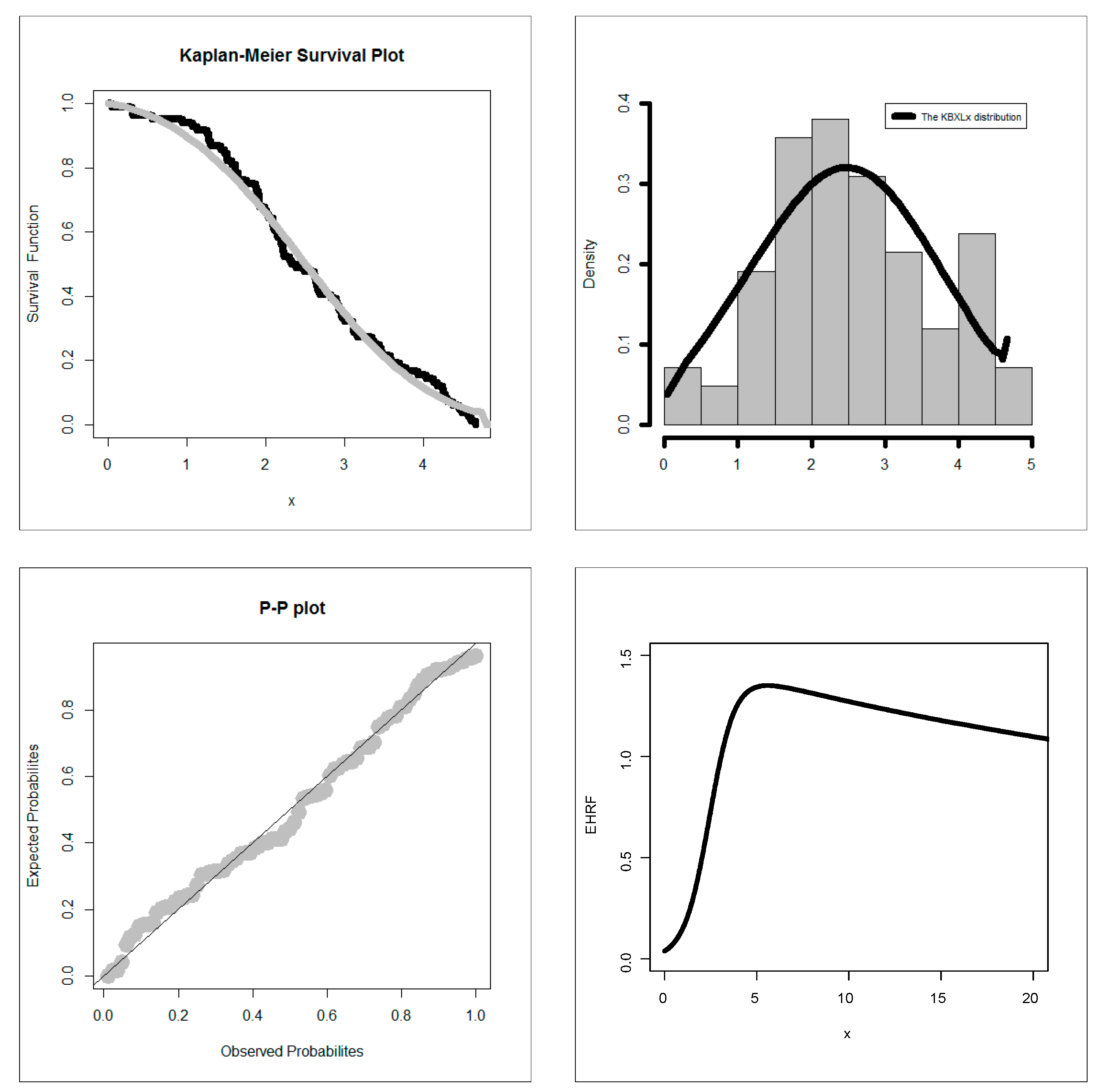
No.	Model	Abbreviation	Author
1	Special generalized mixture Lomax	SGMLx	[29]
2	Odd log-logistic Lx	OLLLx	[30]
3	Reduced OLLLx	ROLLLx	[30]
4	Reduced Burr–Hatke Lx	RBHLx	[6]
5	Transmuted Topp–Leone Lx	TTLLx	[31]
6	Reduced TTLLx	RTTLLx	[31]
7	Gamma Lx	GamLx	[32]
8	Kumaraswamy Lx	KumLx	[33]
9	McDonald Lx	McLx	[33]
10	Beta Lx	BLx	[33]
11	Exponentiated Lx	ExpLx	[34]
12	Lomax	Lx	[35]
13	Proportional reversed hazard rate Lx	PRHRLx	New

).

Dataset I (84 Aircraft Windshield): Times of Failure: The first real-life dataset represents the data on times of failure for 84 aircraft windshields (see [15]). The data observations are: 3.7790, 0.0400, 1.248, 2.154, 2.9640, 4.278, 4.449, 1.6190, 2.0100, 2.688, 3.9240, 1.2810, 2.038,2.224, 3.1170, 1.506, 1.866, 2.0850, 2.890, 4.121, 1.3030, 2.089, 2.902, 4.167, 1.4320, 2.097, 2.934, 4.2400, 0.943, 1.9120, 2.632, 3.5950, 1.0700, 1.914, 2.6460, 3.699, 1.1240, 4.376, 2.3850, 3.443, 0.3010, 1.876, 2.820, 3, 4.035, 1.281, 1.480, 2.135, 2.962, 4.2550, 1.505, 2.4810, 3.467, 0.309, 1.8990, 2.610, 3.4780, 0.557, 1.981, 2.661, 2.190, 3.000, 4.3050, 1.568, 2.1940, 3.103, 1.9110, 2.625,3.5780, 1.615, 2.2230, 3.114, 4.485, 1.652, 2.2290, 3.166, 4.570, 1.652, 2.3000, 3.344, 4.602, 1.7570, 2.324, 3.3760, 4.663. Dataset II (63 Aircraft Windshield): Times of Service: The second real-life dataset represents the times of service for 63 aircraft windshields (see [15]). The data observations are: 0.046, 0.622, 1.978, 3.0030, 0.9000, 2.053, 0.2800, 1.794, 3.483, 1.492, 2.600, 0.150, 3.3040, 0.9960, 3.1020, 0.952, 2.065, 0.487, 2.2400, 4.015, 1.183, 2.3410, 2.717, 2.819, 0.3130, 1.915, 2.820, 0.389, 1.9200, 2.878, 1.580, 2.670, 0.248, 1.7190, 1.092, 2.183, 3.695, 1.1520, 3.6220, 1.085, 2.163, 3.6650, 4.628, 1.0030, 2.137, 3.500, 1.0100, 2.141, 1.9630, 2.950, 2.117, 1.436, 2.592, 0.140, 1.2440, 2.435, 4.806, 1.249, 2.4640, 4.881, 1.262, 2.5430, 5.140. See supplementary for detailed data.

Many other useful real-life datasets can be found in [16,17,18,19,20,21,22,23,24,25,26,27]. For exploring the outliers, the box plot is plotted in Figure 7. Based on Figure 7, we note that no outliers were found. For checking the data normality, the Q–Q plot is sketched in Figure 8. Based on Figure 8, we note that normality nearly exists. For exploring the shape of the HRF for real data, the total time test (TTT) plot (see [28]) is provided (see Figure 9). Based on Figure 9, we note that the HRF is “increasing monotonically” for the two real-life datasets. For exploring the initial shape of real data nonparametrically, the KDE is provided in Figure 10. Figure 11 and Figure 12 give the estimated Kaplan–Meier survival (EKMS) plot, estimated PDF (EPDF), P–P plot and estimated HRF (EHRF) for dataset I and II, respectively.

The following goodness-of-fit (GOF) statistics are used: Akaike information criterion (AIC), Bayesian IC (BIC), consistent AIC (CAIC), Hannan–Quinn IC (HQIC), Cramér-von Mises ($W^{•}$) and Anderson–Darling ($A^{•}$) for comparing the competitive models. For failure time data, the results are listed in

Table 3. Maximum Likelihood Estimation (MLEs) and SEs for Failure Time Data.

Model	Estimates
KBXLx(θ,α,λ,b,a)	0.08869	0.141769	4.47434	1.6099	1.98809
	(0.0097)	(0.00216)	(171.22)	(0.0024)	(0.0021)
McLx(θ,α,λ,b,a)	2.1875	119.1751	12.4171	19.9243	75.6606
	(0.5211)	(140.297)	(20.845)	(38.960)	(147.24)
KLx(θ,β,b,a)	2.6150	100.2756	5.27710	78.6774
	(0.3822)	(120.486)	(9.8116)	(186.01)
TTLLx(θ,β,b,a)	−0.8075	2.47663	(15,608)	(38,628)
	(0.1396)	(0.5418)	(1602.4)	(123.94)
BLx(θ,β,b,a)	3.60360	33.63870	4.83070	118.837
	(0.6187)	(63.715)	(9.2382)	(428.93)
PRHRLx(β,b,a)	3.73 × 10⁶	4.707 × 10⁻1	4.49 × 10⁶
	1.01 × 10⁶	(0.00001)	37.14684
SGMLx(θ,b,a)	−1.04 × 10⁻1	9.83 × 10⁶	1.18 × e⁷
	(0.1223)	(4843.3)	(501.04)
RTTLLx(θ,β,a)	−0.84732	5.52057	1.15678
	(0.1001)	(1.1848)	(0.09588)
OLLLx(θ,b,a)	2.32636	(7.17 × e⁵)	2.34 × 10⁶)
	(2.14 × 10⁻1)	(1.19 × e⁴)	(2.61 × e1)
ExpLx(v,b,a)	3.62610	20,074.5	26,257.7
	(0.6236)	(2041.8)	(99.74)
GamLx(θ,b,a)	3.58760	52,001.4	37,029.7
	(0.5133)	(7955)	(81.16)
ROLLLx(θ,a)	3.890564	0.57316
	(0.36524)	(0.01946)
RBHLx(b,a)	10,801,754	51,367,189
	(983,309)	(232,312)
Lx(b,a)	51,425.4	131,790
	(5933.5)	(296.12)

and

Table 4. -ℓ and Goodness-of-Fit (GOF) Statistics for Failure Time Data.

Model	-ℓ	AIC	CAIC	BIC	HQIC	${\mathit{A}}^{•}$	${\mathit{W}}^{•}$
KBXLx	127.099	264.197	264.966	276.351	269.083	0.512	0.065
McLx	129.802	269.605	270.364	281.818	274.517	0.667	0.086
OLLLx	134.424	274.847	275.147	282.139	277.779	0.941	0.101
TTLLx	135.570	279.140	279.646	288.863	283.049	1.126	0.127
GamLx	138.404	282.808	283.105	290.136	285.756	1.367	0.162
BLx	138.718	285.435	285.935	295.206	289.365	1.408	0.168
ExpLx	141.400	288.799	289.096	296.127	291.747	1.744	0.219
ROLLLx	142.845	289.690	289.839	294.552	291.645	1.957	0.255
SGMLx	143.087	292.175	292.475	299.467	295.106	1.347	0.158
RTTLLx	153.981	313.962	314.262	321.254	316.893	3.753	0.559
PRHRLx	162.877	331.754	332.054	339.046	334.686	1.367	0.161
Lx	164.988	333.977	334.123	338.862	335.942	1.398	0.167
RBHLx	168.604	341.208	341.356	346.070	343.162	1.671	0.207

. Table 3 gives the MaxLEs and StErs for failure time data. Table 4 gives the $-\widehat{\ell }$ and GOF statistics for failure time data. For service time data, the analysis results are listed in

Table 5. MLEs and SEs for Service Time Data.

Model	Estimates
KBXLx(θ,α,λ,b,a)	0.1831	1.6937	0.25705	1.1995	1.52995
	(3.5 × 102)	(2.4124)	(0.3912)	(2.1 × 102)	(2.2 × 102)
BLx(θ,β,b,a)	1.9218	31.2594	4.9684	169.572
	(0.3184)	(316.84)	(50.528)	(339.21)
KLx(θ,β,b,a)	1.6691	60.5673	2.56490	65.0640
	(0.257)	(86.013)	(4.7589)	(177.59)
TTLLx(θ,β,b,a)	(−0.607)	1.78578	2123.391	4822.79
	(0.2137)	(0.4152)	(163.915)	(200.01)
RTTLLx(θ,β,a)	−0.6715	2.74496	1.01238
	(0.18746)	(0.6696)	(0.1141)
PRHRLx(β,b,a)	1.59 × 10⁶	3.93 × 10⁻1	1.30 × 10⁶
	2.01 × 103	0.0004 × 10⁻1	0.95 × 10⁶
SGMLx(θ,b,a)	−1.04 × 10⁻1	6.45 × 10⁶	6.33 × 10⁶
	(4.1 × 10⁻1⁰)	(3.21 × 10⁶)	(3.8573)
GamLx(θ,b,a)	1.9073	35,842.433	39,197.57
	(0.3213)	(6945.074)	(151.653)
OLLLx(θ,b,a)	1.66419	6.340 × 10⁵	2.01 × 10⁶
	(1.79 × 10⁻1)	(1.68 × 10⁴)	7.22 × 10⁶
ExpLx(θ,b,a)	1.9145	22,971.15	32,882
	(0.348)	(3209.53)	(162.2)
RBHLx(b,a)	14,055,522	53,203,423
	(422.01)	(28.5232)
ROLLLx(θ,a)	2.37233	0.69109
	(0.2683)	(0.0449)
Lx(b,a)	99,269.8	207,019.4
	(11,864)	(301.237)

and

Table 6. -ℓ and GOFs Statistics for Service Time Data.

Model	-ℓ	AIC	CAIC	BIC	HQIC	${\mathit{A}}^{•}$	${\mathit{W}}^{•}$
KBXLx	98.0851	206.170	207.223	216.886	210.385	0.219	0.032
KLx	100.866	209.735	210.425	218.308	213.107	0.739	0.122
TTLLx	102.449	212.900	213.589	221.472	216.271	0.943	0.155
GamLx	102.833	211.666	212.073	218.096	214.195	1.112	0.184
SGMLx	102.894	211.788	212.195	218.218	214.317	1.113	0.184
BLx	102.961	213.922	214.612	222.495	217.294	1.134	0.187
ExpLx	103.550	213.099	213.506	219.529	215.628	1.233	0.204
OLLLx	104.904	215.808	216.215	222.238	218.337	0.942	0.155
PRHRLx	109.299	224.597	225.004	231.027	227.126	1.126	0.186
Lx	109.299	222.598	222.798	226.884	224.283	1.127	0.186
ROLLLx	110.729	225.457	225.657	229.744	227.143	2.347	0.391
RTTLLx	112.186	230.371	230.778	236.800	232.900	2.688	0.453
RBHLx	112.601	229.201	229.401	233.487	230.887	1.398	0.232

. Table 5 gives the MaxLEs and StErs for service time data, and Table 6 gives the $-\widehat{\ell }$ and GOFs statistics for the service time data. Based on Table 4 and Table 6, we note that the KBXLx model gives the lowest values for the AIC, CAIC, BIC, HQIC, $A^{•}$ and $W^{•}$among all the fitted models. Hence, it could be chosen as the best model under these criteria.

It is worth mentioning that the presented class of stochastic distributions can have also an important utilization in the insurance industry, risks, reliability, medicine and engineering (see [36,37,38,39,40,41,42,43,44,45,46,47]).

9. Conclusions

A new family of probability distributions based on the Kumaraswamy and Burr X families is derived and studied. Some new bivariate type G families using Farlie–Gumbel–Morgenstern copula, modified Farlie–Gumbel–Morgenstern copula, Clayton copula and Renyi’s entropy copula are derived. Some special models based on exponential, Weibull, Rayleigh, Lomax and Burr XII distributions are presented. Then, special attention is devoted to the Lomax case. Some of its statistical properties, including the quantile function, moments, incomplete moments and mean deviation, are presented. Simulation based on biases and mean squared errors is introduced. Based on this simulation, the maximum likelihood method performs well and can be used for estimating the model parameters. Finally, two real-life applications to illustrate the importance of the new family are proposed.