High-Sensitivity Capsule-Shaped Sensor Based on 2D Photonic Crystals
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Waveguide Characteristics
2.2. The Sensor Characteristics
2.3. The Refractive Index Sensitivity
3. Sensor Optimization Results and Discussion
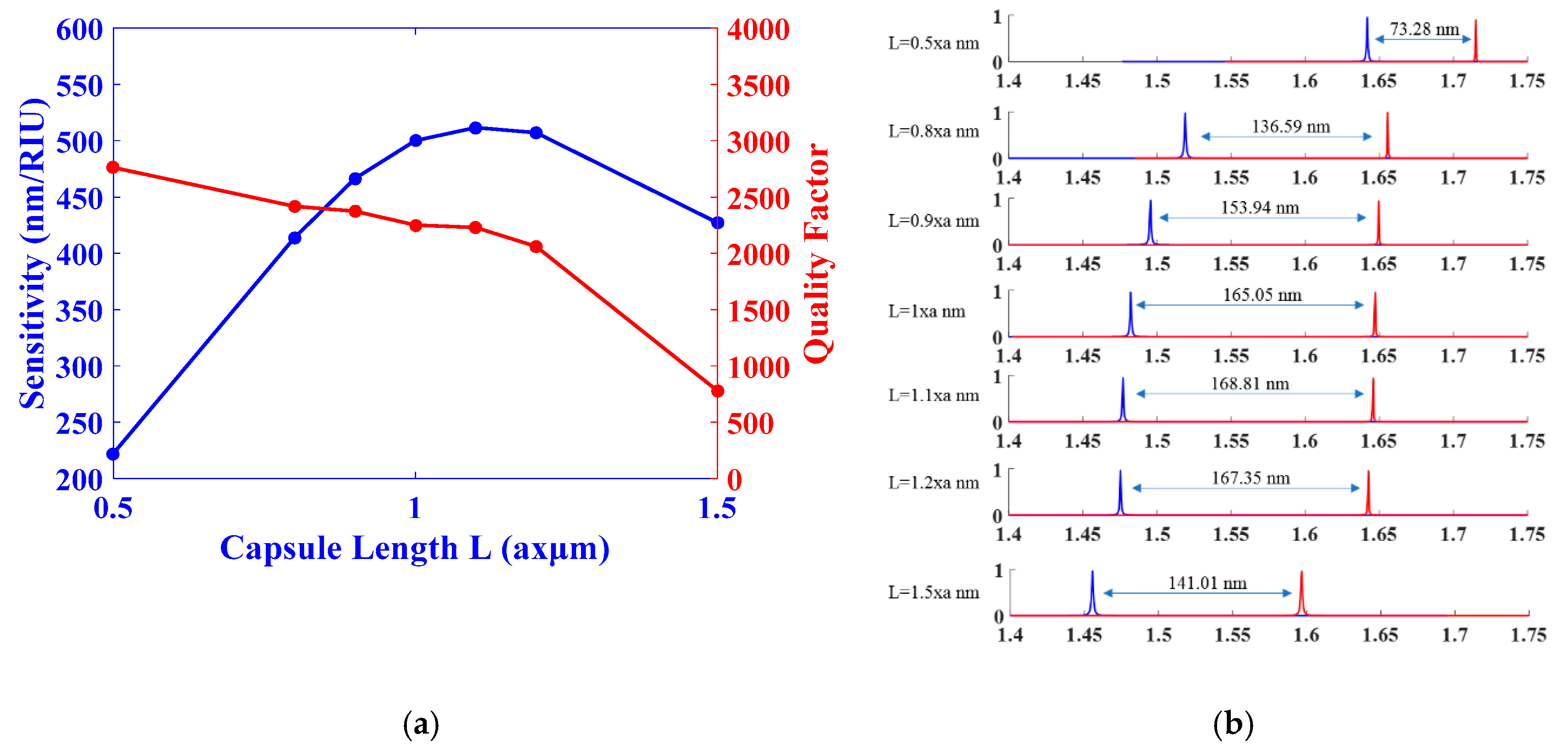
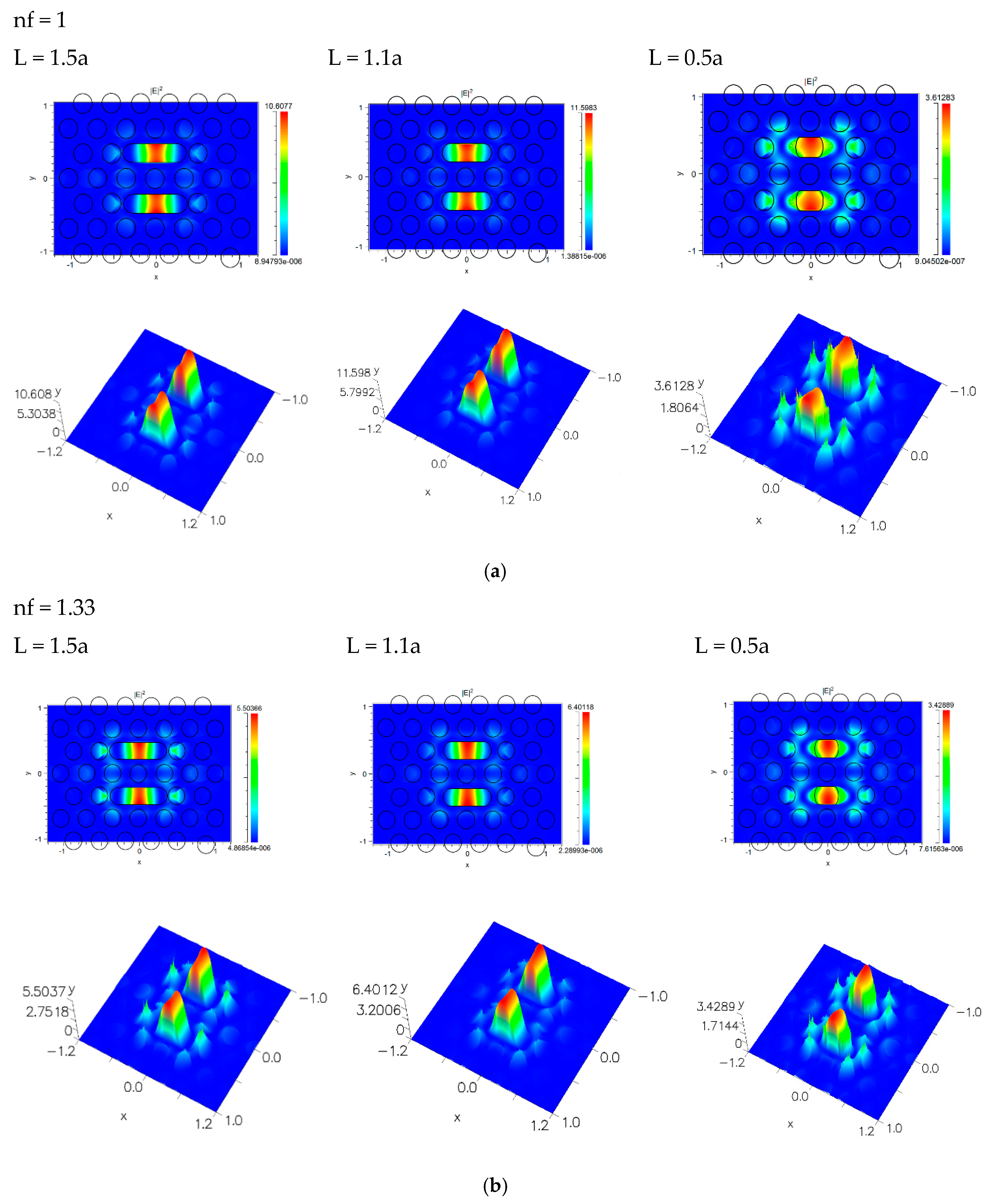
3.1. The Effects of the Capsule Length Sensitivity
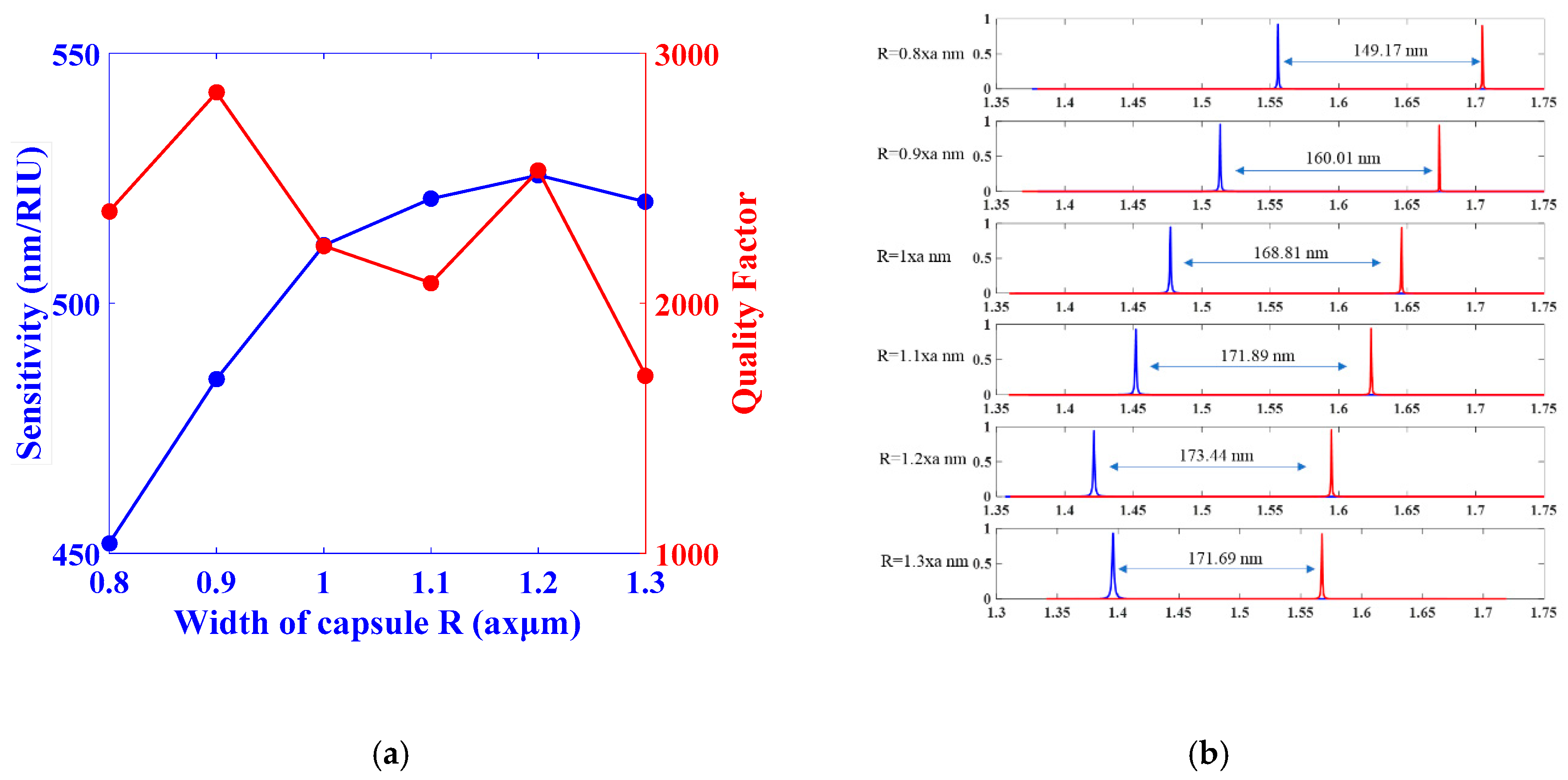
3.2. The Effect of the Capsule Width
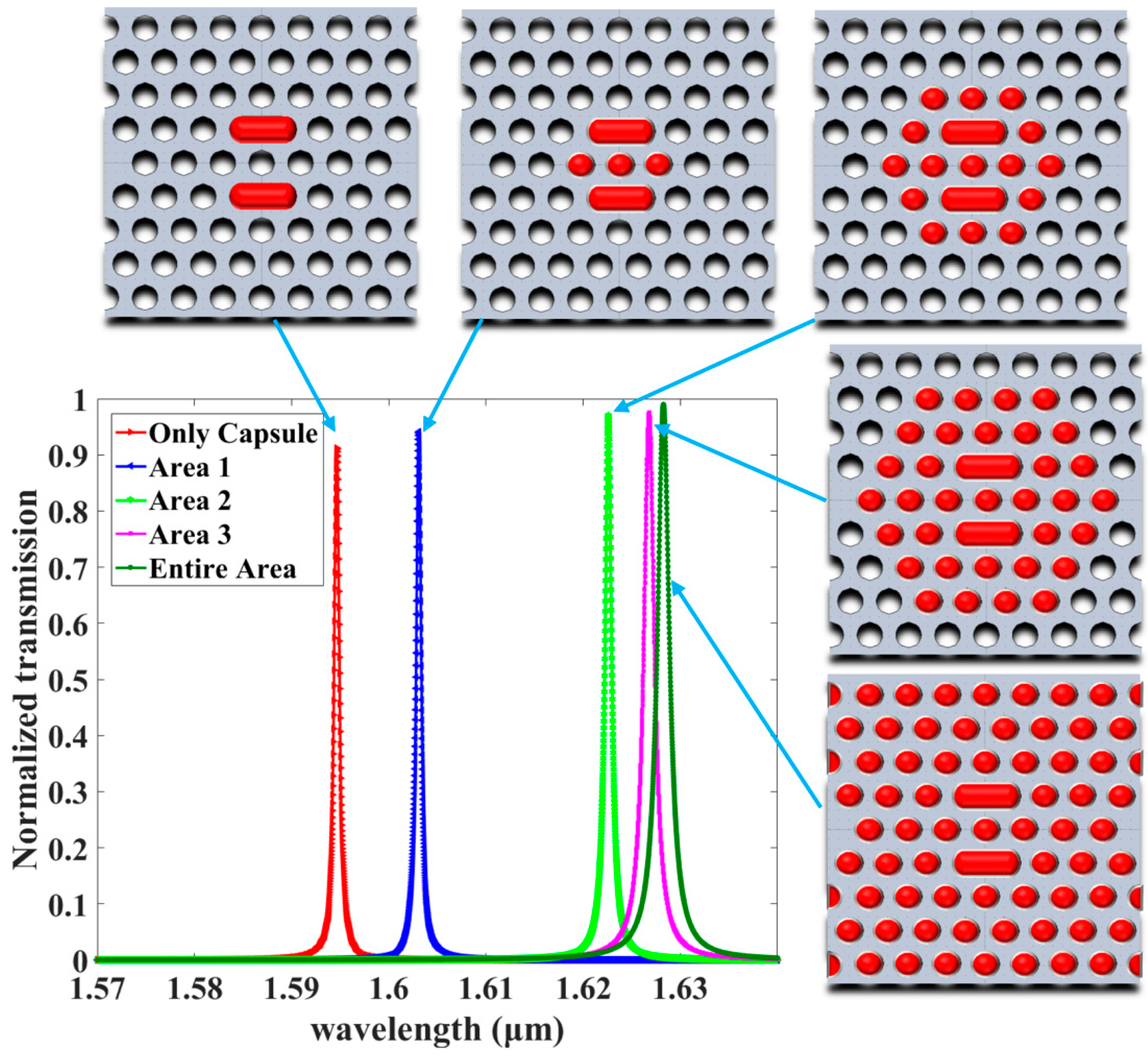
3.3. The Effect of Different Area Infiltration Sensitivity
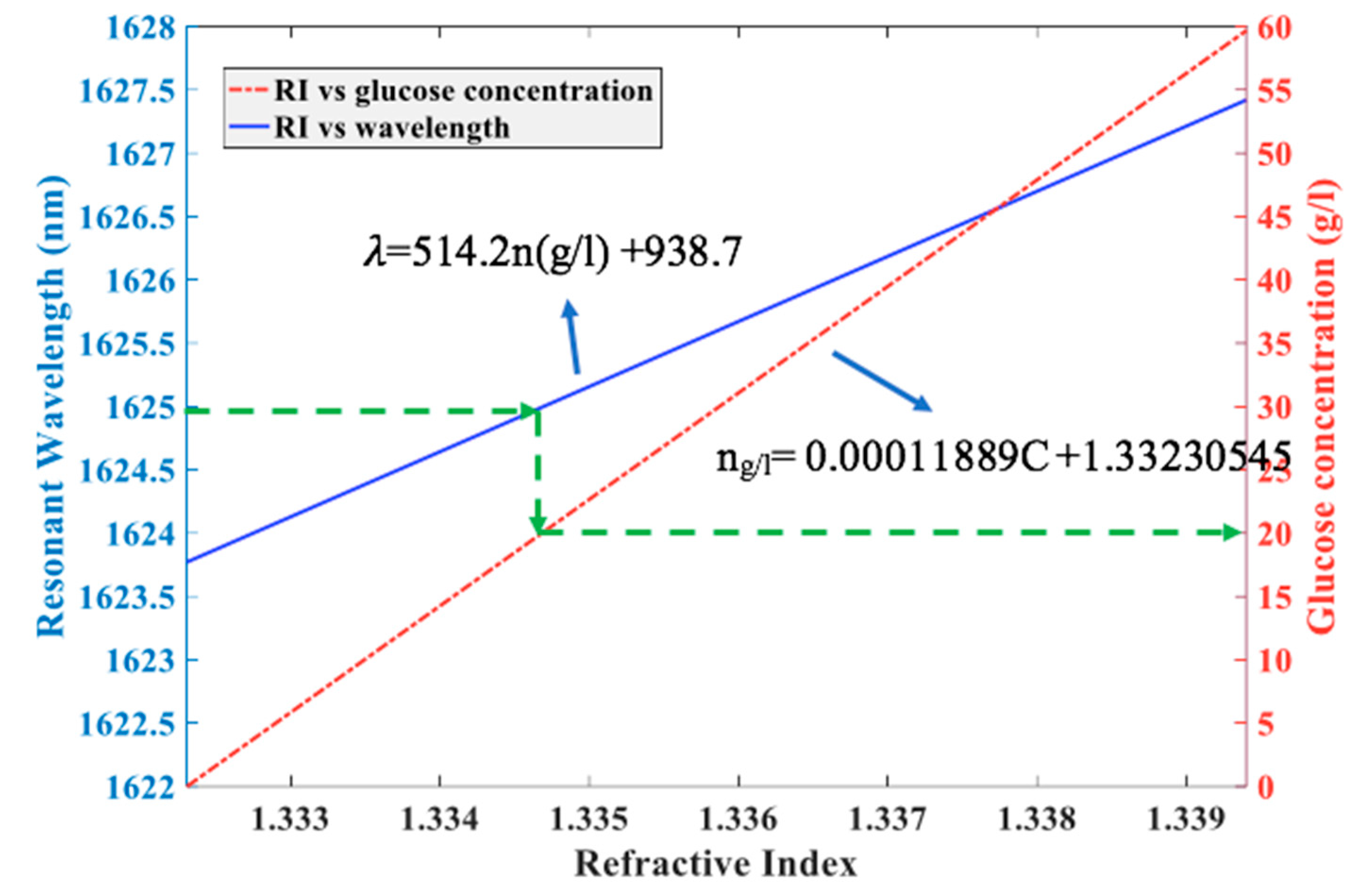
3.4. The Capsule-Shaped Cavity as a Glucose Concentration Sensor
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Arunkumar, R.; Suaganya, T.; Robinson, S. Design and Analysis of 2D Photonic Crystal Based Biosensor to Detect Different Blood Components. Photon Sens. 2018, 9, 69–77. [Google Scholar] [CrossRef]
- Mohammed, N.A.; Hamed, M.M.; Khalaf, A.A.M.; Alsayyari, A.; El-Rabaie, S. High-sensitivity ultra-quality factor and remarkable compact blood components biomedical sensor based on nanocavity coupled photonic crystal. Results Phys. 2019, 14, 102478. [Google Scholar] [CrossRef]
- Romano, S.; Lamberti, A.; Masullo, M.; Penzo, E.; Cabrini, S.; Rendina, I.; Mocella, V. Optical Biosensors Based on Photonic Crystals Supporting Bound States in the Continuum. Materials 2018, 11, 526. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caër, C.; Serna, S.; Zhang, W.; Le Roux, X.; Cassan, É. Liquid sensor based on high-Q slot photonic crystal cavity in silicon-on-insulator configuration. Opt. Lett. 2014, 39, 5792–5794. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.; Wang, Q. Measurement of methane concentration with cryptophane E infiltrated photonic crystal microcavity. Sens. Actuators B Chem. 2015, 209, 431–437. [Google Scholar] [CrossRef]
- Hsiao, F.-L.; Lee, C. Computational Study of Photonic Crystals Nano-Ring Resonator for Biochemical Sensing. IEEE Sens. J. 2010, 10, 1185–1191. [Google Scholar] [CrossRef]
- Dutta, H.S.; Goyal, A.K.; Pal, S. Sensitivity enhancement in photonic crystal waveguide platform for refractive index sensing applications. J. Nanophotonics 2014, 8, 083088. [Google Scholar] [CrossRef]
- Bougriou, F.; Bouchemat, T.; Bouchemat, M.; Paraire, N. Optofluidic sensor using two-dimensional photonic crystal waveguides. Eur. Phys. J. Appl. Phys. 2013, 62, 11201. [Google Scholar] [CrossRef]
- Lai, W.-C.; Chakravarty, S.; Wang, X.; Lin, C.; Chen, R.T. On-chip methane sensing by near-IR absorption signatures in a photonic crystal slot waveguide. Opt. Lett. 2011, 36, 984–986. [Google Scholar] [CrossRef]
- Di Falco, A.; O’Faolain, L.; Krauss, T.F. Chemical sensing in slotted photonic crystal heterostructure cavities. Appl. Phys. Lett. 2009, 94, 063503. [Google Scholar] [CrossRef]
- Arafa, S.; Bouchemat, M.; Bouchemat, T.; Benmerkhi, A.; Hocini, A. Infiltrated photonic crystal cavity as a highly sensitive platform for glucose concentration detection. Opt. Commun. 2017, 384, 93–100. [Google Scholar] [CrossRef]
- Huang, L.; Tian, H.; Zhou, J.; Liu, Q.; Zhang, P.; Ji, Y. Label-free optical sensor by designing a high-Q photonic crystal ring–slot structure. Opt. Commun. 2015, 335, 73–77. [Google Scholar] [CrossRef]
- Butt, M.; Khonina, S.N.; Kazanskiy, N. An array of nano-dots loaded MIM square ring resonator with enhanced sensitivity at NIR wavelength range. Optik 2020, 202, 163655. [Google Scholar] [CrossRef]
- Butt, M.; Kazanskiy, N.L.; Khonina, S.N. Highly Sensitive Refractive Index Sensor Based on Plasmonic Bow Tie Configuration. Photon Sens. 2020, 10, 223–232. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Chou, S.-H.; Hsueh, W.-J. Robust high-Q filter with complete transmission by conjugated topological photonic crystals. Sci. Rep. 2020, 10, 1–7. [Google Scholar] [CrossRef]
- Kunz, K.S.; Luebbers, R.J. The Finite Difference Time Domain Method for Electromagnetics; CRC Press: Boca Roton, FL, USA, 1993. [Google Scholar]
- Bérenger, J.-P. A perfectly matched layer for the absorption of electromagnetic waves. J. Comput. Phys. 1994, 114, 185–200. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.; Li, J. Theoretical research on slow light engineering of slotted photonic crystal waveguides with elliptical holes and optofluidic infiltration. Appl. Opt. 2015, 54, 1639. [Google Scholar] [CrossRef]
- White, I.M.; Fan, X. On the performance quantification of resonant refractive index sensors. Opt. Express 2008, 16, 1020–1028. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Zhao, Y.; Lv, R.-Q. A review for optical sensors based on photonic crystal cavities. Sens. Actuators A Phys. 2015, 233, 374–389. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Xu, Z.; Lu, N.; Zhu, J.; Jin, G. Ultracompact refractive index sensor based on microcavity in the sandwiched photonic crystal waveguide structure. Opt. Commun. 2008, 281, 1725–1731. [Google Scholar] [CrossRef]
- Yeh, Y.-L. Real-time measurement of glucose concentration and average refractive index using a laser interferometer. Opt. Lasers Eng. 2008, 46, 666–670. [Google Scholar] [CrossRef]
- Shiramin, L.A.; Kheradmand, R.; Abbasi, A. High-Sensitive Double-Hole Defect Refractive Index Sensor Based on 2-D Photonic Crystal. IEEE Sens. J. 2013, 13, 1483–1486. [Google Scholar] [CrossRef]
- Rahman-Zadeh, F.; Danaie, M.; Kaatuzian, H. Design of a highly sensitive photonic crystal refractive index sensor incorporating ring-shaped GaAs cavity. Opto Electron. Rev. 2019, 27, 369–377. [Google Scholar] [CrossRef]
- Danaie, M.; Kiani, B.; Mohammad, D.; Behnam, K. Design of a label-free photonic crystal refractive index sensor for biomedical applications. Photon. Nanostructures Fundam. Appl. 2018, 31, 89–98. [Google Scholar] [CrossRef]
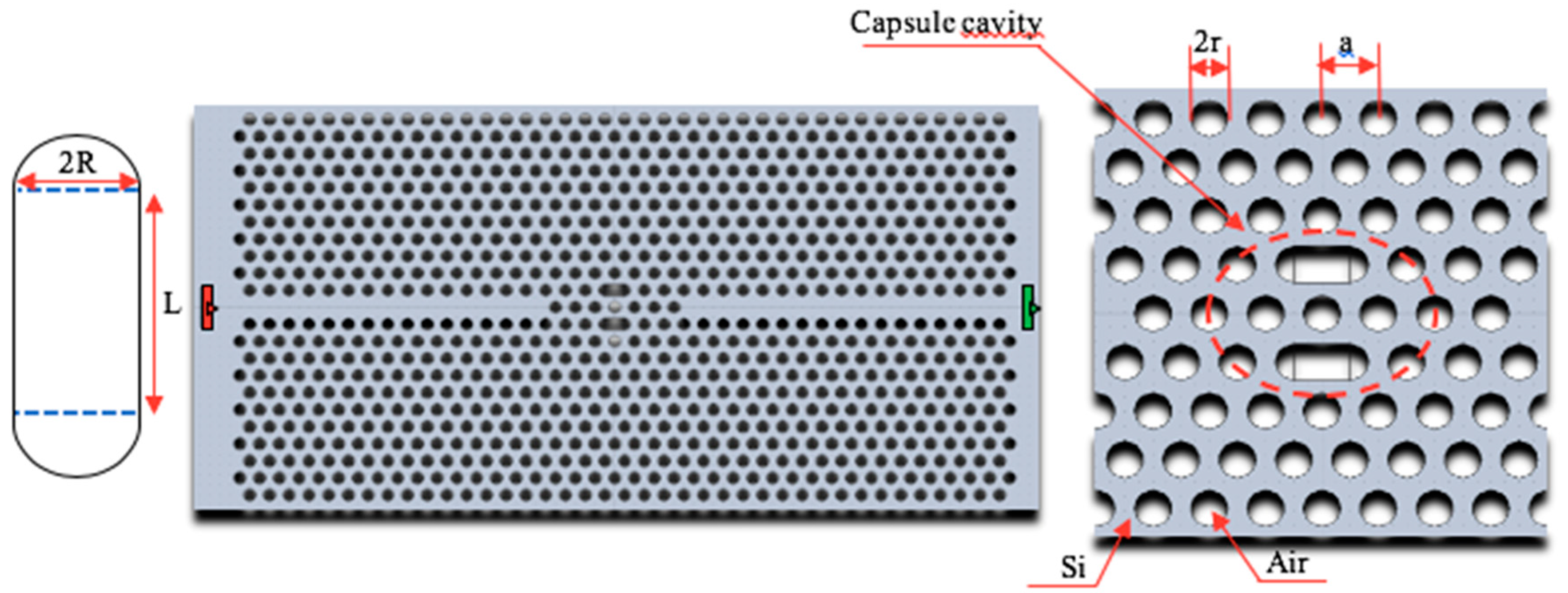
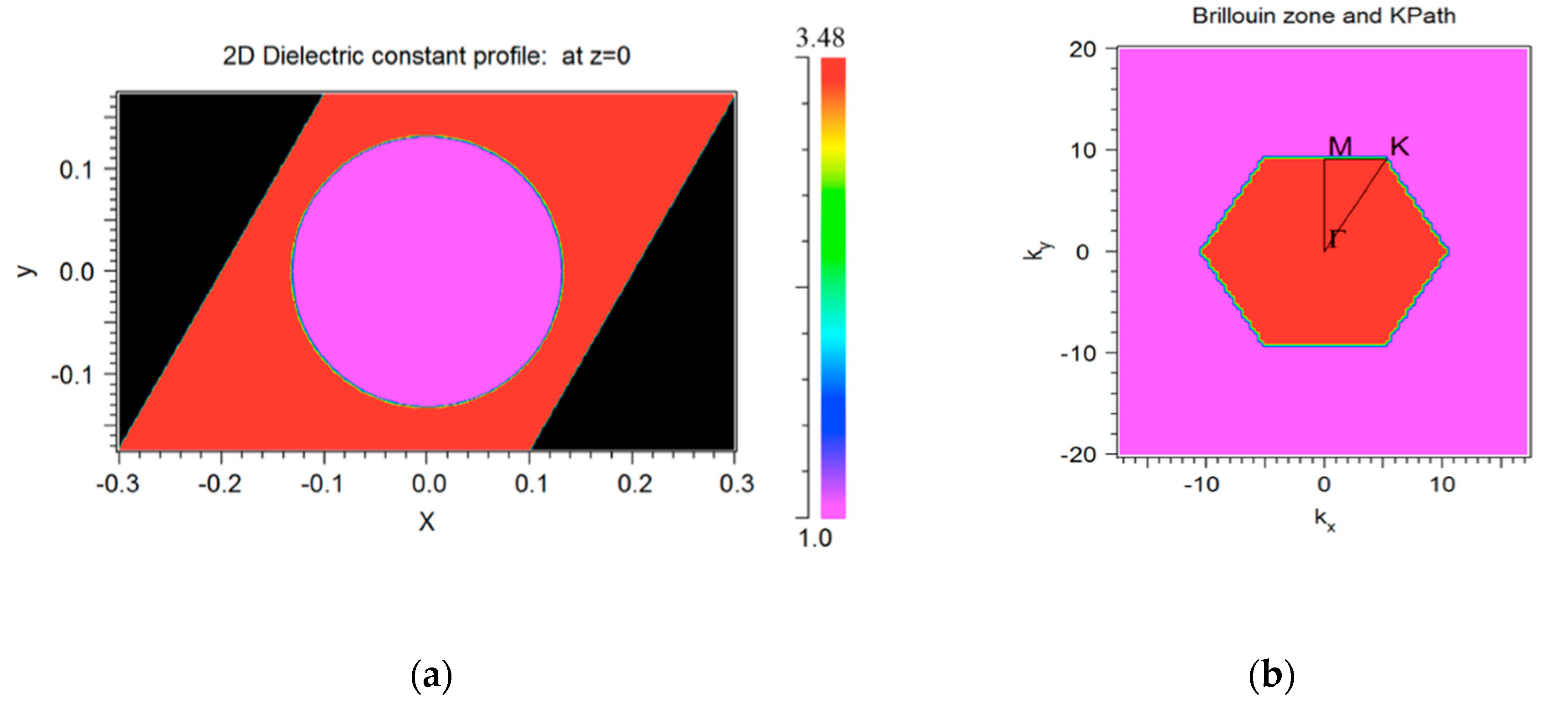
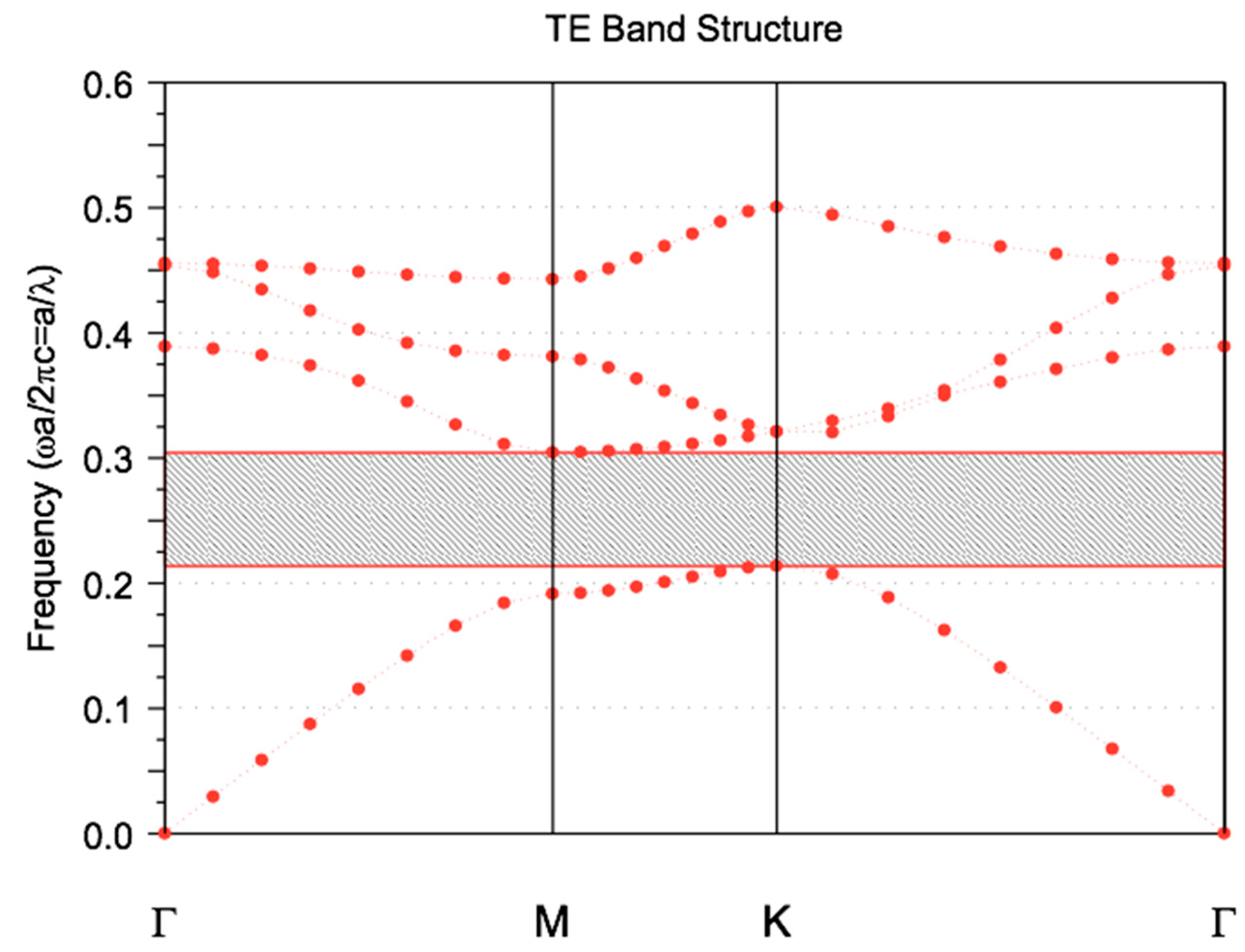
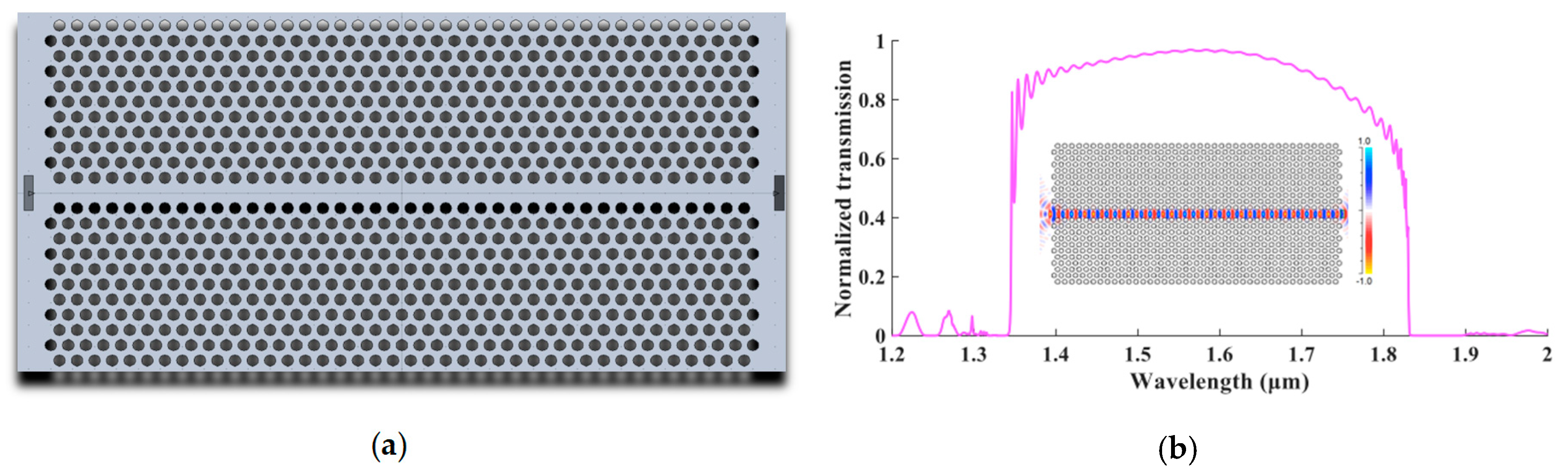
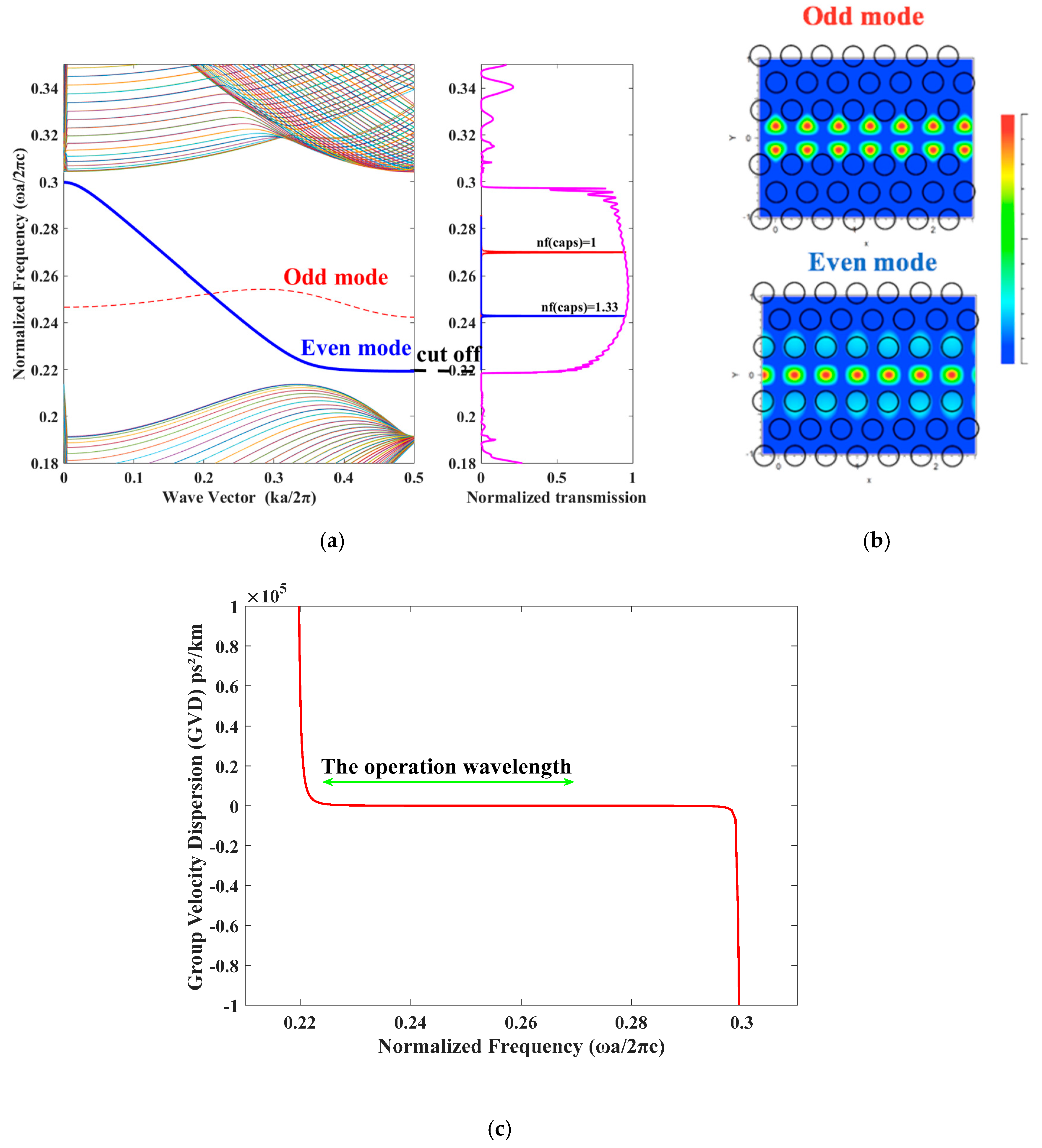
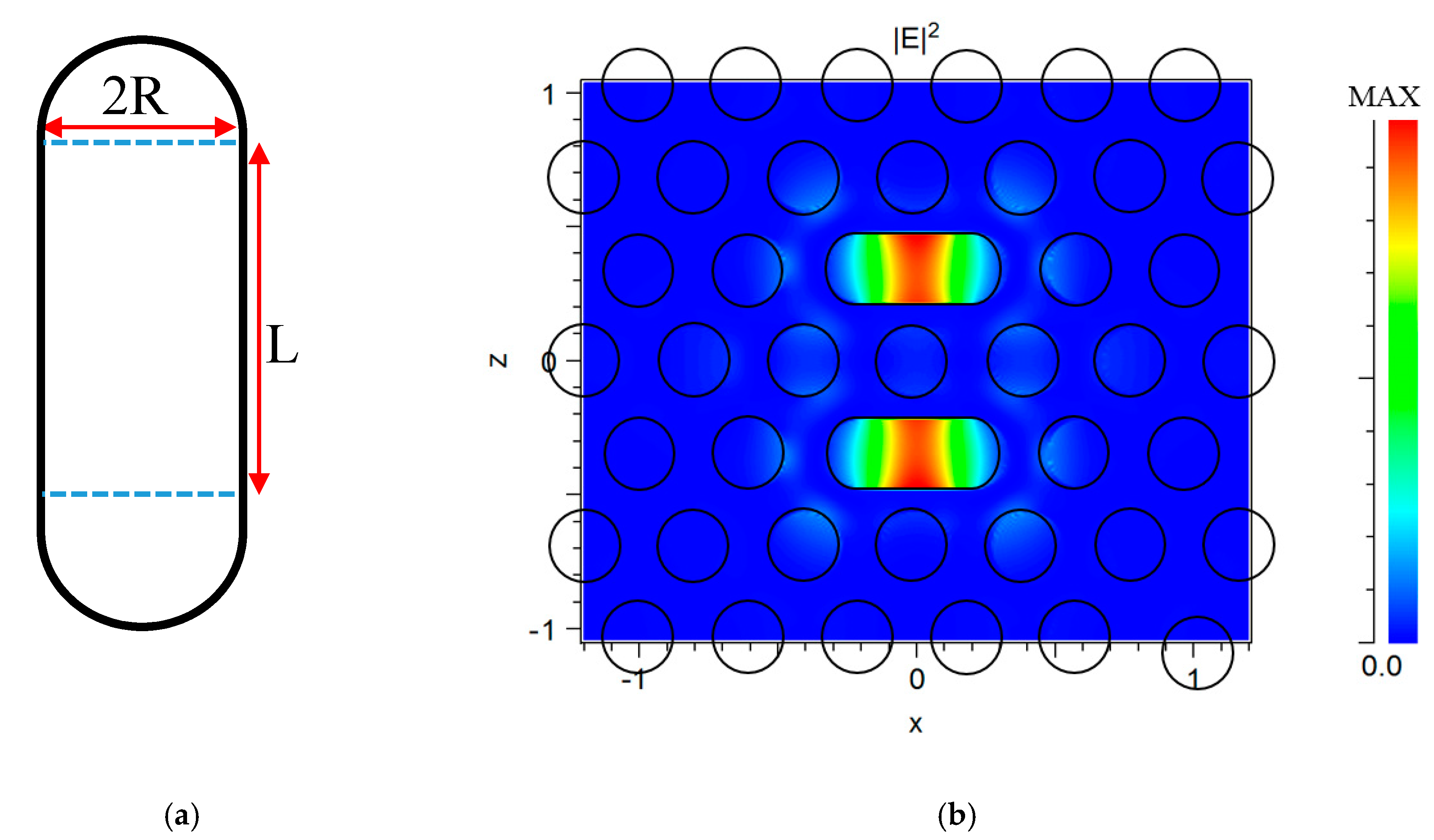
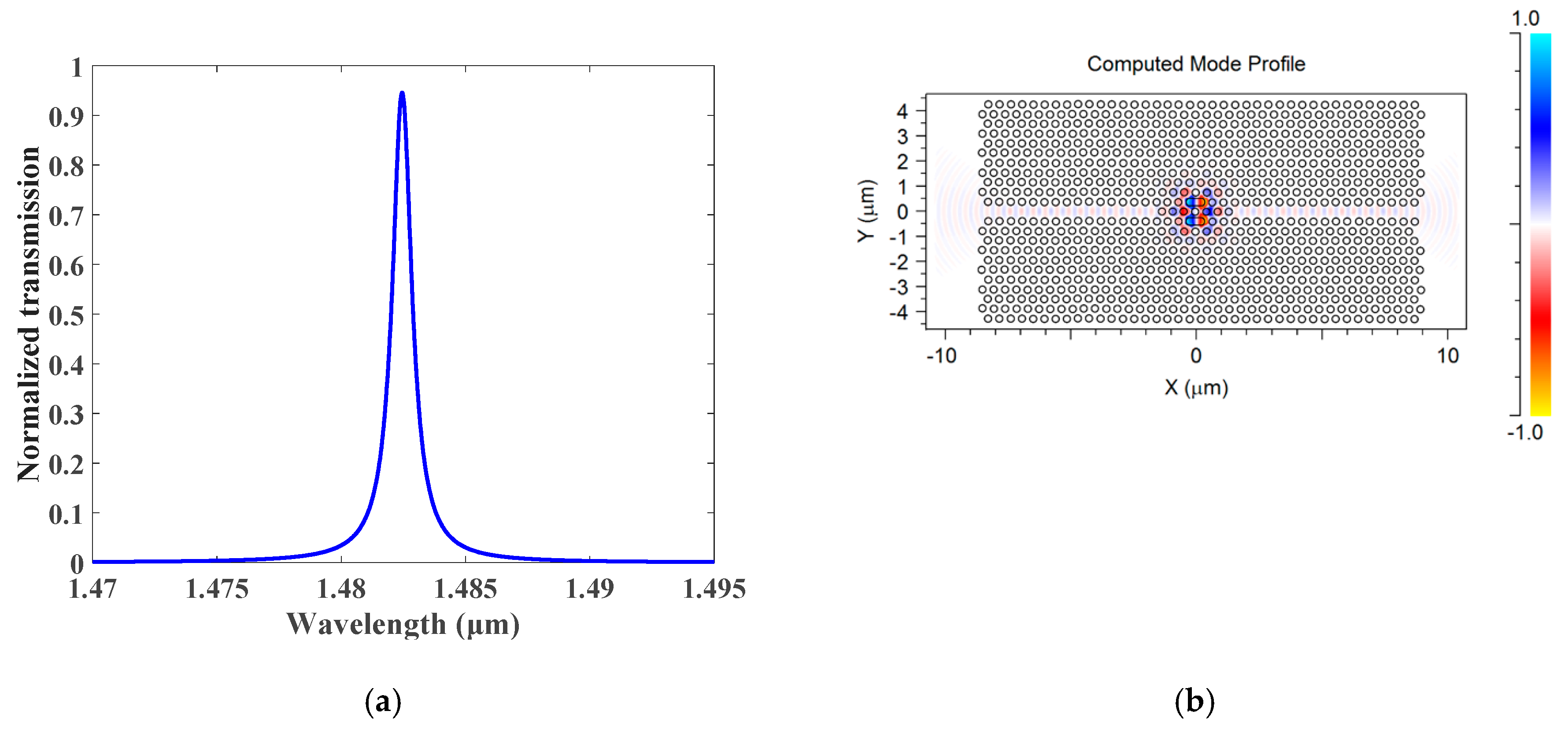
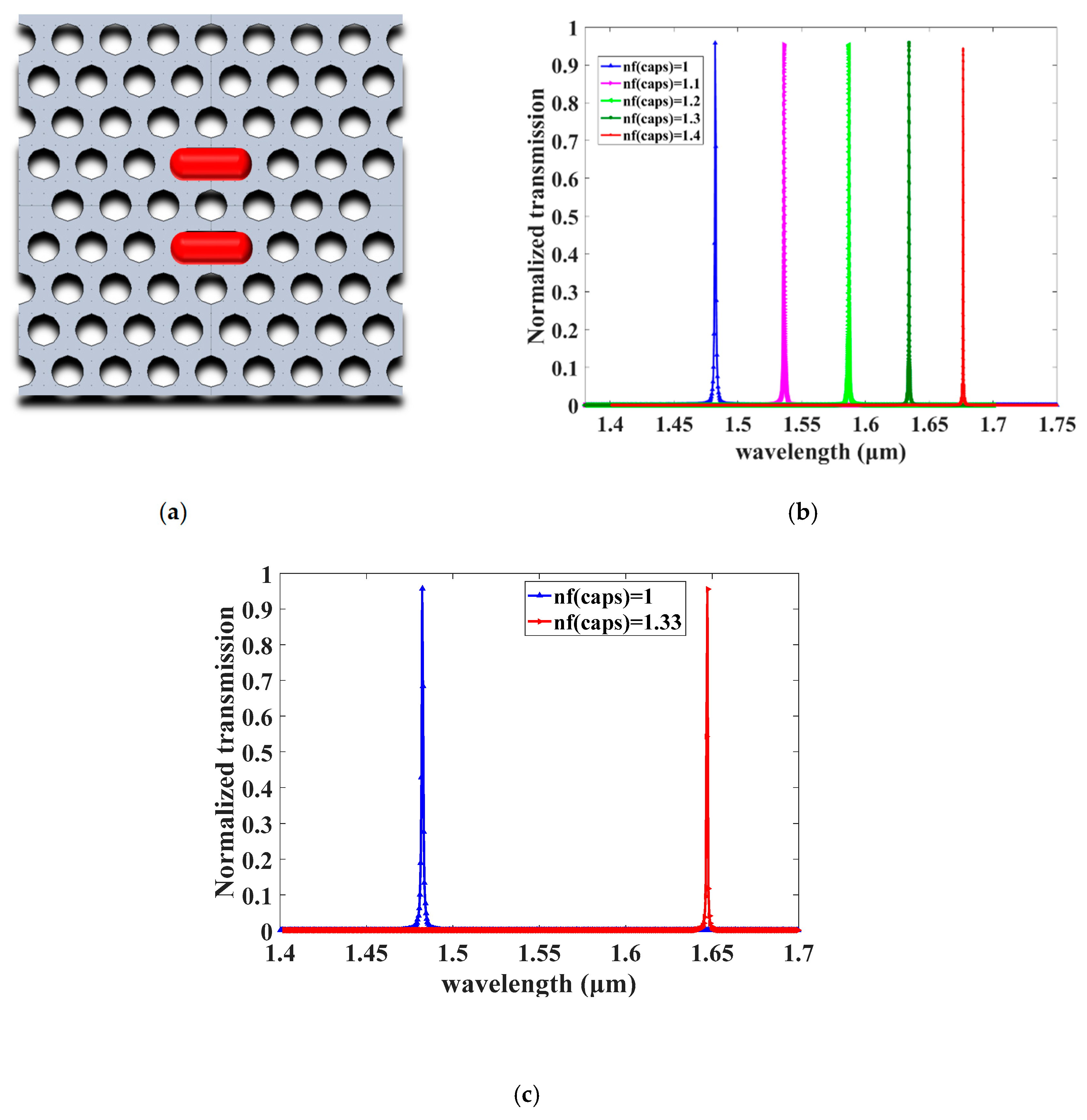


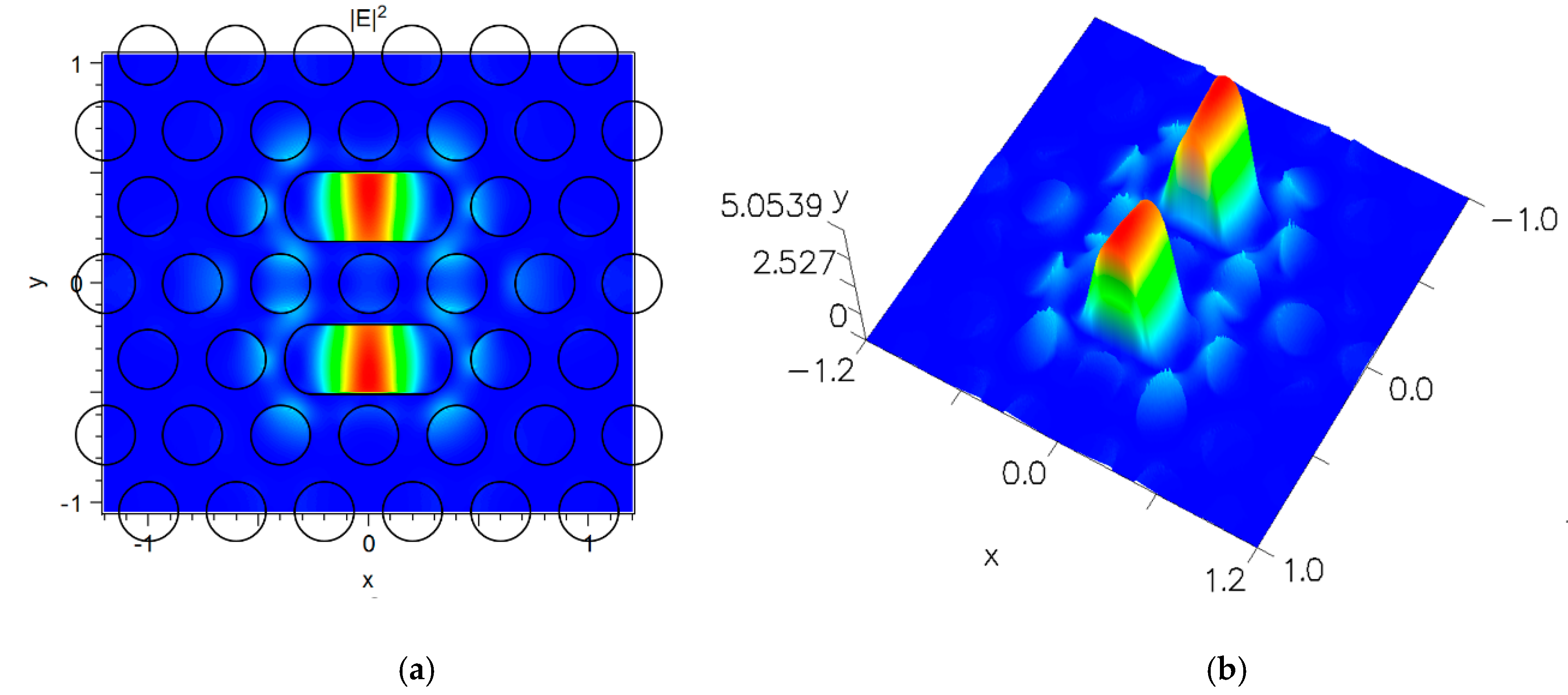

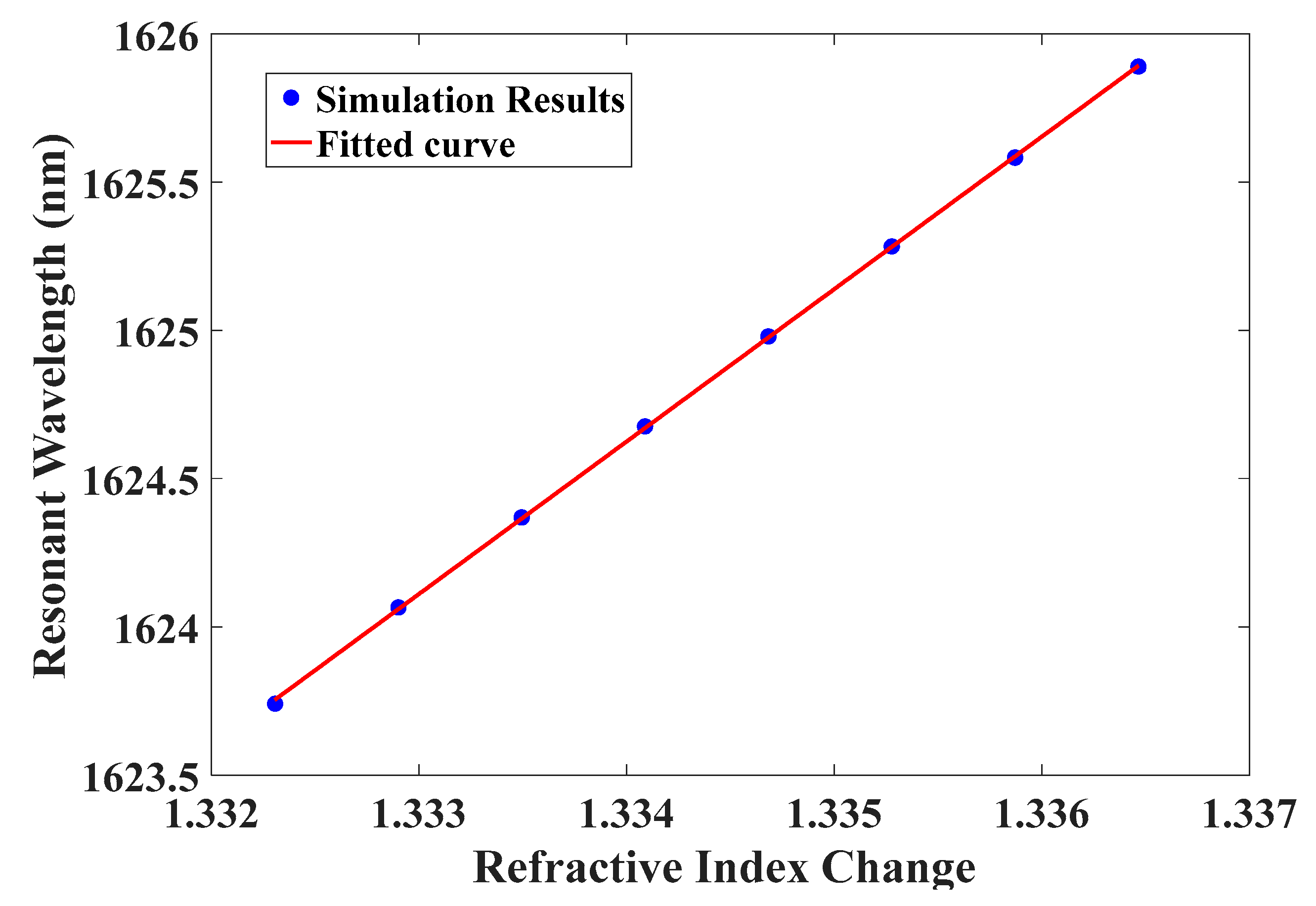
| Length L | nf = 1 | nf = 1.33 | Δλ | S | Q | DL |
|---|---|---|---|---|---|---|
| L = 0.5a | 1641.92 | 1715.205 | 73.28 | 222.08 | 2762.00 | 2.80 × 10−4 |
| L = 0.8a | 1519.08 | 1655.667 | 136.59 | 413.90 | 2417.03 | 1.65 × 10−4 |
| L = 0.9a | 1495.74 | 1649.676 | 153.94 | 466.47 | 2373.63 | 1.49 × 10−4 |
| L = a | 1482.219 | 1647.271 | 165.05 | 500.16 | 2250.20 | 1.46 × 10−4 |
| L = 1.1a | 1477.086 | 1645.9 | 168.81 | 511.56 | 2230.22 | 1.44 × 10−4 |
| L = 1.2a | 1475.4 | 1642.75 | 167.35 | 507.12 | 2061.17 | 1.57 × 10−4 |
| L = 1.5a | 1455.492 | 1596.5 | 141.01 | 427.30 | 779.09 | 4.80 × 10−4 |
| Width R | nf = 1 | nf = 1.33 | Δλ | S | Q | DL |
|---|---|---|---|---|---|---|
| R = 0.8r | 1555.60 | 1704.77 | 149.17 | 452.03 | 2367.74 | 1.59 × 10−4 |
| R = 0.9r | 1513.39 | 1673.40 | 160.01 | 484.87 | 2842.25 | 1.21 × 10−4 |
| R = r | 1477.09 | 1645.90 | 168.81 | 511.56 | 2230.22 | 1.44 × 10−4 |
| R = 1.1r | 1451.70 | 1623.59 | 171.89 | 520.88 | 2081.53 | 1.50 × 10−4 |
| R = 1.2r | 1421.20 | 1594.64 | 173.44 | 525.59 | 2531.18 | 1.21 × 10−4 |
| R = 1.3r | 1395.80 | 1567.49 | 171.69 | 520.26 | 1711.23 | 1.76 × 10−4 |
| Sensing area | Nf = 1 | Nf = 1.33 | S | Q | DL | Transmission |
|---|---|---|---|---|---|---|
| Only Capsule | 1421.20 | 1594.64 | 525.59 | 2531.18 | 1.20 × 10−4 | 91% |
| Area 1 | 1421.20 | 1603.08 | 551.14 | 2410.64 | 1.21 × 10−4 | 94% |
| Area 2 | 1421.20 | 1622.59 | 610.26 | 2192.68 | 1.21 × 10−4 | 97% |
| Area 3 | 1421.20 | 1626.77 | 622.95 | 1265.97 | 2.06 × 10−4 | 97% |
| Entire Area | 1421.20 | 1628.25 | 627.42 | 1112.95 | 2.33 × 10−4 | 99% |
| C (g/L) | n | S | Q | DL | |
|---|---|---|---|---|---|
| 0 | 1.33230545 | 1623.74 | 2055.37 | ||
| 5 | 1.33289990 | 1624.065 | 546.72 | 2066.24 | 1.44 × 10−4 |
| 10 | 1.33349435 | 1624.37 | 529.90 | 2069.26 | 1.48 × 10−4 |
| 15 | 1.33408880 | 1624.675 | 524.29 | 2069.65 | 1.50 × 10−4 |
| 20 | 1.33468325 | 1624.98 | 521.49 | 2070.04 | 1.51 × 10−4 |
| 25 | 1.33527770 | 1625.283 | 519.13 | 2075.71 | 1.51 × 10−4 |
| 30 | 1.33587215 | 1625.583 | 516.72 | 2078.75 | 1.51 × 10−4 |
| 35 | 1.33646660 | 1625.889 | 516.44 | 2084.47 | 1.51 × 10−4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maache, M.; Fazea, Y.; Bile Hassan, I.; Alkahtani, A.A.; Ud Din, I. High-Sensitivity Capsule-Shaped Sensor Based on 2D Photonic Crystals. Symmetry 2020, 12, 1480. https://doi.org/10.3390/sym12091480
Maache M, Fazea Y, Bile Hassan I, Alkahtani AA, Ud Din I. High-Sensitivity Capsule-Shaped Sensor Based on 2D Photonic Crystals. Symmetry. 2020; 12(9):1480. https://doi.org/10.3390/sym12091480
Chicago/Turabian StyleMaache, Mouhssin, Yousef Fazea, Ismail Bile Hassan, Ammar Ahmed Alkahtani, and Ikram Ud Din. 2020. "High-Sensitivity Capsule-Shaped Sensor Based on 2D Photonic Crystals" Symmetry 12, no. 9: 1480. https://doi.org/10.3390/sym12091480
APA StyleMaache, M., Fazea, Y., Bile Hassan, I., Alkahtani, A. A., & Ud Din, I. (2020). High-Sensitivity Capsule-Shaped Sensor Based on 2D Photonic Crystals. Symmetry, 12(9), 1480. https://doi.org/10.3390/sym12091480






