On the Loss of Learning Capability Inside an Arrangement of Neural Networks: The Bottleneck Effect in Black-Holes
Abstract
:1. Introduction
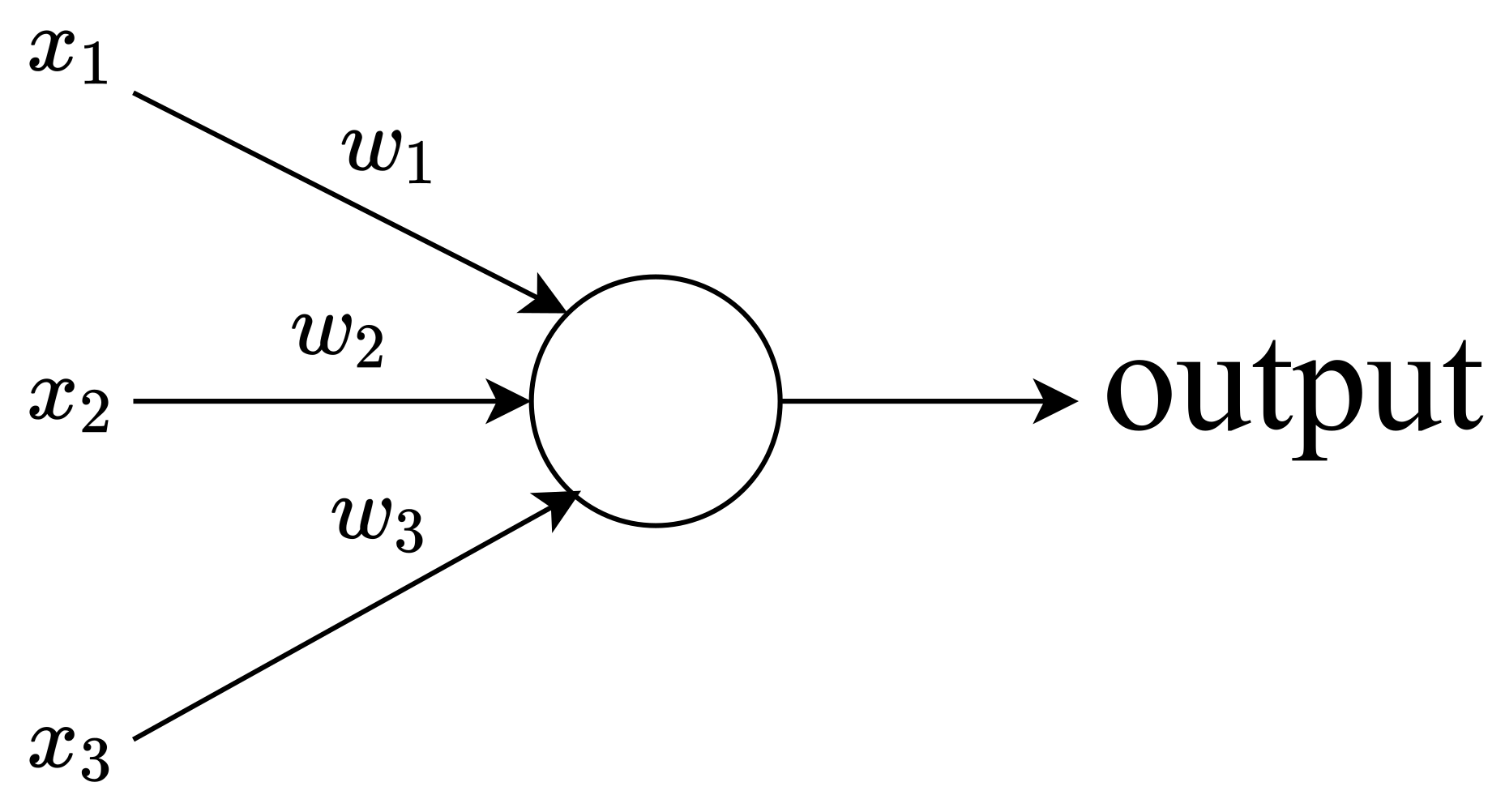
2. Perceptrons: Basic Concepts
3. Sigmoid Neurons
4. The Connection between Neural Networks and Quantum Fields
4.1. Assisted Gaplessness
4.2. Memory Burden
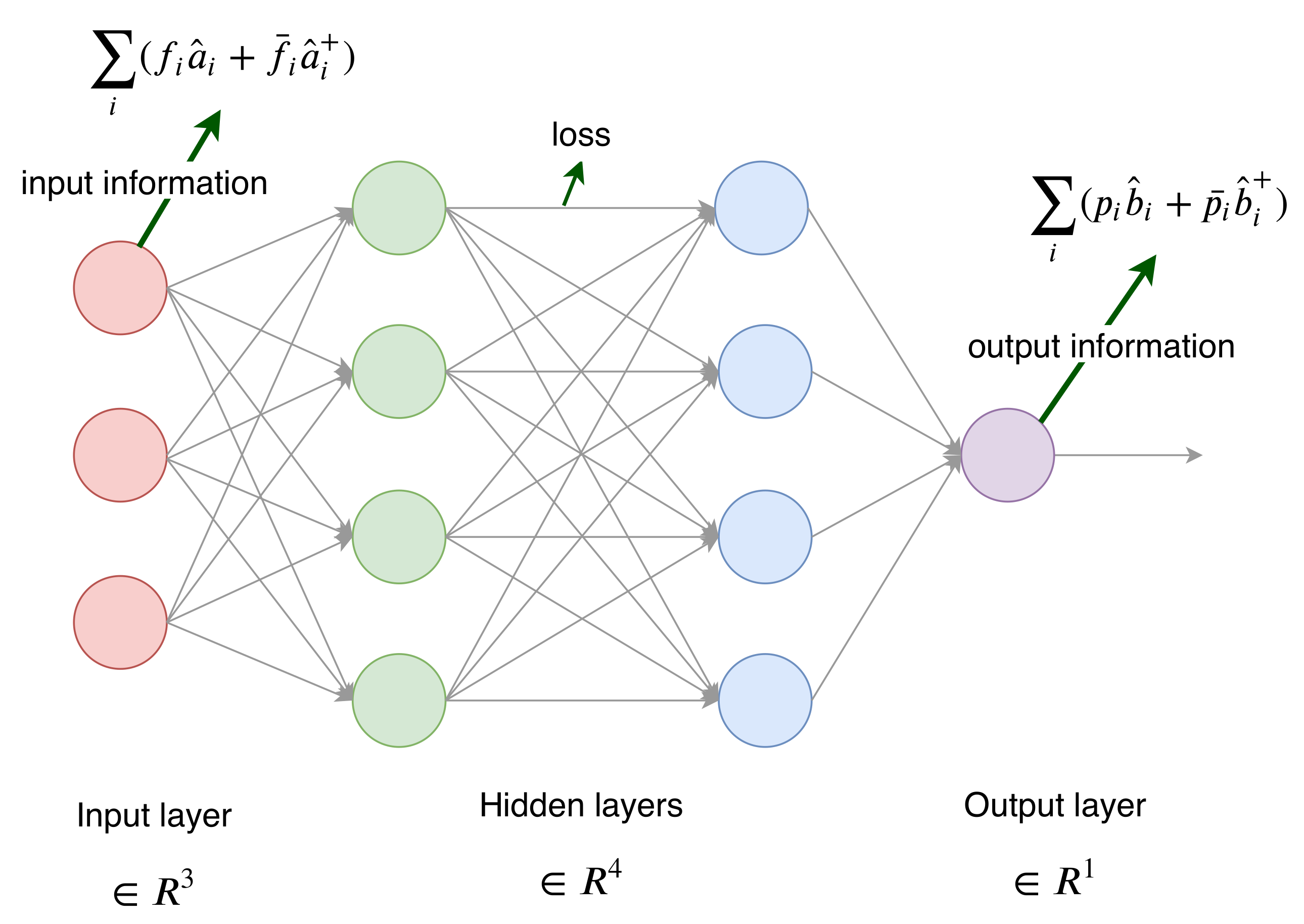
5. Cleaning the Information in Neural Networks
6. The Bottleneck Effect in Black-Holes
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- McCulloch, W.; Pitts, W. A Logical Calculus of Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Hebb, D. The Organization of Behavior; Wiley: New York, NY, USA, 1949; ISBN 978-1-135-63190-1. [Google Scholar]
- Farley, B.G.; Clark, W.A. Simulation of Self-Organizing Systems by Digital Computer. IRE Trans. Inform. Theory 1954, 4, 76–84. [Google Scholar] [CrossRef]
- Nielsen, M. Neural Networks and Deep Learning. Available online: http://neuralnetworksanddeeplearning.com/ (accessed on 31 August 2019).
- Goudet, O.; Duval, B.; Hao, J.K. Gradient Descent based Weight Learning for Grouping Problems: Application on Graph Coloring and Equitable Graph Coloring. arXiv 2019, arXiv:1909.02261. [Google Scholar]
- Harvey, N.J.A.; Liaw, C.; Randhawa, S. Simple and optimal high-probability bounds for strongly-convex stochastic gradient descent. arXiv 2019, arXiv:1909.00843. [Google Scholar]
- Xie, Y.; Wu, X.; Ward, R. Linear Convergence of Adaptive Stochastic Gradient Descent. arXiv 2019, arXiv:1908.10525. [Google Scholar]
- Tishby, N.; Zaslavsky, N. Deep Learning and the Information Bottleneck Principle. arXiv 2015, arXiv:1503.02406. [Google Scholar]
- Shwartz-Ziv, R.; Tishby, N. Opening the Black Box of Deep Neural Networks via Information. arXiv 2017, arXiv:1703.00810. [Google Scholar]
- Susskind, L. The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics; Little Brown and Company, Hachette Book Group USA: New York, NY, USA, 2008. [Google Scholar]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Dvali, G. Critically excited states with enhanced memory and pattern recognition capacities in quantum brain networks: Lesson from black holes. arXiv 2017, arXiv:1711.09079. [Google Scholar]
- Dvali, G. Area law microstate entropy from criticality and spherical symmetry. Phys. Rev. D 2018, 97, 105005. [Google Scholar] [CrossRef] [Green Version]
- Dvali, G. Black Holes as Brains: Neural Networks with Area Law Entropy. arXiv 2018, arXiv:1801.0391. [Google Scholar] [CrossRef] [Green Version]
- DVali, G. Classicalization Clearly: Quantum Transition into States of Maximal Memory Storage Capacity. arXiv 2018, arXiv:1804.06154. [Google Scholar]
- Dvali, G.; Michel, M.; Zell, S. Finding Critical States of Enhanced Memory Capacity in Attractive Cold Bosons. EPJ Quantum Technol. 2019, 6, 1. [Google Scholar] [CrossRef]
- Dvali, G. A Microscopic Model of Holography: Survival by the Burden of Memory. arXiv 2018, arXiv:1810.02336. [Google Scholar]
- Dvali, G.; Eisemann, L.; Michel, M.; Zell, S. Black Hole Metamorphosis and Stabilization by Memory Burden. arXiv 2006, arXiv:2006.00011. [Google Scholar]
- Arraut, I. Black-hole evaporation from the perspective of neural networks. EPL 2018, 124, 50002. [Google Scholar] [CrossRef] [Green Version]
- Israel, W. Event Horizons in Static Vacuum Space-Times. Phys. Rev. 1967, 164, 1776–1779. [Google Scholar] [CrossRef]
- Valatin, J.G. Comments on the theory of superconductivity. Il Nuovo Cimento 1958, 7, 843–857. [Google Scholar] [CrossRef]
- Bogoliubov, N.N. On a new method in the theory of superconductivity. Il Nuovo Cimento 1958, 7, 794–805. [Google Scholar] [CrossRef]
- Arraut, I. Black-Hole evaporation and Quantum-depletion in Bose-Einstein condensates. arXiv 2006, arXiv:2006.09121. [Google Scholar]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; CRC Press/Taylor and Francis Group: Boca Raton, FL, USA, 2018. [Google Scholar]
- Pauli, W. Über den Zusammenhang des Abschlusses der Elektronengruppen im Atom mit der Komplexstruktur der Spektren. Z. Phys. 1925, 31, 765–783. [Google Scholar] [CrossRef]
- Pathria, R.K.; de Beale, P. Statistical Mechanics; Elsevier: Amsterdam, The Netherlands, 1996. [Google Scholar]
- Farley, A.N.S.J.; D’Eath, P.D. Bogoliubov transformations for amplitudes in black-hole evaporation. Phys. Lett. B 2005, 613, 181–188. [Google Scholar] [CrossRef] [Green Version]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arraut, I.; Diaz, D. On the Loss of Learning Capability Inside an Arrangement of Neural Networks: The Bottleneck Effect in Black-Holes. Symmetry 2020, 12, 1484. https://doi.org/10.3390/sym12091484
Arraut I, Diaz D. On the Loss of Learning Capability Inside an Arrangement of Neural Networks: The Bottleneck Effect in Black-Holes. Symmetry. 2020; 12(9):1484. https://doi.org/10.3390/sym12091484
Chicago/Turabian StyleArraut, Ivan, and Diana Diaz. 2020. "On the Loss of Learning Capability Inside an Arrangement of Neural Networks: The Bottleneck Effect in Black-Holes" Symmetry 12, no. 9: 1484. https://doi.org/10.3390/sym12091484



