Model Test Study on the Anisotropic Characteristics of Columnar Jointed Rock Mass
Abstract
:1. Introduction
2. Structural Characteristics of the CJRM
3. Model Tests
3.1. Similar Material and Model Size
3.2. Manufacturing Process of Specimens
3.3. Testing Equipment and Procedure
4. Test Results
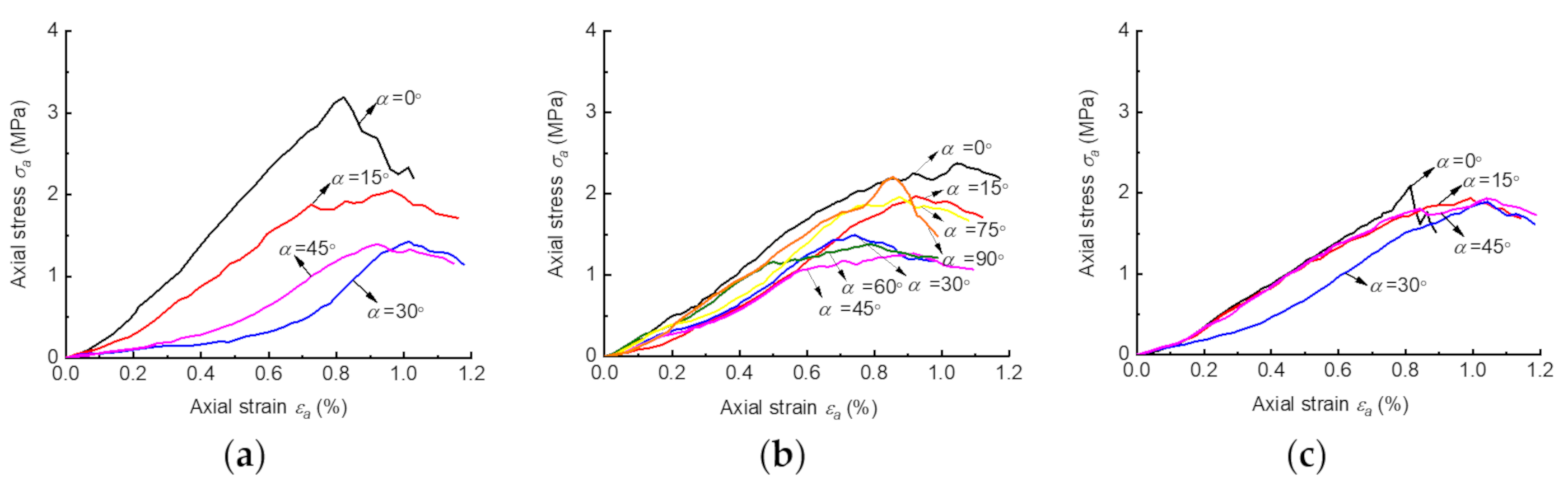
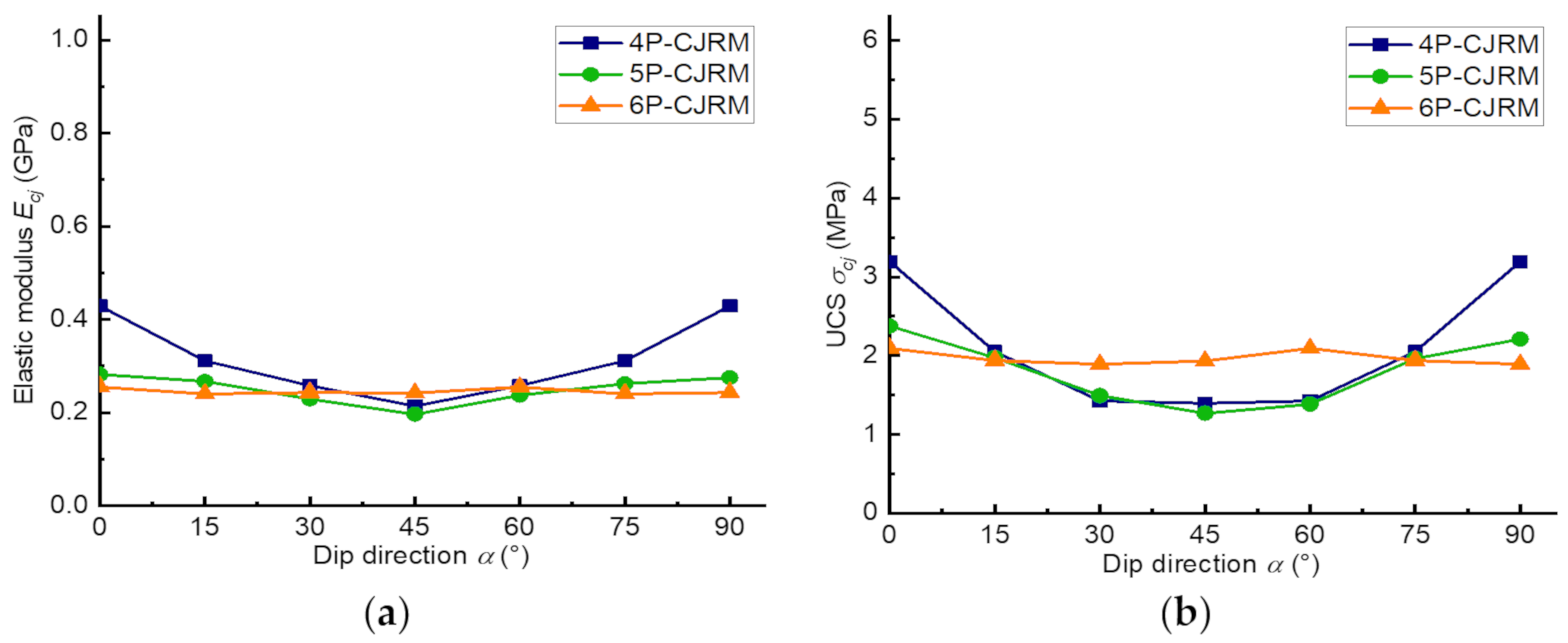
4.1. Deformation and Strength Behavior
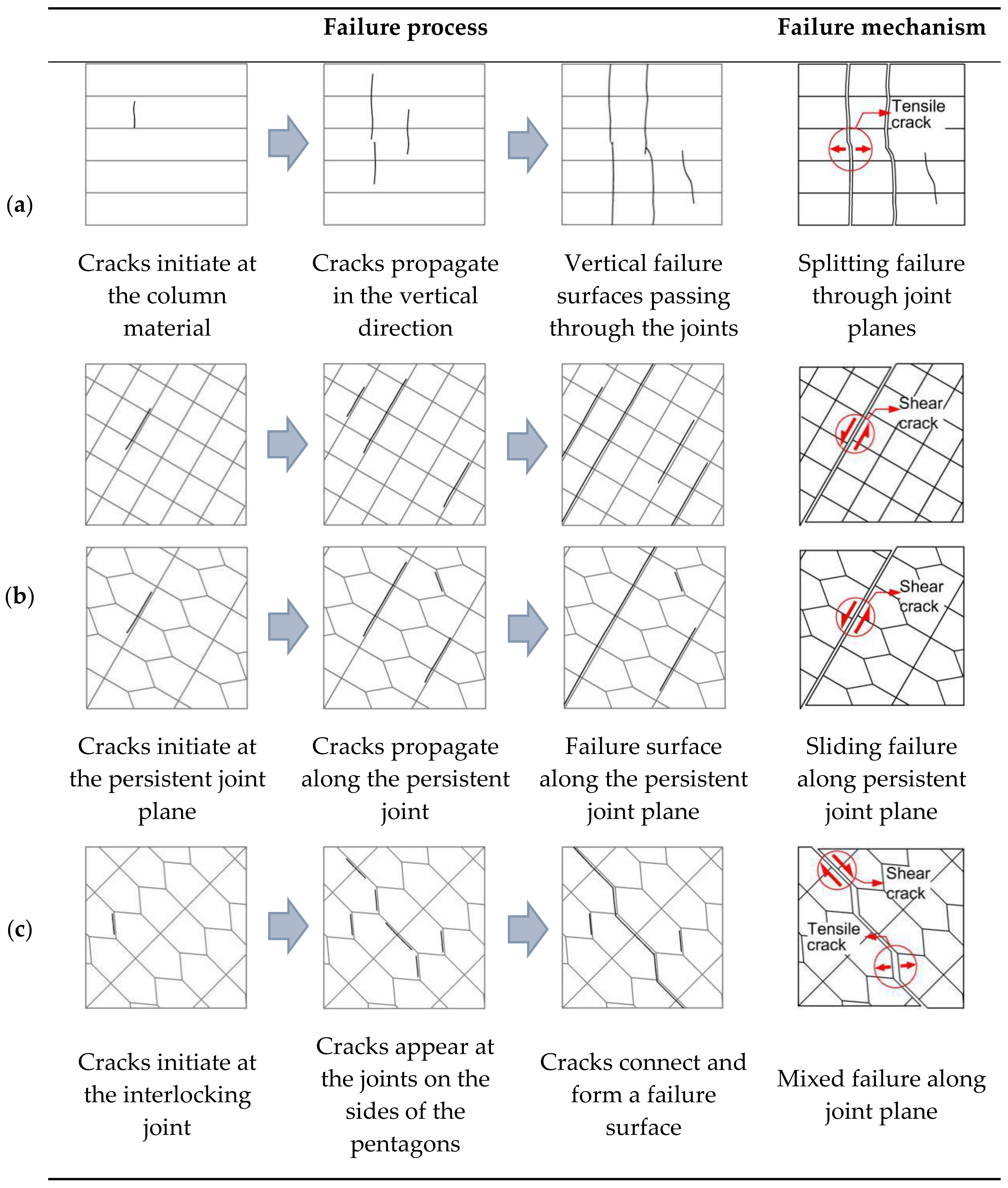
4.2. Failure Modes and Mechanisms
- Mode I:
- Splitting failure through joint planes. This mode occurs in the 4P- and 5P-CJRM specimens with the dip directions of 0, 15, 75 and 90° and in all the 6P-CJRM specimens. As observed from Figure 9a, the cracks initiate at the column material and propagate in the vertical direction. Eventually, failure surfaces passing through the joint planes appear on the specimen. Therefore, no sliding along the joint plane is observed, and the damage of the specimen is tensile failure.
- Mode II:
- Sliding failure along persistent joint plane. This mode occurs in the 4P-CJRM specimens with the dip directions of 30, 45 and 60° and in the 5P-CJRM specimen with the dip direction of 30°. The cracks initiate at the persistent joint plane and propagate along the persistent joint (Figure 9b). Eventually, sliding failure occurs along the persistent joint plane because the shear stress acting on the joint plane is greater than its shear strength.
- Mode III:
- Mixed failure along joint plane. This mode occurs in the 5P-CJRM specimens with the dip directions of 45 and 60°. The cracks initiate at the interlocking joints on the top of the pentagon, and appear at the joints on the sides of the pentagon under the further load (Figure 9c). Eventually, the cracks at the two locations connect and form a failure surface. The initial cracks are caused by tension because the angle between the joint and the load direction is small. The further load makes the columns slide along the sides of the pentagon, and the lateral deformation of the specimen accelerates the propagation of the cracks at the interlocking joints. Therefore, the failure mode of the specimen is mixed failure along the joint plane.
5. Discussion
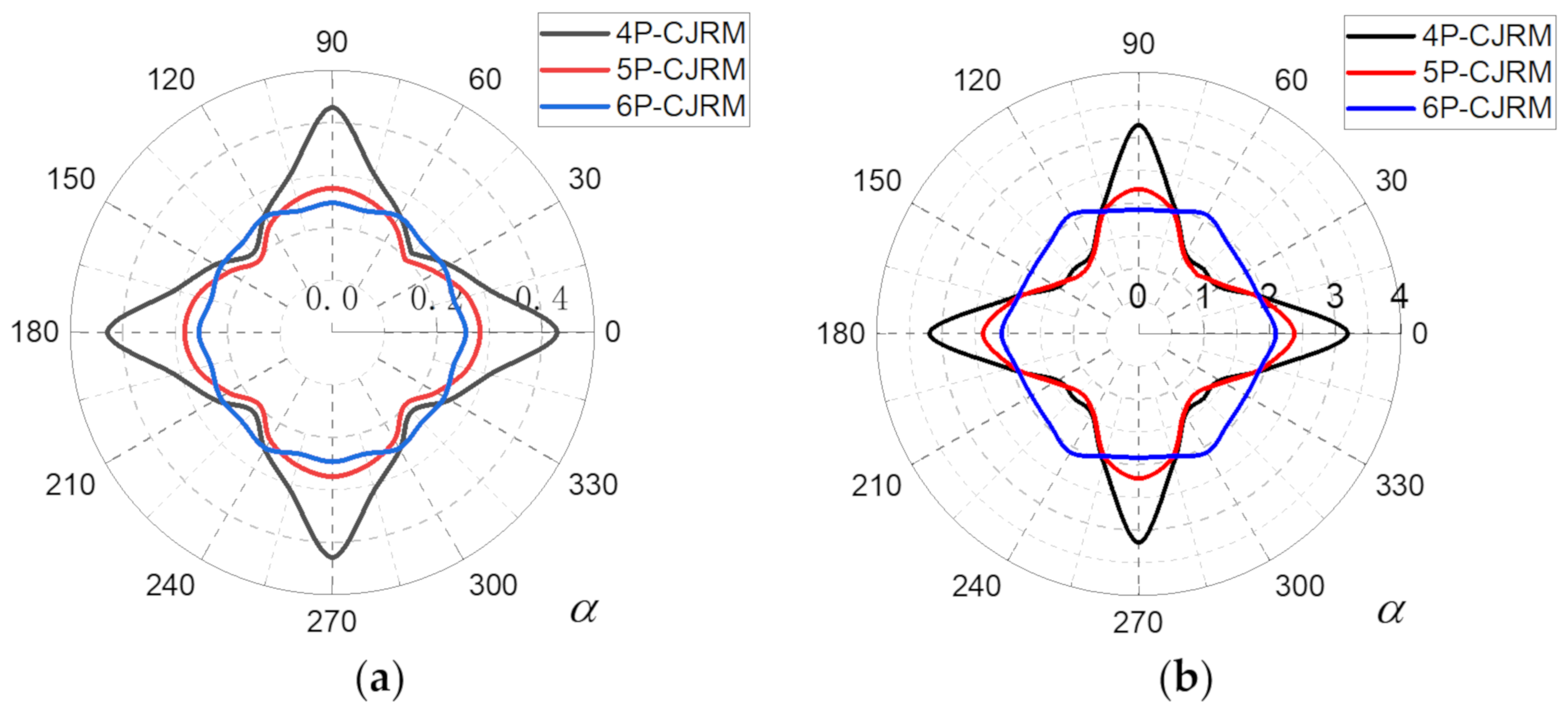
5.1. Anisotropic Degrees in Horizontal Plane
5.2. Anisotropic Characteristics of the Three CJRM Models
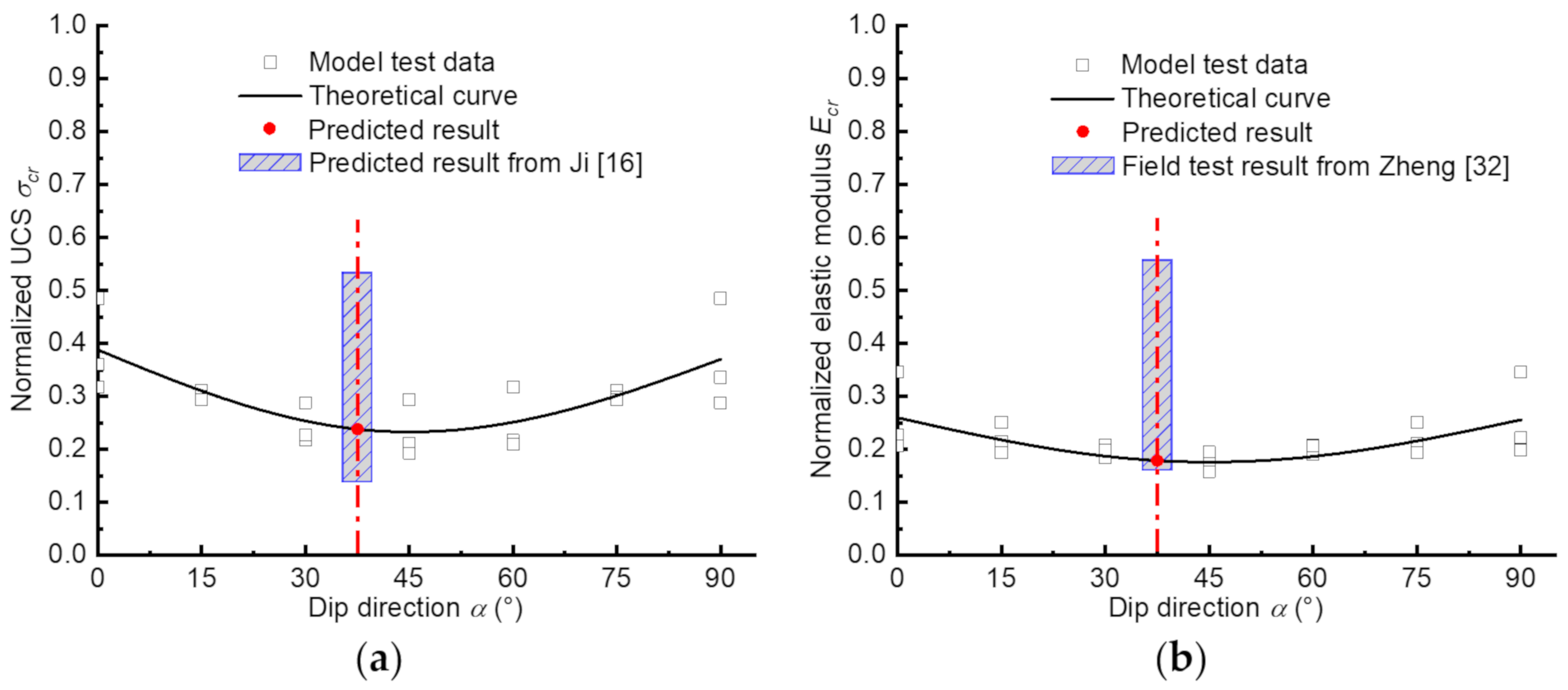
5.3. Theoretical Prediction of Strength and Deformation
6. Conclusions
- (1)
- The differences between the strength and deformation behaviors of the three CJRM models were mainly caused by the structural features of these three models. The curves of 4P-CJRM were symmetrical, while the curves of 6P-CJRM were approximately straight. For 6P-CJRM, the variation curves combined the characteristics of the above two models.
- (2)
- Three typical failure modes of the CJRM specimens with different dip directions α were summarized, including the splitting failure through joint planes, the sliding failure along a persistent joint plane and the mixed failure along a joint plane.
- (3)
- The anisotropy ratio was introduced to classify the anisotropic degrees of the three CJRM models. The anisotropic degrees of the 4P-, 5P- and 6P-CJRM models in the horizontal plane were medium, low and low, respectively.
- (4)
- The anisotropic characteristics of the three CJRM models were described by placing the test results in the polar coordinates. The curves of the 4P- and 5P-CJRM models in the horizontal plane were all an axisymmetric diagram resembling a gyro, which indicated their orthotropy. The curves of the 6P-CJRM were approximately circular, which revealed its quasi-transverse isotropy.
- (5)
- A simple empirical expression was adopted to estimate the strength and deformation of the CJRM, and the derived equations were used in the Baihetan CJRM. The calculated values were all within the ranges of the existing research results, which indicates that the derived empirical equations are valuable for related engineering applications.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jiang, Q.; Feng, X.T.; Hatzor, Y.H.; Hao, X.J.; Li, S.J. Mechanical anisotropy of columnar jointed basalts: An example from the Baihetan hydropower station China. Eng. Geol. 2014, 175, 35–45. [Google Scholar] [CrossRef]
- Niu, Z.; Zhu, Z.; Que, X. Constitutive model of stress-dependent seepage in columnar jointed rock mass. Symmetry 2020, 12, 160. [Google Scholar] [CrossRef] [Green Version]
- Chen, M.; Lu, W.B.; Zhang, W.J.; Yan, P.; Zhou, C.B. An analysis of consolidation grouting effect of bedrock based on its acoustic velocity increase. Rock Mech. Rock Eng. 2015, 48, 1259–1274. [Google Scholar] [CrossRef]
- Feng, X.T.; Hao, X.J.; Jiang, Q.; Li, S.J.; Hudson, J.A. Rock cracking indices for improved tunnel support design: A case study for columnar jointed rock masses. Rock Mech. Rock Eng. 2016, 49, 2115–2130. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, B.; Feng, X.T.; Fan, Q.X.; Wang, Z.L.; Pei, S.F.; Jiang, S. In situ failure investigation and time-dependent damage test for columnar jointed basalt at the Baihetan left dam foundation. Bull. Eng. Geol. Environ. 2018, 78, 3875–3890. [Google Scholar] [CrossRef]
- Zhong, D.N.; Liu, Y.R.; Li, C.; Yang, Q.; Chen, Y.L. Study of unloading relaxation for excavation based on unbalanced force and its application in baihetan arch dam. Rock Mech. Rock Eng. 2020, 52, 1819–1833. [Google Scholar] [CrossRef]
- Chen, B.R.; Li, Q.P.; Feng, X.T.; Xiao, Y.X.; Feng, G.L.; Hu, L.X. Microseismic monitoring of columnar jointed basalt fracture activity: A trial at the Baihetan Hydropower Station China. J. Seismol. 2014, 18, 773–793. [Google Scholar] [CrossRef]
- Hao, X.J.; Feng, X.T.; Yang, C.X.; Jiang, Q.; Li, S.J. Analysis of EDZ development of columnar jointed rock mass in the Baihetan diversion tunnel. Rock Mech. Rock Eng. 2016, 49, 1289–1312. [Google Scholar] [CrossRef]
- Jin, C.Y.; Yang, C.X.; Fang, D.; Xu, S. Study on the failure mechanism of basalts with columnar joints in the unloading process on the basis of an experimental cavity. Rock Mech. Rock Eng. 2015, 48, 1275–1288. [Google Scholar] [CrossRef]
- Lu, W.; Zhu, Z.; Que, X.; Zhang, C.; He, Y. Anisotropic constitutive model of intermittent columnar jointed rock masses based on the cosserat theory. Symmetry 2020, 12, 823. [Google Scholar] [CrossRef]
- Ramamurthy, T.; Arora, V.K. Strength predictions for jointed rocks in confined and unconfined states. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 182. [Google Scholar] [CrossRef]
- Tien, Y.M.; Kuo, M.C.; Juang, C.H. An experimental investigation of the failure mechanism of simulated transversely isotropic rocks. Int. J. Rock Mech. Min. Sci. 2006, 43, 1163–1181. [Google Scholar] [CrossRef]
- Li, B.; Jiang, Y.; Mizokami, T.; Ikusada, K.; Mitani, Y. Anisotropic shear behavior of closely jointed rock masses. Int. J. Rock Mech. Min. Sci. 2014, 71, 258–271. [Google Scholar] [CrossRef] [Green Version]
- Moomivand, H. Effects of orientation, frequency, and number of sets of discontinuities on rock strength under triaxial stresses. Arab. J. Geosci. 2014, 7, 5345–5352. [Google Scholar] [CrossRef]
- Xiao, W.M.; Deng, R.G.; Zhong, Z.B.; Fu, X.M.; Wang, C.Y. Experimental study on the mechanical properties of simulated columnar jointed rock masses. J. Geophys. Eng. 2015, 12, 80–89. [Google Scholar] [CrossRef]
- Ji, H.; Zhang, J.C.; Xu, W.Y.; Wang, R.B.; Wang, H.L.; Yan, L.; Lin, Z.N. Experimental investigation of the anisotropic mechanical properties of a columnar jointed rock mass: Observations from laboratory-based physical modelling. Rock Mech. Rock Eng. 2017, 50, 1919–1931. [Google Scholar] [CrossRef]
- Jin, C.Y.; Li, S.G.; Liu, J.P. Anisotropic mechanical behaviors of columnar jointed basalt under compression. Bull. Eng. Geol. Environ. 2018, 77, 317–330. [Google Scholar] [CrossRef]
- Cui, J.; Jiang, Q.; Feng, X.T.; Li, S.J.; Liu, J.F.; Chen, W.F.; Zhang, J.C.; Pei, S.F. Insights into statistical structural characteristics and deformation properties of columnar jointed basalts: Field investigation in the Baihetan dam base, China. Bull. Eng. Geol. Environ. 2017, 77, 775–790. [Google Scholar] [CrossRef]
- Long, P.E.; Wood, B.J. Structures, textures, and cooling histories of Columbia River basalt flows. Geol. Soc. Am. Bull. 1986, 97, 1144–1155. [Google Scholar] [CrossRef]
- Weinberger, R.; Burg, A. Reappraising columnar joints in different rock types and settings. J. Struct. Geol. 2019, 125, 185–194. [Google Scholar] [CrossRef]
- Phillips, J.C.; Humphreys, M.C.S.; Daniels, K.A.; Brown, R.J.; Witham, F. The formation of columnar joints produced by cooling in basalt at Staffa Scotland. Bull. Volcanol. 2013, 75, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.J.; Zhang, C.Q.; Zhou, H.; Chen, J.L.; Gao, Y.; Liu, N.; Chen, P.Z. Structural characteristics of columnar jointed basalt in drainage tunnel of Baihetan hydropower station and its inflfluence on the behavior of P-wave anisotropy. Eng. Geol. 2019, 264, 105304. [Google Scholar] [CrossRef]
- Lin, Z.N.; Xu, W.Y.; Wang, W.; Wang, H.L.; Wang, R.B.; Ji, H.; Zhang, J.C. Determination of strength and deformation properties of columnar jointed rock mass using physical model tests. KSCE J. Civ. Eng. 2018, 22, 3302–3311. [Google Scholar] [CrossRef]
- Que, X.; Zhu, Z.; Lu, W. Anisotropic constitutive model of pentagonal prism columnar jointed rock mass. Bull. Eng. Geol. Environ. 2020, 79, 269–286. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Chen, J.M.; Huang, T.H. Effect of joint sets on the strength and deformation of rock mass models. Int. J. Rock Mech. Min. Sci. 1998, 35, 75–84. [Google Scholar] [CrossRef]
- Sebastian, R.; Sitharam, T.G. Transmission of elastic waves through a frictional boundary. Int. J. Rock Mech. Min. Sci. 2014, 66, 84–90. [Google Scholar] [CrossRef]
- Xia, Z.F. Research on Similar Material Model Test and Numerical Simulation for Columnar Jointed Rock Mass. Master’s Thesis, Northeastern University, Shenyang, China, 2014. [Google Scholar]
- Yan, D.X.; Xu, W.Y.; Wang, W.; Shi, C.; Shi, A.C.; Wu, G.Y. Research of size effect on equivalent elastic modulus of columnar jointed rock mass. Chin. J. Geotech. Eng. 2012, 34, 243–250. [Google Scholar]
- Ni, H.J.; Xu, W.Y.; Shi, A.C.; Xu, J.R.; Ji, H. Scale effect on equivalent continuum elastic modulus of columnar jointed rock masses by distinct element method. Eng. Mech. 2015, 32, 90–96. [Google Scholar]
- Singh, J.; Ramamurthy, T.; Venkatappa, R.G. Strength anisotropies in rocks. Ind. Geotech. J. 1989, 19, 147–166. [Google Scholar]
- Ramamurthy, T. Strength and modulus responses of anisotropic rocks. In Comprehensive Rock Engineering; Pergamon: Oxford, UK, 1993; Volume 1, pp. 337–349. [Google Scholar]
- Zheng, W.T. Rock Mechanics of Irregular Columnar Jointed Basaltic Mass and Its Application in High Slope and Dam Foundation. Ph.D. Thesis, Hohai University, Nanjing, China, 2008. [Google Scholar]






| Material | Density (g/cm3) | Compressive Strength (MPa) | Elastic Modulus (GPa) | Poisson’s Ratio | Cohesion (MPa) | Friction Angle (°) |
|---|---|---|---|---|---|---|
| Intact basalt 1 | 2.83–2.93 | 47.7–255.0 | 30.0–86.6 | 0.17–0.26 | 10.0–13.0 | 45–50 |
| Rock-like material | 1.17 | 6.58 | 1.24 | 0.19 | 1.37 | 51.3 |
| Shape of Columns | Dip Direction (°) | Elastic Modulus (GPa) | UCS (MPa) |
|---|---|---|---|
| Quadrangular prism | 0 | 0.429 | 3.193 |
| 15 | 0.311 | 2.052 | |
| 30 | 0.258 | 1.427 | |
| 45 | 0.214 | 1.396 | |
| 60 | 0.258 | 1.427 | |
| 75 | 0.311 | 2.052 | |
| 90 | 0.429 | 3.193 | |
| Pentagonal prism | 0 | 0.282 | 2.376 |
| 15 | 0.267 | 1.973 | |
| 30 | 0.229 | 1.495 | |
| 45 | 0.196 | 1.267 | |
| 60 | 0.237 | 1.384 | |
| 75 | 0.262 | 1.962 | |
| 90 | 0.275 | 2.210 | |
| Hexagonal prism | 0 | 0.255 | 2.092 |
| 15 | 0.240 | 1.937 | |
| 30 | 0.243 | 1.892 | |
| 45 | 0.242 | 1.933 | |
| 60 | 0.255 | 2.092 | |
| 75 | 0.240 | 1.937 | |
| 90 | 0.243 | 1.892 |
| Normalized UCS σcr | Normalized Elastic Modulus Ecr |
|---|---|
| σcr = 0.388 − 0.155cos [2(45° − α)] (0° ≤ α < 45°) σcr = 0.370 − 0.137cos[2 (45° − α)] (45° ≤ α ≤ 90°) | Ecr = 0.260 − 0.084cos[2(45° − α)] (0° ≤ α < 45°) Ecr = 0.256 − 0.080cos[2(45° − α)] (45° ≤ α ≤ 90°) |
| Result | Normalized UCS σcr | Normalized Elastic Modulus Ecr |
|---|---|---|
| Calculated result | 0.24 | 0.181 |
| Existing research result 2 | 0.1430.536 | 0.157–0.552 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Que, X.; Niu, Z.; Lu, W. Model Test Study on the Anisotropic Characteristics of Columnar Jointed Rock Mass. Symmetry 2020, 12, 1528. https://doi.org/10.3390/sym12091528
Zhu Z, Que X, Niu Z, Lu W. Model Test Study on the Anisotropic Characteristics of Columnar Jointed Rock Mass. Symmetry. 2020; 12(9):1528. https://doi.org/10.3390/sym12091528
Chicago/Turabian StyleZhu, Zhende, Xiangcheng Que, Zihao Niu, and Wenbin Lu. 2020. "Model Test Study on the Anisotropic Characteristics of Columnar Jointed Rock Mass" Symmetry 12, no. 9: 1528. https://doi.org/10.3390/sym12091528
APA StyleZhu, Z., Que, X., Niu, Z., & Lu, W. (2020). Model Test Study on the Anisotropic Characteristics of Columnar Jointed Rock Mass. Symmetry, 12(9), 1528. https://doi.org/10.3390/sym12091528




