Chiral Soliton Models and Nucleon Structure Functions

Abstract

We outline and review the computations of polarized and unpolarized nucleon structure functions within the bosonized Nambu-Jona-Lasinio chiral soliton model. We focus on a consistent regularization prescription for the Dirac sea contribution and present numerical results from that formulation. We also reflect on previous calculations on quark distributions in chiral quark soliton models and attempt to put them into perspective.

1. Introduction

In this mini-review we reflect on nucleon structure function calculations in chiral soliton models. This is an interesting topic not only because structure functions are of high empirical relevance but maybe even more so conceptually as of how much information about the nucleon structure can be retrieved from soliton models. In this spirit, this paper to quite an extent is a proof of concept review.

Solitons emerge in most nonlinear field theories as classical solutions to the field equations. These solutions have localized energy densities and can be attributed particle like properties. In the context of strong interactions, that govern the structure of hadrons, solitons of meson field configurations are considered as baryons [1].

Nucleon structure functions play an important role in deep inelastic scattering (DIS) that reveals the parton substructure of hadrons. In DIS leptons interact with partons by the exchange of a virtual gauge particle. Here we will mainly consider electrons that exchange a virtual photon with either a pion or a nucleon. The process is called deep inelastic as the produced hadrons are not detected. In a certain kinematical regime, the so-called Bjorken limit to be defined below, the DIS cross-section can be parameterized as the product of the cross-section for scattering off partons and distribution functions that measure the probabilities to find these partons inside the hadron. This is the factorization scheme [2]. In this picture the structure functions are linear combinations of parton distribution functions.

DIS can also be explored without direct reference to partons by writing the cross-section in terms of lepton and hadron components. The latter is the hadron matrix element of a current-current correlator and is parameterized by form factors. The structure functions are obtained from these form factors in a certain regime for the kinematic variables, again the Bjorken limit. The operator product expansion formally relates distribution and structure functions by expressing the hadron matrix elements of the current-current correlator as matrix elements of bilocal and bilinear quark operators in the Bjorken limit. The microscopic theory for the structure of hadrons is quantum-chromo-dynamics (QCD) which is the nonabelian gauge theory $SU\left(N_C\right)$, where $N_C=3$ is the number of color degrees of freedom. Though (perturbative) QCD only relates these functions at different energy scales and does so very successfully [3] within the DGLAP formalism [4,5,6], neither structure nor distribution functions can be computed from first principles in QCD, except, maybe within the lattice formulation [7,8] (Another possibility is to apply QCD renormalization group equations to the empirical data at large energies and scale them down to the point at which the probability interpretation becomes inconsistent [9].). Hence model calculations seem unavoidable for a theoretical approach to the structure functions that contain the information of the nonperturbative nature of hadrons. In such models it may or may not be possible to relate structure and distribution functions. For the quark model that we will employ, regularization stands in the way and we attempt to compute the structure functions directly from the current-current correlator.

Though chiral (soliton) models for baryons have so far not been derived from QCD, there is ample motivation to explore nucleon properties in chiral models. The soliton approach goes back to the Skyrme model [10] while the connection to QCD was later established by considering baryons in a generalized version of QCD with $N_C$ large [1]. Soon after those mainly combinatoric arguments for considering baryons in an effective meson theory, static baryons properties were derived within the Skyrme model [11]. The soliton approach has ever since been very actively explored, cf. the reviews [12,13,14,15,16]. The point of departure for most of these models is an effective meson theory that reflects the major symmetries of QCD on the hadron level. In the low energy regime this is essentially the chiral symmetry with the pions as would-be Goldstone bosons being the basic field degrees of freedom (On the other end, the heavy quark effective symmetry has also been combined with the soliton picture. This is outside the scope of this review. The interested reader may trace relevant publications from Ref. [52] in the recent article [17].). Other mesons like $\omega$ and $\rho$ were then incorporated according to the rules of chiral symmetry. A major endeavor is to determine as many as possible model parameters from mesons to gain a high predictive power in the soliton sector, i.e., for baryon properties. Many of these properties have been reproduced in chiral soliton models to the accuracy that one expects from keeping the leading (and eventually next-to-leading) terms of a power expansion in $\frac{1}{N_C}$ when the actual value is $N_C=3$.

Unfortunately, this is not the case for nucleon structure functions and very early on it was recognized that soliton models based on meson fields disagree with the parton model. Rather than leading to the parton model Callan-Gross relation between the unpolarized structure functions, the Skyrme model yields the Callan-Gross analog for boson constituents [18] when evaluating current-current correlations that eventually lead to the structure functions. This problem is not unexpected as taking a purely meson model as point of departure implicitly relates local quark bilinears to the field degrees of freedom. On the other side, in QCD, the structure functions are related to bilocal quark bilinears and a successful exploration of these functions needs to trace the details of the bosonization procedure. To solve this fundamental problem of the soliton picture it is therefore compulsory to consider a model in which the bosonization is explicitly performed. Such a model starts from a chirally symmetric quark self-interaction and introduces auxiliary boson fields that make feasible the computation of the fermion path integral. Subsequently these boson fields take the role of the mesons in an effective theory. The Skyrme model problem is then approached by formulating the current-current correlations before bosonization. For this purpose we will here consider bosonization [19] of the Nambu-Jona-Lasinio model [20] that has well established soliton solutions [21,22,23]. The model by itself is not renormalizable and the regularization prescription is part of the model definition. Incorporating regularization is the major concern when computing structure functions in a bosonized chiral model. Essentially there are two approaches for computing nucleon structure functions. They differ conceptually but lead to similar results. The one that we will focus on here starts with a fully regularized action and extracts the structure functions from the absorptive part of the Compton tensor. We note that this approach is general enough to also predict the pion structure function [24]. We will take the position that we only identify the symmetries of QCD when adopting this model to describe hadrons. At this stage of the project we will not identify the quark degrees of freedom with those of QCD, which, for example, means that the current quark mass is a free parameter. The theoretical framework has been derived already some time ago [24] while the numerical results arising from costly simulations have only been obtained recently [25,26]. As mentioned above, a major motivation for the soliton picture arises from generalizing QCD to a nonabelian gauge theory with large $N_C$. In this review we will make $N_C$ explicit in formulas, but actual calculations are performed with $N_C=3$.

Formal considerations of QCD relate DIS in the Bjorken limit to hadron matrix elements of bilocal bilinear quark operators. There are soliton model approaches that sandwich the quark operators from the self-consistent chiral soliton in those nucleon matrix elements and impose regularization a posteriori [27,28,29,30,31,32,33,34,35,36,37,38,39]. We will comment on those approaches in Section 7.

The study of structure functions in soliton models has, to quite some extent, been triggered by the so-called proton spin puzzle [40]: Data on the polarized structure function suggested that, together with flavor symmetric relations, almost none of the nucleon spin was due to the spin of the quark constituents. This picture emerges from the nonrelativistic quark model in which the nucleon spin equals the matrix element of the axial singlet current. It is actually this matrix element that relates to the data and chiral soliton models indeed yield a small value, some versions even predict zero [41,42]. See Ref. [43] for a recent review on the present understanding of the proton spin structure.

Earlier we have noted the relevance of structure and/or distribution functions for DIS. There are other regimes of relevance. Let us first make explicit the factorization theorem for the cross-section for electron hadron scattering [2],

$${\sigma }_e(x,Q^2)=\sum _a{\int }_x^{1}d\xi f_a\left(\xi \right){\sigma }_{ea}\left(\frac{x}{\xi },Q^2\right).$$

(1)

Here $f_a\left(\xi \right)$ is the distribution function for parton a with momentum fraction $\xi$ in the hadron and ${\sigma }_{ea}$ is the (Born) cross-section for electron parton scattering. Note that the sum over a also includes different distributions for the same parton such as polarized and unpolarized. Furthermore x and $Q^2$ are Lorentz invariant kinematical variables that will be defined in Section 2. Essentially we are interested in the case where x is fixed but $Q^2$ becomes large. The $f_a\left(\xi \right)$ are equally important for the Drell-Yan process in which two hadrons (A and B) scatter into a lepton-antilepton pair and other hadrons. That pair originates from a virtual gauge boson that is produced by quarks (q) and antiquarks ($\overline{q}$) within the hadrons. Without going into further detail this suggests that the scattering cross-section is parameterized by the same distribution functions as DIS

$$\sigma \sim \sum _a{\int }_{x_A}^{1}d{\xi }_q{f}_q\left({\xi }_q\right){\int }_{x_B}^{1}d{\xi }_{\overline{q}}{f}_{\overline{q}}\left({\xi }_{\overline{q}}\right){\sigma }^{\prime }({\xi }_q,{\xi }_{\overline{q}},Q^2),$$

(2)

where ${\sigma }^{\prime }$ is the cross-section for turning the quark-antiquark pair into a lepton-antileption pair by the exchange of a virtual gauge boson. For the detailed definition of the kinematic variables $x_A$ and $x_B$ for the two hadrons A and B we again refer to Ref. [2]. Here we will not pursue the Drell-Yan process any further because it is not related to a current-current correlation matrix element of a single hadron. However, we will shortly come back to the Drell-Yan process in Section 7.

The expansion, Equation (1) indicates that different distributions $f_a\left(\xi \right)$ contribute with different inverse powers of Q to the total cross-section through ${\sigma }_{ea}$. Accordingly distributions are categorized by their twist which is extracted from the leading inverse power of Q in ${\sigma }_e$. The definition of twist dwells in the operator product expansion and relates to the dimensionality and spin of the operators in that expansion. Here it is sufficient to mention that the leading contribution (as Q increases) has twist-2, distributions that contribute like $1/Q$ to the total cross-section have twist-3 etc. [44].

The following section contains a brief recap of basic definitions in the context of structure functions. Section 3 describes the path from the self-interacting fermion theory to the bosonized chiral model together with a review of the pion structure function calculation. This will be followed by the construction of the soliton in that model in Section 4. We explain the soliton model calculation of structure in Section 5 and discuss the numerical results in Section 6. As mentioned, in Section 7 we will discuss related distribution function calculations in the chiral quark soliton model. Some concluding remarks are contained in Section 8.

2. Framework of Deep Inelastic Scattering

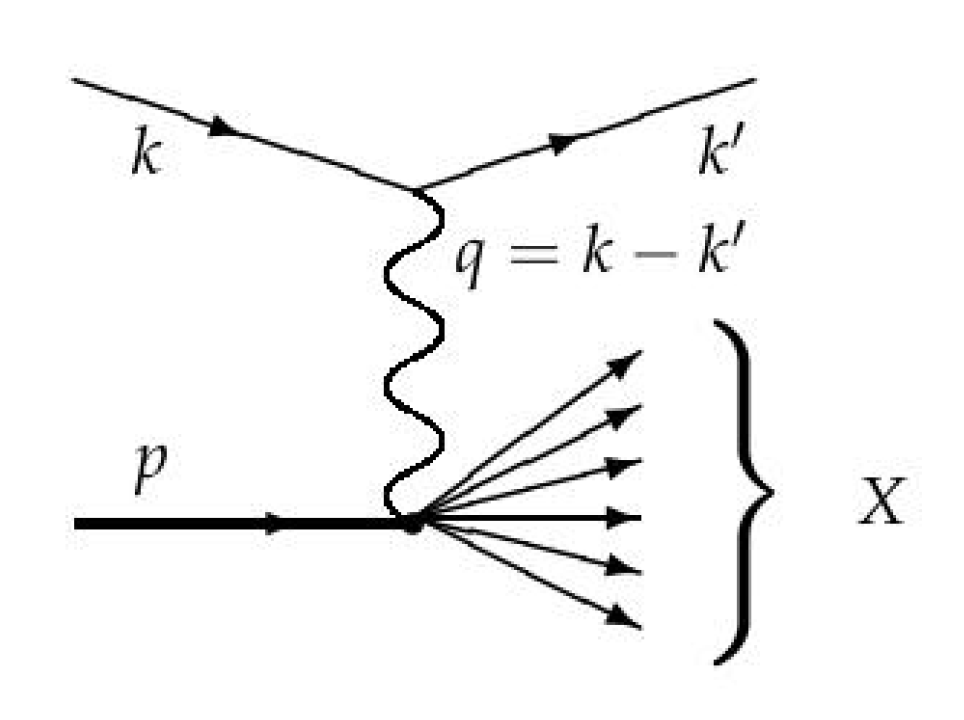
Deep inelastic scattering (DIS) is a major tool to explore the composition of the nucleon. In this process electron scattering produces a virtual photon which then interacts with the charged components of the nucleon. To extract the structure functions, the scattering products need not be detected as they are summed over in the final scattering cross section.

The interaction vertex for the disintegration of the nucleon is the matrix element of the (electromagnetic) current $J_{\mu }\left(\xi \right)$. The cross-section contains the squared absolute value of this matrix element and we sum/integrate over all final states subject to energy momentum conservation. This defines the hadron tensor for electron nucleon scattering

$$W_{\mu \nu }(p,q;s)=\frac{1}{4\pi }\sum _X〈p,s\left|J_{\mu }\left(0\right)\right|X〉〈X\left|J_{\mu }^{†}\left(0\right)\right|p,s〉{\left(2\pi \right)}^4{\delta }^4(p+q-p_X),$$

(3)

where s denotes the nucleon spin. The nucleon momentum is p and $q=k-k^{\prime }$ is the momentum of the virtual photon, see Figure 1. As the interaction is inelastic we have $q_0>0$. This, together with translational invariance, yields

$$W_{\mu \nu }(p,q;s)=\frac{1}{4\pi }\int d^4\xi e^{iq·\xi }〈p,s\left|\right[J_{\mu }\left(\xi \right),J_{\nu }^{†}\left(0\right)\left]\right|p,s〉.$$

(4)

The interaction is space-like and it is customary to introduce $Q^2=-q^2>0$ as well as $\nu =\frac{p·q}{M_N}$ where $M_N$ is the nucleon mass. In the nucleon rest frame $\nu$ is the energy transferred from the electron to the virtual photon. Most prominent is the Bjorken variable

$$x=\frac{Q^2}{2M_N\nu },$$

(5)

which in the parton model denotes the momentum fraction associated with a particular parton. Since on-shell $p^2=M_N^2$, $Q^2$ and x can be taken as the only dynamical Lorentz invariant variables so that the hadron tensor has the form factor decomposition

$$\begin{array}{cc}{W}_{\mu \nu }(p,q;s)\hfill & =\left(-g_{\mu \nu }+\frac{q_{\mu }{q}_{\nu }}{q^2}\right)M_N{W}_1(x,Q^2)\hfill \\ & +\left(p_{\mu }-q_{\mu }\frac{p·q}{q^2}\right)\left(p_{\nu }-q_{\nu }\frac{p·q}{q^2}\right)\frac{1}{M_N}{W}_2(x,Q^2)\hfill \\ \hfill & +\mathrm{i}{ϵ}_{\mu \nu \lambda \sigma }\frac{q^{\lambda }{M}_N}{p·q}\left(\left[G_1(x,Q^2)+G_2(x,Q^2)\right]s^{\sigma }-\frac{q·s}{q·p}{p}^{\sigma }{G}_2(x,Q^2)\right)\hfill \end{array}$$

(6)

for parity conserving processes like electromagnetic scattering of photons. The structure functions are the form factors in the so-called Bjorken scaling limit that takes $Q^2\to \infty$ with x fixed. For the spin independent, unpolarized structure functions $f_1\left(x\right)$ and $f_2\left(x\right)$ that is

$$M_N{W}_1(x,Q^2)\stackrel{\mathrm{Bj}}{⟶}{f}_1\left(x\right)\mathrm{and}\frac{p·q}{M_N}{W}_2(x,Q^2)\stackrel{\mathrm{Bj}}{⟶}{f}_2\left(x\right).$$

(7)

For the spin dependent, polarized structure functions no further scaling is involved and

$$G_1(x,Q^2)\stackrel{\mathrm{Bj}}{⟶}{g}_1\left(x\right)\mathrm{and}{G}_2(x,Q^2)\stackrel{\mathrm{Bj}}{⟶}{g}_2\left(x\right).$$

(8)

Contracting the hadron tensor with the projectors listed in

Table 1. Projection operators which extract the leading large $Q^2$ components from the hadron tensor. The projectors given in the spin independent cases presume the contraction of $W_{\rho \sigma }$ with $S^{\mu \nu \rho \sigma }=g^{\mu \rho }{g}^{\nu \sigma }+g^{\rho \nu }{g}^{\mu \sigma }-g^{\mu \nu }{g}^{\rho \sigma }$. The last row denotes the required spin orientation of the nucleon.

${\mathit{f}}_1$	${\mathit{f}}_2$	${\mathit{g}}_1$	${\mathit{g}}_{\mathit{T}}={\mathit{g}}_1+{\mathit{g}}_2$
$-\frac{1}{2}{g}^{\mu \nu }$	$-x{g}^{\mu \nu }$	$\frac{\mathrm{i}}{2M_N}{ϵ}^{\mu \nu \rho \sigma }\frac{q_{\rho }{p}_{\sigma }}{q·s}$	$\frac{-\mathrm{i}}{2M_N}{ϵ}^{\mu \nu \rho \sigma }{s}_{\rho }{p}_{\sigma }$
$\genfrac{}{}{-1.0pt}{}{\mathrm{spin}}{\mathrm{independent}}$	$\genfrac{}{}{-1.0pt}{}{\mathrm{spin}}{\mathrm{independent}}$	$\overrightarrow{s}\Vert \overrightarrow{q}$	$\overrightarrow{s}\perp \overrightarrow{q}$

extracts the pertinent structure functions. For the unpolarized structure functions these projectors directly lead to the Callan-Gross relation $f_2=2x{f}_1$. Observe also that these projectors are to be combined with appropriate selections for the spin orientation of the nucleon state as indicated in the last row of Table 1.

Even though we employ the Bjorken limit to the form factors, that leading expansion may still contribute with different (inverse) powers of Q to the total cross-section and thus the structure functions may be assigned different (leading) twist.

Similarly to the commutator in the hadron tensor we consider the matrix element of the time-ordered current-current product

$$\begin{array}{cc}\hfill T_{\mu \nu }(p,q;s)& =\mathrm{i}\int d^4\xi e^{\mathrm{i}q·\xi }〈p,s\left|T\left(J_{\mu }\left(\xi \right)J_{\nu }^{†}\left(0\right)\right)\right|p,s〉\hfill \\ \hfill & ={\left(2\pi \right)}^3\sum _X\left\{\frac{{\delta }^3({\overrightarrow{p}}_X-\overrightarrow{q}-\overrightarrow{p})}{p_X^0-q^0-p^0-\mathrm{i}ϵ}〈p,s\left|J_{\mu }\left(0\right)\right|X〉〈X\left|J_{\mu }^{†}\left(0\right)\right|p,s〉\right.\hfill \\ & \left.+\frac{{\delta }^3({\overrightarrow{p}}_X+\overrightarrow{q}-\overrightarrow{p})}{p_X^0+q^0-p^0-\mathrm{i}ϵ}〈p,s\left|J_{\mu }\left(0\right)\right|X〉〈X\left|J_{\mu }^{†}\left(0\right)\right|p,s〉\right\}.\hfill \end{array}$$

(9)

Cauchy’s principal value prescription $\frac{1}{x\pm \mathrm{i}ϵ}=\mathcal{P}\left(\frac{1}{x}\right)\mp \mathrm{i}\pi \delta \left(x\right)$ shows that the imaginary part of the first term is proportional to the hadron tensor as in Equation (3) while the second term does not have an imaginary part for the present kinematical set-up. Hence we have

$$W_{\mu \nu }(p,q;s)=\frac{1}{2\pi }\mathsf{Abs}{T}_{\mu \nu },$$

(10)

where Abs stands for absorptive part. From the physics point of view, $T_{\mu \nu }$ is the forward amplitude for nucleon Compton scattering and the hadron tensor is its absorptive part.

This paves the way towards computing the structure functions in the bosonized quark model. The action for that model is obtained from a functional integral of a self-interacting quark model. Within that formulation matrix elements of time-ordered products are straightforward to compute. Subsequently Cutkosky’s rules are applied to extract their absorptive parts.

3. The Chiral Quark Model

We consider the simplest $SU\left(2\right)$ Nambu-Jona-Lasinio (NJL) model which contains a chirally symmetric quartic fermion interaction in the scalar and pseudoscalar bilinears. In Minkowski space the Lagrangian reads [20],

$${\mathcal{L}}_{\mathrm{NJL}}=\overline{q}\left(\mathrm{i}\partial /-m^0\right)q+\frac{G}{2}\left[{\left(\overline{q}q\right)}^2+{\left(\overline{q}\mathrm{i}{\gamma }_5\overrightarrow{\tau }q\right)}^2\right].$$

(11)

The field $q\left(x\right)$ denotes a spinor with two flavors (up, u and down, d). There are no color interactions but each spinor has $N_C$ color components. Furthermore, $m^0$ and G are the current quark mass (average up and down quark mass) and the dimensionful coupling constant, respectively. The symmetry transformations are $q⟶q+\mathrm{i}\overrightarrow{ϵ}·\overrightarrow{\tau }q$ for $m^0\propto 𝟙$ and $q⟶q+\mathrm{i}{\gamma }_5{\overrightarrow{ϵ}}_5·\overrightarrow{\tau }q$ for $m^0=0$.

The effective bosonized action for the NJL model is constructed with the help of the auxiliary matrix field M that has a quadratic potential and couples linearly to the quark bilinears $\overline{q}q$ and $\overline{q}\mathrm{i}{\gamma }_5\overrightarrow{\tau }q$. Then the fermion part of the functional integral can be computed and its logarithm is an effective action which becomes a nonlinear and nonlocal theory for M [19]. The entries of this matrix are identified with the fields of the low-lying mesons. The model (by invention) breaks chiral symmetry dynamically for sufficiently large G and therefore the most import modes of M are the pseudoscalar pions (${\pi }^{\pm }$, ${\pi }^0$). The members of this isospin triplet would be Goldstone bosons in the chiral limit characterized by $m^0=0$.

At face value the effective action diverges and is not renormalizable. It is therefore mandatory to supplement it with a regularization prescription. It is standard to Wick-rotate to Euclidian space in which the effective action is complex. Apart from the cosmological constant contribution (which diverges quarticly but has no dynamical effect), the real part of this Euclidian action is quadratically divergent while the imaginary part is (conditionally) convergent. It is customary not to regularize the latter in order to properly reproduce the axial anomaly which can be analyzed by introducing photon fields, $\gamma$, (via minimal substitution in ${\mathcal{L}}_{\mathrm{NJL}}$) and studying the decay ${\pi }^0\to \gamma \gamma$. On the other hand, the real part is subjected to standard regularization methods like proper-time [45] or Pauli-Villars [46]. Within the perturbative realm (i.e., zero soliton sector) one can even work with a sharp momentum cut-off [47,48].

We would like to avoid the Wick-rotation because we want any imaginary part in our calculation of the hadron tensor being solely due to the absorptive components that we will extract via Cutkosky’s rules. There is indeed a procedure to identify the Minkowski space analogs of the real and imaginary parts of the Euclidian action [49,50]. To this end we define Dirac operators

$$\begin{array}{cc}\hfill \mathrm{i}\mathbf{D}& =\mathrm{i}\partial /-\left(S+\mathrm{i}{\gamma }_{5}P\right)+v/+a/{\gamma }_5=:\mathrm{i}{\mathbf{D}}^{\left(\pi \right)}+v/+a/{\gamma }_5\hfill \\ \hfill \mathrm{i}{\mathbf{D}}_5& =-\mathrm{i}\partial /-\left(S-\mathrm{i}{\gamma }_{5}P\right)-v/+a/{\gamma }_5=:\mathrm{i}{\mathbf{D}}_5^{\left(\pi \right)}-v/+a/{\gamma }_5,\hfill \end{array}$$

(12)

where $S=\frac{1}{2}(M+M^{†})$ and $P=\frac{1}{2}(M-M^{†})$. Furthermore, $v_{\mu }$ and $a_{\mu }$ denote external (classical) source fields with respect which we will compute functional derivatives to explore correlation functions. Finally, we have also defined Dirac operators without those sources (${\mathbf{D}}^{\left(\pi \right)}$ and ${\mathbf{D}}_5^{\left(\pi \right)}$) for later use. Wick-rotating ${\mathbf{D}}_5$ produces the conjugate of the Wick-rotation of $\mathbf{D}$ so that $\frac{1}{2}\mathrm{Tr}\log \left[\mathbf{D}{\mathbf{D}}_5\right]$ corresponds to the real part of the Euclidian action while its imaginary part is associated with $\frac{1}{2}\mathrm{Tr}\log \left[\mathbf{D}{\left({\mathbf{D}}_5\right)}^{-1}\right]$. The introduction of ${\mathbf{D}}_5$ comes at a price. Some of the Ward identities derived from the standard Dirac operator $\mathbf{D}$ do not hold anymore and rather occur with opposite signs [24]. We will later cure that obstacle by a particular calculational procedure to extract the polarized structure functions. This procedure is part of the regularization scheme. Even though the proper-time scheme has been very successfully applied for the solitons of the NJL model, we do not implement it here. This scheme induces an exponential dependence on the cut-off and it is unclear how to implement the Bjorken limit. Rather we adopt a version of the Pauli-Villars scheme in which the cut-off essentially is additive to the quark mass and does not interfere with the Bjorken limit. With all these preliminaries we are now in a position to write down the effective action for M:

$$\begin{array}{cc}\hfill {\mathcal{A}}_{\mathrm{NJL}}& ={\mathcal{A}}_{\mathrm{R}}+{\mathcal{A}}_{\mathrm{I}}+\frac{1}{4G}\int {\mathrm{d}}^{4}x\mathrm{tr}\left[m^0(M+M^{†})-M{M}^{†}\right]\hfill \\ \hfill {\mathcal{A}}_{\mathrm{R}}& =-\mathrm{i}\frac{N_C}{2}\sum _{i=0}^2{c}_i\mathrm{Tr}\log \left[-\mathbf{D}{\mathbf{D}}_5+{\mathsf{\Lambda }}_i^2-iϵ\right],\hfill \\ \hfill {\mathcal{A}}_{\mathrm{I}}& =-\mathrm{i}\frac{N_C}{2}\mathrm{Tr}\log \left[-\mathbf{D}{\left({\mathbf{D}}_5\right)}^{-1}-iϵ\right].\hfill \end{array}$$

(13)

Here ${\mathcal{A}}_{\mathrm{R}}$ and ${\mathcal{A}}_{\mathrm{I}}$ are the Minkowski analogs of the real and imaginary parts of the Euclidian space effective action. Furthermore, “Tr” denotes the functional trace that includes space-time integration on top of summing over the discrete Dirac and flavor indexes. The Pauli–Villars regularization scheme requires

$$c_0=1,{\mathsf{\Lambda }}_0=0,\sum _{i=0}^2{c}_i=0\mathrm{and}\sum _{i=0}^2{c}_i{\mathsf{\Lambda }}_i^2=0.$$

(14)

For simplicity we reduce the number of regulators by the limiting case ${\mathsf{\Lambda }}_1={\mathsf{\Lambda }}_2=\mathsf{\Lambda }$. For any quantity $Q\left({\mathsf{\Lambda }}^2\right)$ that is subject to regularization we then have

$$\sum _{i=0}^2{c}_{i}Q\left({\mathsf{\Lambda }}_i^2\right)=Q\left(0\right)-Q\left({\mathsf{\Lambda }}^2\right)+{\mathsf{\Lambda }}^2{Q}^{\prime }\left({\mathsf{\Lambda }}^2\right),$$

(15)

where the prime denotes the derivative with respect to the argument. For notational simplicity we will usually write the formulas as on the left hand, understanding that the right hand side is implemented in actual computations.

To analyze the model we need to find the ground state solution, $\langle M\rangle$. For symmetry reasons any nonzero solution can only be a (real) constant that is proportional to the unit matrix. We therefore substitute $\langle M\rangle =m$ in the so-called gap equation

$$\frac{1}{2G}\left(m-m^0\right)=-4\mathrm{i}{N}_{C}m\sum _{i=0}^2{c}_i\int \frac{d^{4}k}{{\left(2\pi \right)}^4}{\left[-k^2+m^2+{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ\right]}^{-1}$$

(16)

that arises from $\frac{\delta A_{\mathrm{NJL}}}{\delta M}=0$. For sufficiently large coupling G this equation has a solution with $m\gg m^0$ which obviously plays the role of a mass parameter when substituted for M into $\mathbf{D}$ (or ${\mathbf{D}}_5$). It is therefore called the constituent quark mass.

Any nontrivial vacuum solution signals dynamical symmetry breaking and applying a symmetry transformation onto that solution leads to (would-be) Goldstone bosons. In this case the relevant transformation is chiral and the would-be Goldstone boson (We expect that boson to be massless only when the original theory has an exact chiral symmetry, $m^{\left(0\right)}=0$.) is the pseudoscalar iso-triplet pion $\overrightarrow{\pi }$. This field is most conveniently introduced via the nonlinear realization

$$M=mU=m\exp \left[\mathrm{i}\frac{g}{m}\overrightarrow{\pi }·\overrightarrow{\tau }\right]=m+\mathrm{i}g\overrightarrow{\pi }·\overrightarrow{\tau }+\mathcal{O}\left({\overrightarrow{\pi }}^2\right),$$

(17)

where U is the chiral field while g is the Yukawa coupling constant. In the next step, we expand the effective action to quadratic order in the pion fields

$${\mathcal{A}}_{\mathrm{NJL}}=g^2\int \frac{d^{4}p}{{\left(2\pi \right)}^4}\overrightarrow{\tilde{\pi }}\left(p\right)·\overrightarrow{\tilde{\pi }}(-p)\left[2N_C{q}^2\mathrm{\Pi }\left(p^2\right)-\frac{1}{2G}\frac{m_0}{m}\right]+\mathcal{O}\left({\overrightarrow{\pi }}^4\right),$$

(18)

which has been written for the Fourier transform $\overrightarrow{\tilde{\pi }}\left(p\right)=d^{4}x{\mathrm{e}}^{-\mathrm{i}p·\xi }\overrightarrow{\pi }\left(\xi \right)$. The quadratic contribution contains the polarization function

$$\begin{array}{cc}\hfill \mathrm{\Pi }\left(p^2\right)& ={\int }_0^{1}dx\mathrm{\Pi }(p^2,x)\hfill \\ \hfill \mathrm{with}\mathrm{\Pi }(p^2,x)& =-\mathrm{i}\sum _{i=0}^2{c}_i\frac{d^{4}k}{{\left(2\pi \right)}^4}{\left[-k^2-x(1-x)p^2+m^2+{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ\right]}^{-2}.\hfill \end{array}$$

(19)

The factor in square brackets in Equation (18) times $g^2$ is the inverse pion propagator. Requiring this propagator to have a pole at the physical pion mass $m_{\pi }$ enforces

$$m^0=4N_{C}Gm{m}_{\pi }^2\mathrm{\Pi }\left(m_{\pi }^2\right).$$

(20)

Furthermore, the residue of that pole should be one thereby relating the Yukawa coupling constant g to other model parameters,

$$\frac{1}{g^2}=4N_C\frac{\partial }{\partial m_{\pi }^2}\left[m_{\pi }^2\mathrm{\Pi }\left(m_{\pi }^2\right)\right].$$

(21)

We construct the axial current from the functional derivative with respect to the axial source $a_{\mu }$

$$A_{\mu }\left(\xi \right)=\frac{\delta {\mathcal{A}}_{\mathrm{NJL}}}{\delta a^{\mu }\left(\xi \right)}{|}_{v_{\nu },a_{\nu }=0}.$$

Expanding $A_{\mu }\left(\xi \right)$ to linear order in $\overrightarrow{\tilde{\pi }}\left(p\right)$ yields the matrix element (a and b are flavor labels)

$$\langle 0|A_{\mu }^{\left(a\right)}\left(\xi \right)|{\tilde{\pi }}^{\left(b\right)}\left(p\right)\rangle \stackrel{!}{=}{\delta }_{ab}{f}_{\pi }\left(p\right)p_{\mu }{\mathrm{e}}^{-\mathrm{i}p·\xi }$$

from which we get the on-shell pion decay constant $f_{\pi }\left(0\right)=f_{\pi }=4N_{c}mg\mathrm{\Pi }\left(m_{\pi }^2\right)$. Taking this together with Equations (20) and (21) gives three equations for four model parameters (g, $\mathsf{\Lambda }$, G and $m^0$) after inserting the empirical data $f_{\pi }=93\mathrm{MeV}$ and $m_{\pi }=138\mathrm{MeV}$. This leaves one parameter, say G, undetermined. We employ the gap Equation (16) to express that undetermined parameter as a function of the constituent quark mass m which we take as the sole variable from now on. After all, we have quite some intuition about m and expect it to be somewhere around $400\mathrm{MeV}$. This procedure is reflected by the first three columns of

Table 2. Model parameters and results. See the main text for their definitions.

$\mathit{m}\left[\mathbf{MeV}\right]$	${\mathit{m}}^0\left[\mathbf{MeV}\right]$	$\mathbf{\Lambda }\left[\mathbf{GeV}\right]$	${\mathit{E}}_{\mathbf{tot}}\left[\mathbf{MeV}\right]$	${\mathit{\alpha }}^2[1/\mathbf{GeV}]$	$\mathbf{\Delta }\mathit{M}\left[\mathbf{MeV}\right]$	${\mathit{g}}_{\mathit{a}}$
350	7.9	0.77	1267	8.65	173	0.85
400	8.4	0.74	1269	5.89	255	0.80
450	8.5	0.73	1257	4.82	311	0.77

in the proceeding section. In this calculation the current quark mass is only about one third of what is obtained within proper-time regularization scheme [22]. This significant difference again suggests that quarks fields of the model are merely some effective degrees of freedom, with little or no relation to fundamental particles.

To apprehend the nucleon structure function calculation let us have a short look at DIS off pions which is characterized by a single structure function, $F\left(x\right)$,

$$\frac{1}{2\pi }\mathsf{Abs}{T}_{\mu \nu }(p,q)\stackrel{\mathrm{Bj}}{⟶}F\left(x\right)\left[-g_{\mu \nu }+\frac{q_{\mu }{q}_{\nu }}{q^2}-\frac{1}{q^2}\left(p_{\mu }-\frac{q_{\mu }}{2x}\right)\left(p_{\nu }-\frac{q_{\nu }}{2x}\right)\right],$$

(22)

where the Bjorken limit defined after Equation (6) has been indicated. In order to compute the Compton amplitude (22) we calculate the time-ordered product

$$T\left(J_{\mu }\left(\xi \right)J_{\nu }\left(0\right)\right)=\frac{{\delta }^2}{\delta v^{\mu }\left(\xi \right)\delta v^{\nu }\left(0\right)}{\mathcal{A}}_{\mathrm{NJL}}{|}_{v_{\mu }=0}$$

(23)

from the action, ${\mathcal{A}}_{\mathrm{NJL}}$ in Equation (12) with $a_{\mu }=0$ and the substitution $v_{\mu }\to v_{\mu }Q$, where $\mathcal{Q}=\frac{1}{3}\mathrm{diag}(2,-1)$ is the quark charge matrix. In principle we would have to fully expand ${\mathcal{A}}_{\mathrm{NJL}}$ to quadratic order in both the photon vector source, $v_{\mu }$ and the pion field $\overrightarrow{\tilde{\pi }}\left(p\right)$. Fortunately there is some simplification in expanding $\mathbf{D}{\mathbf{D}}_5$. Contributions to this product that are quadratic in either of the two fields add Feynman diagrams to the Compton amplitude that depend only on one of the two momenta. This type of local diagrams does not have an absorptive component. It is thus sufficient to consider

$$-\mathbf{D}{\mathbf{D}}_5={\partial }^2+m^2+g{\gamma }_5\left[\partial /,\overrightarrow{\pi }·\overrightarrow{\tau }\right]-\mathrm{i}\left(\partial /v/\mathcal{Q}+v/\mathcal{Q}\partial /\right)+\mathrm{i}g{\gamma }_5\left[\overrightarrow{\pi }·\overrightarrow{\tau },v/\mathcal{Q}\right]+\dots .$$

(24)

Even with this simplification, the expansion of the logarithm in ${\mathcal{A}}_{\mathrm{R}}$ (${\mathcal{A}}_{\mathrm{I}}$ does not contribute) has some unwanted terms with the flavor trace $\mathrm{tr}\left[\overrightarrow{\pi }\mathcal{Q}\overrightarrow{\pi }\mathcal{Q}\right]$ that would lead to different structure functions for the charged and uncharged pions. Fortunately these terms cancel in the Bjorken limit. Even when omitting terms which are suppressed in this limit or eventually do not contribute to the absorptive part, the pion Compton amplitude is still quite cumbersome to compute [24]

$$\begin{array}{cc}\hfill & \int d^4\xi {\mathrm{e}}^{\mathrm{i}q·\xi }\langle \pi \left(p\right)|\frac{{\delta }^2}{\delta v^{\mu }\left(\xi \right)\delta v^{\nu }\left(0\right)}{\mathcal{A}}_{\mathrm{NJL}}{|}_{v_{\mu }=0}|\pi \left(p\right)\rangle \hfill \\ \hfill & =\frac{5g^2{N}_C}{9}\sum _{i=0}^2{c}_i\int \frac{d{}^{4}k}{{\left(2\pi \right)}^4}\frac{1}{-k^2+m^2+{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ}\frac{1}{{\left[-{(k-p)}^2+m^2+{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ\right]}^2}\hfill \\ \hfill & \times \{\frac{-{(k-p)}^2+m^2+{\mathsf{\Lambda }}_i^2}{-{(k+q-p)}^2+m^2+{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ}\mathrm{tr}\left(p/{\gamma }^{\mu }q/{\gamma }^{\nu }+p/{\gamma }^{\nu }q/{\gamma }^{\mu }\right)\hfill \\ \hfill & -\frac{-{(k-p)}^2+m^2+{\mathsf{\Lambda }}_i^2}{-{(k-q-p)}^2+m^2+{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ}\mathrm{tr}\left(p/{\gamma }^{\mu }q/{\gamma }^{\nu }+p/{\gamma }^{\nu }q/{\gamma }^{\mu }\right)\hfill \\ \hfill & +2m^2\left[\frac{\mathrm{tr}\left([k/-p/]{\gamma }^{\nu }q/{\gamma }^{\mu }\right)}{-{(k-q-p)}^2+m^2+{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ}-\frac{\mathrm{tr}\left([k/-p/]{\gamma }^{\mu }q/{\gamma }^{\nu }\right)}{-{(k+q-p)}^2+m^2+{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ}\right]\}.\hfill \end{array}$$

(25)

The last two terms are products of four propagators as expected from an expansion up to fourth order. The first two terms only have three propagators and are represented by diagrams with a pion and a photon at a single vertex. This interaction stems from the last term in Equation (24). As in Equation (9) the absorptive part is extracted by putting all intermediate propagators on-shell according to Cutkosky’s rule

$$\begin{array}{cc}\frac{1}{-k^2+m^2+{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ}\hfill & ⟶-2\mathrm{i}\pi \delta (k^2-m^2-{\mathsf{\Lambda }}_i^2)\hfill \\ \frac{1}{-{(k\pm q-p)}^2+m^2+{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ}\hfill & ⟶-\frac{\mathrm{i}\pi }{q^{-}}\delta \left(q^{+}\pm {(k-p)}^{+}\right).\hfill \end{array}$$

(26)

In the second substitution we introduced light-cone coordinates (the full definition is given in Section 6.3) because they render the implementation of the Bjorken limit quite transparent: $q^{-}\to \infty$ and $q^{+}\to -x{p}^{+}=-\frac{x{m}_{\pi }}{\sqrt{2}}$ (in the pion rest frame). These coordinates bring in the factor $\frac{1}{q^{-}}$ when extracting the absorptive part. A posteriori this justifies the omission of all terms in Equation (25) that did not contain a factor $q/$ in the numerator (The full calculation also produces terms involving ${(k/-p/\pm q/)}^2$ in Equation (25). With Equation (26) it is obvious that they do not contribute to the absorptive part even though they have a finite Bjorken limit.). After taking the traces in color and spinor spaces the structure function can be read off from $T_{11}+T_{22}\stackrel{\mathrm{Bj}}{⟶}2F\left(x\right)$ using, e.g.,

$${\gamma }^{1}q/{\gamma }^1\stackrel{\mathrm{Bj}}{⟶}\frac{1}{2}{q}^{-}{\gamma }^1{\gamma }^{+}{\gamma }^1=-\frac{1}{2}{q}^{-}{\gamma }^{+}.$$

We find

$$\begin{array}{cc}F\left(x\right)\hfill & =-\frac{5\mathrm{i}}{18}\left(4N_C{g}^2\right)\sum _{i=0}^2{c}_i\int \frac{d^{4}k}{{\left(2\pi \right)}^4}\frac{2\pi \delta (k^2-m^2-{\mathsf{\Lambda }}_i^2)}{{\left[-{(k-p)}^2+m^2+{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ\right]}^2}\hfill \\ \hfill & \times \{\left[-{(k-p)}^2+m^2+{\mathsf{\Lambda }}_i^2\right]\left[\delta (k^{+}-p^{+}-q^{+})-\delta (k^{+}-p^{+}+q^{+})\right]p^{+}\hfill \\ \hfill & +m^2\left[\delta (k^{+}-p^{+}+q^{+})-\delta (k^{+}-p^{+}-q^{+})\right](k^{+}-p^{+})\}.\hfill \end{array}$$

(27)

The $\delta$-functions straightforwardly produce the $k^{+}$ integrals fixing this variable to either $m_{\pi }(1-x)$ or $m_{\pi }(1+x)$. The integral over $k^{-}$ can then be computed via the $\delta$-function in first numerator. The result from these two integrals is

$$\begin{array}{cc}\hfill F\left(x\right)& =\frac{5}{18}\left(4N_C{g}^2\right)\sum _{i=0}^2{c}_i\int \frac{d^2{k}_{\perp }}{{\left(2\pi \right)}^3}\left\{\frac{M_i^2\left(x\right)\theta \left(x\right)\theta (1-x)}{x(1-x){\left[M_i^2\left(x\right)-m_{\pi }^2\right]}^2}+\left(x⟷-x\right)\right\},\hfill \end{array}$$

(28)

where $M_i^2\left(x\right)=\frac{1}{x(1-x)}\left[m^2+{\mathsf{\Lambda }}_i^2+k_{\perp }^2\right]$. This expression for the pion structure function was earlier obtained using light-cone wave-functions [49,50,51]. In the chiral limit, $m_{\pi }=0$, this structure function is just a constant on the interval $-1\le x\le 1$. It is interesting to note that the light-cone coordinate momentum variables can also be integrated in the pion polarization function, Equation (19) leading to the same $k_{\perp }$ integral allowing the compact expression

$$F\left(x\right)=\frac{5}{9}\left(4N_C{g}^2\right)\frac{\partial }{\partial p^2}\left[p^2\mathrm{\Pi }(p^2,x)\right]{|}_{p^2=m_{\pi }^2}.$$

(29)

At this point one important aspect has not been considered. As it stands, Equation (29) is the pion structure function at the scale at which the NJL-model is supposed to approximate QCD. Stated otherwise, the structure function computed from Equation (29) approximates the QCD result at a (presumably) low renormalization scale. To allow a comparison with data, the QCD evolution equations must be applied to the model prediction. At that stage, the low renormalization scale enters as a new parameter that is tuned to optimize the agreement with the data at the higher energy scale of the experiments. This calculation has been carried out in Ref. [52]. Here we will not further elaborate on QCD evolution but will get back to it in Section 6 in the context of the nucleon structure functions.

The main lesson learned from this pion structure function study is that the calculation simplifies significantly when identifying the propagators that carry the momentum which is large in the Bjorken limit and ignoring the others (the many terms not shown in Equation (25)) and/or simplifying them by approximating them with free quark propagators.

4. Self-Consistent Soliton

The soliton is a static meson configuration that minimizes the bosonized action. To construct this configuration we define a Dirac Hamiltonian h via the Dirac operators in Equation (12)

$$\mathrm{i}{\mathbf{D}}^{\left(\pi \right)}=\beta (\mathrm{i}{\partial }_t-h)\mathrm{and}\mathrm{i}{\mathbf{D}}_5^{\left(\pi \right)}=(-\mathrm{i}{\partial }_t-h)\beta .$$

(30)

Its diagonalization

$$h{\mathsf{\Psi }}_{\alpha }={ϵ}_{\alpha }{\mathsf{\Psi }}_{\alpha },$$

(31)

yields eigenvalues ${ϵ}_{\alpha }$ and eigen-spinors ${\mathsf{\Psi }}_{\alpha }={\sum }_{\beta }{V}_{\alpha \beta }{\mathsf{\Psi }}_{\alpha }^{\left(0\right)}$ as linear combinations of the free Dirac spinors ${\mathsf{\Psi }}_{\alpha }^{\left(0\right)}$ in a spherical basis.

When constraining the meson configuration to the chiral circle, i.e., parameterizing $M=mU$ with only U being dynamical, the so-called hedgehog configuration [53] minimizes the action in the unit baryon number sector (We refer to the earlier review articles [22,23] for obstacles and their solutions for hedgehog configurations away from the chiral circle.). This, together with (the assumption of) spherical symmetry suggest the ansatz

$$h=\overrightarrow{\alpha }·\overrightarrow{p}+\beta m{U}_5\left(\overrightarrow{r}\right)\mathrm{where}{U}_5\left(\overrightarrow{r}\right)=\exp \left[\mathrm{i}\widehat{r}·\overrightarrow{\tau }{\gamma }_5\mathsf{\Theta }\left(r\right)\right].$$

(32)

The radial profile function $\mathsf{\Theta }\left(r\right)$ is called the chiral angle. The hedgehog configuration, Equation (32), is invariant under so-called grand spin transformations that combine flavor and coordinate rotations. Accordingly, the Dirac and flavor components of the eigenfunctions ${\mathsf{\Psi }}_{\alpha }$ are products of radial functions and grand spin eigenfunctions. The latter are products of spherical harmonic functions, spinors and iso-spinors. Final discretization is accomplished by imposing boundary conditions on the radial functions at a distance D much larger than typical extensions of the chiral angle [54]. Different boundary conditions are equivalent in the limit $D\to \infty$; however, at large but finite D a certain choice may be preferable depending on which quantity is to be computed [55]. All possible boundary conditions require that there is no flux through the sphere at D.

Once the structure of the spinors is established, particular profile functions can be considered. For profiles with $\mathsf{\Theta }\left(0\right)=-\pi$ and ${lim}_{r\to \infty }\mathsf{\Theta }\left(r\right)=0$ the diagonalization, Equation (31) yields a distinct, strongly bound level, (eigenvalue ${ϵ}_{\mathrm{v}}$, eigen-spinor ${\mathsf{\Psi }}_{\mathrm{v}}$) in the grand spin zero channel. This level is referred to as the valence quark level [22]: the wider the chiral angle, the more strongly bound is this distinct level. Its (explicit) occupation ensures unit baryon number.

The functional trace in ${\mathcal{A}}_R$ (${\mathcal{A}}_I$ vanishes for static configurations) is computed as an integral over the time interval T and a discrete sum over the basis levels defined by Equation (31). In the limit $T\to \infty$ the vacuum contribution to the static energy is then extracted from ${\mathcal{A}}_R\to -T{E}_{\mathrm{vac}}$. Collecting pieces, we obtain the total energy functional as [22,23]

$$\begin{array}{cc}\hfill E_{\mathrm{tot}}\left[\mathsf{\Theta }\right]& =\frac{N_C}{2}\left[1+\mathrm{sign}\left({ϵ}_{\mathrm{v}}\right)\right]{ϵ}_{\mathrm{v}}\hfill \\ & -\frac{N_C}{2}\sum _{i=0}^2{c}_i\sum _{\alpha }\left\{\sqrt{{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}_i^2}-\sqrt{{ϵ}_{\alpha }^{\left(0\right)2}+{\mathsf{\Lambda }}_i^2}\right\}+m_{\pi }^2{f}_{\pi }^2\int d^{3}r\left[1-\cos \left(\mathsf{\Theta }\right)\right].\hfill \end{array}$$

(33)

Here we have also subtracted the vacuum energy associated with the nondynamical meson field configuration $\mathsf{\Theta }\equiv 0$ (denoted by the superscript on the energy eigenvalues) that is often called the cosmological constant contribution. This subtraction will also play an important role for the unpolarized isoscalar structure function as it enters via the momentum sum rule. Obviously, the soliton energy is linear in $N_C$ as ascertained for baryon masses in QCD [1].

The soliton profile is then obtained as the profile function $\mathsf{\Theta }\left(r\right)$ that minimizes the total energy $E_{\mathrm{tot}}$ self-consistently subject to the above mentioned boundary conditions on $\mathsf{\Theta }\left(r\right)$. The energy eigenvalues ${ϵ}_{\alpha }$ are functionals of the chiral angle through the diagonalization in Equation (31). Hence the minimization of $E_{\mathrm{tot}}\left[\mathsf{\Theta }\right]$ involves

$$\frac{\delta {ϵ}_{\alpha }}{\delta \mathsf{\Theta }\left(r\right)}=m\int d^3{r}^{\prime }{\mathsf{\Psi }}_{\alpha }^{†}\left({\overrightarrow{r}}^{\prime }\right)\beta \left[-sin\mathsf{\Theta }\left(r^{\prime }\right)+\mathrm{i}{\widehat{r}}^{\prime }·\overrightarrow{\tau }cos\mathsf{\Theta }\left(r^{\prime }\right)\right]{\mathsf{\Psi }}_{\alpha }\left({\overrightarrow{r}}^{\prime }\right)\delta (r-r^{\prime }),$$

by the chain rule. Self-consistency arises as the wave-functions in this functional derivative emerge from diagonalizing an operator that contains $\mathsf{\Theta }\left(r\right)$. Though this Hartree-type problem is quite elaborate, it has been established some time ago [56,57,58] and ever been refined [22,23]. The two main contributions to $E_{\mathrm{tot}}\left[\mathsf{\Theta }\right]$ act in opposite directions: the binding of the distinct level is attractive while the Dirac sea piece (partially) compensates for this reduction. As the binding of the valence level increases with the constituent quark mass m, the soliton is kinematically stable against decaying into $N_C$ unbound quarks for $m\gtrsim 400\mathrm{MeV}$, cf. Table 2.

This soliton represents an object which has unit baryon number but neither good quantum numbers for spin and flavor (isospin). Such quantum numbers are generated by canonically quantizing the time-dependent collective coordinates $A\left(t\right)$ that parameterize the spin-flavor orientation of the soliton via

$$U_5(\overrightarrow{r},t)=A\left(t\right)U_5\left(\overrightarrow{r}\right)A^{†}\left(t\right),$$

(34)

where $U_5\left(\overrightarrow{r}\right)$ is the self-consistent static configuration from Equation (32). For a rigidly rotating soliton the Dirac operator becomes, after transforming to the flavor rotating frame [45],

$$\mathrm{i}{\mathbf{D}}^{\left(\pi \right)}=A\beta \left(\mathrm{i}{\partial }_t-\frac{1}{2}\overrightarrow{\mathsf{\Omega }}·\overrightarrow{\tau }-h\right)A^{†}\mathrm{and}\mathrm{i}{\mathbf{D}}_5^{\left(\pi \right)}=A\left(-\mathrm{i}{\partial }_t+\frac{1}{2}\overrightarrow{\mathsf{\Omega }}·\overrightarrow{\tau }-h\right)\beta A^{†}.$$

(35)

Actual computations involve an expansion with respect to the angular velocities $\overrightarrow{\mathsf{\Omega }}$ that are defined by that time derivative of the collective coordinates as

$$A^{†}\frac{d}{dt}A=\frac{\mathrm{i}}{2}\overrightarrow{\mathsf{\Omega }}·\overrightarrow{\tau }.$$

(36)

According to the canonical quantization rules the angular velocities are replaced by the spin operator

$$\overrightarrow{\mathsf{\Omega }}⟶\frac{1}{{\alpha }^2}\overrightarrow{J}.$$

(37)

The constant of proportionality is the moment of inertia

$$\begin{array}{cc}{\alpha }^2\hfill & =\frac{N_C}{4}\left[1+\mathrm{sign}\left({ϵ}_{\mathrm{v}}\right)\right]\sum _{\beta \ne \mathrm{v}}\frac{|\langle \mathrm{v}|{\tau }_3{|\beta \rangle |}^2}{{ϵ}_{\beta }-{ϵ}_{\mathrm{v}}}\hfill \\ \hfill & +\frac{N_C}{8}\sum _{\alpha \ne \beta }\sum _{i=0}^2{c}_i\frac{|\langle \alpha |{\tau }_3{|\beta \rangle |}^2}{{ϵ}_{\alpha }^2-{ϵ}_{\beta }^2}\left\{\frac{{ϵ}_{\alpha }^2+{ϵ}_{\alpha }{ϵ}_{\beta }+2{\mathsf{\Lambda }}_i^2}{\sqrt{{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}_i^2}}-\frac{{ϵ}_{\beta }^2+{ϵ}_{\alpha }{ϵ}_{\beta }+2{\mathsf{\Lambda }}_i^2}{\sqrt{{ϵ}_{\beta }^2+{\mathsf{\Lambda }}_i^2}}\right\},\hfill \end{array}$$

(38)

expressed by introducing eigenstates $|\alpha \rangle$ of h; i.e., ${\mathsf{\Psi }}_{\alpha }\left(\overrightarrow{r}\right)=\langle \overrightarrow{r}|\alpha \rangle$. The moment of inertia is $\mathcal{O}\left(N_C\right)$ and is extracted as twice the constant of proportionality of the $\mathcal{O}\left({\overrightarrow{\mathsf{\Omega }}}^2\right)$ term in the Lagrange function ($\mathcal{A}/T$). With Equation (37) the expansion in $\overrightarrow{\mathsf{\Omega }}$ is thus equivalent to the one in $\frac{1}{N_C}$. After quantizing the collective coordinates the Hamilton operator is that of a rigid rotor leading to the energy formula

$$E\left(j\right)=E_{\mathrm{tot}}+\frac{1}{2{\alpha }^2}j(j+1),$$

(39)

with spin eigenvalues $j=\frac{1}{2}$ for the nucleon and $j=\frac{3}{2}$ for the $\Delta$-resonance. Note that this energy formula contains a piece linear in $N_C$ and one linear in $\frac{1}{N_C}$. The contribution $\mathcal{O}\left(N_C^0\right)$, which is the vacuum polarization energy from the meson fluctuations, is generally omitted in soliton models. There is no robust calculation of this vacuum polarization energy because these models are not renormalizable. Estimates indicate that the $\mathcal{O}\left(N_C^0\right)$ component significantly reduces the energy [59,60]. Since this part does not depend on the baryon quantum numbers, it is customary to only consider mass differences, in particular, the $\Delta$-nucleon mass difference $\Delta M=\frac{3}{2{\alpha }^2}$. The results shown in Table 2 suggest that $m\approx 400\mathrm{MeV}$ reproduces the experimental value of $293\mathrm{MeV}$ reasonably well.

The nucleon wave-function becomes a (Wigner D) function of the collective coordinates. A useful relation in computing matrix elements of nucleon states $|N\rangle$ is [11]

$$\langle N|D_{ab}|N\rangle =-\frac{4}{3}\langle N|I_a{J}_b|N\rangle \mathrm{with}{D}_{ab}=\frac{1}{2}\mathrm{tr}\left(A^{†}{\tau }_{a}A{\tau }_b\right).$$

(40)

Here $I_a$ and $J_b$ are iso- and spin operators, respectively. The above matrix element arises from the operator identity $I_a=-D_{ab}{J}_b$ which by itself reflects the invariance of the hedgehog configuration under combined isospin and coordinate rotations.

As an example for the computation of a static nucleon property we consider the vacuum contribution to the axial charge, $g_a$, of the nucleon because in Section 5 it will be paradigmatic for how sum rules for structure functions emerge in this model and its treatment. In the first step we require the spatial components of the axial current as functions of the collective coordinates A. This is achieved by expanding the regularized action to leading order in the axial source $a/$ with $a^0=0$

$$\begin{array}{cc}\hfill {\mathcal{A}}_{\mathrm{NJL}}& =-\mathrm{i}\frac{N_C}{2}\sum _{i=0}^2{c}_i\mathrm{Tr}\log \left\{\beta \left({\partial }_t^2+h^2\right)\beta +\beta \left(\mathrm{i}{\partial }_t+h\right)a/{\gamma }_5+a/{\gamma }_5\left(-\mathrm{i}{\partial }_t+h\right)\beta +{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ\right\}\hfill \\ & =-\mathrm{i}\frac{N_C}{2}\sum _{i=0}^2{c}_i\mathrm{Tr}\log \left\{{\partial }_t^2+h^2+\left\{h,a/{\gamma }_5\beta \right\}+{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ\right\}.\hfill \end{array}$$

(41)

The next simplification is that we only need the (space) integral of that current and therefore may take $a/{\gamma }_5\beta =-{\overrightarrow{a}}^{\left(a\right)}·\overrightarrow{\alpha }{\gamma }_5\frac{{\tau }_a}{2}=-{\overrightarrow{a}}^{\left(a\right)}·\overrightarrow{\mathrm{\Sigma }}\frac{{\tau }_a}{2}$ with constant ${\overrightarrow{a}}^{\left(a\right)}$ to compute

$$\begin{array}{cc}\hfill \frac{\partial {\mathcal{A}}_{\mathrm{NJL}}}{\partial {\overrightarrow{a}}^{\left(a\right)}}{|}_{{\overrightarrow{a}}^{\left(a\right)}=0}& =\mathrm{i}\frac{N_C}{2}\sum _{i=0}^2{c}_i\mathrm{Tr}\left\{{\left({\partial }_t^2+h^2+{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ\right)}^{-1}\left\{h,\overrightarrow{\mathrm{\Sigma }}\frac{{\tau }_a}{2}\right\}\right\}\hfill \\ \hfill & =\mathrm{i}\frac{N_C}{2}\sum _{i=0}^2{c}_{i}T\int \frac{d\omega }{2\pi }{\mathrm{Tr}}^{\prime }\left\{{\left(-{\omega }^2+h^2+{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ\right)}^{-1}\left\{h,\overrightarrow{\mathrm{\Sigma }}\frac{{\tau }_a}{2}\right\}\right\}.\hfill \end{array}$$

(42)

As for any path integral, the limit $T\to \infty$ extracts the vacuum (Dirac sea) component. In the next step we want to evaluate the remaining trace ${\mathrm{Tr}}^{\prime }$ using the eigenvalues ${ϵ}_{\alpha }$ and the eigenstates $|\alpha \rangle$ of h. Substituting the rotating hedgehog configuration from Equation (34) and using the cyclic property of the trace yields

$$\begin{array}{cc}\frac{\partial {\mathcal{A}}_{\mathrm{NJL}}}{\partial {\overrightarrow{a}}^{\left(a\right)}}{|}_{{\overrightarrow{a}}^{\left(a\right)}=0}\hfill & =\mathrm{i}\frac{N_C}{2}\sum _{i=0}^2{c}_{i}T\int \frac{d\omega }{2\pi }\sum _{\alpha }\left\{{\left(-{\omega }^2+{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}_i^2-\mathrm{i}ϵ\right)}^{-1}2{ϵ}_{\alpha }〈\alpha \left|\overrightarrow{\mathrm{\Sigma }}{A}^{†}\frac{{\tau }_a}{2}A\right|\alpha 〉\right\}\hfill \\ & =-\frac{N_C}{2}T{D}_{ab}\sum _{i=0}^2{c}_i\sum _{\alpha }\frac{{ϵ}_{\alpha }}{\sqrt{{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}_i^2}}〈\alpha \left|\overrightarrow{\mathrm{\Sigma }}\frac{{\tau }_b}{2}\right|\alpha 〉,\hfill \end{array}$$

(43)

where the frequency integral has been computed by contour integration. The vacuum contribution to the axial charge is then obtained as the proton matrix element

$$g_a^{\left(\mathrm{s}\right)}=\underset{T\to \infty }{lim}\frac{1}{T}〈P\left|2\frac{\partial {\mathcal{A}}_{\mathrm{NJL}}}{\partial a_z^{\left(3\right)}}{|}_{{\overrightarrow{a}}^{\left(3\right)}=0}\right|P〉=\frac{N_C}{6}\sum _{i=0}^2{c}_i\sum _{\alpha }\frac{{ϵ}_{\alpha }}{\sqrt{{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}_i^2}}\langle \alpha |{\mathrm{\Sigma }}_3{\tau }_3|\alpha \rangle ,$$

(44)

with spin projection $J_3=+\frac{1}{2}$. In addition, we have the contribution from the valence quark that we get via a similar derivative after “gauging” the valence level

$$\frac{N_C}{2}\left[1+\mathrm{sign}\left({ϵ}_{\mathrm{v}}\right)\right]{ϵ}_{\mathrm{v}}⟶\frac{N_C}{2}\left[1+\mathrm{sign}\left({ϵ}_{\mathrm{v}}\right)\right]D_{ab}〈\mathrm{v}\left|h+{\overrightarrow{a}}^{\left(a\right)}·\overrightarrow{\mathrm{\Sigma }}\frac{{\tau }_b}{2}\right|\mathrm{v}〉$$

(45)

so that $g_a^{\left(\mathrm{v}\right)}=-\frac{N_C}{6}\left[1+\mathrm{sign}\left({ϵ}_{\mathrm{v}}\right)\right]\langle \mathrm{v}|{\mathrm{\Sigma }}_3{\tau }_3|\mathrm{v}\rangle$. In total we have

$$\begin{array}{cc}\hfill g_a& =g_a^{\left(\mathrm{v}\right)}+g_a^{\left(\mathrm{s}\right)}\hfill \\ & =-\frac{N_C}{6}\left[1+\mathrm{sign}\left({ϵ}_{\mathrm{v}}\right)\right]\langle \mathrm{v}|{\mathrm{\Sigma }}_3{\tau }_3|\mathrm{v}\rangle +\frac{N_C}{6}\sum _{i=0}^2{c}_i\sum _{\alpha }\frac{{ϵ}_{\alpha }}{\sqrt{{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}_i^2}}\langle \alpha |{\mathrm{\Sigma }}_3{\tau }_3|\alpha \rangle .\hfill \end{array}$$

(46)

It is illuminating to make the single cut-off regularization from Equation (15) explicit

$$g_a=-\frac{N_C}{6}\left[1+\mathrm{sign}\left({ϵ}_{\mathrm{v}}\right)\right]\langle \mathrm{v}|{\mathrm{\Sigma }}_3{\tau }_3|\mathrm{v}\rangle +\frac{N_C}{6}\sum _{\alpha }\left[\mathrm{sign}\left({ϵ}_{\alpha }\right)-{ϵ}_{\alpha }\frac{{ϵ}_{\alpha }^2+\frac{3}{2}{\mathsf{\Lambda }}^2}{{\left({ϵ}_{\alpha }^2+{\mathsf{\Lambda }}^2\right)}^{\frac{3}{2}}}\right]\langle \alpha |{\mathrm{\Sigma }}_3{\tau }_3|\alpha \rangle .$$

(47)

The strongly bound valence level is also included in the sum over $\alpha$. As the binding of that level is increased, for example by increasing the constituent quark mass m in the self-consistent construction, the corresponding energy eigenvalue eventually changes sign. The particular combination of valence and sea contributions ensures that $g_a$ is continuous as the terms with $\mathrm{sign}\left({ϵ}_{\mathrm{v}}\right)$ cancel. This feature is universal for any quantity; there is no discontinuity as the sign of the valence energy eigenvalue changes (Taking the “chemical potential” to be zero is a choice anyhow.). This is also true for the energy, Equation (33) and the moment of inertia, Equation (38). This occurs essentially by construction as the prefactor $\frac{1}{2}\left[1+\mathrm{sign}\left({ϵ}_{\mathrm{v}}\right)\right]$ is introduced to ensure unit baryon number (In analogy to $g_a$ the baryon number is obtained from a functional derivative with respect to constant $v_0$. The vacuum contribution stems from ${\mathcal{A}}_{\mathrm{I}}$ and is not regularized. As mentioned earlier ${\mathcal{A}}_{\mathrm{I}}$ is conditionally convergent in the sense that the sum over $\alpha$ must be taken over a symmetric interval.)

$$B=\frac{1}{2}\left[1+\mathrm{sign}\left({ϵ}_{\mathrm{v}}\right)\right]-\frac{1}{2}\sum _{\alpha }\mathrm{sign}\left({ϵ}_{\alpha }\right).$$

Stated otherwise, when the valence level is so strongly bound that its energy eigenvalue is negative, the baryon number is carried by the polarized Dirac sea (vacuum). This is an implicitly assumed feature of topological chiral soliton models like the Skyrme model because the topological current is the leading term in the gradient expansion for the vacuum contribution of the baryon current in chiral quark models [61].

In Table 2 we also list the model predictions for $g_a$. They are about 30% below the empirical value of $1.26$ [62]. Note, however, that only the leading $\frac{1}{N_C}$ result is given. It has been asserted that, because of the time-ordering prescription in the path integral for bosonization, subleading contributions can significantly increase the model prediction [23]. These contributions are, unfortunately, not without further problems. For example, they violate PCAC: In soliton models a partially conserved axial current (PCAC) results from the field equation for the soliton. This equation contains only the leading order in $\frac{1}{N_C}$ and any subleading piece in the axial current is not covered. Altering the field equation accordingly [63] does not produce a stable soliton when the subleading Dirac sea contribution (Early studies [64] omitted that part.) is properly included [23].

5. Hadron Tensor for the Nucleon as Soliton

We now get to a central topic of this short review: extracting the nucleon structure functions from the hadron tensor in the soliton background while realizing regularization from the onset of the action, Equation (13). Here we will consider mainly the example of the leading $\frac{1}{N_C}$ component of the longitudinal polarized structure function, $g_1$. For this example we will also explain how sum rules are established in the fully regularized formulation. For further details on other structure functions, that are obtained using quite a similar procedure, we refer to to original literature [24,25,26].

Similar to the pion structure function in Section 3 we start from the Compton tensor, Equation (23). However, this time we have to account for the nonperturbative nature of the solitonic meson fields and may not approximate ${\mathbf{D}}^{\left(\pi \right)}$ except for the $\frac{1}{N_C}$ expansion. As mentioned in that earlier Section, isospin violating contributions may arise that only cancel once the Bjorken limit is assumed. Can we anticipate this type of cancellations for the soliton configuration at an earlier stage and thus simplify the calculation (somewhat)? As a matter of fact the appearance of these terms is indeed an artifact of the simultaneous expansion in the pion and photon fields, Equation (24). We might equally well have expanded only in the photon field first (taking the charge matrix $\mathcal{Q}$ as part of $v/$, for simplicity)

$$\begin{array}{cc}\hfill & -\mathrm{Tr}\left\{{\left(-{\mathbf{D}}^{\left(\pi \right)}{\mathbf{D}}_5^{\left(\pi \right)}+{\mathsf{\Lambda }}_i^2\right)}^{-1}\right.\hfill \\ & \times \left.\left[\left({\mathbf{D}}^{\left(\pi \right)}v/+v/{\mathbf{D}}_5^{\left(\pi \right)}\right){\left(-{\mathbf{D}}^{\left(\pi \right)}{\mathbf{D}}_5^{\left(\pi \right)}+{\mathsf{\Lambda }}_i^2\right)}^{-1}\left({\mathbf{D}}^{\left(\pi \right)}v/+v/{\mathbf{D}}_5^{\left(\pi \right)}\right)\right]\right\}.\hfill \end{array}$$

(48)

Here square brackets have been introduced to mark those factors that are sensitive to the large photon momentum. Due to the cyclic properties of the trace this is merely a choice but it must contain all vertices with $v/$. In momentum space the propagator inside the square brackets behaves like $1/Q^2$ when assuming the Bjorken limit. In particular this implies that

$$\begin{array}{cc}\left[\dots \right]\hfill & \stackrel{\mathrm{Bj}}{⟶}\left({\mathbf{D}}^{\left(\pi \right)}v/+v/{\mathbf{D}}_5^{\left(\pi \right)}\right){\left(-{\mathbf{D}}^{\left(\pi \right)}{\mathbf{D}}_5^{\left(\pi \right)}\right)}^{-1}\left({\mathbf{D}}^{\left(\pi \right)}v/+v/{\mathbf{D}}_5^{\left(\pi \right)}\right)\hfill \\ \hfill & \stackrel{\mathrm{Bj}}{⟶}-{\mathbf{D}}^{\left(\pi \right)}v/{\left({\mathbf{D}}_5^{\left(\pi \right)}\right)}^{-1}v/-v/{\left({\mathbf{D}}^{\left(\pi \right)}\right)}^{-1}v/{\mathbf{D}}_5^{\left(\pi \right)}.\hfill \end{array}$$

(49)

Terms with either the unit or the ${\left(-{\mathbf{D}}^{\left(\pi \right)}{\mathbf{D}}_5^{\left(\pi \right)}\right)}^{-1}$ operators between two vector sources have been omitted because they will either not depend on the photon momentum, cf. the discussion before Equation (24) or are additionally suppressed by factors of $\frac{1}{Q^2}$. The above replacement tells us that in the Bjorken limit the propagator through which the large photon momentum runs will not contain the cut-offs ${\mathsf{\Lambda }}_i$. In particular there will be no contributions which behave like $\frac{Q^2}{{\mathsf{\Lambda }}_i^2}$; thereby the proper scaling behavior is manifest. In other regularization schemes, like e.g., proper-time, wherein the cut-off is not additive to the loop momenta, the absence of such scaling violating contributions is not apparent. Previously, in Equation (48), we expanded the operator in powers of the pion field leading to complicated three and four vertex quark loops. Now we see that the Bjorken limit enforces the cancellations among those diagrams that we observed for the pion structure function. The expression (49) simplifies even further by noting that the quark propagator between the two photon insertions carries the large photon momentum and should hence be approximated by the free massless propagator,

$$\begin{array}{cc}\hfill \left[\dots \right]& ⟶{\mathbf{D}}^{\left(\pi \right)}v/{\left(\partial /\right)}^{-1}v/-v/{\left(\partial /\right)}^{-1}v/{\mathbf{D}}_5^{\left(\pi \right)}.\hfill \end{array}$$

(50)

The transition from the expression (48) to (50) is illustrated in Figure 2.

Substituting this simplification into Equation (48) leads to

$$\mathrm{Tr}\left\{\left[{\left({\mathbf{D}}^{\left(\pi \right)}\right)}^{-1}-{\left({\mathbf{D}}_5^{\left(\pi \right)}\right)}^{-1}\right]v/{\left(\partial /\right)}^{-1}v/\right\}+\mathrm{reguarlizaion\; terms}.$$

(51)

Essentially we only include small and moderate momenta from the loop integrals for one of the two propagators, keeping in mind that the sum of the momenta in the propagators is subject to the Bjorken limit. The integration regime in which that large momentum is distributed (approximately) equally among the two propagators does not contribute in the Bjorken limit [24].

Having simplified the construction of the Compton tensor with the soliton background in the Bjorken limit we see that it will be sufficient to differentiate (bringing back the charge matrix $\mathcal{Q}$)

$$\begin{array}{cc}{\mathcal{A}}_{\mathsf{\Lambda },\mathrm{R}}^{(2,v)}\hfill & =-\mathrm{i}\frac{N_C}{4}\sum _{i=0}^2{c}_i\mathrm{Tr}\left\{{\left(-{\mathbf{D}}^{\left(\pi \right)}{\mathbf{D}}_5^{\left(\pi \right)}+{\mathsf{\Lambda }}_i^2\right)}^{-1}\right.\hfill \\ & \times \left.\left[{\mathcal{Q}}^{2}v/{\left(\partial /\right)}^{-1}v/{\mathbf{D}}_5^{\left(\pi \right)}-{\mathbf{D}}^{\left(\pi \right)}{(v/{\left(\partial /\right)}^{-1}v/)}_5{\mathcal{Q}}^2\right]\right\}\hfill \end{array}$$

(52)

with respect to the vector sources. As already mentioned after Equation (12) the operator ${\mathbf{D}}_5$, which was introduced to accomplish regularization, produces an unconventional Ward identity because, in contrast to $\mathbf{D}$, this ${\gamma }_5$-odd operator has a relative minus sign between the derivative operator $\mathrm{i}\partial /$ and the axial vector source $a/{\gamma }_5$. To correct this regularization artifact in a way consistent with the Bjorken sum rule [65,66] for the nucleon axial charge, $g_a$, this relative sign must also be reflected in the Dirac decomposition of ${(v/{\left(\partial /\right)}^{-1}v/)}_5=v^{\mu }\frac{{\partial }^{\rho }}{{\partial }^2}{v}^{\nu }{\left({\gamma }_{\mu }{\gamma }_{\rho }{\gamma }_{\nu }\right)}_5$:

$${\gamma }_{\mu }{\gamma }_{\rho }{\gamma }_{\nu }=S_{\mu \rho \nu \sigma }{\gamma }^{\sigma }-\mathrm{i}{ϵ}_{\mu \rho \nu \sigma }{\gamma }^{\sigma }{\gamma }^5\mathrm{while}{\left({\gamma }_{\mu }{\gamma }_{\rho }{\gamma }_{\nu }\right)}_5=S_{\mu \rho \nu \sigma }{\gamma }^{\sigma }+\mathrm{i}{ϵ}_{\mu \rho \nu \sigma }{\gamma }^{\sigma }{\gamma }^5,$$

(53)

where $S_{\mu \rho \nu \sigma }=g_{\mu \rho }{g}_{\nu \sigma }+g_{\rho \nu }{g}_{\mu \sigma }-g_{\mu \nu }{g}_{\rho \sigma }$. We recall that the ${\mathbf{D}}_5$ model, which is not physical, has been solely introduced as a device to allow for a regularization which maintains the anomaly structure of the underlying theory by regularizing ${\mathcal{A}}_{\mathrm{R}}$ and ${\mathcal{A}}_{\mathrm{I}}$ differently. Hence it is not at all surprising that further specification of this regularization prescription is demanded in order to formulate a fully consistent model. We stress that this issue is not specific to the Pauli–Villars scheme. All schemes that regularize the sum, $\log \left(\mathbf{D}\right)+\log \left({\mathbf{D}}_5\right)$ but not the difference, $\log \left(\mathbf{D}\right)-\log \left({\mathbf{D}}_5\right)$ will require the specification (53). Since only the polarized, i.e., spin dependent, structure functions are effected, this issue has not shown up when computing the pion structure function.

For the imaginary part of the action the expression analogous to Equation (52) reads

$$\begin{array}{cc}\hfill {\mathcal{A}}_{\mathsf{\Lambda },\mathrm{I}}^{(2,v)}& =-\mathrm{i}\frac{N_C}{4}\mathrm{Tr}\left\{{\left(-{\mathbf{D}}^{\left(\pi \right)}{\mathbf{D}}_5^{\left(\pi \right)}\right)}^{-1}\left[{\mathcal{Q}}^{2}v/{\left(\partial /\right)}^{-1}v/{\mathbf{D}}_5^{\left(\pi \right)}+{\mathbf{D}}^{\left(\pi \right)}{(v/{\left(\partial /\right)}^{-1}v/)}_5{\mathcal{Q}}^2\right]\right\}\hfill \\ \hfill & =\mathrm{i}\frac{N_C}{4}\mathrm{Tr}\left\{{\left({\mathbf{D}}^{\left(\pi \right)}\right)}^{-1}{\mathcal{Q}}^{2}v/{\left(\partial /\right)}^{-1}v/+{\left({\mathbf{D}}_5^{\left(\pi \right)}\right)}^{-1}{(v/{\left(\partial /\right)}^{-1}v/)}_5{\mathcal{Q}}^2\right\}.\hfill \end{array}$$

(54)

Again, it is understood that the large photon momentum runs only through the operators in square brackets in the first equation. Note that in the unregularized case (${\mathsf{\Lambda }}_i\equiv 0$) the contributions associated with ${\mathbf{D}}_5$ would cancel in the sum of Equations (52) and (54) leaving

$$\begin{array}{cc}\hfill {\mathcal{A}}^{(2,v)}& ={\mathcal{A}}_{\mathsf{\Lambda },\mathrm{R}}^{(2,v)}+{\mathcal{A}}_{\mathsf{\Lambda },\mathrm{I}}^{(2,v)}\hfill \\ \hfill & =\mathrm{i}\frac{N_C}{2}\mathrm{Tr}\left\{{\left({\mathbf{D}}^{\left(\pi \right)}\right)}^{-1}\left[{\mathcal{Q}}^{2}v/{\left(\partial /\right)}^{-1}v/\right]\right\}+\mathrm{regularization\; terms},\hfill \end{array}$$

(55)

and the adjustment, Equation (53) would not be efficacious. Expanding this expression to quadratic order in the pseudoscalar field P produces the standard "handbag" diagram with the propagators connecting the quark-pion and quark-photon vertices [51]. In particular, there are no isospin violating terms of the form $\mathrm{tr}\left(Pv/Pv/\right)$.

In the next step we will detail the calculation of the leading $\frac{1}{N_C}$ contribution from the polarized vacuum (Dirac sea) to the nucleon structure functions. The contribution of the distinct valence level will later be added as for as for the nucleon axial charge, $g_a$, in Equations (45) and (46). For the NJL soliton model this valence quark contribution has been thoroughly discussed in Refs. [67,68]. In other models, like the MIT bag model [69,70,71], the calculation is quite similar [72,73,74,75].

The above discussion and definition of the structure functions (form factors) in the hadron tensor was based on translational invariance. To apply it to a localized soliton configuration we need to restore translational invariance. This is accomplished by introducing a collective coordinate, $\overrightarrow{R}$, which describes the position of the soliton (nucleon) [76] with its momentum $\overrightarrow{p}$ conjugate to this collective coordinate (This procedure is common to all soliton models when e.g., computing form factors [77].), i.e., $\langle \overrightarrow{R}|\overrightarrow{p}\rangle =\sqrt{2E}\exp \left(\mathrm{i}\overrightarrow{R}·\overrightarrow{p}\right)$. Here $E=\sqrt{\overrightarrow{p}{}^2+M_N^2}$ denotes the nucleon energy. The Compton amplitude is then obtained by taking the pertinent matrix element and averaging over the position of the soliton,

$$\begin{array}{cc}{T}_{\mu \nu }^{ab}\hfill & =2\mathrm{i}{M}_N\int d^4\xi \int d^{3}R{e}^{\mathrm{i}q·\xi }〈p,s\left|T\left\{J_{\mu }^a(\xi -R)J_{\nu }^{b†}(-R)\right\}\right|p,s〉\hfill \\ \hfill & =2\mathrm{i}{M}_N\int d^4{\xi }_1\int d^3{\xi }_2{e}^{\mathrm{i}q·({\xi }_1-{\xi }_2)}〈s\left|T\left\{J_{\mu }^a\left({\xi }_1\right)J_{\nu }^{b†}\left({\xi }_2\right)\right\}\right|s〉.\hfill \end{array}$$

(56)

Here we have made use of the fact that the initial and final nucleon states not only have identical momenta but are actually considered in the rest frame. For simplicity we will treat ${\xi }_2$ and R as four-vectors noting that their temporal components vanish, ${\xi }_2^0=R^0=0$. The spin-isospin matrix elements will be evaluated in the space of the collective coordinates A, which have been introduced in Equation (35).

To see how Cutkosky’s rule works in the soliton sector it instructive to briefly (and only formally) consider the leading $\frac{1}{N_C}$ contribution in the unregularized case

$$\begin{array}{cc}\hfill T\left\{J_{\mu }\left({\xi }_1\right)J_{\nu }\left({\xi }_2\right)\right\}& =\mathrm{i}\frac{N_C}{2}\mathrm{Tr}\left\{{\left(-{\mathbf{D}}^{\left(\pi \right)}\right)}^{-1}{\mathcal{Q}}^2\right[{\gamma }_{\mu }{\delta }^4\left(\widehat{x}-{\xi }_1\right){\left(\partial /\right)}^{-1}{\gamma }_{\nu }{\delta }^4\left(\widehat{x}-{\xi }_2\right)\hfill \\ \hfill & +{\gamma }_{\nu }{\delta }^4\left(\widehat{x}-{\xi }_2\right){\left(\partial /\right)}^{-1}{\gamma }_{\mu }{\delta }^4\left(\widehat{x}-{\xi }_1\right)\left]\right\}.\hfill \end{array}$$

(57)

Here $\widehat{x}$ refers to the position operator. The above functional trace is computed by using a plane-wave basis for the operator in the square brackets while the matrix elements of ${\mathbf{D}}^{\left(\pi \right)}$ are evaluated employing the eigenfunctions ${\mathsf{\Psi }}_{\alpha }$ of the Dirac Hamiltonian (32):

$$\begin{array}{cc}\hfill T_{\mu \nu }\left(q\right)& =-M_N{N}_C\int \frac{d\omega }{2\pi }\sum _{\alpha }\int d^4{\xi }_1\int d^3{\xi }_2\int \frac{d^{4}k}{{\left(2\pi \right)}^4}{\mathrm{e}}^{\mathrm{i}{\xi }_1^0(q^0+k^0)}{\mathrm{e}}^{-\mathrm{i}({\overrightarrow{\xi }}_1-{\overrightarrow{\xi }}_2)·(\overrightarrow{q}+\overrightarrow{k})}\frac{1}{k^2+\mathrm{i}ϵ}\hfill \\ \hfill & \times \frac{\omega +{ϵ}_{\alpha }}{{\omega }^2-{ϵ}_{\alpha }^2+\mathrm{i}ϵ}\langle N\left|\right\{{\overline{\mathsf{\Psi }}}_{\alpha }\left({\overrightarrow{\xi }}_1\right){\mathcal{Q}}_A^2{\gamma }_{\mu }k/{\gamma }_{\nu }{\mathsf{\Psi }}_{\alpha }\left({\overrightarrow{\xi }}_2\right){\mathrm{e}}^{\mathrm{i}{\xi }_1^0\omega }\hfill \\ \hfill & -{\overline{\mathsf{\Psi }}}_{\alpha }\left({\overrightarrow{\xi }}_2\right){\mathcal{Q}}_A^2{\gamma }_{\nu }k/{\gamma }_{\nu }{\mathsf{\Psi }}_{\alpha }\left({\overrightarrow{\xi }}_1\right){\mathrm{e}}^{-\mathrm{i}{\xi }_1^0\omega }\left\}\right|N\rangle +\mathcal{O}\left(\frac{1}{N_C}\right).\hfill \end{array}$$

(58)

The dependence on the collective coordinates is contained in ${\mathcal{Q}}_A=A^{†}\mathcal{Q}A$. We clearly recognize the two propagators, one in the massless plane wave basis and the other in the soliton background. Cutkosky’s rule produces respective $\delta$-functions $-2\pi \mathrm{i}\delta \left(k^2\right)$ and $-2\pi \mathrm{i}\delta ({\omega }^2-{ϵ}_{\alpha }^2)$. We perform the frequency integral, write $t={\xi }_1^0$ and employ the prescription from Equation (53) so that the hadron tensor becomes

$$\begin{array}{cc}{W}_{\mu \nu }\hfill & =M_N{N}_C\sum _{\alpha }\mathrm{sign}\left({ϵ}_{\alpha }\right)\int dt\int d^3{\xi }_1\int d^3{\xi }_2\int \frac{d^{4}k}{{\left(2\pi \right)}^4}{\mathrm{e}}^{\mathrm{i}t(q^0+k^0)}{\mathrm{e}}^{-\mathrm{i}({\overrightarrow{\xi }}_1-{\overrightarrow{\xi }}_2)·(\overrightarrow{q}+\overrightarrow{k})}\delta \left(k^2\right)k^{\rho }\hfill \\ & \times \langle N|S_{\mu \rho \nu \sigma }\left\{{\overline{\mathsf{\Psi }}}_{\alpha }\left({\overrightarrow{\xi }}_1\right){\mathcal{Q}}_A^2{\gamma }^{\sigma }{\mathsf{\Psi }}_{\alpha }\left({\overrightarrow{\xi }}_2\right){\mathrm{e}}^{\mathrm{i}{ϵ}_{\alpha }t}-{\overline{\mathsf{\Psi }}}_{\alpha }\left({\overrightarrow{\xi }}_2\right){\mathcal{Q}}_A^2{\gamma }^{\sigma }{\mathsf{\Psi }}_{\alpha }\left({\overrightarrow{\xi }}_1\right){\mathrm{e}}^{-\mathrm{i}{ϵ}_{\alpha }t}\right\}\hfill \\ & -\mathrm{i}{ϵ}_{\mu \rho \nu \sigma }\left\{{\overline{\mathsf{\Psi }}}_{\alpha }\left({\overrightarrow{\xi }}_1\right){\mathcal{Q}}_A^2{\gamma }^{\sigma }{\gamma }_5{\mathsf{\Psi }}_{\alpha }\left({\overrightarrow{\xi }}_2\right){\mathrm{e}}^{\mathrm{i}{ϵ}_{\alpha }t}+{\overline{\mathsf{\Psi }}}_{\alpha }\left({\overrightarrow{\xi }}_2\right){\mathcal{Q}}_A^2{\gamma }^{\sigma }{\gamma }_5{\mathsf{\Psi }}_{\alpha }\left({\overrightarrow{\xi }}_1\right){\mathrm{e}}^{-\mathrm{i}{ϵ}_{\alpha }t}\right\}|N\rangle \hfill \\ & +\mathcal{O}\left(\frac{1}{N_C}\right).\hfill \end{array}$$

(59)

In the above we have four contributions, two for each the unpolarized ($S_{\mu \rho \nu \sigma }$) and polarized (${ϵ}_{\mu \rho \nu \sigma }$) components. One of the two components propagates from ${\xi }_1$ to ${\xi }_2$ and the other in the opposite direction. Typically they are denoted particle and antiparticle distributions. Note, however, that in the present case ${ϵ}_{\alpha }$ may have either sign so that both particle and antiparticles spinors contribute in all terms.

In deriving Equation (59) only the pole from $\omega =+{ϵ}_{\alpha }$ contributed. That will be different when regularization is accounted for. We display the result without further derivation as the calculation for the fully regularized scenario goes along the same lines as above

$$\begin{array}{cc}{T}_{\mu \nu }\left(q\right)\hfill & =-M_N\frac{N_C}{2}\int \frac{d\omega }{2\pi }\sum _{\alpha }\int dt\int d^3{\xi }_1\int d^3{\xi }_2\int \frac{d^{4}k}{{\left(2\pi \right)}^4}{\mathrm{e}}^{\mathrm{i}(q_0+k_0)t}{\mathrm{e}}^{-\mathrm{i}(\overrightarrow{q}+\overrightarrow{k})·({\overrightarrow{\xi }}_1-{\overrightarrow{\xi }}_2)}\frac{1}{k^2+\mathrm{i}ϵ}\hfill \\ & \times \langle N\left|\right\{\left[{\mathrm{e}}^{\mathrm{i}\omega t}{\mathsf{\Psi }}_{\alpha }^{†}\left({\overrightarrow{\xi }}_1\right)\beta {\mathcal{Q}}_A^2{\gamma }_{\mu }k/{\gamma }_{\nu }{\mathsf{\Psi }}_{\alpha }\left({\overrightarrow{\xi }}_2\right)-{\mathrm{e}}^{-\mathrm{i}\omega t}{\mathsf{\Psi }}_{\alpha }^{†}\left({\overrightarrow{\xi }}_2\right)\beta {\mathcal{Q}}_A^2{\gamma }_{\nu }k/{\gamma }_{\mu }{\mathsf{\Psi }}_{\alpha }\left({\overrightarrow{\xi }}_1\right)\right]f_{\alpha }^{+}\left(\omega \right)\hfill \\ & +\left[{\mathrm{e}}^{\mathrm{i}\omega t}{\mathsf{\Psi }}_{\alpha }^{†}\left({\overrightarrow{\xi }}_1\right){\mathcal{Q}}_A^2{({\gamma }_{\mu }k/{\gamma }_{\nu })}_5\beta {\mathsf{\Psi }}_{\alpha }\left({\overrightarrow{\xi }}_2\right)-{\mathrm{e}}^{-\mathrm{i}\omega t}{\mathsf{\Psi }}_{\alpha }^{†}\left({\overrightarrow{\xi }}_2\right){\mathcal{Q}}_A^2{({\gamma }_{\nu }k/{\gamma }_{\mu })}_5\beta {\mathsf{\Psi }}_{\alpha }\left({\overrightarrow{\xi }}_1\right)\right]f_{\alpha }^{-}\left(\omega \right)\left\}\right|N\rangle \hfill \\ & +\mathcal{O}\left(\frac{1}{N_C}\right),\hfill \end{array}$$

(60)

with the spectral functions

$$\begin{array}{c}\hfill f_{\alpha }^{\pm }\left(\omega \right)=\sum _{i=0}^2{c}_i\frac{\omega \pm {ϵ}_{\alpha }}{{\omega }^2-{ϵ}_{\alpha }^2-{\mathsf{\Lambda }}_i^2+\mathrm{i}ϵ}\pm \frac{\omega \pm {ϵ}_{\alpha }}{{\omega }^2-{ϵ}_{\alpha }^2+\mathrm{i}ϵ}.\end{array}$$

(61)

The first term in these spectral functions arises from the regularized real part, and the second from the unregularized imaginary part. Without regularization $f_{\alpha }^{+}\left(\omega \right)\sim \frac{2(\omega +{ϵ}_{\alpha })}{{\omega }^2-{ϵ}_{\alpha }^2+iϵ}$ and $f_{\alpha }^{-}\left(\omega \right)\sim 0$ so that Equation (58) would be recovered.

Before applying Cutkosky’s rule we integrate over the time variable which is distinct from the spatial coordinates because the soliton is static. This integral yields $2\pi \delta (q_0+k_0\pm \omega )$ which we subsequently use to integrate $k_0$. Then the $\delta$-function for the absorptive part of the Compton amplitude is $\delta ({(q_0\pm \omega )}^2-|\overrightarrow{k}{|}^2)$. To perform the spatial integrals we define the Fourier transform of the single particle wave-functions (The single particle wave-functions are parity eigenfunctions so that spatial reflections can be compensated by factors of $\beta$.) as

$${\tilde{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{p}\right)=\int \frac{d^3\xi }{4\pi }{\mathsf{\Psi }}_{\alpha }\left(\overrightarrow{\xi }\right){\mathrm{e}}^{\mathrm{i}\overrightarrow{\xi }·\overrightarrow{p}}$$

(62)

and get

$$\begin{array}{cc}{W}_{\mu \nu }\left(q\right)\hfill & =\mathrm{i}{M}_N\frac{N_C}{\pi }\int \frac{d\omega }{2\pi }\sum _{\alpha }\int d^{3}k\hfill \\ \hfill & \times \langle N\left|\right\{[{\tilde{\mathsf{\Psi }}}_{\alpha }^{†}(\overrightarrow{q}+\overrightarrow{k}){\mathcal{Q}}_A^2\beta {\gamma }_{\mu }k/{\gamma }_{\nu }{\tilde{\mathsf{\Psi }}}_{\alpha }(\overrightarrow{q}+\overrightarrow{k})\delta \left(\right|\overrightarrow{k}{|}^2-{(q_0+\omega )}^2)\hfill \\ & -{\tilde{\mathsf{\Psi }}}_{\alpha }^{†}(\overrightarrow{q}+\overrightarrow{k}){\mathcal{Q}}_A^2{\gamma }_{\nu }k/{\gamma }_{\mu }\beta {\tilde{\mathsf{\Psi }}}_{\alpha }(\overrightarrow{q}+\overrightarrow{k})\delta \left(\right|\overrightarrow{k}{|}^2-{(q_0-\omega )}^2)]f_{\alpha }^{+}\left(\omega \right){|}_{\mathrm{p}}\hfill \\ & +[{\tilde{\mathsf{\Psi }}}_{\alpha }^{†}(\overrightarrow{q}+\overrightarrow{k}){\mathcal{Q}}_A^2{({\gamma }_{\mu }k/{\gamma }_{\nu })}_5\beta {\tilde{\mathsf{\Psi }}}_{\alpha }(\overrightarrow{q}+\overrightarrow{k})\delta \left(\right|\overrightarrow{k}{|}^2-{(q_0+\omega )}^2)\hfill \\ & -{\tilde{\mathsf{\Psi }}}_{\alpha }^{†}(\overrightarrow{q}+\overrightarrow{k}){\mathcal{Q}}_A^2\beta {({\gamma }_{\nu }k/{\gamma }_{\mu })}_5{\tilde{\mathsf{\Psi }}}_{\alpha }(\overrightarrow{q}+\overrightarrow{k})\delta \left(\right|\overrightarrow{k}{|}^2-{(q_0-\omega )}^2)\left]f_{\alpha }^{-}\left(\omega \right){|}_{\mathrm{p}}\right\}|N\rangle ,\hfill \end{array}$$

(63)

where, again, we only wrote the leading $\frac{1}{N_C}$ term. An example for the pole extraction is

$$\begin{array}{cc}\hfill {\left(\sum _{i=0}^2{c}_i\frac{1}{{\omega }^2-{ϵ}_{\alpha }^2-{\mathsf{\Lambda }}_i^2+\mathrm{i}ϵ}\right)}_{\mathrm{p}}& =\sum _{i=0}^2{c}_i\frac{-\mathrm{i}\pi }{{\omega }_{\alpha }}\left[\delta \left(\omega +{\omega }_{\alpha }\right)+\delta \left(\omega -{\omega }_{\alpha }\right)\right],\hfill \end{array}$$

(64)

with ${\omega }_{\alpha }=\sqrt{{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}_i^2}$. To get an expression that looks like a bilocal and bilinear distribution function we shift the integration variable $\overrightarrow{p}=\overrightarrow{q}+\overrightarrow{k}$ and recognize that the single particle wave-functions will have support only for small $\overrightarrow{p}$, as compared to the large momenta in $\overrightarrow{q}$. This allows us to replace $k/$ by $-q/$ in the Bjorken limit (recall that $k_0=-q_0\mp \omega$ from the t integral) for the Dirac matrices sandwiched between the spinors. Furthermore

$$\begin{array}{cc}\hfill |\overrightarrow{k}{|}^2-{(q_0\pm \omega )}^2& =|\overrightarrow{p}-\overrightarrow{q}{|}^2-{(q_0\pm \omega )}^2={\overrightarrow{p}}^2-2\overrightarrow{p}·\widehat{n}|\overrightarrow{q}|+|\overrightarrow{q}{|}^2-{(q_0\pm \omega )}^2\hfill \\ \hfill & \stackrel{\mathrm{Bj}}{⟶}-2\left|\overrightarrow{q}\right|\left[\overrightarrow{p}·\widehat{n}-(M_{N}x\mp \omega )\right].\hfill \end{array}$$

Here $\widehat{n}$ is the unit vector in the direction of the spatial photon momentum $\overrightarrow{q}$. Then

$$\begin{array}{cc}{W}_{\mu \nu }\left(q\right)\hfill & =\mathrm{i}{M}_N\frac{N_C}{2\pi }\int \frac{d\omega }{2\pi }\sum _{\alpha }\int d^{3}p\hfill \\ \hfill & \times \langle N\left|\right\{[{\tilde{\mathsf{\Psi }}}_{\alpha }^{†}\left(\overrightarrow{p}\right){\mathcal{Q}}_A^2\beta {\gamma }_{\mu }n/{\gamma }_{\nu }{\tilde{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{p}\right)\delta (\overrightarrow{p}·\widehat{n}-(M_{N}x-\omega ))\hfill \\ & -{\tilde{\mathsf{\Psi }}}_{\alpha }^{†}\left(\overrightarrow{p}\right){\mathcal{Q}}_A^2{\gamma }_{\nu }n/{\gamma }_{\mu }\beta {\tilde{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{p}\right)\delta (\overrightarrow{p}·\widehat{n}-(M_{N}x+\omega ))]f_{\alpha }^{+}\left(\omega \right){|}_{\mathrm{p}}\hfill \\ & +[{\tilde{\mathsf{\Psi }}}_{\alpha }^{†}\left(\overrightarrow{p}\right){\mathcal{Q}}_A^2{({\gamma }_{\mu }n/{\gamma }_{\nu })}_5\beta {\tilde{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{p}\right)\delta (\overrightarrow{p}·\widehat{n}-(M_{N}x-\omega ))\hfill \\ & -{\tilde{\mathsf{\Psi }}}_{\alpha }^{†}\left(\overrightarrow{p}\right){\mathcal{Q}}_A^2\beta {({\gamma }_{\nu }n/{\gamma }_{\mu })}_5{\tilde{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{p}\right)\delta (\overrightarrow{p}·\widehat{n}-(M_{N}x+\omega ))\left]f_{\alpha }^{-}\left(\omega \right){|}_{\mathrm{p}}\right\}|N\rangle ,\hfill \end{array}$$

(65)

where $n^{\mu }={(1,\widehat{n})}^{\mu }$ is a light-like vector. Equation (65) is well suited for our numerical simulations in Section 6, in particular when treating the $\delta$-functions by averaging the directions of $\widehat{n}$ [28]. However, the similarity with distribution functions is more apparent when returning to coordinate space and writing the $\delta$-functions as integrals of exponential functions

$$\begin{array}{cc}{W}_{\mu \nu }^{\left(s\right)}\left(q\right)\hfill & =\mathrm{i}{M}_N\frac{N_C}{4}\int \frac{d\omega }{2\pi }\sum _{\alpha }\int d^3\xi \int \frac{d\lambda }{2\pi }{\mathrm{e}}^{\mathrm{i}{M}_{n}x\lambda }\hfill \\ & \times \langle N\left|\right\{[{\overline{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{\gamma }_{\mu }n/{\gamma }_{\nu }{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }+\lambda \widehat{n}){\mathrm{e}}^{-\mathrm{i}\lambda \omega }\hfill \\ & -{\overline{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{\gamma }_{\nu }n/{\gamma }_{\mu }{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }-\lambda \widehat{n}){\mathrm{e}}^{\mathrm{i}\lambda \omega }]f_{\alpha }^{+}\left(\omega \right){|}_{\mathrm{p}}\hfill \\ & +[{\overline{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{({\gamma }_{\mu }n/{\gamma }_{\nu })}_5{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }-\lambda \widehat{n}){\mathrm{e}}^{-\mathrm{i}\lambda \omega }\hfill \\ & -{\overline{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{({\gamma }_{\nu }n/{\gamma }_{\mu })}_5{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }+\lambda \widehat{n}){\mathrm{e}}^{\mathrm{i}\lambda \omega }\left]f_{\alpha }^{-}\left(\omega \right){|}_{\mathrm{p}}\right\}|N\rangle ,\hfill \end{array}$$

(66)

where we have added the superscript on $W_{\mu \nu }^{\left(s\right)}\left(q\right)$ to clarify that Equation (66) represents the vacuum (Dirac sea) component only. The valence component is most conveniently obtained by restricting the sum to $\alpha =\mathrm{v}$ and omitting regularization

$$\begin{array}{cc}{W}_{\mu \nu }^{\left(v\right)}\left(q\right)\hfill & =\mathrm{i}\left[1+\mathrm{sign}\left({ϵ}_{\mathrm{v}}\right)\right]M_N\frac{N_C}{4}\int d^3\xi \int \frac{d\lambda }{2\pi }{\mathrm{e}}^{\mathrm{i}{M}_{n}x\lambda }\langle N|\hfill \\ & \times \left\{\left[{\overline{\mathsf{\Psi }}}_{\mathrm{v}}\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{\gamma }_{\nu }n/{\gamma }_{\mu }{\mathsf{\Psi }}_{\mathrm{v}}(\overrightarrow{\xi }-\lambda \widehat{n}){\mathrm{e}}^{\mathrm{i}\lambda {ϵ}_{\mathrm{v}}}-{\overline{\mathsf{\Psi }}}_{\mathrm{v}}\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{\gamma }_{\mu }n/{\gamma }_{\nu }{\mathsf{\Psi }}_{\mathrm{v}}(\overrightarrow{\xi }+\lambda \widehat{n}){\mathrm{e}}^{-\mathrm{i}\lambda {ϵ}_{\mathrm{v}}}\right]\right\}|N\rangle .\hfill \end{array}$$

(67)

Equations (66) and (67) indeed have the form of bilocal and bilinear quark distributions. However, these are the distributions for the quarks in the chiral model interacting self-consistently with the soliton. So far, no connection to distributions in QCD has been incorporated; our calculation is solely based on the electromagnetic interaction within the chiral model. Several features needed consideration to arrive at an expression of the form of distributions. Most importantly and, of course, not surprisingly the Bjorken limit was implemented. In addition, one of the two propagators that occur in the Compton amplitude is taken to be that of a free massless fermion, while the other contains all information about the soliton that resembles the nucleon. Again, this separation is an indirect consequence of the Bjorken limit. Furthermore, we made use of the fact that the (momentum space) quark wave-functions only have support at momenta that are tiny compared to the momentum of the exchanged virtual photon. Finally, we stress that the appearance of single distribution functions in Equation (66) is kind of deceptive as the spectral functions $f_{\alpha }^{(\pm )}\left(\omega \right)$ pick up more than a single pole.

In Section 4 we have computed that axial charge, $g_a$, of the nucleon. It is the prime example to see how sum rules work in the presence of regularization. The Bjorken sum rule [65,66] relates that charge to the x-integral of the isovector combination of longitudinal polarized nucleon structure functions $g_1\left(x\right)$ for proton and neutron. These functions are obtained from the antisymmetric component of the hadron tensor

$$\begin{array}{cc}{W}_{\mu \nu }^{(s,\mathrm{A})}\hfill & =-M_N\frac{N_C}{2}{ϵ}_{\mu \rho \nu \sigma }{\mathrm{n}}^{\rho }\int \frac{d\omega }{2\pi }\sum _{\alpha }\int d^3\xi \int \frac{d\lambda }{2\pi }{\mathrm{e}}^{\mathrm{i}{M}_{N}x\lambda }{\left(\sum _{i=0}^2{c}_i\frac{\omega +{ϵ}_{\alpha }}{{\omega }^2-{ϵ}_{\alpha }^2-{\mathsf{\Lambda }}_i^2+\mathrm{i}ϵ}\right)}_{\mathrm{p}}\hfill \\ & \times 〈N|{\overline{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{\gamma }^{\sigma }{\gamma }_5{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }+\lambda \widehat{n}){\mathrm{e}}^{-\mathrm{i}\omega \lambda }+{\overline{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{\gamma }^{\sigma }{\gamma }_5{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }-\lambda \widehat{n}){\mathrm{e}}^{\mathrm{i}\omega \lambda }|N〉.\hfill \end{array}$$

(68)

The spectral function is fully regularized because it originates from

$$\begin{array}{cc}\hfill f_{\alpha }^{+}\left(\omega \right)-f_{\alpha }^{-}(-\omega )& =\sum _{i=0}^2{c}_i\frac{\omega +{ϵ}_{\alpha }-(-\omega -{ϵ}_{\alpha })}{{\omega }^2-{ϵ}_{\alpha }^2-{\mathsf{\Lambda }}_i^2+\mathrm{i}ϵ}+\frac{\omega +{ϵ}_{\alpha }+(-\omega -{ϵ}_{\alpha })}{{\omega }^2-{ϵ}_{\alpha }^2+\mathrm{i}ϵ}\hfill \\ \hfill & =2\sum _{i=0}^2{c}_i\frac{\omega +{ϵ}_{\alpha }}{{\omega }^2-{ϵ}_{\alpha }^2-{\mathsf{\Lambda }}_i^2+\mathrm{i}ϵ}.\hfill \end{array}$$

Here the prescription from Equation (53) has had a major impact. Without this specification the relative sign between the spectral functions would have been positive resulting in the spectral function $(\omega +{ϵ}_{\alpha })/({\omega }^2-{ϵ}_{\alpha }^2+\mathrm{i}ϵ)$. In that case $W_{\mu \nu }^{(s,\mathrm{A})}$ would have to be associated with unregularized imaginary part of the action in Euclidian space which is not compatible with the sum rules. The reason is that the leading order $\left(\mathrm{in}\frac{1}{N_C}\right)$ contribution to the axial charges stems from the regularized real part of the action.

Taking $\widehat{n}={\widehat{e}}_3$ and the projection operator given in Table 1 we find for the Dirac sea component of the longitudinal polarized structure function

$$\begin{array}{cc}{g}_1^{\left(s\right)}\left(x\right)\hfill & =-\mathrm{i}\frac{M_N{N}_C}{36}〈N\left|I_3\right|N〉\int \frac{d\omega }{2\pi }\sum _{\alpha }\int d^3\xi \int \frac{d\lambda }{2\pi }{\mathrm{e}}^{i{M}_{N}x\lambda }{\left(\sum _{i=0}^2{c}_i\frac{\omega +{ϵ}_{\alpha }}{{\omega }^2-{ϵ}_{\alpha }^2-{\mathsf{\Lambda }}_i^2+iϵ}\right)}_{\mathrm{p}}\hfill \\ & \times \left[{\mathsf{\Psi }}_{\alpha }^{†}\left(\overrightarrow{\xi }\right){\tau }_3\left(1-{\alpha }_3\right){\gamma }_5{\mathsf{\Psi }}_{\alpha }(\xi +\lambda {\widehat{e}}_3){\mathrm{e}}^{-\mathrm{i}\omega \lambda }+{\mathsf{\Psi }}_{\alpha }^{†}\left(\overrightarrow{\xi }\right){\tau }_3\left(1-{\alpha }_3\right){\gamma }_5{\mathsf{\Psi }}_{\alpha }(\xi -\lambda {\widehat{e}}_3){\mathrm{e}}^{\mathrm{i}\omega \lambda }\right],\hfill \end{array}$$

(69)

where we have substituted the matrix element (40) of the collective coordinates, A, sandwiched between nucleon states. To establish a sum rule we first note that $0\le x<\infty$. The upper bound is not unity because the soliton breaks translational invariance. Eventually that will be accounted for by boosting the soliton to the infinite momentum frame [78], as will be discussed in Section 6.3. Furthermore, the two terms in Equation (69) are related by $\lambda \leftrightarrow -\lambda$ which allows us to integrate only one of them but over $-\infty <x<\infty$ thereby producing $\frac{2\pi }{M_N}\delta \left(\lambda \right)$. From parity conservation we have $\int d^3\xi {\mathsf{\Psi }}_{\alpha }^{†}(\overrightarrow{\xi }){\tau }_3{\gamma }_5{\mathsf{\Psi }}_{\alpha }\left(\xi \right)=0$ and the poles are straightforwardly extracted as

$$\begin{array}{cc}{\left(\frac{\omega +{ϵ}_{\alpha }}{{\omega }^2-{ϵ}_{\alpha }^2-{\mathsf{\Lambda }}^2+\mathrm{i}ϵ}\right)}_{\mathrm{p}}\hfill & =-\frac{\mathrm{i}\pi {ϵ}_{\alpha }}{\sqrt{{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}^2}}\left[\delta \left(\omega +\sqrt{{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}^2}\right)+\delta \left(\omega -\sqrt{{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}^2}\right)\right]\hfill \\ \hfill & -\mathrm{i}\pi \left[\delta \left(\omega +\sqrt{{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}^2}\right)-\delta \left(\omega -\sqrt{{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}^2}\right)\right].\hfill \end{array}$$

(70)

Because of $\delta \left(\lambda \right)$ there is no other dependence on $\omega$ in Equation (69) and thus the second square bracket in Equation (70) vanishes when integrating ${\int }_{-\infty }^{\infty }dx{g}_1^{\left(s\right)}\left(x\right)$. Therefore, the vacuum contribution to the Bjorken sum rule (p and n are proton and neutron, respectively)

$${\int }_0^{\infty }dx\left(g_1^{(s,\mathrm{p})}\left(x\right)-g_1^{(s,\mathrm{n})}\left(x\right)\right)=\frac{1}{6}{g}_{\mathrm{A}}^{\left(s\right)}$$

(71)

is immediately verified from Equation (44) after taking care of the isospin matrix elements of the nucleon. Adding the valence level component to this sum rule is a trivial simplification of the calculation leading to Equation (71).

The above example for the verification of a sum rule is (almost) general. The symmetries under $\lambda \leftrightarrow -\lambda$ extend the x integral over whole real axis rather than only the positive half-line. That integral then produces $\delta \left(\lambda \right)$ which turns the bilocal matrix elements into the expectation values that occur in the expressions for the static properties that occur in the particular sum rule. Then the sum rule is verified level by level, i.e., separately for each term in ${\sum }_{\alpha }$. The one exception is the momentum sum rule which involves the isoscalar component of the unpolarized structure function $f_1\left(x\right)$. When adapting the calculation of the Bjorken sum rule to the unpolarized structure function $f_1\left(x\right)$, the integral $\int dxx{f}_1\left(x\right)$ produces the fermion part of the classical soliton energy in Equation (33). However, there is an additional contribution proportional to (The factor x under the integral is written as a derivative with respect to $\lambda$. Integrating by parts and averaging over angles turns this into the expectation value of $\overrightarrow{\alpha }·\overrightarrow{\partial }$.)

$$\left[1+\mathrm{sign}\left({ϵ}_{\mathrm{v}}\right)\right]\int d^3\xi {\mathsf{\Psi }}_{\mathrm{v}}^{†}\left(\overrightarrow{\xi }\right)\overrightarrow{\alpha }·\overrightarrow{\partial }{\mathsf{\Psi }}_{\mathrm{v}}\left(\overrightarrow{\xi }\right)-\sum _{i=0}^2{c}_i\sum _{\alpha }\frac{{ϵ}_{\alpha }}{\sqrt{{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}_i^2}}\int d^3\xi {\mathsf{\Psi }}_{\alpha }^{†}\left(\overrightarrow{\xi }\right)\overrightarrow{\alpha }·\overrightarrow{\partial }{\mathsf{\Psi }}_{\alpha }\left(\overrightarrow{\xi }\right)$$

and the sum rule is only verified when this piece vanishes. One shows that this is indeed the case by recognizing that

$$\overrightarrow{\alpha }·\overrightarrow{\partial }\propto \left[\overrightarrow{\xi }·\overrightarrow{\partial },h\right]-m\left(\overrightarrow{\xi }·\overrightarrow{\partial }{U}_5\left(\xi \right)\right)$$

so that the matrix elements in that unwanted contribution are those of the dilatation operator acting on the soliton. In turn the above sum is the change in energy obtained when squeezing or stretching the soliton infinitesimally. As the soliton minimizes the energy, this change must indeed be zero [24,27,28]. We must thus keep in mind that the momentum sum rule only works when summing all levels. There is a (numerically negligible) complication due to chiral symmetry breaking: for $m_{\pi }\ne 0$ the dilatation term in the sum over the quark levels is not exactly zero but compensates for the local integral in Equation (33). Numerically more concerning is the fact that the nucleon mass has $\mathcal{O}\left(\frac{1}{N_C}\right)$ corrections, Equation (39), which are not contained in this structure function. We also note that the sum rule actually yields $\frac{E_{\mathrm{tot}}}{M_N}-1$, which does not vanish as we have defined the hadron tensor to contain the physical mass parameter. Nevertheless, this sum rule is perfectly suited to test the numerical simulation.

For completeness (and an attempt to frighten the reader) we display the Bjorken limit of the hadron tensor including the next to leading order term for the expansion in $\frac{1}{N_C}$,

$$\begin{array}{cc}{W}_{\mu \nu }^{\left(s\right)}\hfill & \stackrel{\mathrm{Bj}}{⟶}\mathrm{i}{M}_N\frac{N_C}{4}\int \frac{d\omega }{2\pi }\sum _{\alpha }\int d^3\xi \int \frac{d\lambda }{2\pi }{\mathrm{e}}^{\mathrm{i}{M}_{N}x\lambda }\hfill \\ & \times \langle N\left|\right\{\left[{\overline{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{\gamma }_{\mu }n/{\gamma }_{\nu }{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }+\lambda \widehat{n}){\mathrm{e}}^{-\mathrm{i}\lambda \omega }-{\overline{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{\gamma }_{\nu }n/{\gamma }_{\mu }{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }-\lambda \widehat{n}){\mathrm{e}}^{\mathrm{i}\lambda \omega }\right]f_{\alpha }^{+}\left(\omega \right){|}_{\mathrm{p}}\hfill \\ & +\left[{\overline{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{({\gamma }_{\mu }n/{\gamma }_{\nu })}_5{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }-\lambda \widehat{n}){\mathrm{e}}^{-\mathrm{i}\lambda \omega }-{\overline{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{({\gamma }_{\nu }n/{\gamma }_{\mu })}_5{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }+\lambda \widehat{n}){\mathrm{e}}^{\mathrm{i}\lambda \omega }\right]f_{\alpha }^{-}\left(\omega \right){|}_{\mathrm{p}}\hfill \\ & +\frac{\mathrm{i}\lambda }{4}[{\overline{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{\xi }\right)\overrightarrow{\tau }·\overrightarrow{\mathsf{\Omega }}{\mathcal{Q}}_A^2{\gamma }_{\mu }n/{\gamma }_{\nu }{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }+\lambda \widehat{n}){\mathrm{e}}^{-\mathrm{i}\lambda \omega }\hfill \\ & +{\overline{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2\overrightarrow{\tau }·\overrightarrow{\mathsf{\Omega }}{\gamma }_{\nu }n/{\gamma }_{\mu }{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }-\lambda \widehat{n}){\mathrm{e}}^{\mathrm{i}\lambda \omega }]f_{\alpha }^{+}\left(\omega \right){|}_{\mathrm{p}}\hfill \\ & +\frac{\mathrm{i}\lambda }{4}[{\overline{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{\xi }\right)\overrightarrow{\tau }·\overrightarrow{\mathsf{\Omega }}{\mathcal{Q}}_A^2{({\gamma }_{\mu }n/{\gamma }_{\nu })}_5{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }-\lambda \widehat{n}){\mathrm{e}}^{-\mathrm{i}\lambda \omega }\hfill \\ & +{\overline{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2\overrightarrow{\tau }·\overrightarrow{\mathsf{\Omega }}{({\gamma }_{\nu }n/{\gamma }_{\mu })}_5{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }+\lambda \widehat{n}){\mathrm{e}}^{\mathrm{i}\lambda \omega }]f_{\alpha }^{-}\left(\omega \right){|}_{\mathrm{p}}\hfill \\ & +\sum _{\beta }\langle \alpha |\overrightarrow{\tau }·\overrightarrow{\mathsf{\Omega }}|\beta \rangle \left(\right[{\overline{\mathsf{\Psi }}}_{\beta }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{\gamma }_{\mu }n/{\gamma }_{\nu }{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }+\lambda \widehat{n}){\mathrm{e}}^{-\mathrm{i}\lambda \omega }\hfill \\ & -{\overline{\mathsf{\Psi }}}_{\beta }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{\gamma }_{\nu }n/{\gamma }_{\mu }{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }-\lambda \widehat{n}){\mathrm{e}}^{\mathrm{i}\lambda \omega }]g_{\alpha \beta }^{+}\left(\omega \right){|}_{\mathrm{p}}\hfill \\ & +[{\overline{\mathsf{\Psi }}}_{\beta }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{({\gamma }_{\mu }n/{\gamma }_{\nu })}_5{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }-\lambda \widehat{n}){\mathrm{e}}^{-\mathrm{i}\lambda \omega }\hfill \\ & -{\overline{\mathsf{\Psi }}}_{\beta }\left(\overrightarrow{\xi }\right){\mathcal{Q}}_A^2{({\gamma }_{\nu }n/{\gamma }_{\mu })}_5{\mathsf{\Psi }}_{\alpha }(\overrightarrow{\xi }+\lambda \widehat{n}){\mathrm{e}}^{\mathrm{i}\lambda \omega }\left]g_{\alpha \beta }^{-}\left(\omega \right){|}_{\mathrm{p}}\right)\left\}\right|N\rangle ,\hfill \end{array}$$

(72)

with the spectral functions

$$\begin{array}{cc}{g}_{\alpha \beta }^{\pm }\left(\omega \right)\hfill & =\sum _{i=0}^2{c}_i\frac{(\omega \pm {ϵ}_{\alpha })(\omega \pm {ϵ}_{\beta })+{\mathsf{\Lambda }}_i^2}{({\omega }^2-{ϵ}_{\alpha }^2-{\mathsf{\Lambda }}_i^2+\mathrm{i}ϵ)({\omega }^2-{ϵ}_{\beta }^2-{\mathsf{\Lambda }}_i^2+\mathrm{i}ϵ)}\hfill \\ \hfill & \pm \frac{(\omega \pm {ϵ}_{\alpha })(\omega \pm {ϵ}_{\beta })}{({\omega }^2-{ϵ}_{\alpha }^2+\mathrm{i}ϵ)({\omega }^2-{ϵ}_{\beta }^2+\mathrm{i}ϵ)}.\hfill \end{array}$$

(73)

The subleading $\frac{1}{N_C}$ terms contain the angular velocity, Equation (36). These terms arise from the expansions (after transforming $|\omega ,\beta \rangle \to A|\omega ,\beta \rangle$)

$$\langle \omega ,\alpha |{\left({\mathbf{D}}^{\left(\pi \right)}\right)}^{-1}|\omega ,\beta \rangle =\frac{{\delta }_{\alpha \beta }}{\omega -{ϵ}_{\alpha }}+\frac{1}{\omega -{ϵ}_{\alpha }}\langle \alpha |\frac{1}{2}\overrightarrow{\tau }·\overrightarrow{\mathsf{\Omega }}|\beta \rangle \frac{1}{\omega -{ϵ}_{\beta }}+\mathcal{O}\left(\overrightarrow{\mathsf{\Omega }}{}^2\right)$$

(74)

and

$$\langle t,\overrightarrow{\xi }|A\left(\widehat{t}\right)|\omega ,\alpha \rangle =A\left(t\right){\mathrm{e}}^{-\mathrm{i}\omega t}{\mathsf{\Psi }}_{\alpha }\left(\overrightarrow{\xi }\right)=A\left(0\right)\left[1+\frac{\mathrm{i}t}{2}\overrightarrow{\tau }·\overrightarrow{\mathsf{\Omega }}\right]{\mathrm{e}}^{-\mathrm{i}\omega t}{\mathsf{\Psi }}_{\alpha }\left(\overrightarrow{\xi }\right)+\mathcal{O}\left(\overrightarrow{\mathsf{\Omega }}{}^2\right).$$

(75)

The explicit appearance of the time variable is treated in the context of the Fourier transform $t{\mathrm{e}}^{\mathrm{i}{q}_{0}t}=-\mathrm{i}\frac{\partial }{\partial q_0}{\mathrm{e}}^{\mathrm{i}{q}_{0}t}$ while (in the nucleon rest frame) $x=\frac{-q_0^2+\overrightarrow{q}}{2M_N{q}_0}$ allows us to write $\frac{\partial }{\partial q_0}=\frac{\partial x}{\partial q_0}\frac{\partial }{\partial x}$ with

$$\begin{array}{c}\hfill \frac{\partial x}{\partial q_0}=-\frac{1}{M_N}-\frac{q_{0}x}{q_0^2}\stackrel{\mathrm{Bj}}{⟶}-\frac{1}{M_N}.\end{array}$$

This clarifies that the factors of $\mathrm{i}\lambda$ in Equation (72) originated from the explicit appearance of the time variable via the derivative with respect to the Bjorken variable x.

Again, Equation (72) is the vacuum contribution. The valence part is most easily obtained by substituting the cranked valence level wave-function

$$\begin{array}{cc}\hfill {\mathsf{\Psi }}_{\mathrm{v}}^{\left(\mathrm{rot}\right)}(\overrightarrow{r},t)& =\left\{{\mathsf{\Psi }}_{\mathrm{v}}\left(\overrightarrow{r}\right)+\frac{1}{2}\sum _{\alpha \ne \mathrm{v}}{\mathsf{\Psi }}_{\alpha }\left(\overrightarrow{r}\right)\frac{\langle \alpha |\overrightarrow{\tau }·\overrightarrow{\mathsf{\Omega }}|\mathrm{v}\rangle }{{ϵ}_{\mathrm{v}}-{ϵ}_{\alpha }}\right\}\hfill \end{array}$$

(76)

into Equation (67) and taking care of the bilocal dependence on time as in Equation (75).

In this chapter we have reviewed the formal derivation of the hadron tensor for a chiral quark soliton model starting from the electromagnetic coupling before bosonization and making ample use of the Bjorken limit. We have detailed the case of the longitudinal polarized structure function to illuminate the calculational principle and verified the relevant sum rule. Detailed formulas for other structure functions are derived and presented in Refs. [24,25,26].

6. Numerical Results

The results discussed in this section are mostly taken from Refs. [25,26]. There are several steps until we can perform a sensible comparison with experimental data. First we numerically simulate the analytic results from the previous section. This produces structure functions that we call rest frame (RF) structure functions. We will present the results for the RF structure functions in the following two subsections. These structure functions have the unwanted feature that they do not vanish for $\left|x\right|>1$. We will therefore briefly describe a formalism [78] to boost the soliton to the infinite momentum frame (IMF). In the IMF the structure functions indeed vanish for $\left|x\right|>1$. That formalism is essentially adapted from a similar study [79] of the MIT bag model in $D=1+1$. This adoption is made possible as in the Bjorken limit it suffices to restore Lorentz invariance in direction of the (large) photon momentum only. Once support of the structure functions is confined to $\left|x\right|<1$ we can apply the DGLAP evolution formalism and compare with available data in the last subsection. We will only apply a first order evolution as a proof of concept; after all, the model is not constructed for high precision predictions.

We obtain the RF structure functions from the momentum space representation of Equation (65) and the momentum space analog of Equation (72). This momentum space computation is the most costly part of the simulation because we explicitly perform the Fourier transformation, Equation (62), for the eigen-spinors of the self-consistent soliton. Large momenta on a dense grid are needed to maintain the normalization of the spinors (and thus the sum rules). A typical simulation takes several CPU days/weeks on a standard desktop PC. In related work [27,28,30] the expansion coefficients defined after Equation (31) were directly used. Since they are discrete, some smoothing procedure was needed in that treatment of the momentum space wave-functions.

We will refrain from presenting lengthy formulas as, e.g., the extremely bulky expressions involving the Fourier transforms of the radial functions in ${\mathsf{\Psi }}_{\alpha }$ [25,26]. Rather we focus on explaining the treatment of the pole terms without going into too much details. This treatment is nontrivial and interferes with regularization, the central topic of this review and therefore deserves closer consideration. Below we therefore describe some key ingredients that are relevant for all our calculations.

As in Ref. [28] we treat the Dirac $\delta$-functions in Equation (65) by averaging over $\widehat{n}$, that is, we replace these $\delta$-functions by

$$\frac{1}{4\pi }\int d{\mathsf{\Omega }}_{\widehat{n}}\delta \left(E+\overrightarrow{p}·\overrightarrow{n}\right)=\frac{1}{2\left|\overrightarrow{p}\right|}\theta \left(\left|\overrightarrow{p}\right|-\left|E\right|\right)$$

(77)

and generalizations thereof that contain additional factors of $\widehat{n}$ under the solid angle integral. We then need to evaluate expressions like (in sums over single particle levels $\alpha$ but omitting that index)

$$\int \frac{d\omega }{2\pi }\int \frac{d\lambda }{2\pi }\sum _{i=0}^2{c}_i{\left(\frac{\omega +ϵ}{{\omega }^2-{ϵ}^2-{\mathsf{\Lambda }}_i^2+iϵ}\right)}_{\mathrm{p}}\int d^{3}p{\tilde{\mathsf{\Psi }}}^{†}\left(\overrightarrow{p}\right)\tilde{\mathsf{\Psi }}\left(\overrightarrow{p}\right){\mathrm{e}}^{\mathrm{i}(M_{N}x-\widehat{n}·\overrightarrow{p})\lambda }{\mathrm{e}}^{\mathrm{i}\omega \lambda }.$$

(78)

Defining ${\omega }_i=\sqrt{{ϵ}^2+{\mathsf{\Lambda }}_i^2}$ we have (see also Equation (64))

$$\int \frac{d\omega }{2\pi }\sum _{i=0}^2{c}_i{\left(\frac{\omega +ϵ}{{\omega }^2-{ϵ}^2-{\mathsf{\Lambda }}_i^2+iϵ}\right)}_{\mathrm{p}}{\mathrm{e}}^{\mathrm{i}\omega \lambda }=-\frac{\mathrm{i}}{2}\sum _{i=0}^2\frac{c_i}{|{\omega }_i|}\left[\left(ϵ+{\omega }_i\right){\mathrm{e}}^{\mathrm{i}{\omega }_i\lambda }+\left(ϵ-{\omega }_i\right){\mathrm{e}}^{-\mathrm{i}{\omega }_i\lambda }\right]$$

(79)

and therefore

$$\begin{array}{cc}& \int \frac{d\lambda }{2\pi }{\mathrm{e}}^{\mathrm{i}(M_{N}x-\widehat{n}·\overrightarrow{p})\lambda }\int \frac{d\omega }{2\pi }\sum _{i=0}^2{c}_i{\left(\frac{\omega +ϵ}{{\omega }^2-{ϵ}^2-{\mathsf{\Lambda }}_i^2+iϵ}\right)}_{\mathrm{p}}{\mathrm{e}}^{\mathrm{i}\omega \lambda }\hfill \\ & =-\frac{\mathrm{i}}{2}\sum _{i=0}^2\frac{c_i}{|{\omega }_i|}\left[\left(ϵ+{\omega }_i\right)\delta (M_{N}x-\widehat{n}·\overrightarrow{p}+{\omega }_i)+\left(ϵ+{\omega }_i\right)\delta (M_{N}x-\widehat{n}·\overrightarrow{p}-{\omega }_i)\right]\hfill \\ & ⟶-\frac{\mathrm{i}}{4|\overrightarrow{p}|}\sum _{i=0}^2\frac{c_i}{|{\omega }_i|}\left[\left(ϵ+{\omega }_i\right)\theta \left(\right|\overrightarrow{p}|-|M_{N}x+{\omega }_i\left|\right)+\left(ϵ-{\omega }_i\right)\theta \left(\right|\overrightarrow{p}|-|M_{N}x-{\omega }_i\left|\right)\right],\hfill \end{array}$$

(80)

where the arrow denotes the averaging procedure from Equation (77). Note that, due to the step function, the cut-off also appears as the lower boundary of the momentum integral and we treat these boundaries according to the single cut-off prescription, Equation (15)

$$\begin{array}{cc}\sum _{i=0}^2{c}_i{\int }_{|M_{N}x+{\omega }_i|}^{\infty }pdpf(p,{\omega }_i)\hfill & ={\int }_{|M_{N}x+ϵ|}^{\infty }pdpf(p,ϵ)-{\int }_{|M_{N}x+\sqrt{{ϵ}^2+{\mathsf{\Lambda }}^2}|}^{\infty }pdpf(p,\sqrt{{ϵ}^2+{\mathsf{\Lambda }}^2})\hfill \\ & +{\mathsf{\Lambda }}^2{\int }_{|M_{N}x+\sqrt{{ϵ}^2+{\mathsf{\Lambda }}^2}|}^{\infty }pdp\frac{\partial }{\partial {\mathsf{\Lambda }}^2}f(p,\sqrt{{ϵ}^2+{\mathsf{\Lambda }}^2})\hfill \\ & -\frac{{\mathsf{\Lambda }}^2}{2\sqrt{{ϵ}^2+{\mathsf{\Lambda }}^2}}{\left[pf(p,\sqrt{{ϵ}^2+{\mathsf{\Lambda }}^2})\right]}_{p=|M_{N}x+\sqrt{{ϵ}^2+{\mathsf{\Lambda }}^2}|}.\hfill \end{array}$$

(81)

Here $f(p,{\omega }_i)$ contains angular matrix elements like $\int d{\mathsf{\Omega }}_{\overrightarrow{p}}{\tilde{\mathsf{\Psi }}}^{†}\left(\overrightarrow{p}\right)\tilde{\mathsf{\Psi }}\left(\overrightarrow{p}\right)$ or $\int d{\mathsf{\Omega }}_{\overrightarrow{p}}{\tilde{\mathsf{\Psi }}}^{†}\left(\overrightarrow{p}\right)\overrightarrow{\alpha }·\overrightarrow{p}\tilde{\mathsf{\Psi }}\left(\overrightarrow{p}\right)$ multiplied by powers of ${\omega }_i$.

6.1. Unpolarized Structure Functions

We will not present detailed formulas, except for some leading terms of the $\frac{1}{N_C}$ expansion. We refer the reader to Refs. [25,26] for more details (even though some factors of $\pi$ were not written there). As an example we present the expression for the isoscalar component of the unpolarized RF structure function

$$\begin{array}{cc}{\left[f_1^s\left(x\right)\right]}_{I=0}^{\mp }\hfill & =\frac{5M_N{N}_c}{72\pi }\sum _{\alpha }\sum _{i=0}^2{c}_i{\int }_{|M_N{x}_{\alpha }^{\pm }|}^{\infty }pdp\int d{\mathsf{\Omega }}_p\{\pm {\tilde{\mathsf{\Psi }}}_{\alpha }^{†}\left(\overrightarrow{p}\right){\tilde{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{p}\right)\hfill \\ & -\frac{{ϵ}_{\alpha }}{\sqrt{{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}_i^2}}\frac{M_N{x}_{\alpha }^{\pm }}{p}{\tilde{\mathsf{\Psi }}}_{\alpha }^{†}\left(\overrightarrow{p}\right)\widehat{p}·\overrightarrow{\alpha }{\tilde{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{p}\right)\},\hfill \end{array}$$

(82)

where

$$M_N{x}_{\alpha }^{\pm }=M_{N}x\pm \sqrt{{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}_i^2}.$$

(83)

The superscripts ∓ denote the positive (negative) frequency components which are typically referred to as quark and antiquark distribution. They arise from the two poles (for a particular ${\omega }_{\alpha }$) of the $\delta$-function in Equation (64) and materialize in the $\pm \omega$ terms in Equation (65). The total Dirac sea contribution to the isoscalar unpolarized structure function is the sum

$${\left[f_1^s\left(x\right)\right]}_{I=0}={\left[f_1^s\left(x\right)\right]}_{I=0}^{-}+{\left[f_1^s\left(x\right)\right]}_{I=0}^{+}.$$

(84)

On first sight it seems as if the first term under the integral in Equation (82) would not be subject to regularization. This is not the case, as the momentum integral is computed according to Equation (81). Since the isoscalar unpolarized structure functions are related to the classical energy of the soliton by the momentum sum rule, we must still subtract the analog of this calculation that is obtained by substituting spinor wave-functions for $\mathsf{\Theta }=0$. We have numerically checked the sum rule and achieved agreement better than 1%. In view of the many elaborate elements of the simulation, this is more than satisfactory. We get the valence contribution from substituting Equation (76) into the unregularized expression. This then adds

$$\begin{array}{cc}{\left[f_1^{\mathrm{v}}\left(x\right)\right]}_{I=0}^{\mp }\hfill & =-\frac{5M_N{N}_c}{72\pi }\left[1+\mathrm{sign}\left({ϵ}_{\mathrm{v}}\right)\right]{\int }_{M_N\left|x_{\mathrm{v}}^{\pm }\right|}^{\infty }pdp\int d{\mathsf{\Omega }}_p\hfill \\ & \times \left\{\pm {\tilde{\mathsf{\Psi }}}_{\mathrm{v}}^{†}\left(\overrightarrow{p}\right){\tilde{\mathsf{\Psi }}}_{\mathrm{v}}\left(\overrightarrow{p}\right)-\frac{M_N{x}_{\mathrm{v}}^{\pm }}{p}{\tilde{\mathsf{\Psi }}}_{\mathrm{v}}^{†}\left(\overrightarrow{p}\right)\widehat{p}·\overrightarrow{\alpha }{\tilde{\mathsf{\Psi }}}_{\mathrm{v}}\left(\overrightarrow{p}\right)\right\},\hfill \end{array}$$

(85)

to the positive and negative frequency components of the isoscalar unpolarized structure function. In this case there is no need to subtract the $\mathsf{\Theta }=0$ counterpart because this level is not occupied in the baryon number zero sector.

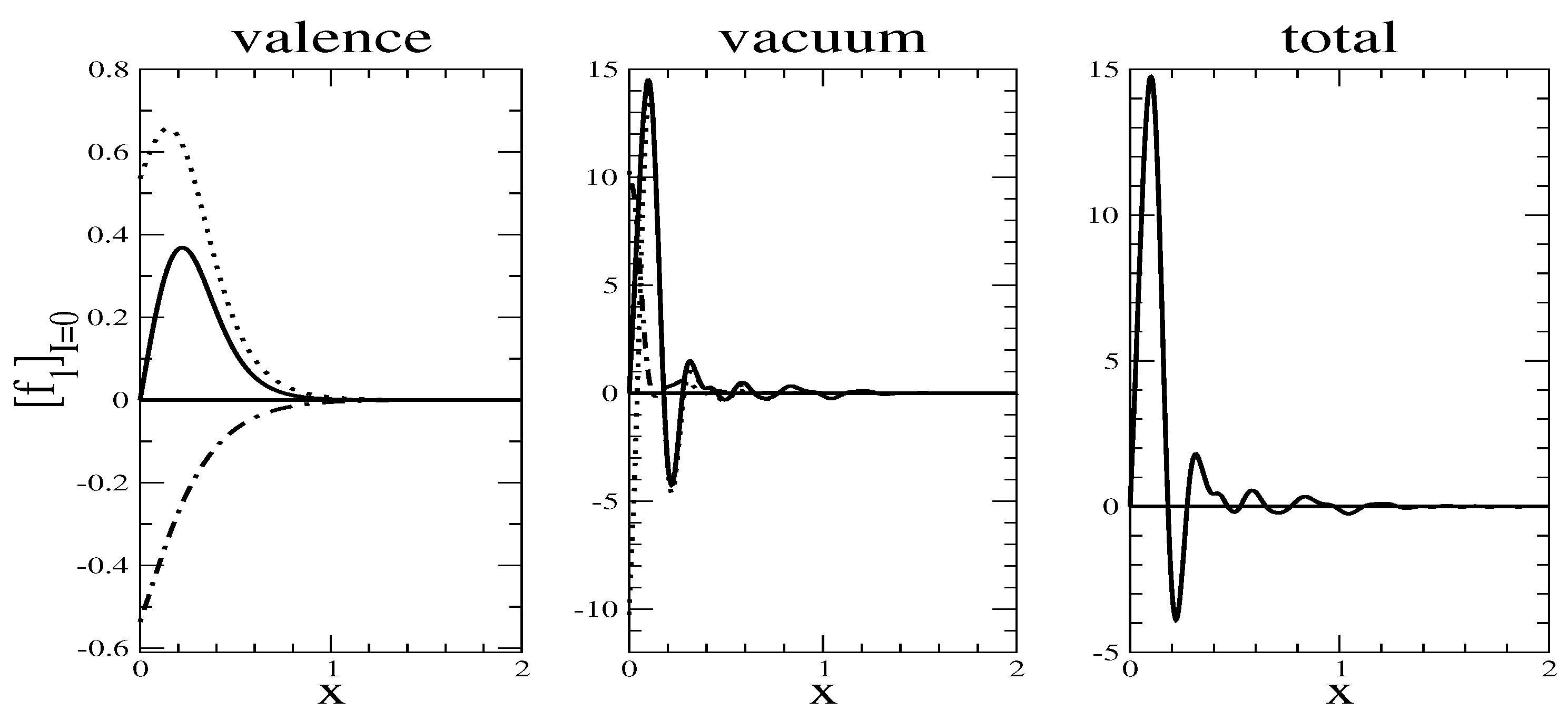
In Figure 3 we present typical numerical results. While the valence contribution is smooth, the vacuum part exhibits large peaks at small x. We consider this as an artifact of the $\mathsf{\Theta }=0$ subtraction, which actually has no dynamical justification other than setting the zero energy scale. However, this is merely a consistency condition on the sum rule which is only an integral over the structure function. This may actually be too strong a condition and we will comment on that in the conclusion.

Figure 4 shows the isovector counterpart which is subleading in $\frac{1}{N_C}$ and does not have any (artificial) $\mathsf{\Theta }=0$ subtraction. Obviously this structure function is dominated by the valence level contribution while the vacuum part is almost negligible.

In Figure 5 we display the numerical results for the unpolarized structure function that enters the Gottfried sum rule, i.e., $f_2^p\left(x\right)-f_2^n\left(x\right)=2x\left[f_1^p\left(x\right)-f_1^n\left(x\right)\right]$, as the Callan-Gross relation holds in the rest frame, cf. Table 1. At large x the vacuum contribution turns slightly negative. Though the valence contribution is generally dominant, the small negative piece persists in the total contribution of this structure function. In

Table 3. The Gottfried sum rule for various values of m. The subscripts “v” and “s” denote the valence and vacuum contributions, respectively. The fourth column contains their sums.

$\mathit{m}\left[\mathbf{MeV}\right]$	${\left[{\mathcal{S}}_{\mathit{G}}\right]}_{\mathbf{v}}$	${\left[{\mathcal{S}}_{\mathit{G}}\right]}_{\mathbf{s}}$	${\mathcal{S}}_{\mathit{G}}$	Emp. Value
400	$0.214$	$0.000156$	$0.214$
450	$0.225$	$0.000248$	$0.225$	$0.235\pm 0.026$ [80]
500	$0.236$	$0.000356$	$0.237$

, we compare our model prediction for the Gottfried sum rule,

$${\mathcal{S}}_G={\int }_0^{\infty }\frac{dx}{x}\left(f_2^p-f_2^n\right),$$

(86)

for various constituent quark masses to that of the value extracted from data by the NM Collaboration [80]. The agreement is astonishingly good. The integral is almost completely saturated by the valence level contribution.

In contrast to the isoscalar unpolarized structure function, the isovector part does not undergo regularization. Such an alternating behavior between (un)regularized quantities is well-known for static properties [22,23] but it is interesting to see that it also holds for structure functions. Of course, that is a prediction of the formalism.

6.2. Polarized Structure Functions

For the polarized structure functions we will only list explicit formulas for the isovector longitudinal piece which is leading in $\frac{1}{N_C}$. Essentially this is the Fourier transform of Equation (69). The vacuum contribution reads

$$\begin{array}{cc}{\left[g_1^s\left(x\right)\right]}_{I=1}^{\mp }\hfill & =-\frac{M_N{N}_c}{36\pi }〈N|I_3|N〉\sum _{\alpha }\sum _{i=0}^2{c}_i\{\mp {\int }_{|M_N{x}_{\alpha }^{\pm }|}^{\infty }dp{M}_N{x}_{\alpha }^{\pm }\int d{\mathsf{\Omega }}_p{\tilde{\mathsf{\Psi }}}_{\alpha }^{†}\left(\overrightarrow{p}\right)\widehat{p}·\overrightarrow{\tau }{\gamma }_5{\tilde{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{p}\right)\hfill \\ & -\frac{{ϵ}_{\alpha }}{\sqrt{{ϵ}_{\alpha }^2+{\mathsf{\Lambda }}_i^2}}{\int }_{|M_N{x}_{\alpha }^{\pm }|}^{\infty }dp{p}^2[A_{\pm }\int d{\mathsf{\Omega }}_p{\tilde{\mathsf{\Psi }}}_{\alpha }^{†}\left(\overrightarrow{p}\right)\overrightarrow{\tau }·\overrightarrow{\sigma }{\tilde{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{p}\right)\hfill \\ & +B_{\pm }\int d{\mathsf{\Omega }}_p{\tilde{\mathsf{\Psi }}}_{\alpha }^{†}\left(\overrightarrow{p}\right)\widehat{p}·\overrightarrow{\tau }\widehat{p}·\overrightarrow{\sigma }{\tilde{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{p}\right)\left]\right\},\hfill \end{array}$$

(87)

where we have introduced the abbreviations, see also Equation (83),

$$\begin{array}{cc}\hfill A_{\pm }& =\frac{1}{2p}\left(1-\frac{{\left(M_N{x}_{\alpha }^{\pm }\right)}^2}{p^2}\right),B_{\pm }=\frac{1}{2p}\left(3\frac{{\left(M_N{x}_{\alpha }^{\pm }\right)}^2}{p^2}-1\right).\hfill \end{array}$$

(88)

As before, the superscripts denote the positive and negative frequency components. The total Dirac sea contribution to $g_1\left(x\right)$ again is the sum of the positive $(+)$ and negative $(-)$ frequency components. The valence quark contribution to the isovector longitudinal polarized structure function reads

$$\begin{array}{cc}{\left[g_1^{\mathrm{v}}\left(x\right)\right]}_{I=1}^{\mp }\hfill & =\frac{M_N{N}_c}{36\pi }\left[1+\mathrm{sign}\left({ϵ}_{\mathrm{v}}\right)\right]〈N|I_3|N〉\hfill \\ & \{\mp {\int }_{|M_N{x}^{\pm }|}^{\infty }dp{M}_N{x}_{\mathrm{v}}^{\pm }\int d{\mathsf{\Omega }}_p{\tilde{\mathsf{\Psi }}}_{\mathrm{v}}^{†}\left(\overrightarrow{p}\right)\widehat{p}·\overrightarrow{\tau }{\gamma }_5{\tilde{\mathsf{\Psi }}}_{\mathrm{v}}\left(\overrightarrow{p}\right)\hfill \\ & -{\int }_{|M_N{x}_{\mathrm{v}}^{\pm }|}^{\infty }dp{p}^2[A_{\pm }\int d{\mathsf{\Omega }}_p{\tilde{\mathsf{\Psi }}}_{\mathrm{v}}^{†}\left(\overrightarrow{p}\right)\overrightarrow{\tau }·\overrightarrow{\sigma }{\tilde{\mathsf{\Psi }}}_{\mathrm{v}}\left(\overrightarrow{p}\right)\hfill \\ & +B_{\pm }\int d{\mathsf{\Omega }}_p{\tilde{\mathsf{\Psi }}}_{\mathrm{v}}^{†}\left(\overrightarrow{p}\right)\widehat{p}·\overrightarrow{\tau }\widehat{p}·\overrightarrow{\sigma }{\tilde{\mathsf{\Psi }}}_{\mathrm{v}}\left(\overrightarrow{p}\right)\left]\right\}.\hfill \end{array}$$

(89)

The numerical results are shown in Figure 6.

The isoscalar counterpart is subleading in $\frac{1}{N_C}$ and we display a typical model prediction in Figure 7.

We have already discussed the Bjorken sum rule for the isovector piece. Its verification serves as a test for the accuracy of the numerical simulation. The isoscalar combination also has a sum rule which gives the matrix element of the isoscalar axial current $\overline{\mathsf{\Psi }}{\gamma }_{\mu }{\gamma }_5\mathsf{\Psi }$. As mentioned, its empirical determination has triggered much of the research on structure functions. Our results for both sum rules are shown in

Table 4. Axial isovector and isoscalar charges for various values of the constituent quark mass m from integrating the longitudinal structure functions. Subscripts are as in Table 3. Data in parenthesis give the numerical results as obtained from the coordinate space representation, cf. Equation (47) and Table 2.

$\mathit{m}\left[\mathbf{MeV}\right]$	$[{\mathit{g}}_{\mathit{A}}{]}_{\mathbf{v}}$	$[{\mathit{g}}_{\mathit{A}}{]}_{\mathbf{s}}$	${\mathit{g}}_{\mathit{A}}$	emp. Value	$[{\mathit{g}}_{\mathit{A}}^0{]}_{\mathbf{v}}$	$[{\mathit{g}}_{\mathit{A}}^0{]}_{\mathbf{s}}$	${\mathit{g}}_{\mathit{A}}^0$	emp. Value
400	$0.734$	$0.065$	$0.799$ ($0.800$)	$1.2601$	$0.344$	$0.0016$	$0.345$ ($0.350$)
450	$0.715$	$0.051$	$0.766$ ($0.765$)	$\pm 0.0025$	$0.327$	$0.0021$	$0.329$ ($0.332$)	$0.33\pm 0.06$
500	$0.704$	$0.029$	$0.733$ ($0.733$)	[62]	$0.316$	$0.0028$	$0.318$ ($0.323$)	[81]

. We note that the isoscalar axial charge is significantly less than one in agreement with phenomenology of the proton spin puzzle [40].

According to the projectors listed in Table 1 the transverse polarized structure function $g_T\left(x\right)$ has matrix elements similar to those above. From its computation we subsequently identify

$$g_2\left(x\right)=g_1\left(x\right)-g_T\left(x\right)$$

(90)

for both the isoscalar and isoscalar combinations. Typical results are shown in Figure 8 and Figure 9. Here it occurs that the vacuum piece dominates. However, that is mainly a consequence of cancellations for the valence contribution via Equation (90).

6.3. Boosting to the Infinite Momentum Frame

It is customary to introduce light-cone coordinates $x^{\pm }=\left(x^0\pm \widehat{n}·\overrightarrow{x}\right)/\sqrt{2}$ to discuss structure functions in the context of the parton model. Using these coordinates the Bjorken limit is particularly transparent

$$q^{-}\to \infty \mathrm{and}x=-\frac{q^{+}}{p^{+}}.$$

As discussed before, the fermion propagator is free and massless in the Bjorken limit. Massless fermions have the singular function $\left\{\mathsf{\Psi }\left(\xi \right),\overline{\mathsf{\Psi }}\left(0\right)\right\}=\frac{1}{2\pi }\partial /\delta \left({\xi }^2\right)ϵ\left({\xi }^0\right)$. This can be used to turn the current-current correlator in the hadron tensor into a matrix element of bilocal bilinear fermion operators [82] (These are fundamental fermion operators, not the eigenfunctions of h in Equation (32).)

$$f_1\left(x\right)=\frac{x}{4\pi }\int d{\xi }^{-}{\mathrm{e}}^{-\mathrm{i}{p}^{+}{\xi }^{-}}\langle N|\overline{\mathsf{\Psi }}\left(\xi \right){\gamma }^{+}{\mathcal{Q}}^2\mathsf{\Psi }\left(0\right)-\overline{\mathsf{\Psi }}\left(0\right){\gamma }^{+}{\mathcal{Q}}^2\mathsf{\Psi }\left(\xi \right){|N\rangle }_{{\xi }^{+}=0,{\xi }_{\perp }=0}.$$

This singles out the coordinate along the photon momentum as the most relevant variable. We will see shortly that this is indeed realized in the IMF, which also has ${\xi }^{+}=0$.

Assuming translational invariance and inserting a complete set of states with momenta $p_n$, the matrix elements of bilocal bilinear quark operators can be shown to be nonzero only when

$$p_n^{+}-(1-x)p^{+}=0.$$

In the vicinity of $x=1$ this can only be fulfilled when the masses of both the partons n and the nucleon are negligible small and/or $p^{+}$ becomes very large. The limit of large $p^{+}$ defines the IMF. It is therefore suggestive to consider the soliton model structure functions in the IMF as well. To boost the system to the IMF, the collective coordinate method of Equation (56) for any local object $\Gamma$ must be extended to

$$\begin{array}{c}\hfill \Gamma (\overrightarrow{\xi },{\xi }^0)⟶S\left(\mathsf{\Lambda }\right)\Gamma ({\overrightarrow{\xi }}^{\prime }-{\overrightarrow{R}}^{\prime },{\xi }^{\prime 0})S^{-1}\left(\mathsf{\Lambda }\right)\mathrm{where}{\xi }^{\prime \mu }={\left({\mathsf{\Lambda }}^{-1}\right)}_{\nu }^{\mu }{\xi }^{\nu }.\end{array}$$

(91)

Here $\mathsf{\Lambda }$ parameterizes a Lorentz transformation and $S\left(\mathsf{\Lambda }\right)$ is the corresponding generator for $\Gamma$. Subsequently, the collective coordinates $\overrightarrow{R}$ are averaged as in Equation (56).

A Lorentz boost with rapidity $\mathsf{\Omega }$ along the light cone transforms the RF coordinates as

$$p^{+}⟶\frac{M_N}{\sqrt{2}}{\mathrm{e}}^{\mathsf{\Omega }}\mathrm{and}{p}^{-}⟶\frac{M_N}{\sqrt{2}}{\mathrm{e}}^{-\mathsf{\Omega }}$$

(92)

while the transverse components are left unchanged. The transformation to the IMF is thus characterized by $\mathsf{\Omega }\to \infty$ which also implies that ${\mathsf{\Lambda }}^{-1}$ singles out ${\xi }^{\prime -}$ so that ${\xi }^{\prime +}\to 0$. In Ref. [78] this transformation was applied together with the collective coordinate average for bilocal bilinear quark composites like those in Equation (59). Essentially that study adapted a two-dimensional MIT bag model calculation [79] to the soliton model by ignoring effects on the transverse coordinates as Lorentz covariance is only restored along $\widehat{n}$. The result is a simple transformation prescription for the structure functions:

$$f_{\mathrm{IMF}}\left(x\right)=\frac{\mathsf{\Theta }\left(1-x\right)}{1-x}{f}_{\mathrm{RF}}\left(-ln(1-x)\right),$$

(93)

where $f_{\mathrm{RF}}$ is any of the structure functions like that in Equation (69) which are obtained from the hadron tensor in the RF according to the calculations in the previous section. Obviously this prescription ensures that the transformed structure functions have support only in the kinematically allowed interval $0\le x\le 1$. Thus the structure function $f_{\mathrm{IMF}}\left(x\right)$ is a suitable input for the DGLAP evolution program. In what follows we will omit the label IMF for the boosted structure functions.

6.4. DGLAP Evolution

Of course, we wish to compare our model predictions with data. In this section we describe the remaining step with focus on the polarized structure functions. All model results presented in this subsection have been obtained for the constitutent quark mass $m=400\mathrm{MeV}$.

So far, we have computed the structure functions within the NJL soliton model, which (at best) approximates QCD at a low mass scale, ${\mu }^2=Q_0^2$ which is thus an adjustable hidden parameter in the approach and can be thought of as the identification scale with QCD. This low mass scale is different from the high energy scales, $Q^2$ at which DIS data are available. To compare with the DIS data, we adopt the leading order Altarelli-Parisi (DGLAP) equations [4,5,6] for parton distributions to evolve the model structure functions. To apply this formalism we, unfortunately, have to identify the model structure functions with QCD distribution functions of quarks since the chiral model is not renormalizable and does not have a renormalization group equation to sum the leading logs.

Let $h^{(I=1)}(x,t)$ be the isovector combination of any twist-2 distribution with $t=ln\left(\frac{Q^2}{{\mathsf{\Lambda }}_{QCD}^2}\right)$. The change in momentum scale is governed by the differential equation

$$\begin{array}{cc}\hfill \frac{d{h}^{(I=1)}(x,t)}{dt}& =\frac{{\alpha }_s\left(t\right)}{2\pi }{C}_R\left(F\right){\int }_x^1\frac{dy}{y}{P}_{qq}\left(y\right)h^{(I=1)}\left(\frac{x}{y},t\right)\hfill \\ \hfill & =:\frac{{\alpha }_s\left(t\right)}{2\pi }{C}_R\left(F\right)P_{qq}\otimes h^{(I=1)}(x,t).\hfill \end{array}$$

(94)

Here ${\alpha }_s\left(t\right)=\frac{4\pi }{{\beta }_{0}t}$, is the running coupling constant of QCD, in which ${\beta }_0=\frac{11}{3}{N}_C-\frac{2}{3}{N}_f$ and $C_R\left(F\right)=\frac{N_f^2-1}{2N_f}$ are combinatoric factors in the QCD renormalization group equation for $N_f$ flavors. Most importantly $P_{qq}\left(y\right)$ is the splitting function that describes the probability of a quark emitting a gluon and a quark with momentum fraction y. This splitting function and those for the isoscalar combination to be discussed below are given in Refs. [4,5,6]. The right-hand-side of Equation (94) serves as the definition of the evolution product “⊗”. As initial condition, $h^{(I=1)}(x,t\left({\mu }^2\right))$, to integrate this differential equation, we take the distributions identified from the boosted structure functions in the IMF. The endpoint of integration is the scale $Q^2$ at which data from experiment are available. We attempt to tune ${\mu }^2$ to optimize the agreement with these data and take the very same identification scale for all evolution calculations.

The isoscalar combinations, $h^{(I=0)}(x,t)$ are more complicated. By the pure nature of the quantum numbers $h^{(I=0)}(x,t)$ mixes with the gluon distribution $g(x,t)$ and the evolution equations are coupled differential equations

$$\begin{array}{cc}\hfill \frac{d{h}^{(I=0)}(x,t)}{dt}& =\frac{{\alpha }_s\left(t\right)}{2\pi }{C}_R\left(F\right)\left[P_{qq}\otimes h^{(I=0)}(x,t)+P_{qg}\otimes g(x,t)\right]\hfill \\ \hfill \frac{dg(x,t)}{dt}& =\frac{{\alpha }_s\left(t\right)}{2\pi }{C}_R\left(F\right)\left[P_{gq}\otimes h^{(I=0)}(x,t)+P_{gg}\otimes g(x,t)\right].\hfill \end{array}$$

(95)

The only sensible identification of the gluon distribution $g(x,t)$ is to have it vanish at ${\mu }^2$, otherwise sum rules would be violated. This is again an unavoidable (and undesirable) identification of QCD degrees of freedom.

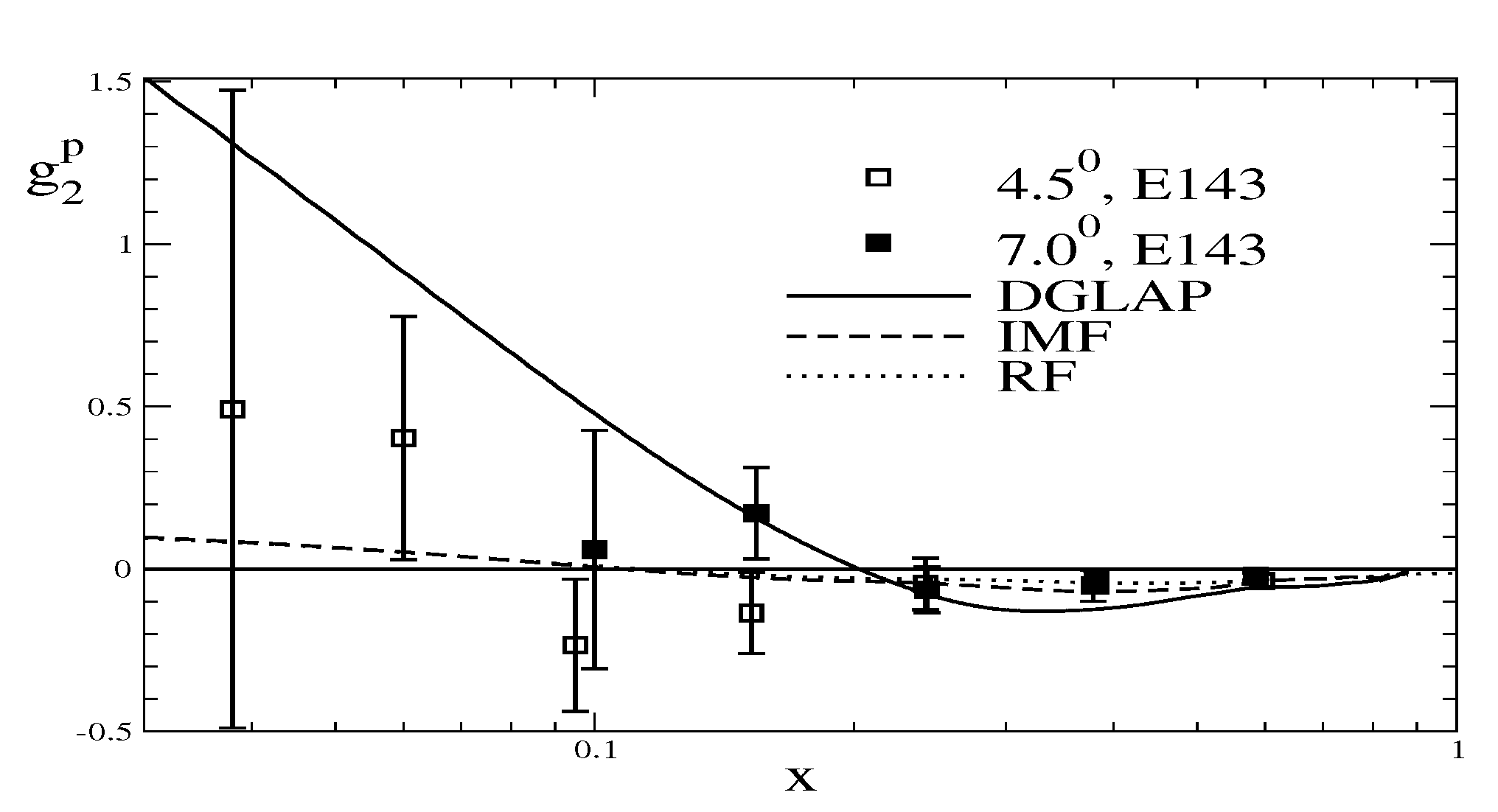
We are now in the position to confront the model prediction with data from experiment. For the longitudinal polarized structure function of the proton, this is done in the left panel of Figure 10.

We chose ${\mu }^2=0.4{\mathrm{GeV}}^2$ and get a reasonable (though not perfect) match with the data after evolving the boosted structure function to the scale of the experiment, $Q^2=3{\mathrm{GeV}}^2$. Any further fine-tuning of ${\mu }^2$ has only marginal effects. The predictions are obviously in the right ballpark, but deviations clearly emerge in detail. Surprisingly, the RF result appears to match data best. This is an indication that the boost formalism overemphasizes the low x regime. For the neutron, data are available in terms of the helium structure function [85] (In Ref. [85] direct neutron data are only given as the ratio ${\mathsf{g}}_1^n\left(x\right)/F_1\left(x\right)$.)

$${\mathsf{g}}_1^{{}^3\mathrm{He}}\left(x\right)\approx P_n{\mathsf{g}}_1^n\left(x\right)+P_p{\mathsf{g}}_1^p\left(x\right)-0.014\left[{\mathsf{g}}_1^p\left(x\right)-4{\mathsf{g}}_1^n\left(x\right)\right],$$

(96)

with $P_n\approx 0.86$ and $P_p\approx -0.028$ arising from the nuclear model. In addition, from Figure 10 we see that in this case the DGLAP evolution indeed brings the model prediction closer to data. At large x we find the structure function to be small and positive while for moderate x the observed negative trough is present but somewhat too strong.

The evolution of the transverse polarized structure functions is even more complicated because $g_2(x,t)$ is the sum of two terms. One has twist-2 [86]

$$g_2^{WW}(x,t)=-g_1(x,t)+{\int }_0^{1}dy\frac{1}{y}{g}_1(y,t)$$

(97)

and the remainder, ${\overline{g}}_2(x,t)=g_2(x,t)-g_2^{WW}(x,t)$ is associated with twist-3. The twist-2 part undergoes the DGLAP evolution described above. For the twist-3 piece we extract Mellin moments

$$M_j\left(Q^2\right)={\int }_0^{1}dx{x}^{j-1}{\overline{g}}_2(x,t)$$

(98)

that scale as

$$\frac{M_j\left(Q^2\right)}{M_j\left({\mu }^2\right)}={\left[\frac{ln\left({\mu }^2\right)}{ln\left(Q^2\right)}\right]}^{\frac{{\gamma }_{j-1}}{{\beta }_0}}.$$

(99)

So far, only the leading large $N_C$ terms of ${\gamma }_{j-1}$ are known [87,88,89]. At the initial scale ${\mu }^2$ we disentangle the twist components, evolve them separately to $Q^2$, invert the Mellin transformation, and put the two components back together to build $g_2(x,t)$. The result of this procedure for the proton channel is compared to available data in Figure 11. Our estimate produces the main structure seen experimentally: $g_2^p(x,t)$ is negative and small in magnitude at large x and increases substantially as x decreases.

Twist-3 by itself is interesting as data have been recently reported [85] for the second moment

$$d_2^{\left(n\right)}\left(Q^2\right)=3{\int }_0^{1}dx{x}^2{\overline{g}}_2^{\left(n\right)}(x,t)$$

(100)

in the neutron channel at two different transferred momenta: $d_2^{\left(n\right)}\left(3.21{\mathrm{GeV}}^2\right)=(-4.21\pm 1.14)\times {10}^{-3}$ and $d_2^{\left(n\right)}\left(4.32{\mathrm{GeV}}^2\right)=(-0.35\pm 1.04)\times {10}^{-3}$ (we added the reported errors in quadrature). Our model calculations for $m=400\mathrm{MeV}$ yield $-4.26\times {10}^{-3}$ and $-4.09\times {10}^{-3}$, respectively. While the lower $Q^2$ result matches the observed value, the higher one differs by about three standard deviations. The results indicate that the large $N_C$ approximation to evolve ${\overline{g}}_2$ requires improvement.

Finally, we comment on the isovector unpolarized structure function that is compared to data in Figure 12, see also Figure 4 and Figure 5. Though the negative contribution to $f_1$ from the Dirac vacuum, cf. Figure 4, around $x=1$ is tiny in the RF, it becomes relatively large when (i) multiplied by x to obtain $f_2$ and (ii) when transformed to the IMF because of the Jacobian factor $1/(1-x)$ thereby worsening the agreement with the experimental data from NMC [80].

To some extent, this dilutes the perfect agreement between the model prediction and data for the Gottfried sum rule, Equation (86), discussed earlier. Under that integral the model result arises from cancellations not seen in the empirical structure function [80].

7. Related Approaches

One of the major obstacles when computing structure functions within chiral quark soliton models is the consistent implementation of the regularization prescription. Various approaches have been undertaken. The numerical results do not differ significantly as the dominant contribution to the structure functions arises from the explicitly occupied valence level (in particular when $m\lesssim 400\mathrm{MeV}$) and this contribution is not subject to regularization. Even though the discrepancies among the various approaches to structure functions in chiral soliton models are presumably smaller than their systematic uncertainties, we will nevertheless comment on alternative approaches in this section.

A simple-minded but not too unrealistic procedure to avoid that problem is to simply ignore the vacuum contribution and compute structure functions in the so-called valence level only approximation. This is guided by the observation that the most important role of the vacuum contribution in chiral quark soliton models is to stabilize the soliton but it is of lesser importance for the predictions of static nucleon properties [22,23]. For example, for $m=400\mathrm{MeV}$ the valence level contributes almost 80% to the moment of inertia in Equation (38). This avenue for the structure functions was taken in the early works reported in Refs. [67,68]. It also allows for a sensitive estimate of $\frac{1}{N_C}$ effects and the separation of isoscalar and -vector components without encountering complicated expressions like those in Equations (72) and (73). The results from Section 6 show that this is indeed a reasonable approximation for the polarized structure functions; maybe to a lesser extent for the unpolarized structure functions.

From Equation (66) we see that the regularized hadron tensor at leading order in $\frac{1}{N_C}$ is a sum of four terms, while the unregularized version only has two. Similarly, when acting with the projection operators from Table 1 to extract a certain structure function, the spectral functions $f_{\alpha }^{(\pm )}\left(\omega \right)$ combine to reduce the number of terms that contribute to the hadron tensor to two as well. We have seen that explicitly for the longitudinal polarized structure function $g_1\left(x\right)$ in Equation (69). These two terms are formally distribution functions that take the fermions forward and backward in space time along the direction of the virtual photon momentum. The (formal) appearance of such distributions is general to all fermion models in the Bjorken limit. It is therefore suggestive to consider distribution functions in such models regardless of whether or not other peculiarities in the model, like regularization, require more detailed consideration. In this context the authors of Refs. [27,28] derived two equivalent expressions for unregularized quark distribution functions (coefficients adjusted to comply with Equation (62))

$$\begin{array}{cc}\hfill D^{\left(1\right)}\left(x\right)& =\frac{2}{\pi }{N}_C{M}_N\sum _{\alpha ,\mathrm{occ}.}\int d^{3}p\tilde{{\overline{\mathsf{\Psi }}}_{\alpha }}\left(\overrightarrow{p}\right)n/\Gamma {\tilde{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{p}\right)\delta (p^3+{ϵ}_{\alpha }-M_{N}x)\hfill \\ \hfill D^{\left(2\right)}\left(x\right)& =-\frac{2}{\pi }{N}_C{M}_N\sum _{\alpha ,\mathrm{non}-\mathrm{occ}.}\int d^{3}p{\widetilde{\overline{\mathsf{\Psi }}}}_{\alpha }\left(\overrightarrow{p}\right)n/\Gamma {\tilde{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{p}\right)\delta (p^3+{ϵ}_{\alpha }-M_{N}x),\hfill \end{array}$$

(101)

in the large $N_C$ limit. Obviously these expression combine to

$$\begin{array}{cc}\hfill D\left(x\right)& =\frac{1}{2}\left[D^{\left(1\right)}\left(x\right)+D^{\left(2\right)}\left(x\right)\right]\hfill \\ \hfill & =-\frac{1}{\pi }{N}_C{M}_N\sum _{\alpha }\mathrm{sign}\left({ϵ}_{\alpha }\right)\int d^{3}p\tilde{{\overline{\mathsf{\Psi }}}_{\alpha }}\left(\overrightarrow{p}\right)n/\Gamma {\tilde{\mathsf{\Psi }}}_{\alpha }\left(\overrightarrow{p}\right)\delta (p^3+{ϵ}_{\alpha }-M_{N}x),\hfill \end{array}$$

(102)

for the Dirac sea contribution which, by definition, has the negative energy levels occupied (occ) and the positive energy levels empty (non-occ). (Equivalent expressions arise from trace identities. E.g., ${\sum }_{\alpha }{ϵ}_{\alpha }=0$ allows to write (for ${ϵ}_{\mathrm{v}}>0$): ${ϵ}_{\mathrm{v}}+\frac{1}{2}{\sum }_{\alpha }\left|{ϵ}_{\alpha }\right|={\sum }_{\alpha ,\mathrm{occ}.}{ϵ}_{\alpha }$. Whether or not such identities hold depends on the particular regularization prescription.) Similarly antiquark distribution functions are obtained with $\overline{D}\left(x\right)=-D(-x)$. Using $D\left(x\right)$, $\overline{D}\left(x\right)$ and suitable linear combinations of the spin flavor matrices $\Gamma$ the authors would then compute the structure functions. Considering, for example, the unregularized version of the first term within the square brackets in Equation (69) and noticing that

$$\left[\omega +{ϵ}_{\alpha }\right]\delta ({\omega }^2-{ϵ}_{\alpha }^2)=\mathrm{sign}\left({ϵ}_{\alpha }\right)\delta (\omega -{ϵ}_{\alpha })$$

(103)

we observe the very same structure as in $D\left(x\right)$. In the notation of Refs. [27,28] the second term in Equation (69) represents the antiquark distribution $\overline{D}\left(x\right)$ that must be added to complete the structure function. Not unexpectedly, without regularization these approaches are thus equivalent. Refs. [27,28] perform a two step regularization for the distributions, first a smoothing function is multiplied in the level sum in Equation (102) with a scale $E_{\max }$. Then the calculation is repeated with a second, larger constituent quark mass and the difference is extrapolated to $E_{\max }\to \infty$. That second constituent quark mass conceptually is a Pauli–Villars mass, $M_{\mathrm{PV}}$. Its numerical value is determined from the pion decay constant $f_{\pi }$ as follows: compute the unregularized polarization functions, Equation (19), that enter $f_{\pi }$ for both m and $M_{\mathrm{PV}}$, multiply both polarization functions by m and $M_{\mathrm{PV}}$, respectively and tune $M_{\mathrm{PV}}$ such that the difference is $f_{\pi }/4N_C$, with $f_{\pi }=93\mathrm{MeV}$. Though the procedure seems plausible, it is not rigorous (The caption to Figure 1 in Ref. [28] suggests that the valence level contribution would also undergo this Pauli-Villars type subtraction. If correctly interpreted, that seems in contradiction to unit baryon number.). Among other questions one might ask why should the second calculation have the same smoothing scale $E_{\max }$; and if different, what is the effect? We also note that a single subtraction does not produce a finite gap equation (In Refs. [27,28] this problem is bypassed by postulating a nonzero constituent quark mass in ${\mathbf{D}}^{\left(\pi \right)}$ and define the model by that operator.), Equation (16), and further obstacles may occur away from the chiral limit when quadratic divergences may occur. In the onset we have distinguished between regularized and nonregularized parts in the action, Equation (13). Any kind of a posteriori regularization faces the dilemma that such a distinction is difficult to implement. There are combinations of distributions that are ultraviolet finite even without regularization. Must they nevertheless undergo regularization? In this context refer to the discussion on the Gottfried sum rule in Section 6. We also note that the restriction to the leading $\frac{1}{N_C}$ terms does not distinguish between isoscalar and -vector components.

Most of those early distribution function calculations did not attempt the DGLAP evolution but rather compared the results with empirical distributions at a low renormalization point; this results from applying the inverse of the DGLAP evolution to data [9].

In Refs. [29,30] similar calculations for the $\frac{1}{N_C}$ corrections to the unpolarized distributions have been performed while Ref. [31] discusses the polarized distributions with subleading $\frac{1}{N_C}$ terms included and also implements the DGLAP evolution program. Similar to our calculations those authors observe that the Dirac sea contribution to the polarized structure functions is almost negligibly small.

The extension to three light flavors has also been addressed. These studies were first performed in the valence level only approximation for the hadron tensor [91] and soon after by formulating distributions incorporating the a posteriori regularization [37,38,39] with a Pauli–Villars mass as described above. Technically the main difference is that the collective coordinates are from $SU\left(3\right)$ and that there are eight instead of three angular velocities. Furthermore flavor symmetry breaking must be included because the strange quark mass (represented by the mass of the pseudoscalar kaon) is much larger than that of the up and down quarks. Of course, that extension allows a closer look at strangeness in the nucleon. In this regard the numerical results of that model calculation agree with data [92,93], at least qualitatively.

Once the identification of distribution functions is accepted, other processes than DIS, that in QCD are described by various bilocal bilinear quark operators, can also be explored within chiral quark soliton models. Let us mention two examples. Transversity distributions complete the description of the nucleon spin [94,95] and are relevant for the Drell–Yan process [96]. There are two of them which are similar to the two polarized structure functions: the transverse $h_T\left(x\right)$ and longitudinal $h_L\left(x\right)$. In the language of distributions the relevant bilocal bilinear quark operators are similar to those for the polarized ones, except for different Dirac matrices. Again, transverse and longitudinal refers to the alignment of spin and external momentum. In the soliton model these distributions were first estimated in the large $N_C$ limit and valence level only approximation [32]. Subsequently $\frac{1}{N_C}$ corrections were included [33] and finally Dirac sea contributions were considered in Refs. [31,34]. Transversity distributions have sum rules with tensor charges, $\langle N\left|{\mathrm{\Sigma }}_3\left({\tau }_3\right)\right|N\rangle$. These charges can be directly computed in the chiral soliton model without any ambiguity from regularizing the Dirac sea component. That component was found to be very small [33] suggesting that the valence level only approximation is reliable for these distributions. This was later confirmed by the computation with the a posteriori regularization prescription [31]. The twist-3 distribution $e\left(x\right)$, which has a sum rule with the $\pi N-\sigma$-term, has been considered in Refs. [35,36]. Again, this distribution is not a structure function accessible in DIS but can be extracted from pion photoproduction [97,98,99]. Even though the relevant bilocal bilinear quark operator is as simple as $\overline{\mathsf{\Psi }}\left(0\right)\left({\tau }_3\right)\mathsf{\Psi }\left(\lambda n\right)$, the actual computation is quite intricate because of a potential $\delta$-function behavior of the isoscalar combination at $x=0$. The sum rule is only satisfied with the inclusion of such a behavior [100]. The model calculation of Refs. [35,36] indeed confirms that singular structure.

Let us also briefly comment on the historical development. Refs. [27,28] mentions that some preliminary results on structure functions had been “announced” in Ref. [101]. However, that reference only states that these calculations are in progress pointing to [27,28]. So it seems fair to state that the first results for structure functions in a soliton model were presented in Ref. [67] according to the journal received dates though there was some delay of the actual publication.

We have seen that, modulo regularization, the matrix elements to be computed are formally the same as if the bilocal bilinear quark operators were directly transferred from QCD to the model. That is, rather than merely taking the NJL model as one for some of the QCD symmetries, it is considered a model for QCD degrees of freedom. This is a frequently adopted point of view, not only for the NJL model but also e.g., the MIT bag model [69,70,71], in particular in the context of structure functions [72,73,74,75]. Furthermore, it opens the door to explore quark distributions other than those parameterizing (electromagnetic) DIS.

8. Conclusions

The standard model for elementary particles is a gauge theory for leptons, quarks, and gauge bosons. To make contact with the world of mesons and baryons, knowledge about their composition in terms of quarks (and gluons) is inevitable. The binding of the fundamental constituents to mesons and baryons, known as color-confinement in QCD, is a nonperturbative effect. Distribution functions that combine to structure functions parameterize this nonperturbative composition of mesons and baryons. These structure functions cannot be computed from first principles in QCD but are either extracted from empirical data, computed in lattice simulations, or obtained from some model estimates. The chiral soliton model is one of the many popular and successful models for baryons. Here meson fields are the model degrees of freedom and solitons, which represent baryons, are (static) solutions to the respective, nonlinear fields equations.

The calculation of nucleon structure functions in chiral soliton models has been a long issue. Traditional soliton models like the Skyrme model and its extensions by incorporating vector mesons in addition to the pions face the problem of only representing local quark bilinear combinations. On the other hand, models that carry through the bosonization, that transforms the quark into a meson theory, are plagued by the need for regularization. Here we have reviewed a method that takes regularization seriously from the initial formulation of the action for the quark model rather than empirically implementing regularization for distribution functions that linearly combine to structure functions. The formal relation between structure functions and quark distributions is no longer obvious when regularization is required. We stress that this formulation only identifies chiral symmetries of QCD with no statement on how the model and QCD quarks relate. Yet all the sum rules that relate integrals of the structure functions to observables like hadron masses, isospin etc. and that are commonly derived from the probability interpretation of distribution functions are also valid in this approach. The project should thus be considered more like a proof of concept rather than attempting precise predictions for the structure functions.

The point of departure is a self-interacting chirally symmetric quark model. It is particularly formulated to make feasible the full process of bosonization. At each step of this calculation regularization is carefully traced resulting in consistently regularized structure functions. The model is defined such that only one part of the bosonized action is regularized in order to maintain the chiral anomaly. Hence it is suggestive that only some of the structure functions will be subject to regularization. The treatment reviewed here is constructive in the sense that it dictates for which structure function regularization must be implemented and for which this is not the case. This goes beyond analyzing whether or not the particular structure function is ultraviolet convergent. The method is also predictive in case the structure function does not have a sum rule that is related to a static property with an established regularization prescription.

Regularization, of course, only concerns the vacuum (Dirac sea) contribution to any observable. In addition, there is always the contribution from the valence level (strongly) bound by the self-consistent soliton. This level contribution must be included to deal with a unit baryon number object. We have actually seen that this level contribution is dominant for almost all structure functions except the isoscalar unpolarized combination. For this combination we see a strong enhancement at small Bjorken x. This was also seen in the numerical simulation of Refs. [27,28], though not quite as drastic as in our case. We recall that the unpolarized isoscalar structure function has a sum rule with the energy, which in soliton models is the classical soliton energy. The standard definition of this energy subtracts the zero soliton vacuum counterpart to get a finite result for the soliton energy and therefore this structure function should undergo an analog subtraction. It is important to note that this energy subtraction has no dynamic effect, i.e., it does not enter the field equation for the soliton. Any additional (finite) subtraction would be possible in a renormalizable theory. Hence this piece is not without ambiguity. Of course, it is very suggestive to subtract the zero soliton energy to determine the binding of the soliton. However, that is only a (regularization) condition for the integrated structure function. Formally, however, the subtraction is obtained from a different action functional. The result that the zero soliton vacuum structure function is not a constant is kind of surprising as it suggests that the trivial vacuum has structure. One may also speculate whether this unexpected result is related to the numerical treatment of discretizing wave-functions with box boundary conditions. In close proximity to the boundary, completeness of the wave-functions is not guaranteed [102]. We are currently exploring this speculation.

The biggest conceptual problem unsolved so far is the fact that the computed structure functions have support for $\left|x\right|>1$ resulting from the soliton not being translationally invariant and that the collective coordinate approach to restore this symmetry is merely an approximation. The computed structure functions are small (or even tiny) for $x>1$ but not exactly zero. In order to apply the DGLAP evolution formalism, the support must be restricted to $\left|x\right|\le 1$. We have adopted a procedure from the $D=1+1$ MIT bag model boosting the rest frame structure functions to the infinite momentum frame. This may overemphasize the small x regime and also interfere with the rotational $\frac{1}{N_C}$ corrections but it maintains the sum rules. Other approaches, that merely omit the $\left|x\right|>1$ piece, multiply a differentiable function that models a function with a step at $x=1$ [31,37,38,39]. Though that may better reproduce the data in the small x regime, this ad hoc approach violates the sum rules, at least formally.

A possible extension of the approach reviewed here would be the consideration of inelastic scattering with neutrino induced interactions. That would bring in a generalization of the Compton tensor that would also include couplings to the axial current as governed by the weak component of the standard model and thus form factors and structure functions that are not disallowed by parity conservation.