A common and visually striking ways to show the fractal character of a complex function such as the classic example of
is to create its filled-in Julia set [
21,
22,
23]. This is done by iterating the function,
an infinite number of times. The appearance of the filled-in Julia set in this example is determined by the
c. Since
, one regards the set of all filled-in Julia sets as parameterized by a two-dimensional space. A succinct representation of this collection of filled-in Julia sets is the Mandelbrot set [
21,
22,
23]. In a recent work, Fowler and McGuinness derived expressions for measuring the size of the bulbs in the Mandelbrot set for
[
24].
4.1. Three-Dimensional and Two-Dimensional Mandelbrot Sets
For the case of the lacunary Möbius fractal as described in Equation (
11) the parameter space is three-dimensional (
, Re
and Im
). Throughout this work, a point in this space will be considered as an element of the Cartesian product
. This means that the succinct representation by a Mandelbrot set is three-dimensional: one real angle and a complex Möbius parameter. There is one of these three-dimensional Mandelbrot sets for each value of
k. The sets are labelled as
.
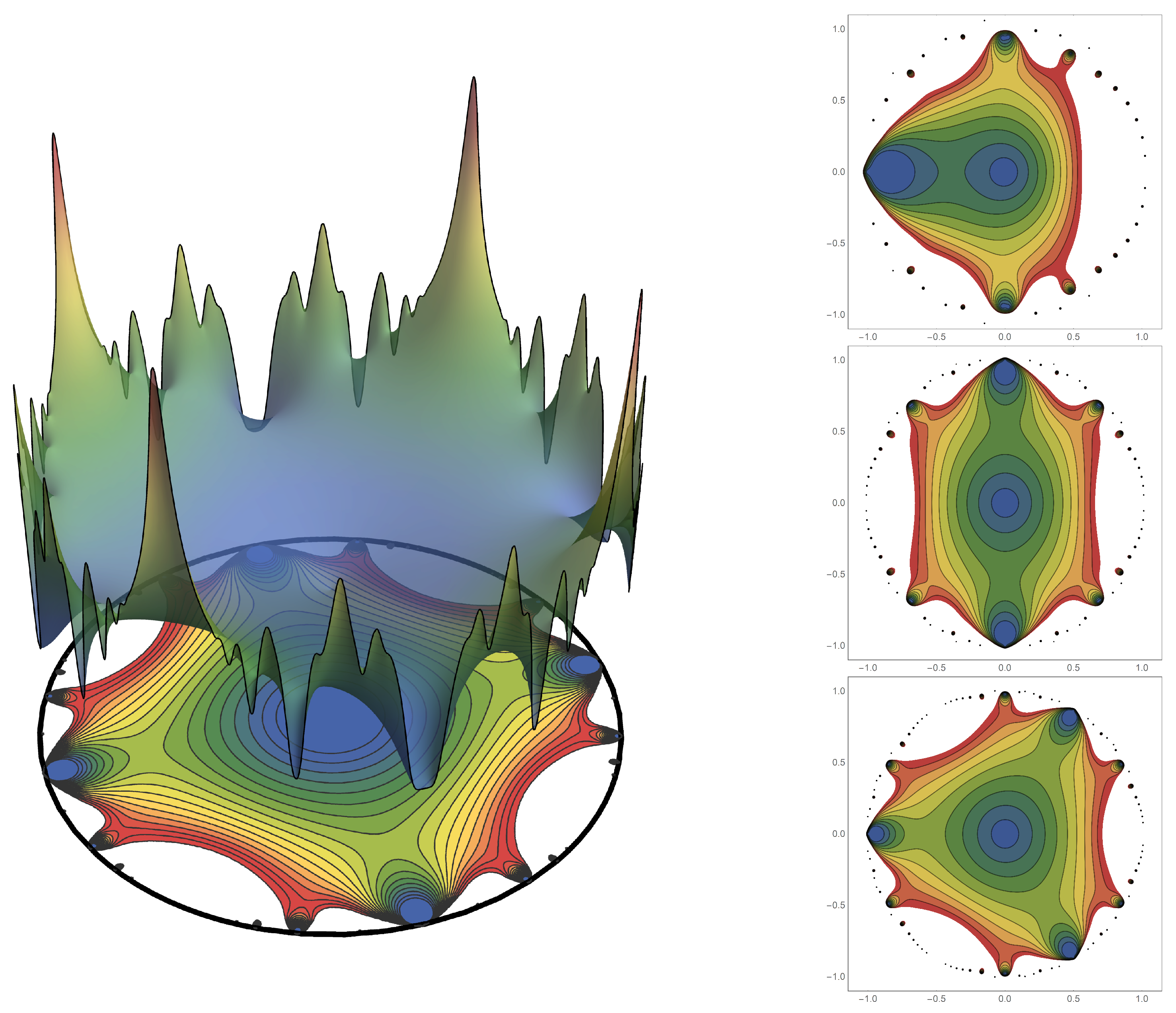
There are certainly some visually interesting representations of these sets, two of which are shown in
Figure 2. where the specific example of
is shown.
Figure 2 collects three such representations of
. The top row and bottom right graphs are three different viewpoints of
shown as a “surface-swarm” representation. In this representation, the Mandelbrot set is plotted with the transparency of its graph based how many points in a small region are not in the same set (
or its complement). For example, if a point is a member of
and so are all its first, second, third, etc nearest neighbors in the lattice of sampled points, then that point will be plotted with very high transparency. The same is true if a point and its neighbors are in the complement of
. Conversely if the collection of nearby points in the sampling lattice differ, which is the case on the (fractal) surface of the Mandelbrot set, then the transparency is much lower. All this results in a smoothed out (because of the inherent averaging) outline of the surface of
. The bulk of the Mandelbrot set and the bulk of its complement are nearly see-through. The surface itself is then colored green if it faces the interior of the Mandelbrot set and colored blue if it faces the exterior of the Mandelbrot set. The surface-swarm representation gives a sense of complexity of the Mandelbrot set but is visually cluttered.
In the interest of space, only
is shown. The surface-swarm graphs for other values of
k have a similar appearance. The main difference is in the number of green diagonal bands (seen best in the top right panel of
Figure 2). The bands are caused be the fact that the Mandelbrot set extends to the edge of the unit disk in
k places and these places twist through parameter for one full rotation. Thus, this results in
k diagonal streaks of green across the face of the cylinder. Indeed there are four such streaks seen in
Figure 2.
A second representation of
, called the “cylinder” representation, is shown in the bottom left of
Figure 2. This is from the same viewpoint as the surface-swam graph in the top left of the figure. In this case the transparency of every plotted point is the same (unlike for the surface swarm). This results in the Mandelbrot set being dark grey in appearance and its complement being light gray. While much is lost here it helps to orient the eye to the parameter space of the Mandelbrot set.
In both of the representations,
is in
. It is clear from both representations that
introduces a twisting in the structure of
. Beyond this observation, it will be more insight to consider subsets of
that are obtains by taking planar slices of these graphs as shown in
Figure 3.
The three-dimensional Mandelbrot sets provide a general overview of the parameters space as a whole but they lack significant value in helping to understand the nature of the fractals. To get a more detailed picture of this one turns to the two-dimensional Mandelbrot sets which are two-dimensional subsets of
. Often these are slices of
that are planes parallel to the three Cartesian planes.
Figure 3 pictorially depicts the relationship between two-dimensional Mandelbrot sets and
. A number of these are explored subsequently.
Figure 4 shows two-dimensional Mandelbrot sets which are similar to the horizontal plane shown in
Figure 3. These four slices occur at
equal to every
from 0 to
. It is clear that the
parameter introduces a twisting of the two-dimensional Mandelbrot set (which was also evident in
itself as seen in
Figure 2). One sees that the
k-fold rotational symmetry persists upon the phase twisting, but a loss of the dihedral mirror symmetry that seen in the first column. The dihedral mirror symmetry is recovered at
. (It is noted that in this work
differs by
from that of reference [
2].) Two main regions emerge as
changes. There is a shrinking central region that appears to maintain a quasi-dihedral mirror symmetry. There is also the development of growing ”arms” off the tips of each lobe.
Two secondary features also emerge upon increasing
. One feature that is a bit unusual for Mandelbrot sets is the wispy fraying of the edges as it twists. This is most noticeable in the graphs shown in the second column of
Figure 4. Another interesting feature is the emergence of “jets” spraying out from the nexus of the lobe and the arm regions. This is most noticeable in the third column of
Figure 4. There is a lot of dynamicism in the filled-in Julia sets coming from the jets. Because of the inherit limit in scope and variety of behavior of the Julia sets, this jet is a an appropriate region to study in detail to understand the characteristics of the whole plane.
Like
Figure 4 and
Figure 5 shows slices of
similar to the vertical planes shown in
Figure 3. The examples
, 3, 4, and 6 are collected. The Re
-
plane is shown across the top row and the Im
-
plane is shown across the bottom row. As
k increases, more arms extend out from the middle. Mirror plane symmetry about the Re
and Im
lines when
k is even, but this mirror symmetry is broken when
k is odd. There is a nexus point at
and Re
(or Im
). The two parts of the Mandelbrot set detach at that point when Re
(or Im
) is not zero. One example of this is shown in the left panel of
Figure 6.
Figure 6 will play a central role for the remainder of this work, because it proves to be fertile ground to gain both qualitative and quantitative insight into the nature of lacunary Möbius fractals, specifically its filled-in Julia sets. The figure shows two slices of
in the left (
plane) and middle (
plane) panels. This particular part of
exhibits some prominent jets that lie along convenient paths, for example
which is marked as a red line in the figure. There is also a nice wispy fray region and, again, a convenient path cuts through it (
, green line). Finally, the right panel of
Figure 6 shows a blow-up of the region marked by the cyan-color box in the middle panel. This shows the intricate behavior of the jet region.
4.2. Filled-In Julia Sets
Each point, p, in represents a complete filled-in Julia set, . The diversity and intricacy of these filled-in Julia sets is stunning. We explore a number of these here. As a matter of notation a family of filled-in Julia sets arising from a path through will be denoted as . In practice, will be discretized so the member of is .
It is also convenient to define the decretized “fill” of a filled-in Julia set , as the number of pixels in the unit disk that are zero (black in the figures). Note the the fill depends on the sampling rate of the filled-in Julia set.
It is particularly interesting to assess the filled-in Julia sets corresponding to points in the jets of the Mandelbrot sets. Because of the nature of the jets one might expect a wide range of diversity among the filled-in Julia sets. This is indeed the case and not only is there a diversity of shapes, the change in the global visual appearance of the filled-in Julia sets along a path
in
is quite abrupt. As a concrete example, the filled-in Julia sets along a path that traverses the jet in
(red line in
Figure 6) is explored in detail. To begin,
Figure 7 shows a sequence of 16 filled in Julia sets corresponding to points along
, where
y runs for the short range from 0 to
. The particular stretch of path through the jet is small but radically different filled-in Julia sets appear. In
Figure 7, the Julia sets are read from left-to-right, top-to-bottom. Thus, for example, the left most Julia set in the second row is given from the point
in parameter space. The initial graph (point
) consist of a relatively nondescript roughly three-lobed shape. The overall appearance changes very little across the top row. The second row marks the beginning of an abrupt transition to a rather elaborate (and beautiful) shape with many intricate clefts and protrusions.
Interestingly, the transition is marked with a disappearance and reappearance of a large portion of the interior of the Julia set. There does appear to be some consistency in certain regions of
that are always in the complement of the filled-in Julia set. But other areas of
are very dynamic. Not only do certain points flicker in and out of the filled-in Julia set, but the size and shapes of the various connected domains differ significantly from on filled-in Julia set to the next, as can be seen in the third row of
Figure 7.
4.3. Dynamicism of the Filled-In Julia Sets
In an effort to pull some quantitative understanding from the dynamic variability of the filled-in Julia sets just discussed, one can define a derivative of sorts to compare Julia sets alone a path in parameter space. This is accomplished by point-wise subtracting adjacent filled-in Julia sets from a collection alone a path. This is normalized by the fill of the initial filled-in Julia set. This a global analysis looking for total change so the sum of the absolute differences is taken. This will be referred to as the JS-derivative and is defined as,
where
is the step size alone
.
Figure 8 shows the JS-derivative for the path
(red line in
Figure 6). It is important to explore the impact of
N and
j on the JS-derivative. The left graph of the
Figure 8 shows and overlay of the JS-derivative for
(brown curve) and
. This shows that the JS-derivative is relatively insensitive to the number of terms in the centered polygonal lacunary series. If fact, most of the data generated in this work used
. The corresponding JS-derivative curve for this case is nearly visually indistinguishable from the
case (data not shown).
The right graph of
Figure 8 shows
(purple curve),
(magenta curve),
(brown curve) and
(blue curve). In contrast to
N, the JS-derivative is quite sensitive to
j, although one does see a convergence of the peak positions. Note the wild disparity of the JS-derivative on the right side of the graph is a result of the Julia sets being mostly “dust” at those parameters. The JS-derivative is unreliable in these conditions, thus care must be taken to visually inspect the filled-in Julia sets being evaluated.
Returning to the qualitative discussion of
Figure 7, the behavior seen in sequence of Julia sets is captured by the JS-derivative in the form of the left most peak (referred to as peak 1). The non-descript roughly three lobed filled-in Julia sets are coming from the left side of peak 1. The largely white graphs of the last of the second row and start of the third row are coming from the peak itself. Finally, the intricate filled-in Julia sets are coming from the right of peak 1.
Figure 9 shows the JS-derivative for a path running through the wispy fray coming of the left side of the bottom lobe in
Figure 6. The abscissa in the JS-derivative graph corresponds to the green line in
Figure 6. Here
where
runs from 0 to
. The figure also shows a few representative filled-in Julia sets. This sets are chosen from points that lie on opposite sides of a peak in the derivative spectrum. The sharp qualitative differences in the global appearance of the filled-in Julia sets occur on opposite sides of sharp JS-derivative peaks. Observationally, the filled-in Julia sets coming from the wispy fray region tend to be a bit less intricate that some of those arising from the jet region. They do, however, experience abrupt changes along a path in parameter space. One clearly sees many peaks in the JS-derivative. These correspond to moving in and out of the wisps of the fray in the Mandelbrot set.
4.4. Fractal Dimension
In this work, fractal dimension was calculated using a modified version of the Hausdorff dimension that was developed in reference [
2] to which the reader is referred.
Figure 10 shows as plot of the fractal dimension of the Julia sets along the path
(red line in
Figure 6). The left graph illustrates the
j dependence on dimension. As with the JS-derivative the dimension is sensitive to
j. And also as with the JS-derivative, the dimension behavior tends to converge. Note that the erratic behavior beginning a little beyond
is due to the fact that the Julia sets are mostly dust in that region. The dimension calculation is unreliable for Julia sets of this type. The same
with the same color scheme as right panel of
Figure 8 is used. Like the JS-derivative, the dimension is relatively insensitive to
N (data not shown). The dimension data for the path
(green line in
Figure 6) is shown in the right panel of
Figure 9.
The right panel of
Figure 10 shows a blow-up on the region
. This is compared to the JS-derivative over the same region (dotted curve). Perhaps not surprisingly, there appears to be a correlation between abrupt changes in the JS-derivative and abrupt changes in the dimension. They do, however, capture these abrupt change events differently to some degree. As a pair, the JS-derivative and the dimension information can provide insight into the nature of these transitions.