Abstract
Protein alignment finds its application in refining results of sequence alignment and understanding protein function. A previous study aligned single molecules, making use of the minimization of sums of the squares of eigenvalues, obtained for the antisymmetric Cartesian coordinate distance matrices Dx and Dy. This is used in our program to search for similarities between amino acids by comparing the sums of the squares of eigenvalues associated with the Dx, Dy, and Dz distance matrices. These matrices are obtained by removing atoms that could lead to low similarity. Candidates are aligned, and trilateration is used to attach all previously striped atoms. A TM-score is the scoring function that chooses the best alignment from supplied candidates. Twenty essential amino acids that take many forms in nature are selected for comparison. The correct alignment is taken into account most of the time by the alignment algorithm. It was numerically detected by the TM-score 70% of the time, on average, and 15% more cases with close scores can be easily distinguished by human observation.
1. Introduction
Just visualizing two simple similar structures leads to an immediate detection of patterns. Similarity is of convenience for humans, but to power automatic decision mechanisms for a PC, it must be measurable. It is mostly used for comparing proteins, but the growing number of PDB structures (currently over 180,000) is many orders of magnitude higher than what the human eye can compare. Because of the large number, it takes days even for current programs to search the database for a query structure. A more reasonable time can be achieved by developing new algorithms [1].
Protein alignment finds its application in refining results of sequence alignment and understanding protein function [2,3]. Choosing the alignment that is most geometrically similar is an easier task compared to evaluating its biological significance [4]. The pursuit of the best method is in progress, with multiple programs being developed during the past decades:
- •
- CAB-Align uses the residue–residue contact area to identify regions of similarity [5].
- •
- Caretta uses rotation-invariant technique signals of distances derived from overlapping contiguous stretches of residues to find an initial superposition [6].
- •
- DALI [7].
- •
- LS-align generates fast and accurate atom-level structural alignments of ligand molecules through an iterative heuristic search of the target function that combines comparisons of inter-atom distance with mass and chemical bonds [8].
- •
- MATT uses a fragment-based approach that allows for local flexibility between fragment pairs from two input structures and then a dynamic programming algorithm to assemble these intermediate pairs [9].
- •
- TM-align uses the length-independent TM-score as a measure of similarity between two proteins in a dynamic programming approach [10].
Some advances have been made in relation to these algorithms, such as parallel re-implementation of mTM-align/TM-align pm-TM-align [11], parMATT [12], heuristic algorithms, and hierarchical organization mTM-align [13].
The 3D variant of the distance matrix alignment method (DALI) uses rotation and translation in order to achieve a smaller distance between equivalent points in the two molecules [14].
In a previous study, the eigenproblem was employed to achieve the proper alignment of single molecules, or the mirror of the proper alignment, and this can be exploited to reduce the number of rotations for which a scoring function needs to run [15].
The eigenproblem is thus defined in the literature as follows:
Given the quadratic matrix A, of the order n, is called the eigenvalue of the matrix A and its associated eigenvector if the relationship is satisfied. The matrix is singular (because ), where I is the unit matrix of the order n. The solutions of the equation represent the eigenvalues of the matrix A.
The determinant is called the characteristic polynomial (ChP) associated with the matrix A. It has a degree equal to the order of the matrix so that the eigenvalues of the matrix A are its roots.
The eigenproblem in relation to geometrical alignment was stated before in the context of surface analysis [16] and control and can go in another direction in the context of amino acids. A subject of the study is a solution to the eigenproblem of amino acid alignment. The Cartesian system is rotated and eventually translated and reflected until the structure arrives at a position characterized by the highest absolute values of the eigenvalues observed on the Cartesian coordinates.
The aim of this study is to find the best geometric alignment of 20 selected amino acids with regard to each other. An extension to the previous study described by Jäntschi [15] has been elaborated. Sums of the squares of eigenvalues (ST = −2Sx − 2Sy − 2Sz) for all three Cartesian coordinate distance matrices (Dx, Dy, and Dz) are compared. By removing atoms, smaller Dx, Dy, and Dz matrices are obtained and more ST sums are added to the comparison. Percentual similarities are found between these sums. Candidates are aligned by the eigenproblem algorithm, and trilateration is used to attach all previously striped atoms. To verify, a TM-score is run on the resulting full-structure candidates.
2. Materials and Methods
In [15], it was shown that the Cartesian distance matrix is antisymmetric and therefore its eigenvalues are purely imaginary, as well as the fact that the best alignment of a molecule is obtained for the minimum value of the sum of the squares of eigenvalues of the Cartesian distance matrix.
Thus, the angle of rotation of the structure must be found around an axis for which the minimum of this amount is obtained. One method of finding the angle of rotation around an axis for the best alignment is as follows: in the case of an amino acid with 5 atoms, we note the vertices of the graph corresponding to the organic compound with . We want to find the optimal angle of rotation around the Oz axis, for example. The characteristic polynomial associated with the matrix of Cartesian distances on Ox can be approximated in this way:
which leads to the problem of finding the rotation angle in the xOy plane so as to obtain the maximum value of the sum
Because the term becomes maximum when , we calculate the amount using the law of motion of the rotation of a body about a fixed axis:
where φ, in turn, takes the value .
Using the interpolation method, we find the value of the angle of rotation around the Oz axis. Similarly, we proceed to find the angle of rotation of the structure around one of the other two axes.
The eigenvalues of the associated Cartesian coordinate distance matrix Dx are always two conjugate purely imaginary solutions: . Sums of the form ST = −2Sx − 2Sy − 2Sz, associated with Dx, Dy, and Dz matrices, are compared in order to find similarities.
Starting from the eigenproblem approach, 20 essential amino acids that take many forms in nature are selected from available databases.
The alignments for these amino acids (downloaded from PubChem), with compound CIDs 750, 5862, 5950, 5951, 5960, 5961, 5962, 6057, 6106, 6137, 6140, 6267, 6274, 6287, 6288, 6305, 6306, 6322, 33032, 145742, are computed. In this example, the one with the fewest heavy atoms is chosen for reference, glycine 00750.sdf. The following tables for the other cases in which the rest of the structures are references can be found in the Supplementary Materials section:
- •
- 3D structural data for heavy atoms
- •
- 3D distance matrix for heavy atoms
Table 1, Table 2 and Table 3 depict the Cartesian coordinate distance matrices for heavy atoms. They are antisymmetric, so their eigenvalues, in Table 4, are imaginary.

Table 1.
First Cartesian coordinate (x) distance matrix for glycine (heavy atoms).

Table 2.
Second Cartesian coordinate (y) distance matrix for glycine (heavy atoms).

Table 3.
Third Cartesian coordinate (z) distance matrix for glycine (heavy atoms).

Table 4.
Eigenvalues for glycine (heavy atoms).
It can be observed that unlike eigenvalues for a symmetric matrix, we obtain a single pair of complementary imaginary numbers regardless of the number of atoms in the compound. Another good part of this approach is that, as shown in Table 5, the polynomial can be expressed with real-value coefficients as a product of a polynomial of degree 2 and a monomial of degree (n − 2), leading to a faster response from the program.

Table 5.
The polynomials of [Dx], [Dy], and [Dz] for glycine (heavy atoms).
Making use of the eigenproblem approach (named the OrigEig function), the other amino acids are aligned to glycine. Candidates with a lower number of atoms than the original are processed while searching for ST similarities. The rest of the atoms are later added using a trilateration algorithm found and used from the literature [17]. Some capabilities are added, such as importing original data (*.sdf or *.xyz by the impCart function); performing *.sdf to *.xyz file conversion; removing hydrogen atoms for convenience; and exporting all compared rotated structures as *.xyz (by the writexyz function), a scoring function based on the TM-score and the creation of *.xls files. The code and its explanation can be found in the Supplementary Materials section, and a schematic overview is available in Figure 1.

Figure 1.
A schematic overview of the algorithm.
The requirements for this application are:
- •
- The “in” and “results” directories, the former containing an “xyz” directory and the latter containing “aligned,” “rotated,” and “tables” directories
- •
- Geometrically optimized amino acid *.xyz or *.sdf files that need to be located in the “in” folder
- •
- The name of the file representing the selected reference amino acid or the number associated with the file (1 representing the first file in the “in” directory)
- •
- Input variable Num.M, which defines how many extra candidates can be taken into consideration in case Num.low is satisfied by only one candidate
- •
- Input variable Num.low, which defines the target percentage differences between ST of two candidates in order to accept and stop searching for candidates with fewer atoms
- •
- Input variable Num.low2, which defines the percentage of the maximum found TM-score such that even lower-scored candidates are exported in *.xls tables and *.xyz files
- •
- Input variables Num.empi1 through 3 needed by the TM-score or another means of choosing between alignments
After the requirements are met, the original eigenproblem algorithm is run in order to be sure that the starting point of the program is a good initial alignment. Then all possible combinations with a smaller number of atoms are found by eliminating atom by atom in the AllE function. Eigenvalues are found for each combination without rotating the candidates. ST sums are compared until the input variables are satisfied or all combinations with a minimum of three atoms are compared. Candidates are aligned by the original eigenproblem approach, possibly good pi/2 rotations are taken into consideration, and trilateration is run. Since the TM-score compares distances between atoms of molecules, candidates are translated on top of the reference structure. Good final candidates are exported.
The following tables are exported as *.xls files in the “results\tables” directory:
- 1.
- 3D structural data for heavy atoms as T1
- 2.
- 3D distance matrix for heavy atoms as T2
- 3.
- Cartesian coordinate distance matrices for heavy atoms as T3–T5
- 4.
- Eigenvalues for above Cartesian coordinate distance matrices as T6
- 5.
- Polynomials for the same Cartesian coordinate distance matrices as T7
- 6.
- A table containing data such as Table A1 available in Appendix A, but no images, named Tscore
The following files are exported as *.xyz geometry files:
- •
- Initial *.sdf files are converted in the “in\xyz” directory.
- •
- In the “results\aligned” directory, the results from the original eigenproblem program are exported.
- •
- In the “results\rotated” directory, all *.xyz files related to the Tscore table can be found.
3. Results
Eigenvalues of all combinations of atoms are computed for each structure. The −2Sx, −2Sy, and −2Sz values of Dx, Dy, and Dz matrices for aligned glycine are −73.557, −27.349, and −0.004, respectively; sum ST = −100.91.
Comparing alanine 005950.sdf to glycine, six possible combinations of five atoms can be found, the fifth having the closest sum to −100.91, as seen in Table 6.

Table 6.
All combinations of five atoms in the case of alanine and their ST sums.
All possible candidates are parsed by the moreData function in the search for a lower percentage difference between ST sums (in the indx function). The targeted percentage difference is defined by Num.low. A multiplier is chosen to extend the search range at the cost of time, Num.M, since the best alignment might not necessarily be the one with the lowest difference between sums. In this case, the following three are chosen by the program: 1, 3, and 5.
The eigenproblem approach is used on the chosen candidates to obtain an eigenvalue-wise rotation alignment. It is suggested that compounds are obtained in their correct alignment or in the mirror of the proper alignment [15]. The search is extended to these possible good rotations (by the first “for” instruction of the align function). To obtain the position of the other unmatched unaligned atoms, a trilateration algorithm (receiving data from the rest of the align function) is found and used from the literature [17].
Since one of these rotations should lead to a good superposition of the two amino acids, the mean values on each of the axes are found for selected atoms of both structures. The selection is based on atoms indexed in the candidate search presented in Table 6. Subtracting for each of the axes, the candidate structure is translated on top of glycine (by the trans function).
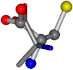
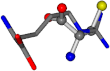
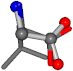
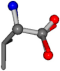
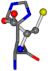
For the resulting candidate combinations, distances are found between pairs of a number of atoms. A MATLAB function matchpairs is used to find atoms that will be superposed based on a linear assignment problem that allows for minimum-cost solutions. These pairs are introduced into a scoring function chosen from the literature, in this case the geometric part of UniAlign-TMscore [2]. All these are executed by the choice function. One change was made since our chosen structures contain a small number of atoms: the 15 subtraction was set to 0 so that we obtained a positive distance under the square root of the empirical scaling factor for distance normalization, d0. This can be modified in empi3. Other scoring functions may be applied. The best result for alanine is superposed in Figure 2 in tube style, on top of glycine, which is presented in ball-and-stick-with-non-colored-bond style.
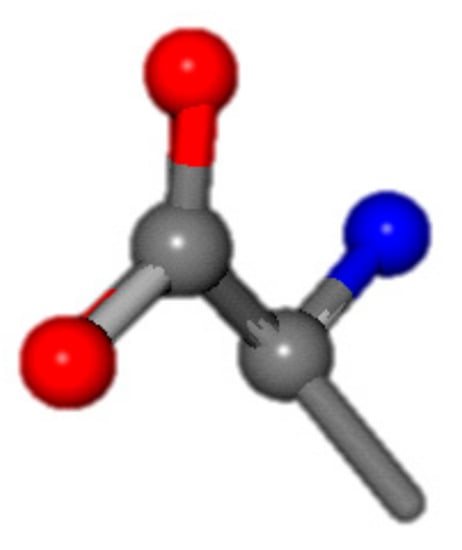
Figure 2.
A 3D view of the best alignment of alanine to glycine.
The best score for each compared structure is exported to the final results in Table A1 available in Appendix A. Using another parameter (Num.low2), scores close to it are added. Elements selected for candidates with fewer atoms are presented in the table since they help make an easy choice between close scores. A *Tscore.xls file is generated at the end of the choice function.
4. Discussion
The TM-score can be used to select a best match from all candidates found by the eigenproblem algorithm, as seen in Table A1 and Table A2 of Appendix A. Of the total of 19 amino acids aligned to glycine, 13 results are singular high-confidence alignments, of which 11 give a high TM-score. Another three (cysteine, lysine, and arginine) give two possible good results each, and the TM-score can be used to distinguish the best one.
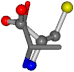
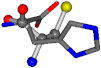
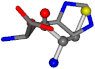
There are some mismatches made by the program. For example, in the case of glutamine 005961, the best score is found for a four-atom alignment instead of the correct five-atom alignment case number 483. Another difficulty can be observed in the cases of tryptophan 006305 and glutamic acid 033032, where a small score is given to the aligned case numbers 4/115, which are the only ones with elemental similarities, as depicted in Table 7.

Table 7.
3D views of the problematic choice of alignments for glycine.
Cysteine is the second amino acid taken as a reference for alignment, and all the candidates that our program outputs are depicted in Table A2 of Appendix A. From the total of 19 amino acids aligned to cysteine, six results can be chosen by the highest TM-score, of which two are singular results. Another five give two or more possible good results each, and the TM-score can be used to distinguish the best one.
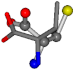
The following eight mismatches are presented for cysteine, of which the first four are available in Table 8:

Table 8.
3D views of the problematic choice of alignments for cysteine.
- •
- In the case of alanine 005950, a small score is given to the aligned case number 269, which is the only one with elemental similarity.
- •
- For valine 006287, threonine 006288, and arginine 006322, the best scores are found for candidates with a lower number of aligned atoms. The best candidates with more aligned atoms are 006287-1, 006288-1, and 6322-19.
- •
- The outputs for aspartic acid 005960, lysine 005962, histidine 006274, and tryptophan 006305 did not contain the expected alignments.
As stated above, a parameter is introduced such that close scores are not ignored. In this case, a score of 80% of the maximum is accepted for output. This percentage can be indicated in the Num.low2 parameter. This is needed so that the best alignment is given as a result, even though it is not the one with the highest TM-score.
Another easy way to choose from these candidates is to view the chosen elements and eliminate candidates that might have close numerical scores but wrong atom types. Other scoring functions or a combination of such means could lead to even better results.
The use and applicability of the eigenproblem goes beyond the alignment of molecules [15] and biochemical similarity. Recent reports include analysis of regular graphs for their properties, including eigen-spectra and automorphisms [18], molecular topology [19,20,21,22], characteristic equations, principal component decomposition [23], algebraic topology and generalized Bertrand curves [24], treatment of fuzzy decisions [25] and tridiagonal matrices [26], commutator tables, and Laplacian [27], systems of differential [28], and integro-differential [29] equations, while challenging problems appear in polynomial root evaluation [30] and the characteristic equation of a square matrix of a great order [31].
5. Conclusions
An application of the eigenproblem was elaborated, aiming to find the best geometric alignment of selected amino acids with regard to each other.
We can conclude that the best alignment does not obey a strict trend. The close results of the same algorithm can be taken into account. Even after running a score function, we can conclude that the alignment with the highest score is not always the best alignment.
To reduce the number of rotations for which a scoring function is run, the present algorithm needs to be restricted with a few parameters. In addition, a combination of multiple approaches could lead to faster results.
Taking glycine as a reference, 84% of the best alignments can be numerically pointed by a scoring function such as the TM-score, of which 68% are exported as single candidates, meaning that the restrictive parameters are relevant to the present comparison. For cysteine, only 58% can benefit from the presented scoring function. An extensive database would reveal a logical way of choosing them and help training for machine learning.
After running the present algorithm with the other amino acids as a reference, the correct alignment was numerically detected by the TM-score 70% of the time, on average, and 15% more cases with close scores can be easily distinguished by human observation. The present algorithm can be sped up by full vectorization. Machine learning needs to be added to scoring functions as a means to reduce the impact of limited description capabilities and predetermined theory-inspired functional form. These shortcomings can be solved by not imposing a strict algorithm but letting machine learning capture properties that are hard to model because of many unmeasured/unknown/undiscovered quantitative structure–activity relationships (QSAR). Machine learning can assimilate the fast-growing volume of high-quality structural and interaction data found in the literature.
Supplementary Materials
The following archive is available online at https://www.mdpi.com/article/10.3390/sym13101849/s1: *.zip archive, containing results in *.xyz format, *.xls tables, and pictures of a 3D view of alignments for each amino acid taken as a reference.
Author Contributions
Conceptualization, L.J.; software, L.J. and D.-M.J.; data curation, D.B.; writing, D.-M.J. and M.A.T.; supervision, L.J. All authors have read and agreed to the published version of the manuscript.
Funding
The present work received financial support through the project “Entrepreneurship for Innovation through Doctoral and Postdoctoral Research,” POCU/380/6/13/123886, co-financed by the European Social Fund, through the Operational Program for Human Capital 2014-2020. This research was funded by the Technical University of Cluj-Napoca open access publication grant.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in the *.zip archive of the Supplementary Materials section of this article.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Aligned amino acids are superposed in Table A1 in tube style on top of glycine, which is presented in ball-and-stick-with-non-colored-bond style. Each amino acid is taken as a reference and presented in its own *Tscore.xls file in the Supplementary Materials section. Three-dimensional renders can be found in the pictures folders of the archive.

Table A1.
All structures aligned to glycine; their candidate indexes as exported by the program in *.xyz format; TM-scores; selected elements; and −2Sx, −2Sy, and −2Sz.
Table A1.
All structures aligned to glycine; their candidate indexes as exported by the program in *.xyz format; TM-scores; selected elements; and −2Sx, −2Sy, and −2Sz.
| 3D Views of Alignment | Aligned Structure and Index | TM-Score | Selected Atoms from 000750 | −2Sx, −2Sy, and −2Sz of the Reference Candidate | Selected Atoms from the Aligned Structure | −2Sx, −2Sy, and −2Sz of the Aligned Candidate |
|---|---|---|---|---|---|---|
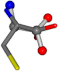 | 005862-13 | 0.49953 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −13.611 −25.8092 −61.4329 |
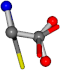 | 005862-14 | 0.59034 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −13.611 −25.8092 −61.4329 |
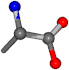 | 005950-3 | 0.97619 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −4.4817 −70.1638 −28.7497 |
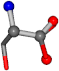 | 005951-41 | 0.80012 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −69.7742 −4.2881 −26.9964 |
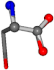 | 005960-37 | 0.86944 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −71.2314 −27.4581 −2.0944 |
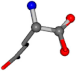 | 005961-33 | 0.84632 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −71.2576 −3.3832 −27.3196 |
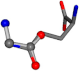 | 005961-170 | 0.95817 | OOCC | −0.0011 −20.6582 −23.8791 | OCNC | −24.0884 −0.0004 −21.1849 |
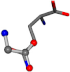 | 005961-173 | 0.93357 | OOCC | −0.0011 −20.6582 −23.8791 | NCOC | −0.0004 −24.0884 −21.1849 |
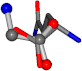 | 005961-198 | 0.79095 | OOCC | −0.0011 −20.6582 −23.8791 | OCOC | −0.2581 −24.3734 −20.2611 |
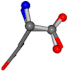 | 005961-283 | 0.82694 | OONCC | −0.0022 −14.8281 −54.3193 | OONCC | −53.2066 −1.5086 −15.0372 |
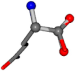 | 005961-483 | 0.85761 | OONCC | −0.0032 −4.3992 −57.2565 | OONCC | −54.6736 −2.475 −21.8424 |
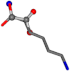 | 005962-12 | 0.75429 | OONCC | −0.004 −27.3493 −73.5567 | CNOCC | −70.2261 −29.0349 −4.2049 |
 | 005962-40 | 0.91715 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −1.5282 −26.4302 −73.3027 |
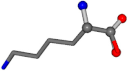
 | 006057-40 | 0.86353 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −2.3691 −27.3223 −70.9619 |
 | 006106-2 | 0.6392 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −8.1806 −61.8107 −30.7736 |
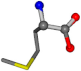 | 006137-40 | 0.86184 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −2.2896 −27.3359 −71.1183 |
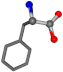 | 006140-40 | 0.86912 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −2.1499 −27.3655 −71.1355 |
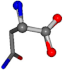 | 006267-2 | 0.86616 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −7.4136 −64.3092 −29.0284 |
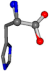 | 006274-41 | 0.83006 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −69.8017 −3.9136 −26.9388 |
 | 006287-15 | 0.69499 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −68.0382 −8.7019 −24.3289 |
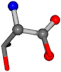 | 006288-65 | 0.92522 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −72.4925 −27.4791 −1.3521 |
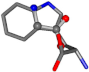 | 006305-1 | 0.80948 | OONCC | −0.004 −27.3493 −73.5567 | CCCCC | −0.0317 −25.8926 −74.5664 |
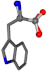 | 006305-4 | 0.66756 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −0.0317 −74.5664 −25.8926 |
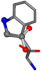 | 006305-42 | 0.7386 | OONCC | −0.004 −27.3493 −73.5567 | CCNCC | −1.1175 −25.7209 −72.1151 |
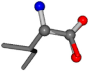 | 006306-11 | 0.82228 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −70.3452 −26.3299 −4.0766 |
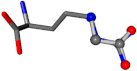 | 006322-14 | 0.97621 | OONCC | −0.004 −27.3493 −73.5567 | NNCNC | −73.6395 −27.5846 −0.0063 |
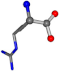 | 006322-93 | 0.99322 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −72.695 −0.0803 −27.8005 |
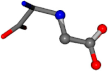 | 033032-69 | 0.96492 | OONCC | −0.004 −27.3493 −73.5567 | OOCCC | −79.1546 −0.3715 −26.9955 |
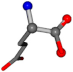 | 033032-115 | 0.93477 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −73.0115 −27.7341 −1.111 |
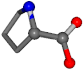 | 145742-4 | 0.92766 | OONCC | −0.004 −27.3493 −73.5567 | OONCC | −6.2518 −65.5464 −27.6594 |

Table A2.
All structures aligned to cysteine; their candidate indexes as exported by the program in *.xyz format; TM-scores; selected elements; and −2Sx, −2Sy, and −2Sz.
Table A2.
All structures aligned to cysteine; their candidate indexes as exported by the program in *.xyz format; TM-scores; selected elements; and −2Sx, −2Sy, and −2Sz.
| 3D Views of Alignment | Aligned Structure and Index | TM-Score | Selected Atoms from 000750 | −2Sx, −2Sy, and −2Sz of the Reference Candidate | Selected Atoms from the Aligned Structure | −2Sx, −2Sy, and −2Sz of the Aligned Candidate |
|---|---|---|---|---|---|---|
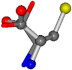 | 000750-6 | 0.48834 | OONCC | −13.611 −25.8092 −61.4329 | OONCC | −73.5567 −27.3493 −0.004 |
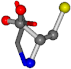 | 000750-8 | 0.42207 | OONCC | −13.611 −25.8092 −61.4329 | OONCC | −73.5567 −0.004 −27.3493 |
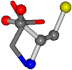 | 000750-10 | 0.44278 | ONCCC | −13.611 −25.8092 −61.4329 | ONCOC | −0.004 −27.3493 −73.5567 |
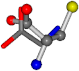 | 000750-11 | 0.44133 | OCCC | −13.611 −25.8092 −61.4329 | OCNC | −73.5567 −27.3493 −0.004 |
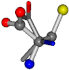 | 005950-148 | 0.50246 | OONCC | −8.3671 −29.9695 −62.0051 | OOCCC | −71.7263 −5.4464 −25.4841 |
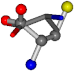 | 005950-164 | 0.5433 | OOCCC | −8.3671 −29.9695 −62.0051 | OOCCC | −71.7263 −25.4841 −5.4464 |
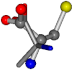 | 005950-248 | 0.60276 | OONCC | −8.3671 −29.9695 −62.0051 | OOCCC | −71.7263 −5.4464 −25.4841 |
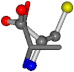 | 005950-269 | 0.56223 | OONCC | −8.3671 −29.9695 −62.0051 | OONCC | −0.31 −73.3751 −27.8286 |
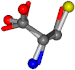 | 005951-16 | 0.78486 | SOONCCC | −37.2279 −107.1892 −159.5151 | OOONCCC | −147.0913 −24.8576 −106.5052 |
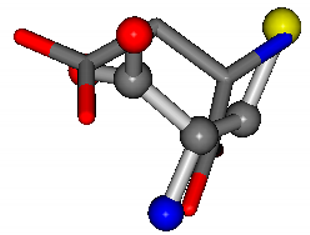 | 005960-1 | 0.42025 | SOONCCC | −37.2279 −107.1892 −159.5151 | NOCOCCC | −11.3045 −110.1124 −182.4483 |
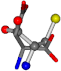 | 005960-6 | 0.4143 | SONCCC | −37.2279 −107.1892 −159.5151 | OCNCCC | −11.3045 −182.4483 −110.1124 |
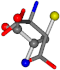 | 005960-7 | 0.3736 | SOONCCC | −37.2279 −107.1892 −159.5151 | NOOOCCC | −182.4483 −110.1124 −11.3045 |
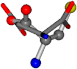 | 005960-10 | 0.42411 | SOOCCC | −37.2279 −107.1892 −159.5151 | CNCCOC | −11.3045 −182.4483 −110.1124 |
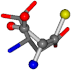 | 005960-12 | 0.40875 | SOONCCC | −37.2279 −107.1892 −159.5151 | OOOCCCC | −182.4483 −110.1124 −11.3045 |
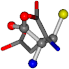 | 005960-13 | 0.39022 | OONCC | −37.2279 −107.1892 −159.5151 | OCCCC | −110.1124 −11.3045 −182.4483 |
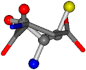 | 005960-14 | 0.39347 | SOONCCC | −37.2279 −107.1892 −159.5151 | ONCOCCC | −11.3045 −110.1124 −182.4483 |
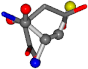 | 005960-15 | 0.45748 | SOONCCC | −37.2279 −107.1892 −159.5151 | CCNOCOC | −11.3045 −110.1124 −182.4483 |
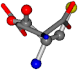 | 005960-24 | 0.42411 | SOOCCC | −37.2279 −107.1892 −159.5151 | CNCCOC | −110.1124 −11.3045 −182.4483 |
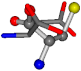 | 005960-25 | 0.37188 | SOOCCC | −37.2279 −107.1892 −159.5151 | CONCOC | −182.4483 −110.1124 −11.3045 |
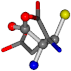 | 005960-26 | 0.39022 | OONCC | −37.2279 −107.1892 −159.5151 | OCCCC | −11.3045 −110.1124 −182.4483 |
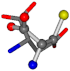 | 005960-27 | 0.40875 | SOONCCC | −37.2279 −107.1892 −159.5151 | OOOCCCC | −24.9542 −207.716 −70.9892 |
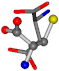 | 005960-28 | 0.39485 | SOONCCC | −37.2279 −107.1892 −159.5151 | NOOOCCC | −207.716 −24.9542 −70.9892 |
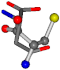 | 005960-31 | 0.3717 | SOONCCC | −37.2279 −107.1892 −159.5151 | OCCOCOC | −24.9542 −207.716 −70.9892 |
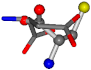 | 005960-35 | 0.42601 | SOCCC | −37.2279 −107.1892 −159.5151 | OCCOC | −24.9542 −207.716 −70.9892 |
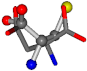 | 005960-37 | 0.42553 | SOONCCC | −37.2279 −107.1892 −159.5151 | OOOCCCC | −207.716 −70.9892 −24.9542 |
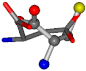 | 005960-43 | 0.43719 | SOOCCC | −37.2279 −107.1892 −159.5151 | OOCOCC | −207.716 −70.9892 −24.9542 |
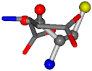 | 005960-49 | 0.42601 | SOCCC | −37.2279 −107.1892 −159.5151 | OCCOC | −70.9892 −24.9542 −207.716 |
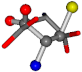 | 005960-50 | 0.46341 | SOOCCC | −37.2279 −107.1892 −159.5151 | COCOCC | −207.716 −70.9892 −24.9542 |
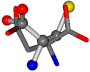 | 005960-52 | 0.42553 | SOONCCC | −37.2279 −107.1892 −159.5151 | OOOCCCC | −207.716 −70.9892 −24.9542 |
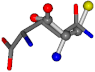 | 005961-14 | 0.61685 | SCCC | −31.8416 −89.3906 −126.7171 | OCCC | −1.4071 −33.3867 −210.7718 |
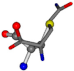 | 005961-155 | 0.55368 | SOOCCC | −5.2465 −88.3648 −122.3962 | COOCNC | −118.8959 −26.4831 −65.5527 |
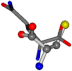 | 005961-179 | 0.5482 | SOONCC | −28.5971 −38.2796 −135.5565 | OCCNCC | −14.3175 −66.8735 −113.4675 |
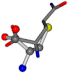 | 005961-230 | 0.59214 | SOOCCC | −28.5971 −38.2796 −135.5565 | COOCNC | −118.8959 −26.4831 −65.5527 |
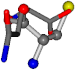 | 005961-239 | 0.55869 | SOOCCC | −28.5971 −38.2796 −135.5565 | OCNCOC | −118.8959 −65.5527 −26.4831 |
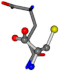 | 005961-242 | 0.56355 | SNCCC | −28.9822 −86.0507 −136.5352 | CNCOC | −210.7718 −1.4071 −33.3867 |
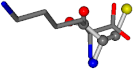 | 005962-1 | 0.43119 | SONCCC | −37.2279 −107.1892 −159.5151 | OCNCOC | −8.8452 −80.0543 −237.5683 |
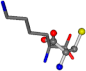 | 005962-2 | 0.39314 | SONCCC | −31.7674 −35.7196 −105.9193 | OCNCOC | −8.8452 −237.5683 −80.0543 |
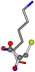 | 005962-3 | 0.41372 | SONCCC | −37.2279 −107.1892 −159.5151 | CNOCOC | −237.5683 −8.8452 −80.0543 |
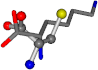 | 005962-15 | 0.44908 | SOONCCC | −37.2279 −107.1892 −159.5151 | COONCCC | −8.8452 −80.0543 −237.5683 |
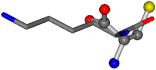 | 005962-18 | 0.40717 | SOOCCC | −37.2279 −107.1892 −159.5151 | ONCCCC | −237.5683 −80.0543 −8.8452 |
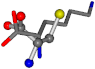 | 005962-23 | 0.44908 | SOONCCC | −37.2279 −107.1892 −159.5151 | COONCCC | −237.5683 −8.8452 −80.0543 |
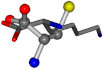 | 005962-25 | 0.4643 | SOOCCC | −37.2279 −107.1892 −159.5151 | COOCCC | −237.5683 −80.0543 −8.8452 |
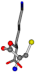 | 005962-30 | 0.40299 | OONCC | −31.7674 −35.7196 −105.9193 | CNOCC | −7.4698 −103.8043 −62.1387 |
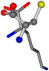 | 005962-32 | 0.39753 | SONCCC | −31.7674 −35.7196 −105.9193 | OONCCC | −103.8043 −62.1387 −7.4698 |
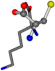 | 005962-34 | 0.44778 | OONCC | −31.7674 −35.7196 −105.9193 | OONCC | −103.8043 −7.4698 −62.1387 |
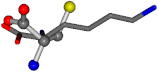 | 005962-39 | 0.41984 | SOOCCC | −31.7674 −35.7196 −105.9193 | COOCNC | −7.4698 −62.1387 −103.8043 |
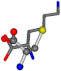 | 005962-40 | 0.46743 | SONCCC | −31.7674 −35.7196 −105.9193 | COOCNC | −7.4698 −62.1387 −103.8043 |
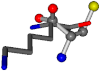 | 005962-46 | 0.38057 | SOOCCC | −31.7674 −35.7196 −105.9193 | OCNCOC | −7.4698 −62.1387 −103.8043 |
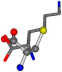 | 005962-48 | 0.46743 | SONCCC | −31.7674 −35.7196 −105.9193 | COOCNC | −103.8043 −7.4698 −62.1387 |
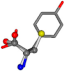 | 006057-16 | 0.76753 | SOONCCC | −37.2279 −107.1892 −159.5151 | COONCCC | −173.9182 −101.9463 −23.1192 |
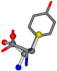 | 006057-144 | 0.62652 | SOONCCC | −28.5971 −38.2796 −135.5565 | COONCCC | −13.4258 −40.6418 −148.5831 |
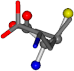 | 006106-16 | 0.54749 | SOOCCC | −37.2279 −107.1892 −159.5151 | COOCCC | −28.1552 −71.8562 −208.2835 |
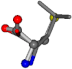 | 006106-83 | 0.68249 | SOONCCC | −37.2279 −107.1892 −159.5151 | COONCCC | −37.4924 −148.3439 −113.3827 |
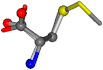 | 006137-18 | 0.8267 | SOONCCC | −37.2279 −107.1892 −159.5151 | COONCCC | −156.8033 −107.15 −27.0805 |
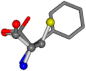 | 006140-5 | 0.65026 | SOONCCC | −11.1453 −70.4461 −121.9608 | COONCCC | −9.3713 −53.8297 −141.0272 |
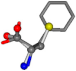 | 006140-28 | 0.76831 | SOONCCC | −37.2279 −107.1892 −159.5151 | COONCCC | −173.9288 −101.9683 −23.0865 |
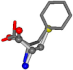 | 006140-228 | 0.62808 | SOONCCC | −28.5971 −38.2796 −135.5565 | COONCCC | −108.7941 −87.3884 −5.489 |
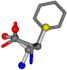 | 006140-256 | 0.62895 | SOONCCC | −28.5971 −38.2796 −135.5565 | COONCCC | −13.4284 −40.6224 −148.603 |
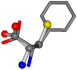 | 006140-453 | 0.69151 | SOONCCC | −31.8416 −89.3906 −126.7171 | COONCCC | −148.4493 −83.8248 −16.8891 |
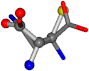 | 006267-150 | 0.75426 | SOOCCC | −28.5971 −38.2796 −135.5565 | OONCCC | −114.7445 −56.4402 −32.1581 |
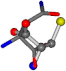 | 006267-270 | 0.64267 | OONCCC | −30.6696 −83.1536 −110.9209 | CNOCOC | −157.5302 −52.8112 −14.0738 |
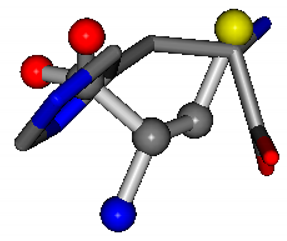 | 006274-11 | 0.52022 | SOOCC | −30.6696 −83.1536 −110.9209 | CCNCC | −29.2987 −34.082 −161.888 |
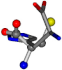 | 006274-20 | 0.51619 | OCCC | −37.2279 −107.1892 −159.5151 | CCCN | −8.53 −238.2463 −49.0387 |
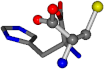 | 006274-44 | 0.47052 | OONCC | −31.7674 −35.7196 −105.9193 | OONCC | −104.752 −19.0687 −49.267 |
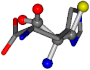 | 006274-75 | 0.48041 | SOOCCC | −11.1453 −70.4461 −121.9608 | CNOCCC | −27.4473 −30.9096 −145.1067 |
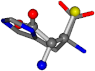 | 006274-78 | 0.58417 | SOOCCC | −11.1453 −70.4461 −121.9608 | CNCCCC | −145.1067 −30.9096 −27.4473 |
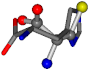 | 006274-83 | 0.48041 | SOOCCC | −11.1453 −70.4461 −121.9608 | CNOCCC | −145.1067 −27.4473 −30.9096 |
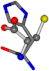 | 006274-140 | 0.47356 | SOONCC | −28.9822 −86.0507 −136.5352 | NCOCCC | −7.9674 −210.2593 −33.7955 |
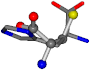 | 006274-151 | 0.5215 | SOOCCC | −28.9822 −86.0507 −136.5352 | CNCCCC | −210.2593 −7.9674 −33.7955 |
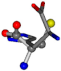 | 006274-170 | 0.48165 | OCCC | −28.9822 −86.0507 −136.5352 | CCCN | −6.8009 −203.291 −41.7099 |
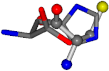 | 006274-175 | 0.48518 | SOOCCC | −28.9822 −86.0507 −136.5352 | CCCCNC | −6.8009 −41.7099 −203.291 |
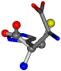 | 006274-184 | 0.48165 | OCCC | −28.9822 −86.0507 −136.5352 | CCCN | −41.7099 −6.8009 −203.291 |
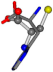 | 006274-188 | 0.47675 | SOONCCC | −28.9822 −86.0507 −136.5352 | NOOCCCC | −175.3227 −13.4702 −62.6855 |
 | 006274-195 | 0.54066 | SOCCC | −28.9822 −86.0507 −136.5352 | ONCCC | −13.4702 −175.3227 −62.6855 |
 | 006274-253 | 0.51888 | SOOCCC | −28.9822 −86.0507 −136.5352 | CCCCCC | −170.4509 −72.8278 −7.6721 |
 | 006274-266 | 0.49887 | OONCC | −30.6696 −83.1536 −110.9209 | NCCCC | −29.2987 −161.888 −34.082 |
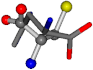 | 006274-270 | 0.47705 | OONC | −30.6696 −83.1536 −110.9209 | CNCC | −29.2987 −161.888 −34.082 |
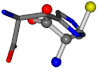 | 006274-275 | 0.4984 | SOOCCC | −30.6696 −83.1536 −110.9209 | NCCNCC | −29.2987 −34.082 −161.888 |
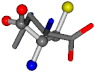 | 006274-284 | 0.47705 | OONC | −30.6696 −83.1536 −110.9209 | CNCC | −34.082 −29.2987 −161.888 |
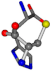 | 006274-291 | 0.47128 | SOONCC | −31.8416 −89.3906 −126.7171 | OCNCCC | −9.7892 −202.8613 −35.0825 |
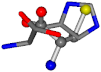 | 006274-303 | 0.47216 | SOOCCC | −31.8416 −89.3906 −126.7171 | CCCCCC | −202.8613 −35.0825 −9.7892 |
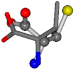 | 006287-1 | 0.44763 | SOONCCC | −37.2279 −107.1892 −159.5151 | COONCCC | −28.463 −162.9622 −112.2806 |
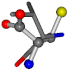 | 006287-10 | 0.50113 | ONCCC | −37.2279 −107.1892 −159.5151 | COCNC | −28.463 −112.2806 −162.9622 |
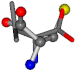 | 006287-14 | 0.43465 | SOONCCC | −37.2279 −107.1892 −159.5151 | OCCNCCC | −28.463 −112.2806 −162.9622 |
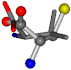 | 006287-20 | 0.43271 | SOOCCC | −37.2279 −107.1892 −159.5151 | COOCCC | −28.463 −112.2806 −162.9622 |
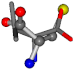 | 006287-22 | 0.43465 | SOONCCC | −37.2279 −107.1892 −159.5151 | OCCNCCC | −162.9622 −28.463 −112.2806 |
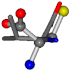 | 006287-24 | 0.46687 | SOOCCC | −37.2279 −107.1892 −159.5151 | OCCCCC | −162.9622 −112.2806 −28.463 |
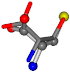 | 006288-1 | 0.48391 | SOONCCC | −37.2279 −107.1892 −159.5151 | OOONCCC | −43.0635 −66.5743 −180.8565 |
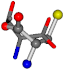 | 006288-3 | 0.45585 | SOONCCC | −11.1453 −70.4461 −121.9608 | OCCNOCC | −43.0635 −180.8565 −66.5743 |
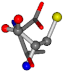 | 006288-6 | 0.45633 | OONCCC | −37.2279 −107.1892 −159.5151 | CNOCCC | −43.0635 −180.8565 −66.5743 |
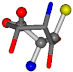 | 006288-13 | 0.51827 | SONCCC | −37.2279 −107.1892 −159.5151 | NCOCCC | −180.8565 −66.5743 −43.0635 |
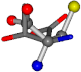 | 006288-26 | 0.5201 | SOOCCC | −37.2279 −107.1892 −159.5151 | OCOCCC | −180.8565 −66.5743 −43.0635 |
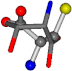 | 006288-28 | 0.51827 | SONCCC | −37.2279 −107.1892 −159.5151 | NCOCCC | −8.4024 −103.7817 −61.1853 |
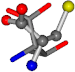 | 006288-37 | 0.42733 | SONCCC | −31.7674 −35.7196 −105.9193 | OONCOC | −8.4024 −61.1853 −103.7817 |
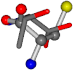 | 006288-72 | 0.42211 | SOOCCC | −11.1453 −70.4461 −121.9608 | OCNCOC | −29.1037 −62.1843 −111.9187 |
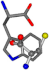 | 006305-1 | 0.50837 | SONCCC | −37.2279 −107.1892 −159.5151 | CCCCCC | −1.9654 −82.3993 −214.7367 |
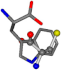 | 006305-2 | 0.56881 | SONCCC | −37.2279 −107.1892 −159.5151 | CCNCCC | −3.6968 −75.0753 −224.1486 |
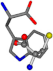 | 006305-5 | 0.48382 | SONCCC | −37.2279 −107.1892 −159.5151 | CCNCCC | −2.4671 −82.2841 −211.504 |
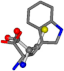 | 006305-9 | 0.54483 | SOONCCC | −37.2279 −107.1892 −159.5151 | COONCCC | −1.9654 −214.7367 −82.3993 |
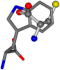 | 006305-23 | 0.47679 | SONCCC | −37.2279 −107.1892 −159.5151 | CNCCCC | −214.7367 −1.9654 −82.3993 |
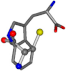 | 006305-35 | 0.51784 | SONCCC | −37.2279 −107.1892 −159.5151 | CNCCCC | −224.1486 −3.6968 −75.0753 |
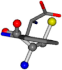 | 006305-36 | 0.50682 | OOCCC | −37.2279 −107.1892 −159.5151 | CNCCC | −75.0753 −224.1486 −3.6968 |
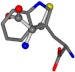 | 006305-44 | 0.51678 | SOONCCC | −37.2279 −107.1892 −159.5151 | CCCCCCC | −224.1486 −75.0753 −3.6968 |
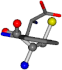 | 006305-49 | 0.50682 | OOCCC | −37.2279 −107.1892 −159.5151 | CNCCC | −75.0753 −3.6968 −224.1486 |
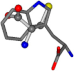 | 006305-59 | 0.51678 | SOONCCC | −37.2279 −107.1892 −159.5151 | CCCCCCC | −1.8573 −208.8667 −86.2881 |
 | 006305-60 | 0.53173 | SONCCC | −37.2279 −107.1892 −159.5151 | CNCCCC | −208.8667 −1.8573 −86.2881 |
 | 006305-88 | 0.49077 | SONCCC | −37.2279 −107.1892 −159.5151 | NCCCCC | −0.5256 −221.8958 −77.1639 |
 | 006305-93 | 0.4984 | SONCCC | −37.2279 −107.1892 −159.5151 | CCCCCC | −0.5256 −77.1639 −221.8958 |
 | 006305-97 | 0.56351 | SOONCCC | −37.2279 −107.1892 −159.5151 | CCCCCNC | −0.5256 −77.1639 −221.8958 |
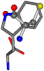 | 006305-98 | 0.56197 | SONCCC | −37.2279 −107.1892 −159.5151 | CNCCCC | −221.8958 −0.5256 −77.1639 |
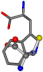 | 006305-105 | 0.56351 | SOONCCC | −37.2279 −107.1892 −159.5151 | CCCCCNC | −221.8958 −0.5256 −77.1639 |
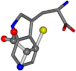 | 006305-110 | 0.56356 | SONCCC | −37.2279 −107.1892 −159.5151 | CNCCCC | −211.504 −2.4671 −82.2841 |
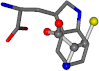 | 006305-138 | 0.50276 | SOONCCC | −37.2279 −107.1892 −159.5151 | NCOCCCC | −1.4469 −210.87 −83.7564 |
 | 006305-163 | 0.59418 | SONCCC | −37.2279 −107.1892 −159.5151 | CCCCNC | −0.0058 −216.4546 −93.9712 |
 | 006305-186 | 0.49257 | OOCCC | −37.2279 −107.1892 −159.5151 | CCCCC | −48.5216 −239.5349 −13.6686 |
 | 006305-188 | 0.48355 | SONCCC | −37.2279 −107.1892 −159.5151 | CNCCCC | −13.6686 −239.5349 −48.5216 |
 | 006305-199 | 0.49257 | OOCCC | −37.2279 −107.1892 −159.5151 | CCCCC | −48.5216 −13.6686 −239.5349 |
 | 006305-200 | 0.47666 | SOOCCC | −37.2279 −107.1892 −159.5151 | CCNCCC | −239.5349 −48.5216 −13.6686 |
 | 006306-26 | 0.59343 | SOONCCC | −37.2279 −107.1892 −159.5151 | OCCNCCC | −187.941 −40.4448 −79.4912 |
 | 006306-106 | 0.68164 | SOCCC | −5.2465 −88.3648 −122.3962 | NCCCC | −20.4327 −39.2382 −155.9536 |
 | 006306-141 | 0.57733 | OONCCC | −5.2465 −88.3648 −122.3962 | CNCCCC | −18.3555 −160.9526 −36.9999 |
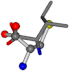 | 006306-175 | 0.54571 | SOOCCC | −28.5971 −38.2796 −135.5565 | COOCNC | −28.3736 −66.0039 −109.0218 |
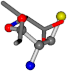 | 006306-181 | 0.54665 | SOOCCC | −28.5971 −38.2796 −135.5565 | OCNCOC | −28.3736 −66.0039 −109.0218 |
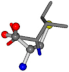 | 006306-183 | 0.54571 | SOOCCC | −28.5971 −38.2796 −135.5565 | COOCNC | −109.0218 −28.3736 −66.0039 |
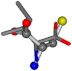 | 006306-226 | 0.56045 | SOONCCC | −28.9822 −86.0507 −136.5352 | OCCNCCC | −152.9247 −33.7788 −64.0308 |
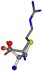 | 006322-2 | 0.55916 | SOOCCC | −28.5971 −38.2796 −135.5565 | COOCNC | −27.3384 −62.6263 −111.6846 |
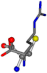 | 006322-19 | 0.4956 | SOONCCC | −37.2279 −107.1892 −159.5151 | COONCCC | −158.5429 −38.7577 −80.7785 |
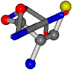 | 006322-42 | 0.5614 | SOOCCC | −28.5971 −38.2796 −135.5565 | OCNCOC | −27.3384 −62.6263 −111.6846 |
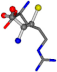 | 006322-44 | 0.46472 | SOOCCC | −28.5971 −38.2796 −135.5565 | NOOCCC | −111.6846 −27.3384 −62.6263 |
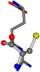 | 006322-56 | 0.49042 | ONCCC | −28.9822 −86.0507 −136.5352 | CNCNC | −221.7222 −6.933 −23.1061 |
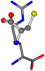 | 006322-60 | 0.4524 | SNCC | −28.9822 −86.0507 −136.5352 | NCNC | −221.7222 −23.1061 −6.933 |
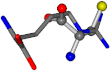 | 006322-69 | 0.51145 | SOOCCC | −28.9822 −86.0507 −136.5352 | NCCNCC | −221.7222 −6.933 −23.1061 |
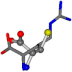 | 006322-90 | 0.4613 | SOONCCC | −28.9822 −86.0507 −136.5352 | COCNCCC | −204.5901 −27.1111 −18.7144 |
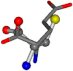 | 033032-13 | 0.56115 | SOONCCC | −37.2279 −107.1892 −159.5151 | COONCCC | −157.6594 −87.1404 −38.0414 |
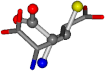 | 033032-66 | 0.45269 | SOONCCC | −31.8416 −89.3906 −126.7171 | COONCCC | −12.4748 −35.4453 −199.7397 |
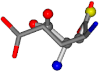 | 033032-69 | 0.51437 | SOCCC | −31.8416 −89.3906 −126.7171 | OCCOC | −199.7397 −35.4453 −12.4748 |
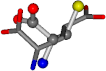 | 033032-74 | 0.45269 | SOONCCC | −31.8416 −89.3906 −126.7171 | COONCCC | −199.7397 −12.4748 −35.4453 |
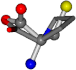 | 145742-21 | 0.59575 | SOOCCC | −37.2279 −107.1892 −159.5151 | COOCNC | −24.7574 −57.3704 −227.05 |
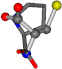 | 145742-28 | 0.53132 | SONCCC | −11.1453 −70.4461 −121.9608 | CCCCCN | −145.192 −12.4766 −45.8437 |
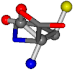 | 145742-29 | 0.52833 | OONCCC | −11.1453 −70.4461 −121.9608 | OCNCCC | −45.8437 −145.192 −12.4766 |
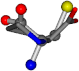 | 145742-43 | 0.48734 | SOCCC | −11.1453 −70.4461 −121.9608 | CCNCC | −145.192 −45.8437 −12.4766 |
References
- Dong, R.; Pan, S.; Peng, Z.; Zhang, Y.; Yang, J. MTM-ALIGN: A server for fast protein structure database search and multiple protein structure alignment. Nucleic Acids Res. 2018, 46, 380–386. [Google Scholar] [CrossRef]
- Zhao, C.; Sacan, A. UniAlign: Protein structure alignment meets evolution. Bioinformatics 2015, 31, 3139–3146. [Google Scholar] [CrossRef][Green Version]
- Hasegawa, H.; Holm, L. Advances and pitfalls of protein structural alignment. Curr. Opin. Struct. Biol. 2009, 19, 341–348. [Google Scholar] [CrossRef] [PubMed]
- Kolodny, R.; Koehl, P.; Levitt, M. Comprehensive evaluation of protein structure alignment methods: Scoring by geometric measures. J. Mol. Biol. 2005, 346, 1173–1188. [Google Scholar] [CrossRef] [PubMed]
- Terashi, G.; Takeda-Shitaka, M. CAB-Align: A flexible protein structure alignment method based on the residue-residue contact area. PLoS ONE 2015, 10, e0141440. [Google Scholar] [CrossRef] [PubMed]
- Akdel, M.; Durairaj, J.; de Ridder, D.; van Dijk, A.D.J. Caretta-A multiple protein structure alignment and feature extraction suite. comput. struct. Biotechnol. J. 2020, 18, 981–992. [Google Scholar] [CrossRef]
- Holm, L. Using dali for protein structure comparison. In Structural Bioinformatics; Gáspári, Z., Ed.; Methods in Molecular Biology; Springer: New York, NY, USA, 2020; Volume 2112, pp. 29–42. ISBN 978-1-07-160269-0. [Google Scholar]
- Hu, J.; Liu, Z.; Yu, D.-J.; Zhang, Y. LS-Align: An atom-level, flexible ligand structural alignment algorithm for high-throughput virtual screening. Bioinformatics 2018, 34, 2209–2218. [Google Scholar] [CrossRef] [PubMed]
- Menke, M.; Berger, B.; Cowen, L. Matt: Local flexibility aids protein multiple structure alignment. PLoS Comput. Biol. 2008, 4, 88–99. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y. TM-Align: A protein structure alignment algorithm based on the tm-Score. Nucleic Acids Res. 2005, 33, 2302–2309. [Google Scholar] [CrossRef]
- Chen, W.; Yao, C.; Guo, Y.; Wang, Y.; Xue, Z. PmTM-Align: Scalable pairwise and multiple structure alignment with apache spark and openmp. BMC Bioinform. 2020, 21, 426. [Google Scholar] [CrossRef]
- Shegay, M.V.; Suplatov, D.A.; Popova, N.N.; Švedas, V.K.; Voevodin, V.V. ParMATT: Parallel multiple alignment of protein 3D-structures with translations and twists for distributed-memory systems. Bioinformatics 2019, 35, 4456–4458. [Google Scholar] [CrossRef] [PubMed]
- Dong, R.; Peng, Z.; Zhang, Y.; Yang, J. MTM-Align: An algorithm for fast and accurate multiple protein structure alignment. Bioinformatics 2018, 34, 1719–1725. [Google Scholar] [CrossRef]
- Holm, L. DALI and the persistence of protein shape. Protein Sci. 2020, 29, 128–140. [Google Scholar] [CrossRef] [PubMed]
- Jäntschi, L. The eigenproblem translated for alignment of molecules. Symmetry 2019, 11, 1027. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, M.; Ma, J.; Liu, X.; Kobbelt, L.; Bao, H. Spectral quadrangulation with orientation and alignment control. In Proceedings of the ACM SIGGRAPH Asia 2008 Papers, Singapore, 10–13 December 2018; Hart, J.C., Ed.; Association for Computing Machinery: New York, NY, USA, 2008; Volume 147, pp. 1–9. [Google Scholar]
- Norrdine, A.; Kasmi, Z.; Ahmed, K.; Motzko, C.; Schiller, J. MQTT-Based Surveillance System of IoT Using UWB Real Time Location System. In Proceedings of the 2020 International Conferences on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData) and IEEE Congress on Cybermatics (Cybermatics), Rhodes, Greece, 2–6 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 216–221. [Google Scholar] [CrossRef]
- Xu, Z.; Huang, X.; Jimenez, F.; Deng, Y. A new record of graph enumeration enabled by parallel processing. Mathematics 2019, 7, 1214. [Google Scholar] [CrossRef]
- Medina, L.; Nina, H.; Trigo, M. On distance signless laplacian spectral radius and distance signless laplacian energy. Mathematics 2020, 8, 792. [Google Scholar] [CrossRef]
- Hayat, S.; Khan, S.; Khan, A.; Liu, J.-B. Valency-based molecular descriptors for measuring the π-electronic energy of lower polycyclic aromatic hydrocarbons. Polycycl. Aromat. Compd. 2020, 1, 1–17. [Google Scholar] [CrossRef]
- Hayat, S.; Khan, S. Quality testing of spectrum-based valency descriptors for polycyclic aromatic hydrocarbons with applications. J. Mol. Struct. 2021, 1228, 129789. [Google Scholar] [CrossRef]
- Tomescu, M.A.; Jäntschi, L.; Rotaru, D.I. Figures of graph partitioning by counting, sequence and layer matrices. Mathematics 2021, 9, 1419. [Google Scholar] [CrossRef]
- Jukic, S.; Saracevic, M.; Subasi, A.; Kevric, J. Comparison of ensemble machine learning methods for automated classification of focal and non-focal epileptic EEG signals. Mathematics 2020, 8, 1481. [Google Scholar] [CrossRef]
- Zhang, C.; Pei, D. Generalized bertrand curves in minkowski 3-space. Mathematics 2020, 8, 2199. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Dashtian, Z.; Weber, G.-W.; Tomaskova, H.; Soltani, M.; Mousavi, N.S. An integrated decision-making approach for green supplier selection in an agri-food supply chain: Threshold of robustness worthiness. Mathematics 2021, 9, 1304. [Google Scholar] [CrossRef]
- Wei, Y.; Zheng, Y.; Jiang, Z.; Shon, S. A study of determinants and inverses for periodic tridiagonal toeplitz matrices with perturbed corners involving mersenne numbers. Mathematics 2019, 7, 893. [Google Scholar] [CrossRef]
- Gasiński, L.; Papageorgiou, N.S. Resonant anisotropic (p,q)-equations. Mathematics 2020, 8, 1332. [Google Scholar] [CrossRef]
- Moaaz, O.; Furuichi, S.; Muhib, A. New comparison theorems for the nth order neutral differential equations with delay inequalities. Mathematics 2020, 8, 454. [Google Scholar] [CrossRef]
- Kamran, K.; Shah, Z.; Kumam, P.; Alreshidi, N.A. A meshless method based on the laplace transform for the 2D multi-term time fractional partial integro-differential equation. Mathematics 2020, 8, 1972. [Google Scholar] [CrossRef]
- Sharma, J.R.; Kumar, S.; Jäntschi, L. On a class of optimal fourth order multiple root solvers without using derivatives. Symmetry 2019, 11, 1452. [Google Scholar] [CrossRef]
- Kumar, D.; Sharma, J.R.; Jäntschi, L. A novel family of efficient weighted-newton multiple root iterations. Symmetry 2020, 12, 1494. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).