Abstract
In this work, we determined the total effective vascular compliance of a global closed-loop model for the cardiovascular system by performing an infusion test of 500 mL of blood in four minutes. Our mathematical model includes a network of arteries and veins where blood flow is described by means of a one-dimensional nonlinear hyperbolic PDE system and zero-dimensional models for other cardiovascular compartments. Some mathematical modifications were introduced to better capture the physiology of the infusion test: (1) a physiological distribution of vascular compliance and total blood volume was implemented, (2) a nonlinear representation of venous resistances and compliances was introduced, and (3) main regulatory mechanisms triggered by the infusion test where incorporated into the model. By means of presented in silico experiment, we show that effective total vascular compliance is the result of the interaction between the assigned constant physical vascular compliance and the capacity of the cardiovascular system to adapt to new situations via regulatory mechanisms.
1. Introduction
The vascular compliance of the circulatory system is defined as the slope of the relationship between intravascular volume and circulatory filling pressure; this property reflects the inherent elasticity of the vascular system. Changes in vascular compliance are of primary importance in the control of cardiovascular function and extracellular fluid volume regulation [1]. In animals, an estimation of total vascular compliance can be obtained by determining Mean Circulatory Filling Pressure (MCFP)-blood volume curves. MCFP refers to the pressure, constant in all vascular districts, that can be obtained by stopping the heart and waiting for blood to redistribute in the vascular system according to the capacity of the different districts [2]. Compliance is thus defined as the change in blood volume divided by the change in MCFP, thus total vascular compliance (TVC) is
where V is total blood volume and is unstressed blood volume, i.e., the blood volume contained in the vascular system for zero MCFP. Different methods were used to evaluate the TVC in different animal species [2,3,4]; some of them imply stopping the circulation to measure MCFP, while others require the use of anesthesia and extensive surgery, as in the constant cardiac output reservoir technique [5,6], to determine compliance as the ratio of a change in volume to a change in venous pressure. However, the values for total vascular compliance are very close whatever the method adopted; in dogs, values from 1.4 to 4.2 mL/kg/mmHg were observed with an average of 2.57 mL/kg/mmHg [3,5,7,8].
Classical estimation of MCFP requires stopping systemic flow, posing ethical limitations to its application to humans. To avoid this methodological limitation, a different index of capacitance was introduced as a measure of total vascular compliance. This method was first presented in [9] and then used in [10,11,12,13,14,15,16,17]; it involves simultaneous recording of right atrial pressure and volume changes induced by transfusion, bleeding, or rapid iso-oncotic dextran infusion. Based on the experiment first presented in [9], London et al. [10] determined the total effective vascular compliance (TEVC) using an infusion of 500 mL of 6% dextran carried out within four minutes in a large forearm vein in control and hypertensive patients in supine position. Dextran is an osmotically neutral fluid that is used in intravenous solutions as volume expanders to replace lost blood in emergency situations; it is effective in expanding and maintaining the plasma volume. According to the authors of [18], total blood volume after dextran infusion increased only by the amount of solution administered. The slope of the relationship between central venous pressure (CVP) and blood volume was called TEVC in order to differentiate it from the compliance obtained from MCFP measurements [9]. CVP, usually considered as representative of the right atrial pressure, depends on the venous return and the pumping ability of the heart, thus it does not rely exclusively upon vascular volume and the elastic properties of the vascular bed [19]. Moreover, a four-minute long infusion is not rapid enough to prevent the participation of some regulatory mechanisms such as the short-term regulation of blood pressure, which occurs within seconds. Modification in CVP and also arterial pressure due to blood volume variations activates various reflexes that modify specific cardiovascular system properties like vascular compliance, vascular tone, heart rate, etc. [20]. In turn, such modifications influence the final CVP change for a given blood volume variation and thus the estimated TEVC [6,21]. Even if CVP is influenced by several factors during blood volume changes via transfusion or bleeding, Echt et al. [9] showed that the pressure–volume relationship is practically linear; in normal men, it ranges from 2.1 to 2.7 mL/kg. It was shown [6,22] that 1–3% of this value can be attributed to the compliance of arterial circulation, while approximately 20% of total vascular compliance represents compliance of the cardiopulmonary circulation [12].
In mathematical models of the human circulation, the vascular compliance, that is, the relationship between stressed volume and the transmural pressure of a vascular segment, is generally represented by either linear or nonlinear relationships that include physical parameters. The values assigned to these parameters are usually based on experimental evidence of effective compliance and blood volume distribution among different vascular compartments. For example, in the lumped model of the entire circulation proposed by Sun et al. [23], the elastance (the inverse of the compliance) and volume in each vascular territory were estimated from the blood volume distribution in [24]. Ursino et al. [25] proposed a model of the cardiovascular system represented as six lumped compartments arranged in series, which synthesizes the main hemodynamic properties of the systemic arterial, systemic venous, pulmonary arterial, and pulmonary venous, as well as of the left and right cardiac volumes. In that work, a total vascular compliance was assigned based on human and animal TEVC [26], and then this value was distributed among different compartments following literature data on blood flow distribution. Mynard and Smolich [27] adopted a vascular compliance of 170 mL/mmHg for the entire circulation, that was distributed in the following way: 1.7 mL/mmHg in the arterial circulation, following [28], 146 mL/mmHg in the venous circulation, based on [29], and 6.7 and 15.8 mL/mmHg in the arterial and venous pulmonary circulation respectively. The same was done in the previous version of the global mathematical model adopted here [30]. As we can see in these works, mathematical modelers set the total vascular compliance equal to a parameter. However, this parameter value is usually based on the index of TEVC that is the result of an experiment wherein the elastic properties of the vascular system interact with the pumping ability of the heart and the reflex control of blood pressure. This choice is necessary to represent the vascular capacity, that is the amount of blood held by the systemic vascular bed at a specific pressure. However, this assumption could lead to inappropriate results, especially if we move from the baseline status, i.e., the model state for which the model was parametrized and validated.
The aim of this mathematical work was to determine in silico the effective total vascular compliance of a global mathematical model for the cardiovascular system. To this end, we reproduced the experiment of London et al. [10]. Changes in blood volume and changes in central venous pressure were recorded during the infusion. The model used for this kind of test is based on the works in [30,31,32]. It is composed of networks of major arteries and veins where blood flow is described by means of a mathematical model consisting of a nonlinear hyperbolic PDE system. This system can be derived assuming axial symmetry of flow [33] or using a more general framework based on mass and momentum balance, as well as a specialized version of Reynolds transport theorem, as proposed in [34]. Other cardiovascular compartments, i.e., heart, pulmonary circulation, microvasculature, venous valves, Starling resistors and cerebrospinal fluid dynamics, are described by lumped parameter models. A high-order well-balanced nonlinear numerical scheme based on the ADER [35] (Arbitrary high-order DERivatives) framework was used for discretization of one-dimensional blood flow equations. Compared to previous versions of the mathematical model, some changes were introduced to better capture the main physiological processes involved in the infusion test as well as to update modeling assumptions that needed to be improved in order to consider a deviation from the baseline state. First of all, we performed a physiologically sound parametrization of the mathematical model in the baseline pre-infusion status: this required the introduction of the unstressed volume in all vascular compartments. Assuming that each vascular compartment has an average pressure, a value of compliance was assigned such that the stressed volume together with the unstressed volume gave the desired total blood volume. As the major part of total blood volume is located in the lumped-parameters model of the venules/distal veins, nonlinear resistances and compliances were introduced in the venous 0D compartments to take into account the distension of the vasculature during volume expansion. Moreover, the global mathematical model of the circulation was coupled to a model for short-term regulation of pressure that considers the activity of high- and low-pressure baroreceptors. Such activity was represented by sigmoid functions, featuring a symmetric response to low/high arterial and/or venous pressure deviations from baseline values, that generate efferent sympathetic and parasympathetic firing rates. Results reported here show that a good parametrization of the vascular compliance and blood volume of the human body gives a reasonable representation of the vascular capacity in the baseline setting. However, when total blood volume is changed with the infusion test, this parametrization becomes necessary but not sufficient for reproducing the effective behaviour of the human circulation. The main short-term regulatory mechanisms of arterial pressure play an essential role in the capacity of the model to correctly describe experimental results. In fact, TEVC reflects the interaction between the assigned parameters but also the functioning of the regulatory mechanisms.
The rest of the paper is structured as follows. In Section 2, we present the global closed-loop mathematical model of the human circulation and the modifications introduced in this work as well as the baroreflex control mechanism. Section 3 presents the main results about the infusion test; the evaluation of the TEVC; and how mean arterial pressure, cardiac output, heart rate, and cardiopulmonary blood volume change during the blood volume expansion; moreover, a discussion on the modeling choices and the main outcomes is provided. Section 4 summarizes the main findings and poses some directions for further investigations.
2. Materials and Methods
In this section, we briefly describe the closed-loop model of the cardiovascular system used in this work, focusing on the main improvements with respect to previous versions of the model. These include the parametrization of the global model with the introduction of total blood volume and the nonlinear relationship in venous resistances and compliances. Moreover, we present the equations that describe the functioning of baroreflex control mechanisms considered in our work and how we performed the infusion test reported in [10].
2.1. A Global Closed-Loop Model for the Human Circulation
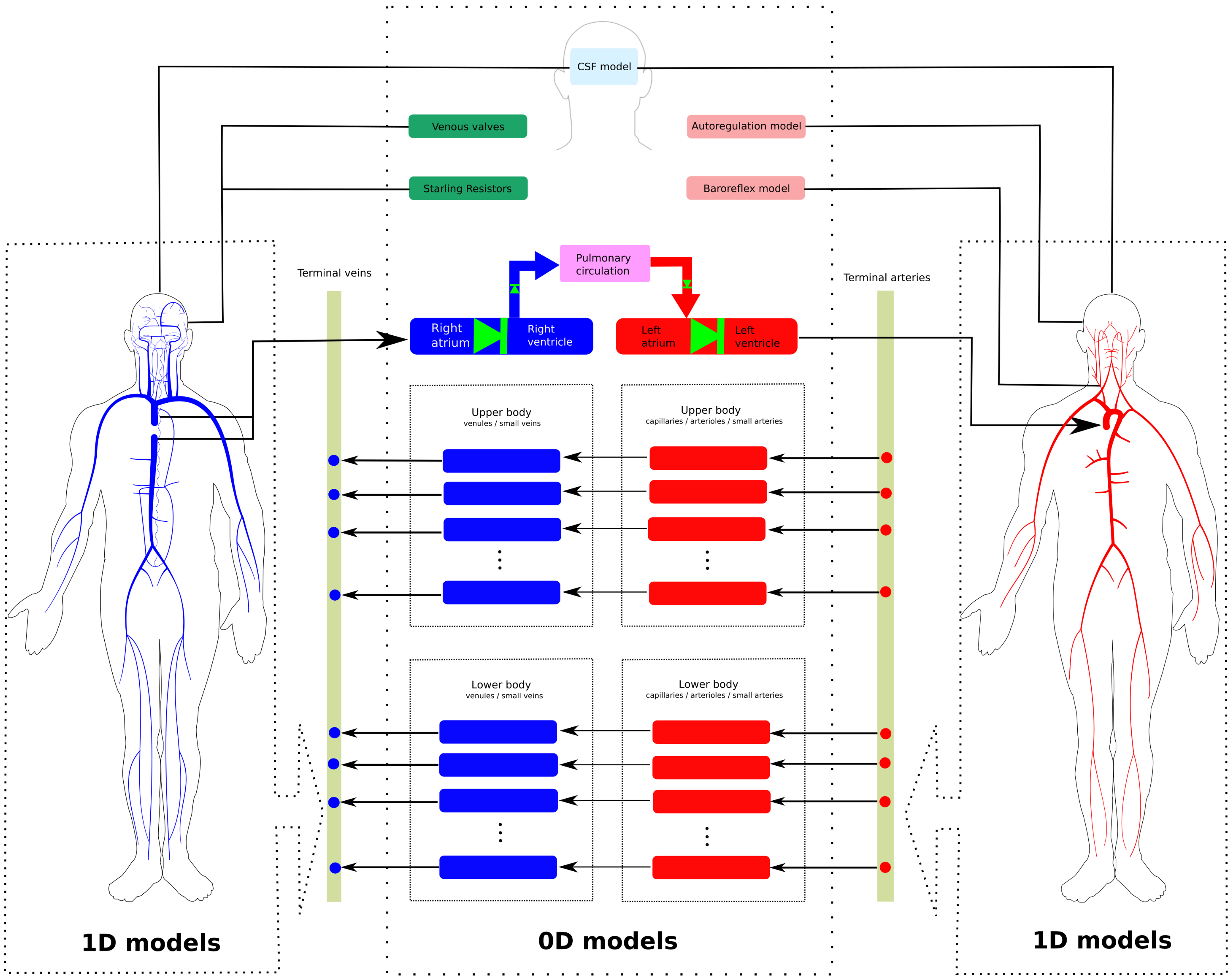
The mathematical model used in this work is an extension of the closed-loop model for the entire human circulation presented in [31,32]. It is a geometric multi-scale type model which includes one-dimensional models for blood flow in major vessels and zero-dimensional lumped-parameters models describing blood flow in the remaining compartments. Figure 1 illustrates schematically the structure of the model: it includes 323 vessels, comprising arteries and veins; four heart chambers and cardiac valves; 3 compartments for the pulmonary circulation; 31 compartmental models describing the connections between terminal arteries and veins through the microcirculation; 17 venous valves; 21 Starling resistors; and one cerebrospinal fluid compartment.
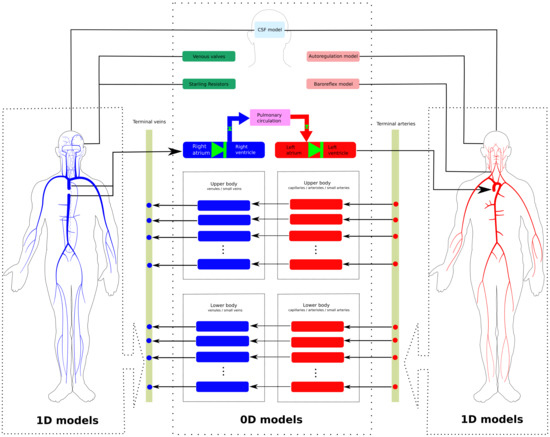
Figure 1.
Schematic representation of the global model used in this work [30]. 1D models refer to networks of major arteries and veins, which are modeled using evolutionary partial differential equations, providing space- and time-resolved blood pressure and flow. Rectangles represent lumped-parameter models, which are used to describe the heart chambers, the pulmonary circulation, the microcirculation, as well as brain and CSF dynamics. Such compartments are modeled using ordinary differential equations, which provide time-resolved hemodynamic variables.
Blood flow in major vessels—arteries and veins—was modeled using a 1D system of partial differential equations. A complete derivation of the governing equations can be found in [36], where such equations were derived from conservation principles. A vessel is represented as a single compliant rectilinear tube with impermeable walls. Moreover, blood is assumed to be an incompressible Newtonian fluid. The resulting system of equations is given by
The first equation represents the conservation of mass in the flexible tube, while the second one describes momentum balance. The three unknowns of the problem are the cross-sectional area of the vessel’s lumen, ; the blood flow rate across a section of the vessel, ; and the cross-sectionally averaged internal pressure, . is the Coriolis coefficient linked to the velocity profile, here taken equal to 1 to represent a flat velocity profile, is the blood density, and f is the friction force per unit length of the tube. The problem has more unknowns than equations, thus an extra closure condition is required. This condition couples the internal blood flow distribution with the mechanical properties of the solid moving vessel wall. We adopted a pressure-area relation which describes the viscoelastic nature of vessels wall
In this tube law, the internal pressure is expressed as a function of the cross-sectional area and other parameters. The first part of the tube law represents the elastic behaviour of the vessel wall. It depends on , the vessel cross-sectional area for which the transmural pressure () is zero. The parameters m and n are two real numbers that can be derived from experimental measurements; throughout this work, we assume and for arteries, while we assume and for veins. Moreover, is a positive function representing the vessel stiffness, which accounts for mechanical and geometrical properties of the vessel; in this work, was obtained from the reference wave speed assumed for each vessel, distinguishing arteries, veins, and dural sinuses [30]. is the reference pressure while is the external pressure, generally prescribed. The second term of the tube law describes the viscoelastic nature of vessel walls; it depends on the time partial derivative of the cross-sectional area of the vessel and on , a constant related to the viscoelastic properties of the vessel wall and expressed, following the work in [37], as
where is the wall viscosity and is the wall thickness. The value of these parameters are chosen such that the hysteresis behaviour of pressure-area plots in peripheral arteries and veins reproduces the physiological behaviour. We refer the reader to [30] for more details about the chosen parameters of the viscoelastic term in the tube law.
The friction term on the right hand side, which depends on the local velocity profile, is set as follows
with being the blood dynamic viscosity. This formulation is obtained by assuming a fully developed laminar flow in an axially symmetric tube.
Note that , , and are variable material and geometrical parameters that depend on x. To deal with parameters that vary in space, the system in
(2) is rewritten as in Toro and Siviglia [38,39], obtaining a first-order system whose vector of unknowns is . When the tube law in Equation (3) is inserted in the momentum balance equation in system (2), the problem becomes an advection-diffusion-reaction problem as a second-order spatial derivative of the flow variable arises. Using a relaxation technique [40], one can obtain a nonlinear hyperbolic PDE system that is solved using a high-order well-balanced nonlinear numerical scheme based on ADER [35] (Arbitrary high-order DERivatives) framework for networks of elastic and viscoelastic vessels [41,42] and an explicit local time-stepping temporal discretization (LTS) approach [43]. We refer the reader to the works in [35,44] for an up-to-date review of the ADER scheme, to the works in [45,46] for full details about the high-order well-balanced scheme in the framework of path-conservative schemes, to the works in [41,42,47] for clarification about the hyperbolic reformulation of the parabolic system incorporating the viscoelastic nature of the vessel wall mechanics, and finally to the works in [43,48] for the local time-stepping procedure which is implemented so that the local time step is defined at the level of the vessels (and not computational cells).
Lumped-parameter models for the microcirculation describe the connection between arteries and veins through arterioles, capillaries, and venules; the generic vascular bed model used for all microvasculature beds is based on the three-element Windkessel model. This model is characterized by
- characteristic impedances that couple any number of connecting 1D arteries/veins to lumped-parameter models for the microvasculature ( or ) and regulate the pressure drop between 1D domains and vascular beds,
- peripheral resistances and compliances divided between arterioles and capillaries , and
- venous compartments with related compliances (), which represent venules and distal veins not included in the 1D network.
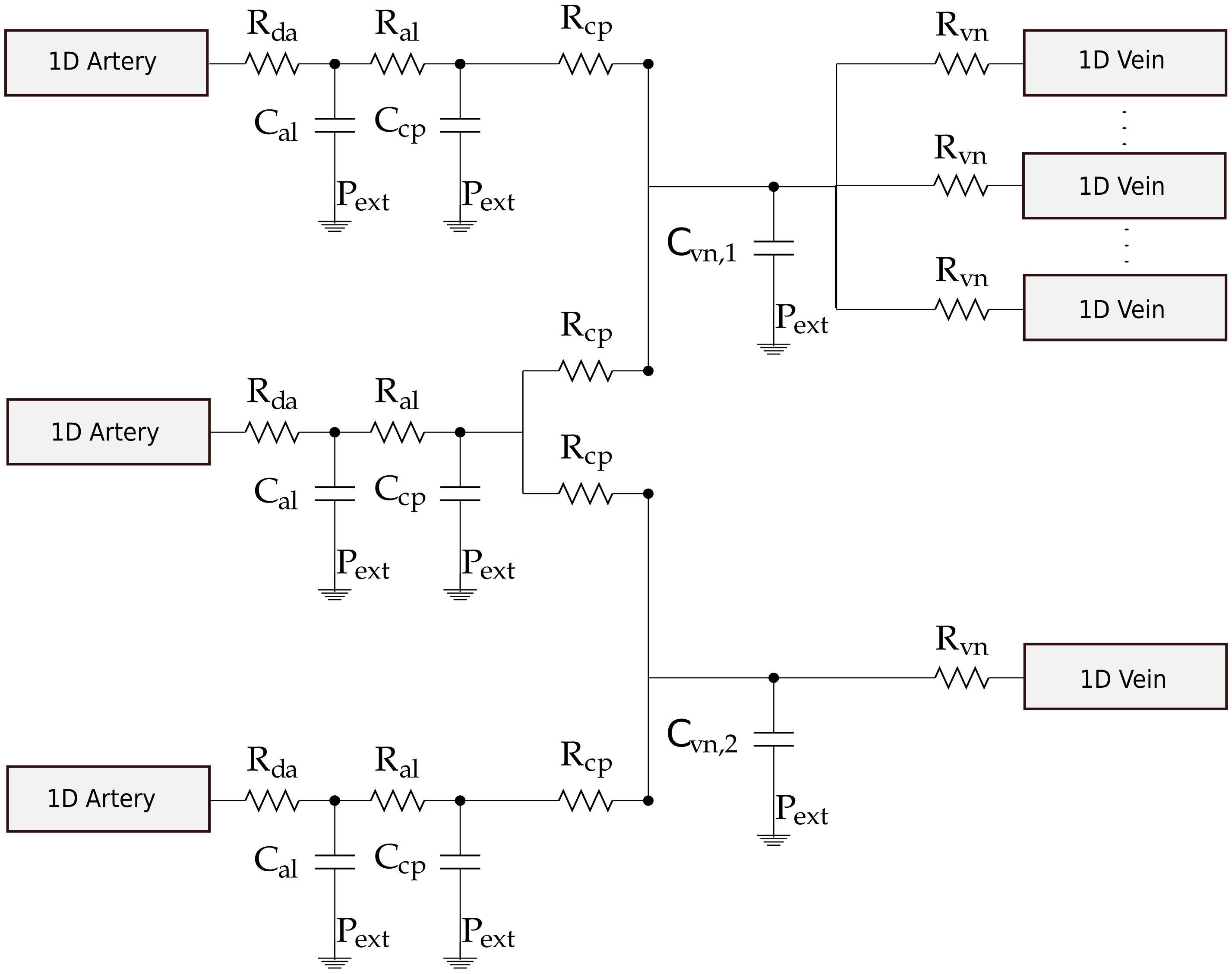
Figure 2 shows an example of a generic terminal vascular beds connecting three 1D arteries and multiple 1D veins.
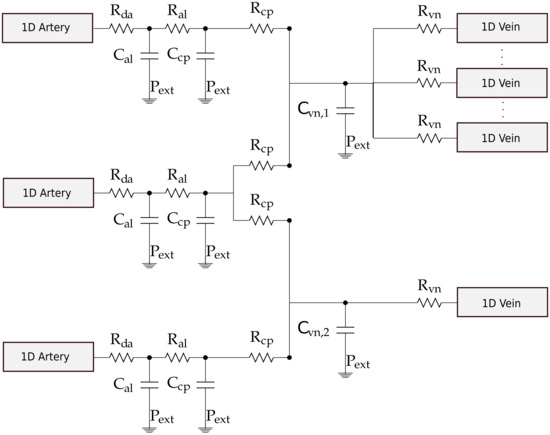
Figure 2.
Example of a generic complex vascular bed connecting three 1D arteries to multiple 1D veins [30]. Each connecting artery can be linked to one or both venous capacitors , while each venous capacitor can be connected to any number of terminal veins. Each 1D artery is connected to arterioles compartments , that in turn is connected to either one or two capillaries compartments . The pressure drop between 1D arteries and the vascular beds is regulated by while on the venous side by .
The heart model considers the “time-varying elastance” model [23,49] to describe the dynamics of relaxation/contraction of the four cardiac chambers, while cardiac valves were modeled as in [50]. For each heart chamber, the time-varying elastance is defined by
where and are respectively the maximal elastance at systole and the baseline elastance, while is the normalized time-varying elastance taken as in [23].
The pulmonary circulation is divided into arteries, capillaries, and veins, and it was modeled as in [23]; each compartment is characterized by a pulmonary resistance and a pulmonary inertance that are used for the evolution of the fluid exchange between compartments and by an exponential pressure–volume relationship describing vascular capacitance. Venous circulation was equipped by venous valves which governs the flow across the interface between two vessels. Starling resistors were placed at the confluence of cortical veins in the dural sinuses; they prevent the vein collapse maintaining the blood pressure upstream the collapsed segment higher than the intracranial pressure. Both venous valves and Starling resistors were represented by the model presented in [50]. Finally, the blood circulation model was coupled to a simple cerebrospinal fluid model. This model, based on the works in [32,51], is characterized by a simple compartment representing the cranial and spinal cavity with elastic behaviour. An ordinary differential equation which depends on cerebral blood volume (cerebral arteries, arterioles, capillaries, venules, and veins), capillaries, and superior sagittal sinus pressures was used for the evaluation of the intracranial pressure that was then adopted as external pressure in cerebral 1D vessels and lumped-parameters compartments.
The parameters needed for the implementation of the global closed-loop model were defined in order to simulate a young healthy subject. Unless specified otherwise in this work, the parametrization is the same as the one reported in [30]. We refer the reader to the works in [30,31,32] for more details about the model description, parameter selection, and validation of the baseline state.
2.2. Compliances, Unstressed Volumes, and Total Blood Volume Distribution
As in this work we would like to describe a change in blood volume through an infusion test, we first defined basal parameters describing total blood volume and total vascular compliance. Following the work in [14], the total vascular compliance is ∼2.1 mL/mmHg/kg for humans; ∼70% of this value may characterize the systemic circulation, while the remaining part is ascribed to the pulmonary circulation [20]. Moreover, the systemic vascular compliance may be divided between systemic arterial and venous compliances, assuming that ∼3% of the systemic compliance is in the arterial side [5]. For the pulmonary circulation, few data are available about the distinction between arterial and venous compliances; we considered here that 20% of total pulmonary compliance is in the arterial side, as in [25]. Table 1 reports the compliance value for each vascular territory. As in [30], arterial and venous compliance were distributed in 1D vessels following the work in [49]. Moreover, after determination of 1D vessel vascular compliance, the remaining part of the arterial compliance was distributed among in arterioles according to [49] and 15% of the arterioles compliance was assigned to the capillaries (see Figure 2). The remaining part of the venous compliance was assigned to venule compartments according to blood flow distribution. For the heart circulation, atria and ventricular baseline elastances were set as in previous works [30].

Table 1.
Basal value for model parameters of compliance and unstressed volume in the main vascular compartments.
Total blood volume was reported to be in the range of 75 to 80 mL/kg body weight for a normal male subject [52,53]. Stressed volume is usually approximately 30–40% of total volume [54,55]. The unstressed volume is the volume in a compartment when the transmural pressure is equal to zero. In previous version of the model [30,31,32], only the stressed component of the total blood volume was considered in lumped-parameters models of the microcirculation, heart, and pulmonary circulation. We added here the unstressed part in order to have complete control on total blood volume.
Using assigned compliances as in Table 1 and pressures as in previous works [30], we set for each vascular territories the amount of unstressed volume such that the total blood volume distribution among different vascular compartments follows those reported in the literature. For the heart circulation, we fixed 50 mL of unstressed volume (one sixth of the cardiac blood volume), 20 mL for each atrium, and 5 mL in each ventricle, as suggested in [25,56]. In the pulmonary circulation, we set 70 mL of unstressed volume, divided between arteries and capillaries, and 490 mL of unstressed volume in venous compartment [56]. Concerning the systemic circulation, we considered 715 mL of arterial unstressed volume, distributed between 1D arteries and arterioles, and 2500 mL of venous unstressed blood that was assigned to capillaries, venules, and 1D veins [56]. In the arterial part, we evaluated the unstressed volume of 1D arteries as the volume in each vessel at zero-transmural pressure according to tube law in Equation (3), and then subtracted it to the total amount of arterial unstressed volume; the remaining part was distributed between arterioles compartments of vascular beds according to flow distribution in venous capacitors (, see Figure 2). The same was done for the venous circulation; after subtracting 1D venous unstressed volume from total venous unstressed volume, the remaining part was distributed between capillaries (15%) and venules (85%) following the flow distribution in venous capacitors. Table 1 summarizes the assigned compliances and unstressed volume distribution.
2.3. Nonlinear Venous Resistances and Compliances
In order to take into account the distension of the vasculature during the infusion test, we modified the resistances that characterize the venous vascular beds in a nonlinear manner according to blood volume variation. The resistances that are located between capillaries and venules compartments and the characteristic impedances that couple 1D veins to venules compartment ( and , see Figure 2) in the vascular beds were modified at each time step according to the following relationship:
where stands for or at time t, is the corresponding reference resistance in the baseline condition, is the current volume in the capacitor, and is the reference volume of the venous capacitor at the baseline condition.
In order to account for the nonlinear pressure–volume relation of the venous system during the blood infusion test, we applied a nonlinear pressure–volume relation to zero-dimensional venules compartments. The equation describing this behaviour is the following:
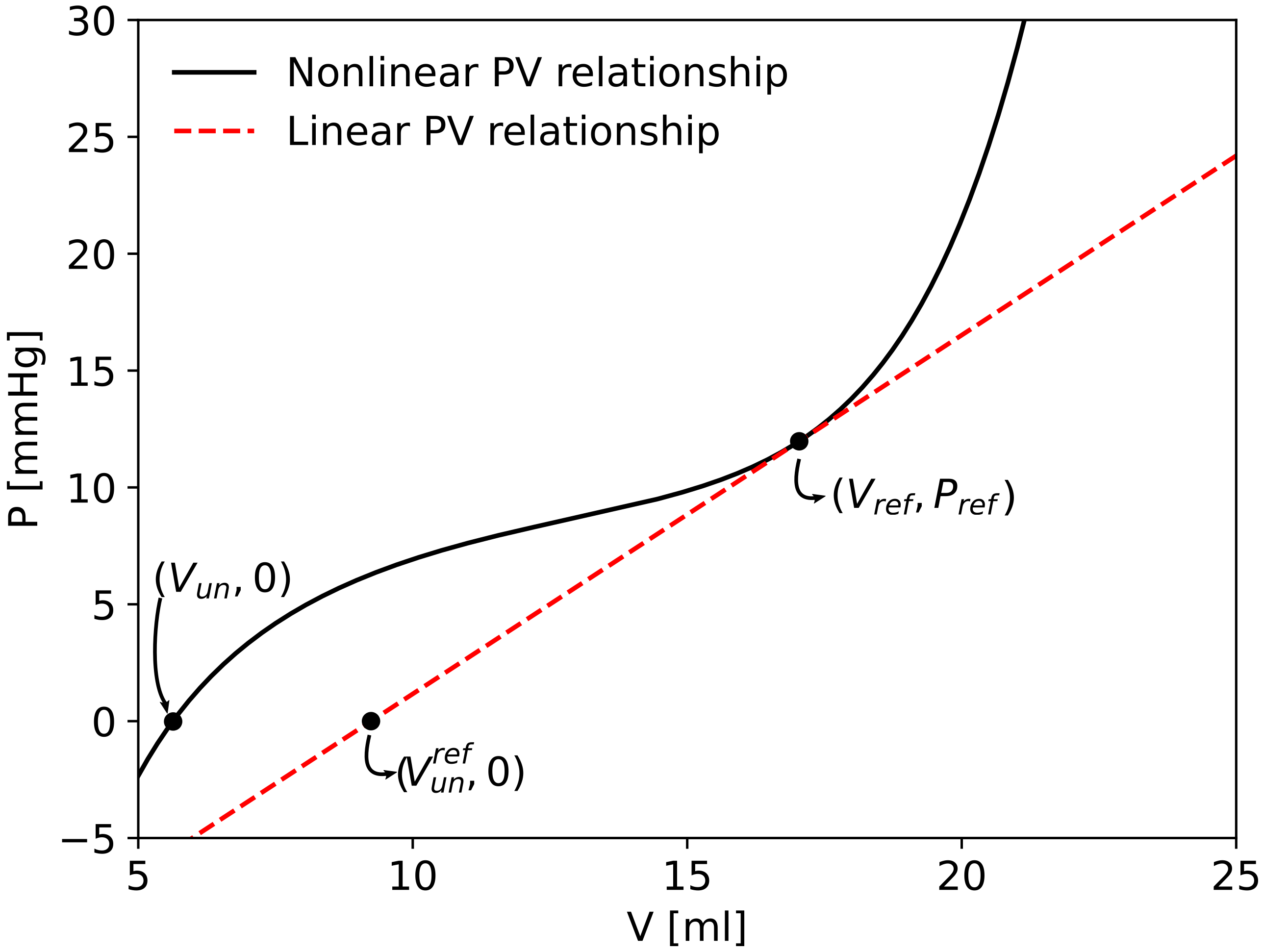
where m and n are set to be 10 and −3/2, respectively, as it is usually done for 1D veins. and constitute the basal point of the pressure-volume relationship with the basal value of compliance as in the linear case. The value of the parameter K is assigned by imposing the passage of the curve through and , that is, . Given this nonlinear pressure–volume relationship, the unstressed volume in the venules compartments was modified imposing zero transmural pressure in Equation (8). Figure 3 compares the linear and nonlinear pressure-volume relation of one venule compartment of the right forearm. As a result of this parametrization procedure we recover the linear compliance case if we set and .
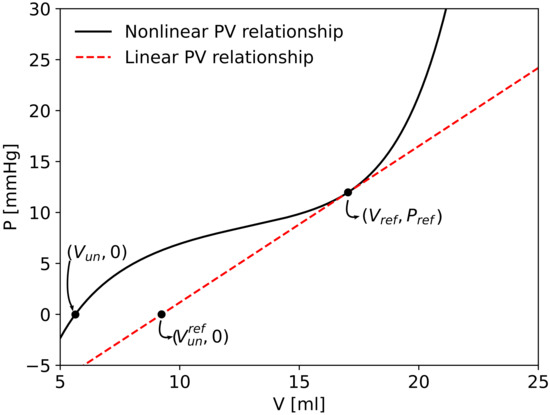
Figure 3.
Comparison between linear and nonlinear pressure–volume relationship in one venule/vein compartment of the right forearm. is the basal point of the pressure-volume relationship with linear basal value of compliance and reference unstressed volume . Following the nonlinear pressure–volume relationship, the unstressed volume was calculated imposing zero transmural pressure.
2.4. The Baroreflex Regulation
The baroreflex model adopted in this work is based on [57,58,59]. It includes the activity of high- and low-pressure receptors. The set of parameters undergoing regulation is = { H, E, R, C, V}, where H is the heart rate, E is the maximum value of elastance of the four cardiac chambers, R is the arterial resistance, and C and V are the venous compliance and unstressed volume (i.e., the venous tone). In our closed-loop model, R refers to the proximal resistance of 1D terminal arteries and to the resistance of arteriolar compartment of vascular beds for all vascular districts, except for the brain, which is directly regulated by cerebral autoregulation with the model presented in [30]. C and V refers to compliance and unstressed volume of venules compartment of non-intracranial vascular beds and 1D veins; changes in compliance and unstressed volume of 1D veins are reflected in variation of reference area and stiffness K of these vessels, as explained later at the end of this section.
The arterial baroreflex is activated by the mean arterial pressure (over a cardiac cycle) in the aortic arch and in both carotid arteries. We assumed that the receptors located in all these arteries behave in the same manner [58]. The low-pressure baroreceptors are activated by the right atrial pressure. The level of activation of the afferent nervous system is evaluated as
where , , , and are the mean pressure over the previous cardiac cycle of right carotid artery, left carotid artery, aortic arch, and right atrium, respectively.
Alterations in the arterial pressure and/or in the venous pressure affect the firing rates of afferent fibers. These fibers reach the central nervous system which in turn generates efferent sympathetic and parasympathetic nerve activity. An enhanced firing rate results in an enhanced parasympathetic response and a reduced sympathetic activity. It was experimentally proved in vagotomized animals that the efferent responses in heart rate and arterial resistances follow a sigmoid relationship. For this reason, the sympathetic and parasympathetic firing rates are modeled via sigmoid functions that depend on arterial and venous pressure changes [57,58,59]. The sympathetic and parasympathetic activity are described by the following expressions:
where is a linear combination of pressure changes
and the index i ranges the set . and are the baseline arterial and venous activation, respectively. The values of the sympathetic and parasympathetic responses range between 0 and 1; when is equal to 0, i.e., when the model is operating in the baseline setting with and , both and assume the value 0.5. approaches 1 when is less than 0 while it tends to 0 when is larger than 1; this implies that the sympathetic nerve activity is reduced when the relative change of arterial and/or venous pressure from the baseline values increases. By contrast, the parasympathetic response assumes its maximum value 1 when tends to infinity. and are the maximum open loop gains of the arterial and cardiopulmonary baroreceptor mechanisms, each evaluated when the other mechanism is not operating. is set equal to zero for all variables in , expect for R and V, on which both arterial and low-pressure baroreceptors work in synergism; in this case, the total open loop gain results from a nonlinear superimposition of the action of the two classes of receptors [59]. Finally, is a parameter which determines the slope of the sigmoidal characteristic at its central point, chosen to be equal to −1 as in [59]. The efferent responses are governed by first order ordinary differential equations. These equations read as
where
is the characteristic time constant, while , , and are defined using physiologically admissible threshold values. Table 2 reports parameters for the baroreflex model, which were taken from [57,58,59]. Following the works in [57,58], a symmetric response to deviations was assumed by setting minimum and maximum threshold values at equal distance from the central point of the sigmoid function.

Table 2.
Parameters for the efferent pathways of the baroreceptors and for the arterial and venous gain in Equation (15) for all .
The baroreflex regulation changes venous compliance and unstressed volume; in order to maintain constant total blood volume, we reset the venous pressure in 0D venules compartments modifying the reference pressure in Equation (8), according to the modified compliance and unstressed volume given by the baroreflex model. The same is done in one-dimensional veins. The venous pressure is reset by changing reference area and stiffness of 1D veins. In each computational cell of a vein, given and the unstressed area and compliance determined by the baroreflex regulation, the modified reference area and vessel stiffness are evaluated solving the following nonlinear system:
where
The first equation of system (16) is derived from the definition of unstressed area, that is, the area for which the transmural pressure is equal to zero; the second equation relies upon the definition of compliance in a one-dimensional vessel, that is the integral average over the length of the domain of the inverse of the pressure changes with respect to area variation, when area is the reference area of the vessel.
2.5. Determination of Total Effective Compliance
The TEVC of the above-described computational model was computed by reproducing in silico the experiment reported in [10]. A 500 mL blood infusion in four minutes was simulated adding a flow source at the level of the left atrium, starting from a periodic solution in the baseline setting. In all the simulations, the infusion started at 80 s and ended at 320 s; after the expansion, the new periodic state was reached in 40 s and the simulations were stopped at 400 s. Main cardiovascular indexes were recorded after completion of the infusion’s generated transient, i.e., after a periodic state was reached for the new situation with increased blood volume. During the simulated infusion test, the mean central venous pressure (right atrial pressure) over a cardiac cycle was plotted against changes in total blood volume. The effective compliance was evaluated in the following three scenarios:
- (1)
- Linear case: linear resistances and compliances in 0D venous compartments were applied. The use of linear resistances implies that in Equation (7) during the entire simulation. With linear compliance, pressure in 0D venules compartments is evaluated with and in Equation (8); this is equivalent towhere is the unstressed volume of the linear pressure–volume relationship (see Figure 3) and is the basal value of compliance in Equation (8).
- (2)
- (3)
- Baroreflex case: in this case, the model presented in Section 2.4 was applied with parameters of Table 2 in conjunction with nonlinear resistances and compliances in venules/distal veins compartments.
The numerical results were compared to experimental results reported in [10].
3. Discussion
3.1. Control of Vascular Blood Volume
The mathematical model adopted in this paper departs from the Müller–Toro mathematical model [30,31,32] for the systemic and pulmonary circulations in the entire human body. In previous versions of the model, the unstressed component of blood volume was included only in vessels described by one-dimensional models according to the nonlinear relationship between area and pressure described by the tube law in Equation (3). By contrast, in the models for heart, pulmonary circulation, and microvasculature, only the stressed component (that determines flow in the circulation) of blood volume was considered. While this modeling assumption was sufficient in previous applications of the model, in this case a complete control of the total blood volume in the circulation became necessary as we were interested in the total capacitance of the vascular system and the short-term cardiovascular homeostasis. The introduction of the unstressed volumes was generally adopted in fully lumped-parameters models of the circulation [25,60,61,62]. This is the first global model with one-dimensional representation of major arteries and veins with total control of blood volume. The presence of the unstressed volumes in the venous part of the circulation is of primary importance when the baroreflex control of the arterial pressure is considered.
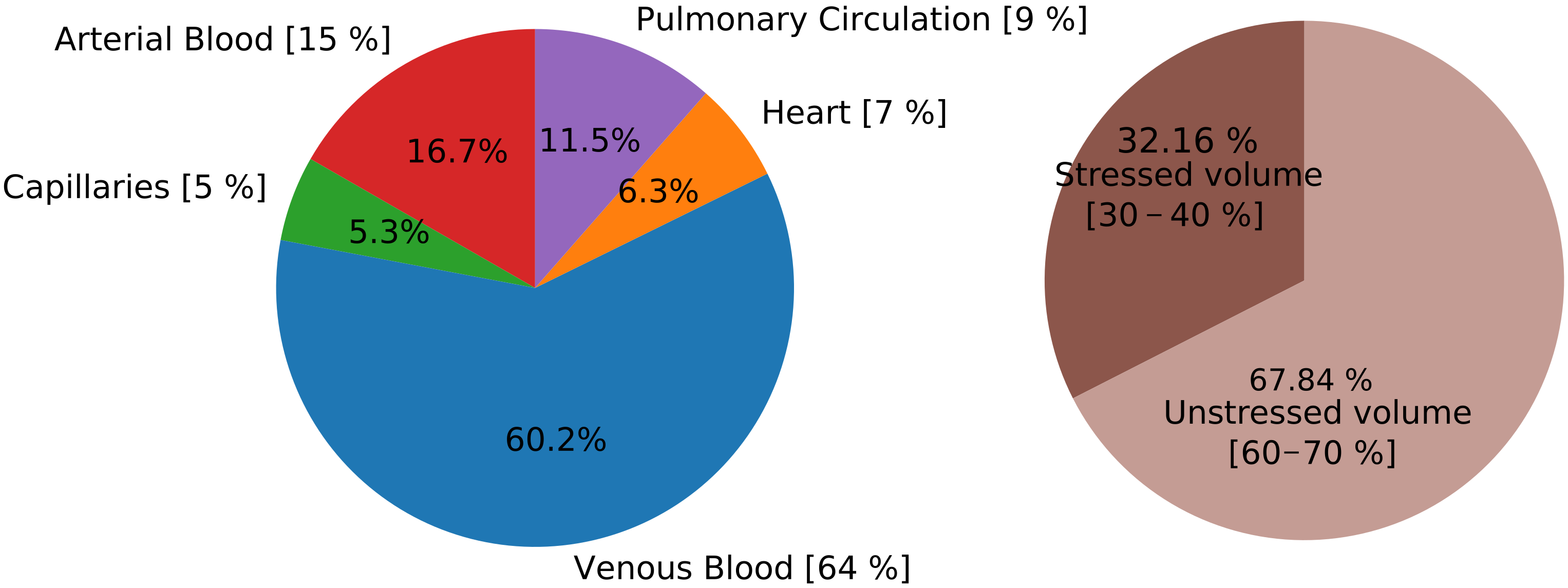
Vascular compliance (for the evaluation of the stressed volumes) and unstressed volume for each vascular territory had to be assigned for the determination of the capacitance of the vascular system. The mathematical model proposed here was parametrized with values of compliances and unstressed volumes based on literature data for humans and animals, as described in Section 2.2. Total blood volume was set to 5520 mL, of which about 70% is unstressed blood volume (3745 mL). Figure 4 shows the total blood volume distribution in different vascular territories; this distribution agrees with literature observations [24,63]. The same happens for the main cardiovascular indexes and the pressures of different vascular compartments. Table 3 reports main cardiovascular indexes computed on model results and general literature data, as well as London et al. [10]. The first part of the table refers to variables of the systemic circulation, mean arterial pressure, pulse pressure, cardiac output, and central venous pressure. Arterial compliance was evaluated as the ratio between stroke volume and brachial pulse pressure, as routinely performed in clinical practice [28]. We can observe that even if the arterial compliance parameter is assigned to be 4 mL/mmHg (Table 1), the effective value of the arterial compliance evaluated as proposed in [28] is in the physiological range. The second part of Table 3 shows the main cardiac indexes, heart rate, arterial elastance, left ventricle elastance, arterial–ventricular coupling index, maximum left ventricular volume, and minimum pressure rate of left ventricle. The computed values are in line with literature observations and the model is able to represent a normal functioning heart.
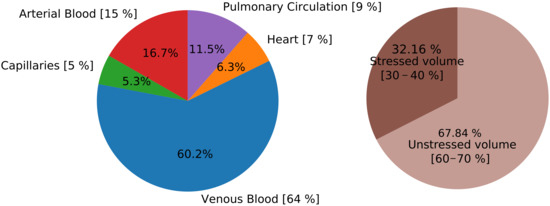
Figure 4.
Total blood volume distribution. In the left pie chart, distribution among different vascular compartments, while in the right frame distribution between stressed and unstressed volume. In square brackets, reference blood volume distribution [24]. Total blood volume is set to be 5520 mL. Arterial blood: 1D arteries and arterioles; Venous Blood: 1D veins and venules; Heart: sum of volume of the four cardiac chambers; Pulmonary circulation: arterial, capillaries and venous blood of pulmonary compartments.

Table 3.
Cardiovascular indexes. Current Value: computed numerical value; Ref. Value: literature reference value with mean and standard deviation. (S/D)BP: systolic/diastolic aortic blood pressure; MBP: mean blood pressure; PP: pulse pressure in aortic root and in brachial artery; PP: ratio between pulse pressure in brachial artery and aortic root; CO: cardiac output; C: arterial compliance evaluated as the ratio between stroke volume and brachial pulse pressure [28]; CVP: central venous pressure; H: heart rate; E: arterial elastance; E: left ventricle elastance; E/E: arterial-ventricular coupling index; LV: maximum left ventricle volume; LV: averaged left ventricle volume; max. : maximum pressure rate of left ventricle; min. : minimum pressure rate of left ventricle.
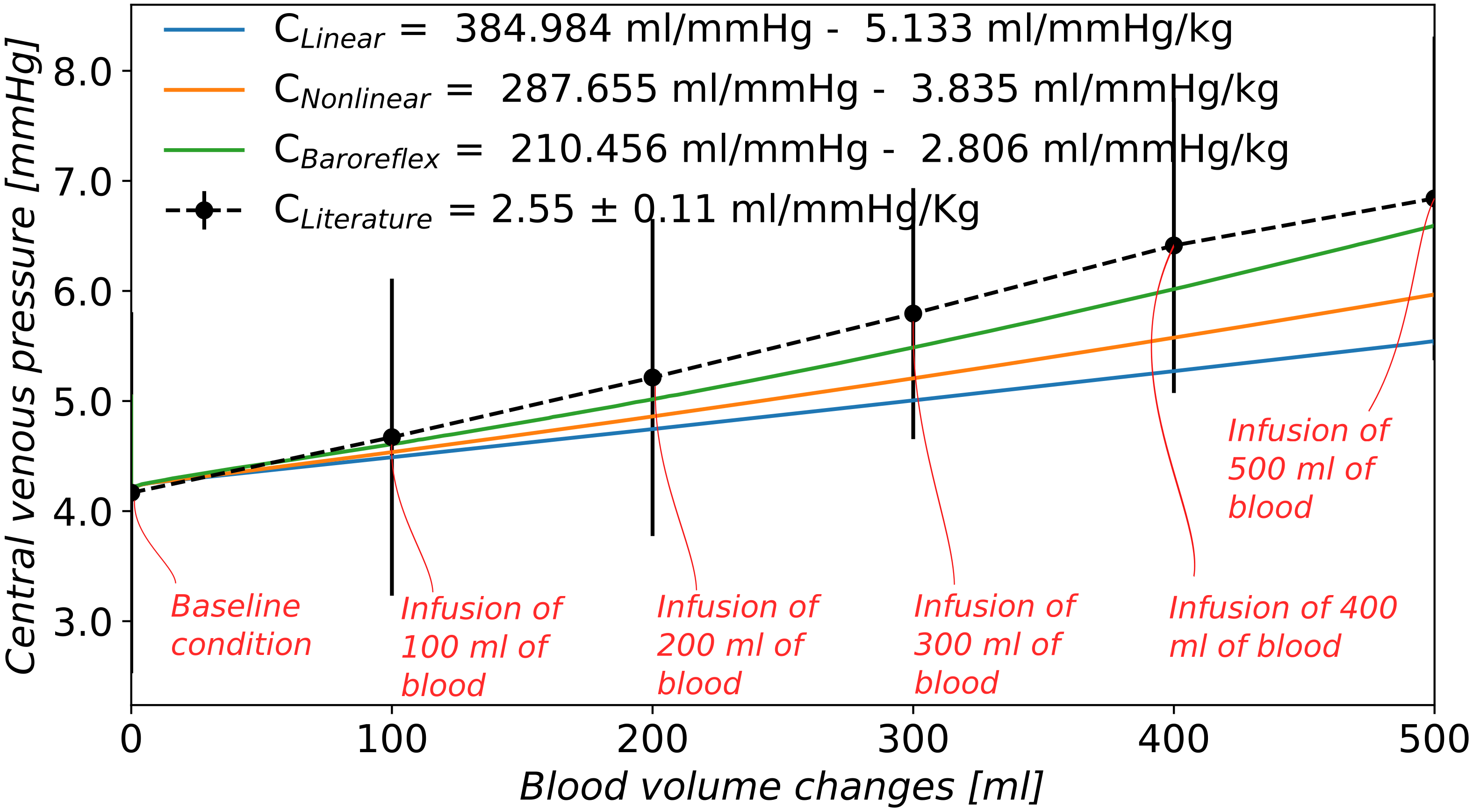
Figure 5 shows the relationship between changes in blood volume and changes in central venous pressure for the three scenarios considered here, as well as experimental results reported by London et al. [10]. As in the literature, this relationship is practically linear. The value of TEVC is expressed in brackets in mL/mmHg and then normalized to the body weight, considered to be 75 kg. Even if the physical parametrization of the model concerning compliance distribution and total blood volume was assigned following physiological measurements based on the literature, the TEVC of the computational model is not comparable to literature data if one considers the model setup with linear venule resistance and compliance and no baroreflex (Figure 5): 5.13 mL/mmHg compared to 2.55 ± 0.11 mL/mmHg in [10], 2.7 in [15], and 2.3 in [9]. A reasonable value of TEVC can be reached changing the physical parameter for the venous compliance. According to sensitivity analysis not reported here, venous compliance and unstressed volume are the main determinants of the TEVC of the global model in case of linear resistances and compliances and without regulation; variations in these parameters could improve the effective behaviour of the mathematical model. Reducing the compliance of the systemic venous circulation from mL/mmHg to mL/mmHg and the total blood volume to 4800 mL, the resulting TEVC was 2.7 mL/mmHg when we considered linear resistances and compliances in the venous lumped parameters compartments and we neglected the autonomic nervous system control by the baroreceptors. In this case, the capacitance of the vascular system was changed by modified venous compliance, i.e., stressed volume, without changes in unstressed volume. With this setting, the unstressed volume was 78% of total blood volume, while the blood distribution between vascular compartments was the following: 19.3% of arterial blood, 6.1% of blood in capillaries, 53.7% of venous blood, 7.3% of blood in cardiac circulation, and 13.2% in lungs. In the baseline condition, the mean arterial pressure and cardiac output were 92.53 mmHg and 90.87 mL/s, respectively, while the baseline central venous pressure was 4.28 mmHg. We observed that this parametrization led to a physiological status of the mathematical model in the baseline setting, and the numerical effective compliance was comparable to the literature. However, the changes in main cardiovascular indexes during the infusion were unreasonable: the mean arterial pressure and the cardiac output increased by more than 35% and the cardiopulmonary blood volume changed by 25%. Even if the baroreflex control was activated, the authors did not find physiological parameters for the baroreflex model that were able to control the main cardiovascular indexes as in [10]. These observations highlight the importance of including both, realistic physical parameters, appropriate mathematical models for physical processes and relevant physiological processes regarding the adaptation of the cardiovascular system to deviations from baseline conditions. These elements are essential in order to reproduce experimental observations that imply large deviations of the model with respect to the baseline condition for which the model was parametrized (and/or conceived).
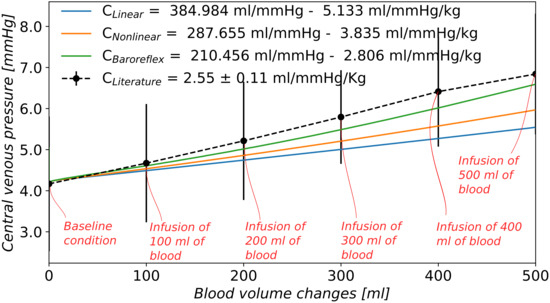
Figure 5.
Computed TEVC by means of an infusion test of 500 mL of blood in 4 min. Changes in mean central venous pressure are plotted against changes in total blood volume and the inverse of the slope of their linear relationship is the value of the effective compliance. : linear relationship for resistances and compliances in venules compartments; : nonlinear resistances and compliances in venules compartments; : nonlinear resistances and compliances and baroreflex control; : London et al. [10] experimental results on 9 controls subjects (mean value of the group and ± 1 standard deviation).
3.2. Nonlinearities in Venous Compartments
Another modeling improvement of this work regards the introduction of nonlinear equations for the determination of venous resistances and compliances. As shown in Figure 5, when linear venous compliances and constant resistances were considered, the computed TEVC was higher with respect to experimentally measured compliance. During the infusion test, the central venous pressure evaluated in the right atrium increased by 1.3 mmHg, while in terminal veins and venules compartments, the change in venous pressure was twice the one observed in central veins. Echt et al. [9] evaluated changes in central and peripheral venous pressures during infusion of 500 mL of 6% dextran solution within 3 min. The central venous pressure was recorded in the right atrium while the peripheral pressure was measured in a vein in the distal third of the left forearm. The central venous pressure rose from 6.6 mmHg to 9.8 mmHg after infusion of 500 mL of blood while the peripheral venous pressure increased from 10.2 mmHg to 12.9 mmHg. A comparable increase in pressure was measured in both vascular locations. During the infusion test, the increased blood volume distends the blood vessels, thus reducing their resistance and the resistance to venous return. Guyton et al. [66] studied the effect of blood transfusion or hemorrhage on the venous return curve. The slope of the curve which relates venous return and right atrial pressure is a measure of the resistance to venous return; the more vertical the slope, the less is the resistance to the return of blood to the heart. In dogs, it was observed that blood transfusion modified the slope of the venous return-right atrial pressure relation: increased blood volume distended the blood vessels and hence it decreased the resistance to blood flow. These considerations lead to the introduction of a nonlinear relationship between compartment volume and resistance of the post-capillary compartments. Vessel resistance is proportional to the inverse of radius to the power four and volume is proportional to the radius squared; thus, for a given vessel length, volume behaves as the inverse square root of the resistance; according to Equation (7), if the volume increases with respect to the reference volume, the resistance will decrease. This kind of relation was previously used by [67] to describe the biomechanics of the arterial–arteriolar cerebrovascular bed, while in [68] it was used also for the venous cerebral compartments. In [30], this relation was adopted to describe changes in cerebral arterial vasculature caused by an autoregulation model. In this work, we applied this nonlinear relation between resistance and volume to all venous compartments. The use of nonlinear resistances in venous compartments decreased the effective compliance of the mathematical model of the human circulation by 18.8% (from 5.133 mL/mmHg/kg to 4.168 mL/mmHg/kg).
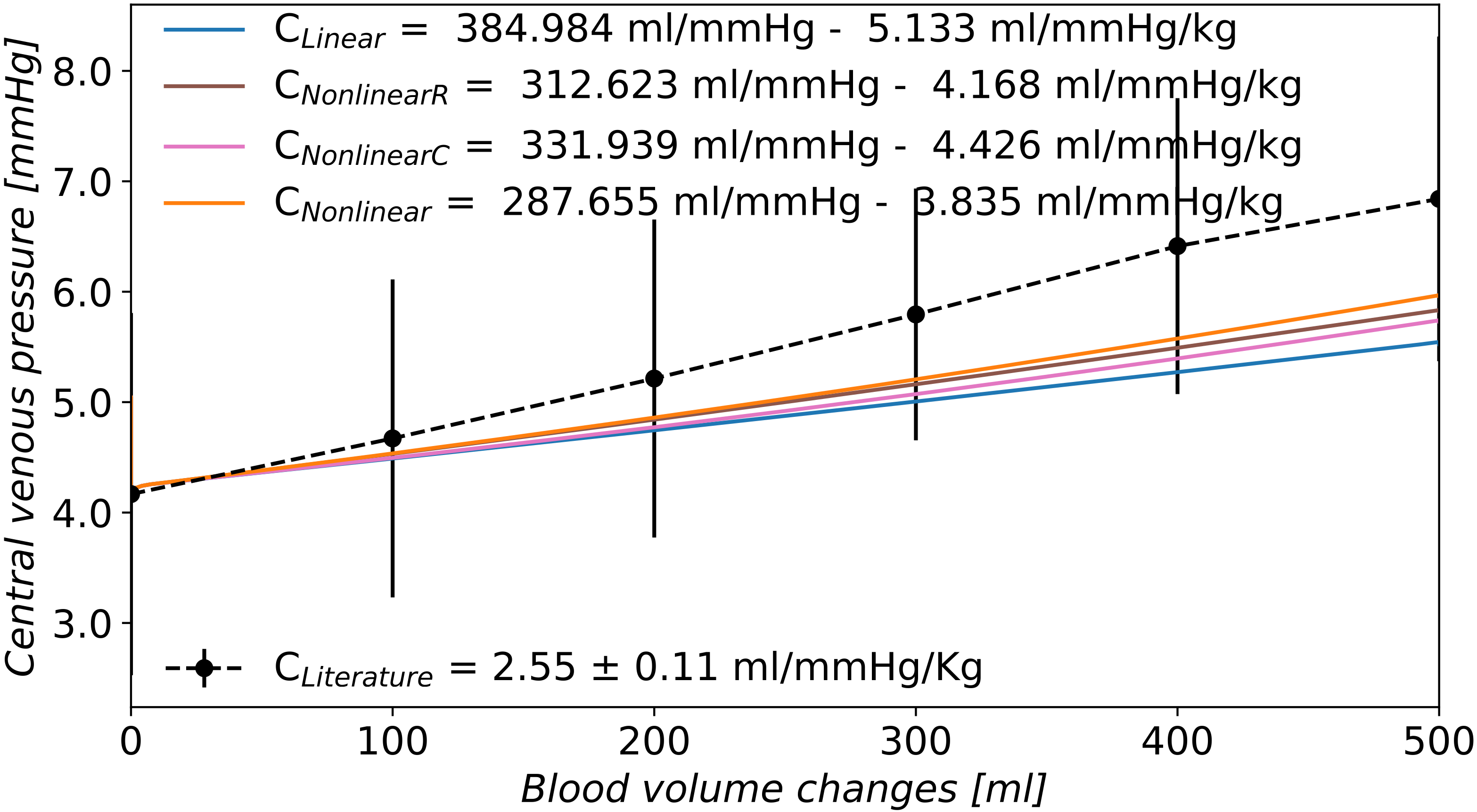
According to the work in [20], the relationship between total contained volume in the vasculature and the transmural pressure is nonlinear. As most of the total blood volume is contained in the venous circulation, a good approximation of the behaviour of the venous compartments is essential for obtaining reasonable results in the determination of TEVC. The 1D venous network adopted in this work contains all the main large veins. However, most of the venous blood volume and the larger portion of venous compliance were assigned to the 0D compartments which represent venules/distal veins. For this reason, a nonlinear relationship between volume and pressure based on 1D veins tube law was applied to 0D venous compartments. The law that represents venous compliance (Equation (8)) is such that the actual compliance is similar to the reference linear compliance in baseline volume condition. If the volume in the compartment is higher than the reference volume, the transmural pressure evaluated according to the nonlinear pressure–volume relationship will be higher with respect to linear compliance case. Ursino et al. [25] showed how the nonlinear behaviour of the relationship between pressure and volume influenced the computational results on the hemorrhage test; the use of linear pressure–volume curves is acceptable provided that moderate blood volume changes are simulated. As pointed out by Drees and Rothe [3], the use of linear compliances is probably adequate in the physiological pressure range, but in the context of highest blood volume changes the extrapolation of the results may produce unacceptable errors. The presence of nonlinear compliances in venous compartments improved the computational effective compliance by 13.78% (from 5.133 mL/mmHg/kg in linear case (1) to 4.426 mL/mmHg/kg). Compared to the case of nonlinear resistances, the sensitivity of the effective compliance to nonlinear compliances is lower than to nonlinear resistances. When both resistances and compliances are nonlinear, the effective compliance improved from 5.133 mL/mmHg/kg in scenario (1) to 3.835 mL/mmHg/kg in scenario (2). Figure 6 compares the computed effective compliance in case of: linear resistances and compliances of venule compartments (scenario (1)), variable resistances according to volume variation and linear compliances, constant resistances and nonlinear compliances, nonlinear resistances and compliances (scenario (2)). It can be observed that when both resistances and compliances are nonlinear, the computed effective compliance is closer to the literature value of TEVC.
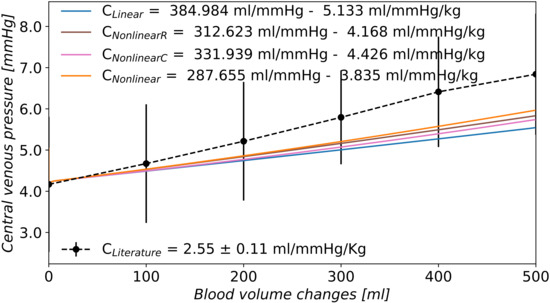
Figure 6.
Comparison between linear and nonlinear resistances and compliances of venule compartments. : linear relationship for resistances and compliances in venules compartments; : nonlinear resistances in venule compartments (Equation (7)); : nonlinear compliances in venule compartments (Equation (Figure 3)); : nonlinear resistances and compliances in venules compartments; : London et al. [10] experimental results on 9 controls subjects (mean value of the group and ± 1 standard deviation).
3.3. Baroreflex
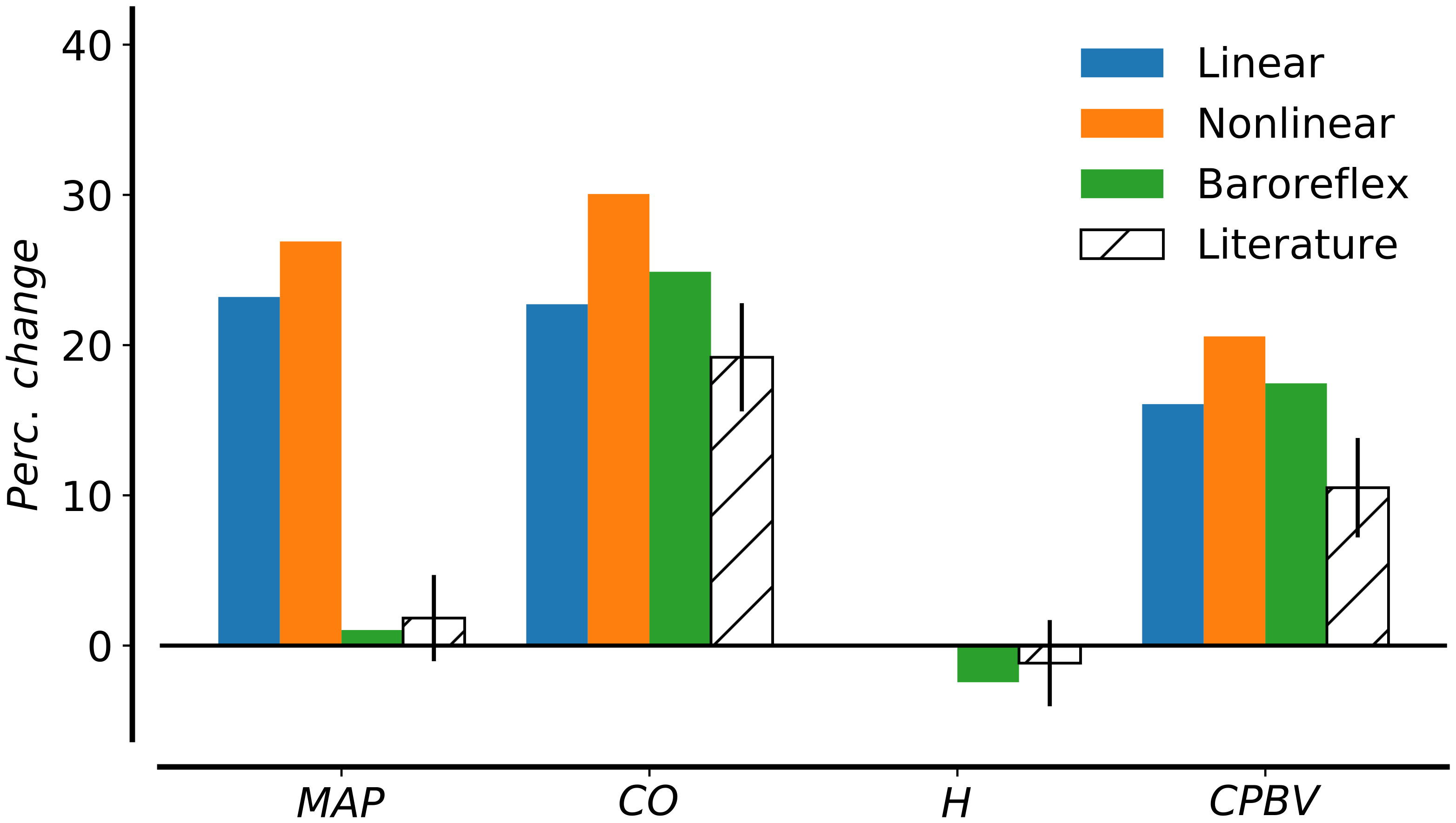
London et al. [10] performed the infusion test of 500 mL of 6% dextran within 4 min in 9 control patient in supine position. They found that an increase in total blood volume changes the mean arterial pressure by 3%. Even if the study was carried out in the shortest possible time, short-term cardiovascular regulation is considered to play a role in maintaining arterial blood pressure. Figure 7 shows the variation in main cardiovascular indexes during the expansion compared to London’s data (mean error and standard deviations) [10]. The variables under consideration are mean arterial pressure (MAP), cardiac output (CO), heart rate (HR), and cardiopulmonary blood volume. Heart rate is evaluated as the inverse of the duration of the cardiac cycle while cardiopulmonary blood volume is the sum of blood in heart and lungs. Mean arterial pressure and cardiac output increased by more than 20% (23.20% and 22.72%, respectively) in case of linear venules resistances and compliances. The increment in these quantities was even higher in the case of nonlinear venules resistances and compliances. The cardiopulmonary blood volume increased by 16.07% during the infusion test. Computational results revealed the need for baroreflex control to limit the changes in mean arterial pressure. The baroreflex represents the main neural mechanism involved in short-term regulation of arterial pressure. Two categories of baroreceptors can be distinguished according to their location: high-pressure arterial baroreceptors and low-pressure baroreceptors (also known as cardiopulmonary or volume receptors). The first group of baroreceptors is located in the carotid arteries and the aortic arch, and they are activated by a variation in systemic blood pressure. Afferent signals will then be processed; the response to deviations from a nominal state will be conveyed by efferent fibers and ultimately result in changes in vascular resistance, heart rate and cardiac contractility and venous tone. Cardiopulmonary receptors compose an heterogeneous group of sensors [69]. Despite their heteromorphism, cardiopulmonary receptors tonically inhibit the vasomotor center in analogy to arterial baroreceptors. Low-pressure baroreceptors are located in large systemic veins and the atria of the heart (at the junction of the venae cavae and the pulmonary veins). They act on arterial resistance, venous tone, and heart rate [70]. These low-pressure receptors minimize arterial pressure changes when the blood volume variation is too small to be detected by high-pressure receptors; they activate reflexes parallel to the arterial baroreflexes to ensure a stronger control of arterial pressure. Moreover, they participate in the control of renin release and vasopressin secretion, with effects on salt and water retention, production of urine and long-term control of arterial pressure. However, as the goal of this paper was to simulate an infusion of blood in four minutes, only the short-term pressure regulation by high- and low-pressure baroreceptors was considered.
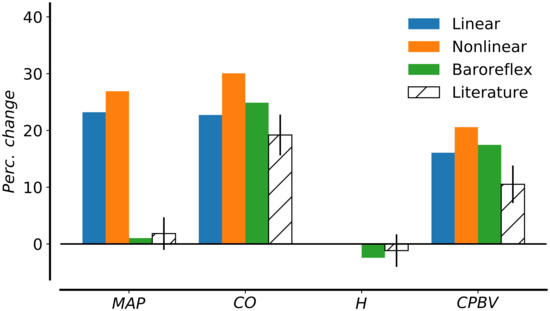
Figure 7.
Changes in hemodynamic parameters before and after expansion. Comparison between computational results for scenario (1) with linear resistances and compliances, scenario (2) with nonlinear relationship in venous compartments, and scenario (3) with nonlinearities and baroreflex control. Computed results are compared to literature data from [10]. Parameters under consideration are MAP, mean arterial pressure; CO, cardiac output; H, heart rate; CPBV, cardiopulmonary blood volume.
In this work, the mathematical function representing the nervous responses for both high- and low receptors was a sigmoid function, which ranges between the low and high saturation values symmetrically with respect to the baseline central point. It was experimentally proved in anesthetized dogs [71] that the firing rate of high-pressure receptors acted in an asymmetrical way in response to increasing or decreasing carotid pressure, like in an hysteresis loop. Moreover, this asymmetry was more evident in the parasympathetic activity than in the sympathetic one [69]: the parasympathetic firing rate response is faster when the blood pressure increases than in response to a decrease in pressure. For simplicity, the asymmetrical behaviour of the firing rate was neglected in this work; however, other mathematical models of the baroreflex activity considered the asymmetry of the firing rates, in particular in the control of the heart rate, where the parasympathetic nerve activity plays a role [72,73].
The control of heart rate by atrial receptors is called the Bainbridge reflex. In 1915, Bainbridge [74] reported that if 200 to 400 mL of blood or saline was injected into a 10 kg dog over a period of 1.5 to 4 min then its heart rate increased; this increase did not seem to be tied to arterial blood pressure because the heart rate rose regardless of whether arterial blood pressure changed, but it increased whenever central venous pressure increased sufficiently to increase ventricular end-diastolic pressure and cause ventricular dilation. The Bainbridge reflex occurs especially if the initial heart rate is low [20]; on the other hand, with more rapid heart rate, the infusion ordinarily slows the heart. Several studies have failed to demonstrate a Bainbridge effect in humans [75]. This reflex might be poorly developed or less sensitive in humans than in dogs, thus species-dependent. Moreover, a 10% volume expansion stimulates also the aortic receptors; it has been shown that the reflex generated by aortic receptors was able to reverse the tachycardic Bainbridge reflex into a bradycardic response [20]. The resulting effect could maintain constant heart rate. In view of these considerations, we applied the effects of cardiopulmonary receptors to arterial resistance and venous unstressed volume, neglecting the Brainbidge reflex on the heart rate, in agreement with work done in [59]. According to the sigmoid function, which describes the heart rate variation by means of the sympathetic and parasympathetic activity from arterial baroreceptors, the assumption of omitting the low-pressure receptors control of heart rate may lead to insignificant changes in heart rate if the changes in arterial pressure are small.
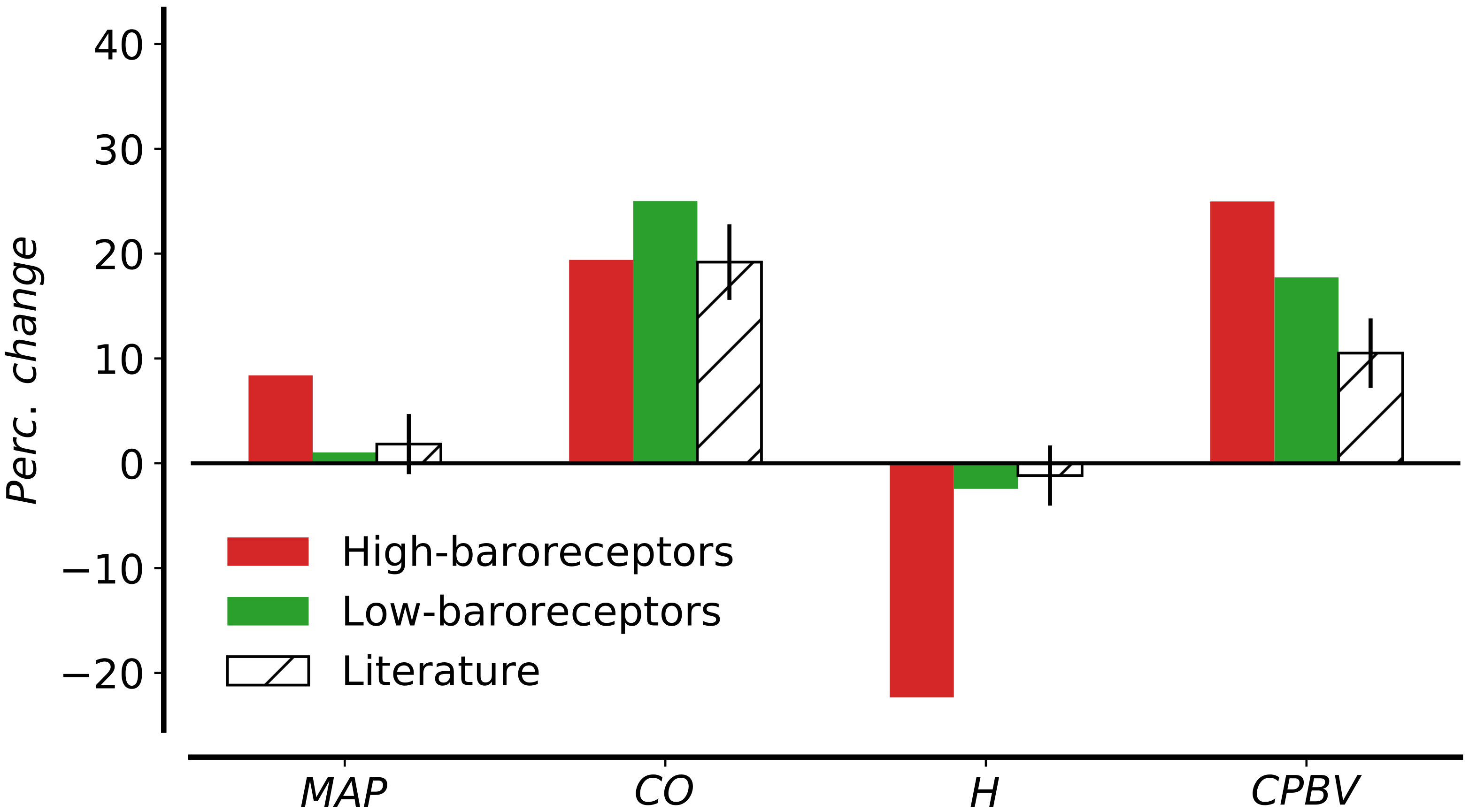
Mathematical models of human cardiovascular system [57,58,76] were applied to study the effects of short-term regulation of arterial pressure during hemorrhage. These works included only the high-pressure baroreceptors which were sufficient to appropriately control the arterial pressure. We performed an hemorrhage test for the validation of the parameters of the arterial baroreflex model, obtaining reasonable results in comparison with animals and humans data [77,78], as well as other mathematical models [57]. There is literature evidence on the activation of cardiopulmonary receptors when there are variations in total blood volume. Gupta et al. [79] demonstrated in dogs that the firing rate from the low-pressure receptors decreased in proportion to the loss of blood volume, concluding that the low-pressure receptors are primarily responsible for the reflex maintenance of arterial pressure. Abboud et al. [80] stressed that both arterial pressure and cardiac filling pressure increase with expansion of blood volume and activate the arterial baroreceptors as well as cardiopulmonary baroreceptors with vagal afferents. The mathematical model presented in Section 2.4 was first validated for a hemorrhage test; even if the underlying model with high-pressure receptors alone was able to reproduce physiological variation in mean arterial pressure during hemorrhage test, this was not the case for the infusion test. According to a sensitivity analysis study, arterial resistance is positively correlated to arterial pressure while negatively correlated to right atrial pressure. This means that a decrease in arterial resistance might decrease the arterial pressure and increase the central venous pressure. Therefore, the effect of the baroreflex control on arterial resistance is twofold: it helps controlling the arterial pressure during the infusion and it increases the central venous pressure, decreasing the total effective compliance. As reported in [10], the infusion test did not significantly change the arterial pressure, so the variation in arterial resistance might be due to the action of the low-pressure receptors. Figure 8 compares the percentage change in mean arterial pressure and other cardiovascular indexes during the infusion test under the action of either high-pressure baroreceptors ( for all ) or low-pressure receptors alone ( for all ). In the first case, the mean arterial pressure increases by 9%, leading to 20% variation in heart rate. On the contrary, under the action of the low-pressure receptors alone, the value of the mean arterial pressure is almost equal to the pre-infusion one due to the variation in arterial resistance and venous unstressed volume. When the two types of receptors work together, the mean arterial pressure increases only by 1.03% after the volume expansion; the cardiac output and the cardiopulmonary blood volume increase by 24.11% and 16.98%, respectively, while the heart rate decreases by 2.44% (as shown in Figure 7). As blood volume is infused in the circulation, the pressure in carotid arteries and aortic arch increases and activates the sympathetic control of the high-pressure baroreceptors; the low-pressure receptors are in turn activated by changes in right atrial pressure. The variation in arterial resistance and the unstressed volume was modified mainly by the receptors in the low-pressure system while the other variables undergoing regulation remain almost constant during the infusion, as we see in the efferent responses (Figure 9). The 39% variation in arterial resistance increased the right atrial pressure up to 6.3 mmHg, decreasing the TEVC to 2.806 mL/mmHg/kg. This change in arterial resistance is such that the variation in total systemic vascular resistance evaluated as ratio between mean arterial pressure and cardiac output reflects the one observed in [10].
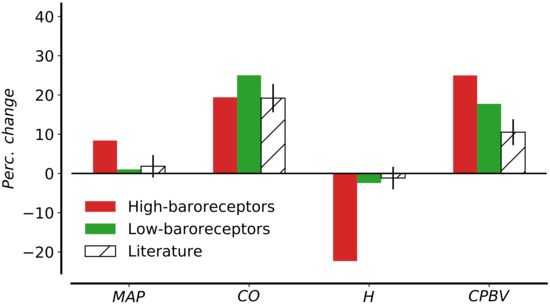
Figure 8.
Changes in hemodynamic parameters before and after expansion. Comparison between simulation with high-baroreceptors alone ( for all ) and simulation with complete baroreflex control with both high- and low-pressure receptors. Computed results are compared to literature data from [10]. Parameters under consideration are MAP, mean arterial pressure; CO, cardiac output; H, heart rate; CPBV, cardiopulmonary blood volume.
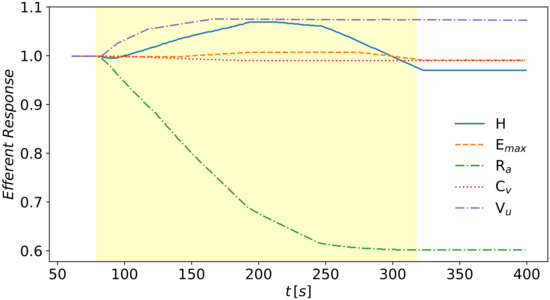
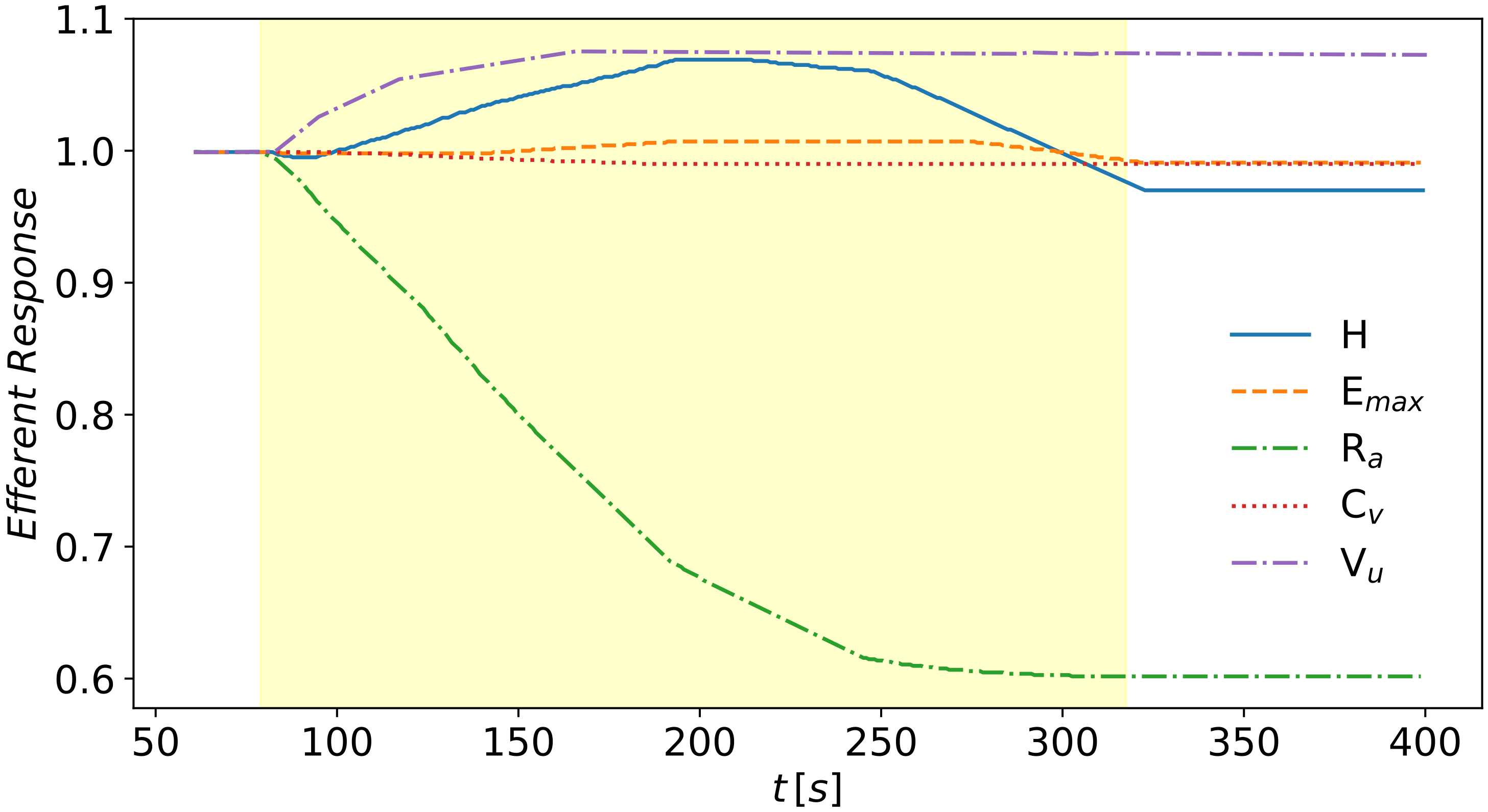
Figure 9.
Efferent response of the baroreflex model during the volume expansion evaluated at the beginning of the cardiac output by a first order differential Equation (14). Infusion starts at 80 s and it ends at 320 s. The parameters undergoing regulation are H, heart rate, , maximum elastance of cardiac chambers, , arterial resistance in terminal arteries and arterioles’ compartments, , venous compliance, , venous unstressed volume.
Concerning the unstressed volume, few data are available about the entity of changes in venous tone during infusion or hemorrhagic events. Even if there are several techniques for the determination of body venous tone, all of them present technical limitations; in whole animals, information on body venous tone or capacitance cannot be obtained with intact cardiovascular reflex system. The MCFP method was used for the evaluation of whole body venous tone or venoconstrictor influence; however, this method is unable to obtain reliable readings of compliance and unstressed volume. First, the amount of unstressed volume was linearly extrapolated from the blood volume/MCFP relationship; however, this relies on the assumption that there is a linear volume–pressure relationship, but this is not generally valid. Moreover, changes in blood volume activate cardiovascular reflexes that modify the unstressed volume, which in turn initiate other regulatory mechanisms. The volume/MCFP relationship has been obtained in animals with suppressed autonomic reflex [81] and even then the effects of vasoactive agents, such as angiotensin II, vasopressin or endothelium-derived relaxing and contracting factors modified the volume of blood, leading to over- or underestimation of changes in compliance and/or unstressed volume. There is evidence that a change in blood volume induced a larger change in unstressed volume than compliance [3]. Echt et al. [9] measured venous tone in the arm during blood volume changes by means of venous occlusion plethysmography in the left forearm. Using forearm volume and pressure, the volume elasticity coefficient at an intravenous pressure of 15 mmHg was used as measure of venous tone. Their observations failed to reveal changes in venous tone with moderate (±10%) changes in central blood volume; they did not excluded the possibility of venous tone variation, probably these changes took place in other parts of the capacitance system. Figure 9 shows the percentage alteration of the parameters controlled by the baroreflex model during blood infusion. The venous compliance remained almost constant during the infusion, while the unstressed volume varied by less that 10%, according to venous pressure changes and the threshold and saturation points given by previous works [59]. From literature evidence, it is difficult to establish the real variation of unstressed volume or compliance per se, without combining the baroreceptors activity with other reflex control mechanisms. However, we are aware that such variation in unstressed volume is necessary to control the mean arterial pressure and cardiac output as in the physiological experiment, especially when other cardiovascular regulatory system are not taken in consideration. The local sensitivity analysis (not reported here) of the principal parameters of the global mathematical model with linear relationship for resistances and compliances and without baroreflex control revealed that the venous unstressed volume is one of the major determinants of computed mean arterial pressure and mean central venous pressure. Both arterial and venous pressures were negatively correlated to venous unstressed volume; an increase of 20% in venous unstressed volume caused a decrease of 10.11% in mean arterial pressure and 13.32% in mean central venous pressure.
4. Conclusions
A mathematical model of the human circulation was used to estimate the TEVC of a mathematical model for human circulation, evaluating the changes in central venous pressure with respect to changes in blood volume during an infusion test. In order to perform this experiment the original model was modified. The main changes regarded (i) the introduction of total blood volume, including both stressed and unstressed volume, (ii) the parametrization of vascular compliance and its distribution between different vascular compartments, (iii) the use of nonlinear pressure–volume relations for venule compartments, and (iv) the use of resistances for capillaries and venules featuring a nonlinear dependence from compartment volume. We showed that a physiological parametrization of the mathematical model, in particular the assignment of physical compliance and unstressed volume in different vascular compartments, is necessary but not sufficient for obtaining a TEVC in agreement with experimental data. In fact, major physiological mechanisms must be considered, such as, for example, the short-term control of arterial pressure by baroreceptors which is crucial for obtaining modeling results that are in agreement with observed variations in mean arterial pressure, cardiac output, heart rate, and cardiopulmonary blood volume during the infusion test.
As we pointed out previously, other reflex mechanisms are activated to control volume homeostasis and to re-establish baseline cardiovascular variables after blood volume changes. Increased blood volume leads to increased cardiac output, which in turn increases the capillary pressure; due to the capillary fluid shift mechanism, fluid starts to flow out of the circulation through the tissue capillary walls to readjust the blood volume. Moreover, increased venous pressure gradually distend the veins by the reflex called stress-relaxation; the venous blood reservoirs (the unstressed volume in the liver and spleen) distend or contract, modifying the mean systemic pressure. Finally, excess blood flow in the peripheral tissues activates autoregulatory mechanisms of blood flow control. This kind of local control occurs within seconds to minutes and provide rapid regulation of tissue blood flow by means of local vasodilation or vasoconstriction of small terminal vessels (arterioles and pre-capillaries), thus modifying the peripheral vascular resistance and resistance to venous return. Drees and Rothe [3] measured variation in mean circulatory pressure at 0.5, 2, and 5 min after randomized changes in blood volume in dogs; they showed the reflexogenic control of vascular capacity evaluating the changes in effective compliance with time. They concluded that the compensation after about 30 s was mostly from passive viscoelastic creep and fluid shifts; less than half of the compensation for hemorrhage during the first 5 min came from the stress-relaxation venoconstriction. Even if the infusion considered in this work was performed in the shortest possible time, four minutes are long enough to start reflex mechanisms other than the baroreflex control. This is one of the main limitations of the present work. In future work, all these mentioned mechanisms should be taken into account to better represent the physiology of this infusion test. This will imply the introduction of a model for solute transport that permits to study the transcapillary fluid shift during the infusion experiment.
London et al. [11,26] showed the strong positive relationships between compliance and cardiopulmonary, interstitial and extracellular fluid volumes. As demonstrated by animal experiments and by immersion in man, the filling pressure of the heart is monitored through cardiac mechanoreceptors controlling renal function, extracellular fluid volume and thirst via the autonomic nervous system. Thus, even if the effective compliance was evaluated by an infusion within four minutes, a complete control of the volume in the circulation should be obtained only if other body fluid compartments are added to the mathematical model and the main regulatory mechanisms that participate in the long-term regulation of arterial pressure are included. This link with other body fluids was stressed in the evaluation of effective compliance in arterial hypertensive patients. It has been shown [1,11,12,26] that hypertensive patients are characterized by decreased TEVC, mainly in the venous compartment, due to complex hemodynamic abnormalities with alterations in main fluid volume control mechanisms. A decreased venous compliance could increase the cardiac output, causing the activation of regulatory mechanisms that modify the total peripheral resistance; this could be an initiating factor in hypertension. Future work will focus on the estimation of the effective compliance in the context of remodeling that is cause/consequence of arterial hypertension.
A further aspect that leaves room for improvement is that of local autoregulation. Previous versions of this model included the myogenic response of cerebral autoregulation. In this work, we did not consider the local control, but a global regulation of venous resistances. One should differentiate regulation with local mechanisms to brain and heart and global control to the remaining vascular territories, as proposed in [82]. Finally, note that even if the short-term control of arterial pressure by baroreceptors adopted in this work produced results in agreement with experimental observations available in the literature, an aspect that could be addressed in future developments is to consider a more refined baroreflex model that would account for the asymmetrical response of receptors and that would be able to generate an hysteresis loop for the nervous receptors activity, first of all in the cardiac regulation.
While the parametrization of the mathematical model provided in this work and the consequent adaptation of the cardiovascular system to the infusion test might not be totally accurate, especially because of lack of experimental data available for model parametrization, we believe that the results presented here should contribute to raise awareness about the difference of effective and physical parameters, as well as about the need to enrich the set of physiological processes that models like the one considered here need to incorporate, especially if large deviations from the baseline model state are to be described.
Author Contributions
Conceptualization, methodology and validation M.C., E.F.T. and L.O.M.; investigation, M.C.; writing—original draft preparation, M.C.; writing—review and editing, E.F.T. and L.O.M.; visualization, M.C.; supervision, E.F.T. and L.O.M. All authors have read and agreed to the published version of the manuscript.
Funding
M.C. acknowledges the University of Trento for financing her PhD studentship. L.O.M. acknowledges funding from the Italian Ministry of Education, University and Research (MIUR) in the frame of the Departments of Excellence Initiative 2018–2022 attributed to the Department of Mathematics of the University of Trento (grant L. 232/2016) and in the frame of the PRIN 2017 project Innovative numerical methods for evolutionary partial differential equations and applications.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Safar, M.E.; London, G.M.; Simon, A.C.; Weiss, Y.A. (Eds.) Arterial and Venous Systems in Essential Hypertension. In Developments in Cardiovascular Medicine; Springer: Dordrecht, The Netherlands, 1987; Volume 63. [Google Scholar]
- Guyton, A.C.; Polizo, D.; Armstrong, G.G. Mean Circulatory Filling Pressure Measured Immediately after Cessation of Heart Pumping. Am. J. Physiol.-Leg. Content 1954, 179, 261–267. [Google Scholar] [CrossRef] [Green Version]
- Drees, J.A.; Rothe, C.F. Reflex Venoconstriction and Capacity Vessel Pressure-Volume Relationships in Dogs. Circ. Res. 1974, 34, 360–373. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Samar, R.E.; Coleman, T.G. Measurement of Mean Circulatory Filling Pressure and Vascular Capacitance in the Rat. Am. J. Physiol.-Heart Circ. Physiol. 1978, 234, H94–H100. [Google Scholar] [CrossRef] [PubMed]
- Shoukas, A.A.; Sagawa, K. Total Systemic Vascular Compliance Measured as Incremental Volume-Pressure Ratio. Circ. Res. 1971, 28, 277–289. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shoukas, A.A.; Sagawa, K. Control of Total Systemic Vascular Capacity by the Carotid Sinus Baroreceptor Reflex. Circ. Res. 1973, 33, 22–33. [Google Scholar] [CrossRef] [Green Version]
- Henry, J.P.; Gauer, O.H.; Sieker, H.O. The Effect of Moderate Changes in Blood Volume on Left and Right Atrial Pressures. Circ. Res. 1956, 4, 91–94. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Holtz, J.; Bassenge, E.; Kinadeter, H.; Kolin, A. Increased Effective Vascular Compliance and Venous Pooling of Intravascular Volume during Sustained Venodilation in Conscious Dogs. Basic Res. Cardiol. 1981, 76, 657–669. [Google Scholar] [CrossRef] [PubMed]
- Echt, M.; Duweling, J.; Gauer, O.H.; Lange, L. Effective Compliance of the Total Vascular Bed and the Intrathoracic Compartment Derived from Changes in Central Venous Pressure Induced by Volume Changes in Man. Circ. Res. 1974, 34, 61–68. [Google Scholar] [CrossRef] [Green Version]
- London, G.; Safar, M.; Weiss, Y.; Simon, C. Total Effective Compliance of the Vascular Bed in Essential Hypertension. Am. Heart J. 1978, 95, 325–330. [Google Scholar] [CrossRef]
- London, G.M.; Safar, M.E.; Simon, A.C.; Alexandre, J.M.; Levenson, J.A.; Weiss, Y.A. Total Effective Compliance, Cardiac Output and Fluid Volumes in Essential Hypertension. Circulation 1978, 57, 995–1000. [Google Scholar] [CrossRef] [Green Version]
- London, G.M.; Safar, M.E.; Payen, D.M.; Gitelman, R.C.; Guerin, A.M. Total, Peripheral and Intrathoracic Effective Compliances of the Vascular Bed in Normotensive and Hypertensive Patients. In Contributions to Nephrology; Bahlmann, J., Liebau, H., Eds.; S. Karger AG: Basel, Switzerland, 1982; Volume 30, pp. 144–153. [Google Scholar]
- Safar, M.E.; London, G.M.; Levenson, J.A.; Simon, A.C.; Chau, N.P. Rapid Dextran Infusion in Essential Hypertension. Hypertension 1979, 1, 615–623. [Google Scholar] [CrossRef] [Green Version]
- Safar, M.E.; London, G.M. Arterial and Venous Compliance in Sustained Essential Hypertension. Hypertension 1987, 10, 133–139. [Google Scholar] [CrossRef] [Green Version]
- Gauer, O.H.; Henry, J.P.; Sieker, H.O. Changes in Central Venous Pressure after Moderate Hemorrhage and Transfusion in Man. Circ. Res. 1956, 4, 79–84. [Google Scholar] [CrossRef] [Green Version]
- Warren, J.V.; Brannon, E.S.; Weens, H.S.; Stead, E. Effect of Increasing the Blood Volume and Right Atrial Pressure on the Circulation of Normal Subjects by Intravenous Infusions. Am. J. Med. 1948, 4, 193–200. [Google Scholar] [CrossRef]
- Koubenec, H.J.; Risch, W.D.; Gauer, O.H. Effective Compliance of the Circulation in the Upright Sitting Posture. Pflügers Arch. Eur. J. Physiol. 1978, 374, 121–124. [Google Scholar] [CrossRef] [PubMed]
- Witham, A.C.; Fleming, J.W.; Bloom, W.L. The effect of the intravenous administration of dextran on cardiac output and other circulatory dynamics. J. Clin. Investig. 1951, 30, 897–902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pang, C.C.Y. Measurement of body venous tone. J. Pharmacol. Toxicol. Methods 2000, 44, 341–360. [Google Scholar] [CrossRef]
- Rothe, C.F. Reflex Control of Veins and Vascular Capacitance. Physiol. Rev. 1983, 63, 1281–1342. [Google Scholar] [CrossRef]
- Ludbrook, J.; Graham, W.F. The Role of Cardiac Receptor and Arterial Baroreceptor Reflexes in Control of the Circulation during Acute Change of Blood Volume in the Conscious Rabbit. Circ. Res. 1984, 54, 424–435. [Google Scholar] [CrossRef] [Green Version]
- Simon, A.C.; Safar, M.E.; Levenson, J.A.; London, G.M.; Levy, B.I.; Chau, N.P. An evaluation of large arteries compliance in man. Am. J. Physiol.-Heart Circ. Physiol. 1979, 237, H550–H554. [Google Scholar] [CrossRef]
- Sun, Y.; Beshara, M.; Lucariello, R.; Chiaramida, S. A Comprehensive Model for Right–Left Heart Interaction under the Influence of Pericardium and Baroreflex. Am. J. Physiol. 1997, 272, H1499–H1515. [Google Scholar] [CrossRef] [Green Version]
- Guyton, A.C.; Hall, J.E. Guyton and Hall TextBook of Medical Physiology, 12th ed.; Saunders/Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Ursino, M.; Antonucci, M.; Belardinelli, E. Role of Active Changes in Venous Capacity by the Carotid Baroreflex: Analysis with a Mathematical Model. Am. J. Physiol.-Heart Circ. Physiol. 1994, 267, H2531–H2546. [Google Scholar] [CrossRef] [PubMed]
- Safar, M.E.; London, G.M. Venous System in Essential Hypertension. Clin. Sci. 1985, 69, 497–504. [Google Scholar] [CrossRef] [PubMed]
- Mynard, J.; Smolich, J. One-Dimensional Haemodynamic Modeling and Wave Dynamics in the Entire Adult Circulation. Ann. Biomed. Eng. 2015, 43, 1443–1460. [Google Scholar] [CrossRef] [PubMed]
- Alfie, J.; Waisman, G.D.; Galarza, C.R.; Cámera, M.I. Contribution of Stroke Volume to the Change in Pulse Pressure Pattern with Age. Hypertension 1999, 34, 808–812. [Google Scholar] [CrossRef] [Green Version]
- Takatsu, H.; Gotoh, K.; Suzuki, T.; Ohsumi, Y.; Yagi, Y.; Tsukamoto, T.; Terashima, Y.; Nagashima, K.; Hirakama, S. Quantitative estimation of compliance of human systemic veins by occlusion plethysmography with radionucleotide: Methodology and the Effect of Nitroglycerin. Jpn. Circ. J. 1989, 53, 245–254. [Google Scholar] [CrossRef] [PubMed]
- Toro, E.F.; Celant, M.; Zhang, Q.; Contarino, C.; Agarwal, N.; Linninger, A.A.; Müller, L.O. Cerebrospinal fluid dynamics coupled to the global circulation in holistic setting: Mathematical models, numerical methods and applications. 2021; under review. [Google Scholar]
- Müller, L.O.; Toro, E.F. A Global Multiscale Mathematical Model for the Human Circulation with Emphasis on the Venous System. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 681–725. [Google Scholar] [CrossRef]
- Müller, L.O.; Toro, E.F. Enhanced Global Mathematical Model for Studying Cerebral Venous Blood Flow. J. Biomech. 2014, 47, 3361–3372. [Google Scholar] [CrossRef]
- Barnard, A.L.; Hunt, W.; Timlake, W.; Varley, E. A Theory of Fluid Flow in Compliant Tubes. Biophys. J. 1966, 6, 717–724. [Google Scholar] [CrossRef] [Green Version]
- Hughes, T.J.; Lubliner, J. On the One-Dimensional Theory of Blood Flow in the Larger Vessels. Math. Biosci. 1973, 18, 161–170. [Google Scholar] [CrossRef]
- Toro, E.F.; Millington, R.C.; Nejad, L.A.M. Towards Very High–Order Godunov Schemes. In Godunov Methods: Theory and Applications; Toro, E.F., Ed.; Kluwer Academic/Plenum Publishers: New York, NY, USA, 2001; pp. 905–937. [Google Scholar]
- Formaggia, L.; Quarteroni, A. (Eds.) Cardiovascular Mathematics: Modeling and Simulation of the Circulatory System; Number 1 in MS & A: Modeling, Simulation & Applications; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Alastruey, J.; Khir, A.; Matthys, K.; Segers, P.; Sherwin, S.; Verdonck, P.; Parker, K.; Peiró, J. Pulse Wave Propagation in a Model Human Arterial Network: Assessment of 1-D Visco-Elastic Simulations against In Vitro Measurements. J. Biomech. 2011, 44, 2250–2258. [Google Scholar] [CrossRef] [PubMed]
- Toro, E.F.; Siviglia, A. Flow in Collapsible Tubes with Discontinuous Mechanical Properties: Mathematical Model and Exact Solutions. Commun. Comput. Phys. 2013, 13, 361–385. [Google Scholar] [CrossRef]
- Spilimbergo, A.; Toro, E.F.; Müller, L.O. One-Dimensional Blood Flow with Discontinuous Properties and Transport: Mathematical Analysis and Numerical Schemes. Commun. Comput. Phys. 2021, 29, 649–697. [Google Scholar] [CrossRef]
- Cattaneo, C. A Form of Heat-Conduction Equations which Eliminates the Paradox of Instantaneous Propagation. Comptes Rendus Mathématique l’Academie Sci. 1958, 247, 431–433. [Google Scholar]
- Montecinos, G.I.; Toro, E.F. Reformulations for General Advection-Diffusion-Reaction Equations and Locally Implicit ADER Schemes. J. Comput. Phys. 2014, 275, 415–442. [Google Scholar] [CrossRef]
- Montecinos, G.I.; Müller, L.O.; Toro, E.F. Hyperbolic Reformulation of a 1D Viscoelastic Blood Flow Model and ADER Finite Volume Schemes. J. Comput. Phys. 2014, 266, 101–123. [Google Scholar] [CrossRef]
- Müller, L.O.; Blanco, P.J.; Watanabe, S.M.; Feijóo, R.A. A High-Order Local Time Stepping Finite Volume Solver for One-Dimensional Blood Flow Simulations: Application to the ADAN Model. Int. J. Numer. Methods Biomed. Eng. 2015, 32, e02761. [Google Scholar] [CrossRef]
- Toro, E.F. The ADER Path to High-Order Godunov Methods. Continuum Mechanics, Applied Mathematics and Scientific Computing: Godunov’s Legacy—A Liber Amicorum to Professor Godunov; Springer: Berlin/Heidelberg, Germany, 2020; pp. 359–366. [Google Scholar]
- Müller, L.O.; Parés, C.; Toro, E.F. Well-Balanced High-Order Numerical Schemes for One-Dimensional Blood Flow in Vessels with Varying Mechanical Properties. J. Comput. Phys. 2013, 242, 53–85. [Google Scholar] [CrossRef]
- Müller, L.O.; Toro, E.F. Well-Balanced High-Order Solver for Blood Flow in Networks of Vessels with Variable Properties. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 1388–1411. [Google Scholar] [CrossRef]
- Toro, E.; Montecinos, G. Advection-Diffusion-Reaction Equations: Hyperbolisation and High-Order ADER Discretizations. SIAM J. Sci. Comput. 2014, 36, A2423–A2457. [Google Scholar] [CrossRef]
- Dumbser, M.; Käser, M.; Toro, E.F. An Arbitrary High Order Discontinuous Galerkin Method for Elastic Waves on Unstructured Meshes v: Local Time Stepping and p–Adaptivity. Geophys. J. Int. 2007, 171, 695–717. [Google Scholar] [CrossRef] [Green Version]
- Liang, F.; Takagi, S.; Himeno, R.; Liu, H. Biomechanical Characterization of Ventricular-Arterial Coupling during Aging: A Multi-Scale Mode Study. J. Biomech. 2009, 42, 692–704. [Google Scholar] [CrossRef]
- Mynard, J.; Davidson, M.; Penny, D.; Smolich, J. A Simple, Versatile Valve Model for Use in Lumped Parameter and One-Dimensional Cardiovascular Models. Int. J. Numer. Methods Biomed. Eng. 2012, 28, 626–641. [Google Scholar] [CrossRef]
- Ursino, M.; Lodi, C. A Simple Mathematical Model of the Interaction between Intracranial Pressure and Cerebral Hemodynamics. J. Appl. Physiol. 1997, 82, 1256–1269. [Google Scholar] [CrossRef]
- Falz, R.; Fikenzer, S.; Hoppe, S.; Busse, M. Normal Values of Hemoglobin Mass and Blood Volume in Young, Active Women and Men. Int. J. Sport. Med. 2019, 40, 236–244. [Google Scholar] [CrossRef] [PubMed]
- Davy, K.P.; Seals, D.R. Total Blood Volume in Healthy Young and Older Men. J. Appl. Physiol. 1994, 76, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- Magder, S. Volume and Its Relationship to Cardiac output and Venous Return. Crit. Care 2016, 20, 271. [Google Scholar] [CrossRef] [Green Version]
- Greenway, C.V.; Lautt, W.W. Blood Volume, the Venous System, Preload, and Cardiac Output. Can. J. Physiol. Pharmacol. 1986, 64, 383–387. [Google Scholar] [CrossRef] [PubMed]
- Davis, T.L. Teaching Physiology through Interactive Simulation of Hemodynamics. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1991. [Google Scholar]
- Danielsen, M. Modeling of Feedback Mechanisms Which Control the Heart Function in a View to an Implementation in Cardiovascular Models. Ph.D. Thesis, Roskilde University Center, Roskilde, Denmark, 1998. [Google Scholar]
- Blanco, P.J.; Trenhago, P.R.; Fernandes, L.G.; Feijóo, R.A. On the Integration of the Baroreflex Control Mechanism in a Heterogeneous Model of the Cardiovascular System. Int. J. Numer. Methods Biomed. Eng. 2012, 28, 412–433. [Google Scholar] [CrossRef] [PubMed]
- Ursino, M.; Innocenti, M. Modeling Arterial Hypotension During Hemodialysis. Artif. Organs 2008, 21, 873–890. [Google Scholar] [CrossRef]
- Ursino, M.; Magosso, E. Acute Cardiovascular Response to Isocapnic Hypoxia. I. A Mathematical Model. Am. J. Physiol.-Heart Circ. Physiol. 2000, 279, H149–H165. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lim, E.; Chan, G.S.H.; Dokos, S.; Ng, S.C.; Latif, L.A.; Vandenberghe, S.; Karunanithi, M.; Lovell, N.H. A Cardiovascular Mathematical Model of Graded Head-Up Tilt. PLoS ONE 2013, 8, e77357. [Google Scholar] [CrossRef] [Green Version]
- Liang, F.; Liu, H. Simulation of Hemodynamic Responses to the Valsalva Maneuver: An Integrative Computational Model of the Cardiovascular System and the Autonomic Nervous System. J. Physiol. Sci. 2006, 56, 45–65. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Levick, J.R. An Introduction to Cardiovascular Physiology, 5th ed.; Hodder Arnold: London, UK, 2010. [Google Scholar]
- McEniery, C.; Ian, Y.; Ahmad Qasem, R.; Wilkinson, I.; Cockcroft, J. Normal Vascular Aging: Differential Effects on Wave Reflection and Aortic Pulse Wave Velocity: The Anglo-Cardiff Collaborative Trial (ACCT). J. Am. Coll. Cardiol. 2005, 46, 1753–1760. [Google Scholar] [CrossRef] [Green Version]
- Najjar, S.; Schulman, S.; Gerstenblith, G.; Fleg, J.; Kass, D.; O’Connor, F.; Becker, L.; Lakatta, E. Age and gender affect ventricular-vascular coupling during aerobic exercise. J. Am. Coll. Cardiol. 2004, 44, 611–617. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guyton, A.C.; Lindsey, A.W.; Kaufmann, B.N.; Abernathy, J.B. Effect of Blood Transfusion and Hemorrhage on Cardiac Output and on the Venous Return Curve. Am. J. Physiol.-Leg. Content 1958, 194, 263–267. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Payne, S. A Model of the Interaction between Autoregulation and Neural Activation in the Brain. Math. Biosci. 2006, 204, 260–281. [Google Scholar] [CrossRef] [PubMed]
- Cirovic, S.; Walsh, C.; Fraser, W.D. Mathematical study of the role of non-linear venous compliance in the cranial volume-pressure test. Med. Biol. Eng. Comput. 2003, 41, 579–588. [Google Scholar] [CrossRef]
- Persson, P.B.; Kirchheim, H.R. (Eds.) Baroreceptor Reflexes; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Mark, A.L.; Mancia, G. Cardiopulmonary Baroreflexes in Humans. In Comprehensive Physiology; Terjung, R., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Coleridge, H.M.; Coleridge, J.C.; Kaufman, M.P.; Dangel, A. Operational Sensitivity and Acute Resetting of Aortic Baroreceptors in Dogs. Circ. Res. 1981, 48, 676–684. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ottesen, J.; Olufsen, M. Functionality of the Baroreceptor Nerves in Heart Rate Regulation. Comput. Methods Programs Biomed. 2011, 101, 208–219. [Google Scholar] [CrossRef] [PubMed]
- Ricketts, J.H.; Head, G.A. A Five-Parameter Logistic Equation for Investigating Asymmetry of Curvature in Baroreflex Studies. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 1999, 277, R441–R454. [Google Scholar] [CrossRef]
- Bainbridge, F.A. The Influence of Venous Filling upon the Rate of the Heart. J. Physiol. 1915, 50, 65–84. [Google Scholar] [CrossRef] [PubMed]
- Takeshita, A.; Mark, A.L.; Eckberg, D.L.; Abboud, F.M. Effect of Central Venous Pressure on Arterial Baroreflex Control of Heart Rate. Am. J. Physiol.-Heart Circ. Physiol. 1979, 236, H42–H47. [Google Scholar] [CrossRef] [PubMed]
- Ursino, M. Interaction between Carotid Baroregulation and the Pulsating Heart: A Mathematical Model. Am. J. Physiol.-Heart Circ. Physiol. 1998, 275, H1733–H1747. [Google Scholar] [CrossRef] [PubMed]
- Hosomi, H.; Sagawa, K. Sinovagal Interaction in Arterial Pressure Restoration after 10% Hemorrhage. Am. J. Physiol.-Regul. Integr. Comp. Physiol. 1979, 237, R203–R209. [Google Scholar] [CrossRef]
- Kumada, M.; Sagawa, K. Aortic Nerve Activity during Blood Volume Changes. Am. J. Physiol.-Leg. Content 1970, 218, 961–965. [Google Scholar] [CrossRef] [PubMed]
- Gupta, P.; Henry, J.; Sinclair, R.; Von Baumgarten, R. Responses of Atrial and Aortic Baroreceptors to Nonhypotensive Hemorrhage and to Tranfusion. Am. J. Physiol.-Leg. Content 1966, 211, 1429–1437. [Google Scholar] [CrossRef]
- Abboud, F.M.; Thames, M.D. Interaction of Cardiovascular Reflexes in Circulatory Control. In Comprehensive Physiology; American Cancer Society: Atlanta, GA, USA, 2011; Chapter 19; pp. 675–753. [Google Scholar]
- Trippodo, N.C. Total Circulatory Capacity in the Rat. Effects of Epinephrine and Vasopressin on Compliance and Unstressed Volume. Circ. Res. 1981, 49, 923–931. [Google Scholar] [CrossRef] [Green Version]
- Albanese, A.; Cheng, L.; Ursino, M.; Chbat, N.W. An integrated mathematical model of the human cardiopulmonary system: Model development. Am. J. Physiol.-Heart Circ. Physiol. 2016, 310, H899–H921. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).