Cogging Torque Reduction in PMSM in Wide Temperature Range by Response Surface Methodology

Abstract

In this paper, a wide temperature range permanent magnet synchronous motor (PMSM) is designed, which can be used as the servo mechanism of an electric actuator in a missile. Considering the operating characteristics of the actuator with large environmental temperature change and large temperature rise, the magnetic material characteristics at different temperatures are analyzed, and the influence of eccentric magnetic poles on the cogging torque is deduced. In order to reduce cogging torque in a wide temperature range, the poles of the motor are optimized based on the response surface method. By utilizing temperature rise calculations, the scheme that may exceed the maximum working temperature of the material is eliminated. Then, the response surfaces of the cogging torque with pole arc coefficient, thickness and asymmetry at different temperatures are established, and the optimal value ranges of the three parameters are determined. The minimum upper limits of cogging torque and meeting the specified output torque at different temperatures are used as the judging criteria, and the optimal schemes for different working environments are determined. Finally, a prototype is developed, and the output torque is more than 10 N·m, and the cogging torque is less than 0.2 N·m in a wide temperature range.

1. Introduction

As the executive body of the missile guidance and control system, the actuator directly determines the dynamic quality of the missile flight process and the final strike effect of the missile. The permanent magnet synchronous motor (PMSM) is often considered as an electric actuator servo mechanism due to its advantages of high energy density and strong overload capacity [1,2]. At this time, considering the particularity of its working state and working environment, the motor needs to widen its temperature range adaptability.

The wide temperature range of the motor can be divided into internal temperature rise and external environment temperature. First of all, in order to compel the missile to reach a sufficient flight speed in a short of period time, generally only 100–500 s, the electric actuator will provide acceleration through a large current, which causes a large temperature rise inside the motor. Secondly, as a special aircraft, the temperature around the missile is greatly affected by the changes of flight altitude and space. When the missile flies in direct sunlight areas, the external high temperature environment deteriorates the heat dissipation conditions of the motor, reducing the magnetic performance of the permanent magnet or destroying the winding insulation layer. When the missile flies in the area that avoids direct sunlight, the external temperature is much lower than ground temperature, and the electromagnetic parameters and mechanical structure changes of the motor will also affect its stability.

The current research on PMSM in wide temperature ranges mainly focuses on the material properties of the motor at specific high or low temperatures. Polish scholar Dlugiewicz et al. designed a low-temperature PMSM for rocket propulsion fuel pumps in 2012. The operating temperature is −165 °C or −240 °C. In the process of testing the prototype, it was observed that the low-temperature impact would not affect the magnetic properties of the selected permanent magnet materials [3]. Newell MA et al. took the lunar rover as the object and conducted research on whether permanent magnets loses magnetism under high temperature conditions, high temperature resistance of electronic devices and high temperature resistance insulation materials [4]. Paper [5] researched the low-temperature and high-speed PMSM and analyzed the material selection and low-temperature application, which selected SmCo (pointing out that NdFeB is not suitable for low temperature environments below 140 K) as the permanent magnet material and set the working temperature of the motor as −196 °C. However, due to the limited conditions, only water-cooling tests were carried out on the prototype. Considering the influence of low temperature on material properties, the article [6] established and simulated a multi-physics model of electromagnetic, fluid, heat and stress coupling and proposed a low-temperature temperature design method. The results indicated that PMSM has superiority in wastage compared with induction motors in this environment. Vahid Ghorbanian et al. conducted experimental measurements on the properties of silicon steel, permanent magnet materials and other materials at different temperatures and imported finite element software to establish the design space for various objectives, including comprehensive system efficiency, speed limit, motor starting quality, average torque, total harmonic distortion and power factor and finally proposed the optimal design scheme at different temperatures [7]. Oguzhan Ocak et al. proposed a new magnet step-skew approach for surface mounted permanent magnet motors in order to reduce the cogging torque and torque pulsations as well as to increase output torque quality [8]. In [9], a temperature-dependent permanent magnet hysteresis model is proposed to consider the change of the permanent magnet working point and the deterioration of magnetic performance caused by temperature rise. The model has high accuracy within 25–120 °C and can be used for permanent magnets, electromagnetic and thermal analysis of motors.

These existing studies have obtained some design criteria to ensure that PMSM can work normally and output enough torque in a wide temperature range, but there is still a lack of research on the change of PMSM cogging torque in a wide temperature range.

During the flight, the missile is affected by various complex factors such as air resistance and bearing friction resistance, and it is inevitable that the actual flight trajectory will deviate from the preset one. In order to ensure guidance accuracy, the trajectory correction work is usually performed by generating lateral power between the actuator and the air. Therefore, torque fluctuations of the actuator directly affect the accuracy of trajectory correction [10]. As the main factor of PMSM torque fluctuation, the analysis and reduction in cogging torque in wide temperature range are necessary for improving the accuracy of missile guidance and control. Commonly used methods to suppress PMSM torque fluctuation include selecting appropriate pole slot matching [11], chamfering the magnetic pole [12], changing the pole arc coefficient [13], adopting skewed-slot stator or skewed-pole rotor [14,15], auxiliary slots [16], unequal tooth width fit [17] and unequal notch width fit [18], etc.

Aiming at the cogging torque characteristics of PMSM in a wide temperature range, this paper firstly analyzes the temperature characteristics of materials and the influence of poles structure parameters on the cogging torque at different temperatures. Then, under the condition that the output torque meets the requirements and the temperature of the motor does not exceed the maximum working temperature of materials, the response surface method is used to obtain the optimal solution of the magnetic pole structure parameters in order to reduce cogging torque. Finally, a prototype is developed for experimental verification.

2. Cogging Torque Characteristics of PMSM in a Wide Temperature Range

2.1. Basic Parameters of PMSM

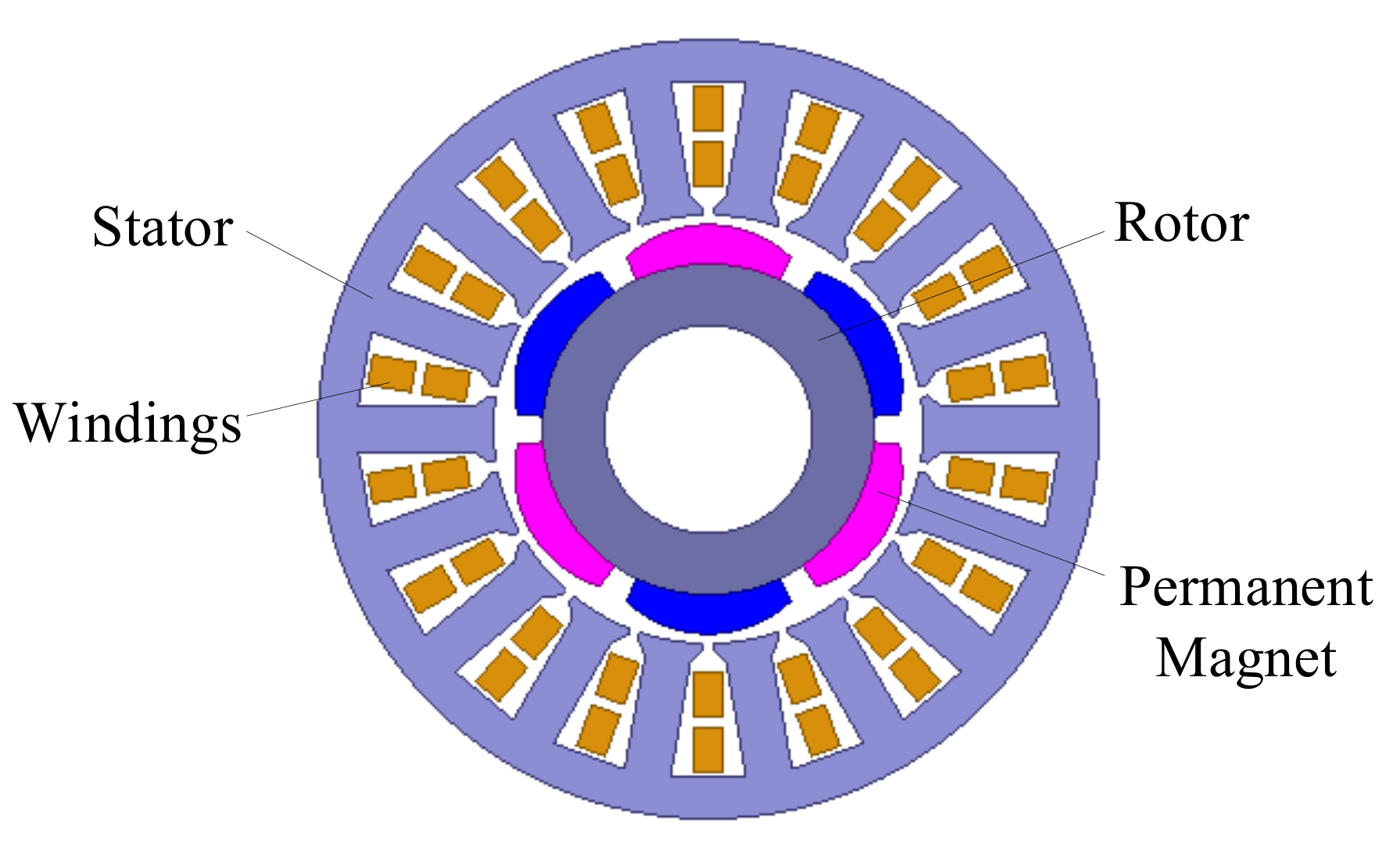
A surface-mounted inner rotor PMSM with six poles and eighteen slots is preliminarily designed, and the output torque is required to be no less than 10 Nm during operation, as shown in Figure 1. Some of its size parameters are shown in

Table 1. Partially determined parameters of PMSM.

Project	Unit	Value
Outer diameter of stator	mm	120
Stator inner diameter	mm	66
Air gap	mm	1.5
Rotor outer diameter	mm	63
Rotor inner diameter	mm	32
Tooth width	mm	7
Groove depth	mm	19.5
Back yoke thickness	mm	6.5

.

2.2. Magnetic Material Properties in a Wide Temperature Range

When the PMSM works in a wide temperature range environment, it is necessary to consider the effect of temperature changes on the performance of each component material. According to different materials, the motor is divided into three parts: iron core, windings and permanent magnet.

The motor core is composed of laminated silicon steel sheets, which can effectively reduce the eddy current and iron loss, improve motor efficiency and reduce heat and temperature rise during motor operation. The research shows that the temperature change has little effect on the magnetic permeability of silicon steel materials below 500 °C, which can be ignored.

In the design of PMSM, the most commonly used winding material is copper. Given the length and cross-sectional area, the current transmission capacity of copper depends on the conductivity. In the temperature range studied in this paper, the conductivity of copper changes linearly with temperature. The conductivity of copper at 20 °C is 58,000,000 S/m, and the temperature coefficient is −0.38%. The insulation level of copper wire is R, of which the temperature tolerance is 240 °C.

The common permanent magnet materials in the design of PMSM are ferrite, NdFeB and SmCo. In normal operation, the demagnetization curves and recovery curves of the permanent magnet are straight lines that coincide with each other. In this temperature range, the magnetic properties of these three types of permanent magnets all decrease as the temperature rises. The magnetic properties at different temperatures are as follows:

$$B_{rT}=\left[1+{\alpha }_{Br}\left(T-20\right)\right]·B_{r20}$$

(1)

$$H_{cT}=\frac{B_{rT}}{\mu }$$

(2)

where B_rT is the remanence at T °C, α_Br is the temperature coefficient of the remanence, H_cT is the magnetic coercivity at T °C and μ is the relative permeability, which is a constant.

However, as the temperature changes further, the demagnetization curve of the permanent magnet will bend downwards. If the working point of the permanent magnet drops below the inflection point, permanent demagnetization will occur. Among them, ferrite will undergo permanent demagnetization at low temperatures, while NdFeB and SmCo will undergo permanent demagnetization at high temperatures. In order to ensure reliability during the operation, the maximum demagnetization operating point of permanent magnet needs to be verified in order to ensure that it is above the inflection point.

A concept of critical field strength is introduced here. The critical field strength H_K of the permanent magnet refers to the magnetic field strength when B_i = 0.9 B_r, and its ratio to the intrinsic coercivity H_cj is defined as the rectangularity Q of the permanent magnet material. When thee rectangularity is greater, the resistance to external magnetic fields is stronger. Under normal circumstances, the rectangularity of permanent magnetic materials changes very little with temperature, so this change can be ignored in the actual application process.

Then, the magnetic density value B_rKT and the magnetic field intensity value H_cKT at the inflection point of permanent magnet are defined. Suppose the ratio of magnetic density to remanence at the inflection point (B_rKT, H_cKT) is k, then the following is the case.

$$B_{rKT}=k·B_{rT}$$

(3)

$$H_{cKT}=\left(1-k\right)·H_{cT}$$

(4)

In order to ensure that the recovery line of the operating point coincides with the demagnetization curve, the critical field strength H_KT is required to be greater than the magnetic field strength H_cKT at the inflection point.

$$H_{cjT}=\frac{H_{KT}}{Q}\ge \frac{H_{cKT}}{Q}=\frac{\left(1-k\right)H_{cT}}{Q}=\frac{\left(1-k\right)B_{rT}}{\mu Q}$$

(5)

That is to say that the following is the case:

$$H_{cj20}=\frac{H_{cjT}}{1+{\alpha }_{H_{cj}}\left(T-20\right)}\ge \frac{\left(1-k\right)\left[1+{\alpha }_{Br}\left(T-20\right)\right]B_{r20}}{\mu Q\left[1+{\alpha }_{Hcj}\left(T-20\right)\right]}$$

(6)

$$k\ge \frac{\mu Q\left[1+{\alpha }_{Hcj}\left(T-20\right)\right]H_{cj20}}{\left[1+{\alpha }_{Br}\left(T-20\right)\right]B_{r20}}$$

(7)

where H_cjT is the intrinsic coercivity at temperature T °C, and α_Hcj is the intrinsic coercivity temperature coefficient.

The above formula can be used to select suitable permanent magnet materials conveniently. Usually, according to the parameters provided by the manufacturer, Q, μ, α_Br and α_Hcj of the permanent magnet material can be known. If the ratio of the magnetic density at the inflection point of the demagnetization curve to the remanence does not exceed k = 10% in high temperature operating, the required relationship between H_cj20 and B_r20 can be calculated by the formula. Then, the permanent magnet material which meets the requirements of B_rKT can be selected according to B_r20. The maximum demagnetization operating point of the permanent magnet can be checked with the aforementioned methods, which verifies whether the permanent magnet will be permanently demagnetized when in operation and ensures the reliability of the PMSM.

2.3. Eccentric Magnetic Pole Asymmetric Structure

The PMSM designed in this paper adopts surface-mounted poles with radial magnetization. If the traditional equal thickness tile-shaped permanent magnets are adopted, the air gap flux density waveform of the motor is approximately a rectangular wave with large harmonic content. Then, it will cause large cogging torque, resulting in cogging torque and noise, which greatly affects the accuracy of missile guidance. Therefore, this paper selects the eccentric magnetic pole structure shown in Figure 2 to suppress the cogging torque of PMSM.

R_m is the radius of the inner arc of permanent magnet, h is the eccentric distance between the inner and outer arcs, h_m is the thickness of the central magnetization direction of permanent magnet and h_m(θ) is the thickness in the magnetizing direction of permanent magnet at different angles. The following can be obtained.

$$h_m\left(\theta \right)=h\cos \theta +\sqrt{{\left(R_m+h_m-h\right)}^2-{\left(h\sin \theta \right)}^2}-R_m$$

(8)

Due to the slot of the stator and rotor, the reluctance around the permanent magnet is different. When the rotor moves relative to the stator, the magnetic field energy inside the motor will change, thereby generating cogging torque. When the windings are open, the cogging torque T_cog of PMSM can be expressed as follows:

$$T_{cog}=-\frac{\partial W}{\partial \alpha }$$

(9)

where W is the magnetic field energy storage of PMSM, and α is the relative angle of the stator and rotor.

The magnetic field energy change of PMSM is mainly reflected in the air gap, and the following equation can be obtained as follows:

$$W=\frac{1}{2{\mu }_0}{\displaystyle {\int }_V{B}^2\mathrm{d}V}$$

(10)

where μ₀ is the air gap permeability, and V is the air gap volume.

Assuming that the permeability of permanent magnet is approximately equal to that of air and by ignoring the effects of magnetic flux leakage and saturated slot effects, the distribution of air gap magnetic density along the armature surface at different temperatures can be expressed as follows.

$$B\left(\theta ,\alpha ,T\right)=B_{rT}\left(\theta \right)\frac{h_m\left(\theta \right)}{h_m\left(\theta \right)+\delta \left(\theta ,\alpha \right)}$$

(11)

By performing Fourier expansion on the two components of the above expression, the following can be obtained:

$$B_{rT}{}^2\left(\theta \right)={\alpha }_p{B}_{rT}{}^2+{\displaystyle \sum _{n=1}^{\infty }\frac{2}{n\pi }{B}_{rT}{}^2\sin \left(n{\alpha }_p\pi \right)}\cos \left(2np\theta \right)$$

(12)

$${\left[\frac{h_m\left(\theta \right)}{h_m\left(\theta \right)+\delta \left(\theta ,\alpha \right)}\right]}^2=G_0+{\displaystyle \sum _{n=1}^{\infty }{G}_n\cos nz\left(\theta +\alpha \right)}$$

(13)

where p is the number of pole pairs, z is the number of stator slots, B_r is the permanent magnet remanence and α_p is the pole arc coefficient.

By substituting Formula (1) and (10)–(13) into (9), the analytical formula of cogging torque at different temperatures can be obtained as follows.

$$T_{cog}\left(\alpha ,T\right)=\frac{\pi z{L}_a}{4{\mu }_0}\left(R_2^2-R_1^2\right)·{\displaystyle \sum _{n=1}^{\infty }n{G}_n{B}_{r20}{}_{\frac{nz}{2p}}\left[1+{\alpha }_{B_r}\left(T-20\right)\right]\sin nz\alpha }$$

(14)

It can be observed that the lowest order $B_{r{T}_{\frac{nz}{2p}}}$ plays a major role in cogging torque. Therefore, Fourier decomposition of B_rT²(θ) is performed to obtain $B_{r{T}_{\frac{nz}{2p}}}$. If it decreases after using eccentric magnetic poles, this pole structure can be used to suppress cogging torque at this temperature; if an increase is observed after using eccentric magnetic poles, this method cannot be used.

Figure 3 shows the B_rT(θ) Fourier decomposition coefficients of magnetic poles with different eccentricity at 20 °C. This paper adopts a 6-pole and 18-slot PMSM, and the main effect on the cogging torque is B_rT3. When the poles adopt the asymmetric structure, the B_rT3 amplitude decreases significantly, indicating that the eccentric magnetic pole structure is suitable for this kind of motor with pole slot matching. However, as the eccentricity increases, the amplitude of B_rT3 decreases first and increases after, which indicates that there is an optimal eccentricity suppressing the cogging torque of PMSM to the greatest extent.

2.4. Relationship between Cogging Torque and Pole Parameters at Different Temperatures

According to the above theoretical analysis, different eccentricity can suppress the cogging torque to different degrees. Moreover, this paper adds pole arc coefficient and thickness as research variables. These three parameters can determine the structure size of eccentric magnetic poles. In addition, permanent magnet materials with various magnetic properties differ in performances and further change with wide temperature range. These factors may change the suppression effect of eccentric magnetic poles on cogging torque. Therefore, this paper analyzes the variation of cogging torque with pole arc coefficient, thickness and eccentricity with different permanent magnet materials and different temperatures.

In order to achieve the high power density of PMSM, this paper does not consider ferrite with poor magnetic properties as the permanent magnet material and mainly analyzes the differences in PMSM output characteristics with NdFeB and SmCo as the magnetic poles. The selected NdFeB is N30UH, and the selected SmCo is SmCo28. The remanence and coercivity of these two materials at room temperature are basically the same. However, the properties of each can vary differently with temperature. The α_Br of N30UH is −0.12%/°C, and the α_Br of SmCo28 is −0.03%/°C.

Figure 4 shows the variation trend of cogging torque with N30UH at different temperatures. It can be observed that the cogging torque decreases to a minimum near the pole arc coefficient of 0.85. The variations of cogging torque with pole thickness vary greatly at different temperatures. The developing trend is relatively complex, some of which increases while others decreases. The cogging torque is suppressed with the increase in pole eccentricity, and the downward trend is basically linear at high temperatures while there is an obvious inflection point at low temperature.

Figure 5 shows the variation trend of cogging torque with SmCo28 at different temperatures. It can be obesrved that the cogging torque also decreases to a minimum near the pole arc coefficient of 0.85, and the change magnitude is basically the same; the variation of cogging torque with pole thickness at every temperatures is different, but it basically shows a downward trend; the cogging torque of PMSM at different temperatures basically shows a linear downward trend with pole eccentricity.

In addition, the sensitivity of cogging torque with respect to temperature with two structures is analyzed, as shown in Figure 6. At room temperature, the cogging torque of structure 1 is greater than that of structure 2, and the variation of cogging torque with temperature is also significantly greater. SmCo28 can significantly reduce the variation of cogging torque with structure 1, which decreases the maximum value of torque fluctuation at different temperatures. Therefore, SmCo28 is more suitable as the permanent magnet material for structure size 1. For structure 2, the cogging torque excited by two kinds of permanent magnet is both small at different temperatures. Thus, by considering costs, it is more appropriate to choose N30UH as the permanent magnet material.

3. Magnetic Pole Optimization Method for Wide Temperature Range PMSM Based on Response Surface

3.1. Optimization Flow Chart

The relationship between cogging torque and magnetic pole parameters under different temperatures is studied above. The following part studies the magnetic pole size scheme with small cogging torque at different temperatures, considering the wide temperature range that PMSM may encounter. Firstly, the temperature rise of PMSM at different ambient temperatures is calculated. Then, the response surface of temperature and multiple magnetic pole structure parameters is established, and the appropriate range of each parameter is determined. Finally, a scheme in which the minimum upper limit of cogging torque and output torque meets the performance requirements in wide temperature ranges is selected. The optimization flowchart is shown in Figure 7.

3.2. Wide Temperature Range

As a high-speed and long-range aircraft, missile’s flight can be divided into rising stage, mid-flight stage and reentry stage, and the surrounding environment of it will change greatly. The rising stage is the process from launching to flying out of the atmosphere. The mid-flight stage is the process of flying towards the target area. The reentry stage is the process of reaching the target area, returning to the atmosphere and hitting the target. In these processes, the missile will experience external environments of low temperature, normal temperature and high temperature alternately. Coupled with the temperature rise of the missile actuator during the operation, the temperature change inside the PMSM is more complex, and the PMSM performance is more affected by the wide temperature range.

The lowest temperature of the atmosphere referring to the low-temperature environment is set at about −100 °C in this paper. The normal temperature is set at 20 °C, while the high temperature with respect to the highest surface temperature after being exposed to direct sunlight is about 100 °C. It is assumed that the initial internal temperature of the PMSM is the same as the ambient temperature, and the motor uses natural heat dissipation. The transient thermal analysis of PMSM is carried out by using MotorCAD software under the condition of a 90 A current running for 500 s at these three initial temperatures. This software calculates the temperature rise based on the thermal network, which is shown in Figure 8.

Take the PMSM with a pole arc coefficient of 0.85, thickness of 6 mm and eccentricity of 12 mm as an example. According to the calculation results, after 500 s of operation at the initial 20 °C, the temperature of windings reaches about 113 °C, and the temperature of permanent magnet reaches 73 °C. After 500 s of operation at low temperature −100 °C, the temperature of windings reaches −26 °C, and the temperature of the permanent magnet reaches −57 °C. After 500 s of operation at high temperature 100 °C, the temperature of windings reaches about 224 °C, and the temperature of permanent magnet part reaches about 173 °C. The higher the temperature, the smaller the convection coefficient between the PMSM and the outside world and heat dissipation becomes more difficult. Copper consumption increases as copper conductivity decreases. Then, the temperature will further rise, which is the same as the calculated results.

The temperature tolerance of copper wire used in this article is 240 °C. With N30UH, it is 180 °C, and it is 300 °C for SmCo28. All of them are higher than the final calculated temperature of PMSM at different initial temperatures. Therefore, the material damage or failure cannot be considered in the PMSM of this size scheme. If the final temperature of a certain part in other size PMSM is higher than the temperature tolerance of the material, the scheme needs to be eliminated by considering material reliability.

Since copper conductivity change caused by winding temperature rise does not affect the torque characteristics of PMSM, the temperature range of windings is not considered below. The wide temperature range that the permanent magnet can reach is set at −100–180 °C.

3.3. Principles of Response Surface Method

Response surface method is a commonly used optimization method in engineering. It takes the response of the system as a function of one or more factors and uses graphic technology to display this functional relationship so that researchers can intuitively select the optimal conditions in the experimental design [19,20]. To construct such response surfaces, a large number of experimental data should be obtained first, and then the appropriate mathematical model is established by using the multiple linear regression method, and the mathematical model is used for plotting.

This paper uses a 4-order response surface model and considers the interaction of various variables. The model formula is described as follows:

$$\begin{array}{c}y={\beta }_0+{\displaystyle \sum _{i=1,i<j}^k{\beta }_{i,j}{x}_i{x}_j+{\displaystyle \sum _{i=1}^k{\beta }_{ii}{x}_i^2+}}{\displaystyle \sum _{i=1,i\ne j}^k{\beta }_{i,j}^{\prime }{x}_i{x}_j^2}\\ +{\displaystyle \sum _{i=1}^k{\beta }_{iii}{x}_i^3+}{\displaystyle \sum _{i=1,i\ne j}^k{\beta }_{i,j}^{″}{x}_i{x}_j^3}+{\displaystyle \sum _{i=1}^k{\beta }_{iiii}{x}_i^4}+\epsilon \end{array}$$

(15)

where ${\beta }_0$, ${\beta }_i$, ${\beta }_{ii}$, ${\beta }_{iii}$,${\beta }_{iiii}$, ${\beta }_{i,j}$, ${\beta }_{i,j}^{\prime }$ and ${\beta }_{i,j}^{″}$ are the regression coefficients of response surface, ε is the fitting error and k is the number of independent variables. By using matrix B to represent all regression coefficients, the above formula can be expressed in matrix form.

$$Y=XB+\epsilon$$

(16)

The least squares method is used to estimate the regression coefficient of the equation. In the response surface, when approaching the optimal solution, the curvature error between the response surface and the actual model is small, then the necessary condition for the existence of the optimal solution in the model is that the first partial derivative of the least squares expression is zero. Thus, the following can be obtained:

$$\left\{\begin{array}{l}Q(B)={\displaystyle \sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2={(Y-XB)}^T(Y-XB)}\\ \frac{\partial Q(B)}{\partial {\beta }_i}=-2X^{T}Y+2X^{T}B=0\end{array}\right.$$

(17)

where Q is the square of the fitting error, and n is the number of test samples.

The estimation formula of regression coefficient can be obtained as follows.

$$B={(X^{T}X)}^{-1}{X}^{T}Y$$

(18)

The finally fitted response surface model is as follows.

$$\widehat{Y}=XB$$

(19)

4. Optimization Result in Wide Temperature Range

According to the method described above, this paper optimized the PMSM with N30UH and SmCo28, respectively. The goal is to reduce the cogging torque of PMSM at different temperatures while ensuring that the output torque always meets the requirements in wide temperature range.

A total of 800 initial sample data were obtained by dividing the temperature into eight levels, the pole arc coefficient and thickness into five levels and the magnetic pole eccentricity into four levels. Then, these three size parameters are selected as independent variable X, and the maximum cogging torque in wide temperature range is selected as the response value Y. The three cases of PMSM working in wide temperature range, low temperature or high temperature are analyzed, respectively, to find the scheme with the minimum upper limit of cogging torque.

Firstly, the response surfaces of PMSM and the green contour in wide temperature ranges are constructed, as shown in Figure 9 and Figure 10. The darker the color on the response surface, the smaller the cogging torque. The sparser the contour line, the lesser the sensitivity of the cogging torque relative to the change of magnetic pole size and the smaller the influence of machining error on cogging torque. Therefore, the final scheme should be selected in the area with dark color and sparse contour lines, which is the red frame area.

It can be observed that the pole arc coefficient and eccentricity have great influence on cogging torque in wide temperature ranges, while pole thickness has little. The upper limit of cogging torque with two permanent magnet materials both reach the minimum near the pole arc coefficient of 0.85. The cogging torque of the N30UH PMSM decreases with the increase in pole eccentricity. The cogging torque of the SmCo28 PMSM firstly decreases and then increases at the pole eccentricity close to 15 mm. By comparison, it can be found that the cogging torque is more affected by the change of the magnetic pole size when N30UH is adopted.

After finding the scheme with the minimum cogging torque according to the response surface results, finite element calculation is also needed to ensure that the output torque of the final PMSM scheme in wide temperature ranges can always meet the basic performance requirements greater than 10 N·m. Finally, the magnetic pole optimization results of PMSM with two permanent magnet materials in wide temperature ranges are shown in

Table 2. The optimal magnetic pole size and cogging torque results under different working environments.

Permanent Magnets	Working Environment	Polar Arc Coefficient	Pole Thickness (mm)	Pole Eccentricity (mm)	Cogging Torque (N·m)
N30UH	Wide temperature range	0.87	6.90	0.87	0.21
	Low temperature	0.88	6.95	0.88	0.13
	High temperature	0.86	6.50	0.86	0.08
SmCo28	Wide temperature range	0.85	6.02	0.85	0.15
	Low temperature	0.87	5.70	0.87	0.07
	High temperature	0.88	6.95	0.88	0.12

.

Since the temperature rise calculation above shows that the final temperature of permanent magnet reaches −57 °C when the PMSM works at the low temperature of −100 °C and the final temperature reaches 173 °C when the PMSM works at the high temperature of 100 °C, therefore, the PMSMs operating in the low temperature range of −100 °C~−50 °C and the high temperature range of 100 °C~180 °C are also optimized. The optimal magnetic pole schemes under different working environments are also recorded in Table 2.

The results show that when the PMSM works in wide temperature ranges or low temperature environments, the upper limit of cogging torque with SmCo28 is lower, which is a better choice for permanent magnet materials. When the PMSM works in the high temperature environment selected in this paper, it is better to choose N30UH as the permanent magnet material.

According to finite element analysis, no-load back EMF, output torque and cogging torque of SmCo28 PMSM in wide temperature ranges are shown in Figure 11. The no-load back EMF amplitude is 88.22 V at 20 °C, 90.20 V at −100 °C and 85.24 V at 100 °C. The average output torque is 10.44 N·m at 20 °C, 10.80 N·m at −100 °C and 10.19 N·m at 100 °C. The peak-to-peak cogging torque is 0.146 N·m at 20 °C, 0.15 N·m at −100 °C and 0.144 N·m at 100 °C.

5. Prototype and Experiment

In order to verify the effectiveness of optimization, a PMSM prototype is developed based on the scheme with SmCo28 in wide temperature range in Table 2. The outer stator is composed of iron core and three-phase Y-connected windings. The inner rotor is composed of permanent magnets and a back yoke. The rotor is supported by the bearing and drives the bearing to rotate.

Firstly, the no-load back EMF and cogging torque of PMSM at room temperature are measured. The experimental test platform is shown in Figure 12. The rated speed of the PMSM driven by the prime mover is controlled at 13,500 rpm, and the output results are obtained through the dynamometer under no-load operation. As shown in Figure 13 and Figure 14, the measured value of no-load back EMF and cogging torque are both slightly larger than the simulated value. This is because the actual air gap length of prototype is reduced by about 0.15 mm due to the machining accuracy of stator lamination and magnetic steel.

Then, the PMSM prototype, reducer and lead screw are assembled into an integrated actuator by using the connecting mechanism, as shown in Figure 15, which can directly output thrust in a linear direction. The actuator is connected to the rocker arm and the torsion bar of test bench for load test, as shown in Figure 16.

According to the transmission relationship between the actuator and the loading tooling and the torsion stiffness of the torsion bar, the output torque corresponding to the linear force of 100 kN is 15 N·m theoretically. Therefore, the output torque of PMSM can be derived by measuring the linear force output by the actuator. When the PMSM is excited by 90 A rated phase current, the simulation value of output torque is 10.44 N·m; that is, the design value of linear force is 69.6 kN. The actual measured linear force under a rated load is 73.7 kN, which means that the corresponding output torque is 11.07 N·m, which is slightly larger than the design value. This is because the smaller air gap results in larger air gap flux density than the simulation model.

Finally, in order to observe the suppression effect of cogging torque in wide temperature range, the actuator is placed in the thermostat, and the output fluctuation of actuator at different temperatures is tested, as shown in Figure 17. Since the actuator has been integrated, it is difficult to directly test the cogging torque of PMSM. Therefore, the actuator is connected with the tension and pressure sensor, it is operated under light load and the output linear force waveform is observed, as shown in Figure 18.

At 20 °C and 120 °C, the peak value of output linear force is about 1.0 kN, corresponding to cogging torque of 0.15 N·m. At −55 °C, the peak value of output linear force is about 1.1 kN, corresponding to cogging torque of 0.165 N·m. It can be observed that in a wide temperature range, the amplitude change of the actuator output torque can be ignored, the torque fluctuation has been effectively suppressed and the cogging torque is always less than 0.2 N·m. Therefore, the PMSM designed in this paper has good adaptability in wide temperature range.

6. Conclusions

In this paper, the wide temperature range PMSM is taken as the research object, the law of magnetic material performance changing with temperature is revealed, and the suppression effect of eccentric magnetic pole structure on cogging torque at different temperatures is analyzed. Unreasonable schemes are screened out by using temperature rise calculation, and the optimal permanent magnet material selection and magnetic pole structure parameters in wide temperature range, low temperature and high temperature environment are determined based on response surfaces so that the upper limit of cogging torque at different temperatures does not exceed 0.2 N·m. Finally, a prototype is developed, and no-load experiments, load experiments and wide temperature range experiments are carried out, which proved the effectiveness of optimization work.

In the future, the application of water cooling, oil cooling, heat pipe cooling and other cooling methods and the inhibition effect of temperature rise can be studied in the actuator. At the same time, we will further analyze the variation law of motor inductance and other disturbance factors with temperature and carry out anti-interference control strategy research.