Classification of Integrodifferential C∗-Algebras
Abstract
:1. Introduction
2. Characterization of AF-Algebras. Infinite Product of Matrices with Integer Entries
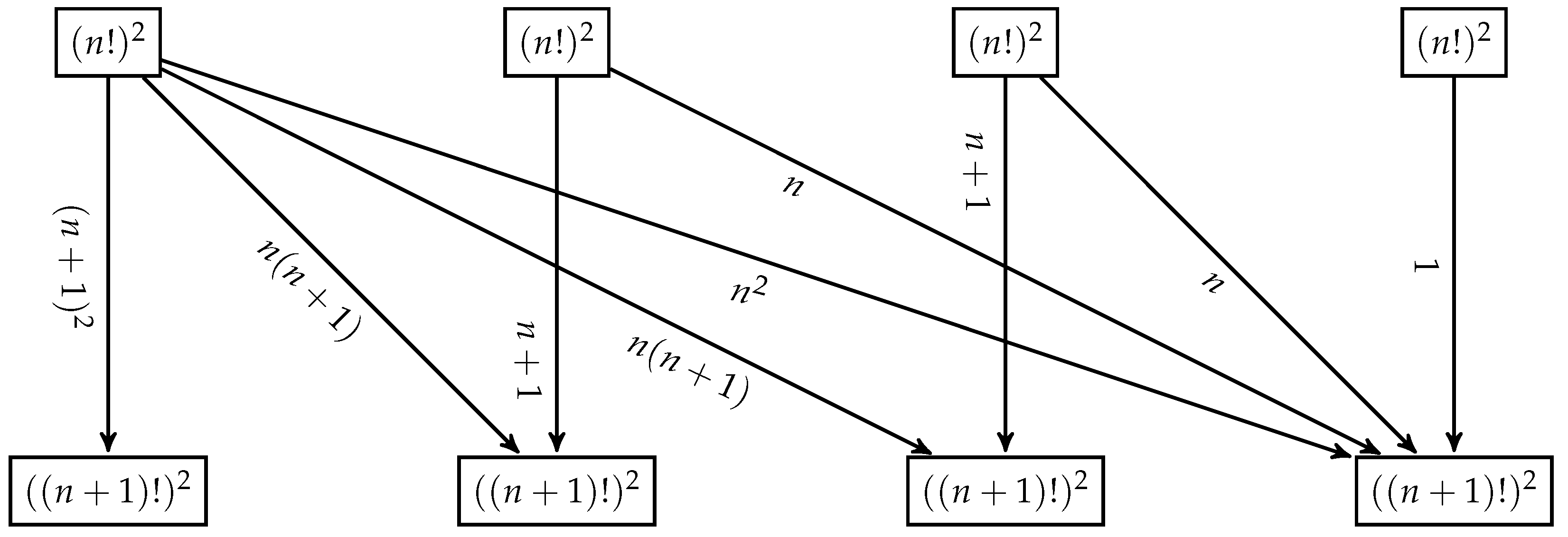
3. Main Results
4. Proof of the Main Results
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rosenkranz, M. A new symbolic method for solving linear two-point boundary value problems on the level of operators. J. Symb. Comput. 2005, 39, 171–199. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Keigher, W. On differential Rota-Baxter algebras. J. Pure Appl. Algebra 2008, 212, 522–540. [Google Scholar] [CrossRef] [Green Version]
- Bavula, V.V. The algebra of integro-differential operators on an affine line and its modules. J. Pure Appl. Algebra 2013, 217, 495–529. [Google Scholar] [CrossRef] [Green Version]
- Guo, L.; Regensburger, G.; Rosenkranz, M. On integro-differential algebras. J. Pure Appl. Algebra 2014, 218, 456–473. [Google Scholar] [CrossRef] [Green Version]
- Pimsner, M.; Voiculescu, D. Imbedding the irrational rotation C*-algebra into an AF-algebra. J. Oper. Theory 1980, 4, 201–220. [Google Scholar]
- Rieffel, M.A. C*-algebras associated with irrational rotations. Pac. J. Math. 1981, 93, 415–429. [Google Scholar] [CrossRef] [Green Version]
- Yin, H.S. A simple proof of the classification of rational rotation C*-algebras. Proc. Am. Math. Soc. 1986, 98, 469–470. [Google Scholar] [CrossRef]
- Elliot, G.A.; Niu, Z. All irrational extended rotation algebras are AF algebras. Can. J. Math. 2015, 67, 810–826. [Google Scholar] [CrossRef] [Green Version]
- Kutsenko, A. Isomorphism between one-dimensional and multidimensional finite difference operators. Commun. Pure Appl. Anal. 2021, 20, 359–368. [Google Scholar] [CrossRef]
- Bratteli, O. Inductive limits of finite dimensional C*-algebras. Trans. Am. Math. Soc. 1972, 171, 195–234. [Google Scholar] [CrossRef] [Green Version]
- Davidson, K. C*-Algebras by Example. In Fields Institute Monographs; American Mathematical Society: Providence, RI, USA, 1997. [Google Scholar]
- Nyland, P.K. Bratteli Diagrams; Norwegian University of Science and Technology: Trondheim, Norway, 2016. [Google Scholar]
- Elliot, G.A. On the classiffication of inductive limits of sequences of semisimple finite-dimensional algebras. J. Algebra 1980, 38, 29–44. [Google Scholar] [CrossRef] [Green Version]
- Effros, E.G.; Handelman, D.E.; Shen, C.-L. Dimension groups and their affine representations. Am. J. Math. 1980, 102, 385–407. [Google Scholar] [CrossRef]
- Rordam, M.; Larsen, F.; Laustsen, N.J. An Introduction to K-Theory for C*-Algebras; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Amini, M.; Elliott, G.A.; Golestani, N. The category of Bratteli diagrams. Can. J. Math. 2015, 67, 990–1023. [Google Scholar] [CrossRef] [Green Version]
- Ghasemi, S.; Kubis, W. Universal AF-algebras. J. Funct. Anal. 2020, 279, 108590. [Google Scholar] [CrossRef]
- Glimm, J.G. On a certain class of operator algebras. Trans. Am. Math. Soc. 1960, 95, 318–340. [Google Scholar] [CrossRef]
- Kutsenko, A.A. Matrix representations of multidimensional integral and ergodic operators. Appl. Math. Comput. 2020, 369, 124818. [Google Scholar] [CrossRef] [Green Version]


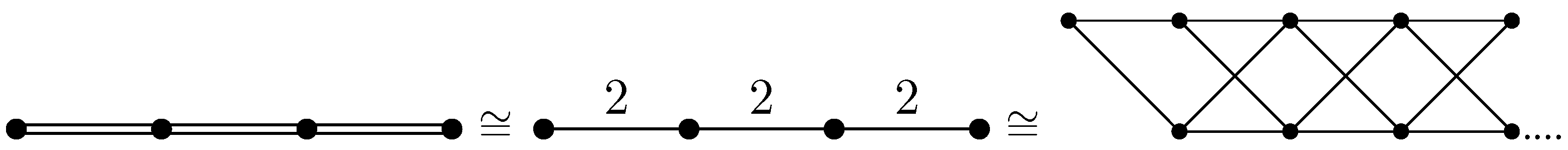
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kutsenko, A.A. Classification of Integrodifferential C∗-Algebras. Symmetry 2021, 13, 1900. https://doi.org/10.3390/sym13101900
Kutsenko AA. Classification of Integrodifferential C∗-Algebras. Symmetry. 2021; 13(10):1900. https://doi.org/10.3390/sym13101900
Chicago/Turabian StyleKutsenko, Anton A. 2021. "Classification of Integrodifferential C∗-Algebras" Symmetry 13, no. 10: 1900. https://doi.org/10.3390/sym13101900




