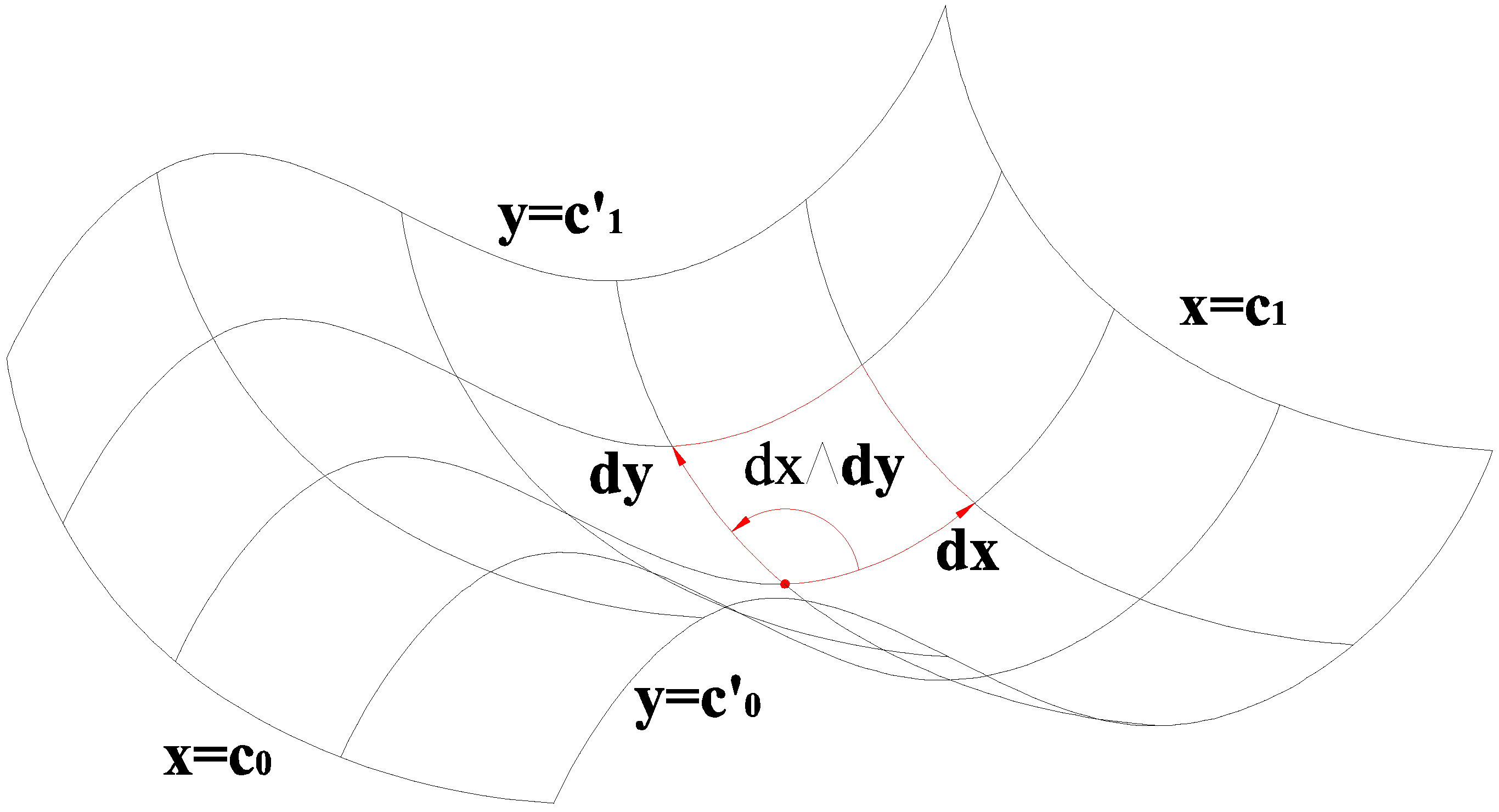Theory of Spinors in Curved Space-Time

Abstract

By means of Clifford Algebra, a unified language and tool to describe the rules of nature, this paper systematically discusses the dynamics and properties of spinor fields in curved space-time, such as the decomposition of the spinor connection, the classical approximation of the Dirac equation, the energy-momentum tensor of spinors and so on. To split the spinor connection into the Keller connection ${\mathsf{{\rm Y}}}_{\mu }\in {\mathsf{\Lambda }}^1$ and the pseudo-vector potential ${\mathsf{\Omega }}_{\mu }\in {\mathsf{\Lambda }}^3$ not only makes the calculation simpler, but also highlights their different physical meanings. The representation of the new spinor connection is dependent only on the metric, but not on the Dirac matrix. Only in the new form of connection can we clearly define the classical concepts for the spinor field and then derive its complete classical dynamics, that is, Newton’s second law of particles. To study the interaction between space-time and fermion, we need an explicit form of the energy-momentum tensor of spinor fields; however, the energy-momentum tensor is closely related to the tetrad, and the tetrad cannot be uniquely determined by the metric. This uncertainty increases the difficulty of deriving rigorous expression. In this paper, through a specific representation of tetrad, we derive the concrete energy-momentum tensor and its classical approximation. In the derivation of energy-momentum tensor, we obtain a spinor coefficient table $S_{ab}^{\mu \nu }$, which plays an important role in the interaction between spinor and gravity. From this paper we find that Clifford algebra has irreplaceable advantages in the study of geometry and physics.

1. Introduction

The Dirac equation for spinor is a magic equation, which includes many secrets of nature. The interaction between spinors and gravity is the most complicated and subtle interaction in the universe, which involves the basic problem of a unified quantum theory and general relativity. The spinor connection has been constructed and researched in many works [1,2,3,4,5]. The spinor field is used to explain the accelerating expansion of the universe and dark matter and dark energy [6,7,8,9,10,11]. In the previous works, we usually used spinor covariant derivative directly, in which the spinor connection takes a compact form and its physical meaning becomes ambiguous. In this paper, by means of Clifford algebra, we split the spinor connection into geometrical and dynamical parts $({\mathsf{{\rm Y}}}_{\mu },{\mathsf{\Omega }}_{\mu })$, respectively [12]. This form of connection is determined by metric, independent of Dirac matrices. Only in this representation, we can clearly define classical concepts such as coordinate, speed, momentum and spin for a spinor, and then derive the classical mechanics in detail. ${\mathsf{{\rm Y}}}_{\mu }\in {\mathsf{\Lambda }}^1$ only corresponds to the geometrical calculations, but ${\mathsf{\Omega }}_{\mu }\in {\mathsf{\Lambda }}^3$ leads to dynamical effects. ${\mathsf{\Omega }}_{\mu }$ couples with the spin $S^{\mu }$ of a spinor, which provides location and navigation functions for a spinor with little energy. This term is also related with the origin of the magnetic field of a celestial body [12]. So this form of connection is helpful in understanding the subtle relation between spinor and space-time.

The classical theory for a spinor moving in gravitational field is firstly studied by Mathisson [13], and then developed by Papapetrou [14] and Dixon [15]. A detailed derivation can be found in [16]. By the commutator of the covariant derivative of the spinor $[{\nabla }_{\alpha },{\nabla }_{\beta }]$, we obtain an extra approximate acceleration of the spinor as follows

$$\begin{array}{c}\hfill a_{\alpha }\left(x^{\mu }\right)=-\frac{\hslash }{4m}{R}_{\alpha \beta \gamma \delta }\left(x^{\mu }\right)u^{\beta }\left(x^{\mu }\right)S^{\gamma \delta }\left(x^{\mu }\right),\end{array}$$

(1)

where $R_{\alpha \beta \gamma \delta }$ is the Riemann curvature, $u^{\alpha }$ 4-vector speed and $S^{\gamma \delta }$ the half commutator of the Dirac matrices.

Equation (1) leads to the violation of Einstein’s equivalence principle. This problem was discussed by many authors [16,17,18,19,20,21,22,23]. In [17], the exact Cini–Touschek transformation and the ultra-relativistic limit of the fermion theory were derived, but the Foldy–Wouthuysen transformation is not uniquely defined. The following calculations also show that the usual covariant derivative ${\nabla }_{\mu }$ includes cross terms, which is not parallel to the speed $u^{\mu }$ of the spinor.

To study the coupling effect of spinor and space-time, we need the energy-momentum tensor (EMT) of spinor in curved space-time. The interaction of spinor and gravity is considered by H. Weyl as early as in 1929 [24]. There are some approaches to the general expression of EMT of spinors in curved space-time [4,8,25,26]; however, the formalisms are usually quite complicated for practical calculation and different from each other. In [6,7,8,9,11], the space-time is usually Friedmann–Lemaitre–Robertson–Walker type with diagonal metric. The energy-momentum tensor $T_{\mu \nu }$ of spinors can be directly derived from Lagrangian of the spinor field in this case. In [4,25], according to the Pauli’s theorem

$$\begin{array}{c}\hfill \delta {\gamma }^{\alpha }=\frac{1}{2}{\gamma }_{\beta }\delta g^{\alpha \beta }+[{\gamma }^{\alpha },M],\end{array}$$

(2)

where M is a traceless matrix related to the frame transformation, the EMT for Dirac spinor $\varphi$ was derived as follows,

$$\begin{array}{c}\hfill T^{\mu \nu }=\frac{1}{2}\Re \langle {\varphi }^{†}({\gamma }^{\mu }i{\nabla }^{\nu }+{\gamma }^{\nu }i{\nabla }^{\mu })\varphi \rangle ,\end{array}$$

(3)

where ${\varphi }^{†}={\varphi }^{+}\gamma$ is the Dirac conjugation, ${\nabla }^{\mu }$ is the usual covariant derivatives for spinor. A detailed calculation for variation of action was performed in [8], and the results were a little different from (2) and (3).

The following calculation shows that, M is still related with $\delta g^{\mu \nu }$, and provides nonzero contribution to $T^{\mu \nu }$ in general cases. The exact form of EMT is much more complex than (3), which includes some important effects overlooked previously. The covariant derivatives operator $i{\nabla }_{\mu }$ for spinor includes components in grade-3 Clifford algebra ${\mathsf{\Lambda }}^3$, which is not parallel to the classical momentum $p_{\mu }\in {\mathsf{\Lambda }}^1$. The derivation of rigorous $T_{\mu \nu }$ is quite difficult due to non-uniqueness representation and complicated formalism of vierbein or tetrad frames. In this paper, we provide a systematical and detailed calculation for EMT of spinors. We clearly establish the relations between tetrad and metric at first, and then solve the Euler derivatives with respect to $g_{\mu \nu }$ to obtain an explicit and rigorous form of $T_{\mu \nu }$.

From the results we find some new and interesting conclusions. Besides the usual kinetic energy momentum term, we find three kinds of other additional terms in EMT of bispinor. One is the self interactive potential, which acts like negative pressure. The other reflects the interaction of momentum $p^{\mu }$ with tetrad, which vanishes in classical approximation. The third is the spin-gravity coupling term ${\mathsf{\Omega }}_{\alpha }{S}^{\alpha }$, which is a higher-order infinitesimal in weak field, but becomes important in a neutron star. All these results are based on Clifford algebra decomposition of usual spin connection ${\mathsf{\Gamma }}_{\mu }$ into geometrical part ${\mathsf{{\rm Y}}}_{\mu }$ and dynamical part ${\mathsf{\Omega }}_{\mu }$, which not only makes calculation simpler, but also highlights their different physical meanings. In the calculation of tetrad formalism, we find a new spinor coefficient table $S_{ab}^{\mu \nu }$, which plays an important role in the interaction of spinor with gravity and appears in many places.

This paper is an improvement and synthesis of the previous works arXiv:gr-qc/0610001 and arXiv:gr-qc/0612106. The materials in this paper are organized as follows: In the next section, we specify notations and conventions used in the paper, and derive the spinor connections in form of Clifford algebra. In Section 3, we set up the relations between tetrad and metric, which is the technical foundations of classical approximation of Dirac equation and EMT of spinor. We derive the classical approximation of spinor theory in Section 4, and then calculate the EMT in Section 5. We provide some simple discussions in the last section.

2. Simplification of the Spinor Connection

Clifford algebra is a unified language and efficient tool for physics. The variables and equations expressed by Clifford algebra have a neat and elegant form, and the calculation has a standard but simple procedure [12]. At first we introduce some notations and conventions used in this paper. We take $\hslash =c=1$ as units. The element of space-time is described by

$$\begin{array}{c}\hfill d\mathbf{x}={\gamma }_{\mu }d{x}^{\mu }={\gamma }^{\mu }d{x}_{\mu }={\gamma }_a\delta X^a={\gamma }^a\delta X_a,\end{array}$$

(4)

in which ${\gamma }_a$ stands for tetrad, and ${\gamma }^a$ for co-frame, which satisfies the following $C{\ell }_{1,3}$ Clifford algebra,

$$\begin{array}{cc}& {\gamma }_a{\gamma }_b+{\gamma }_b{\gamma }_a=2{\eta }_{ab},{\gamma }_{\mu }{\gamma }_{\nu }+{\gamma }_{\nu }{\gamma }_{\mu }=2g_{\mu \nu },\end{array}$$

(5)

$$\begin{array}{cc}& {\gamma }_{\mu }=f_{\mu }^a{\gamma }_a,{\gamma }^{\mu }=f_a^{\mu }{\gamma }^a,{\eta }_{ab}=diag(1,-1,-1,-1).\end{array}$$

(6)

The relation between the local frame coefficient $(f_a^{\mu },f_{\mu }^a)$ and metric is given by

$$\begin{array}{c}\hfill f_{\mu }^a{f}_b^{\mu }={\delta }_b^a,f_{\mu }^a{f}_a^{\nu }={\delta }_{\mu }^{\nu },f_a^{\mu }{f}_b^{\nu }{\eta }^{ab}=g^{\mu \nu },f_{\mu }^a{f}_{\nu }^b{\eta }_{ab}=g_{\mu \nu }.\end{array}$$

(7)

We use the Latin characters $(a,b\in \{0,1,2,3\left\}\right)$ for the Minkowski indices, Greek characters $(\mu ,\nu \in \{0,1,2,3\left\}\right)$ for the curvilinear indices, and $(j,k,l,m,n\in \{1,2,3\left\}\right)$ for spatial indices. For local frame coefficient in matrix form $\left(f_{\mu }^a\right)$ and $\left(f_a^{\mu }\right)$, the curvilinear index $\mu$ is row index and Minkowski index a is column index. The Pauli and Dirac matrices in Minkowski space-time are given by

$$\begin{array}{cc}& {\sigma }^a\equiv \left\{\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),\left(\begin{array}{cc}0& 1\\ 1& 0\end{array}\right),\left(\begin{array}{cc}0& -i\\ i& 0\end{array}\right),\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\right\},\end{array}$$

(8)

$$\begin{array}{cc}& {\tilde{\sigma }}^a\equiv ({\sigma }^0,-\overrightarrow{\sigma }),\overrightarrow{\sigma }=({\sigma }^1,{\sigma }^2,{\sigma }^3),\end{array}$$

(9)

$$\begin{array}{cc}& \begin{array}{c}{\gamma }^a\equiv \left(\begin{array}{cc}0& {\tilde{\sigma }}^a\\ {\sigma }^a& 0\end{array}\right),{\gamma }^5=\left(\begin{array}{cc}I& 0\\ 0& -I\end{array}\right).\hfill \end{array}\end{array}$$

(10)

Since the Clifford algebra is isomorphic to the matrix algebra, we need not distinguish tetrad ${\gamma }^a$ and matrix ${\gamma }^a$ in algebraic calculation.

There are several definitions for Clifford algebra [27,28]. Clifford algebra is also called geometric algebra. If the definition is directly related to geometric concepts, it will bring great convenience to the study and research of geometry [12,29].

Definition 1.

Assume the element of an $n=p+q$ dimensional space-time ${\mathbb{M}}^{p,q}$ over $\mathbb{R}$ is given by $\left(4\right)$. The space-time is endowed with distance $ds=\left|d\mathbf{x}\right|$ and oriented volumes $d{V}_k$ calculated by

$$\begin{array}{ccc}\hfill d{\mathbf{x}}^2& =& \frac{1}{2}({\gamma }_{\mu }{\gamma }_{\nu }+{\gamma }_{\nu }{\gamma }_{\mu })d{x}^{\mu }d{x}^{\nu }=g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }={\eta }_{ab}\delta X^a\delta X^b,\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill d{V}_k& =& d{\mathbf{x}}_1\wedge d{\mathbf{x}}_2\wedge \cdots \wedge d{\mathbf{x}}_k={\gamma }_{\mu \nu \cdots \omega }d{x}_1^{\mu }d{x}_2^{\nu }\cdots d{x}_k^{\omega },(1\le k\le n),\hfill \end{array}$$

(12)

in which the Minkowski metric $\left({\eta }_{ab}\right)=diag(I_p,-I_q)$, and Grassmann basis ${\gamma }_{\mu \nu \cdots \omega }={\gamma }_{\mu }\wedge {\gamma }_{\nu }\wedge \cdots \wedge {\gamma }_{\omega }\in {\mathsf{\Lambda }}^k{\mathbb{M}}^{p,q}$. Then the following number with basis

$$\begin{array}{c}\hfill C=c_{0}I+c_{\mu }{\gamma }^{\mu }+c_{\mu \nu }{\gamma }^{\mu \nu }+\cdots +c_{12\cdots n}{\gamma }^{12\cdots n},(\forall c_k\in \mathbb{R})\end{array}$$

(13)

together with multiplication rule of basis given in $\left(11\right)$ and associativity define the $2^n$-dimensional real universalClifford algebra $C{\ell }_{p,q}$.

The geometrical meanings of elements $d\mathbf{x},d\mathbf{y},d\mathbf{x}\wedge d\mathbf{y}$ are shown in Figure 1.

Figure 1 shows that the exterior product is oriented volume of the parallel polyhedron of the line element vectors, and the Grassmann basis ${\gamma }_{ab\cdots c}$ is just the orthonormal basis of k-dimensional volume. Since the length of a line element and the volumes of each grade constitute the fundamental contents of geometry, the Grassmann basis set becomes units to represent various geometric and physical quantities, which are special kinds of tensors.

By straightforward calculation we have [5,12,29]

Theorem 1.

For $C{\ell }_{1,3}$, we have the following useful relations

$$\begin{array}{cc}& I,{\gamma }^a,{\gamma }^{ab}=\frac{i}{2}{ϵ}^{abcd}{\gamma }_{cd}{\gamma }^5,{\gamma }^{abc}=i{ϵ}^{abcd}{\gamma }_d{\gamma }^5,{\gamma }^{0123}=-i{\gamma }^5.\end{array}$$

(14)

$$\begin{array}{cc}& {\gamma }^{\mu }{\gamma }^{\nu }=g^{\mu \nu }+{\gamma }^{\mu \nu },{\gamma }^{\mu \nu }{\gamma }^{\omega }={\gamma }^{\mu }{g}^{\nu \omega }-{\gamma }^{\nu }{g}^{\mu \omega }+{\gamma }^{\mu \nu \omega }.\end{array}$$

(15)

The above theorem provides several often used relations between the Clifford products and the Grassmann products. Since the calculations of geometric and physical quantities are mostly in the form of Clifford products, but only by expressing these forms as Grassmann products, their geometric and physical significance is clear. Thus the above transformation relations become fundamental and important.

For Dirac equation in curved space-time without torsion, we have [1,2,3,4,30],

$$\begin{array}{c}\hfill {\gamma }^{\mu }(i{\nabla }_{\mu }-e{A}_{\mu })\varphi =m\varphi ,{\nabla }_{\mu }\varphi =({\partial }_{\mu }+{\mathsf{\Gamma }}_{\mu })\varphi ,\end{array}$$

(16)

in which the spinor connection is given by

$$\begin{array}{ccc}\hfill {\mathsf{\Gamma }}_{\mu }& \equiv & \frac{1}{4}{\gamma }_{\nu }{\gamma }_{;\mu }^{\nu }=\frac{1}{4}{\gamma }^{\nu }{\gamma }_{\nu ;\mu }=\frac{1}{4}{\gamma }^{\nu }({\partial }_{\mu }{\gamma }_{\nu }-{\mathsf{\Gamma }}_{\mu \nu }^{\alpha }{\gamma }_{\alpha }).\hfill \end{array}$$

(17)

The total spinor connection ${\gamma }^{\mu }{\mathsf{\Gamma }}_{\mu }\in {\mathsf{\Lambda }}^1\cup {\mathsf{\Lambda }}^3$. Clearly, ${\gamma }^{\mu }{\mathsf{\Gamma }}_{\mu }$ is a Clifford product, and its geometric and physical significance is unclear. Only by projecting it onto the Grassmann basis ${\gamma }_a$ and ${\gamma }_{abc}$, its geometric and physical meanings become clear [12].

Theorem 2.

Dirac equation $\left(16\right)$ can be rewritten in the following Hermitian form

$$\begin{array}{c}\hfill ({\alpha }^{\mu }{\widehat{p}}_{\mu }-S^{\mu }{\mathsf{\Omega }}_{\mu })\varphi =m{\gamma }^0\varphi ,\end{array}$$

(18)

in which ${\alpha }^{\mu }$ is current operator, ${\widehat{p}}_{\mu }$ momentum and $S^{\mu }$ spin operator,

$$\begin{array}{c}\hfill {\alpha }^{\mu }=diag({\sigma }^{\mu },{\tilde{\sigma }}^{\mu }),{\widehat{p}}_{\mu }=i({\partial }_{\mu }+{\mathsf{{\rm Y}}}_{\mu })-e{A}_{\mu },S^{\mu }=\frac{1}{2}diag({\sigma }^{\mu },-{\tilde{\sigma }}^{\mu }),\end{array}$$

(19)

where ${\mathsf{{\rm Y}}}_{\mu }$ is Keller connection and ${\mathsf{\Omega }}_{\mu }$ Gu–Nester potential, they are respectively defined as

$$\begin{array}{ccc}\hfill {\mathsf{{\rm Y}}}_{\nu }& \equiv & \frac{1}{2}{f}_a^{\mu }({\partial }_{\nu }{f}_{\mu }^a-{\partial }_{\mu }{f}_{\nu }^a)=\frac{1}{2}\left[{\partial }_{\nu }(ln\sqrt{g})-f_a^{\mu }{\partial }_{\mu }{f}_{\nu }^a\right],\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}^{\alpha }& \equiv & \frac{1}{2}{f}_d^{\alpha }{f}_a^{\mu }{f}_b^{\nu }{\partial }_{\mu }{f}_{\nu }^e{ϵ}^{abcd}{\eta }_{ce}=\frac{1}{4\sqrt{g}}{ϵ}^{\alpha \mu \nu \omega }{\eta }_{ab}{f}_{\omega }^a({\partial }_{\mu }{f}_{\nu }^b-{\partial }_{\nu }{f}_{\mu }^b).\hfill \end{array}$$

(21)

Proof. 

By (14) and (15), we have the following Clifford calculus

$$\begin{array}{ccc}\hfill {\gamma }^{\mu }{\mathsf{\Gamma }}_{\mu }& =& \frac{1}{4}{\gamma }^{\mu }{\gamma }^{\nu }({\partial }_{\mu }{\gamma }_{\nu }-{\mathsf{\Gamma }}_{\mu \nu }^{\alpha }{\gamma }_{\alpha })=\frac{1}{4}(g^{\mu \nu }+{\gamma }^{\mu \nu })({\partial }_{\mu }{\gamma }_{\nu }-{\mathsf{\Gamma }}_{\mu \nu }^{\alpha }{\gamma }_{\alpha })\hfill \\ & =& \frac{1}{4}({\gamma }_{;\mu }^{\mu }+{\gamma }^{\mu \nu }{\partial }_{\mu }{\gamma }_{\nu })=\frac{1}{4}({\partial }_{\mu }{\gamma }^{\mu }+{\partial }_{\mu }ln\left(\sqrt{g}\right){\gamma }^{\mu })+\frac{1}{4}{f}_a^{\mu }{f}_b^{\nu }{\partial }_{\mu }{f}_{\nu }^c{\gamma }^{ab}{\gamma }_c\hfill \\ & =& \frac{1}{4}[{\gamma }^a{\partial }_{\mu }{f}_a^{\mu }+\left(f_a^{\nu }{\partial }_{\mu }{f}_{\nu }^a\right){\gamma }^{\mu }]+\frac{1}{4}{f}_a^{\mu }{f}_b^{\nu }{\partial }_{\mu }{f}_{\nu }^d{\gamma }^{ab}{\gamma }^c{\eta }_{cd}\hfill \\ & =& \frac{1}{4}{f}_a^{\mu }{\gamma }^{\nu }(-{\partial }_{\mu }{f}_{\nu }^a+{\partial }_{\nu }{f}_{\mu }^a)+\frac{1}{4}{f}_a^{\mu }{f}_b^{\nu }{\partial }_{\mu }{f}_{\nu }^d({\eta }^{bc}{\gamma }^a-{\eta }^{ac}{\gamma }^b+{\gamma }^{abc}){\eta }_{cd}\hfill \\ & =& \frac{1}{2}{f}_a^{\mu }{\gamma }^{\nu }({\partial }_{\nu }{f}_{\mu }^a-{\partial }_{\mu }{f}_{\nu }^a)+\frac{1}{4}{f}_a^{\mu }{f}_b^{\nu }{\partial }_{\mu }{f}_{\nu }^e{\gamma }^{abc}{\eta }_{ce}\hfill \\ & =& {\mathsf{{\rm Y}}}_{\mu }{\gamma }^{\mu }+\frac{i}{2}{\mathsf{\Omega }}^{\alpha }{\gamma }_{\alpha }{\gamma }^5.\hfill \end{array}$$

(22)

Substituting it into (16) and multiplying the equation by ${\gamma }^0$, we prove the theorem. □

The following discussion shows that ${\mathsf{{\rm Y}}}_{\mu }$ and ${\mathsf{\Omega }}_{\mu }$ have different physical meanings. ${\partial }_{\mu }+{\mathsf{{\rm Y}}}_{\mu }$ as a whole operator is similar to the covariant derivatives ${\nabla }_{\mu }$ for vector, it only has a geometrical effect; however, ${\mathsf{\Omega }}_{\mu }$ couples with the spin of a particle and leads to the magnetic field of a celestial body [12]. ${\mathsf{\Omega }}_{\mu }\equiv 0$ is a necessary condition for the metric to be diagonalized. If the gravitational field is generated by a rotating ball, the corresponding metric, similar to the Kerr one, cannot be diagonalized. In this case, the spin-gravity coupling term has a non-zero coupling effect.

In axisymmetric and asymptotically flat space-time we have the line element in quasi-spherical coordinate system [31]

$$\begin{array}{cc}& d\mathbf{x}={\gamma }_0\sqrt{U}(dt+Wd\phi )+\sqrt{V}({\gamma }_{1}dr+{\gamma }_{2}rd\theta )+{\gamma }_3\sqrt{U^{-1}}rsin\theta d\phi ,\end{array}$$

(23)

$$\begin{array}{cc}& d{\mathbf{x}}^2=U{(dt+Wd\phi )}^2-V(d{r}^2+r^{2}d{\theta }^2)-U^{-1}{r}^2{sin}^2\theta d{\phi }^2,\end{array}$$

(24)

in which $(U,V,W)$ is just functions of $(r,\theta )$. As $r\to \infty$ we have

$$\begin{array}{c}\hfill U\to 1-\frac{2m}{r},W\to \frac{4L}{r}{sin}^2\theta ,V\to 1+\frac{2m}{r},\end{array}$$

(25)

where $(m,L)$ are mass and angular momentum of the star, respectively. For common stars and planets we always have $r\gg m\gg L$. For example, we have $m\dot{=}3$ km for the sun. The nonzero tetrad coefficients of metric (23) are given by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{f}_t^0=\sqrt{U},f_r^1=\sqrt{V},f_{\theta }^2=r\sqrt{V},f_{\phi }^3=\frac{rsin\theta }{\sqrt{U}},f_{\phi }^0=\sqrt{U}W,\hfill \\ f_0^t=\frac{1}{\sqrt{U}},f_1^r=\frac{1}{\sqrt{V}},f_2^{\theta }=\frac{1}{r\sqrt{V}},f_3^{\phi }=\frac{\sqrt{U}}{rsin\theta },f_3^t=\frac{-\sqrt{U}W}{rsin\theta }.\hfill \end{array}\right.\end{array}$$

(26)

Substituting (26) into (21) or the following (54), we obtain

$$\begin{array}{ccc}\hfill {\mathsf{\Omega }}^{\alpha }& =& f_0^t{f}_1^r{f}_2^{\theta }{f}_3^{\phi }(0,{\partial }_{\theta }{g}_{t\phi },-{\partial }_r{g}_{t\phi },0)\hfill \\ & =& {\left(V{r}^{2}sin\theta \right)}^{-1}\left(0,{\partial }_{\theta }\left(UW\right),-{\partial }_r\left(UW\right),0\right)\hfill \\ & \to & \frac{4L}{r^4}(0,2rcos\theta ,sin\theta ,0).\hfill \end{array}$$

(27)

By (27) we find that the intensity of ${\mathsf{\Omega }}^{\alpha }$ is proportional to the angular momentum of the star, and its force line is given by

$$\begin{array}{c}\hfill \frac{d{x}^{\mu }}{ds}={\mathsf{\Omega }}^{\mu }\Rightarrow \frac{dr}{d\theta }=\frac{2rcos\theta }{sin\theta }\iff r=R{sin}^2\theta .\end{array}$$

(28)

Equation (28) shows that, the force lines of ${\mathsf{\Omega }}^{\alpha }$ is just the magnetic lines of a magnetic dipole. According to the above results, we know that the spin-gravity coupling potential of charged particles will certainly induce a macroscopic dipolar magnetic field for a star, and it should be approximately in accordance with the Schuster–Wilson–Blackett relation [12].

For diagonal metric

$$\begin{array}{c}\hfill g_{\mu \nu }=\mathrm{diag}(N_0^2,-N_1^2,-N_2^2,-N_3^2),\sqrt{g}=N_0{N}_1{N}_2{N}_3,\end{array}$$

(29)

where $N_{\mu }=N_{\mu }\left(x^{\alpha }\right)$, we have ${\mathsf{\Omega }}_{\mu }\equiv 0$ and

$$\begin{array}{c}\hfill {\gamma }^{\mu }=\left(\frac{{\gamma }^0}{N_0},\frac{{\gamma }^1}{N_1},\frac{{\gamma }^2}{N_2},\frac{{\gamma }^3}{N_3}\right),{\mathsf{{\rm Y}}}_{\mu }=\frac{1}{2}{\partial }_{\mu }ln\left(\frac{\sqrt{g}}{N_{\mu }}\right).\end{array}$$

(30)

For Dirac equation in Schwarzschild metric,

$$\begin{array}{c}\hfill g_{\mu \nu }=diag(B\left(r\right),-A\left(r\right),-r^2,-r^2{sin}^2\theta ),\end{array}$$

(31)

we have

$$\begin{array}{c}\hfill {\gamma }^{\mu }=\left(\frac{{\gamma }^0}{\sqrt{B}},\frac{{\gamma }^1}{\sqrt{A}},\frac{{\gamma }^2}{r},\frac{{\gamma }^3}{rsin\theta }\right),{\mathsf{{\rm Y}}}_{\mu }=\left(1,\frac{1}{r}+\frac{B^{\prime }}{4B},\frac{1}{2}cot\theta ,0\right).\end{array}$$

(32)

The Dirac equation for free spinor is given by

$$\begin{array}{c}\hfill i\left(\frac{{\gamma }^0}{\sqrt{B}}{\partial }_t+\frac{{\gamma }^1}{\sqrt{A}}({\partial }_r+\frac{1}{r}+\frac{B^{\prime }}{4B})+\frac{{\gamma }^2}{r}({\partial }_{\theta }+\frac{1}{2}cot\theta )+\frac{{\gamma }^3}{rsin\theta }{\partial }_{\phi }\right)\varphi =m\varphi .\end{array}$$

(33)

Setting $A=B=1$, we obtain the Dirac equation in a spherical coordinate system. In contrast with the spinor in the Cartesian coordinate system, the spinor in the (33) includes an implicit rotational transformation [12].

3. Relations between Tetrad and Metric

Different from the cases of vector and tensor, in general relativity the equation of spinor fields depends on the local tetrad frame. The tetrad ${\gamma }^{\alpha }$ can be only determined by metric to an arbitrary Lorentz transformation. This situation makes the derivation of EMT quite complicated. In this section, we provide an explicit representation of tetrad and derive the EMT of spinor based on this representation. For convenience to check the results by computer, we denote the element by $d{x}^{\mu }=(dx,dy,dz,cdt)$ and $\delta X^a=(\delta X,\delta Y,\delta Z,c\delta T)$.

For metric $g_{\mu \nu }$, not losing generality we assume that, in the neighborhood of $x^{\mu }$, $d{x}^0$ is time-like and $(d{x}^1,d{x}^2,d{x}^3)$ are space-like. This means $g_{00}>0$, $g_{kk}\le 0(k\ne 0)$, and the following definitions of $J_k$ are real numbers

$$\begin{array}{cc}& J_1=\sqrt{-g_{11}},J_2=\sqrt{\left|\begin{array}{cc}{g}_{11}& g_{12}\\ g_{21}& g_{22}\end{array}\right|},J_3=\sqrt{-\left|\begin{array}{ccc}{g}_{11}& g_{12}& g_{13}\\ g_{21}& g_{22}& g_{23}\\ g_{31}& g_{32}& g_{33}\end{array}\right|},J_0=\sqrt{-det\left(g\right)}.\end{array}$$

(34)

$$\begin{array}{cc}& u_1=\left|\begin{array}{cc}{g}_{11}& g_{12}\\ g_{31}& g_{32}\end{array}\right|,u_2=\left|\begin{array}{cc}{g}_{11}& g_{12}\\ g_{01}& g_{02}\end{array}\right|,u_3=\left|\begin{array}{cc}{g}_{21}& g_{22}\\ g_{31}& g_{32}\end{array}\right|,\end{array}$$

(35)

$$\begin{array}{cc}& v_1=\left|\begin{array}{ccc}{g}_{12}& g_{13}& g_{10}\\ g_{22}& g_{23}& g_{20}\\ g_{32}& g_{33}& g_{30}\end{array}\right|,v_2=\left|\begin{array}{ccc}{g}_{11}& g_{13}& g_{10}\\ g_{21}& g_{23}& g_{20}\\ g_{31}& g_{33}& g_{30}\end{array}\right|,v_3=\left|\begin{array}{ccc}{g}_{11}& g_{12}& g_{10}\\ g_{21}& g_{22}& g_{20}\\ g_{31}& g_{32}& g_{30}\end{array}\right|.\end{array}$$

(36)

The following conclusions can be checked by computer program.

Theorem 3.

For LU decomposition of matrix $\left(g_{\mu \nu }\right)$

$$\begin{array}{c}\hfill \left(g_{\mu \nu }\right)=L\left({\eta }_{ab}\right)L^{+},\left(g^{\mu \nu }\right)=U\left({\eta }_{ab}\right)U^{+},U=L^{*}={\left(L^{+}\right)}^{-1},\end{array}$$

(37)

with positive diagonal elements, we have the following unique solution

$$\begin{array}{c}\hfill L=\left(L_{\mu }^a\right)=\left(\begin{array}{cccc}-\frac{g_{11}}{J_1}& 0& 0& 0\\ -\frac{g_{21}}{J_1}& \frac{J_2}{J_1}& 0& 0\\ -\frac{g_{31}}{J_1}& \frac{u_1}{J_1{J}_2}& \frac{J_3}{J_2}& 0\\ -\frac{g_{01}}{J_1}& \frac{u_2}{J_1{J}_2}& -\frac{v_3}{J_2{J}_3}& \frac{J_0}{J_3}\end{array}\right),\end{array}$$

(38)

$$\begin{array}{c}\hfill U=\left(U_a^{\mu }\right)=\left(\begin{array}{cccc}\frac{1}{J_1}& \frac{g_{21}}{J_1{J}_2}& \frac{u_3}{J_2{J}_3}& \frac{v_1}{J_3{J}_0}\\ 0& \frac{J_1}{J_2}& -\frac{u_1}{J_2{J}_3}& -\frac{v_2}{J_3{J}_0}\\ 0& 0& \frac{J_2}{J_3}& \frac{v_3}{J_3{J}_0}\\ 0& 0& 0& \frac{J_3}{J_0}\end{array}\right).\end{array}$$

(39)

Theorem 4.

For any solution of tetrad $\left(7\right)$ in matrix form $\left(f_{\mu }^a\right)$ and $\left(f_a^{\mu }\right)$, there exists a local Lorentz transformation $\delta {X^{\prime }}^a={\mathsf{\Lambda }}_b^a\delta X^b$ independent of $g_{\mu \nu }$, such that

$$\begin{array}{c}\hfill \left(f_{\mu }^a\right)=L{\mathsf{\Lambda }}^{+},\left(f_a^{\mu }\right)=U{\mathsf{\Lambda }}^{-1},\end{array}$$

(40)

where $\mathsf{\Lambda }=\left({\mathsf{\Lambda }}_b^a\right)$ stands for the matrix of Lorentz transformation.

Proof. 

For any solution (7) we have

$$\begin{array}{c}\hfill \left(g_{\mu \nu }\right)=L\left({\eta }_{ab}\right)L^{+}=\left(f_{\mu }^a\right)\left({\eta }_{ab}\right){\left(f_{\mu }^a\right)}^{+}\iff L^{-1}\left(f_{\mu }^a\right)\left({\eta }_{ab}\right){\left(L^{-1}\left(f_{\mu }^a\right)\right)}^{+}=\left({\eta }_{ab}\right).\end{array}$$

(41)

So we have a Lorentz transformation matrix $\mathsf{\Lambda }=\left({\mathsf{\Lambda }}_b^a\right)$, such that

$$\begin{array}{c}\hfill L^{-1}\left(f_{\mu }^a\right)={\mathsf{\Lambda }}^{+}\iff \left(f_{\mu }^a\right)=L{\mathsf{\Lambda }}^{+},or{f}_{\mu }^a=L_{\mu }^b{\mathsf{\Lambda }}_b^a.\end{array}$$

(42)

Similarly we have $\left(f_a^{\mu }\right)=U{\mathsf{\Lambda }}^{-1}$. The proof is finished. □

The decomposition (37) is similar to the Gram–Schmidt orthogonalization for vectors $d{x}^{\mu }$ in the order $dt\to dz\to dy\to dx$. In matrix form, by (37) we have $\delta X=L^{+}dx$ and

$$\begin{array}{ccc}\hfill d{s}^2& =& g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }={\eta }_{ab}\delta X^a\delta X^b\hfill \\ & =& {\left(L_t^{T}dt\right)}^2-{(L_x^{X}dx+L_y^{X}dy+L_z^{X}dz+L_t^{X}dt)}^2\hfill \\ & & -{(L_y^{Y}dy+L_z^{Y}dz+L_t^{Y}dt)}^2-{(L_z^{Z}dz+L_t^{Z}dt)}^2.\hfill \end{array}$$

(43)

Equation (43) is a direct result of (38), but (43) manifestly shows the geometrical meanings of the tetrad components $L_{\mu }^a$. Obviously, (43) is also the method of completing the square to calculate the tetrad coefficients $f_{\mu }^a$.

The above theorems Theorems 3 and 4 provide the solution of the Equation (7), and the geometric meaning of the solution is (4). In differential geometry, the element (4) is more fundamental than the distance formula $d{s}^2=g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }$, because (4) clarifies the geometric meanings of the basis vectors ${\gamma }_{\mu }$ and ${\gamma }_a$, and Clifford algebra (5) or (11) as well as Grassmann algebra (12) and (13) provide the calculating rules of the basis [12,29].

For $LU$ decomposition (39), we define a spinor coefficient table by

$$\begin{array}{ccc}\hfill S_{ab}^{\mu \nu }& \equiv & \left(\begin{array}{cccc}0& -U_1^{\{\mu }{U}_2^{\nu \}}& -U_1^{\{\mu }{U}_3^{\nu \}}& -U_1^{\{\mu }{U}_0^{\nu \}}\\ U_2^{\{\mu }{U}_1^{\nu \}}& 0& -U_2^{\{\mu }{U}_3^{\nu \}}& -U_2^{\{\mu }{U}_0^{\nu \}}\\ U_3^{\{\mu }{U}_1^{\nu \}}& U_3^{\{\mu }{U}_2^{\nu \}}& 0& -U_3^{\{\mu }{U}_0^{\nu \}}\\ U_0^{\{\mu }{U}_1^{\nu \}}& U_0^{\{\mu }{U}_2^{\nu \}}& U_0^{\{\mu }{U}_3^{\nu \}}& 0\end{array}\right)=-S_{ba}^{\mu \nu },\hfill \end{array}$$

(44)

in which

$$\begin{array}{c}\hfill U_a^{\{\mu }{U}_b^{\nu \}}=\frac{1}{2}(U_a^{\mu }{U}_b^{\nu }+U_a^{\nu }{U}_b^{\mu })=U_b^{\{\mu }{U}_a^{\nu \}}.\end{array}$$

(45)

$S_{ab}^{\mu \nu }=U_a^{\{\mu }{U}_b^{\nu \}}\mathrm{sign}(a-b)=-S_{ba}^{\mu \nu }$ is not a tensor for indices $(a,b)$, it is symmetrical for Riemann indices $(\mu ,\nu )$ but anti-symmetrical for Minkowski indices $(a,b)$. For diagonal metric we have $S_{ab}^{\mu \nu }\equiv 0$. It should be stressed again, $S_{ab}^{\mu \nu }$ is not a tensor for indices $(a,b)$; however, for any local Lorentz transformation $\delta X^{\prime }=\mathsf{\Lambda }\delta X$, if taking (44) as the proper values and setting Lorentz transformation

$$\begin{array}{c}\hfill \left(S_{ab}^{\prime \mu \nu }\right)={\mathsf{\Lambda }}^{*}\left(S_{cd}^{\alpha \beta }\right){\mathsf{\Lambda }}^{-1},{\mathsf{\Lambda }}^{*}\equiv {\left({\mathsf{\Lambda }}^{-1}\right)}^{+},\end{array}$$

then $S_{ab}^{\mu \nu }$ becomes a tensor for indices $(a,b)$.

By representation of (38), (39) and relation (40), we can check the following results by straightforward calculation.

Theorem 5.

For tetrad $\left(40\right)$, we have

$$\begin{array}{ccc}\hfill \frac{\partial f_{\alpha }^n}{\partial g_{\mu \nu }}& =& \frac{1}{4}({\delta }_{\alpha }^{\mu }{f}_m^{\nu }+{\delta }_{\alpha }^{\nu }{f}_m^{\mu }){\eta }^{nm}+\frac{1}{2}{S}_{ab}^{\mu \nu }{f}_{\alpha }^a{\eta }^{nb}.\hfill \end{array}$$

(46)

$$\begin{array}{ccc}\hfill \frac{\partial f_a^{\alpha }}{\partial g_{\mu \nu }}& =& -\frac{1}{4}(f_a^{\mu }{g}^{\alpha \nu }+f_a^{\nu }{g}^{\mu \alpha })-\frac{1}{2}{S}_{ab}^{\mu \nu }{f}_n^{\alpha }{\eta }^{nb}.\hfill \end{array}$$

(47)

Or equivalently,

$$\begin{array}{ccc}\hfill \frac{\partial {\gamma }_{\alpha }}{\partial g_{\mu \nu }}& =& \frac{1}{4}({\delta }_{\alpha }^{\mu }{\gamma }^{\nu }+{\delta }_{\alpha }^{\nu }{\gamma }^{\mu })+\frac{1}{2}{S}_{ab}^{\mu \nu }{f}_{\alpha }^a{\gamma }^b.\hfill \end{array}$$

(48)

$$\begin{array}{ccc}\hfill \frac{\partial {\gamma }^{\alpha }}{\partial g_{\mu \nu }}& =& -\frac{1}{4}(g^{\mu \alpha }{\gamma }^{\nu }+g^{\nu \alpha }{\gamma }^{\mu })-\frac{1}{2}{S}_{ab}^{\mu \nu }{f}_n^{\alpha }{\gamma }^a{\eta }^{nb}.\hfill \end{array}$$

(49)

Or equivalently,

$$\begin{array}{ccc}\hfill \delta {\gamma }_{\alpha }& =& \frac{1}{2}{\gamma }^{\beta }(\delta g_{\alpha \beta }+S_{ab}^{\mu \nu }{f}_{\alpha }^a{f}_{\beta }^b\delta g_{\mu \nu }),\hfill \end{array}$$

(50)

$$\begin{array}{ccc}\hfill \delta {\gamma }^{\lambda }& =& -\frac{1}{2}{g}^{\lambda \beta }{\gamma }^{\alpha }(\delta g_{\alpha \beta }+S_{ab}^{\mu \nu }{f}_{\alpha }^a{f}_{\beta }^b\delta g_{\mu \nu })=-g^{\lambda \alpha }\delta {\gamma }_{\alpha }.\hfill \end{array}$$

(51)

For any given vector $A^{\mu }$, we have

$$\begin{array}{ccc}\hfill A^{\alpha }\frac{\partial {\gamma }_{\alpha }}{\partial g_{\mu \nu }}& =& \frac{1}{4}(A^{\mu }{\gamma }^{\nu }+A^{\nu }{\gamma }^{\mu })+\frac{1}{4}{S}_{ab}^{\mu \nu }(A^a{\gamma }^b-A^b{\gamma }^a),\hfill \end{array}$$

(52)

$$\begin{array}{ccc}\hfill A_{\alpha }\frac{\partial {\gamma }^{\alpha }}{\partial g_{\mu \nu }}& =& -\frac{1}{4}(A^{\mu }{\gamma }^{\nu }+A^{\nu }{\gamma }^{\mu })+\frac{1}{4}{S}_{ab}^{\mu \nu }(A^a{\gamma }^b-A^b{\gamma }^a).\hfill \end{array}$$

(53)

In (46)–(53), we set $\frac{\partial {\gamma }^{\alpha }}{\partial g_{\mu \nu }}=\frac{\partial {\gamma }^{\alpha }}{\partial g_{\nu \mu }}=\frac{1}{2}\frac{d{\gamma }^{\alpha }}{d{g}_{\mu \nu }}$ for $\mu \ne \nu$ to obtain the tensor form. $\frac{d}{d{g}_{\mu \nu }}$ is the total derivative for $g_{\mu \nu }$ and $g_{\nu \mu }$. $S_{ab}^{\mu \nu }$ is transformed from $\left(44\right)$.

The following derivation only use the property $S_{ab}^{\mu \nu }=-S_{ba}^{\mu \nu }$. For ${\mathsf{\Omega }}^{\alpha }$, we have

$$\begin{array}{c}\hfill {\mathsf{\Omega }}^d=\frac{1}{4}{ϵ}^{abcd}{f}_a^{\alpha }{S}_{bc}^{\mu \nu }{\partial }_{\alpha }{g}_{\mu \nu },{\mathsf{\Omega }}^{\alpha }=-\frac{1}{4}{ϵ}^{dabc}{f}_d^{\alpha }{f}_a^{\beta }{S}_{bc}^{\mu \nu }{\partial }_{\beta }{g}_{\mu \nu }.\end{array}$$

(54)

4. The Classical Approximation of Dirac Equation

In this section, we derive the classical mechanics for a charged spinor moving in gravity, and disclose the physical meaning of connections ${\mathsf{{\rm Y}}}_{\mu }$ and ${\mathsf{\Omega }}_{\mu }$. By covariance principle, the Dirac Equation (18) is valid and covariant in any regular coordinate system; however, in order to obtain the energy eigenstates of a spinor we need to solve the Hamiltonian system of quantum mechanics, and in order to derive its classical mechanics we need to calculate the spatial integrals of its Noether charges such as coordinates, energy and momentum. These computations cannot be realized in an arbitrary coordinate system, but must be performed in a coordinate system with realistic global simultaneity; that is, we need the Gu’s natural coordinate system (NCS) [12,32]

$$\begin{array}{c}\hfill d{s}^2=g_{tt}d{t}^2-{\overline{g}}_{kl}d{x}^{k}d{x}^l,d\tau =\sqrt{g_{tt}}dt=f_t^{0}dt,dV=\sqrt{\overline{g}}{d}^{3}x.\end{array}$$

(55)

in which $ds$ is the proper time element, $d\tau$ the Newton’s absolute cosmic time element and $dV$ the absolute volume element of the space at time t. NCS generally exists and the global simultaneity is unique. Only in NCS we can clearly establish the Hamiltonian formalism and calculate the integrals of Noether charges. In NCS, we have

$$\begin{array}{c}\hfill f_t^0=\sqrt{g_{tt}},f_0^t=\frac{1}{\sqrt{g_{tt}}},{\gamma }_t=\sqrt{g_{tt}}{\gamma }_0,{\gamma }^t=\frac{1}{\sqrt{g_{tt}}}{\gamma }^0.\end{array}$$

(56)

Then by (20) we obtain

$$\begin{array}{ccc}\hfill {\mathsf{{\rm Y}}}_{\mu }& =& \frac{1}{2}\left({\partial }_{t}ln\sqrt{\overline{g}},f_k^a{\partial }_j{f}_a^j+{\partial }_{k}ln\sqrt{g}\right),{\mathsf{{\rm Y}}}^t=g^{tt}{\mathsf{{\rm Y}}}_t,{\mathsf{{\rm Y}}}^k=-{\overline{g}}^{kl}{\mathsf{{\rm Y}}}_l.\hfill \end{array}$$

(57)

In NCS, to lift and lower the index of a vector means ${\mathsf{\Omega }}^t=g^{tt}{\mathsf{\Omega }}_t,{\mathsf{\Omega }}^k=-{\overline{g}}^{kl}{\mathsf{\Omega }}_l$.

More generally, we consider the Dirac equation with electromagnetic potential $e{A}^{\mu }$ and nonlinear potential $N\left(\check{\gamma }\right)=\frac{1}{2}w{\check{\gamma }}^2$, where $\check{\gamma }={\varphi }^{+}{\gamma }_0\varphi$. Then (18) can be rewritten in Hamiltonian formalism

$$\begin{array}{c}\hfill i{\alpha }^t{\nabla }_t\varphi =\mathbf{H}\varphi ,\mathbf{H}=-{\alpha }^k{\widehat{p}}_k+e{\alpha }^t{A}_t+S^{\mu }{\mathsf{\Omega }}_{\mu }+(m-N^{\prime }){\gamma }_0,\end{array}$$

(58)

where $\mathbf{H}$ is the Hamiltonian or energy of the spinor, ${\alpha }^t=f_0^t{\alpha }^0={\left(\sqrt{g_{tt}}\right)}^{-1}$ and ${\nabla }_{\mu }={\partial }_{\mu }+{\mathsf{{\rm Y}}}_{\mu }$. Since $d\tau =f_t^{0}dt$ is the realistic time of the universe, only $i{\alpha }^t{\nabla }_t=i{\partial }_{\tau }$ is the true energy operator for a spinor. $g_{tt}$ represents the gravity, and it cannot be generally merged into $d\tau$ as performed in a semi-geodesic coordinate system.

In traditional quantum theory, we simultaneously take coordinate, speed, momentum and wave function of a particle as original concepts. This situation is the origin of logical confusion. As a matter of fact, only wave function $\varphi$ is independent concept and dynamical Equation (58) is fundamental in logic. Other concepts of the particle should be defined by $\varphi$ and (58). Similarly to the case in flat space-time [33], we define some classical concepts for the spinor.

Definition 2.

The coordinate $\overrightarrow{X}$ and speed $\overrightarrow{v}$ of the spinor is defined as

$$\begin{array}{c}\hfill X^k\left(t\right)\equiv {\int }_{R^3}{x}^k{\left|\varphi \right|}^2\sqrt{\overline{g}}{d}^{3}x={\int }_{R^3}{x}^k{q}^t\sqrt{g}{d}^{3}x,v^k\equiv \frac{d}{d\tau }{X}^k=f_0^t\frac{d}{dt}{X}^k,\end{array}$$

(59)

where $R^3$ stands for the total simultaneous hypersurface, $q^{\mu }={\varphi }^{+}{\alpha }^{\mu }\varphi ={\check{\alpha }}^{\mu }$ is the current.

By definition (59) and current conservation law $q_{;\mu }^{\mu }={\left(\sqrt{g}\right)}^{-1}{\partial }_{\mu }\left(q^{\mu }\sqrt{g}\right)=0$, we have

$$\begin{array}{ccc}\hfill v^j& =& f_0^t{\int }_{R^3}{x}^j{\partial }_t\left(q^t\sqrt{g}\right)d^{3}x=-f_0^t{\int }_{R^3}{x}^j{\partial }_k\left(q^k\sqrt{g}\right)d^{3}x\hfill \\ & =& f_0^t{\int }_{R^3}{q}^j\sqrt{g}{d}^{3}x\to {\int }_{R^3}{q}^j\sqrt{\overline{g}}{d}^{3}x.\hfill \end{array}$$

(60)

Since a spinor has only a very tiny structure, together with normalizing condition ${\int }_{R^3}{q}^t\sqrt{g}{d}^{3}x=1$, we obtain the classical point-particle model for the spinor as [33]

$$\begin{array}{c}\hfill q^{\mu }\to u^{\mu }\sqrt{1-v^2}{\delta }^3(\overrightarrow{x}-\overrightarrow{X}),v^2={\overline{g}}_{kl}{v}^k{v}^l,u^{\mu }=\frac{d{X}^{\mu }}{ds}=\frac{v^{\mu }}{\sqrt{1-v^2}},\end{array}$$

(61)

where the Dirac-$\delta$ means ${\int }_{R^3}{\delta }^3(\overrightarrow{x}-\overrightarrow{X})\sqrt{\overline{g}}{d}^{3}x=1$.

Theorem 6.

For any Hermitian operator $\widehat{P}$, $P\equiv {\int }_{R^3}\sqrt{\overline{g}}{\varphi }^{+}\widehat{P}\varphi d^{3}x$ is real for any ϕ. We have the following generalized Ehrenfest theorem,

$$\begin{array}{c}\hfill \frac{dP}{dt}=\Re {\int }_{R^3}\sqrt{g}{\varphi }^{+}\left({\alpha }^t{\partial }_t\widehat{P}-i{f}_0^t[\widehat{P},f_t^0]\mathbf{H}+i[\mathbf{H},\widehat{P}]\right)\varphi d^{3}x,\end{array}$$

(62)

where ℜ means taking the real part.

Proof. 

By (57) and (58), we have

$$\begin{array}{ccc}\hfill \frac{dP}{dt}& =& \frac{d}{dt}{\int }_{R^3}\sqrt{\overline{g}}{\varphi }^{+}\widehat{P}\varphi d^{3}x\hfill \\ & =& \Re {\int }_{R^3}\sqrt{\overline{g}}\left({\varphi }^{+}\left({\partial }_t\widehat{P}\right)\varphi +i{\left(i{\partial }_t\varphi \right)}^{+}\widehat{P}\varphi -i{\varphi }^{+}\widehat{P}\left(i{\partial }_t\varphi \right)+{\varphi }^{+}\widehat{P}\varphi {\partial }_{t}ln\sqrt{\overline{g}}\right)d^{3}x\hfill \\ & =& \Re {\int }_{R^3}\sqrt{\overline{g}}\left({\varphi }^{+}\left({\partial }_t\widehat{P}\right)\varphi +i{f}_t^0{\left(\mathbf{H}\varphi \right)}^{+}\widehat{P}\varphi -i{\varphi }^{+}\widehat{P}\left(f_t^0\mathbf{H}\varphi \right)\right)d^{3}x\hfill \\ & =& \Re {\int }_{R^3}\sqrt{g}{\varphi }^{+}\left({\alpha }^t{\partial }_t\widehat{P}-i{f}_0^t[\widehat{P},f_t^0]\mathbf{H}+i[\mathbf{H},\widehat{P}]\right)\varphi d^{3}x\hfill \\ & & +\Re {\int }_{R^3}\sqrt{g}{\varphi }^{+}({\partial }_k{\alpha }^k+{\alpha }^k{\partial }_{k}ln\sqrt{g}-2{\alpha }^k{\mathsf{{\rm Y}}}_k)\widehat{P}\varphi d^{3}x\hfill \\ & =& \Re {\int }_{R^3}\sqrt{g}{\varphi }^{+}\left({\alpha }^t{\partial }_t\widehat{P}-i{f}_0^t[\widehat{P},f_t^0]\mathbf{H}+i[\mathbf{H},\widehat{P}]\right)\varphi d^{3}x.\hfill \end{array}$$

(63)

Then we prove (62). The proof clearly shows the connection ${\mathsf{{\rm Y}}}^{\mu }$ has only geometrical effect, which cancels the derivatives of $\sqrt{g}$. Obviously, we cannot obtain (62) from the conventional definition of spinor connection ${\mathsf{\Gamma }}_{\mu }$. □

Definition 3.

The 4-dimensional momentum of the spinor is defined by

$$\begin{array}{c}\hfill p^{\mu }=\Re {\int }_{R^3}\left({\varphi }^{+}{\widehat{p}}^{\mu }\varphi \right)\sqrt{\overline{g}}{d}^{3}x.\end{array}$$

(64)

For a spinor at energy eigenstate, we have classical approximation $p^{\mu }=m{u}^{\mu }$, where m defines the classicalinertial massof the spinor.

Theorem 7.

For momentum of the spinor $p_{\mu }=\Re {\int }_{R^3}\sqrt{\overline{g}}{\varphi }^{+}{\widehat{p}}_{\mu }\varphi d^{3}x$, we have

$$\begin{array}{c}\hfill \frac{d}{d\tau }{p}_{\mu }=f_0^t\Re {\int }_{R^3}\sqrt{g}\left(e{F}_{\mu \nu }{q}^{\nu }+{\check{S}}^a{\partial }_{\mu }{\mathsf{\Omega }}_a-{\partial }_{\mu }N-{\varphi }^{+}\left({\partial }_{\mu }{\alpha }^{\nu }\right){\widehat{p}}_{\nu }\varphi \right)d^{3}x,\end{array}$$

(65)

in which

$$\begin{array}{c}\hfill F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu },{\check{S}}^a={\varphi }^{+}{S}^a\varphi .\end{array}$$

(66)

Proof. 

Substituting $\widehat{P}={\widehat{p}}_{\mu }$ and $\mathbf{H}\varphi ={\alpha }^{t}i{\nabla }_t\varphi$ into (62), by straightforward calculation we obtain

$$\begin{array}{ccc}\hfill \frac{d}{d\tau }{p}_{\mu }& =& f_0^t\Re {\int }_{R^3}\sqrt{g}{\varphi }^{+}\left(-e{\alpha }^t{\partial }_t{A}_{\mu }-\left({\partial }_{\mu }{\alpha }^t\right)i{\nabla }_t+{\alpha }^k{\partial }_k{\widehat{p}}_{\mu }\right)\varphi d^{3}x\hfill \\ & & +f_0^t\Re {\int }_{R^3}\sqrt{g}{\varphi }^{+}\left({\partial }_{\mu }(-{\alpha }^k{\widehat{p}}_k+e{\alpha }^t{A}_t+S^{\nu }{\mathsf{\Omega }}_{\nu }-N^{\prime }{\gamma }_0)\right)\varphi d^{3}x\hfill \\ & =& f_0^t\Re {\int }_{R^3}\sqrt{g}\left(e{F}_{\mu \nu }{q}^{\nu }+{\varphi }^{+}{\partial }_{\mu }\left(S^{\nu }{\mathsf{\Omega }}_{\nu }\right)\varphi -{\partial }_{\mu }N\right)d^{3}x-K_{\mu },\hfill \end{array}$$

(67)

in which

$$\begin{array}{ccc}\hfill K_{\mu }& =& f_0^t\Re {\int }_{R^3}\sqrt{g}{\varphi }^{+}\left({\partial }_{\mu }{\alpha }^{\nu }\right){\widehat{p}}_{\nu }\varphi d^{3}x.\hfill \end{array}$$

(68)

By $S^{\mu }{\mathsf{\Omega }}_{\mu }=S^a{\mathsf{\Omega }}_a$, we prove the theorem. □

For a spinor at particle state [33], by classical approximation $q^{\mu }\to v^{\mu }{\delta }^3(\overrightarrow{x}-\overrightarrow{X})$ and local Lorentz transformation, we have

$$\begin{array}{ccc}\hfill {\int }_{R^3}e{F}_{\mu \nu }{q}^{\nu }\sqrt{g}{d}^{3}x& \to & f_t^{0}e{F}_{\mu \nu }{u}^{\nu }\sqrt{1-v^2},\hfill \end{array}$$

(69)

$$\begin{array}{ccc}\hfill {\int }_{R^3}{\varphi }^{+}{S}^a\varphi \left({\partial }_{\mu }{\mathsf{\Omega }}_a\right)\sqrt{g}{d}^{3}x& \to & f_t^0{\overline{S}}^a{\partial }_{\mu }{\mathsf{\Omega }}_a\sqrt{1-v^2}=f_t^0{\partial }_{\mu }\left({\overline{S}}^a{\mathsf{\Omega }}_a\right)\sqrt{1-v^2},\hfill \\ \hfill {\int }_{R^3}{\partial }_{\mu }N\sqrt{g}{d}^{3}x& =& {\int }_{R^3}{\partial }_{\mu }\left(N\sqrt{g}\right)d^{3}x-{\int }_{R^3}N{\mathsf{\Gamma }}_{\mu \nu }^{\nu }\sqrt{g}{d}^{3}x\hfill \end{array}$$

(70)

$$\begin{array}{ccc}& \to & {\delta }_{\mu }^t\frac{d}{dt}\left(f_t^0\overline{w}\sqrt{1-v^2}\right)-f_t^0{\mathsf{\Gamma }}_{\mu \nu }^{\nu }\overline{w}\sqrt{1-v^2},\hfill \end{array}$$

(71)

in which the proper parameters ${\overline{S}}^a={\int }_{R^3}{\varphi }^{+}{S}^a\varphi d^{3}X$ is almost a constant, ${\overline{S}}^a$ equals to $\pm \frac{1}{2}\hslash$ in one direction but vanishes in other directions. $\overline{w}={\int }_{R^3}N{d}^{3}X$ is scale dependent. Then (65) becomes

$$\begin{array}{c}\hfill \frac{d}{ds}{p}_{\mu }\to e{F}_{\mu \nu }{u}^{\nu }+{\partial }_{\mu }\left({\overline{S}}^{\nu }{\mathsf{\Omega }}_{\nu }\right)+\overline{w}\left({\mathsf{\Gamma }}_{\mu \alpha }^{\alpha }-{\delta }_{\mu }^t\frac{d}{dt}\zeta \right)-\frac{K_{\mu }}{\sqrt{1-v^2}},\end{array}$$

(72)

where $\zeta =ln\left(f_t^0\overline{w}\sqrt{1-v^2}\right)$.

Now we prove the following classical approximation of $K_{\mu }$,

$$\begin{array}{c}\hfill K_{\mu }\to -\frac{1}{2}\left({\partial }_{\mu }{g}_{\alpha \beta }\right)m{u}^{\alpha }{u}^{\beta }\sqrt{1-v^2}.\end{array}$$

(73)

For $LU$ decomposition of metric, by (47) we have

$$\begin{array}{ccc}\hfill \frac{\partial f_a^{\nu }}{\partial g_{\alpha \beta }}& =& -\frac{1}{4}(f_a^{\alpha }{g}^{\nu \beta }+f_a^{\beta }{g}^{\alpha \nu })-\frac{1}{2}{S}_{ab}^{\alpha \beta }{f}_n^{\nu }{\eta }^{nb},\hfill \end{array}$$

(74)

where $S_{ab}^{\mu \nu }=-S_{ba}^{\mu \nu }$ is anti-symmetrical for indices $(a,b)$. Thus we have

$$\begin{array}{ccc}\hfill \left({\partial }_{\mu }{\alpha }^{\nu }\right){\widehat{p}}_{\nu }& =& {\partial }_{\mu }{g}_{\alpha \beta }\frac{\partial f_a^{\nu }}{\partial g_{\alpha \beta }}{\alpha }^a{\widehat{p}}_{\nu }={\partial }_{\mu }{g}_{\alpha \beta }\left(-\frac{1}{4}({\alpha }^{\alpha }{\widehat{p}}^{\beta }+{\alpha }^{\beta }{\widehat{p}}^{\alpha })-\frac{1}{2}{S}_{ab}^{\alpha \beta }{f}_n^{\nu }{\eta }^{nb}{\alpha }^a{\widehat{p}}_{\nu }\right)\hfill \\ & =& -\frac{1}{4}{\partial }_{\mu }{g}_{\alpha \beta }\left(({\alpha }^{\alpha }{\widehat{p}}^{\beta }+{\alpha }^{\beta }{\widehat{p}}^{\alpha })+2S_{ab}^{\alpha \beta }{\alpha }^a{\widehat{p}}^b\right).\hfill \end{array}$$

(75)

For classical approximation we have

$$\begin{array}{c}\hfill {\check{\alpha }}^a={\varphi }^{+}{\alpha }^a\varphi \to v^a{\delta }^3(\overrightarrow{x}-\overrightarrow{X}),{\widehat{p}}^b\varphi \to m{u}^b\varphi ,S_{ab}^{\alpha \beta }=-S_{ba}^{\alpha \beta }.\end{array}$$

(76)

Substituting (76) into (75), we obtain

$$\begin{array}{c}\hfill {\int }_{R^3}\sqrt{g}{\varphi }^{+}\left({\partial }_{\mu }{\alpha }^{\nu }\right){\widehat{p}}_{\nu }\varphi d^{3}x\to -\frac{1}{2}{f}_t^0\left({\partial }_{\mu }{g}_{\alpha \beta }\right)p^{\alpha }{u}^{\beta }\sqrt{1-v^2}.\end{array}$$

(77)

So (73) holds.

In the central coordinate system of the spinor, by relations

$$\begin{array}{c}\hfill {\mathsf{\Gamma }}_{\alpha \beta }^{\nu }=\frac{1}{2}{g}^{\mu \nu }({\partial }_{\alpha }{g}_{\mu \beta }+{\partial }_{\beta }{g}_{\mu \alpha }-{\partial }_{\mu }{g}_{\alpha \beta }),\frac{d}{d\tau }{g}_{\mu \nu }=\sqrt{1-v^2}{u}^{\alpha }{\partial }_{\alpha }{g}_{\mu \nu },\end{array}$$

(78)

it is easy to check

$$\begin{array}{c}\hfill g_{\mu \nu }{\mathsf{\Gamma }}_{\alpha \beta }^{\nu }{p}^{\alpha }{u}^{\beta }\sqrt{1-v^2}-p^{\nu }\frac{d{g}_{\mu \nu }}{d\tau }=-\frac{1}{2}\left({\partial }_{\mu }{g}_{\alpha \beta }\right)p^{\alpha }{u}^{\beta }\sqrt{1-v^2}.\end{array}$$

(79)

Substituting (79) into (73) we obtain

$$\begin{array}{c}\hfill K_{\mu }\to g_{\mu \nu }{\mathsf{\Gamma }}_{\alpha \beta }^{\nu }{p}^{\alpha }{u}^{\beta }\sqrt{1-v^2}-p^{\nu }\frac{d{g}_{\mu \nu }}{d\tau }.\end{array}$$

(80)

Substituting (80) and $ds=\sqrt{1-v^2}d\tau$ into (72), we obtain Newton’s second law for the spinor

$$\begin{array}{ccc}\hfill \frac{d}{ds}{p}^{\mu }& +& {\mathsf{\Gamma }}_{\alpha \beta }^{\mu }{p}^{\alpha }{u}^{\beta }=g^{\alpha \mu }\left(e{F}_{\alpha \beta }{u}^{\beta }+\overline{w}({\mathsf{\Gamma }}_{\alpha \beta }^{\beta }-{\delta }_{\alpha }^t\frac{d}{dt}ln\zeta )+{\partial }_{\alpha }\left({\overline{S}}^{\nu }{\mathsf{\Omega }}_{\nu }\right)\right).\hfill \end{array}$$

(81)

The classical mass m weakly depends on speed v if $\overline{w}\ne 0$.

By the above derivation we find that Newton’s second law is not as simple as it looks, because its universal validity depends on many subtle and compatible relations of the spinor equation. A complicated partial differential equation system (58) can be reduced to a 6-dimensional dynamics (59) and (81) is not a trivial event, which implies the world is a miracle designed elaborately. If the spin-gravity coupling potential $S_{\mu }{\mathsf{\Omega }}^{\mu }$ and nonlinear potential $\overline{w}$ can be ignored, (81) satisfies ‘mass shell constraint’ $\frac{d}{dt}\left(p^{\mu }{p}_{\mu }\right)=0$ [33,34]. In this case, the classical mass of the spinor is a constant and the free spinor moves along geodesic. In some sense, only vector potential is strictly compatible with Newtonian mechanics and Einstein’s principle of equivalence.

Clearly, the additional acceleration in (81) ${\mathsf{\Omega }}_{\mu }\in {\mathsf{\Lambda }}^3$ is different from that in (1), which is in ${\mathsf{\Lambda }}^2$. The approximation to derive (1) $\hslash \to 0$ may be inadequate, because ℏ is a universal constant acting as unit of physical variables. If $\overline{w}=0$, (81) obviously holds in all coordinate system due to the covariant form, although we derive (81) in NCS; however, if $\overline{w}>0$ is large enough for dark spinor, its trajectories will manifestly deviate from geodesics, so the dark halo in a galaxy is automatically separated from ordinary matter. Besides, the nonlinear potential is scale dependent [12].

For many body problem, dynamics of the system should be juxtaposed (58) due to the superposition of Lagrangian,

$$\begin{array}{c}\hfill i{\alpha }^t({\partial }_t+{\mathsf{{\rm Y}}}_t){\varphi }_n={\mathbf{H}}_n{\varphi }_n,{\mathbf{H}}_n=-{\alpha }^k{\widehat{p}}_k+e{\alpha }^t{A}_t+(m_n-N_n^{\prime }){\gamma }_0+{\mathsf{\Omega }}_{\mu }{S}^{\mu }.\end{array}$$

(82)

The coordinate, speed and momentum of n-th spinor are defined by

$$\begin{array}{c}\hfill {\overrightarrow{X}}_n\left(t\right)={\int }_{R^3}\overrightarrow{x}{q}_n^t\sqrt{g}{d}^{3}x,{\overrightarrow{v}}_n=\frac{d}{d\tau }{\overrightarrow{X}}_n,p_n^{\mu }=\Re {\int }_{R^3}{\varphi }_n^{+}{\widehat{p}}^{\mu }{\varphi }_n\sqrt{\overline{g}}{d}^{3}x.\end{array}$$

(83)

The classical approximation condition for point-particle model reads,

$$\begin{array}{c}\hfill q_n^{\mu }\to u_n^{\mu }\sqrt{1-v_n^2}{\delta }^3(\overrightarrow{x}-{\overrightarrow{X}}_n),u_n^{\mu }\equiv \frac{d{X}_n^{\mu }}{d{s}_n}=(1,{\overrightarrow{v}}_n)/\sqrt{1-v_n^2}.\end{array}$$

(84)

Repeating the derivation from (72) to (76), we obtain classical dynamics for each spinor,

$$\begin{array}{c}\hfill \frac{d}{d{s}_n}{p}_n^{\mu }+{\mathsf{\Gamma }}_{\alpha \beta }^{\mu }{p}_n^{\alpha }{u}_n^{\beta }=g^{\alpha \mu }\left(e_n{F}_{\alpha \beta }{u}_n^{\beta }+{\overline{w}}_n({\mathsf{\Gamma }}_{\alpha \beta }^{\beta }-{\delta }_{\alpha }^t\frac{d}{dt}ln{\zeta }_n)+{\partial }_{\alpha }\left({\overline{S}}^{\nu }{\mathsf{\Omega }}_{\nu }\right)\right).\end{array}$$

(85)

5. Energy-Momentum Tensor of Spinors

Similarly to the case of metric $g_{\mu \nu }$, the definition of Ricci tensor can also differ by a negative sign. We take the definition as follows

$$\begin{array}{c}\hfill R_{\mu \nu }\equiv {\partial }_{\alpha }{\mathsf{\Gamma }}_{\mu \nu }^{\alpha }-{\partial }_{\mu }{\mathsf{\Gamma }}_{\nu \alpha }^{\alpha }-{\mathsf{\Gamma }}_{\mu \beta }^{\alpha }{\mathsf{\Gamma }}_{\nu \alpha }^{\beta }+{\mathsf{\Gamma }}_{\mu \nu }^{\alpha }{\mathsf{\Gamma }}_{\alpha \beta }^{\beta },R=g^{\mu \nu }{R}_{\mu \nu }.\end{array}$$

(86)

For a spinor in gravity, the Lagrangian of the coupling system is given by

$$\begin{array}{c}\hfill \mathcal{L}=\frac{1}{2\kappa }(R-2\mathsf{\Lambda })+{\mathcal{L}}_m,{\mathcal{L}}_m=\Re \langle {\varphi }^{+}{\alpha }^{\mu }{\widehat{p}}_{\mu }\varphi \rangle -{\varphi }^{+}{\mathsf{\Omega }}_{\mu }{S}^{\mu }\varphi -m{\varphi }^{+}{\gamma }^0\varphi +N,\end{array}$$

(87)

in which $\kappa =8\pi G$, $\mathsf{\Lambda }$ is the cosmological constant, and $N=\frac{1}{2}w{\check{\gamma }}^2$ the nonlinear potential. Variation of the Lagrangian (87) with respect to $g_{\mu \nu }$, we obtain Einstein’s field equation

$$\begin{array}{c}\hfill G^{\mu \nu }+\mathsf{\Lambda }{g}^{\mu \nu }+\kappa T^{\mu \nu }=0,G^{\mu \nu }\equiv R^{\mu \nu }-\frac{1}{2}{g}^{\mu \nu }R=-\frac{\delta \left(R\sqrt{g}\right)}{\sqrt{g}\delta g_{\mu \nu }}.\end{array}$$

(88)

where $\frac{\delta }{\delta g_{\mu \nu }}$ is the Euler derivatives, and $T^{\mu \nu }$ is EMT of the spinor defined by

$$\begin{array}{ccc}\hfill T^{\mu \nu }& =& -2\frac{\delta \left({\mathcal{L}}_m\sqrt{g}\right)}{\sqrt{g}\delta g_{\mu \nu }}=-2\frac{\partial {\mathcal{L}}_m}{\partial g_{\mu \nu }}+2({\partial }_{\alpha }+{\mathsf{\Gamma }}_{\alpha \gamma }^{\gamma })\frac{\partial {\mathcal{L}}_m}{\partial \left({\partial }_{\alpha }{g}_{\mu \nu }\right)}-g^{\mu \nu }{\mathcal{L}}_m.\hfill \end{array}$$

(89)

By detailed calculation we have

Theorem 8.

For the spinor ϕ with nonlinear potential $N\left(\check{\gamma }\right)$, the total EMT is given by

$$\begin{array}{ccc}\hfill T^{\mu \nu }& =& \frac{1}{2}\Re \langle {\varphi }^{+}({\alpha }^{\mu }{\widehat{p}}^{\nu }+{\alpha }^{\nu }{\widehat{p}}^{\mu }+2S_{ab}^{\mu \nu }{\alpha }^a{\widehat{p}}^b)\varphi \rangle +g^{\mu \nu }(N^{\prime }\check{\gamma }-N)+K^{\mu \nu }+{\tilde{K}}^{\mu \nu },\hfill \end{array}$$

(90)

$$\begin{array}{ccc}\hfill K^{\mu \nu }& =& \frac{1}{2}{ϵ}^{abcd}{\check{S}}_d\left(\frac{1}{2}{f}_a^{\beta }{S}_{bc}^{\mu \nu }{g}^{\lambda \kappa }+\frac{\partial \left(f_a^{\beta }{S}_{bc}^{\mu \nu }\right)}{\partial g_{\lambda \kappa }}-\frac{\partial \left(f_a^{\beta }{S}_{bc}^{\lambda \kappa }\right)}{\partial g_{\mu \nu }}\right){\partial }_{\beta }{g}_{\lambda \kappa },\hfill \end{array}$$

(91)

$$\begin{array}{ccc}\hfill {\tilde{K}}^{\mu \nu }& =& \frac{1}{4}{ϵ}^{abcd}{S}_{cd}^{\mu \nu }({\partial }_a{\check{S}}_b-{\partial }_b{\check{S}}_a),{\check{S}}_{\mu }\equiv {\varphi }^{+}{S}_{\mu }\varphi .\hfill \end{array}$$

(92)

Proof. 

The Keller connection $i{\mathsf{{\rm Y}}}_{\alpha }$ is anti-Hermitian and actually vanishes in $\Re \langle {\varphi }^{+}{\alpha }^{\alpha }{\widehat{p}}_{\alpha }\varphi \rangle$. By (89) and (53), we obtain the component of EMT related to the kinematic energy as

$$\begin{array}{ccc}\hfill T_p^{\mu \nu }& \equiv & -2\frac{\delta }{\delta g_{\mu \nu }}\Re \langle {\varphi }^{+}{\alpha }^{\alpha }{\widehat{p}}_{\alpha }\varphi \rangle =-2\Re \langle {\varphi }^{+}\left(\frac{\partial {\alpha }^{\alpha }}{\partial g_{\mu \nu }}\right)(i{\partial }_{\alpha }-e{A}_{\alpha })\varphi \rangle \hfill \\ & =& \frac{1}{2}\Re \langle {\varphi }^{+}({\alpha }^{\mu }{\widehat{p}}^{\nu }+{\alpha }^{\nu }{\widehat{p}}^{\mu }+2S_{ab}^{\mu \nu }{\alpha }^a{\widehat{p}}^b)\varphi \rangle ,\hfill \end{array}$$

(93)

where we take $A_{\mu }$ as independent variable. By (54) we obtain the variation related with spin-gravity coupling potential as

$$\begin{array}{ccc}& & \frac{\partial \left({\varphi }^{+}{\mathsf{\Omega }}^d{S}_d\varphi \right)}{\partial g_{\mu \nu }}=\frac{1}{4}{ϵ}^{abcd}{\check{S}}_d\frac{\partial \left(f_a^{\alpha }{S}_{bc}^{\lambda \kappa }\right)}{\partial g_{\mu \nu }}{\partial }_{\alpha }{g}_{\lambda \kappa },\hfill \\ \hfill ({\partial }_{\alpha }& +& {\mathsf{\Gamma }}_{\alpha \beta }^{\beta })\frac{\partial \left({\varphi }^{+}{\mathsf{\Omega }}^d{S}_d\varphi \right)}{\partial \left({\partial }_{\alpha }{g}_{\mu \nu }\right)}=\frac{1}{4}{ϵ}^{abcd}({\partial }_{\alpha }+{\mathsf{\Gamma }}_{\alpha \beta }^{\beta })\left(f_a^{\alpha }{S}_{bc}^{\mu \nu }{\check{S}}_d\right)\hfill \end{array}$$

(94)

$$\begin{array}{ccc}& =& \frac{1}{4}{ϵ}^{abcd}\left[S_{bc}^{\mu \nu }{\partial }_a{\check{S}}_d+{\check{S}}_d\left(\frac{\partial \left(f_a^{\alpha }{S}_{bc}^{\mu \nu }\right)}{\partial g_{\lambda \kappa }}+\frac{1}{2}{f}_a^{\alpha }{S}_{bc}^{\mu \nu }{g}^{\lambda \kappa }\right){\partial }_{\alpha }{g}_{\lambda \kappa }\right].\hfill \end{array}$$

(95)

Then we have the EMT for term ${\mathsf{\Omega }}^{\mu }{\check{S}}_{\mu }$ as

$$\begin{array}{c}\hfill T_s^{\mu \nu }=-2\frac{\partial \left({\mathsf{\Omega }}^d{\check{S}}_d\right)}{\partial g_{\mu \nu }}+2({\partial }_{\alpha }+{\mathsf{\Gamma }}_{\alpha \beta }^{\beta })\frac{\partial \left({\mathsf{\Omega }}^d{\check{S}}_d\right)}{\partial \left({\partial }_{\alpha }{g}_{\mu \nu }\right)}=K^{\mu \nu }+{\tilde{K}}^{\mu \nu }.\end{array}$$

(96)

Substituting Dirac Equation (18) into (87), we get ${\mathcal{L}}_m=N-N^{\prime }\check{\gamma }$. For nonlinear potential $N=\frac{1}{2}w{\check{\gamma }}^2$, we have ${\mathcal{L}}_m=-N$. Substituting all the results into (89), we prove the theorem. □

For EMT of compound systems, we have the following useful theorem [12].

Theorem 9.

Assume matter consists of two subsystems I and II, namely ${\mathcal{L}}_m={\mathcal{L}}_I\left(\varphi \right)+{\mathcal{L}}_{II}\left(\psi \right)$, then we have

$$\begin{array}{c}\hfill T^{\mu \nu }=T_I^{\mu \nu }+T_{II}^{\mu \nu }.\end{array}$$

(97)

If the subsystems I and II have not interaction with each other, namely,

$$\begin{array}{c}\hfill \frac{\delta }{\delta \psi }{\mathcal{L}}_I\left(\varphi \right)=\frac{\delta }{\delta \varphi }{\mathcal{L}}_{II}\left(\psi \right)=0,\end{array}$$

(98)

then the two subsystems have independent energy-momentum conservation laws, respectively,

$$\begin{array}{c}\hfill T_{I;\nu }^{\mu \nu }=0,T_{II;\nu }^{\mu \nu }=0.\end{array}$$

(99)

For classical approximation of EMT, we have ${\varphi }^{+}{S}_{ab}^{\mu \nu }{\alpha }^a{\widehat{p}}^b\varphi \to S_{ab}^{\mu \nu }{u}^a{p}^b=0$. By the symmetry of the spinor, the proper value ${\int }_{R^3}{\tilde{K}}^{\mu \nu }{d}^{3}X=0$. By the structure and covariance, we should have

$$\begin{array}{c}\hfill K^{\mu \nu }=k_1{\check{S}}_{\alpha }{\mathsf{\Omega }}^{\alpha }{g}^{\mu \nu }+k_2({\mathsf{\Omega }}^{\mu }{\check{S}}^{\nu }+{\mathsf{\Omega }}^{\nu }{\check{S}}^{\mu }),\end{array}$$

(100)

where $k_1,k_2$ are constants to be determined. By (82), we find that the energy of spin-gravity interaction is just ${\check{S}}^{\mu }{\mathsf{\Omega }}_{\mu }$. Besides, if $A^{\mu }=0$, the spinor is an independent system and its energy-momentum conservation law $T_{;\nu }^{\mu \nu }=0$ holds, so its classical approximation should give (81) as $F_{\mu \nu }=0$. This means we have $k_1=1$ and $k_2=0$, or equivalently $K_t^t={\check{S}}^{\mu }{\mathsf{\Omega }}_{\mu }$. For the classical approximation of (90), by the summation of energy we have the total EMT as

$$\begin{array}{c}\hfill T^{\mu \nu }\to \left[m{u}^{\mu }{u}^{\nu }+({\overline{S}}^{\alpha }{\mathsf{\Omega }}_{\alpha }+\overline{w})g^{\mu \nu }\right]\sqrt{1-v^2}{\delta }^3(\overrightarrow{x}-\overrightarrow{X}).\end{array}$$

(101)

$\overline{w}>0$ acts like negative pressure, which is scale dependent. If the metric is diagonalizable, then we have ${\mathsf{\Omega }}_{\mu }\equiv 0$, so the term ${\overline{S}}^{\alpha }{\mathsf{\Omega }}_{\alpha }$ vanishes in cosmology.

Some previous works usually use one spinor to represent matter field. This may be not the case, because spinor fields only has a very tiny structure. Only to represent one particle by one spinor field, the matter model can be comparable with general relativity, classical mechanics and quantum mechanics [11,12,33]. By the superposable property of Lagrangian, the many body system should be described by the following Lagrangian

$$\begin{array}{c}\hfill {\mathcal{L}}_m=\sum _n\left(\Re \langle {\varphi }_n^{+}{\alpha }^{\mu }{\widehat{p}}_{\mu }{\varphi }_n\rangle -{\check{S}}_n^{\mu }{\mathsf{\Omega }}_{\mu }-m_n{\check{\gamma }}_n+N_n\right).\end{array}$$

(102)

The classical approximation of EMT becomes

$$\begin{array}{c}\hfill T^{\mu \nu }\to \sum _n\left[m_n{u}_n^{\mu }{u}_n^{\nu }+({\overline{w}}_n+{\check{S}}_n^{\alpha }{\mathsf{\Omega }}_{\alpha })g^{\mu \nu }\right]\sqrt{1-v_n^2}{\delta }^3(\overrightarrow{x}-{\overrightarrow{X}}_n),\end{array}$$

(103)

which leads to the EMT for average field of spinor fluid as follows

$$\begin{array}{c}\hfill T^{\mu \nu }=(\rho +P)U^{\mu }{U}^{\nu }+(W-P)g^{\mu \nu }.\end{array}$$

(104)

The self potential becomes negative pressure W, which takes the place of cosmological constant $\mathsf{\Lambda }$ in Einstein’s field equation. W has very important effects in astrophysics [12].

6. Discussion and Conclusions

From the calculation of this paper, we can find that Clifford algebra is indeed a unified language and efficient tool to describe the laws of nature. To represent the physical and geometric quantities of Clifford algebra, the formalism is neat and elegant and the calculation and derivation are simple and standard. The decomposition of spinor connection into ${\mathsf{{\rm Y}}}_{\mu }$ and ${\mathsf{\Omega }}_{\mu }$ by Clifford algebra, not only makes the calculation simpler, but also highlights their different physical meanings. ${\mathsf{{\rm Y}}}_{\mu }\in {\mathsf{\Lambda }}^1$ only corresponds to geometric calculations similar to the Levi–Civita connection, but ${\mathsf{\Omega }}_{\mu }\in {\mathsf{\Lambda }}^3$ results in physical effects. ${\mathsf{\Omega }}_{\mu }$ is coupled with the spin of spinor field, which provides position and navigation functions for the spinor, and is the origin of the celestial magnetic field. ${\mathsf{\Omega }}_{\mu }\equiv 0$ is a necessary condition of the diagonalizablity of metric, which seems to be also sufficient.

In the theoretical analysis of the spinor equation and its classical approximation, we must use Gu’s natural coordinate system with realistic cosmic time. This is a coordinate system with universal applicability and profound philosophical significance, which can clarify many misunderstandings about the concept of space-time. The energy-momentum tensor of the spinor field involves the specific representation of the tetrad. Through the $LU$ decomposition of metric, we set up the clear relationship between the frame and metric, and then derive the exact EMT of spinor. In the derivation, we discover a new non-tensor spinor coefficient table $S_{ab}^{\mu \nu }$, which has some wonderful properties and appears in many places in the spinor theory, but the specific physical significance needs to be further studied.

We usually use limits such as $\hslash \to 0$ and $c\to \infty$ in classical approximation of quantum mechanics. In some cases, such treatment is inappropriate. $(\hslash ,c)$ are constant units for physical variables, how can they take limits? In the natural unit system used in this paper or the dimensionless equations, we do not even know where the constants are. We can only make approximations such as $\left|v\right|\ll c$ or (61) while the average radius of the spinor is much smaller than its moving scale. Most paradoxes and puzzles in physics are caused by such ambiguous statements or overlapping concepts in different logical systems. A detailed discussion of these issues is given in [12,33].

This paper clearly shows how general relativity, quantum mechanics and classical mechanics are all compatible. Newton’s second law is not as simple as it looks, its universal validity depends on many subtle and compatible relations of the spinor equation as shown in Section 4. A complicated Dirac equation of spinor can be reduced to a 6-dimensional ordinary differential dynamics is not a trivial event, which implies that the world is a miracle designed elaborately. In fact, all the fundamental physical theories can be unified in the following framework expressed by the Clifford algebra [12,33]:

${\mathbf{A}}_{\mathbf{1}}.$The element of space-time is described by

$$\begin{array}{c}\hfill d\mathbf{x}={\gamma }_{\mu }d{x}^{\mu }={\gamma }_a\delta X^a,\end{array}$$

(105)

where the basis ${\gamma }_a$ and ${\gamma }_{\mu }$ satisfy the $C{\ell }_{1,3}$ Clifford algebra (5).

${\mathbf{A}}_{\mathbf{2}}.$The dynamics for a definite physical system takes the form as

$$\begin{array}{c}\hfill {\gamma }^{\mu }{\partial }_{\mu }\Psi =\mathcal{F}\left(\Psi \right),\end{array}$$

(106)

where $\Psi ={({\psi }_1,{\psi }_2,\cdots ,{\psi }_n)}^T$, and $\mathcal{F}\left(\Psi \right)$ consists of some Clifford numbers of Ψ, so that the total equation is covariant.

${\mathbf{A}}_{\mathbf{3}}.$The dynamic equation of a physical system satisfies the action principle

$$\begin{array}{c}\hfill S=\int \mathcal{L}(\Psi ,\partial \Psi )\sqrt{g}{d}^{4}x,\end{array}$$

(107)

where the Lagrangian $\mathcal{L}\in \mathbb{R}$ is a superposable scalar.

${\mathbf{A}}_{\mathbf{4}}.$Nature is consistent, i.e., for all solutions to (106) we always have

$$\begin{array}{c}\hfill \Psi \left(\mathbf{x}\right)\in L^{\infty }\left({\mathbb{M}}^{1,3}\right).\end{array}$$

(108)