Improving the Convergence of Interval Single-Step Method for Simultaneous Approximation of Polynomial Zeros
Abstract
:1. Introduction
2. Materials and Method
2.1. Interval Single-Step Method
2.2. Interval Trio Symmetric Single-Step (ITMSS) Method
3. Results
3.1. Convergence Analysis
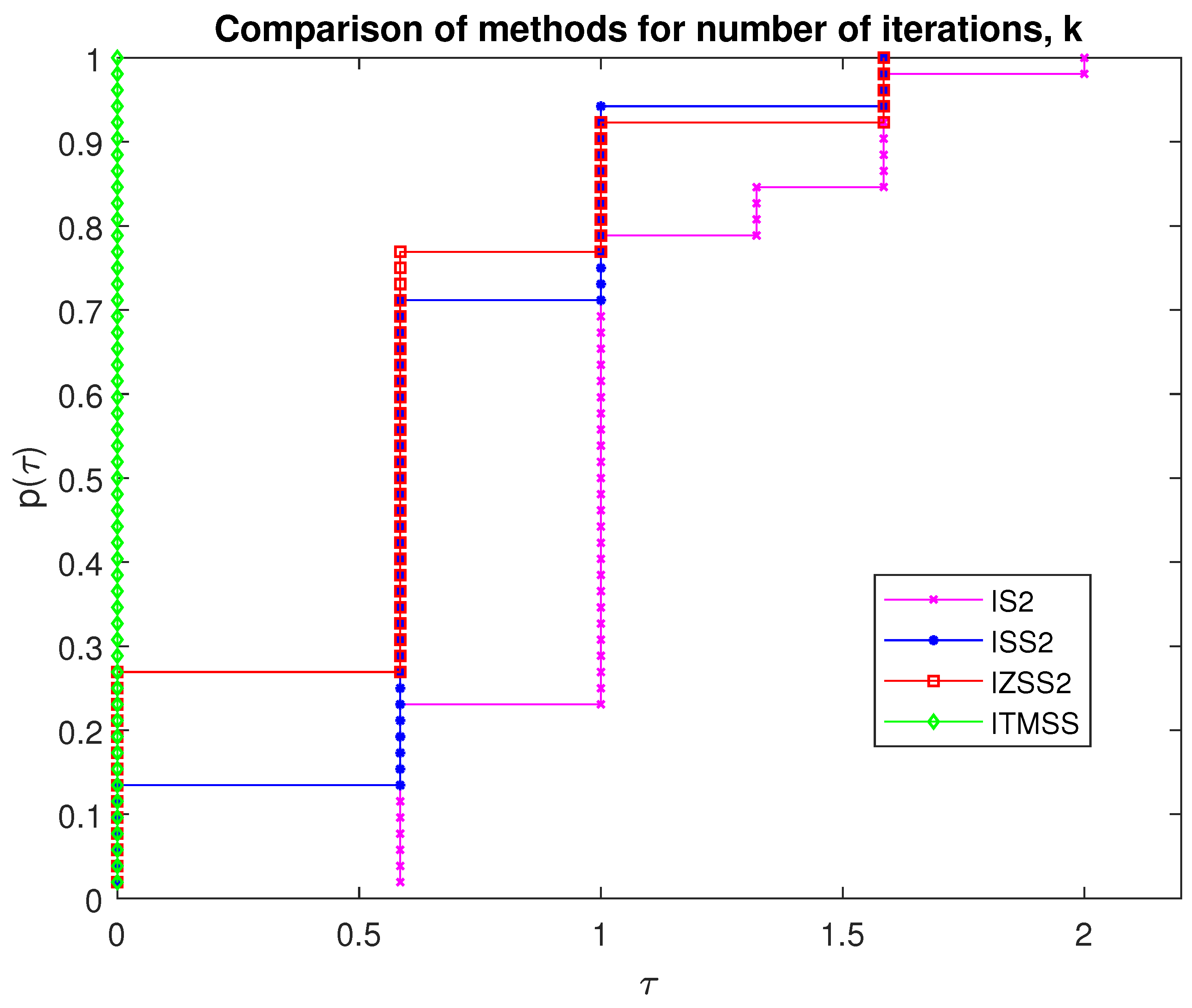
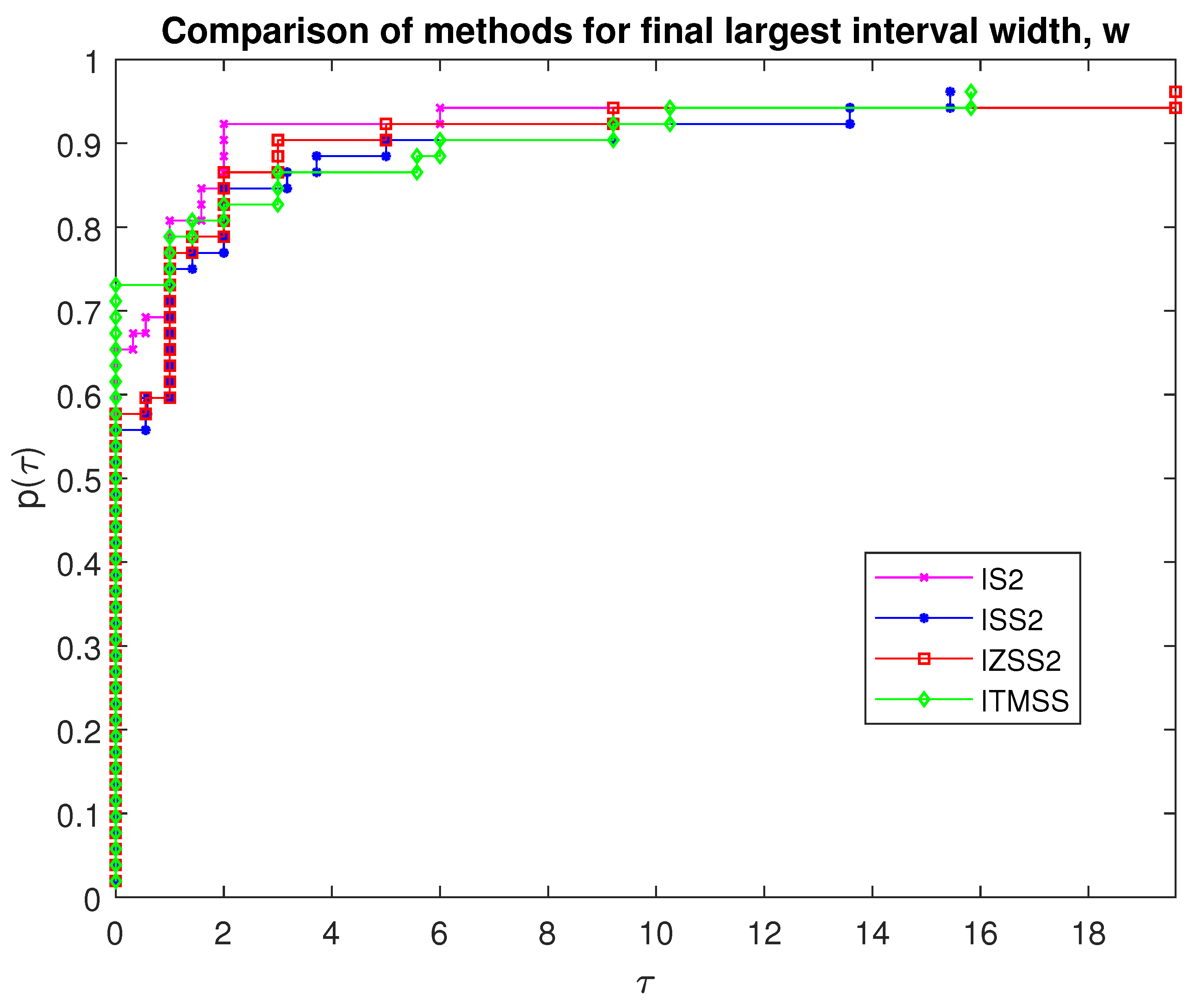
3.2. Numerical Experiments
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| IS2 | Interval single-step method |
| ISS2 | Interval symmetric single-step method |
| IZSS2 | Interval zoro-symmetric single-step method |
| ITMSS | Interval trio midpoint symmetric single-step method |
References
- Ohura, R.; Minamoto, T. A blind digital image watermarking method based on the dyadic wavelet packet transform and fast interval arithmetic techniques. Int. J. Wavelets Multiresolution Inf. Process. 2015, 13, 1550040. [Google Scholar] [CrossRef]
- Rump, S.M.; Ogita, T.; Morikura, Y.; Oishi, S.I. Interval arithmetic with fixed rounding mode. Nonlinear Theory and Its Applications. IEICE 2016, 7, 362–373. [Google Scholar]
- Pereira, D.R.; Papa, J.P.; Saraiva, G.F.R.; Souza, G.M. Automatic classification of plant electrophysiological responses to environmental stimuli using machine learning and interval arithmetic. Comput. Electron. Agric. 2018, 145, 35–42. [Google Scholar] [CrossRef] [Green Version]
- Orozco-Gutierrez, M.L. An Interval-Arithmetic-Based Approach to the Parametric Identification of the Single-Diode Model of Photovoltaic Generators. Energies 2020, 13, 932. [Google Scholar] [CrossRef] [Green Version]
- Pan, W.; Feng, L.; Zhang, L.; Cai, L.; Shen, C. Time-series interval prediction under uncertainty using modified double multiplicative neuron network. Expert Syst. Appl. 2021, 184, 115478. [Google Scholar] [CrossRef]
- Weierstrass, K. Neuer Beweis des Satzes, dass jede ganze rationale Funktion einer Veranderlichen dargestellt werden kann als ein Product aus lineare Funktionen derselben Veranderlichen. Gesammelte Werke 1967, 3, 251–269. [Google Scholar]
- Proinov, P.D.; Cholakov, S.I. Semilocal Convergence of Chebyshev-like Root-finding Method for Simultaneous Approximation of Polynomial Zeros. Appl. Math. Comput. 2014, 236, 669–682. [Google Scholar] [CrossRef]
- Proinov, P.D.; Petkova, M.D. Convergence of The Two-point Weierstrass Root-finding Method. Jpn. J. Ind. Appl. Math. 2014, 31, 279–292. [Google Scholar] [CrossRef]
- Proinov, P.D.; Vasileva, M.T. On a Family of Weierstrass-type Root-finding Methods with Accelerated Convergence. Appl. Math. Comput. 2014, 273, 957–968. [Google Scholar] [CrossRef] [Green Version]
- Proinov, P.D.; Ivanov, S.I. On The Convergence of Halley’s Method for Simultaneous Computation of Polynomial Zeros. J. Numer. Math. 2015, 23, 379–394. [Google Scholar] [CrossRef]
- Proinov, P.D.; Vasileva, M.T. On The Convergence of High-order Ehrlich-type Iterative Methods for Approximating All Zeros of A Polynomial Simultaneously. J. Inequalities Appl. 2015, 2015, 336. [Google Scholar] [CrossRef]
- Proinov, P.D. On The Local Convergence of Ehrlich Method for Numerical Computation of Polynomial Zeros. Calcolo 2016, 253, 413–426. [Google Scholar] [CrossRef]
- Proinov, P.D. Relationships Between Different Types of Initial Conditions for Simultaneous Root Finding Methods. Appl. Math. Lett. 2016, 52, 102–111. [Google Scholar] [CrossRef]
- Proinov, P.D.; Petkova, M.D. A New Semilocal Convergence Theorem for the Weierstrass Method for Finding Zeros of A Polynomial Simultaneously. J. Complex. 2014, 30, 366–380. [Google Scholar] [CrossRef]
- Cholakov, S.I.; Vasileva, M.T. A Convergence Analysis of A Fourth-order Method for Computing All Zeros of A Polynomial Simultaneously. J. Comput. Appl. Math. 2017, 321, 270–283. [Google Scholar] [CrossRef]
- Kyncheva, V.K.; Yotov, V.V.; Ivanov, S.I. Convergence of Newton, Halley and Chebyshev Iterative Methods as Methods for Simultaneous Determination of Multiple Polynomial Zeros. J. Appl. Numer. Math. 2017, 112, 146–154. [Google Scholar] [CrossRef]
- Proinov, P.D.; Ivanov, S.I. Convergence Analysis of Sakurai–Torii–Sugiura Iterative Method for Simultaneous Approximation of Polynomial Zeros. J. Comput. Appl. Math. 2019, 357, 56–70. [Google Scholar] [CrossRef]
- Gargantini, I.; Henrici, P. Circular Arithmetic and The Determination of Polynomial Zeros. Numer. Math. 1971, 18, 305–320. [Google Scholar] [CrossRef]
- Petković, M.S. On an iterative method for simultaneous inclusion of polynomial complex zeros. J. Comput. Appl. Math. 1982, 8, 51–56. [Google Scholar] [CrossRef] [Green Version]
- Monsi, M.; Wolfe, M.A. Interval Versions of Some Procedures for The Simultaneous Estimation of Complex Polynomial Zeros. Appl. Math. Comput. 1988, 28, 191–209. [Google Scholar] [CrossRef]
- Alefeld, G.; Herzberger, J. On the Convergence Speed of Some Algorithms for The Simultaneous Approximation of Polynomial Roots. SIAM J. Numer. Anal. 1974, 11, 237–243. [Google Scholar] [CrossRef] [Green Version]
- Moore, R.E. Methods and Applications of Interval Analysis, 1st ed.; SIAM: Philadelphia, PA, USA, 1979. [Google Scholar]
- Alefeld, G.; Herzberger, J. Introduction to Interval Computations, 1st ed.; Academic Press: New York, NY, USA, 1983. [Google Scholar]
- Salim, N.R. Convergence of Interval Symmetric Single-step Method for Simultaneous Inclusion of Real Polynomial Zeros. Ph.D. Thesis, Universiti Putra Malaysia, Seri Kembangan, Malaysia, 2012. [Google Scholar]
- Salim, N.R.; Monsi, M.; Hassan, M.A.; Leong, W.J. On The Convergence Rate of Symmetric Single-step Method ISS for Simultaneous Bounding Polynomial Zeros. Appl. Math. Sci. 2011, 5, 3731–3741. [Google Scholar]
- Jamaludin, N.; Monsi, M.; Hassan, N. The Performance of The Interval Midpoint Zoro Symmetric Single-step (IMZSS2-5D) Procedure to Converge Simultaneously to The Zeros. In AIP Conference Proceedings, Proceeding of The International Conference on Mathematics, Engineering and Industrial Applications 2018 (ICoMEIA 2018), Kuala Lumpur, Malaysia, 24–26 July 2018; Zin, S.M., Abdullah, N., Khazali, K.A.M., Roslan, N., Rusdi, N.A., Saad, R.M., Yazid, N.M., Zain, N.A.M., Eds.; AIP Publishing LLC: Melville, NY, USA, 2018; Volume 2013, p. 020033. [Google Scholar]
- Durand, E. Solutions numéRiques des Équations algéBriques: Systèmes de Plusieurs Équations; Masson: Paris, France, 1960; Volume 2. [Google Scholar]
- Kerner, I.O. Ein gesamtschrittverfahren zur berechnung der nullstellen von polynomen [A complete procedure for calculating the zeros of polynomials]. Numer. Mathl Sci. 2015, 8, 290–294. [Google Scholar] [CrossRef]
- Rusli, S.F.; Monsi, M.; Hassan, M.A.; Leong, W.J. On the interval zoro symmetric single-step procedure for simultaneous finding of real polynomial zeros. Appl. Math. Sci. 2011, 5, 3693–3706. [Google Scholar]
- Chen, C.Y.; Ghazali, A.H.; Leong, W.J. Scaled parallel iterative method for finding real roots of nonlinear equations. Optimization 2021, 1–17. [Google Scholar] [CrossRef]
- Ortega, J.M.; Rheinboldt, W.C. Numerical Solution of Nonlinear Problems: Studies in Numerical Analysis 2. Symp. Spons. Nav. Res. 1970, 2, 122–143. [Google Scholar]
- Salim, N.R.; Monsi, M.; Hassan, N. On The Performances of IMZSS2 Method for Bounding Polynomial Zeros Simultaneously. In Proceedings of the 7th International Conference on Research and Education in Mathematics (ICREM7), Kuala Lumpur, Malaysia, 25–27 August 2015; Majid, Z.A., Salim, N.R., Laham, M.F., Gopal, K., Phang, P.S., Mahad, Z., Eds.; IEEE: Piscataway, NJ, USA, 2015; pp. 5–9. [Google Scholar]
- Rump, S.M. INTLAB — INTerval LABoratory. In Developments in Reliable Computing; Csendes, T., Ed.; Springer: Dordrecht, The Netherlands, 1999; pp. 77–104. [Google Scholar]
- Dolan, E.D.; Moré, J.J. Benchmarking optimization software with performance profiles. Math. Program. 2002, 91, 201–213. [Google Scholar] [CrossRef]
| Step 0: | Given initial intervals and . |
| Set the stopping criterion | |
| Step 1: | For set . Compute |
| Step 2.1: | Compute |
| , | |
| Step 2.2: | Compute |
| Step 2.3: | Compute |
| , | |
| Step 2.4: | Set |
| Step 3: | If , for every then stop. Else, set and |
| , and go to Step 1. |
| k | i | Largest Interval Width in Every Iteration | |||
|---|---|---|---|---|---|
| IS2 Method | ISS2 Method | IZSS2 Method | ITMSS Method | ||
| 1 | 1 | ||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 2 | 1 | ||||
| 2 | |||||
| 3 | |||||
| 4 | 0.00000000000000000 | ||||
| 3 | 1 | Already Converge | Already Converge | ||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 4 | 1 | Already Converge | |||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| k | i | Largest Interval Width in Every Iteration | |||
|---|---|---|---|---|---|
| IS2 Method | ISS2 Method | IZSS2 Method | ITMSS Method | ||
| 1 | 1 | ||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 2 | 1 | ||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 3 | 1 | Already Converge | |||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 4 | 1 | Already Converge | |||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salim, N.R.; Chen, C.Y.; Mahad, Z.; Sapar, S.H. Improving the Convergence of Interval Single-Step Method for Simultaneous Approximation of Polynomial Zeros. Symmetry 2021, 13, 1971. https://doi.org/10.3390/sym13101971
Salim NR, Chen CY, Mahad Z, Sapar SH. Improving the Convergence of Interval Single-Step Method for Simultaneous Approximation of Polynomial Zeros. Symmetry. 2021; 13(10):1971. https://doi.org/10.3390/sym13101971
Chicago/Turabian StyleSalim, Nur Raidah, Chuei Yee Chen, Zahari Mahad, and Siti Hasana Sapar. 2021. "Improving the Convergence of Interval Single-Step Method for Simultaneous Approximation of Polynomial Zeros" Symmetry 13, no. 10: 1971. https://doi.org/10.3390/sym13101971
APA StyleSalim, N. R., Chen, C. Y., Mahad, Z., & Sapar, S. H. (2021). Improving the Convergence of Interval Single-Step Method for Simultaneous Approximation of Polynomial Zeros. Symmetry, 13(10), 1971. https://doi.org/10.3390/sym13101971






