Quantum Game Application to Recovery Problem in Mobile Database
Abstract
:1. Introduction
Motivation and Contribution
2. State-of-the-Art
The Need to Extend the Related Work
3. Quantum Game-Based Recovery Model
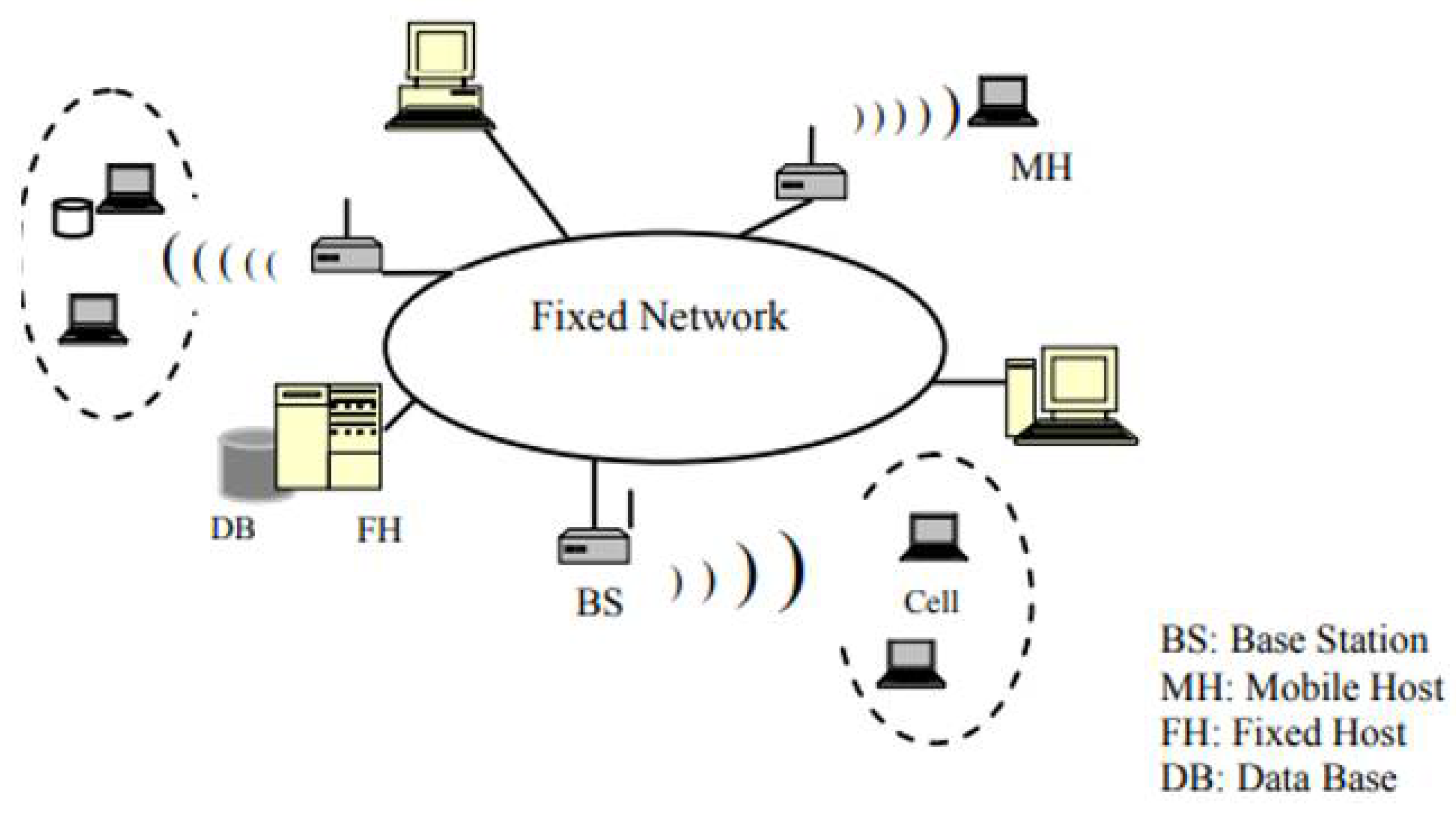
3.1. Mobile System Architecture
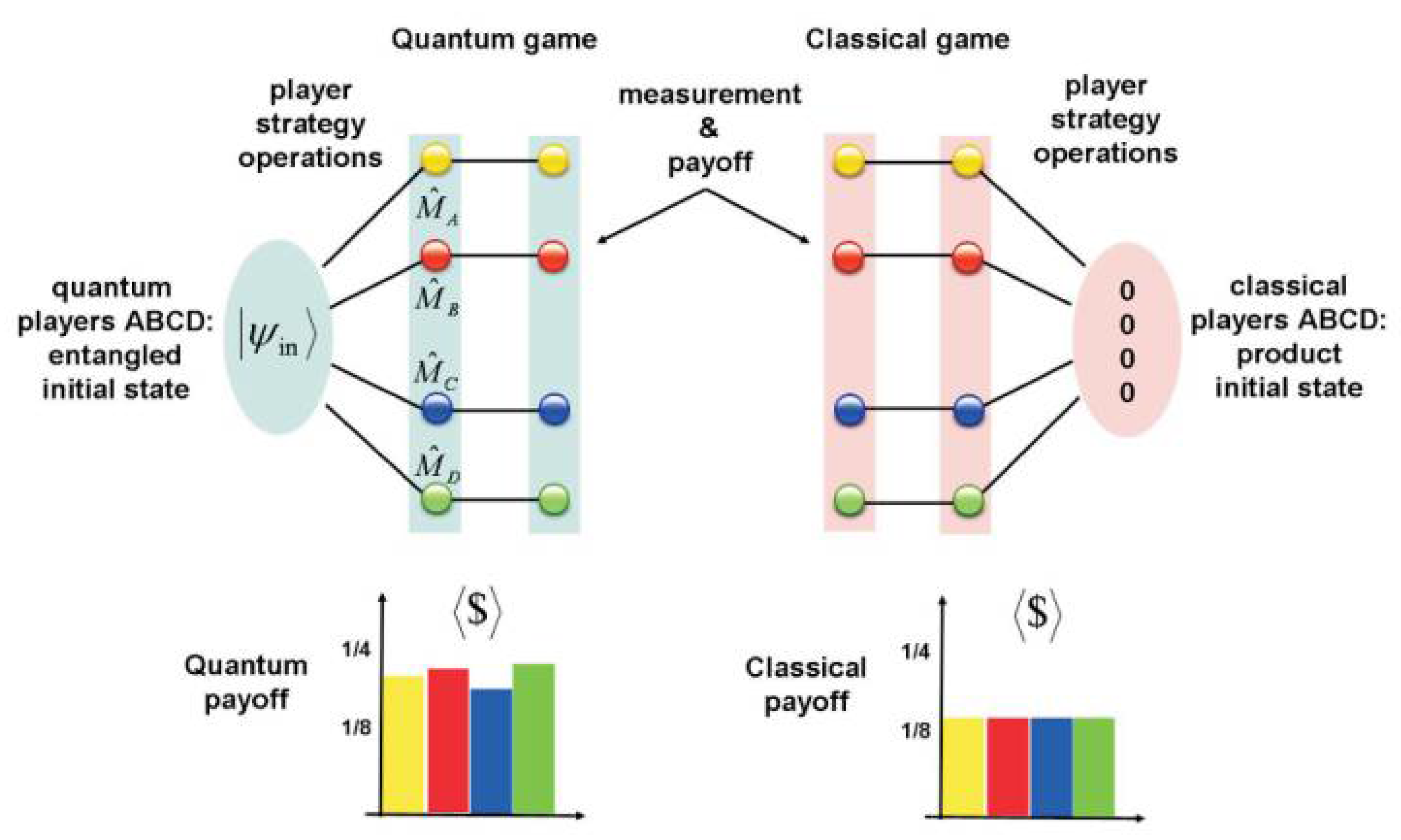
3.2. Recovery Modeling Using Quantum Game
| Game | Parameter |
|---|---|
| Number of Players | Three Players |
| Game Type | Non Cooperative (No interaction between players) |
| Game Form | Strategic form |
| Evolutionary Game Theory | No |
| Strategy type | Pure not Mixed |
| Payoff Functions | TIME, Memory, Recovery Done Probability |
| The Winning Algorithm | The highest NE(Quantum Nash) in the reward matrix |
3.2.1. Recovery Algorithms and Its Parameters
3.2.2. Build Knowledge Base
3.2.3. Build Payoff Matrix
| Symbol | Meaning |
|---|---|
| Quantum game model | |
| Number of players | |
| Game player | |
| Player’s strategy | |
| Payoff function or utility | |
| Best response for a player i |
3.2.4. Quantum Nash Equilibrium for Selection
4. Discussion
4.1. Simulation Setup
4.2. Simulation Results
4.2.1. Experiment One
| Variable | Meaning |
|---|---|
| Channel type | Channel/Wireless Channel |
| MAC type | Mac/802_11 |
| Radio-propagation model | Propagation/Two Ray Ground |
| Network interface type | Phy/wireless Phy |
| Interface queue type | queue/drop tail/priqueue |
| Antenna model | Antenna/Omni Antenna |
| Link layer type | LL |
| Routing protocol | Destination-Sequenced Distance Vector (DSDV) |
| Coordinate of topology | 670 m × 670 m |
| Max packet in ifq | 500 |
| Time to stop simulation | 250 |
| Algorithm/Log Size | 5 KB | 30 KB | 60 KB | 90 KB | 120 KB | 150 KB |
|---|---|---|---|---|---|---|
| Log Management | 1 | 1.3 | 1.8 | 2.5 | 3.3 | 3.5 |
| Mobile Agent | 1.1 | 1.5 | 1.9 | 2.4 | 3 | 3.15 |
| Hybrid Method | 1.2 | 1.6 | 1.7 | 2.3 | 2.8 | 3 |
| Proposed Model | 1 | 1.4 | 1.8 | 2.3 | 2.7 | 2.75 |
4.2.2. Experiment Two

4.2.3. Experiment Three

4.2.4. Experiment Four

4.2.5. Experiment Five
4.2.6. Experiment Six


5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rathika, R.; Prakash, T.; Aloysius, A. A survey on mobile computing security. Int. J. Res. Anal. Rev. 2019, 6, 645–649. [Google Scholar]
- Anandhakumar, M.; Ramaraj, E.; Venkatesan, N. Query issues in mobile database systems. Asia Pac. J. Res. 2014, 1, 24–36. [Google Scholar]
- Ibikunle, F.; Adegbenjo, A. Management issues and challenges in mobile database system. Int. J. Eng. Sci. Emerg. Technol. 2013, 5, 1–6. [Google Scholar]
- Su, H. The processing technology in mobile database transaction system. Int. J. Database Theory Appl. 2015, 8, 51–60. [Google Scholar] [CrossRef]
- Patil, P. Mobile computing: Issues and limitations. Int. J. Comput. Sci. Mob. Appl. 2016, 4, 1–6. [Google Scholar]
- Nisar, J.; Trumboo, O.N. Database for mobile application. Int. J. Trend Sci. Res. Dev. 2018, 2, 853–854. [Google Scholar] [CrossRef]
- Mobarek, A.; Abdelrhman, S.; Abdel-Mutal, A.; Adam, S.; Elbadri, N.; Ahmed, T.M. Transaction processing, techniques in mobile database: An overview. Int. J. Comput. Sci. Appl. 2015, 5, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Selvarani, D.; Ravi, T. A survey on data and transaction management in mobile databases. Int. J. Database Manag. Syst. 2012, 4, 1211. [Google Scholar] [CrossRef]
- Ramaj, V.; Januzaj, Y.; Januzaj, Y. Transactions management in mobile database. Int. J. Comput. Sci. Issues 2016, 13, 39–44. [Google Scholar]
- Ahmed, I.; Karvonen, H.; Kumpuniemi, T.; Katz, M. Wireless communications for the hospital of the future: Requirements challenges and solutions. Int. J. Wirel. Inf. Netw. 2020, 27, 4–17. [Google Scholar] [CrossRef] [Green Version]
- Kumar, P. Fault tolerance approach in mobile distributed systems. Int. J. Comput. Appl. 2015, 975, 8887. [Google Scholar]
- Chandna, A. Mobile database design: A key factor in mobile computing. In Proceedings of the 5th National Conference on Computing for Nation Development, New Delhi, India, 10–11 March 2011; pp. 1–4. [Google Scholar]
- Kumar, V. Mobile database recovery. In Fundamentals of Pervasive Information Management Systems, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013; pp. 219–238. [Google Scholar]
- Murthy, D.; Jack, N. Game theoretic modelling of service agent warranty fraud. J. Oper. Res. Soc. 2017, 68, 1399–1408. [Google Scholar] [CrossRef]
- Bonau, S. A Case for Behavioral Game Theory. J. Game Theory 2017, 6, 7–14. [Google Scholar]
- Quezada, L.; Dong, S. Quantum version of a generalized Monty Hall game and its possible applications to quantum secure communications. Ann. Physik 2021, 533, 2000427. [Google Scholar] [CrossRef]
- Zabaleta, O.; Barrangú, J.; Arizmendi, C. Quantum game application to spectrum scarcity problems. Phys. A Stat. Mech. Its Appl. 2017, 15, 455–461. [Google Scholar] [CrossRef] [Green Version]
- Babu, S.; Mohan, U.; Arthanari, T. Modeling coopetition as a quantum game. Int. Game Theory Rev. 2020, 22, 2040001. [Google Scholar] [CrossRef]
- Schmid, C.; Flitney, A.P.; Wieczorek, W.; Kiesel, N.; Weinfurter, H.; Hollenberg, L.C. Experimental implementation of a four-player quantum game. New J. Phys. 2010, 12, 063031. [Google Scholar] [CrossRef] [Green Version]
- Satria, D.; Park, D.; Jo, M. Recovery for overloaded mobile edge computing. Future Gener. Comput. Syst. 2017, 70, 138–147. [Google Scholar] [CrossRef]
- Mokhtar, Y.F.; Darwish, S.M.; Madbouly, M.M. An enhanced database recovery model based on game theory for mobile applications. Adv. Intell. Syst. Comput. 2021, 1261, 16–25. [Google Scholar]
- Saraswat, B.K.; Suryavanshi, R.; Yadav, D.S. A comparative study of checkpointing algorithms for distributed systems. Int. J. Pure Appl. Math. 2018, 118, 1595–1603. [Google Scholar]
- Silberschatz, A.; Korth, H.F.; Sudarshan, S. Recovery system. In Database System Concepts, 7th ed.; McGraw-Hill Education: New York, NY, USA, 2020; pp. 907–957. [Google Scholar]
- George, S.E.; Chen, I.R. Movement-based checkpointing and logging for failure recovery of database applications in mobile environments. Distrib. Parallel Databases 2008, 23, 189–205. [Google Scholar] [CrossRef]
- Jaggi, P.; Singh, A. Log based recovery with low overhead for large mobile computing systems. J. Inf. Sci. Eng. 2013, 29, 969–984. [Google Scholar]
- Chowdhury, C.; Neogy, S. Checkpointing using mobile agents for mobile computing system. Int. J. Recent Trends Eng. 2009, 1, 26–29. [Google Scholar]
- Mansouri, H.; Badache, N.; Aliouat, M.; Pathan, A. A new efficient checkpointing algorithm for distributed mobile computing. Control. Eng. Appl. Inform. 2015, 17, 43–54. [Google Scholar]
- Mahmoodi, M.; Baraani, A.; Khayyambashi, M. Recovery time improvement in the mobile database systems. In Proceedings of the International Conference on Signal Processing Systems, Singapore, 15–17 May 2009; pp. 688–692. [Google Scholar]
- Pamila, M.J.; Thanushkodi, K. Log management support for recovery in mobile computing environment. arXiv 2009, arXiv:0908.0076. [Google Scholar]
- Chowhan, R.S. Mobile agent programming paradigm and its application scenarios. Int. J. Curr. Microbiol. Appl. Sci. 2018, 7, 3269–3273. [Google Scholar] [CrossRef]
- Belghiat, A.; Kerkouche, E.; Chaoui, A.; Beldjehem, M. Mobile agent-based software systems modeling approaches: A comparative study. J. Comput. Inf. Technol. 2016, 24, 149–163. [Google Scholar] [CrossRef] [Green Version]
- Kekgathetse, M.; Letsholo, K. A survey on database synchronization algorithms for mobile device. J. Theor. Appl. Inf. Technol. 2016, 86, 1–9. [Google Scholar]
- Bhagat, A.R.; Bhagat, V.B. Mobile database review and security aspects. Int. J. Comput. Sci. Mob. Comput. 2014, 3, 1174–1182. [Google Scholar]
- Liang, X.; Yan, Z. A survey on game theoretical methods in human–machine networks. Future Gener. Comput. Syst. 2019, 92, 674–693. [Google Scholar] [CrossRef]
- Shaha, H.; Kakkada, V.; Patela, R.; Doshi, N. A survey on game theoretic approaches for privacy preservation in data mining and network security. Procedia Comput. Sci. 2019, 155, 686–691. [Google Scholar] [CrossRef]
- Orbay, B.Z.; Sevgi, L. Game theory and engineering applications. IEEE Antennas Propag. Mag. 2014, 56, 256–267. [Google Scholar]
- Gerasimou, G. Dominance-solvable multi-criteria games with incomplete preferences. Econ. Theory Bull. 2019, 7, 165–171. [Google Scholar] [CrossRef] [Green Version]
- Trivedi, H.; Mali, M. A Review on Network Simulator and its Installation. Int. J. Res. Sci. Innov. 2014, 1, 115–116. [Google Scholar]
- Gayathri, C.; Vadivel, R. An overview: Basic concept of network simulation tools. Int. J. Adv. Res. Comput. Commun. Eng. 2017, 6, 19–22. [Google Scholar]
- Fang, Y.; Chlamtac, I.; Fei, H. Failure recovery of HLR mobility databases and parameter optimization for PCS networks. J. Parallel Distrib. Comput. 2000, 60, 431–450. [Google Scholar] [CrossRef] [Green Version]


| Player | Player 3 Hybrid Method (Strategy ) | ||||
|---|---|---|---|---|---|
| Player 2 Mobile Agent Method | |||||
| Player 1 Log Management Method | Strategy | …. | |||
| ) | ) | …. | ) | ||
| ) | ) | …. | ) | ||
| …. | …. | …. | …. | ||
| ) | …. | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madbouly, M.M.; Mokhtar, Y.F.; Darwish, S.M. Quantum Game Application to Recovery Problem in Mobile Database. Symmetry 2021, 13, 1984. https://doi.org/10.3390/sym13111984
Madbouly MM, Mokhtar YF, Darwish SM. Quantum Game Application to Recovery Problem in Mobile Database. Symmetry. 2021; 13(11):1984. https://doi.org/10.3390/sym13111984
Chicago/Turabian StyleMadbouly, Magda M., Yasser F. Mokhtar, and Saad M. Darwish. 2021. "Quantum Game Application to Recovery Problem in Mobile Database" Symmetry 13, no. 11: 1984. https://doi.org/10.3390/sym13111984
APA StyleMadbouly, M. M., Mokhtar, Y. F., & Darwish, S. M. (2021). Quantum Game Application to Recovery Problem in Mobile Database. Symmetry, 13(11), 1984. https://doi.org/10.3390/sym13111984







