Next Article in Journal
Special Issue: “Symmetries in Quantum Mechanics and Statistical Physics”
Previous Article in Journal
Trusting Testcases Using Blockchain-Based Repository Approach
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Symmetry
Volume 13
Issue 11
10.3390/sym13112026
symmetry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Molecular, Supramolecular Structures Combined with Hirshfeld and DFT Studies of Centrosymmetric M(II)-azido {M=Ni(II), Fe(II) or Zn(II)} Complexes of 4-Benzoylpyridine

by
Morsy A. M. Abu-Youssef
1,*,
Vratislav Langer
2,
Assem Barakat
3,
Matti Haukka
4 and
Saied M. Soliman
1,*
1
Department of Chemistry, Faculty of Science, Alexandria University, P.O. Box 426, Ibrahimia, Alexandria 21321, Egypt
2
Department of Chemical and Biological Engineering, Chalmers University of Technology, SE-41296 Gothenburg, Sweden
3
Department of Chemistry, College of Science, King Saud University, P.O. Box 2455, Riyadh 11451, Saudi Arabia
4
Department of Chemistry, University of Jyväskylä, P.O. Box 35, FI-40014 Jyväskylä, Finland
*
Authors to whom correspondence should be addressed.
Symmetry 2021, 13(11), 2026; https://doi.org/10.3390/sym13112026
Submission received: 26 September 2021 / Revised: 7 October 2021 / Accepted: 19 October 2021 / Published: 26 October 2021
(This article belongs to the Section Chemistry: Symmetry/Asymmetry)
Browse Figures
Versions Notes

Abstract

:
The supramolecular structures of the three metal (II) azido complexes [Fe(4bzpy)4(N3)2]; 1, [Ni(4bzpy)4(N3)2]; 2 and [Zn(4bzpy)2(N3)2]n; 3 with 4-benzoylpyridine (4bzpy) were presented. All complexes contain hexa-coordinated divalent metal ions with a slightly distorted octahedral MN6 coordination sphere. Complexes 1 and 2 are monomeric with terminal azido groups while 3 is one-dimensional coordination polymer containing azido groups with μ(1,1) and μ(1,3) bridging modes of bonding. Hirshfeld analysis was used to quantitatively determine the different contacts affecting the molecular packing in the studied complexes. The most common interactions are the polar O…H and N…H interactions and the hydrophobic C…H contacts. The charges at the M(II) sites are calculated to be 1.004, 0.847, and 1.147 e for complexes 1–3, respectively. The degree of asymmetry is the highest in the case of the terminal azide in complexes 1 and 2 while was found the lowest in the μ(1,1) and μ(1,3) azide bonding modes in the Zn(II) complex 3. These facts were further explained in terms of atoms in molecules (AIM) topological parameters.

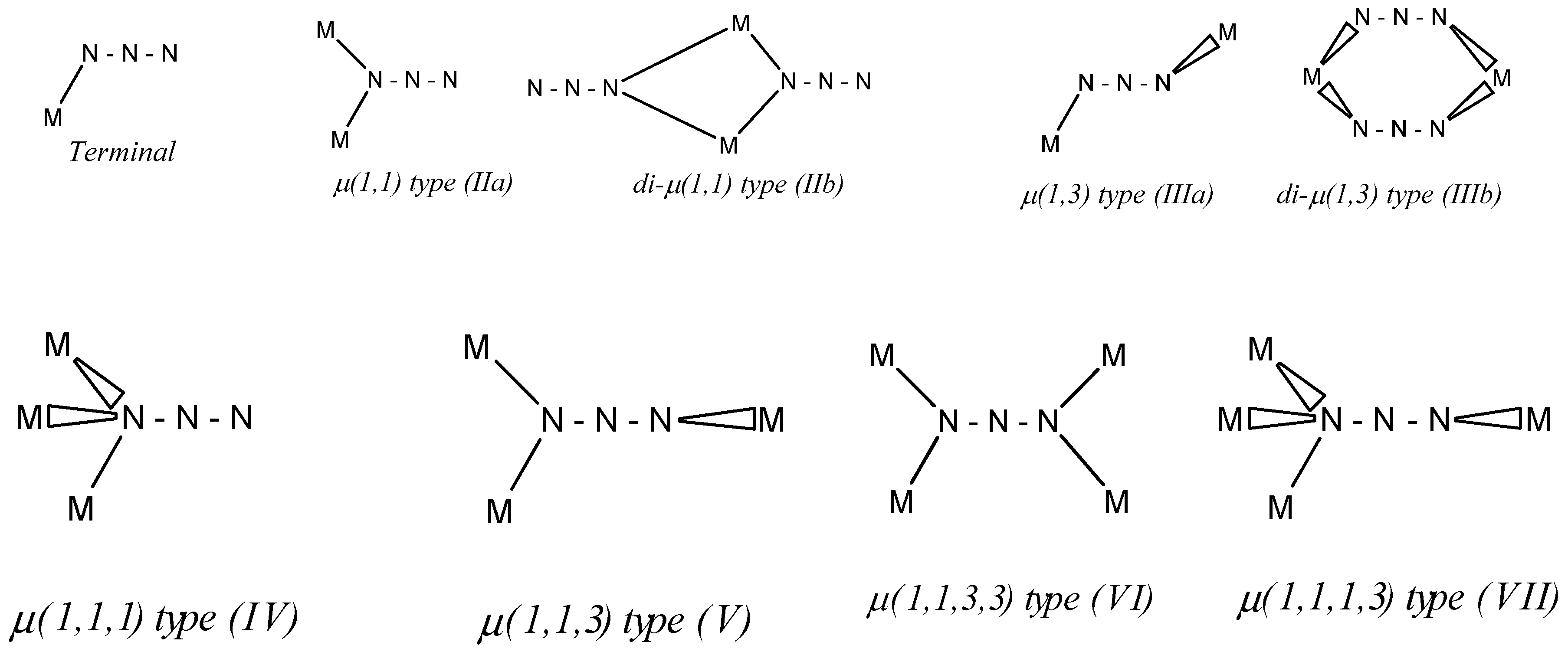
1. Introduction

In supramolecular solid-state chemistry of metal-organic complexes, the framework constructions are based on the arrangement of the molecular building blocks by strong hydrogen bonds or dative coordination bonds. An important class of supramolecular chemistry known as metallosupramolecular chemistry which is based upon the self-assembly of metal ions and organic ligands [1,2]. Metallosupramolecular chemistry has an important contribution to the spectacular development of crystal engineering [3,4,5,6,7,8,9,10]. Self-assembly is one of the most appropriate synthetic routes to build metallosupramolecular structures with interesting multidimensional and topological structures [11,12,13,14,15,16,17,18,19,20]. These can be achieved by proper selection of the suitable metal ion, ligand, and co-ligand [21,22]. The coordination number and geometry, charge, HSAB behavior of the metal ion as well as the denticity, shape, size, HSAB behavior of the ligands are vital factors in controlling the desired network topology [21,22].
Azide ion N3¯ is linear and symmetric with equal N-N distances; the covalent azides are linear but asymmetric with unequal N-N distances [23]. The importance of the coordinated azides is due to the capability of the azide group to have different modes of bonding as it acts as a terminal ligand (mono-dentate) or bridging ligand with several types of bonding modes (Scheme 1). Furthermore, the azide complexes may contain more than one of these modes of bonding in the same compound. Dori and Ziolo [24] have divided the azide complexes into three main groups (terminal, end-on bridging, end-to-end bridging). Hence, the azide anion is a versatile ligand that can bridge metal centers [25]. The coordinated azide was found to be linear and asymmetric in the first investigated complex [Co(NH3)5N3](N3)2 of the terminal mode of bonding [26]. Now, many azido complexes have been investigated showing different types of bonding modes. In light of the interesting coordination behavior of azide-containing complexes, the aim of the present work is to shed light on the structural diversity of three metal-azido complexes (Ni(II), Fe(II), and Zn(II)) with 4-benzoylpyridine (4bzpy) as N-donor organic ligand. The molecular and supramolecular structure features of these complexes were also investigated and discussed.

2. Materials and Methods

2.1. Materials and Instrumentation

The CHN analyses were carried out using a Perkin–Elmer analyzer. The Ni, Fe, and Zn were analyzed by a Perkin-Elmer Analyst 300, AAS atomic absorption spectrophotometer. The 4-benzoylpyridine ligand was purchased from Aldrich Company and other chemicals were of analytical grade quality and used without further purification.

2.2. Syntheses

2.2.1. [Fe(4bzpy)4(N3)2]; 1

Complex 1 was synthesized by mixing a 5 mL ethanolic solution of 4-benzoylpyridine (67.7 mg, 0.4 mmol) with an aqueous solution of FeSO4·7H2O (27.8 mg, 0.1 mmol) in an ice bath. To the resulting mixture, 1 mL saturated aqueous solution of L-ascorbic acid was added followed by the addition of 2 mL aqueous solution of NaN3 (65.0 mg, 1 mmol) dropwise with constant stirring then the mixture was placed in a refrigerator at ca. 4 °C. Red crystals of complex 1 were obtained with a yield of 62.1 mg, 71.2%. Anal. Calc. data: C, 66.06; H, 4.16; N, 16.05; Fe, 6.40. Found: C, 66.11; H, 4.11; N, 15.95; Fe, 6.31%.

2.2.2. [Ni(4bzpy)4(N3)2]; 2

A 10 mL aqueous solution of NiSO4·7H2O (28.1 mg, 0.1 mmol) and 5 mL ethanolic solution of 4-benzoylpyridine (67.7 mg, 0.4 mmol) was mixed then 2 mL aqueous solution of NaN3 (65.0 mg, 1 mmol) was added dropwise with continuous stirring. The clear mixture was left to evaporate slowly at room temperature, green crystals were obtained after one week with a yield of 60.7 mg, 69.3%. Anal. Calc. data: C, 65.85; H, 4.14; N, 16.00; Ni, 6.70. Found: 65.62; H, 4.01; N, 15.83; Ni, 6.59%.

2.2.3. [Zn(4bzpy)2(N3)2]n; 3

ZnSO4·7H2O (28.8 mg, 0.1 mmol) was dissolved in 10 mL water and mixed with 5 mL of 4-benzoylpyridine in ethanol (33.8 mg, 0.2 mmol), followed by a dropwise addition of NaN3 solution (65.0 mg, 1 mmol in 2 mL). After two weeks, colorless crystals were obtained from the clear mixture with a yield of 39.4 mg, 76.4%. Anal. Calc. data: C, 55.88; H, 3.52; N, 21.72; Zn, 12.68. Found: C, 55.61; H, 3.43; N, 21.66; Zn, 12.54%.

2.3. X-ray Structure Determination

Crystallographic measurements details of complexes 1–3 are given in Table 1 and Supplementary Materials [27,28,29,30,31]. Crystal Explorer program [32] was used for Hirshfeld calculations.

2.4. Computational Details

With the aid of the Gaussian 09 software package [33], natural charge calculations [34] were performed using WB97XD and MPW1PW91 methods [35,36] at the X-ray structure coordinates and employing the TZVP basis sets. Atoms in molecules (AIM) [37] topology analyses were performed using the Multiwfn program [38].

3. Results and Discussion

3.1. Structure Description

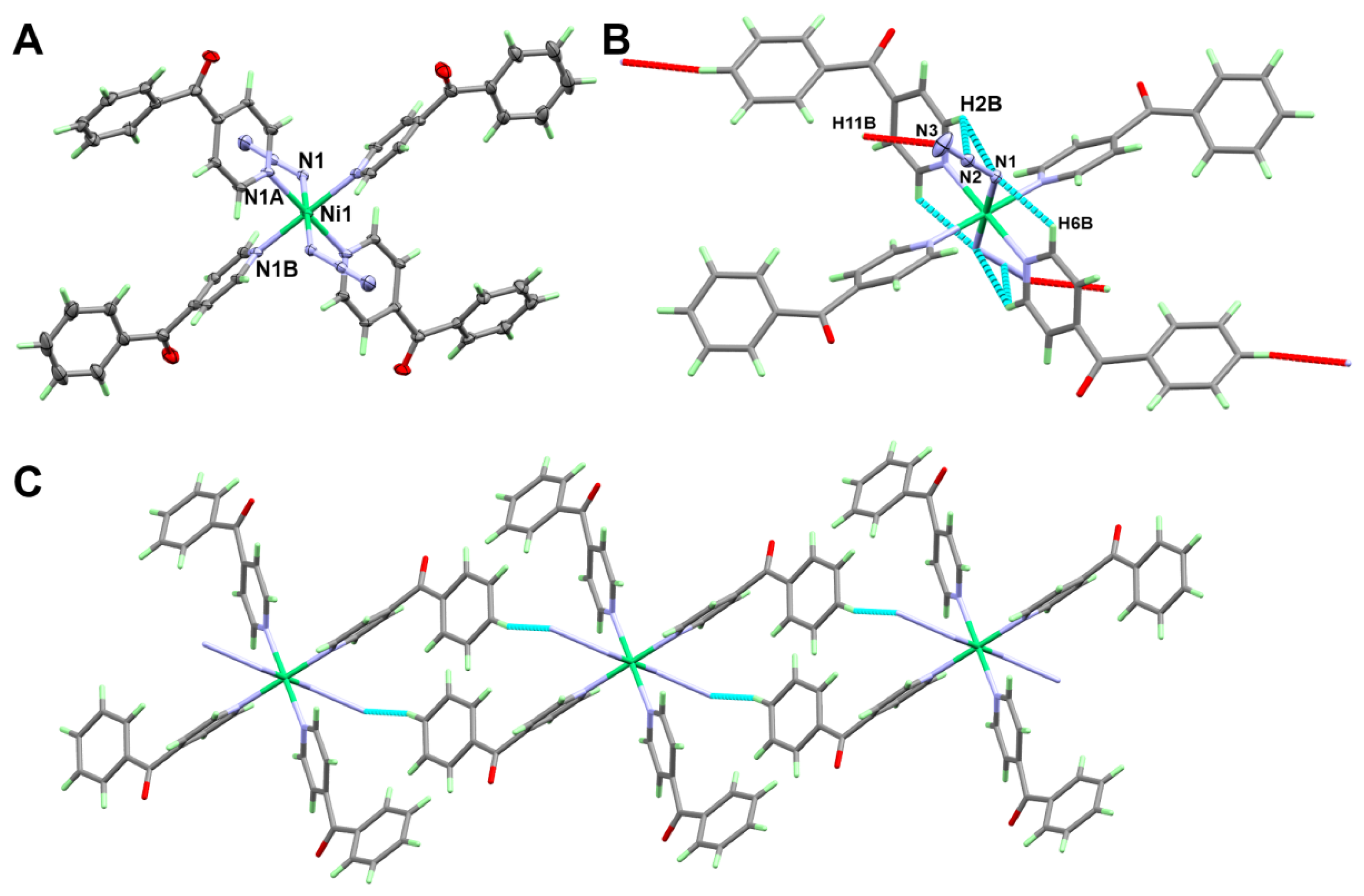
3.1.1. Structure of [Fe(4bzpy)4(N3)2]; 1

The structure of complex 1 comprised four 4bzpy molecules coordinating the Fe(II) central metal ion via the pyridine nitrogen atom. The coordination sphere of the Fe(II) is completed by two terminally coordinated trans-azide ions (Figure 1A). The [Fe(4bzpy)4(N3)2] complex possesses an inversion center located at the Fe atom, hence the asymmetric unit comprised half [Fe(4bzpy)4(N3)2] molecule. The most important geometrical parameters including bond distances and angles are listed in Table 2. The Fe-N(pyridine) distances (Fe1-N11: 2.2604(11) Å and Fe1-N21: 2.2929(11) Å) are shorter than the Fe-N(azide) (Fe1-N1: 2.1080(12) Å). All trans-N-Fe-N angles have exactly the ideal values for the perfect octahedron while the cis-N-Fe-N bond angles are close to 90° (87.96(4)–2.03(4)°). Hence, the coordination environment around Fe(II) could be described as a slightly distorted octahedron.
The structure of 1 comprised two intramolecular C-H...N interactions with donor-acceptor distances of 3.254(2) and 3.123(2) Å for the C22-H22…N2 and C26-H26…N1 interactions, respectively (Table 3). In addition, the neutral complex units are connected with each other via weak C-H…O interactions with a donor-acceptor distance of 3.419(2) Å. Presentation of the inter- and intra-molecular contacts, as well as the molecular packing, is shown in Figure 1B,C, respectively.

3.1.2. Structure of [Ni(4bzpy)4(N3)2]; 2

Similar to 1, the [Ni(4bzpy)4(N3)2]; 2 is a neutral complex comprising the central Ni(II) ion coordinated to four 4bzpy molecules and two terminally coordinated azide ions in trans positions (Figure 2). Moreover, complex 2 possesses an inversion center located at the Ni atom, hence the asymmetric unit comprised half molecule. The Ni-N(pyridine) distances (Ni1-N1A: 2.133(4) Å and Ni1-N1B: 2.180(4) Å) are shorter than the Ni-N(azide) (Ni1-N1: 2.091(4) Å). All trans-N-Ni-N bond angles are 180° while cis-N-Ni-N bond angles (87.38(14)–92.62(14)°) are slightly more deviated from 90° compared to 1. Hence, the octahedral coordination environment around Ni(II) is slightly more distorted than 1.
In this complex, there are three intramolecular C-H...N interactions with donor-acceptor distances of 3.139(6), 3.147(7), and 3.123(2) Å for the C2B-H2B…N1, C2B-H2B…N2 and C6B-H6B...N1 interactions, respectively as well as one intermolecular C-H...N interaction (Table 3 and Figure 1B). The donor–acceptor distance of the intermolecular C-H...N interaction is 3.508(9) Å (C11B-H11B...N3) and the packing scheme is shown in Figure 2C.

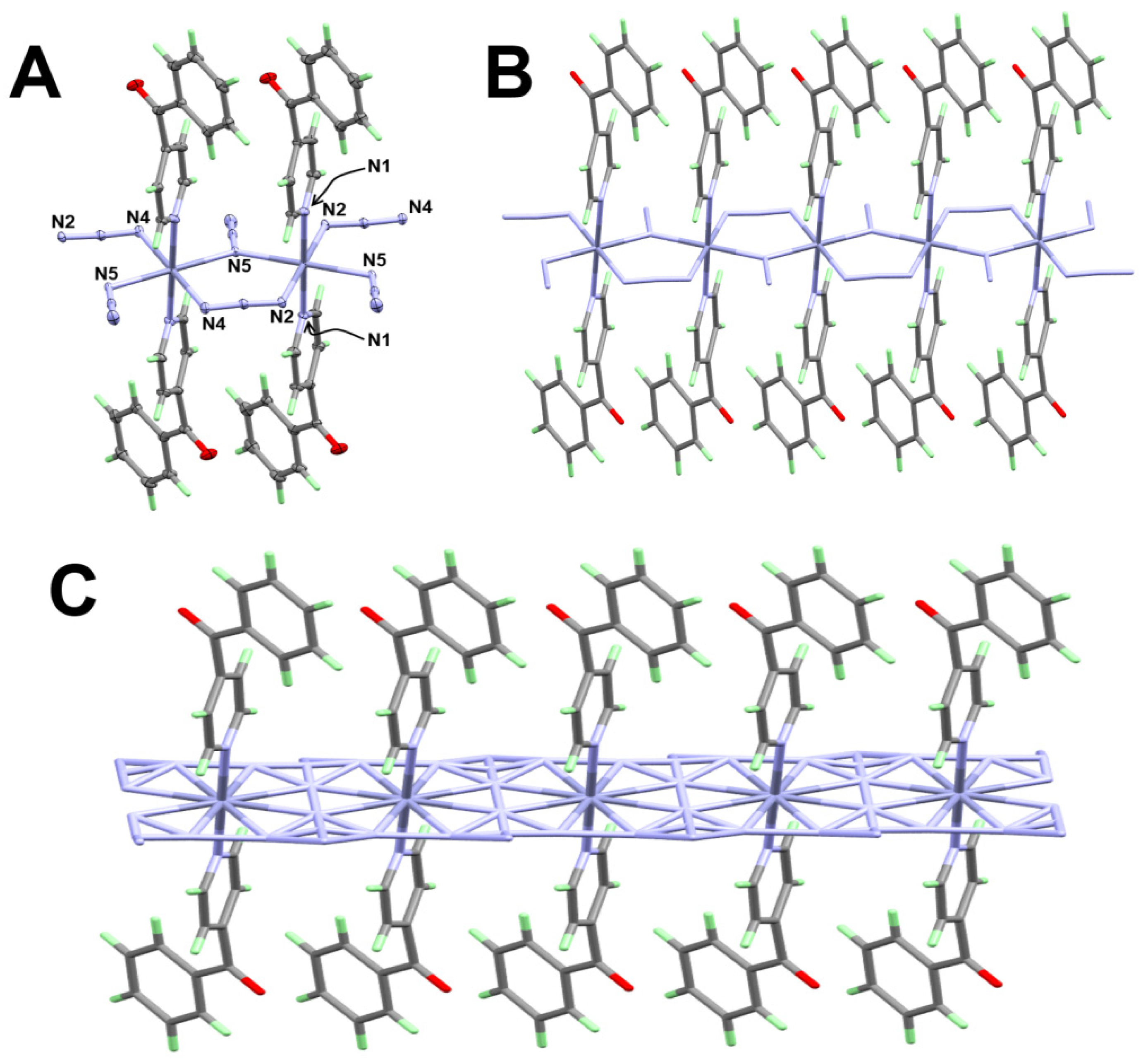
3.1.3. Structure of [Zn(4bzpy)2(N3)2]n; 3

In contrast to complexes 1 and 2 which are monomeric, the [Zn(4bzpy)2(N3)2]n; 3 complex has a polymeric network. In this complex, the Zn(II) is coordinated with two trans 4bzpy molecules and four azide ions where each two trans ligands are symmetrically related (Figure 3). Due to symmetry consideration, the asymmetric unit comprised a half [Zn(4bzpy)2(N3)2] unit. There are two azide ions that are differently coordinated with the Zn(II). There is one azide ion that has μ(1,1)-type IIa coordination mode connecting the Zn(II) centers along the polymer array where the Zn-N distances are 2.177(2) and 2.205(2) Å, for Zn1-N52 and Zn1-N5 bonds, respectively. The other azide ion has μ(1,3) type IIIa coordination mode which also connects the Zn(II) centers along the polymer array where the Zn1-N5 and Zn1-N2 distances are 2.199(2) and 2.212(2) Å, respectively. The Zn to nitrogen distances of the coordinated 4bzpy are 2.198(1) Å. Hence, the coordination environment of the two Zn(II) centers could be described as a slightly distorted octahedron where all the trans-N-Zn-N bond angles are equal to the expected value for the ideal case (180°) while the cis-N-Zn-N bond angles deviate slightly from 90° (Table 4).

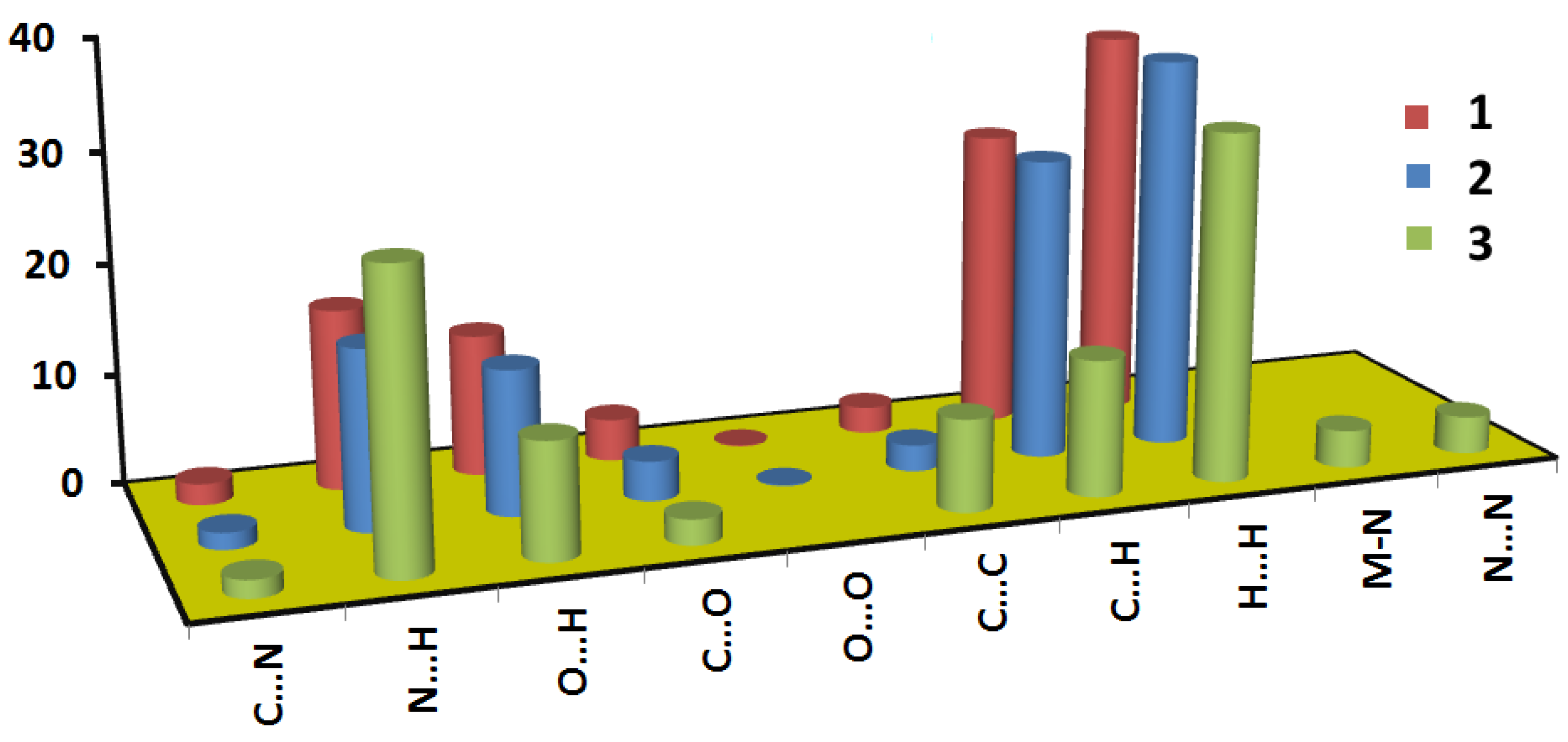
3.2. Hirshfeld Analysis

The different Hirshfeld surfaces [39,40,41,42] are shown in Figure S1 (Data) while the intermolecular contacts and their percentages are shown in Figure 4. In the case of complex 3, the Hirshfeld calculations were performed for one of the disordered parts of this complex as the results of the two parts are almost the same. The polar O…H and N…H hydrogen bonding interactions as well as the hydrophobic C…H contacts are the most common interactions in the crystal structure of the studied systems. The O…H contact percentages are 12.8, 13.1 and 10.5% for 1, 2, and 3, respectively. The shortest O...H contacts are O27...H112 (2.491 Å), O7B...H12A (2.499 Å), and O1...H8 (2.571 Å), respectively. The N…H contacts contributed by 16.3, 16.2, and 26.5%, for 1, 2, and 3, respectively, and the N3...H211 (2.507 Å), N3...H11B (2.453 Å), and N2...H5 (2.488 Å) are the shortest N...H contacts, respectively. On the other hand, the nonpolar C…H contact percentages are 27.1, 27.4, and 10.5%, respectively. The shortest C...H distances that belong to the C-H...π interactions are C23...H10 (2.678 Å), C3B...H10A (2.650 Å), and C4...H12 (2.680 Å), respectively.
It is clear that these interactions appeared as red regions with shorter distances than the vdWs radii sum of the two atoms sharing the contact (Figure 5). The O…H contacts are the shortest in complexes 1 and 2 compared to 3. On other hand, the N…H and C…H interactions appeared the shortest in the case of complex 2. The percentages of the C…C/C…N contacts are 4.3, 3.9, and 10.0% from the whole fingerprint area of complexes 1, 2, and 3, respectively, suggesting the presence of some π–π stacking interactions which are considered of less significance as these interactions appeared as blue regions in the dnorm maps. The polymeric nature of complex 3 was revealed by the presence of a large red region corresponding to the Zn–N(azido) coordination interactions (lower right part of Figure 5).

3.3. Natural Charges

Natural charges calculated using the NBO method employing two DFT functional (MPW1PW91 and Wb97XD) are listed in Table 5. Since the results of the two DFT functionals are almost the same, the discussion will be therefore limited to one of these two methods for simplicity. The charge at the Fe, Ni, and Zn centers are calculated using the MPW1PW91 method to be 1.004, 0.847, and 1.147 e, respectively. For the two monomeric complexes, the organic ligand compensated the charge of the divalent metal ion (M(II)) to a higher extent in the case of complex 2 than that in complex 1. The four 4bzpy ligands compensated the Ni(II) by about 0.596 e while the two azide groups donated 0.556 e to the Ni(II) ion. The corresponding values in the Fe(II) complexes are 0.414 and 0.562 e, respectively. In contrast, complex 3 has four azido groups coordinating the Zn(II) in μ(1,1) and μ(1,3) bonding fashion. Each one of the μ(1,1) and μ(1,3) azido groups has a natural charge less than −1 by 0.304 and 0.319 e, respectively, indicating that the four azido groups compensated the Zn(II) charge to a higher extent (~0.622 e) compared to those in complexes 1 and 2. These results are further revealed by the lower negative charge density transferred from the two 4bzpy ligand units (0.19 e) in this complex.

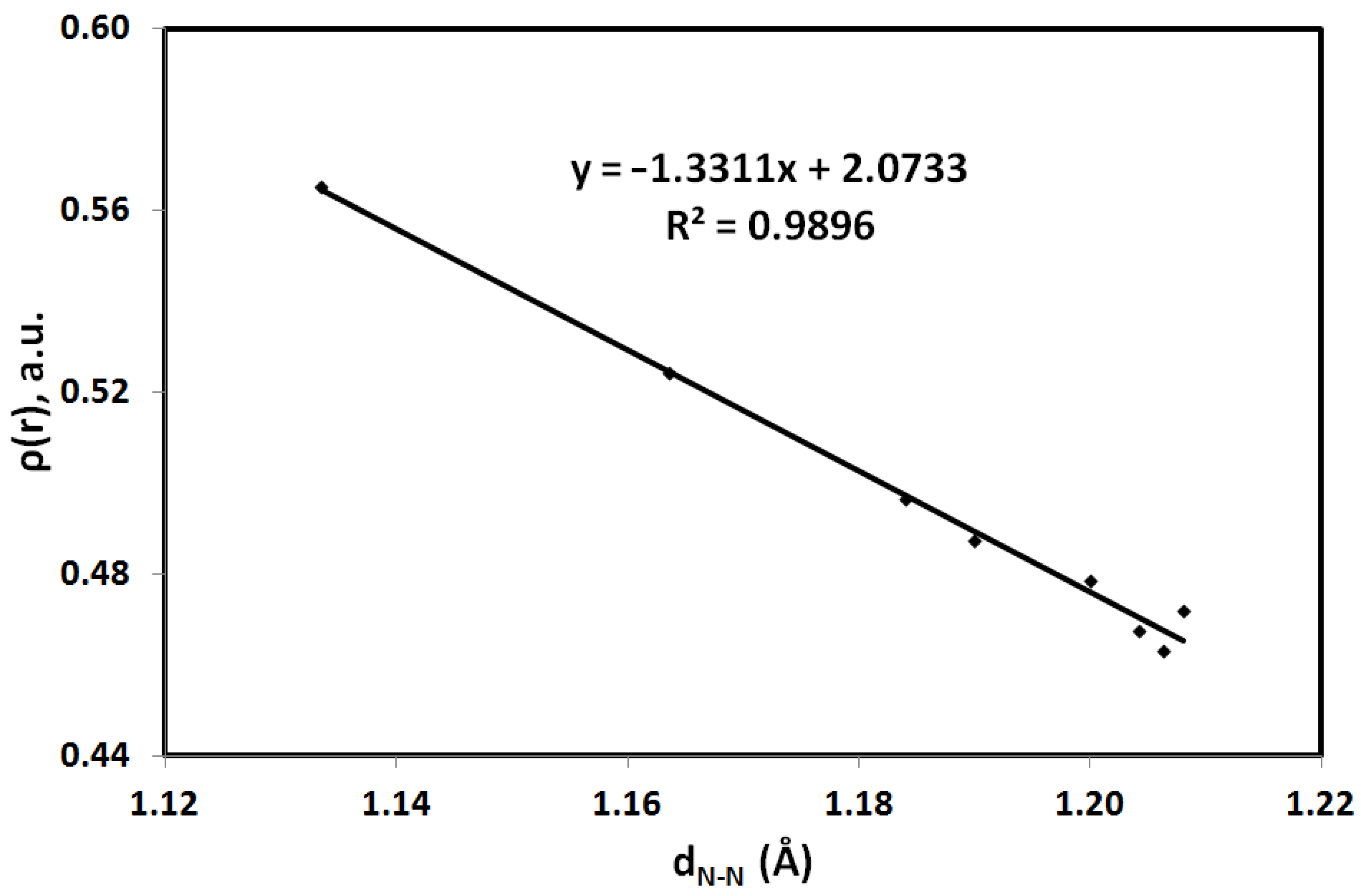
3.4. AIM Studies

It is well known covalent azides are linear and asymmetric while the azide ion (N3¯) is symmetric with equal N-N distances [23]. A rationale for the inequivalence within the bound azide was given by considering the ground state electronic structure of the azide in terms of contribution [43] from two resonance structures (A) and (B) shown in Figure 6.
Topological parameters of the atoms in molecules (AIM) [37] theory have great importance in describing the nature and strength of atom–atom interactions [44,45,46,47,48,49]. In this study, we employed these parameters to describe the degree of asymmetry of the azido group in the three complexes presented in this work. The electron density (ρ(r)) at the (3, −1) bond critical point (BCP; Figure 7) is a good measure for the bond strength. The N-N distances (dN-N) and the corresponding topological parameters at the N-N BCPs in the studied complexes are summarized in Table 6. It is clear that in all complexes, the two N-N bonds of an azido group are not identical. The degree of asymmetry is the highest in the case of the terminal azide in the Fe(II) and Ni(II) complexes. This could be simply confirmed by calculating the difference (Δd) between the two N-N bond distances in these azido groups which are also listed in the same table. The most symmetric situation occurred in the azide groups of the Zn(II) complex where the two azido groups coordinating the Zn(II) ion either in a μ(1,3) or μ(1,1) mode of bonding. Interestingly, the electron density (ρ(r)) topological parameter correlated well with the N-N distances of the azido groups (Figure 8). There is a clear dramatic decrease in the ρ(r) values with increasing N-N distances which could be used as a measure for the degree of asymmetry of the coordinated azido group. In addition, the high ρ(r) and negative ∇2ρ(r) at the N-N BCPs indicate clear covalent interactions.
On other hand, the AIM parameters for the M-N bonds are listed in Table 7. Based on the low electron density (ρ(r) < 0.10 au) values, positive H(r) and positive ∇2ρ(r) as well as V(r)/G(r) < 1, one could conclude that all M-N bonds belong to closed-shell interactions. It is clear that the M–N interactions of the terminal azido groups in the Fe and Ni complexes have some higher covalency as indicated from the slightly negative H(r) and V(r)/G(r) ratios are slightly higher than 1 [50,51,52,53].

4. Conclusions

Using self-assembly of metal(II) salts heptahydrate, azide, and 4-benzoylpyridine (4bzpy) in a water-alcohol mixture, the monomeric [Fe(4bzpy)4(N3)2]; 1 and [Ni(4bzpy)4(N3)2]; 2 complexes as well as the [Zn(4bzpy)2(N3)2]n; 3 coordination polymer were synthesized. In the latter, the Zn(4bzpy)2 moiety has two 4bzpy located trans to one another and acting as axial ligands of the octahedron. The two azido groups having μ(1,1) and μ(1,3) bridging modes in the equatorial plane are connecting the Zn(4bzpy)2 moieties leading to the formation of a one-dimensional coordination polymer. Complexes 1 and 2 contain two terminal azides in trans position and four 4bzpy ligand units. The packing of molecular units is controlled by N...H, O...H, and C...H intermolecular interactions. The bonding modes of the azido groups in the studied complexes were discussed using AIM calculations.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/sym13112026/s1, X-ray structure determination, Figure S1: Hirshfeld surfaces of the studied complexes.

Author Contributions

Conceptualization, M.A.M.A.-Y. and S.M.S.; synthesis and characterization, A.B. and M.A.M.A.-Y.; X-ray crystal structure, V.L. and M.H.; computational investigation, S.M.S.; funding acquisition, A.B.; writing—original manuscript, S.M.S.; revision and editing, M.A.M.A.-Y., V.L., A.B., M.H. and S.M.S.; All authors have read and agreed to the published version of the manuscript.

Funding

The authors would like to extend their sincere appreciation to the Researchers Supporting Project (RSP-2021/64), King Saud University, Riyadh, Saudi Arabia.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Constable, E.E.C. Novel oligopyridines for metallosupramolecular chemistry. Pure Appl. Chem. 1996, 68, 253–260. [Google Scholar] [CrossRef]
  2. Constable, E.C.; Lehn, J.-M.; Atwood, L.; Davis, J.E.D.; MacNicol, D.D.; Vögtle, F. Comprehensive Supramolecular Chemistry; Pergamon: New York, NY, USA; Elsevier Science Ltd.: Amsterdam, The Netherlands; Oxford: Oxford, UK, 1996. [Google Scholar]
  3. Champness, N.R. Coordination frameworks—Where next? Dalton Trans. 2006, 877–880. [Google Scholar] [CrossRef]
  4. Moulton, B.; Zaworotko, M.J. From Molecules to Crystal Engineering:  Supramolecular Isomerism and Polymorphism in Network Solids. Chem. Rev. 2001, 101, 1629–1658. [Google Scholar] [CrossRef]
  5. Wuest, J.D. Engineering crystals by the strategy of molecular tectonics. Chem. Commun. 2005, 5830–5873. [Google Scholar] [CrossRef]
  6. Biradha, K.; Sarkar, M.; Rajput, L. Crystal engineering of coordination polymers using 4,4′-bipyridine as a bond between transition metal atoms. Chem. Commun. 2006, 4169–4179. [Google Scholar] [CrossRef] [PubMed]
  7. Zhou, Y.; Hong, M.; Wu, X. Lanthanide–transition metal coordination polymers based on multiple N- and O-donor ligand. Chem. Commun. 2006, 135–143. [Google Scholar] [CrossRef] [PubMed]
  8. Madalan, M.; Avarvari, N.; Andruh, M. Metal complexes as second-sphere ligands. New J. Chem. 2006, 521–523. [Google Scholar] [CrossRef]
  9. Abu-Youssef, M.A.M.; Langer, V.; Öhrstrom, L. A unique example of a high symmetry three- and four-connected hydrogen bonded 3D-network. Chem. Comm. 2006, 10, 1082–1084. [Google Scholar] [CrossRef] [PubMed]
  10. Abu-Youssef, M.A.M.; Langer, V. 1D, 2D and 3D cadmium(II) polymeric complexes with quinoline-4-carboxylato anion, quinazoline and 2,5-dimethylpyrazine. Polyhedron 2005, 25, 1187–1194. [Google Scholar] [CrossRef]
  11. Kahn, O. Chemistry and Physics of Supramolecular Magnetic Materials. Acc. Chem. Res. 2000, 33, 647–657. [Google Scholar] [CrossRef] [PubMed]
  12. Eddaoudi, M.; Moler, D.B.; Li, H.; Chen, B.; Reineke, T.M.; O’Keeffe, M.; Yaghi, O.M. Modular chemistry: Secondary building units as a basis for the design of highly porous and robust metal-organic carboxylate frameworks. Acc. Chem. Res. 2001, 34, 319–330. [Google Scholar] [CrossRef]
  13. Kitagawa, S.; Kitaura, R.; Noro, S. Functional porous coordination polymers. Angew. Chem. Int. Ed. 2004, 43, 2334–2375. [Google Scholar] [CrossRef]
  14. Kepert, J. Advanced functional properties in nanoporous coordination framework materials. Chem. Commun. 2006, 695–700. [Google Scholar] [CrossRef]
  15. Kitagawa, S.; Noro, S.; Nakamura, T. Pore surface engineering of microporous coordination polymers. Chem. Commun. 2006, 701–707. [Google Scholar] [CrossRef] [PubMed]
  16. Evans, O.R.; Lin, W. Crystal Engineering of NLO Materials Based on Metal−Organic Coordination Networks. Acc. Chem. Res. 2002, 35, 511–522. [Google Scholar] [CrossRef]
  17. Coronado, E.; Galán-Mascarós, J.-R. Hybrid molecular conductors. J. Mater. Chem. 2005, 15, 66–74. [Google Scholar] [CrossRef]
  18. Bradshaw, D.; Claridge, J.B.; Cussen, E.J.; Prior, T.J.; Rosseinsky, M.J. Design, chirality, and flexibility in nanoporous molecule-based materials. Acc. Chem. Res. 2005, 38, 273–282. [Google Scholar] [CrossRef] [PubMed]
  19. Coronado, E.; Day, P. Magnetic molecular conductors. Chem. Rev. 2004, 104, 5419–5448. [Google Scholar] [CrossRef] [PubMed]
  20. Farhoud, M.; Abu-Youssef, M.A.M.; El-Ayan, U. Kerr Effect and Thermal Analysis of Some 3D and 1D polymeric Cadmium (II) and Zinc (II) Azido Complexes. Nonlinear Opt. Quantum Opt. 2006, 36, 1–15. [Google Scholar]
  21. Lehn, J.-M. Supramolecular Chemistry—Concepts and Perspectives; VCH: Weinheim, Germany, 1995. [Google Scholar]
  22. Lehn, J.-M. Toward self-organization and complex matter. Science 2002, 295, 2400–2403. [Google Scholar] [CrossRef] [Green Version]
  23. Evans, B.L.; Yofee, A.D.; Gray, P. Physics and Chemistry of the Inorganic Azides. Chem. Rev. 1959, 59, 515–568. [Google Scholar] [CrossRef]
  24. Dori, Z.; Ziolo, R.F. Chemistry of coordinated azides. Chem. Rev. 1973, 73, 247–254. [Google Scholar] [CrossRef]
  25. Ribas, J.; Escure, A.; Monfort, M.; Vicente, R.; Cortes, R.; Lezama, L.; Rojo, T. Polynuclear NiII and MnII azido bridging complexes. Structural trends and magnetic behaviour. Coord. Chem. Rev. 1999, 1027, 193–195. [Google Scholar]
  26. Palenik, G.J. The Structure of Coordination Compounds I. The Crystal and Molecular Structure of Azidopentamminecobalt(III) Azide. Acta Crystallogr. 1964, 17, 360–367. [Google Scholar] [CrossRef] [Green Version]
  27. SAINT. Siemens Analytical X-ray Instruments Inc.; SAINT: Madison, WI, USA, 1995. [Google Scholar]
  28. Sheldrick, G.M. SADABS; University of Göttingen: Göttingen, Germany, 1996. [Google Scholar]
  29. Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. 2008, A64, 112–122. [Google Scholar] [CrossRef] [Green Version]
  30. Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Cryst. 2015, A71, 3–8. [Google Scholar] [CrossRef] [Green Version]
  31. Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Cryst. 2015, C71, 3–8. [Google Scholar]
  32. Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. Crystal Explorer17 (2017) University of Western Australia. Available online: http://hirshfeldsurface.net (accessed on 12 June 2017).
  33. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. GAUSSIAN 09; Revision A02; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
  34. Glendening, E.D.; Reed, A.E.; Carpenter, J.E.; Weinhold, F. NBO; Version 3.1 CI; University of Wisconsin: Madison, WI, USA, 1998. [Google Scholar]
  35. Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  36. Adamo, C.; Barone, V. Exchange functionals with improved long-range behavior and adiabatic connection methods without adjustable parameters: The mPW and mPW1PW models. J. Chem. Phys. 1998, 108, 664–675. [Google Scholar] [CrossRef]
  37. Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
  38. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comp. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
  39. Hirshfeld, F.L. Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta. 1977, 44, 129–138. [Google Scholar] [CrossRef]
  40. Spackman, M.A.; Jayatilaka, D. Hirshfeld surface analysis. Cryst. Eng. Comm. 2009, 11, 19–32. [Google Scholar] [CrossRef]
  41. Spackman, M.A.; McKinnon, J.J. Fingerprinting intermolecular interactions in molecular crystals. Cryst. Eng. Comm. 2002, 4, 378–392. [Google Scholar] [CrossRef]
  42. McKinnon, J.J.; Jayatilaka, D.; Spackman, M.A. Towards quantitative analysis of intermolecular interactions with Hirshfeld surfaces. Chem. Commun. 2007, 3814–3816. [Google Scholar] [CrossRef]
  43. Pauling, L. The Natural of the Chemical Bond; Cornell University Press: Ithaca, NY, USA, 1967. [Google Scholar]
  44. Matta, C.F.; Hernandez-Trujillo, J.; Tang, T.-H.; Bader, R.F.W. Hydrogen–Hydrogen Bonding: A Stabilizing Interaction in Molecules and Crystals. Chem. Eur. J. 2003, 9, 1940–1951. [Google Scholar] [CrossRef] [PubMed]
  45. Grabowski, S.J.; Pfitzner, A.; Zabel, M.; Dubis, A.T.; Palusiak, M. Intramolecular H...H Interactions for the Crystal Structures of [4-((E)-But-1-enyl)-2,6-dimethoxyphenyl]pyridine-3-carboxylate and [4-((E)-Pent-1-enyl)-2,6-dimethoxyphenyl]pyridine-3-carboxylate; DFT Calculations on Modeled Styrene Derivatives. J. Phys. Chem. B 2004, 108, 1831–1837. [Google Scholar] [CrossRef]
  46. Matta, C.F.; Castillo, N.; Boyd, R.J. Characterization of a Closed-Shell Fluorine−Fluorine Bonding Interaction in Aromatic Compounds on the Basis of the Electron Density. J. Phys. Chem. A 2005, 109, 3669–3681. [Google Scholar] [CrossRef] [PubMed]
  47. Pendás, A.M.; Francisco, E.; Blanco, M.A.; Gatti, C. Bond Paths as Privileged Exchange Channels. Chem. Eur. J. 2007, 13, 9362–9371. [Google Scholar] [CrossRef]
  48. Gibbs, G.V.; Cox, D.F.; Crawford, T.D.; Rosso, K.M.; Ross, N.L.; Downs, R.T. Classification of metal-oxide bonded interactions based on local potential- and kinetic-energy densities. J. Chem. Phys. 2006, 124, 084704. [Google Scholar] [CrossRef]
  49. Dinda, S.; Samuelson, A.G. The Nature of Bond Critical Points in Dinuclear Copper(I) Complexes. Chem. A Eur. J. 2012, 18, 3032–3042. [Google Scholar] [CrossRef]
  50. Cremer, D.; Kraka, E. Chemical Bonds without Bonding Electron Density—Does the Difference Electron-Density Analysis Suffice for a Description of the Chemical Bond? Angew. Chem. Int. Ed. Engl. 1984, 23, 627–628. [Google Scholar] [CrossRef]
  51. Jenkins, V.; Morrison, I. The chemical character of the intermolecular bonds of seven phases of ice as revealed by ab initio calculation of electron densities. Chem. Phys. Lett. 2000, 317, 97–102. [Google Scholar] [CrossRef]
  52. Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E. From weak to strong interactions: A comprehensive analysis of the topological and energetic properties of the electron density distribution involving X–H…F–Y systems. J. Chem. Phys. 2002, 117, 5529–5542. [Google Scholar] [CrossRef]
  53. Varadwaj, P.R.; Marques, H.M. The physical chemistry of coordinated aqua-, ammine-, and mixed-ligand Co2+ complexes: DFT studies on the structure, energetics, and topological properties of the electron density. Phys. Chem. Chem. Phys. 2010, 12, 2126–2138. [Google Scholar] [CrossRef] [PubMed]
Symmetry 13 02026 sch001 550
Scheme 1. Coordination modes of azide ligands in metal complexes.
Scheme 1. Coordination modes of azide ligands in metal complexes.
Symmetry 13 02026 sch001
Symmetry 13 02026 g001 550
Figure 1. X-ray structure with atom numbering; (A) hydrogen bond contact; (B) packing view (C) for 1.
Figure 1. X-ray structure with atom numbering; (A) hydrogen bond contact; (B) packing view (C) for 1.
Symmetry 13 02026 g001
Symmetry 13 02026 g002 550
Figure 2. X-ray structure with atom numbering; (A) hydrogen bond contact; (B) packing view (C) for 2.
Figure 2. X-ray structure with atom numbering; (A) hydrogen bond contact; (B) packing view (C) for 2.
Symmetry 13 02026 g002
Symmetry 13 02026 g003 550
Figure 3. X-ray structure showing atom numbering; (A) 1D polymer array (B) and 1D polymer showing the disordered azide ions (C) for 3.
Figure 3. X-ray structure showing atom numbering; (A) 1D polymer array (B) and 1D polymer showing the disordered azide ions (C) for 3.
Symmetry 13 02026 g003
Symmetry 13 02026 g004 550
Figure 4. Summary of the intermolecular contacts in complexes 1–3.
Figure 4. Summary of the intermolecular contacts in complexes 1–3.
Symmetry 13 02026 g004
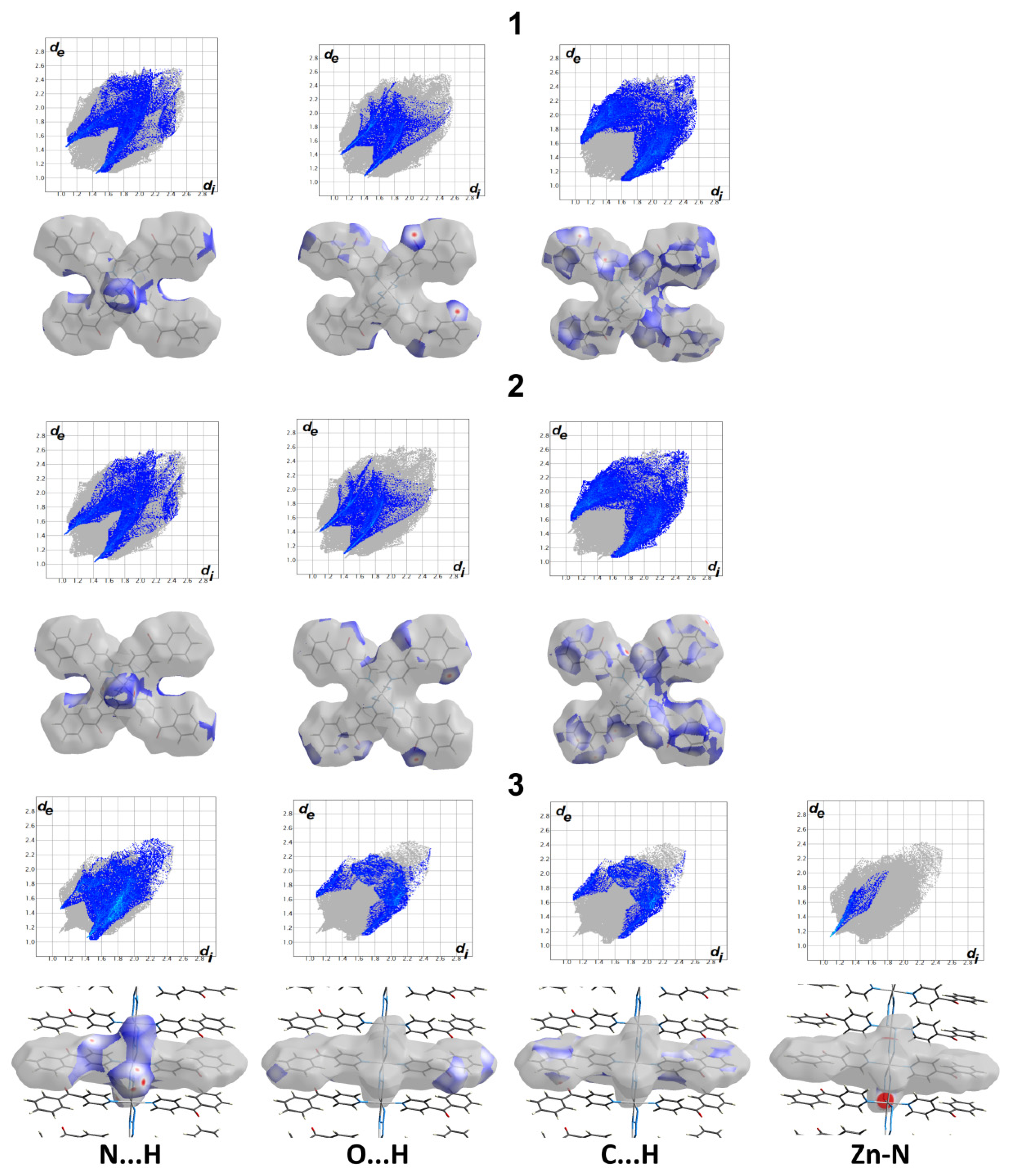
Symmetry 13 02026 g005 550
Figure 5. The decomposed dnorm and FP plots of the N…H, O...H, and C…H contacts in the studied complexes as well as the bridging Zn–N coordination interactions in 3.
Figure 5. The decomposed dnorm and FP plots of the N…H, O...H, and C…H contacts in the studied complexes as well as the bridging Zn–N coordination interactions in 3.
Symmetry 13 02026 g005
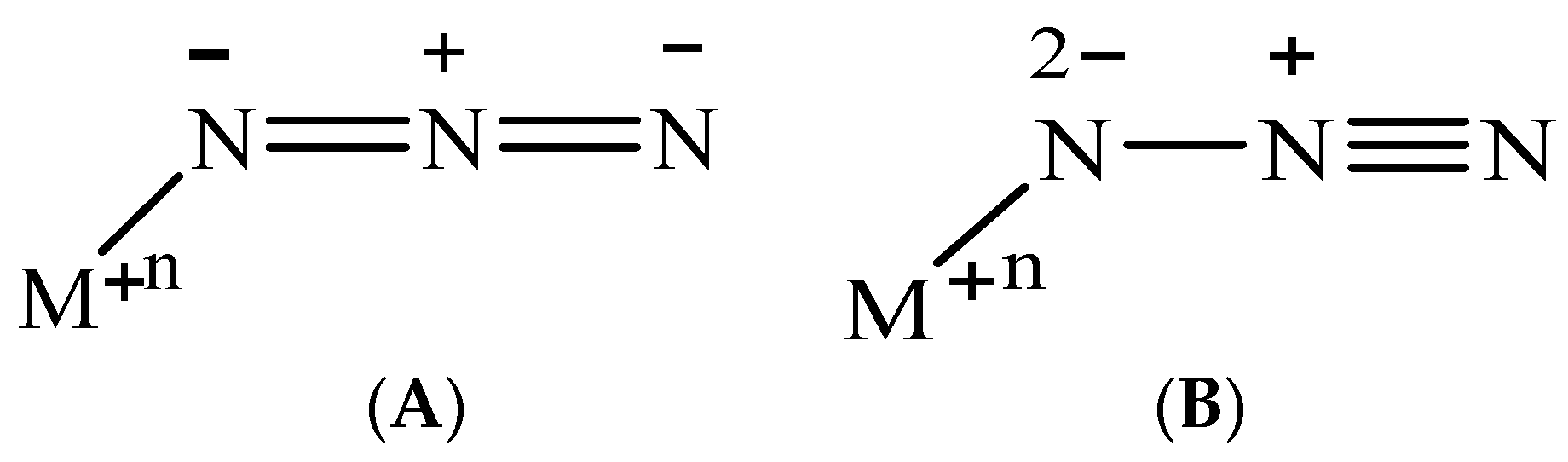
Symmetry 13 02026 g006 550
Figure 6. Simple presentation of the resonance structures of the metal coordinated azides.
Figure 6. Simple presentation of the resonance structures of the metal coordinated azides.
Symmetry 13 02026 g006
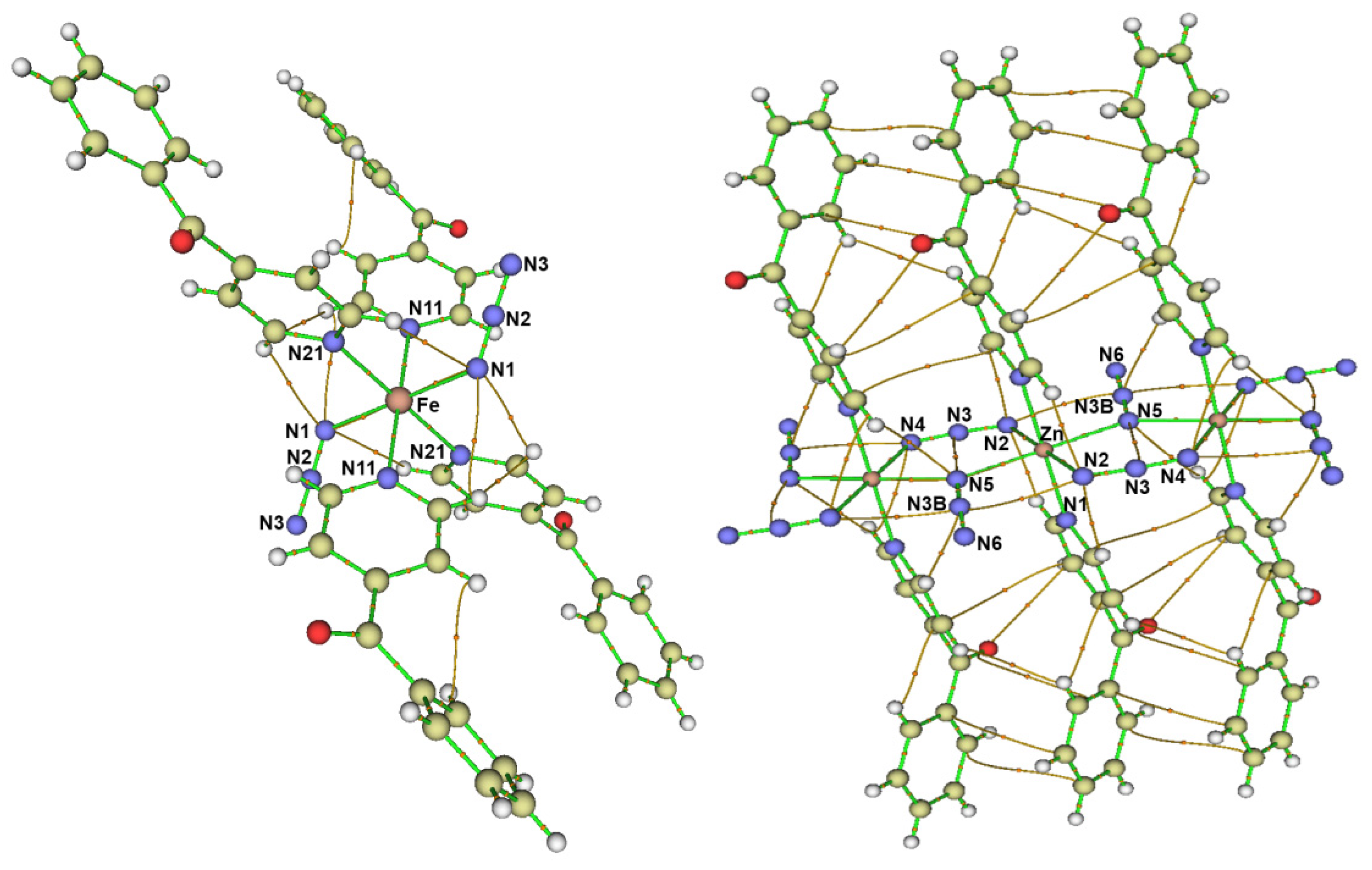
Symmetry 13 02026 g007 550
Figure 7. The bond critical points (BCP; orange dots) and bond paths for complexes 1 and 3. For complex 2, the BCPs are the same as in 1 but Fe, N11, and N21 are replaced by Ni, N1A, and N1B, respectively.
Figure 7. The bond critical points (BCP; orange dots) and bond paths for complexes 1 and 3. For complex 2, the BCPs are the same as in 1 but Fe, N11, and N21 are replaced by Ni, N1A, and N1B, respectively.
Symmetry 13 02026 g007
Symmetry 13 02026 g008 550
Figure 8. Correlations between the azido N-N distances and the electron density (ρ(r)).
Figure 8. Correlations between the azido N-N distances and the electron density (ρ(r)).
Symmetry 13 02026 g008
Table
Table 1. Crystal data for the metal(II)-azido complexes.
Table 1. Crystal data for the metal(II)-azido complexes.
123
Empirical formulaC48H36FeN10O4C48H36N10NiO4C24H18N8O2Zn
fw872.72875.58515.83
temp (K)173(2) 173(2) 173(2)
λ(Å)0.71073 0.71073 0.71073
cryst systTriclinicTriclinicTriclinic
space groupPPP?1
a (Å)6.98090(10) 6.9531(4) 4.0405(1)
b (Å)12.16860(10) 11.9596(7) 8.30040(10)
c (Å)12.49150(10) 12.4219(8) 16.4323(2)
α (deg)92.7020(10)87.2790(10)89.0500(10)
β (deg)90.2030(10)89.6840(10)83.0480(10)
γ (deg)91.6290(10)88.3160(10)83.3630(10)
V (Å3)1059.504(19)1031.34(11)543.383(9)
Z111
ρcalc (Mg/m3)1.3681.4101.576
μ(Mo Kα) (mm−1)0.4140.5301.172
No. reflns.18342112979272
Unique reflns.721136263768
GOOF (F2)1.0231.0071.066
Rint0.03780.09510.0307
R1 a (I ≥ 2σ)0.04310.07250.0312
wR2 b (I ≥ 2σ)0.06580.17760.0717
Largest diff. peak and hole e.Å−30.404/−0.5290.771/−0.6190.524/−0.437
CCDC2,110,4242,110,4252,110,426
a R1 = Σ||Fo|—|Fc||/Σ|Fo|. b wR2 = [Σ[w(Fo2—Fc2)2]/Σ[w(Fo2)2]]1/2.
Table
Table 2. The most important geometrical parameters in complexes 1 and 2.
Table 2. The most important geometrical parameters in complexes 1 and 2.
BondDistance ÅBondDistance Å
12
Fe1-N12.1080(12)Ni1-N12.091(4)
Fe1-N112.2604(11)Ni1-N1A2.133(4)
Fe1-N212.2929(11)Ni1-N1B2.180(4)
BondsAngle °BondsAngle °
N11 1-Fe1-N11180.00(5)N1 1-Ni1-N1B 191.81(14)
N11 1-Fe1-N21 192.03(4)N1-Ni1-N1B 188.19(14)
N11-Fe1-N21 187.96(4)N1 1-Ni1-N1180.0
N21-Fe1-N21 1180.0N1 1-Ni1-N1A88.42(15)
N1-Fe1-N11 189.46(4)N1 1-Ni1-N1A 191.58(15)
N1-Fe1-N1190.54(4)N1A-Ni1-N1B92.62(14)
N1 1-Fe1-N2188.42(4)N1A 1-Ni1-N1B87.38(14)
N1-Fe1-N2191.58(4)N1A-Ni1-N1A 1180.0
Symm. code: 1 -X,1-Y,1-Z Symm. code: 1 1-X,1-Y,1-Z
Table
Table 3. The parameters of the C-H…N and C-H…O interactions (Å and °).
Table 3. The parameters of the C-H…N and C-H…O interactions (Å and °).
D-H...Ad(D-H)d(H...A)d(D...A)<(DHA)
1
C22-H22…N20.952.583.254(2)128
C26-H26…N1 10.952.543.123(2)120
C112-H112…O27 20.952.603.419(2)145
Symm. Codes: 1 -x,1-y,1-z and 2 -1-x,1-y,2-z
2
C2B-H2B…N10.952.543.139(6)121
C2B-H2B…N20.952.483.147(7)127
C6B-H6B...N1 30.952.413.004(6)120
C11B-H11B...N3 40.952.583.508(9)165
Symm. Codes:3 1-x,1-y,1-z4 -x,1-y,2-z
Table
Table 4. The most important geometrical parameters in complex 3.
Table 4. The most important geometrical parameters in complex 3.
BondDistance ÅBondDistance Å
Zn1-N5 12.177(2)Zn1-N52.205(2)
Zn1-N12.198(1)Zn1-N4 12.212(2)
Zn1-N22.199(2)
BondsAngle °BondsAngle °
N5 1-Zn1-N191.00(6)N1-Zn1-N289.60(7)
N5 2-Zn1-N189.00(6)N2 3-Zn1-N2180.00(7)
N1 3-Zn1-N2 389.60(7)N1-Zn1-N588.69(6)
N1-Zn1-N2 390.40(7)N1-Zn1-N5 391.31(6)
Symm. Codes: 1 -x, -y + 2, -z + 1; 2 x + 1, y, z; 3 -x + 1, -y + 2, -z + 1.
Table
Table 5. The natural charges at metal center, 4bzpy and azido groups a.
Table 5. The natural charges at metal center, 4bzpy and azido groups a.
123
Fe1.004 (1.008)Ni0.847 (0.864)Zn1.147 (1.153)
2(4bzpy)0.217 (0.228)2(4bzpy)0.298 (0.300)4bzpy0.093 (0.091)
N3¯−0.719 (−0.731)N3¯−0.722 (−0.732)N3¯μ(1,1)−0.696 (−0.701)
N3¯μ(1,3)−0.681 (0.687)
a MPW1PW91 (WB97XD).
Table
Table 6. The N-N distances (dN-N) and the corresponding topological parameters in the studied complexes.
Table 6. The N-N distances (dN-N) and the corresponding topological parameters in the studied complexes.
CPXdN-NΔdρ(r), a.u∇2ρ(r) a
N1-N21.2040.04050.4675−1.2160
N2-N31.164 0.5242−1.3276
N1-N21.2060.07280.4631−1.4209
N2-N31.133 0.5653−1.8049
N6-N3B1.2070.0170.4721−1.0357
N5-N3B1.190 0.4873−1.3938
N2-N31.1990.0150.4787−1.0351
N3-N41.184 0.4967−1.3545
a Laplacian of electron density.
Table
Table 7. The AIM parameters for the M-N bonds in complexes 1–3 using MPW1PW91 method a.
Table 7. The AIM parameters for the M-N bonds in complexes 1–3 using MPW1PW91 method a.
Bond ρ(r); a.u.H(r) b; a.u.V(r)/G(r) c∇ρ(r) d
Complex 1
Fe1-N110.03460.00100.9850.2646
Fe1-N210.03190.00110.9810.2422
Fe1-N10.0501−0.00061.0070.3528
Complex 2
Ni1-N1B0.03570.00210.9730.3252
Ni1-N1A0.04080.00170.9810.3720
Ni1-N50.0612−0.00951.1020.3347
Complex 3
Zn1-N10.0389−0.06470.9410.2770
Zn1-N410.0369−0.06260.9380.2770
Zn1-N50.0437−0.06581.0100.2575
Zn1-N510.0525−0.07851.0620.2770
Zn1-N20.0297−0.04970.9240.2316
a The WB97XD method gave almost the same results. b Total energy density c potential to kinetic energy density. d Laplacian of electron density.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Abu-Youssef, M.A.M.; Langer, V.; Barakat, A.; Haukka, M.; Soliman, S.M. Molecular, Supramolecular Structures Combined with Hirshfeld and DFT Studies of Centrosymmetric M(II)-azido {M=Ni(II), Fe(II) or Zn(II)} Complexes of 4-Benzoylpyridine. Symmetry 2021, 13, 2026. https://doi.org/10.3390/sym13112026

AMA Style

Abu-Youssef MAM, Langer V, Barakat A, Haukka M, Soliman SM. Molecular, Supramolecular Structures Combined with Hirshfeld and DFT Studies of Centrosymmetric M(II)-azido {M=Ni(II), Fe(II) or Zn(II)} Complexes of 4-Benzoylpyridine. Symmetry. 2021; 13(11):2026. https://doi.org/10.3390/sym13112026

Chicago/Turabian Style

Abu-Youssef, Morsy A. M., Vratislav Langer, Assem Barakat, Matti Haukka, and Saied M. Soliman. 2021. "Molecular, Supramolecular Structures Combined with Hirshfeld and DFT Studies of Centrosymmetric M(II)-azido {M=Ni(II), Fe(II) or Zn(II)} Complexes of 4-Benzoylpyridine" Symmetry 13, no. 11: 2026. https://doi.org/10.3390/sym13112026

APA Style

Abu-Youssef, M. A. M., Langer, V., Barakat, A., Haukka, M., & Soliman, S. M. (2021). Molecular, Supramolecular Structures Combined with Hirshfeld and DFT Studies of Centrosymmetric M(II)-azido {M=Ni(II), Fe(II) or Zn(II)} Complexes of 4-Benzoylpyridine. Symmetry, 13(11), 2026. https://doi.org/10.3390/sym13112026

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop