Investigation and Control of Damping in VSC–MTDC System with DC Circuit Breakers
Abstract
:1. Introduction
2. VSC–MTDC System Modeling
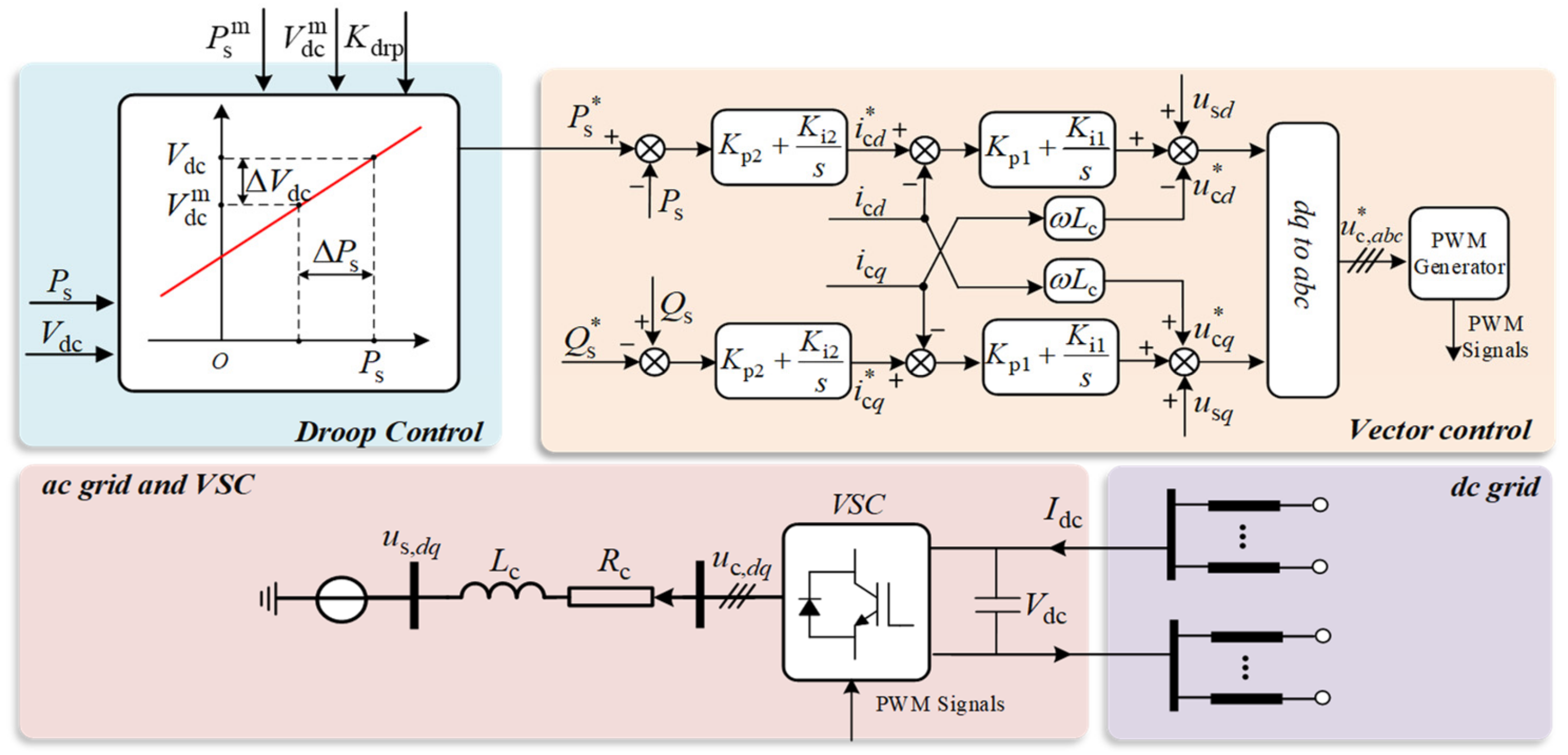
2.1. Average-Value Model
2.2. Controller Modeling
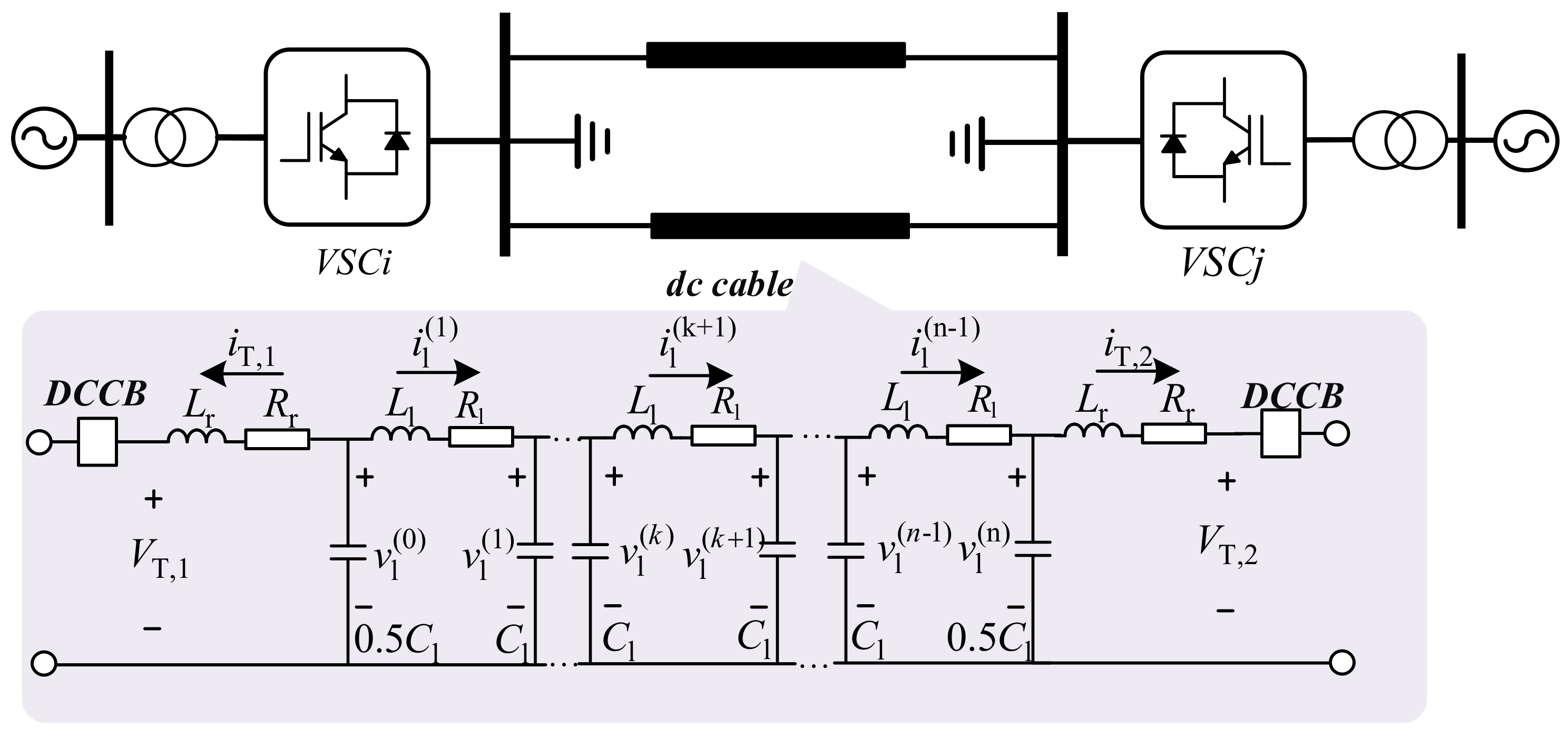
2.3. DC Cable Network Modeling
2.4. Formulation of the Overall Linearized System
3. Modal Analysis
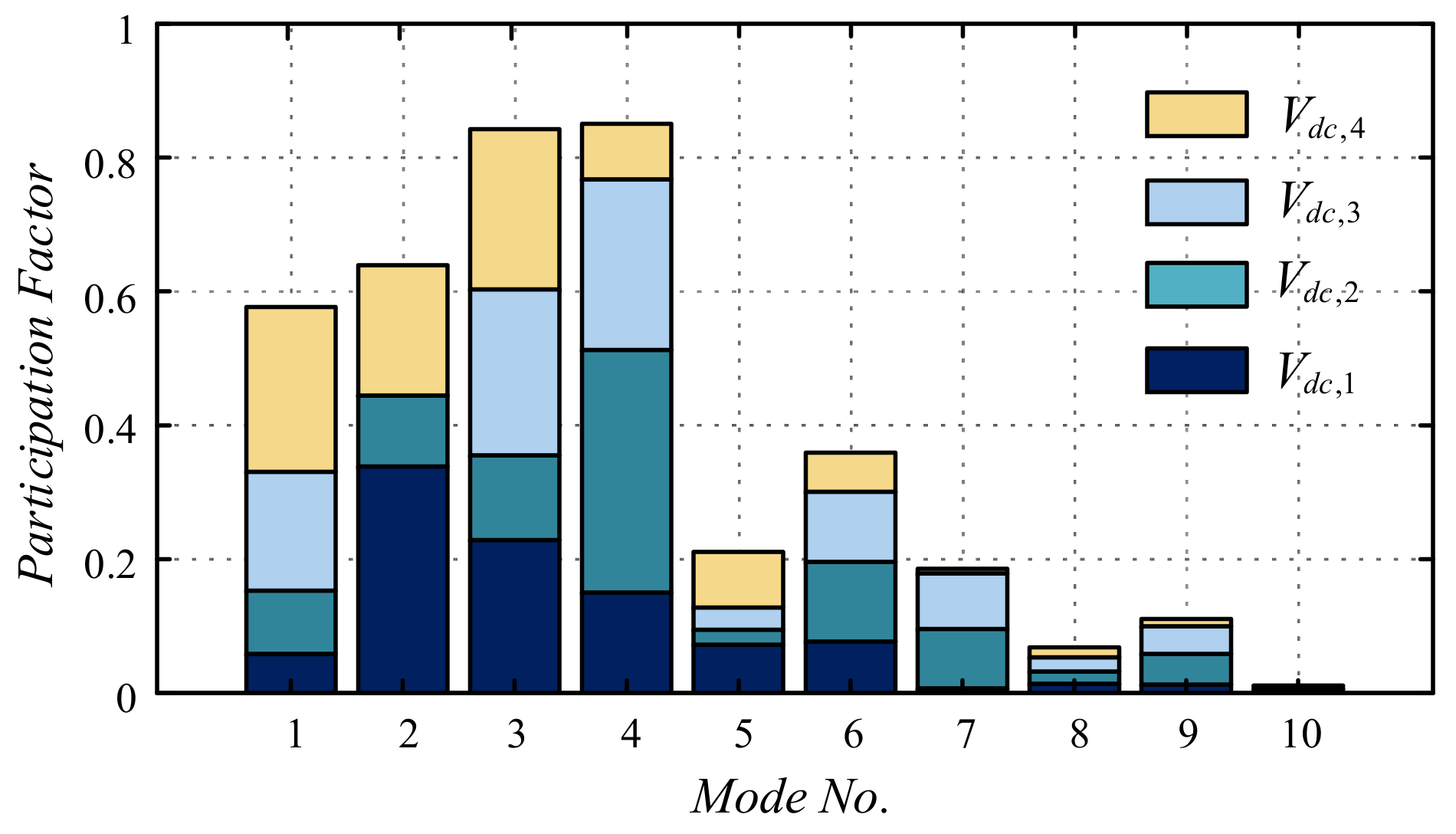
3.1. Participation Factor Analysis
3.2. Participation Sensitivity Analysis
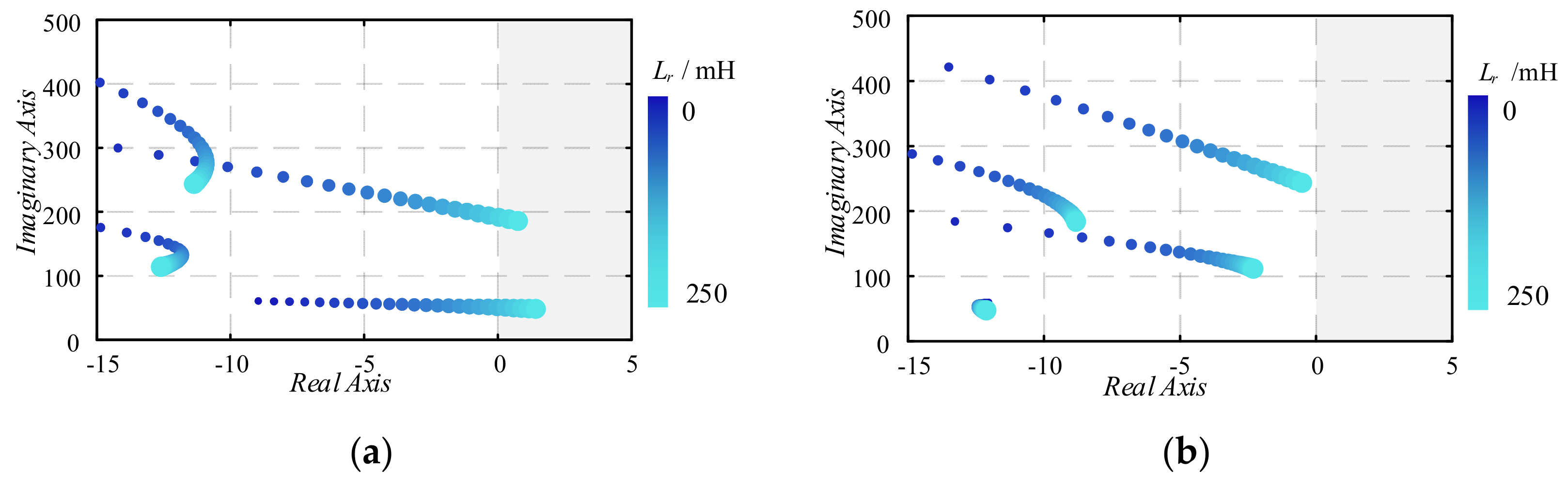
3.2.1. Impact of DC Reactor
3.2.2. Impact of Power Flow
4. Additional Damping Control Strategy for MTDC
4.1. Parametric Sensitivity Analysis
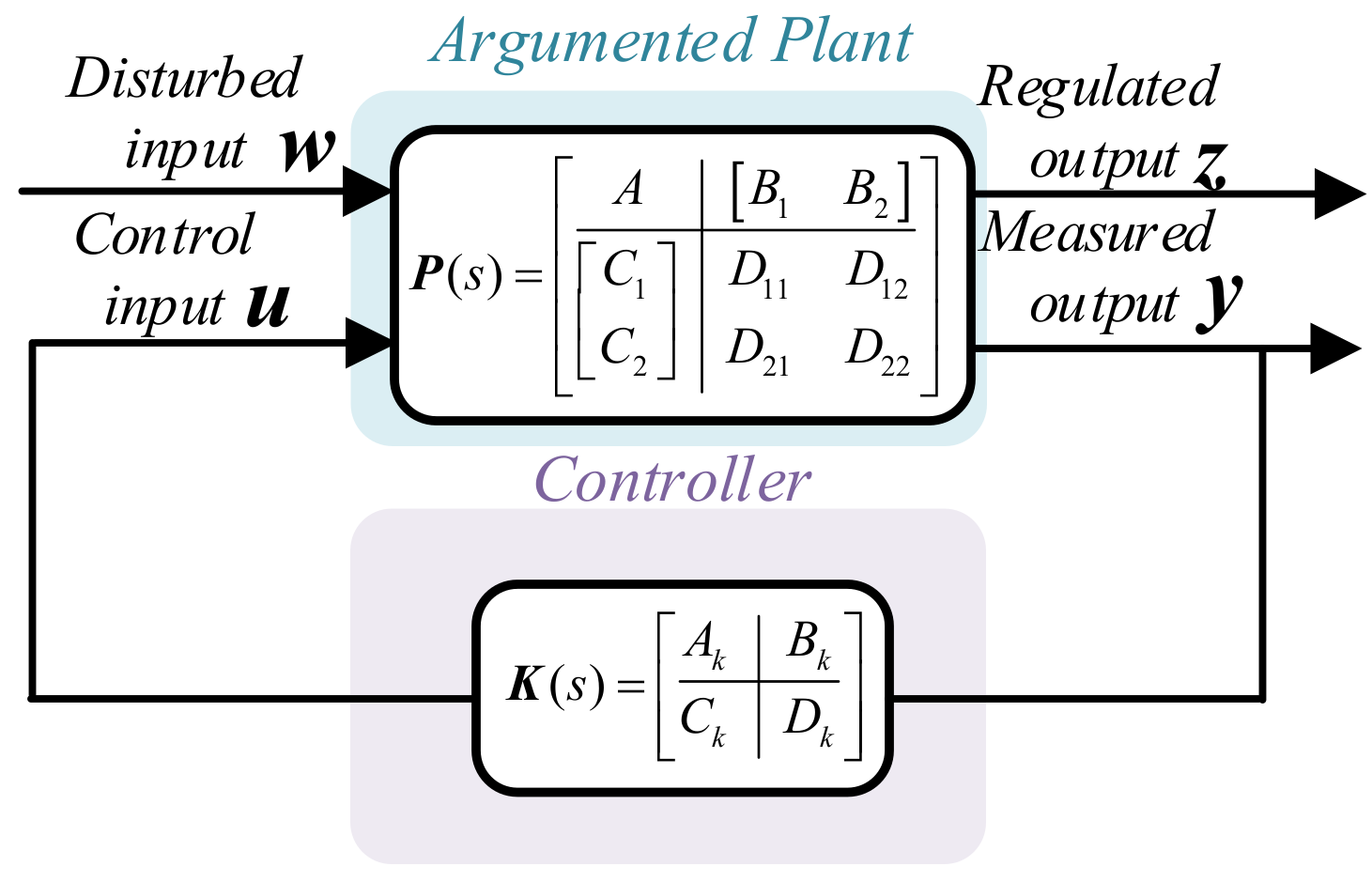
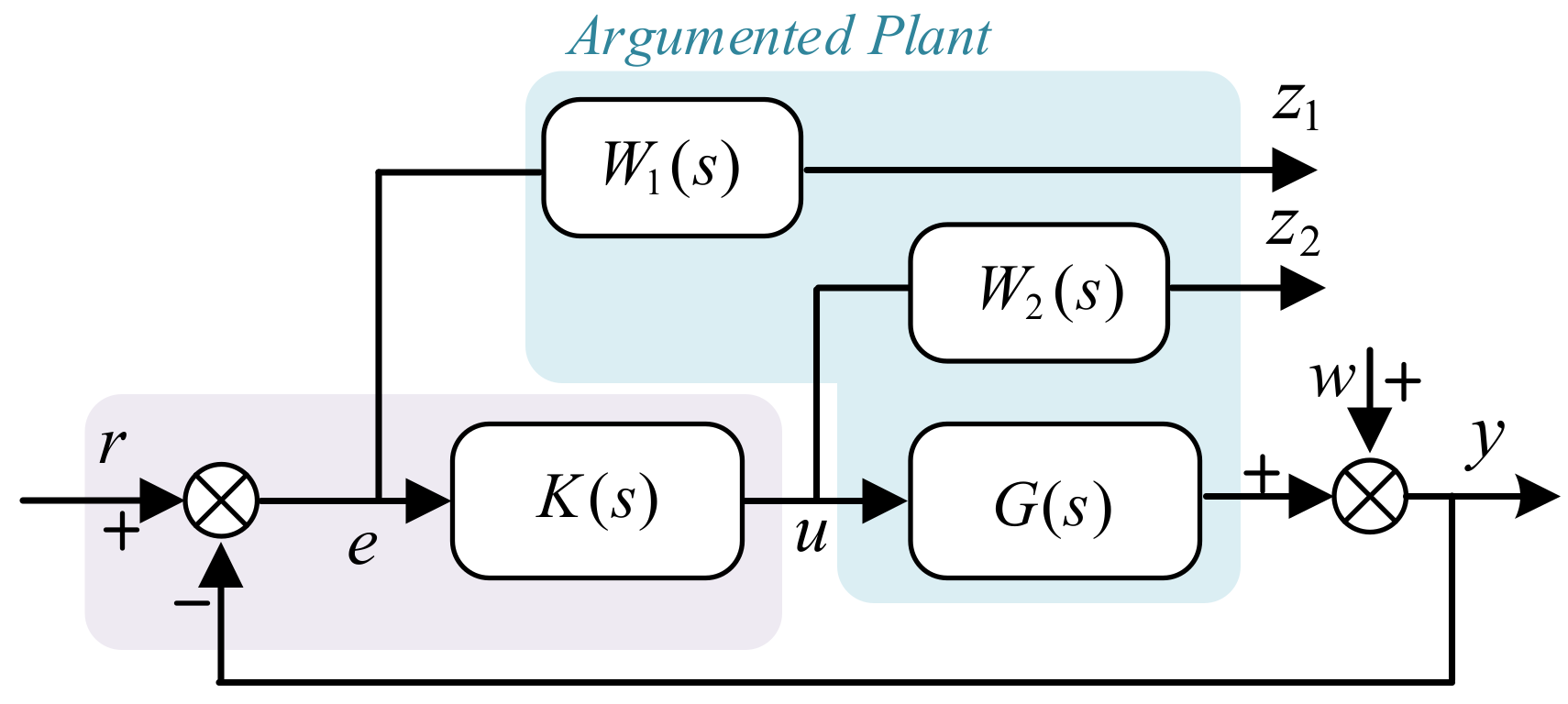
4.2. DC Power System Stabilizer Design Utilizing H∞ Mix-Sensitivity Optimization
4.2.1. Selection of W1(s)
4.2.2. Selection of W2(s)
5. Case Study
5.1. Eigenvalue Analysis
5.2. Eigenvalue Analysis
5.2.1. Impact of DC Reactor Evaluation of Influence of DCCBs
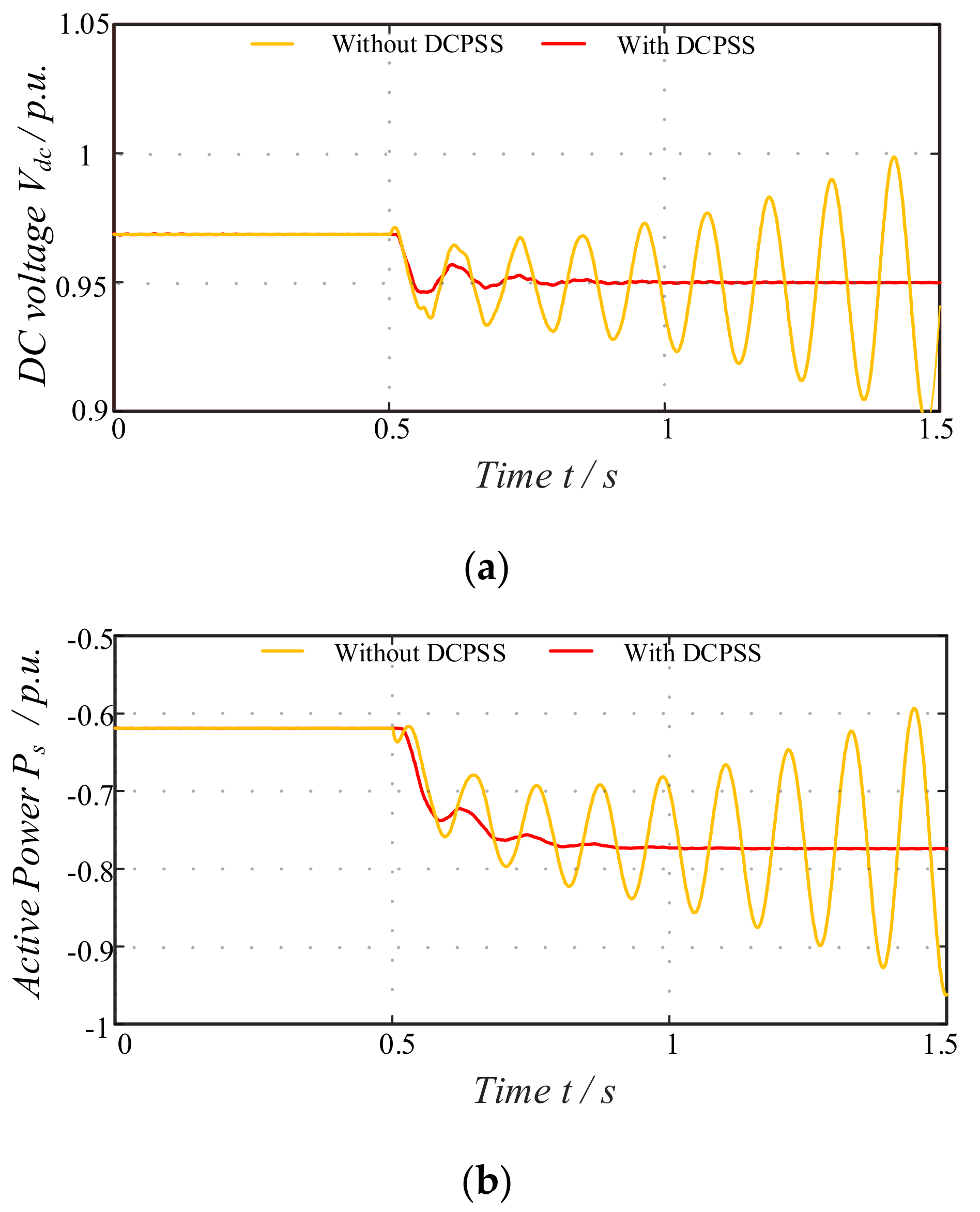
5.2.2. Instability Suppression Scenario
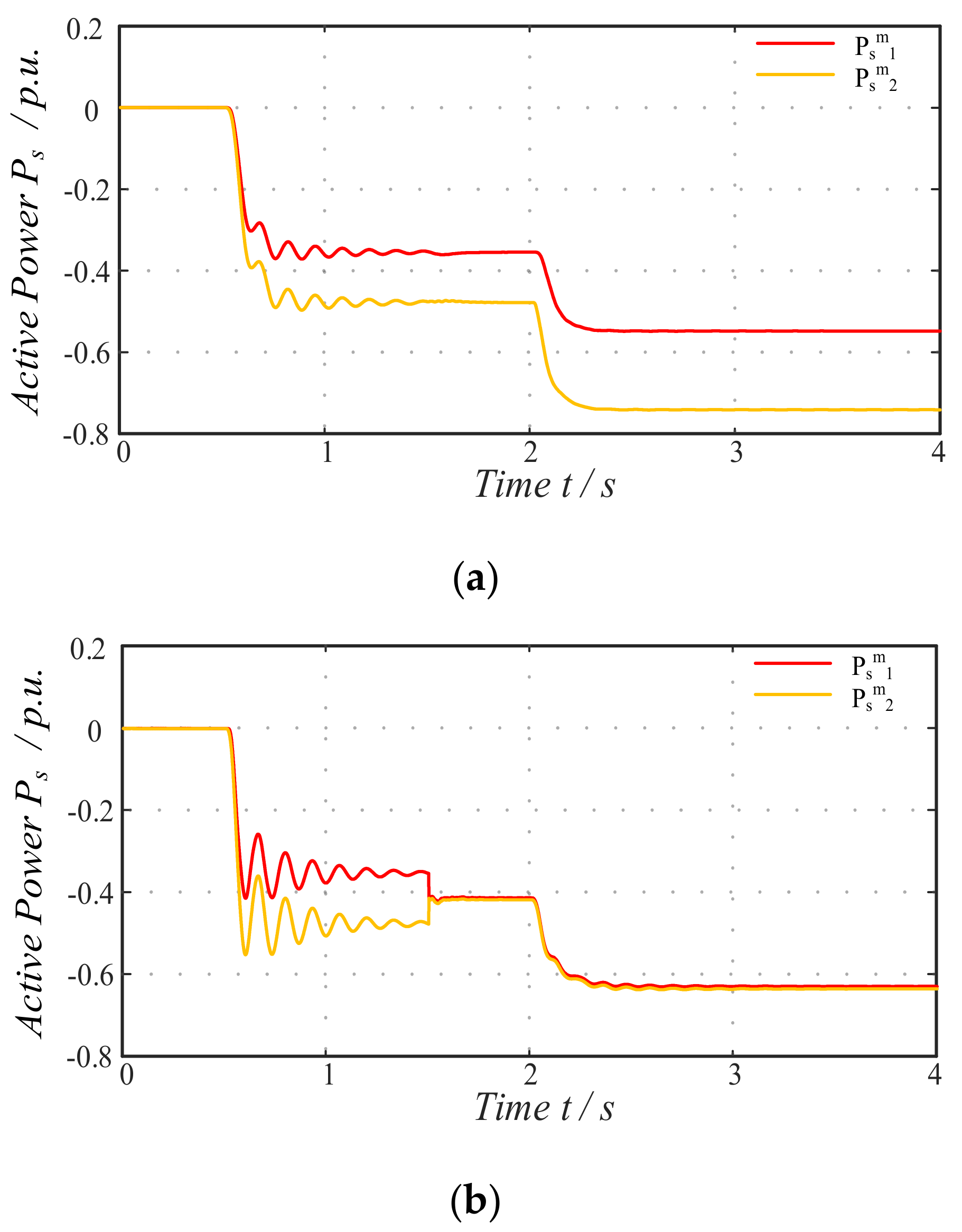
5.2.3. Accurate Power Sharing between VSCs
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| N1, NC | Total number of cables and converters in a MTDC system |
| VSCi, VSCj | The i-th and j-th voltage-sourced converter in a MTDC system |
| Vdc0 | The steady-state value of a DC voltage |
| ΔVdc0 | The small signal value of a DC voltage |
| Vdc, Ps | The measurement value of a DC voltage and the active power injections atthe point of the common coupling |
| Psm, Ps* | The modulation value of a droop controller and the reference value of an active power controller |
| Lr, Rr | The inductance and resistance of a DC reactor |
| Kp, Ki | The proportional coefficient and integral coefficient of a PI controller |
| en, zn | The error and its integral values of the n-th PI controller. (n = 1, 2, 3, 4) |
References
- Abedin, T.; Lipu, M.S.H.; Hannan, M.A.; Ker, P.J.; Rahman, S.A.; Yaw, C.T.; Tiong, S.K.; Muttaqi, K.M. Dynamic modeling of hvdc for power system stability assessment: A review, issues, and recommendations. Energies 2021, 14, 4829. [Google Scholar] [CrossRef]
- Flourentzou, N.; Agelidis, V.G.; Demetriades, G.D. VSC-based HVDC power transmission systems: An overview. IEEE Trans. Power Electron. 2009, 24, 592–602. [Google Scholar] [CrossRef]
- Rodriguez, P.; Rouzbehi, K. Multi-terminal DC grids: Challenges and prospects. J. Mod. Power Syst. Clean Energy 2017, 5, 515–523. [Google Scholar] [CrossRef] [Green Version]
- Lei, Z.; Zou, Y.; Yu, J.; Vittal, V.; Wang, Z. Modeling, control, and protection of modular multilevel converter-based multi-terminal HVDC systems: A review. CSEE J. Power Energy Syst. 2017, 3, 340–352. [Google Scholar]
- Sun, J.; Wang, H.; Zhu, X.; Pu, Q. A self-regulation strategy for the power fluctuation of the islanded voltage source converter (VSC) station delivering large-scale wind power. Energies 2020, 13, 560. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.P.; Zhao, C. The research of SM topology with DC fault tolerance in MMC-HVDC. IEEE Trans. Power Deliv. 2015, 30, 1561–1568. [Google Scholar] [CrossRef]
- Zeng, R.; Xu, L.; Yao, L.; Morrow, D.J. Precharging and DC Fault Ride-Through of Hybrid MMC-Based HVDC Systems. IEEE Trans. Power Deliv. 2015, 30, 1298–1306. [Google Scholar] [CrossRef] [Green Version]
- Miyara, R.; Nakadomari, A.; Matayoshi, H.; Takahashi, H.; Hemeida, A.M.; Senjyu, T. A Resonant Hybrid DC Circuit Breaker for Multi-Terminal HVDC Systems. Sustainability 2020, 12, 7771. [Google Scholar] [CrossRef]
- Schmitt, D.; Wang, Y.; Weyh, T.; Marquardt, R. DC-side fault current management in extended multiterminal-HVDC-grids. In Proceedings of the International Multi-Conference on Systems, Signals & Devices, Chemnitz, Germany, 21–24 March 2012. [Google Scholar]
- Kontos, E.; Pinto, R.T.; Rodrigues, S.; Bauer, P. Impact of HVDC transmission system topology on multiterminal DC network faults. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 June 2015. [Google Scholar]
- Bayo-Salas, A.; Beerten, J.; Rimez, J.; Hertem, D.V. analysis of control interactions in multi-infeed VSC HVDC connections. IET Gener. Transm. Distrib. 2016, 10, 1336–1344. [Google Scholar] [CrossRef]
- Bidadfar, A.; Nee, H.P.; Zhang, L.; Harnefors, L.; Namayantavana, S.; Abedi, M. Power system stability analysis using feedback control system modeling including HVDC transmission links. IEEE Trans. Power Syst. 2016, 31, 116–124. [Google Scholar] [CrossRef]
- Zhang, Z.; Lee, J.; Han, C.; Jeong, S.; Jang, G. An advance index to evaluate the stability of MMC-HVDC and offshore wind power generation. In Proceedings of the IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP 2019), Xi’an, China, 21–24 October 2019. [Google Scholar]
- Yuan, Z.; Zhengchun, D.; Li, G. Analysis on the dynamic behaviours and interactions of VSC-MTDC grid. IET Gener. Transm. Distrib. 2018, 12, 1756–1764. [Google Scholar] [CrossRef]
- Pinares, G.; Bongiorno, M. Analysis and mitigation of instabilities originated from DC-side resonances in VSC-HVDC systems. IEEE Trans. Ind. Appl. 2016, 52, 2807–2815. [Google Scholar] [CrossRef]
- Amin, M.; Molinas, M.; Lyu, J.; Cai, X. Impact of power flow direction on the stability of VSC-HVDC seen from the impedance Nyquist Plot. IEEE Trans. Power Electron. 2017, 32, 8204–8217. [Google Scholar] [CrossRef]
- Chaudhuri, N.R.; Majumder, R.; Chaudhuri, B. Stability analysis of VSC MTDC grids connected to multimachine AC systems. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012. [Google Scholar]
- Kalcon, G.O.; Adam, G.P.; Anaya-Lara, O.; Lo, S.; Uhlen, K. Small-signal stability analysis of multi-terminal VSC-based DC transmission systems. IEEE Trans. Power Syst. 2012, 27, 1818–1830. [Google Scholar] [CrossRef]
- Jie, Y.; Kaipei, L.; Dongxu, W. Small signal stability analysis of VSC-HVSC applied to passive network. Proc. CSEE 2015, 35, 2400–2408. [Google Scholar]
- Das, K.; Guo, F.; Nuño, E.; Cutululis, N.A. Frequency stability of power system with large share of wind power under storm conditions. J. Mod. Power Syst. Clean Energy 2020, 8, 219–228. [Google Scholar] [CrossRef]
- Azizi, N.; Moradi CheshmehBeigi, H.; Rouzbehi, K. Optimal placement of direct current power system stabiliser (DC-PSS) in multi-terminal HVDC grids. IET Gener. Transm. Distrib. 2020, 14, 2315–2322. [Google Scholar] [CrossRef]
- Li, Y.; Tang, G.; Ge, J.; He, Z.; Wu, Y. Modeling and damping control of modular multilevel converter based DC grid. IEEE Trans. Power Syst. 2018, 33, 723–735. [Google Scholar] [CrossRef]
- Herrera, M.L.; Subramanyam, S.A.; Zhang, X. Robust control and optimal operation of multiple microgrids with configurable interconnections. In Proceedings of the 2019 IEEE Green Technologies Conference, Lafayette, LA, USA, 3–5 April 2019. [Google Scholar]
- Wu, W.; Wu, X.; Jing, L. Active damping control of multi-port DC power flow controller for suppressing power oscillation of MMC-MTDC under unbalanced grid. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE 2020), Detroit, MI, USA, 11–15 October 2020. [Google Scholar]
- Jiebei, Z.; Zhipeng, S.; Siqi, B.; Xialin, L.; Booth Campbell, D.; Qiu, W.; Hongjie, J.; Chengshan, W. Coordinated flexible damping mechanism with inertia emulation capability for MMC-MTDC transmission systems. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 1. [Google Scholar] [CrossRef]
- Cao, W.; Han, M.; Zhang, X.; Xie, W.; Agundis-Tinajero, G.; Guerrero, J.M. A novel power sharing scheme of controlling parallel-operated inverters in islanded microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5732–5746. [Google Scholar] [CrossRef]
- Zhou, K.; Doyle, J.C.; Glover, K. Robust and Optimal Control, 2st ed.; Prentice Hall: Hoboken, NJ, USA, 1995; pp. 373–399. [Google Scholar]
- Pal, B.; Chaudhuri, B. Robust Control in Power Systems, 1st ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005; pp. 79–81. [Google Scholar]
- Chen, S.; Malik, O.P. H∞ optimisation-based power system stabiliser design. IEE Proc. Gener. Transm. Distrib. 1995, 142, 179–184. [Google Scholar] [CrossRef]
- Prieto-Araujo, E.F.; Bianchi, D.; Junyent-Ferre, A.; Gomis-Bellmunt, O. Methodology for droop control dynamic analysis of multiterminal VSC-HVDC grids for offshore wind farms. IEEE Trans. Power Deliv. 2011, 26, 2476–2485. [Google Scholar] [CrossRef]
- Chaudhuri, B.; Pal, B.C.; Zolotas, A.C.; Jaimoukha, I.M.; Green, T.C. Mixed-sensitivity approach to h-infinity control of power system oscillations employing multiple facts devices. IEEE Trans. Power Syst. 2003, 18, 1149–1156. [Google Scholar] [CrossRef] [Green Version]
- Banerjee, A.; Chaudhuri, N.R. Robust damping of inter-area oscillation in AC-MTDC grids using H∞ Mixed-sensitivity approach. In Proceedings of the IEEE Power and Energy Society General Meeting (PESGM 2016), Boston, MA, USA, 17–21 July 2016. [Google Scholar]
- Banerjee, A.; Chaudhuri, N.R.; Kavasseri, R.G. A novel explicit disturbance model-based robust damping of interarea oscillations through MTDC grids embedded in AC systems. In Proceedings of the IEEE Power & Energy Society General Meeting (PESGM 2019), Atlanta, GA, USA, 4–9 April 2019. [Google Scholar]
- Gahinet, P.; Nemirovskii, A.; Laub, A.J.; Chilali, M. The LMI control toolbox. In Proceedings of the 33rd IEEE Conference on Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994. [Google Scholar]
- Chilali, M.; Gahinet, P. H∞ design with pole placement constraints: An LMI approach. IEEE Trans. Autom. Control 1996, 41, 358–367. [Google Scholar] [CrossRef]



| VSC1 | VSC2 | VSC3 | VSC4 | ||
|---|---|---|---|---|---|
| Equilibrium I | 0.9604 | 0.9465 | 0.9269 | 0.9121 | |
| −0.3961 | −0.5353 | 0.4000 | 0.5000 | ||
| Equilibrium II | 1.0377 | 1.0500 | 1.0668 | 1.0793 | |
| 0.3771 | 0.4997 | −0.5000 | −0.4000 |
| Mode | Eigenvalue (p.u.) | Damping Ratio ζ (%) | Frequency (rad/s) |
|---|---|---|---|
| M1 | −4.06 ± 56.00i | 0.072 | 56.15 |
| M2 | −11.94 ± 141.94i | 0.084 | 142.45 |
| M3 | −7.14 ± 247.84i | 0.029 | 247.95 |
| M4 | −11.89 ± 334.36i | 0.035 | 335 |
| Mode | Poles | Damping Ratio ξ | ωn (rad/s) | |||
|---|---|---|---|---|---|---|
| Open Loop | Closed Loop | Open Loop | Closed Loop | Open Loop | Closed Loop | |
| M1 | −4.06 ± 56.00i | −13.69 ± 56.39i | 0.072 | 0.236 | 56.15 | 58 |
| M2 | −11.94 ± 141.94i | −12.97 ± 143.9i | 0.084 | 0.09 | 142.4 | 144 |
| M3 | −7.14 ± 247.84i | −10.80± 139.8i | 0.029 | 0.07 | 247.9 | 140 |
| Mode | Poles | Damping Ratio ξ | ωn (rad/s) | |||
| Open Loop | Closed Loop | Open Loop | Closed Loop | Open Loop | Closed Loop | |
| M1 | −4.06 ± 56.00i | −19.45 ± 54.48i | 0.072 | 0.430 | 56.15 | 53.9 |
| M2 | −11.94 ± 141.94i | −20.23 ± 141.9i | 0.084 | 0.14 | 142.4 | 143 |
| M3 | −7.14 ± 247.84i | −27.6 ± 246.5i | 0.029 | 0.11 | 247.9 | 248 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, W.; Gao, J.; Zhou, G.; Zhang, Y.; Zhang, K.; Han, J.; Dong, L. Investigation and Control of Damping in VSC–MTDC System with DC Circuit Breakers. Symmetry 2021, 13, 2037. https://doi.org/10.3390/sym13112037
Ma W, Gao J, Zhou G, Zhang Y, Zhang K, Han J, Dong L. Investigation and Control of Damping in VSC–MTDC System with DC Circuit Breakers. Symmetry. 2021; 13(11):2037. https://doi.org/10.3390/sym13112037
Chicago/Turabian StyleMa, Wenzhong, Jianyi Gao, Guanyu Zhou, Yan Zhang, Kuitong Zhang, Jia Han, and Lei Dong. 2021. "Investigation and Control of Damping in VSC–MTDC System with DC Circuit Breakers" Symmetry 13, no. 11: 2037. https://doi.org/10.3390/sym13112037
APA StyleMa, W., Gao, J., Zhou, G., Zhang, Y., Zhang, K., Han, J., & Dong, L. (2021). Investigation and Control of Damping in VSC–MTDC System with DC Circuit Breakers. Symmetry, 13(11), 2037. https://doi.org/10.3390/sym13112037





