A Prabhakar Fractional Approach for the Convection Flow of Casson Fluid across an Oscillating Surface Based on the Generalized Fourier Law
Abstract
:1. Introduction
2. Preliminaries of Fractional Calculus
3. Problem Formulation
4. Results of the Problem
4.1. Temperature Field’s Outcome
4.2. Velocity Field’s Outcome
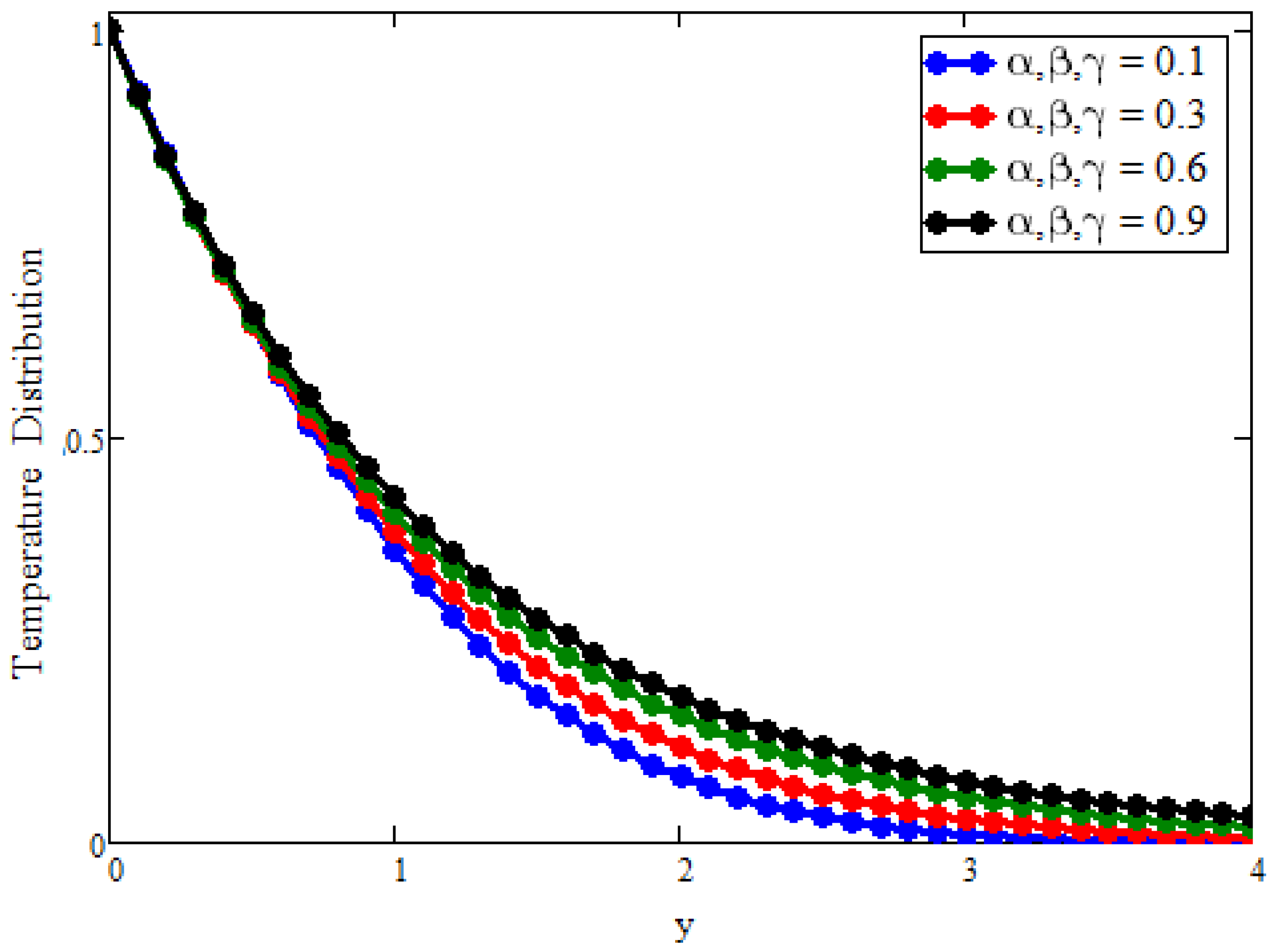
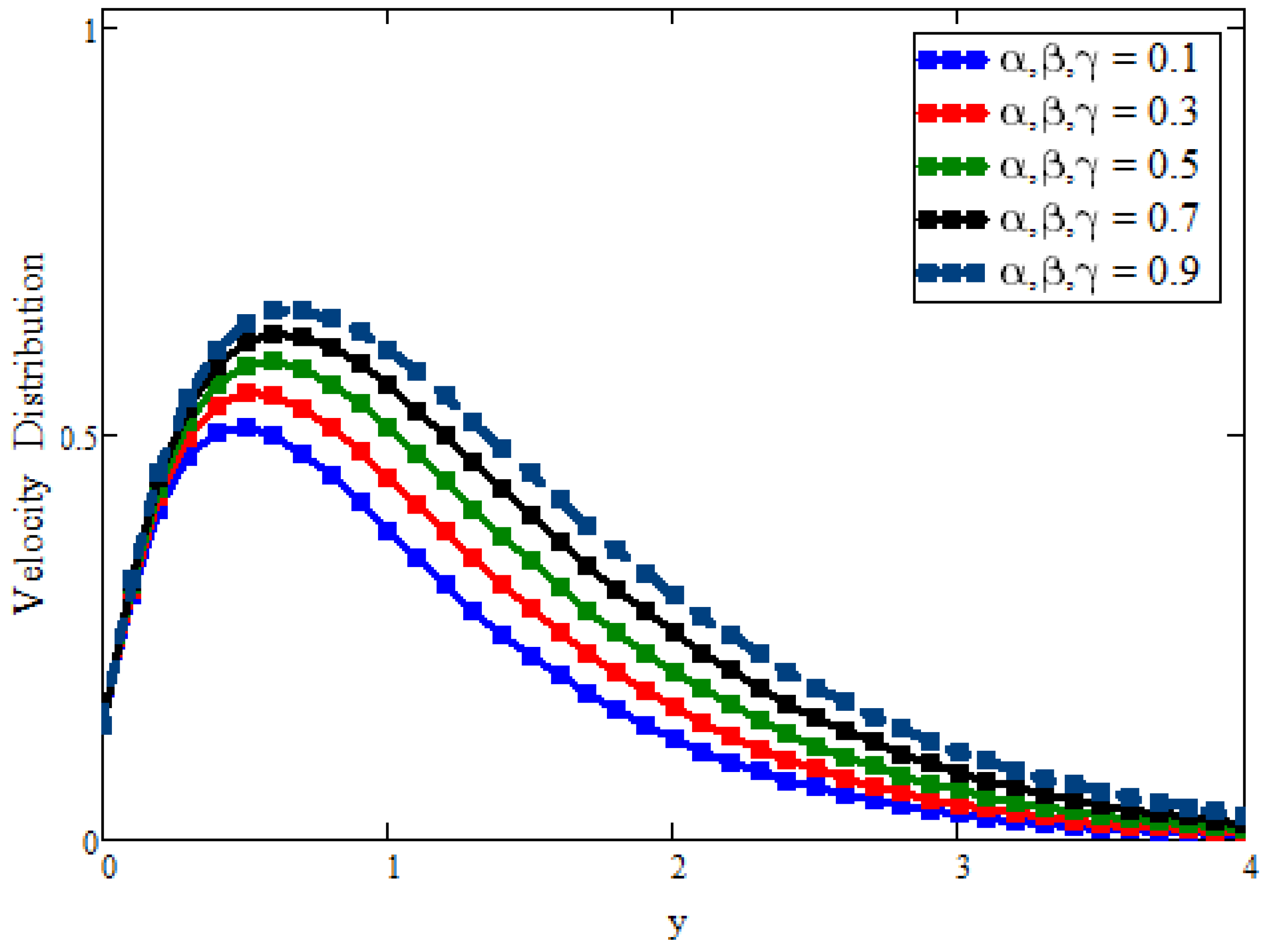
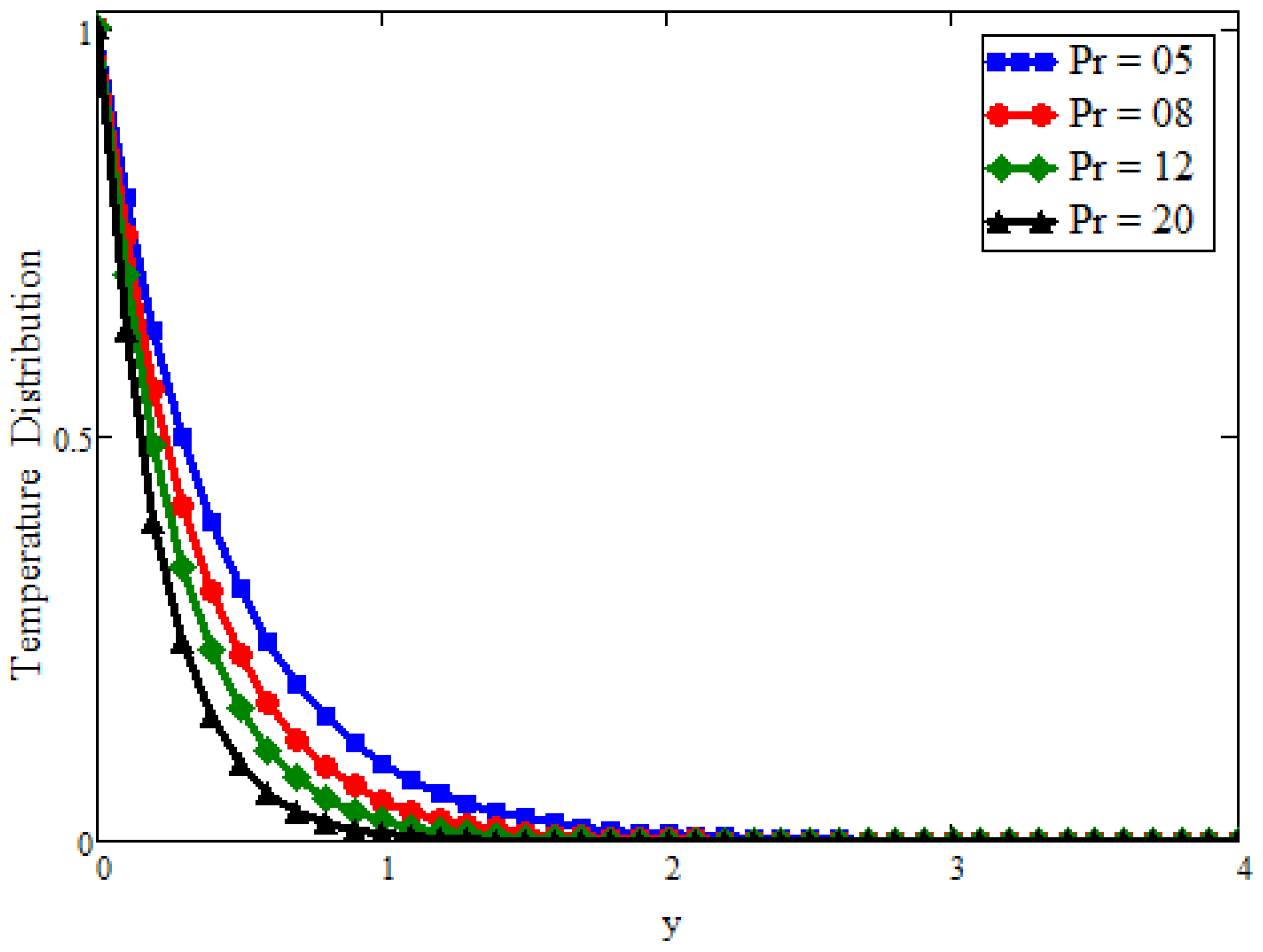
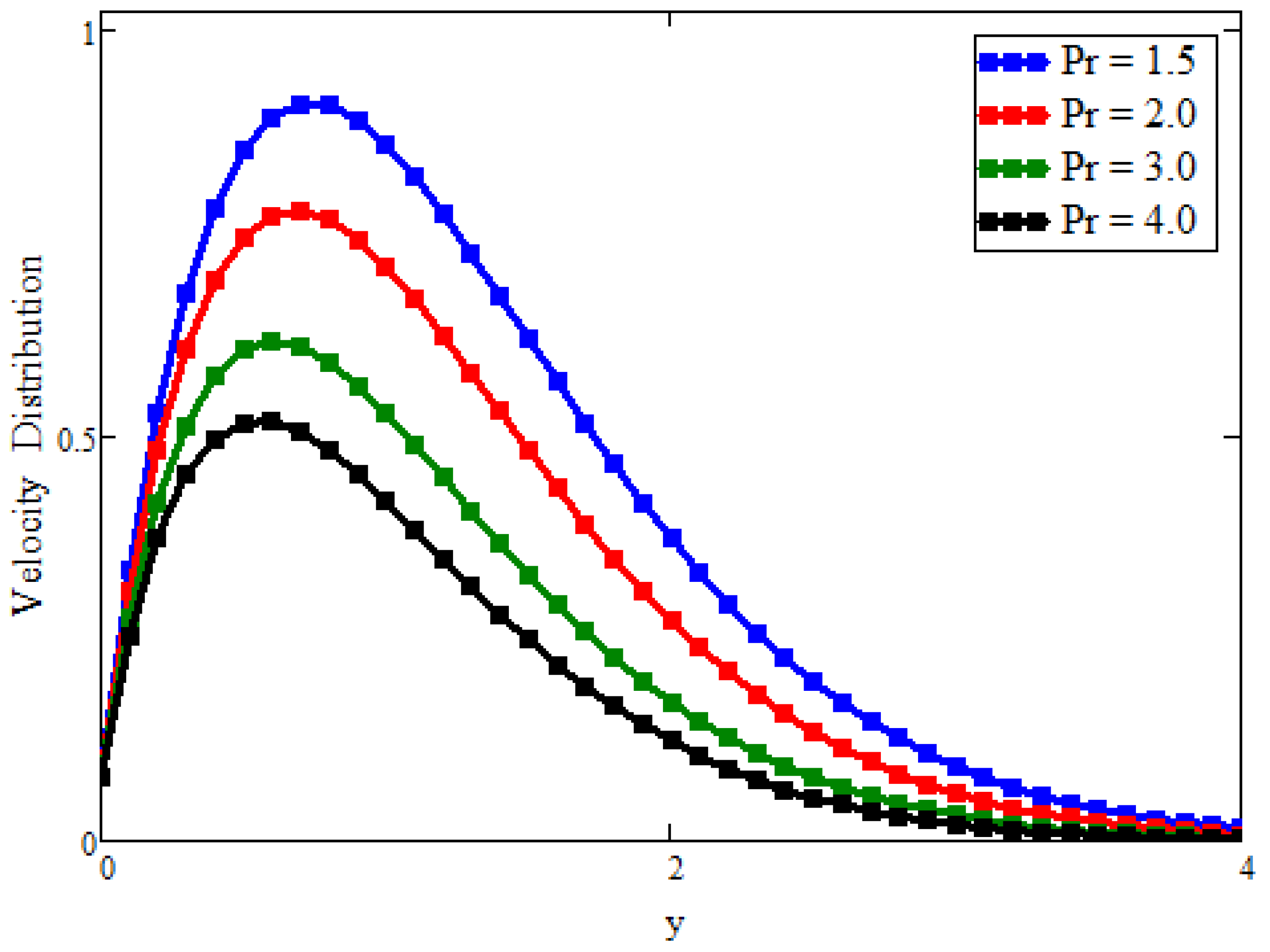
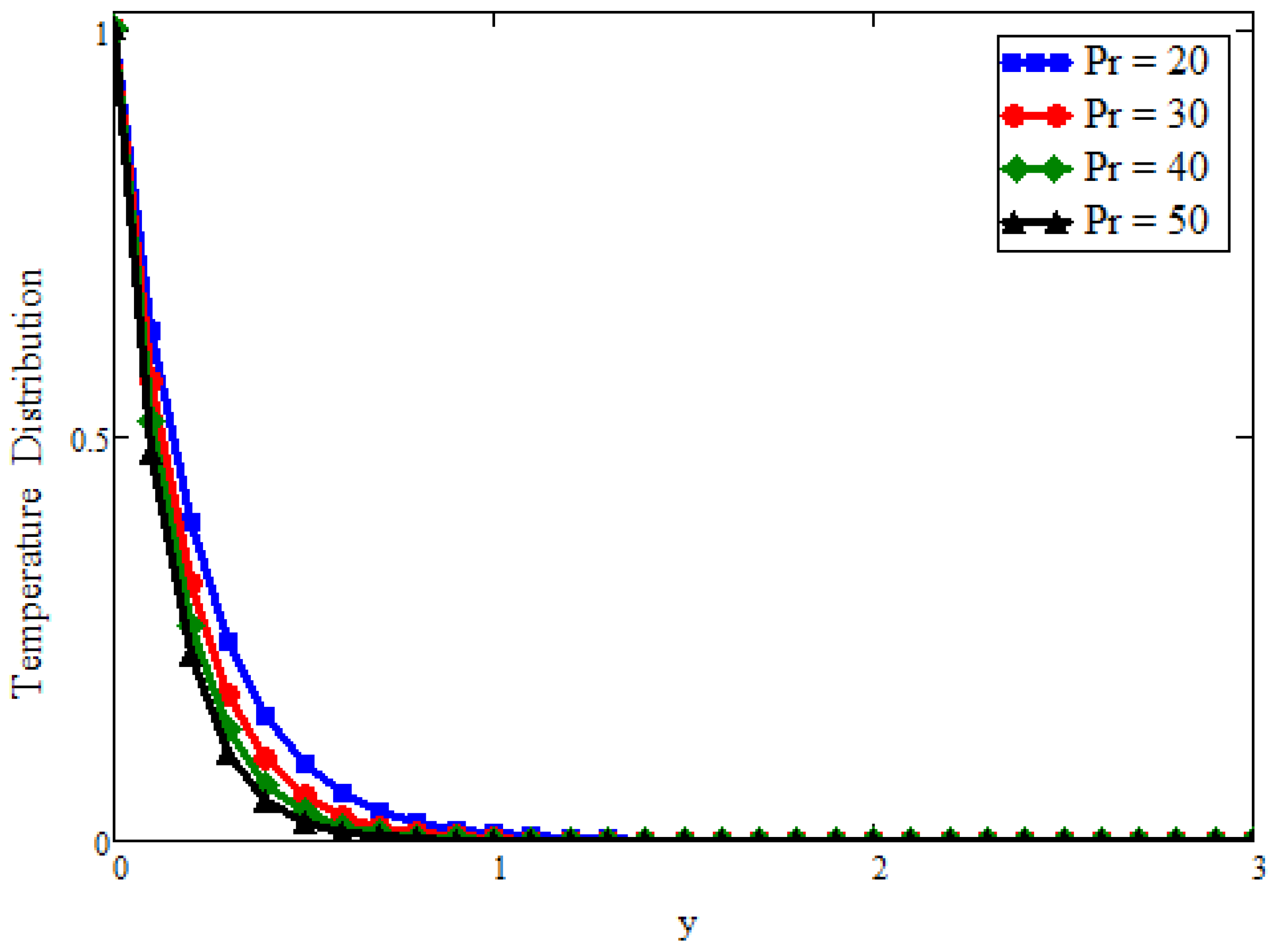
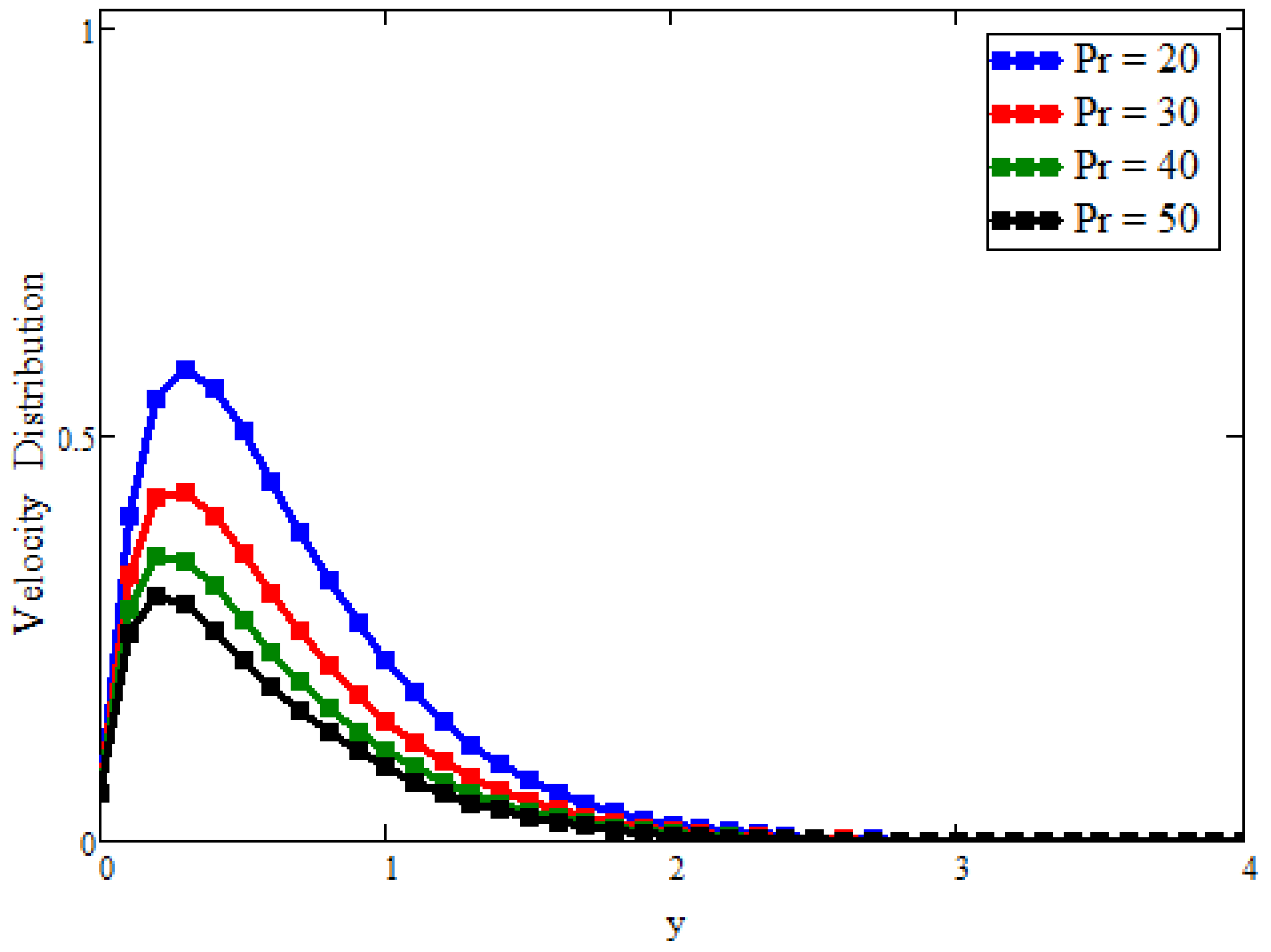
5. Graphically Results and Discussion
6. Conclusions
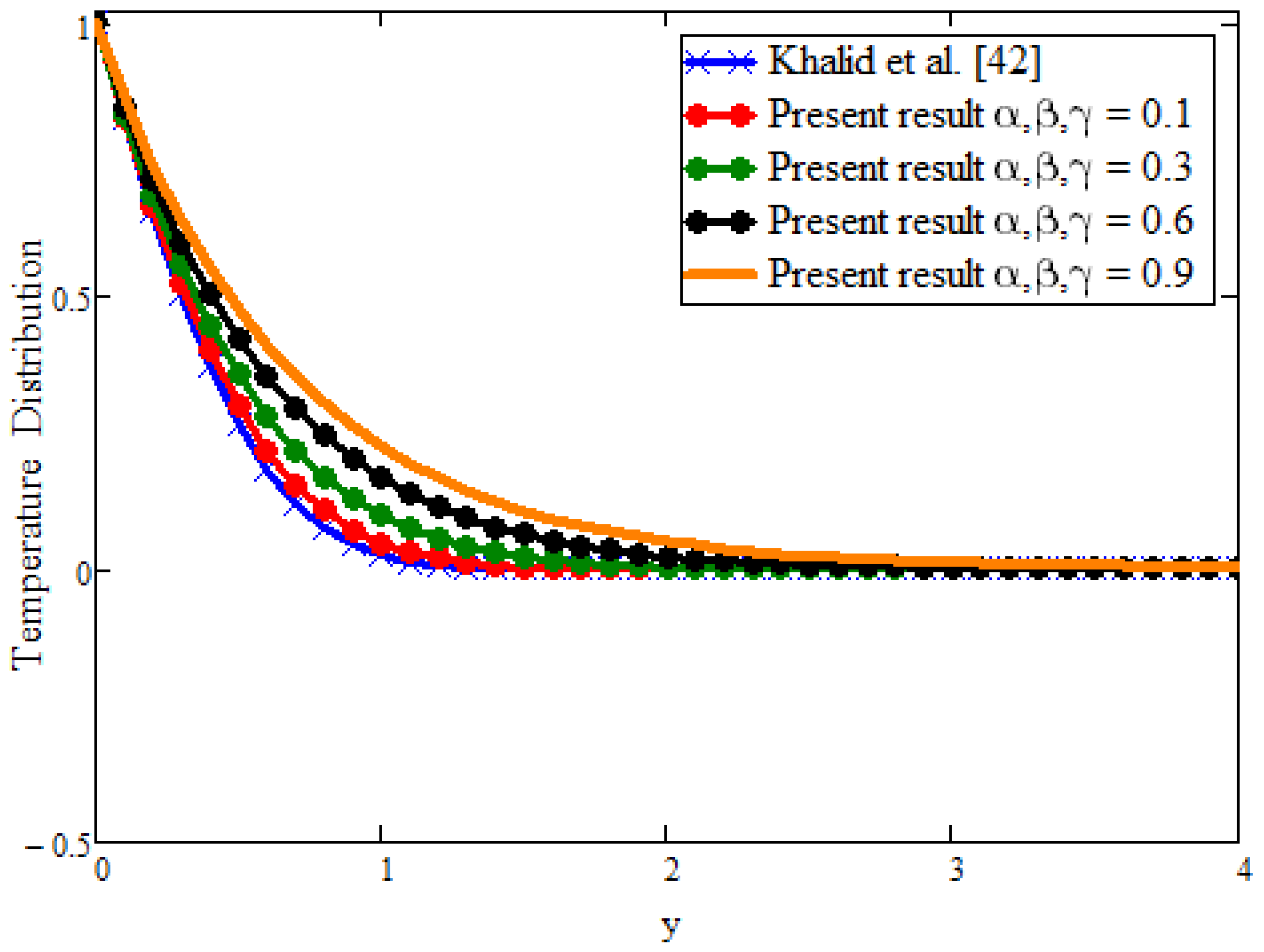
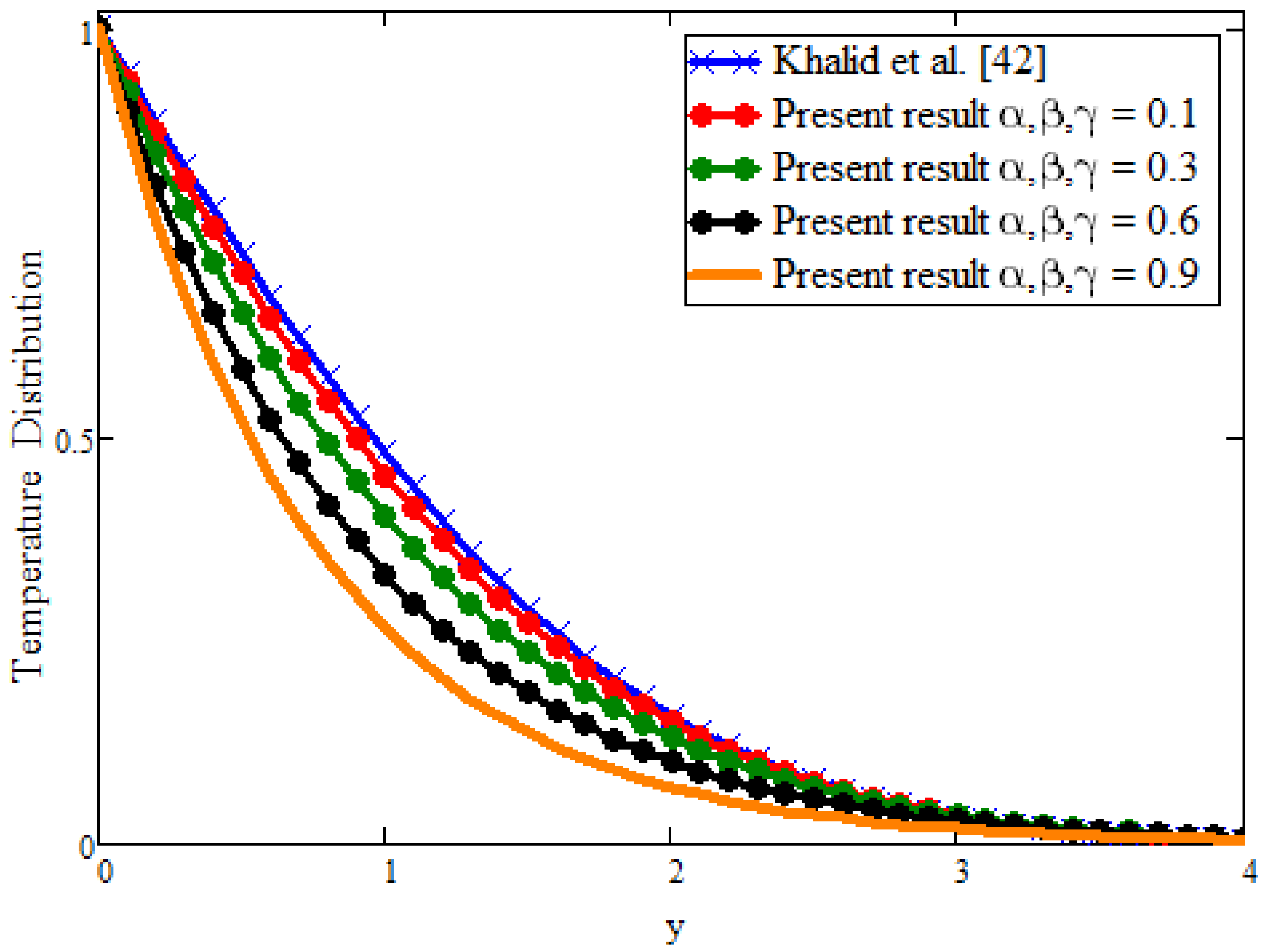
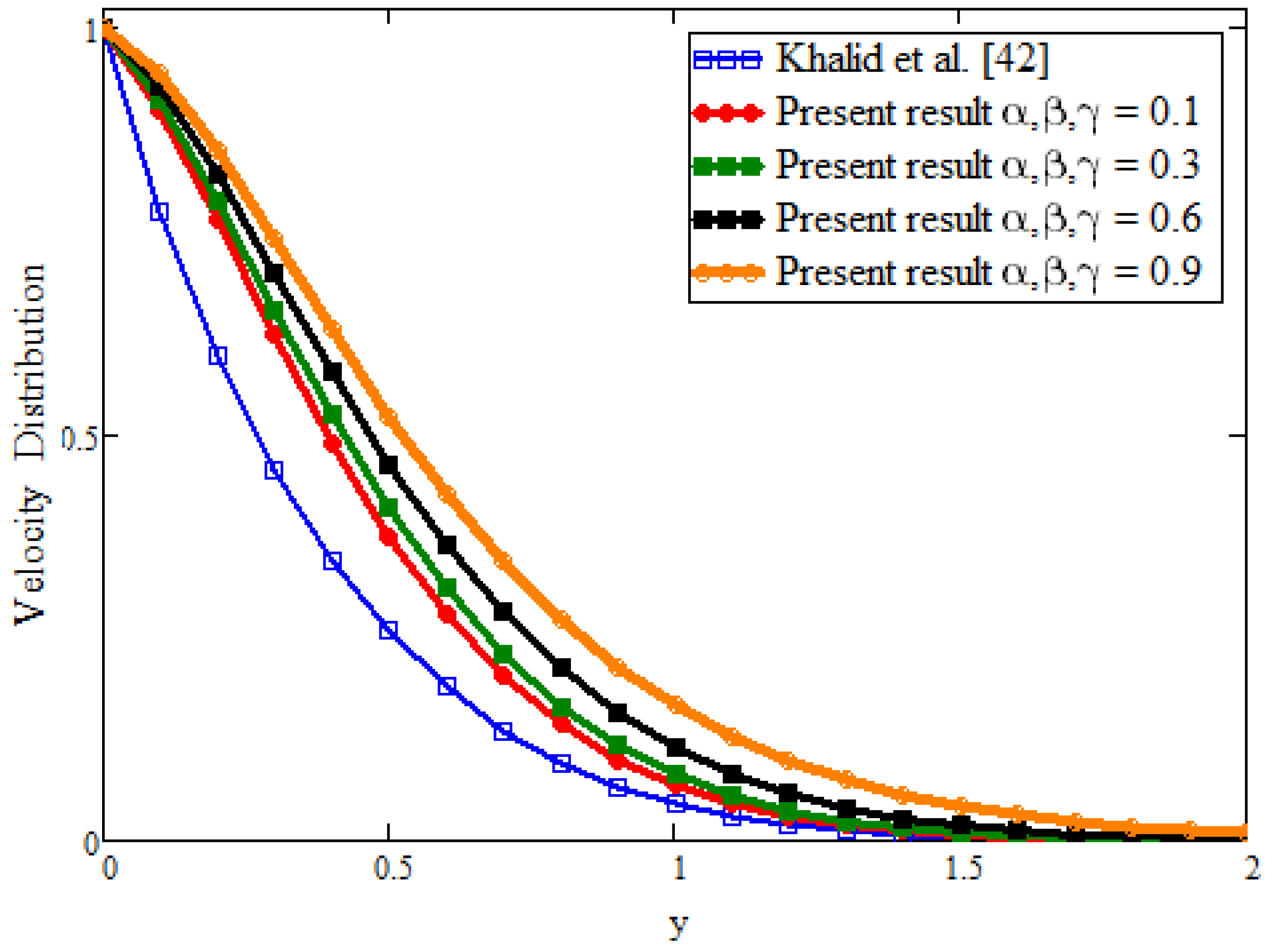
- For fractional parameters, the energy and momentum boundary layer can be controlled with different values of the time.
- The Prabhakar fractional model holds for small and larger values of the Prandtl number.
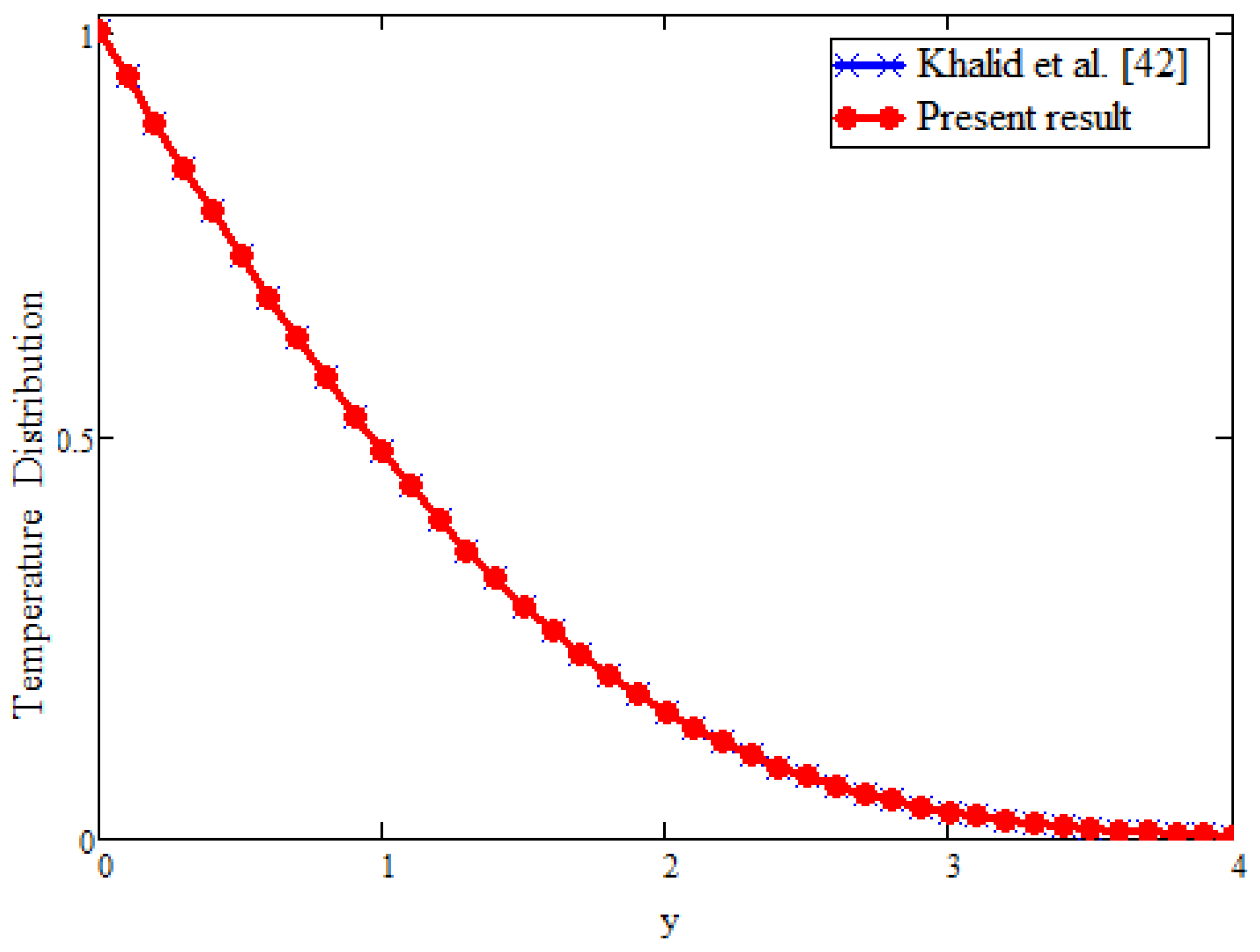
- For validation, recent results are recovered and presented graphically in the graphic section and show good agreement.
- The fractional derivative approach can be useful in fitting the real data where needed instead of classical approach.
- In the limiting case, when fractional parameters are taken = 0 and = 1 for both velocity and temperature, we find the solutions obtained with ordinary derivatives from the existing literature.
- This model is a linear fractional model with oscillation at the boundary displaying the laminar flow. It is possible when the fractional model is non-linear with turbulence and not handled with integral transform. Then, in order to handle the turbulence, some numerical methods are required, such as finite element method, RK-4, etc.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Explaination |
| Prandtl number | |
| Groshof number | |
| Casson Parameter | |
| Yield stress of fluid | |
| Critical value of non-Newtonian | |
| Density | |
| Unit step function | |
| Plastic dynamic viscosity | |
| Frequency of oscillation | |
| Specific heat | |
| Thermal conductivity | |
| i | Unit vector |
| Velocity field | |
| Fractional parameter | |
| Heat capacity ratio | |
| t | Time |
| Amplitude of plate oscillation | |
| Fractional parameter | |
| Temperature | |
| Fluid temperature plate at raised | |
| Fluid temperature of plate at rest | |
| Fractional parameter | |
| Dimensionless temperature |
References
- Casson, N. A flow equation for pigment-oil suspensions of the printing ink type. In Rheol. Disperse Syst.; Pergamon Press: Oxford, UK, 1959. [Google Scholar]
- Pramanik, S. Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation. Ain Shams Eng. J. 2014, 5, 205–212. [Google Scholar] [CrossRef] [Green Version]
- Dash, R.K.; Mehta, K.N.; Jayaraman, G. Casson fluid flow in a pipe filled with a homogeneous porous medium. Int. J. Eng. Sci. 1996, 34, 1145–1156. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ching, D.L.C.; Khan, I.; Kumar, D.; Nisar, K.S. A new model of fractional Casson fluid based on generalized Fick’s and Fourier’s laws together with heat and mass transfer. Alex. Eng. J. 2020, 59, 2865–2876. [Google Scholar] [CrossRef]
- Ndolane, S.E.N.E. A new approach for the solutions of the fractional generalized Casson fluid model described by Caputo fractional operator. Adv. Theory Nonlinear Anal. Its Appl. 2020, 4, 373–384. [Google Scholar]
- Arif, M.; Kumam, P.; Kumam, W.; Khan, I.; Ramzan, M. A Fractional Model of Casson Fluid with Ramped Wall Temperature: Engineering Applications of Engine Oil. Comput. Math. Methods 2021, e1162. [Google Scholar] [CrossRef]
- Ali, F.; Sheikh, N.A.; Khan, I.; Saqib, M. Solutions with Wright function for time fractional free convection flow of Casson fluid. Arab. J. Sci. Eng. 2017, 42, 2565–2572. [Google Scholar] [CrossRef]
- Raza, A.; Khan, S.U.; Farid, S.; Khan, M.I.; Sun, T.C.; Abbasi, A.; Khan, M.I.; Malik, M.Y. Thermal activity of conventional Casson nanoparticles with ramped temperature due to an infinite vertical plate via fractional derivative approach. Case Stud. Therm. Eng. 2021, 27, 101191. [Google Scholar] [CrossRef]
- Khan, I.; Shah, N.A.; Vieru, D. Unsteady flow of generalized Casson fluid with fractional derivative due to an infinite plate. Eur. Phys. J. Plus 2016, 131, 1–12. [Google Scholar] [CrossRef]
- Saqib, M.; Shafie, S.; Khan, I.; Chu, Y.M.; Nisar, K.S. Symmetric MHD channel flow of nonlocal fractional model of BTF containing hybrid nanoparticles. Symmetry 2020, 12, 663. [Google Scholar] [CrossRef]
- Koffi, M.; Andreopoulos, Y.; Jiji, L. Heat transfer enhancement by induced vortices in the vicinity of a rotationally oscillating heated plate. Int. J. Heat Mass Transf. 2017, 112, 862–875. [Google Scholar] [CrossRef]
- Akcay, S.; Akdag, U.; Palancioglu, H. Experimental investigation of mixed convection on an oscillating vertical flat plate. Int. Commun. Heat Mass Transf. 2020, 113, 104528. [Google Scholar] [CrossRef]
- Song, Y.Q.; Raza, A.; Al-Khaled, K.; Farid, S.; Khan, M.I.; Khan, S.U.; Shi, Q.H.; Malik, M.Y.; Khan, M.I. Significances of exponential heating and Darcy’s law for second grade fluid flow over oscillating plate by using Atangana-Baleanu fractional derivatives. Case Stud. Therm. Eng. 2021, 27, 101266. [Google Scholar] [CrossRef]
- Ali, F.; Khan, I.; Shafie, S. Closed form solutions for unsteady free convection flow of a second grade fluid over an oscillating vertical plate. PLoS ONE 2014, 9, e85099. [Google Scholar] [CrossRef] [Green Version]
- Haider, M.I.; Asjad, M.I.; Ali, R.; Ghaemi, F.; Ahmadian, A. Heat transfer analysis of micropolar hybrid nanofluid over an oscillating vertical plate and Newtonian heating. J. Therm. Anal. Calorim. 2021, 144. [Google Scholar] [CrossRef]
- Shah, N.A.; Khan, I. Heat transfer analysis in a second grade fluid over and oscillating vertical plate using fractional Caputo–Fabrizio derivatives. Eur. Phys. J. C 2016, 76, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Sheikholeslami, M.; Kataria, H.R.; Mittal, A.S. Effect of thermal diffusion and heat-generation on MHD nanofluid flow past an oscillating vertical plate through porous medium. J. Mol. Liq. 2018, 257, 12–25. [Google Scholar] [CrossRef]
- Fang, Z.W.; Sun, H.W.; Wang, H. A fast method for variable-order Caputo fractional derivative with applications to time-fractional diffusion equations. Comput. Math. Appl. 2020, 80, 1443–1458. [Google Scholar] [CrossRef]
- Dassios, I.; Baleanu, D. Optimal solutions for singular linear systems of Caputo fractional differential equations. Math. Methods Appl. Sci. 2021, 44, 884–7896. [Google Scholar] [CrossRef] [Green Version]
- Ali, R.; Akgül, A.; Asjad, M.I. Power law memory of natural convection flow of hybrid nanofluids with constant proportional Caputo fractional derivative due to pressure gradient. Pramana 2020, 94, 1–11. [Google Scholar] [CrossRef]
- Baleanu, D.; Jajarmi, A.; Mohammadi, H.; Rezapour, S. A new study on the mathematical modelling of human liver with Caputo–Fabrizio fractional derivative. Chaos Solitons Fractals 2020, 134, 109705. [Google Scholar] [CrossRef]
- Alizadeh, S.; Baleanu, D.; Rezapour, S. Analyzing transient response of the parallel RCL circuit by using the Caputo–Fabrizio fractional derivative. Adv. Differ. Equ. 2020, 2020, 55. [Google Scholar] [CrossRef]
- Shah, K.; Jarad, F.; Abdeljawad, T. On a nonlinear fractional order model of dengue fever disease under Caputo-Fabrizio derivative. Alex. Eng. J. 2020, 59, 2305–2313. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Hajji, M.A.; Al-Mdallal, Q.M.; Jarad, F. Analysis of some generalized ABC–fractional logistic models. Alex. Eng. J. 2020, 59, 2141–2148. [Google Scholar] [CrossRef]
- Thabet, S.T.; Abdo, M.S.; Shah, K.; Abdeljawad, T. Study of transmission dynamics of COVID-19 mathematical model under ABC fractional order derivative. Results Phys. 2020, 19, 103507. [Google Scholar] [CrossRef] [PubMed]
- Ghanbari, B.; Atangana, A. A new application of fractional Atangana–Baleanu derivatives: Designing ABC-fractional masks in image processing. Phys. A Stat. Mech. Appl. 2020, 542, 123516. [Google Scholar] [CrossRef]
- Garra, R.; Gorenflo, R.; Polito, F.; Tomovski, Ž. Hilfer–Prabhakar derivatives and some applications. Appl. Math. Comput. 2014, 242, 576–589. [Google Scholar] [CrossRef] [Green Version]
- Benchohra, M.; Bouriah, S.; Nieto, J.J. Terminal value problem for differential equations with Hilfer–Katugampola fractional derivative. Symmetry 2019, 11, 672. [Google Scholar] [CrossRef] [Green Version]
- Asif, M.; Ul Haq, S.; Islam, S.; Abdullah Alkanhal, T.; Khan, Z.A.; Khan, I.; Nisar, K.S. Unsteady flow of fractional fluid between two parallel walls with arbitrary wall shear stress using Caputo–Fabrizio derivative. Symmetry 2019, 11, 449. [Google Scholar] [CrossRef] [Green Version]
- Polito, F.; Tomovski, Z. Some properties of Prabhakar-type fractional calculus operators. arXiv 2015, arXiv:1508.03224. [Google Scholar] [CrossRef]
- Elnaqeeb, T.; Shah, N.A.; Mirza, I.A. Natural convection flows of carbon nanotubes nanofluids with Prabhakar-like thermal transport. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Shah, N.A.; Fetecau, C.; Vieru, D. Natural convection flows of Prabhakar-like fractional Maxwell fluids with generalized thermal transport. J. Therm. Anal. Calorim. 2021, 143, 2245–2258. [Google Scholar] [CrossRef]
- Eshaghi, S.; Ghaziani, R.K.; Ansari, A. Stability and dynamics of neutral and integro-differential regularized Prabhakar fractional differential systems. Comput. Appl. Math. 2020, 39, 1–21. [Google Scholar] [CrossRef]
- Tanveer, M.; Ullah, S.; Shah, N.A. Thermal analysis of free convection flows of viscous carbon nanotubes nanofluids with generalized thermal transport: A Prabhakar fractional model. J. Therm. Anal. Calorim. 2021, 144, 2327–2336. [Google Scholar] [CrossRef]
- Alidousti, J. Stability region of fractional differential systems with Prabhakar derivative. J. Appl. Math. Comput. 2020, 62, 135–155. [Google Scholar] [CrossRef]
- Derakhshan, M. New Numerical Algorithm to Solve Variable-Order Fractional Integrodifferential Equations in the Sense of Hilfer-Prabhakar Derivative. Abstr. Appl. Anal. 2021, 2021, 8817794. [Google Scholar]
- Asjad, M.I.; Sarwar, N.; Hafeez, M.B.; Sumelka, W.; Muhammad, T. Advancement of Non–Newtonian Fluid with Hybrid Nanoparticles in a Convective Channel and Prabhakar’s Fractional Derivative—Analytical Solution. Fractal Fract. 2021, 5, 99. [Google Scholar] [CrossRef]
- Basit, A.; Asjad, M.I.; Akgül, A. Convective flow of a fractional second grade fluid containing different nanoparticles with Prabhakar fractional derivative subject to non-uniform velocity at the boundary. Math. Methods Appl. Sci. 2021. [Google Scholar] [CrossRef]
- Wang, F.; Asjad, M.I.; Zahid, M.; Iqbal, A.; Ahmad, H.; Alsulami, M.D. Unsteady thermal transport flow of Casson nanofluids with generalized Mittag–Leffler kernel of Prabhakar’s type. J. Mater. Res. Technol. 2021, 14, 1292–1300. [Google Scholar] [CrossRef]
- Sene, N.; Srivastava, G. Generalized Mittag–Leffler input stability of the fractional differential equations. Symmetry 2019, 11, 608. [Google Scholar] [CrossRef] [Green Version]
- Iyiola, O.; Oduro, B.; Zabilowicz, T.; Iyiola, B.; Kenes, D. System of time fractional models for COVID-19: Modeling, analysis and solutions. Symmetry 2021, 13, 787. [Google Scholar] [CrossRef]
- Khalid, A.; Khan, I.; Shafie, S. Exact solutions for unsteady free convection flow of Casson fluid over an oscillating vertical plate with constant wall temperature. In Abstract and Applied Analysis; Hindawi: London, UK, 2015; Volume 2015. [Google Scholar]
- Asjad, M.I.; Basit, A.; Iqbal, A.; Shah, N.A. Advances in transport phenomena with nanoparticles and generalized thermal process for vertical plate. Phys. Scr. 2021, 96, 114001. [Google Scholar] [CrossRef]
- Garra, R.; Garrappa, R. The Prabhakar or three parameter Mittag–Leffler function: Theory and application. Commun. Nonlinear Sci. Numer. Simul. 2018, 56, 314–329. [Google Scholar] [CrossRef] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarwar, N.; Asjad, M.I.; Sitthiwirattham, T.; Patanarapeelert, N.; Muhammad, T. A Prabhakar Fractional Approach for the Convection Flow of Casson Fluid across an Oscillating Surface Based on the Generalized Fourier Law. Symmetry 2021, 13, 2039. https://doi.org/10.3390/sym13112039
Sarwar N, Asjad MI, Sitthiwirattham T, Patanarapeelert N, Muhammad T. A Prabhakar Fractional Approach for the Convection Flow of Casson Fluid across an Oscillating Surface Based on the Generalized Fourier Law. Symmetry. 2021; 13(11):2039. https://doi.org/10.3390/sym13112039
Chicago/Turabian StyleSarwar, Noman, Muhammad Imran Asjad, Thanin Sitthiwirattham, Nichaphat Patanarapeelert, and Taseer Muhammad. 2021. "A Prabhakar Fractional Approach for the Convection Flow of Casson Fluid across an Oscillating Surface Based on the Generalized Fourier Law" Symmetry 13, no. 11: 2039. https://doi.org/10.3390/sym13112039






