Effect of Ventricular Elasticity Due to Congenital Hydrocephalus
Abstract
:1. Introduction
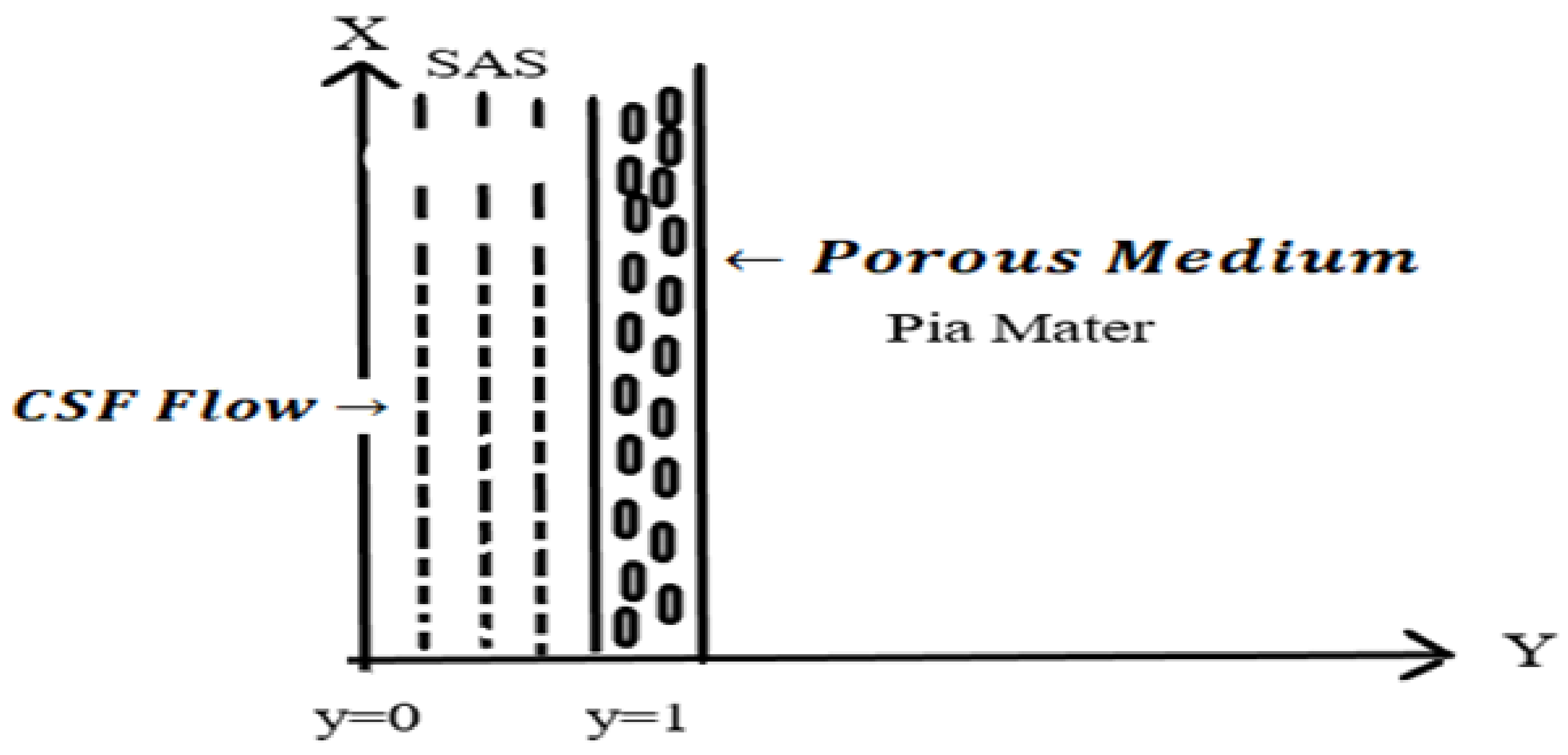
2. Mathematical Formulation
3. Method of Solution
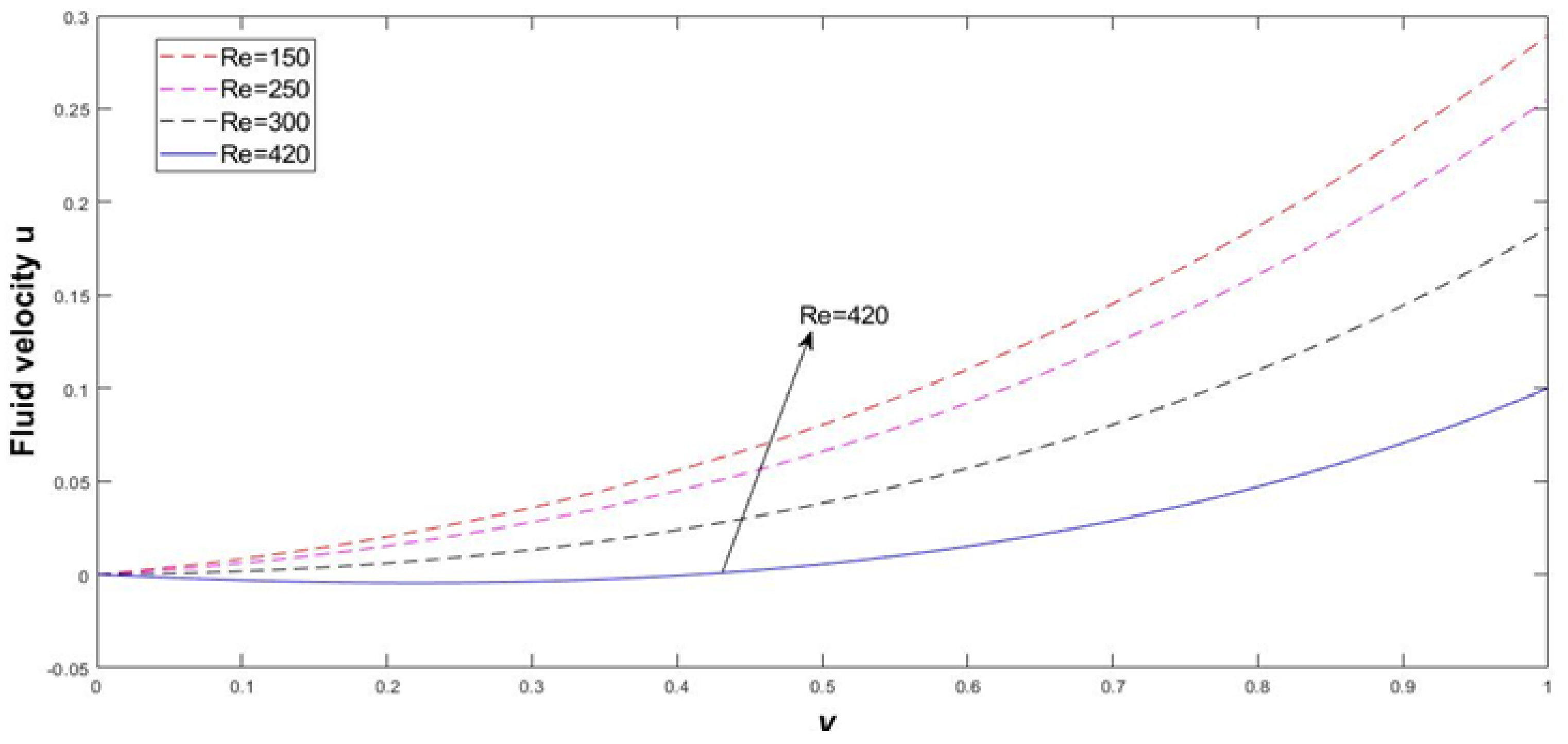
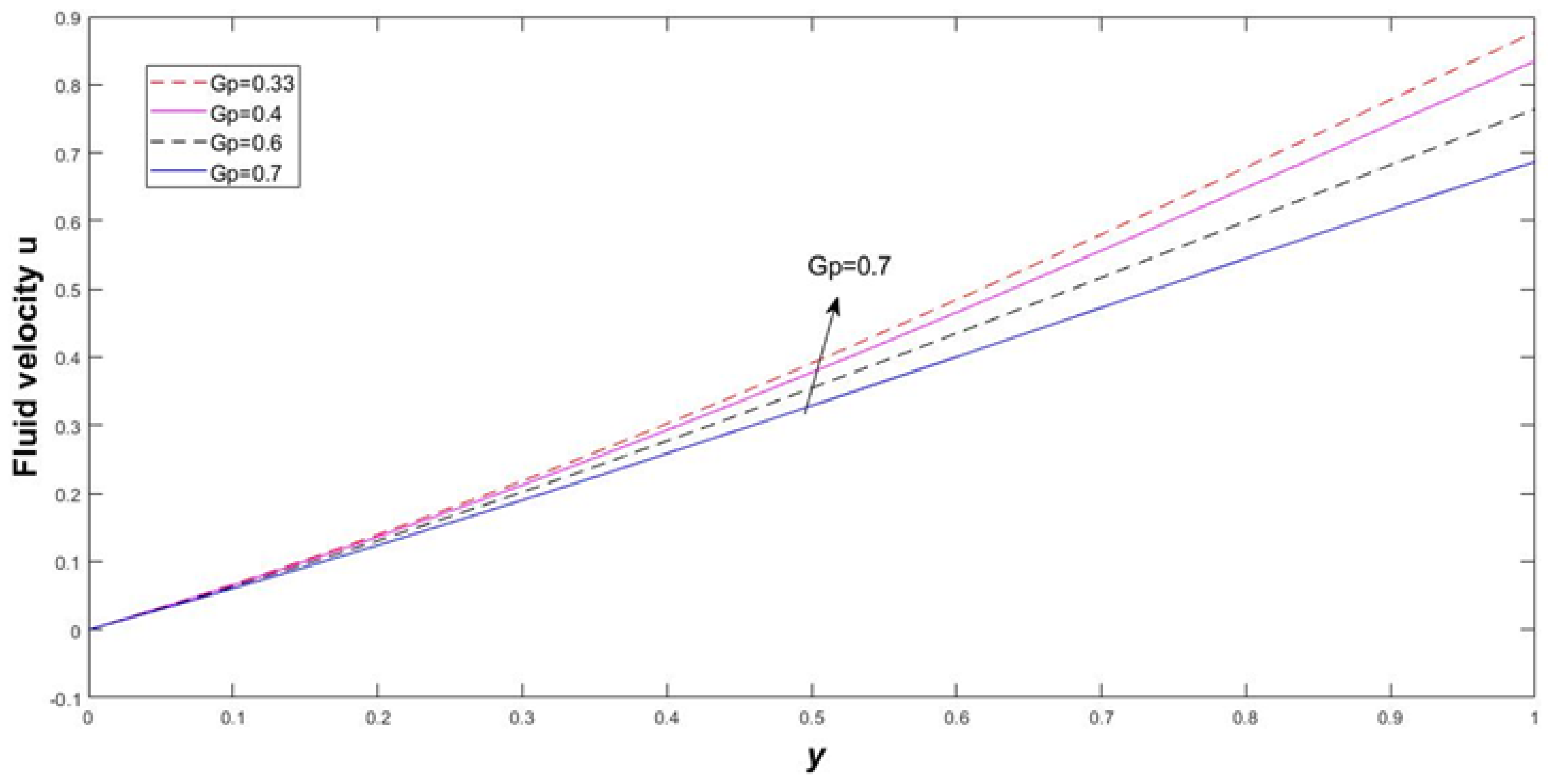
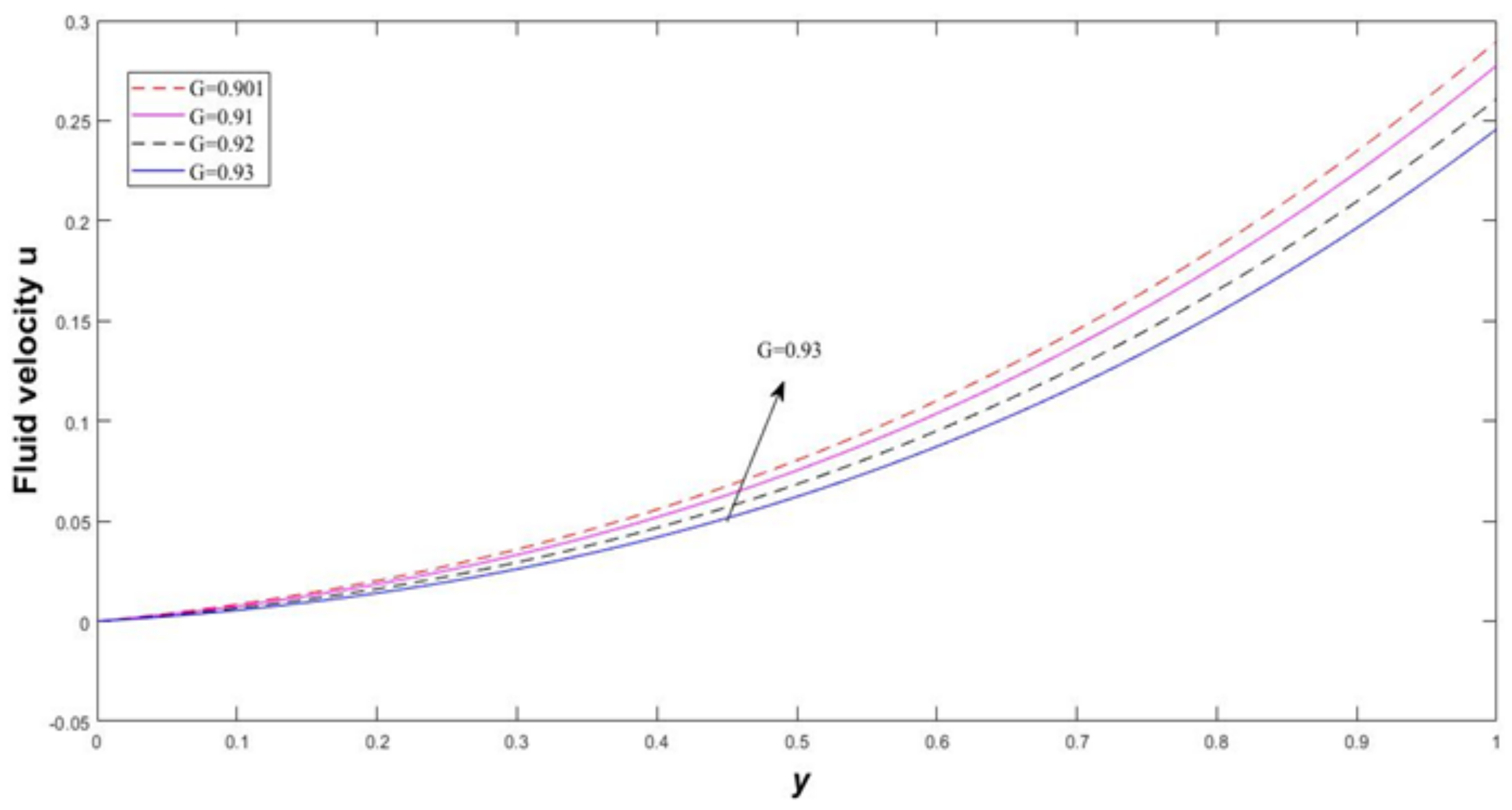
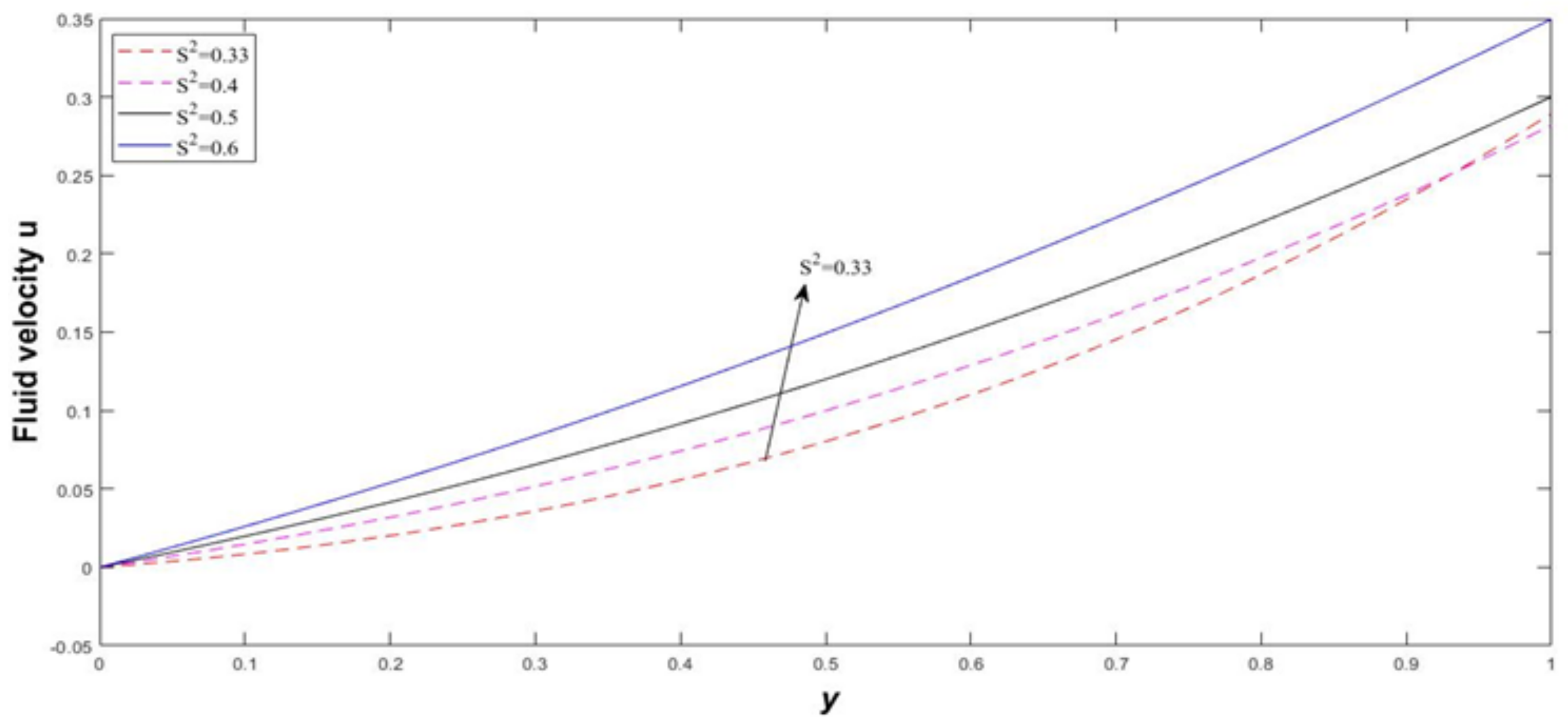
4. Results and Discussion
Error Approximation for Dimensionless Number (Re)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| CSF | cerebrospinal fluid |
| cartesian coordinates | |
| dimensionless cartesian coordinates | |
| time parameter | |
| t | dimensionless time parameter |
| concentration of the fluid | |
| c | dimensionless concentraion |
| subarachnoid space | |
| fluid pressure | |
| velocity of the fluid flow | |
| dimensionless velocity of the fluid flow | |
| h | characteristics length |
| initial velocity of the fluid flow | |
| positive real constant | |
| initial concentration of the fluid | |
| Velocity of the fluid | |
| Kinematic viscosity of the fluid | |
| Density of the fluid | |
| G | (elasticity) Young’s modulus of the fluid flow |
| p | dimensionless constant pressure |
| K | chemical reaction parameter |
| g | dimensionless pressure |
| k | Permeability of the porous medium |
| D | Coefficient of mass diffusivity of the fluid |
| Peclet number for mass transfer | |
| Reynolds Number | |
| Darcy Number | |
| particle mass parameter | |
| perturbation parameter () |
Appendix A
References
- Bering, E.A.; Sato, O. Hydrocephalus: Changes in Formation and Absorption of Cerebrospinal Fluid Within the Cerebral Ventricles. J. Neurosurg. 1963, 20, 1050–1063. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Linninger, A.A.; Xenos, M.; Zhu, D.C.; Somayaji, M.R.; Kondapalli, S.; Penn, R.D. Cerebrospinal Fluid Flow in the Normal and Hydrocephalic Human Brain. IEEE Trans. Biomed. Eng. 2007, 54, 291–302. [Google Scholar] [CrossRef] [PubMed]
- Kalyanasundaram, S.; Calhoun, V.D.; Leong, K.W. A finite element model for predicting the distribution of drugs delivered intracranially to the brain. Am. J. Physiol. Integr. Comp. Physiol. 1997, 273, R1810–R1821. [Google Scholar] [CrossRef] [PubMed]
- Ursino, M. A mathematical study of human intracranial hydrodynamics part 1—The cerebrospinal fluid pulse pressure. Ann. Biomed. Eng. 1988, 16, 379–401. [Google Scholar] [CrossRef] [PubMed]
- Symss, N.P.; Oi, S. Theories of cerebrospinal fluid dynamics and hydrocephalus: Historical trend. J. Neurosurg. Pediatr. 2013, 11, 170–177. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gholampour, S. FSI simulation of CSF hydrodynamic changes in a large population of non-communicating hydrocephalus patients during treatment process with regard to their clinical symptoms. PLoS ONE 2018, 13, e0196216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kauffman, J.; Drapaca, C.S. A Fractional Pressure-Volume Model of Cerebrospinal Fluid Dynamics in Hydrocephalus. In Mechanics of Biological Systems and Materials; Barthelat, F., Zavattieri, P., Korach, C., Prorok, B., Grande-Allen, K., Eds.; Springer: Cham, Switzerland, 2014; Volume 4. [Google Scholar] [CrossRef]
- Pandey, S.; Jin, Y.; Gao, L.; Zhou, C.C.; Cui, D.M. Negative-Pressure Hydrocephalus: A Case Report on Successful Treatment Under Intracranial Pressure Monitoring with Bilateral Ventriculoperitoneal Shunts. World Neurosurg. 2017, 99, 812.e7–812.e12. [Google Scholar] [CrossRef] [PubMed]
- Miller, K.; Wittek, A.; Tavner, A.C.R.; Joldes, G.R. Biomechanical Modelling of the Brain for Neurosurgical Simulation and Neuroimage Registration. In Biomechanics of the Brain. Biological and Medical Physics, Biomedical Engineering; Miller, K., Ed.; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Gholampour, S.; Fatouraee, N.; Seddighi, A.S. Numerical simulation of cerebrospinal fluid hydrodynamics in the healing process of hydrocephalus patients. J. Appl. Mech. Tech. Phys. 2017, 58, 386–391. [Google Scholar] [CrossRef]
- Sharp, M.K.; Carare, R.O.; Martin, B.A. Dispersion in porous media in oscillatory flow between flat plates: Applications to intrathecal, periarterial and paraarterial solute transport in the central nervous system. Fluids Barriers CNS 2019, 16, 13. [Google Scholar] [CrossRef]
- Apura, J.; Tiago, J.; Moura, A.; Lourenço, J.A.; Sequeira, A. The effect of ventricular volume increase in the amplitude of intracranial pressure. Comput. Methods Biomech. Biomed. Eng. 2019, 22, 889–900. [Google Scholar] [CrossRef]
- Yamada, S.; Kelly, E. Cerebrospinal Fluid Dynamics and the Pathophysiology of Hydrocephalus: New Concepts. Semin. Ultrasound CT MRI 2016, 37, 84–91. [Google Scholar] [CrossRef] [PubMed]
- Liou, W.W.; Yang, Y.; Yamada, S. Cerebrospinal Fluid Flow Simulations in Brain Ventricles With Elastic Wall Responses. In Proceedings of the 6th International Conference on Computational and Mathematical Biomedical Engineering—CMBE2019, Sendai City, Japan, 10–12 June 2019. [Google Scholar]
- Soza, G.; Grosso, R.; Nimsky, C.; Hastreiter, P.; Fahlbusch, R.; Greiner, G. Determination of the elasticity parameters of brain tissue with combined simulation and registration. Int. J. Med. Robot. Comput. Assist. Surg. 2005, 1, 87. [Google Scholar] [CrossRef]
- Yan’kova, G.S.; Cherevko, A.A.; Khe, A.K.; Bogomyakova, O.B.; Tulupov, A.A. Study of Hydrocephalus Using Poroelastic Models. J. Appl. Mech. Tech. Phys. 2020, 61, 14–24. [Google Scholar] [CrossRef]
- Dreglea, A.I.; Shishskin, G.I. Robust numerical method based on Blasius approach for flow past a flat plate in the case of heat transfer for large Reynolds numbers. In Proceedings of the CMAM-1, Minsk, Belarus, 21–25 July 2003; pp. 19–20. [Google Scholar]
- Dreglea, A.I.; Shishskin, G.I. Numerical method based on Blasius approach for flow past flat plate in the case of heat transfer for large Reinolds numbers. In Proceedings of the Annual Symposium of Irish Society for Scientific and Engineering Computation, Belfield, Dublin, Ireland, 23–24 May 2003; p. 14. [Google Scholar]
- Albanese, A.; Cheng, L.; Ursino, M.; Chbat, N.W. An integrated mathematical model of the human cardiopulmonary system: Model development. Am. J. Physiol. Circ. Physiol. 2016, 310, H899–H921. [Google Scholar] [CrossRef] [PubMed]
- Gholampour, S.; Fatouraee, N. Boundary conditions investigation to improve computer simulation of cerebrospinal fluid dynamics in hydrocephalus patients. Commun. Biol. 2021, 4, 394. [Google Scholar] [CrossRef] [PubMed]
- Gupta, D.; Singla, R.; Dash, C. Pathophysiology of Hydrocephalus. In Hydrocephalus; Ammar, A., Ed.; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Miller, K. (Ed.) Biomechanics of the Brain; Biological and Medical Physics, Biomedical Engineering; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Hemalatha, B.; Senthamil, S. Effect of Cerebrospinal Fluid Dynamics with Hydrocephalus in Porous Medium. Turk. J. Comput. Math. Educ. 2021, 12, 5666–5671. [Google Scholar]

| Re | Velocity of Fluid Flow | Relative Error | |Error|% | |
|---|---|---|---|---|
| True Value | Measured Value | |||
| 150 | −4.19 × | 1.4536 × | −0.776109002 | 77.61090023 |
| 250 | −1.87 × | 6.4925 × | −0.776109002 | 77.61090023 |
| 317 | −8.37 × | 2.8998 × | −0.776109002 | 77.61090023 |
| 322 | −3.74 × | 1.2952 × | −0.776109002 | 77.61090023 |
| 340 | −1.67 × | −1.6688 × | −0.776109002 | 77.61090023 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balasundaram, H.; Sathiamoorthy, S.; Santra, S.S.; Ali, R.; Govindan, V.; Dreglea, A.; Noeiaghdam, S. Effect of Ventricular Elasticity Due to Congenital Hydrocephalus. Symmetry 2021, 13, 2087. https://doi.org/10.3390/sym13112087
Balasundaram H, Sathiamoorthy S, Santra SS, Ali R, Govindan V, Dreglea A, Noeiaghdam S. Effect of Ventricular Elasticity Due to Congenital Hydrocephalus. Symmetry. 2021; 13(11):2087. https://doi.org/10.3390/sym13112087
Chicago/Turabian StyleBalasundaram, Hemalatha, Senthamilselvi Sathiamoorthy, Shyam Sundar Santra, Rifaqat Ali, Vediyappan Govindan, Aliona Dreglea, and Samad Noeiaghdam. 2021. "Effect of Ventricular Elasticity Due to Congenital Hydrocephalus" Symmetry 13, no. 11: 2087. https://doi.org/10.3390/sym13112087









