The Predictive Power of Transition Matrices

Abstract

When working with Markov chains, especially if they are of order greater than one, it is often necessary to evaluate the respective contribution of each lag of the variable under study on the present. This is particularly true when using the Mixture Transition Distribution model to approximate the true fully parameterized Markov chain. Even if it is possible to evaluate each transition matrix using a standard association measure, these measures do not allow taking into account all the available information. Therefore, in this paper, we introduce a new class of so-called "predictive power" measures for transition matrices. These measures address the shortcomings of traditional association measures, so as to allow better estimation of high-order models.

1. Introduction

Transition matrices such as the ones summarizing a Markov chain contain a certain amount of information, but this amount is not so straightforward to quantify. When the transition matrix is estimated from an observed dataset, we generally consider the contingency table associated with the transition matrix, and we evaluate the quantity of information it contains using a measure of association. There exist many different measures of association, some being derived from the chi-square statistic (e.g., Cramer’s V), some being defined as the proportion of reduction in error (e.g., Theil’s u, Goodman & Kruskal $\lambda$ & $\tau$), and others being based on the concept of similarity and dissimilarity (e.g., Goodman and Kruskal $\gamma$, Kendall’s ${\tau }_b$, Somers’s d) [1,2]. All these measures have in common that they take as a reference situation the perfect independence between rows and columns of the contingency table, then they quantify the strength of association as a function of the distance between the reference situation and the contingency table of interest.

The concept of a measure of association is particularly relevant in the social sciences, because the vast majority of variables used for analysis are categorical in nature, often without a precise ordering of the modalities. The number of modalities of a variable can sometimes be very large, for example in the case of an exhaustive classification of all the types of diplomas that can be obtained. Moreover, the number of potential explanatory factors for a phenomenon can also be very large, because social phenomena are often closely linked to one another (family, school and professional trajectories, for example). Measures of association are therefore extremely useful for comparing different factors with each other and ranking them according to their explanatory power.

Numerous measures of association have been defined to take into account the characteristics of the different variables studied. Many of these measures are highly specialized. For example, the Pearson correlation coefficient is intended to measure a linear relationship between two continuous variables, to the exclusion of other forms of relationship. The notion of predictive power described in this article follows the same logic in that it is intended to best express the row-to-column relationship that may exist within a specific object, a transition matrix. On the other hand, other measures of a more general nature have also been proposed. Recently, one can note the concept of Maximum Information Coefficient (MIC, [3]). It should be noted, however, that too much generality of a coefficient can also make it unsuitable for certain uses. For example, because the MIC is symmetric, it does not apply to transition matrices associated with one-way Markov chains running from the past to the future. Similarly, if one wants to be able to distinguish between several types of relationships (linear, exponential, parabolic, etc.), it is necessary to use tools that allow one to distinguish a particular form of relationship.

If we concentrate on the transition matrix of a Markov chain, the rows and columns are not interchangeable. According to the standard notation, the rows represent the past observation and the columns represent the current observation. Therefore, a measure of the quantity of information must be asymmetrical with the columns depending on the rows. Among the previously cited association measures, some of them such as Theil’s u are in line with this requirement, but they measure the degree of dependence between rows and columns rather than the quantity of information provided by the matrix to predict the column variable.

The following example highlights the difference between both concepts. Let $Q_1$ and $Q_2$ be two transition matrices associated with first-order Markov chains:

$$Q_1=\left(\begin{array}{ccc}\frac{1}{3}& \frac{1}{3}& \frac{1}{3}\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}\end{array}\right),Q_2=\left(\begin{array}{ccc}0.6& 0.3& 0.1\\ 0.6& 0.3& 0.1\\ 0.6& 0.3& 0.1\end{array}\right).$$

Both transition matrices represent a situation of perfect independence between the rows and columns in the sense that the information provided by a specific row cannot help to better predict the corresponding column, and vice versa. Consequently, all the measures mentioned above take a value of zero meaning perfect independence. From another point of view, if the goal is to predict the most likely column, then $Q_2$ provides more information than $Q_1$, since whatever the row, the first column occurs 60% of the time, while the probability of occurrence of all columns is identical in $Q_1$. Consequently, if you need to guess the most likely column, you would prefer to have $Q_2$ instead of $Q_1$. This example simply demonstrates that traditional measures of association do not take into account all the information contained in a transition matrix. Put differently, the concept of association measures the degree of difference between the rows of the matrix. On the contrary the concept of predictive power that we introduce in this article considers in addition the degree of difference between the columns. While it is sufficient for all rows to be equal for the association to be zero, zero predictive power additionally requires that the columns be equal (or equivalently that all row distributions be equal to the uniform distribution).

The distinction between a measure of association and a measure of predictive power proves important when working with Markovian models. If we consider a high-order Markov chain and we want to approximate it through a Mixture Transition Distribution (MTD) model [4], then it is useful to evaluate the role and importance of each lag in the overall model. This is very important, because by its construction, the MTD model will be all the better as the contribution of each lag on the present is similar. This is also the starting point for the traditional estimation algorithm of the MTD model [5,6]. If matrices $Q_1$ and $Q_2$ above represent the direct relationship between lag 1 and the present, and lag 2 and the present, respectively, then using an association measure such as Theil’s u would just indicate that both lags are absolutely non-informative on the present situation, when in fact $Q_2$ gives a clear indication of the most likely current situation. Therefore, evaluating the two matrices through a measure of the predictive power rather than an association measure is clearly better.

Of course, one could argue that if the transition matrix of a Markov chain has all rows equal, then it corresponds to a zero-order model, which is an independence model. This is true, but once again, even independence models can be more or less informative regarding the variable of interest. For instance, if we assume that a condition can have three causes and our model points with a 60% probability to one of them, we are in a better position to determine the best treatment than if all three causes are equally likely.

The concept of predictive power was first introduced by the author in a now out of print book about Markov chains written in French [7], but until then the concept had not been really developed and it had never been published in English. In this article, we define which properties are required for a statistic to be a measure of the predictive power of a transition matrix rather than a measure of association, then we define such a statistic, we provide two alternatives, and we illustrate the behaviour of these measures through practical examples.

2. Properties of a Measure of the Predictive Power

Traditional measures of association evaluate the distance between an empirical matrix and a matrix with perfect independence between rows and columns. The more different the rows of the matrix, the higher the association. On the other hand, the predictive power of a matrix measures the degree of certainty about the column. As can be deduced from the example of Section 1, when the association is null, the predictive power can be non-null, but when the predictive power is null, the association is null too. Formally, we define the following desired qualities for a measure of the predictive power:

• The predictive power takes values between zero and one.
• The predictive power reaches its minimal value of zero only when all rows of the transition matrix are uniform distributions.
• The predictive power reaches its maximal value of one only when whatever the row of the matrix, there is always a probability of one to be in one of the columns (not necessarily the same column for each row).
• The predictive power increases weakly monotonously with the certainty of the columns.

The first point is required for the sake of clarity and simplicity of use of the measure. Indeed, it would be perfectly possible to consider, for example, a measure ranging from −1 to +1, but then it would be difficult to understand what a negative rather than a positive value could mean. The second and third requirements ensure that when the measure takes its minimum, then it is not possible to transform the matrix (by exchanging some elements of the underlying contingency table) into another one with even less predictive power, and vice versa regarding the maximum value. Finally, the fourth requirement ensures that all possible situations represented by a transition matrix can be ordered in a non-decreasing manner, hence ensuring their comparability.

Different concepts are available to fulfill all of these requirements and to build a suitable measure. We present three possibilities in the next section.

3. Measures of Predictive Power

3.1. An Entropy-Based Measure

Shannon’s entropy is a well known measure of uncertainty that is as the basis of Theil’s u measure of association [8]. Let $p=(p_1,p_2,\dots ,p_c)$, $p_j\ge 0,\forall j=1,\dots ,c$, ${\sum }_{j=1}^c{p}_j=1$ the probability distribution of a multinomial variable taking values in $1,\dots ,c$. Then, Shannon’s entropy for p is

$$H\left(p\right)=-\sum _j{p}_j{log}_2{p}_j,$$

and to have a measure taking values between zero and one, we standardize $H\left(p\right)$ to obtain

$$\begin{array}{c}\hfill p{p}_H\left(p\right)=1+\frac{{\sum }_j{p}_j{log}_2{p}_j}{{log}_{2}c}.\end{array}$$

(1)

The transition matrix $Q=\left[q_{i,j}\right]$ of a Markov chain can be viewed as a collection of r probability distributions, one per row. Therefore, we can apply Equation (1) separately on each row of the transition matrix, and average the results to obtain a measure of the predictive power for the whole transition matrix Q:

$$\begin{array}{ccc}\hfill P{P}_H\left(Q\right)& =& \sum _{i=1}^r{w}_{i}p{p}_{Hi}\hfill \\ & =& 1+\frac{{\sum }_i{w}_i{\sum }_j{q}_{i,j}{log}_2{q}_{i,j}}{{log}_{2}c},\hfill \end{array}$$

(2)

where $w_i$ are non-negative row weights summing to one. Since ${log}_2\left(0\right)$ is undefined, the computation of the above equations must be performed only on non-null elements of the transition matrix Q. Of course, if this computation is performed on the transition matrix of a Markov chain of order $\ell >1$, this matrix will have $c^{\ell }-c$ structural zeros on each row, corresponding to impossible transitions between the situation represented by the row and the situation represented by the column. In such a case, these strucural zeros are entirely excluded from the computation, which is similar to the usual convention to not count structural zeros as parameters to be estimated [9].

Even if the $P{P}_H$ measure is based on the same principle as Theil’s u measure, it is clearly different. The corresponding Theil’s u measure is written

$$u=\frac{{\sum }_i{\sum }_j{q}_{i,j}{log}_2\left(\frac{q_{i,.}{q}_{.,j}}{q_{i,j}}\right)}{{\sum }_j{log}_2{q}_{.,j}}$$

(3)

where $q_{i,.}$ and $q_{.,j}$ are the total relative frequency of row i and column j, respectively. The comparison of Equations (2) and (3) shows that the predictive power takes into account each row separately through the weights $w_i$, which is not the case for u. More generally, u is a mutual information measure, which means that it is based on the joint share of information that rows use to predict columns and simultaneously that columns use to predict rows [10]. By removing this mutual information share, the predictive power is able to better focus on only predicting the column based on the row.

There are at least two possibilities for choosing the weights $w_i$. First, when only the transition matrix Q is known, but not the underlying contingency table, then the logical choice is to have all weights equal to the inverse of the number of rows, $1/r$, i.e., 1/c in the case of the transition matrix of a first-order Markov chain, and $1/c^{\ell }$ in the case of an ℓ-th order chain. On the other hand, when the contingency table is known, then we can use this information to weight the predictive power of each row in function of the number of data points used to estimate the probabilities of this row. If we note $n_i·$ the number of data points used to compute the i-th row and n the total number of data points in the whole contingency table, then

$$w_i=\frac{n_i·}{n}.$$

The advantage of the second approach is to give more emphasis on the most likely rows, which is the most likely situation. Consider for instance the two following contingency tables and their corresponding transition matrices:

$$\begin{array}{c}\hfill C{T}_3=\left(\begin{array}{cc}1& 9\\ 30& 30\end{array}\right),Q_3=\left(\begin{array}{cc}0.1& 0.9\\ 0.5& 0.5\end{array}\right),\\ \hfill C{T}_4=\left(\begin{array}{cc}5& 45\\ 10& 10\end{array}\right),Q_4=\left(\begin{array}{cc}0.1& 0.9\\ 0.5& 0.5\end{array}\right).\end{array}$$

The transition matrices are identical, but this is not the case for their underlying contingency tables. When computed on $Q_3$ or $Q_4$, without any additional information, the predictive power is in both cases 0.2655. However, if we compute it on the underlying contingency tables, we obtain 0.0759 for $C{T}_3$ and 0.3793 for $C{T}_4$. From the transition matrices, we can deduce that the first row is much more informative than the second one to predict correctly the column, with probabilities very far from the uniform distribution. However, the contingency tables show in addition that on $C{T}_3$, being on the first row is a quite rare situation, occurring 1/7 of the time, when the first row of $C{T}_4$ is active 5/7 of the time. Therefore, even if both transition matrices seem to describe the same process, determining the most likely column is a lot easier with the process represented by $C{T}_4$ than by the one of $C{T}_3$. Consequently, it is appropriate that the predictive power of $C{T}_4$ and $Q_4$ is greater than that of $C{T}_3$ and $Q_3$. This is what is reflected by the use of weights proportional to the frequency of the rows instead of equal weights. For comparison, the Theil’s u computed on $C{T}_3$ and $C{T}_4$ gives 0.0670 and 0.1719, respectively. On the resulting transition matrix, the value is 0.1666. The behavior is thus similar to that observed with the predictive power, but of course, given the specificities of the two types of measures, the values are different.

A third possibility is to choose ad hoc weights in function of the situation to be analyzed, but in this case, the justification of the weights is left to the user of the predictive power measure, without clear mathematical justification.

3.2. Alternative Measures

As defined in the previous section, the $p{p}_H$ measure fulfills all requirements to be a measure of the predictive power of a transition matrix. However, other possibilities do exist. We present hereafter two alternative measures of the predictive power.

One possibility is based on a difference. Consider the probability distribution p defined in the previous section. The difference between the largest and smallest probabilities is

$$\begin{array}{c}\hfill p{p}_D\left(p\right)=\underset{j}{max}\left(p_j\right)-\underset{j}{min}\left(p_j\right).\end{array}$$

(4)

By construction, $0\le p{p}_D\left(p\right)\le 1$. Then, by computing the same difference on all rows of a transition matrix and by averaging, we define a second measure of the predictive power of a matrix:

$$\begin{array}{c}\hfill P{P}_D\left(S\right)=\sum _i{w}_i\left(\underset{j}{max}\left(s_{i,j}\right)-\underset{j}{min}\left(s_{i,j}\right)\right).\end{array}$$

(5)

Another possibility is to consider the variability of a probability distribution p:

$$\begin{array}{c}\hfill p{p}_V\left(p\right)=\frac{\left(c{\sum }_j{p}_j^2\right)-1}{c-1}.\end{array}$$

(6)

Again, since the $p_j$ are probabilities, the above quantity is bounded by zero and one. Then by computing this variability on each row of a matrix and by averaging, we obtain a third measure of the predictive power:

$$\begin{array}{c}\hfill P{P}_V\left(S\right)=\frac{\left(c{\sum }_i{w}_i{\sum }_j{s}_{i,j}^2\right)-1}{c-1}.\end{array}$$

(7)

All the three measures fulfill all requirements of a predictive power measure. However, they differ on some aspects. For instance, $p{p}_D$ uses only two probabilities on each row of the transition matrix, so it is less informative than the two other measures as soon as $c>2$.

4. Examples

4.1. Theoretical Examples

In this section, we present different example to demonstrate the behavior of the three measures of the predictive power introduced in this article, and to compare them with the classical Theil’s u measure of association. We consider Theil’s u as a gold standard because (1) it is an association measure with a large spectrum of applications which does not suffer the shortcomings that other measures such as Goodman and Kruskall’s $\lambda$ do [11]; (2) it is based on the same underlying concept, Shannon’s entropy, as our main measure of the predictive power does. However, conclusions would be similar to another association measure.

We define hereafter four pairs of transition matrices and we will examine the evolution of the measures of predictive power when we go from the first to the second matrix of each pair, using 99 intermediary steps. The R statistical environment was used for all computations [12]. The first pair of matrices represents a transition from independence ($BE{G}_1$) to perfect prediction of the columns ($EN{D}_1$):

$$BE{G}_1=\left(\begin{array}{cc}0.5& 0.5\\ 0.5& 0.5\end{array}\right),EN{D}_1=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right).$$

The second pair of matrices represents a transition between two different situations of independence. In matrix $BE{G}_2$, the two columns are equiprobable, when the second column has a probability of one in matrix $EN{D}_2$:

$$BE{G}_2=\left(\begin{array}{cc}0.5& 0.5\\ 0.5& 0.5\end{array}\right),EN{D}_2=\left(\begin{array}{cc}0& 1\\ 0& 1\end{array}\right).$$

The last two pairs of matrices represent two cases of evolution between non-extreme situations, without independence or perfect predicion:

$$BE{G}_3=\left(\begin{array}{cc}0.1& 0.9\\ 0.4& 0.6\end{array}\right),EN{D}_3=\left(\begin{array}{cc}0.2& 0.8\\ 0.5& 0.5\end{array}\right),$$

$$BE{G}_4=\left(\begin{array}{cc}0.2& 0.8\\ 0& 1\end{array}\right),EN{D}_4=\left(\begin{array}{cc}0.4& 0.6\\ 1& 0\end{array}\right).$$

Ninety-nine intermediate matrices were computed between each pair of transition matrices, with the step matrix i defined as follows

$$MA{T}_i=\left(\frac{nbs-i+1}{nbs}\right)BEG+\left(\frac{i-1}{nbs}\right)END$$

where $nbs=100$. Then, the equal-weight version of the three predictive power measures, as well as Theil’s u, were computed on each matrix. Figure 1 summarizes the results.

On the two top subfigures, the three measures of the predictive power evolves exactly in the same way, but this is not the case for Theil’s u: On the top-left subfigure it behaves exactly as $P{P}_H$ does, while it takes only the zero value in the top-right subfigure. Since Theil’s u and $P{P}_H$ are based on the same concept, it is not surprising that they evolve in a similar way for situations other than independence (top-left), but the comparison of these two situations exemplifies the difference between the concepts of predictive power and of association. When a transition matrix corresponds to a situation of independence, association measures always take value zero (top-right), but the predictive power can take a different value as long as there is a different probability to belong to each column. On the contrary, the three measures of the predictive power behave similarly in the two top situations, because in both cases the evolution is between rows that are uniform probability distributions to rows that give a probability of one to belong to one of the column, whatever the column it is.

The two situations depicted at the bottom of Figure 1 do not represent such extreme cases. On the left, both rows of the transition matrix tend to be closer to a uniform distribution in the $EN{D}_3$ matrix than in the $BE{G}_3$ matrix, so globally both the predictive power and the association diminish gradually. On the right, the two rows of the transition matrix exhibit a different and opposite behavior. When the first row becomes closer to the uniform distribution, the second rows evolves between two situations indicating both a perfect prediction of one of the column, but between these two extreme situations, the probability distribution moves towards, then away, from the uniform distribution. It results in different measures that all pass through a minimum before increasing again, with Theil’s u reaching its minimum sooner than the three measures of the predictive power. Both $P{P}_H$ and $P{P}_V$ reach their minimum of, respectively, 0.057 and 0.077 for the matrix.

$$\left(\begin{array}{cc}0.308& 0.692\\ 0.540& 0.460\end{array}\right),$$

$P{P}_V$ reaches its minimum of 0.2 for

$$\left(\begin{array}{cc}0.3& 0.7\\ 0.5& 0.5\end{array}\right),$$

and Theil’s u reaches its minimum of zero for

$$\left(\begin{array}{cc}0.25& 0.75\\ 0.25& 0.75\end{array}\right).$$

It can be seen in Figure 1 that $P{P}_D$ adopts only straight line evolutions, in contrast with the other measures. This is due to the construction of the measure itself, the difference between two probabilities, not including a non-linearity such as the ones involved by a logarithm ($P{P}_H$) or a squared value ($P{P}_V$).

The next two examples are based on larger transition matrices of size $(4\times 4)$, matrices

$$BE{G}_5=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0.25& 0.25& 0.25& 025\\ 0.2& 0.4& 0.1& 0.3\\ 0& 0.5& 0.4& 0.1\end{array}\right),EN{D}_5=\left(\begin{array}{cccc}0& 0& 0& 1\\ 0.6& 0& 0& 0.5\\ 0.2& 0.4& 0.1& 0.3\\ 0& 0.7& 0.3& 0\end{array}\right),$$

and

$$BE{G}_6=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\\ 0& 0& 0& 1\end{array}\right),EN{D}_6=\left(\begin{array}{cccc}0& 0& 0& 1\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 1& 0& 0& 0\end{array}\right)$$

respectively. Figure 2 summarizes the results.

First of all, we see that $P{P}_D$ takes generally higher values than the three other measures. Since this behavior was already observed in Figure 1 with matrices of a smaller size, it is not related to the number of rows and columns of the matrix. On all examples, $P{P}_H$ and $P{P}_V$ exhibit quite similar behaviors, even if the exact values are different. On the right subfigure, Theil’s u takes exactly the same values as $P{P}_H$ does, what was also observed on the top-left subfigure of Figure 1, the reason being the same.

4.2. Life Course Example

When analyzing life courses, it is usual to consider several dimensions simultaneously that can influence each other [13]. For example, it is usual for relationships to exist between a person’s career path and their family situation. Moreover, these relationships are often different for women and men [14]. In order to construct a relevant explanatory model, it is therefore necessary to be able to quantify the respective influence of the different life domains on the one under study.

Here we consider data from a retrospective biographical survey conducted as part of the Swiss Household Panel [15]. We consider a sample of 847 individuals, 421 women and 424 men for whom we have complete data between the ages of 20 and 65. Three life domains are considered: work activity (four categories: full-time work; part-time work; inactive or unemployed; retired); family status (five categories: single; couple without children; couple with children; single-parent family; other) and health problems (two categories: had a significant health problem in the last 12 months; no health problem). The objective is to study the influence of family situation, health status and past work activity on current work activity. Before building an explanatory model, it is necessary to determine which present or past events can best explain current work activity. To do this, we construct a transition matrix between each potentially explanatory event and current work activity and then calculate its predictive power.

Table 1. Predictive power of the potentially explanatory events, separately for women and men.

	Lags
	t – 5	t – 4	t – 3	t – 2	t – 1	t
Women
Work activity	0.424	0.481	0.556	0.653	0.788	-
Family status	0.164	0.170	0.176	0.182	0.187	0.190
Health problems	0.102	0.103	0.103	0.103	0.104	0.104
Men
Work activity	0.729	0.752	0.780	0.821	0.878	-
Family status	0.640	0.642	0.643	0.644	0.645	0.646
Health problems	0.622	0.622	0.622	0.622	0.623	0.623

summarizes the results for women and men.

The relationships between the three domains and current work activity are very different for women and men. For women, only past work activity can explain a significant part of current work activity, whereas for men, family situation and health problems are also important. For both women and men, the predictive power of family situation and health problems is stable over time, whereas work activity is more predictive the closer the period considered. Thus, predictive power allows us to quickly identify the events most likely to lead to a successful explanatory model. In this example, a model for women might be based primarily on work history, whereas family situation and health problems might also be important for men.

5. Conclusions

Association and predictive power are two close but different concepts measuring two different aspects of a transition matrix or of a contingency table. The main difference is that with the concept of association, all situations of independence correspond to the value of zero, when the predictive power differentiate further between independence situations that provide no information on the most likely column of the transition matrix or contingency table, and situations that provide some kind of information about the columns. In that sense, predictive power extends the concept of association for situations in which it is important to differentiate between the columns.

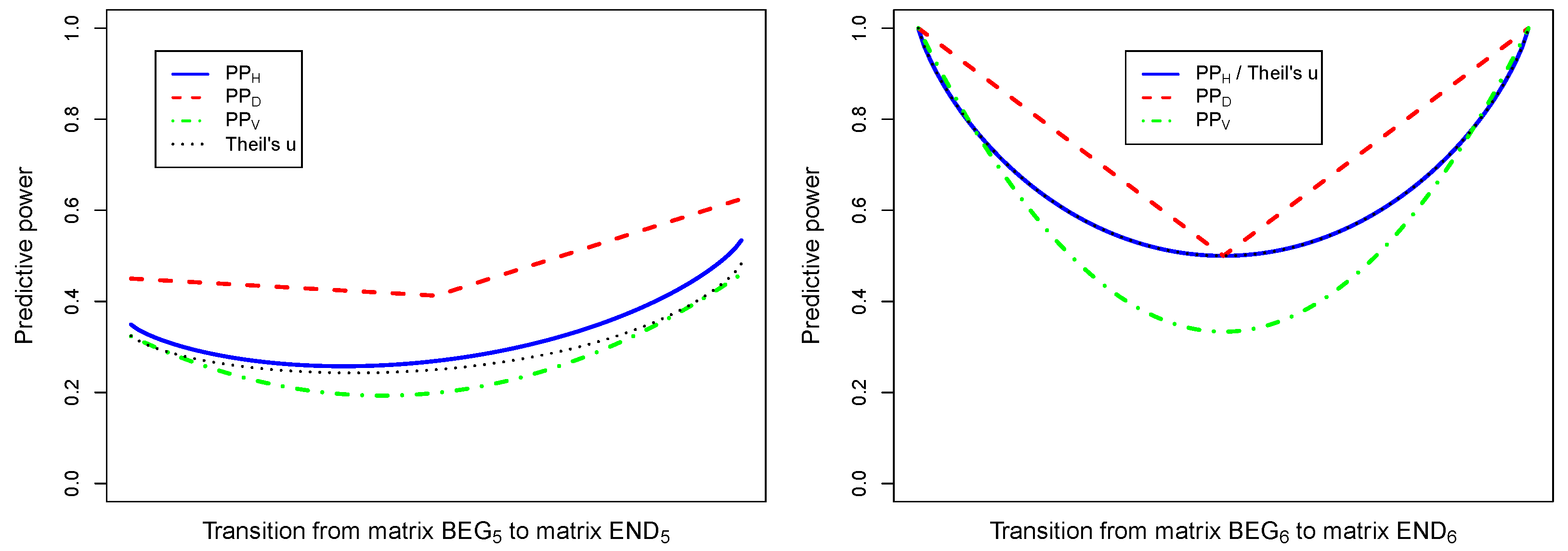
By nature, the concept of predictive power is not symmetric. This is illustrated by the discussion of the comparison between predictive power and Theil’s u, as well as by the various numerical examples provided in Section 4. However, predictive power coefficients are useful for detecting and quantifying situations in which symmetry reduces the complexity of a problem into a simpler problem. Therefore, predictive power should not be viewed as a symmetric concept per se, but as a tool for detecting symmetry.

A specific situation in which the predictive power proves useful is for the initialization of the estimation algorithm of the MTD model [5]. Let a discrete random variable take two different values, and suppose that we want to model a second-order Markov chain. Suppose that empirically the links between lags 1 and 2 and the present, as computed from a dataset, are summarized by the matrices $BE{G}_2$ and $EN{D}_2$ used in Section 4. If $BE{G}_2$ is the direct relationship between lag 1 and the present, and $EN{D}_2$ is the direct relationship between lag 2 and the present, then using Theil’s u (as suggested in [5]) would not let us to determine which matrix should be given more importance as starting value. Moreover, we could also wrongly conclude that since both matrices present a null association, then the Markovian process is of order zero and there is no interest in using a second-order model. On the other hand, using a measure of the predictive power such as $P{P}_H$, we would conclude that lag 1 does not explain the present situation ($P{P}_H$ = 0), on the contrary of lag 2 ($P{P}_H$ = 1), so lag 2 should be given more weight than lag 1 in the initialization of the estimation process. We could also be certain that a second-order model is of interest.

In this article, we presented a concept derived from that of association, but allowing better distinguishing the respective importance of each column of a matrix. We believe that by allowing going beyond what is measured by the association concept alone, this new tool will allow to distinguish more finely between close situations, as it may be necessary when using the MTD model to approximate high order Markov chains. Now that measures of the predictive power of transition matrices have been defined, a next step could be to validate them. For this, a simulation approach could be considered by building theoretical causal models that could be used to generate artificial data in which the degree of dependence between the past and the present is fixed. Then, different measures of predictive power could be calculated and compared to verify that their values are closely correlated with the theoretical degree of causality.