Train Derailment Process Analysis on Heavy Haul Railway Bridge under Ship Impact
Abstract
:1. Introduction
2. Materials and Methods
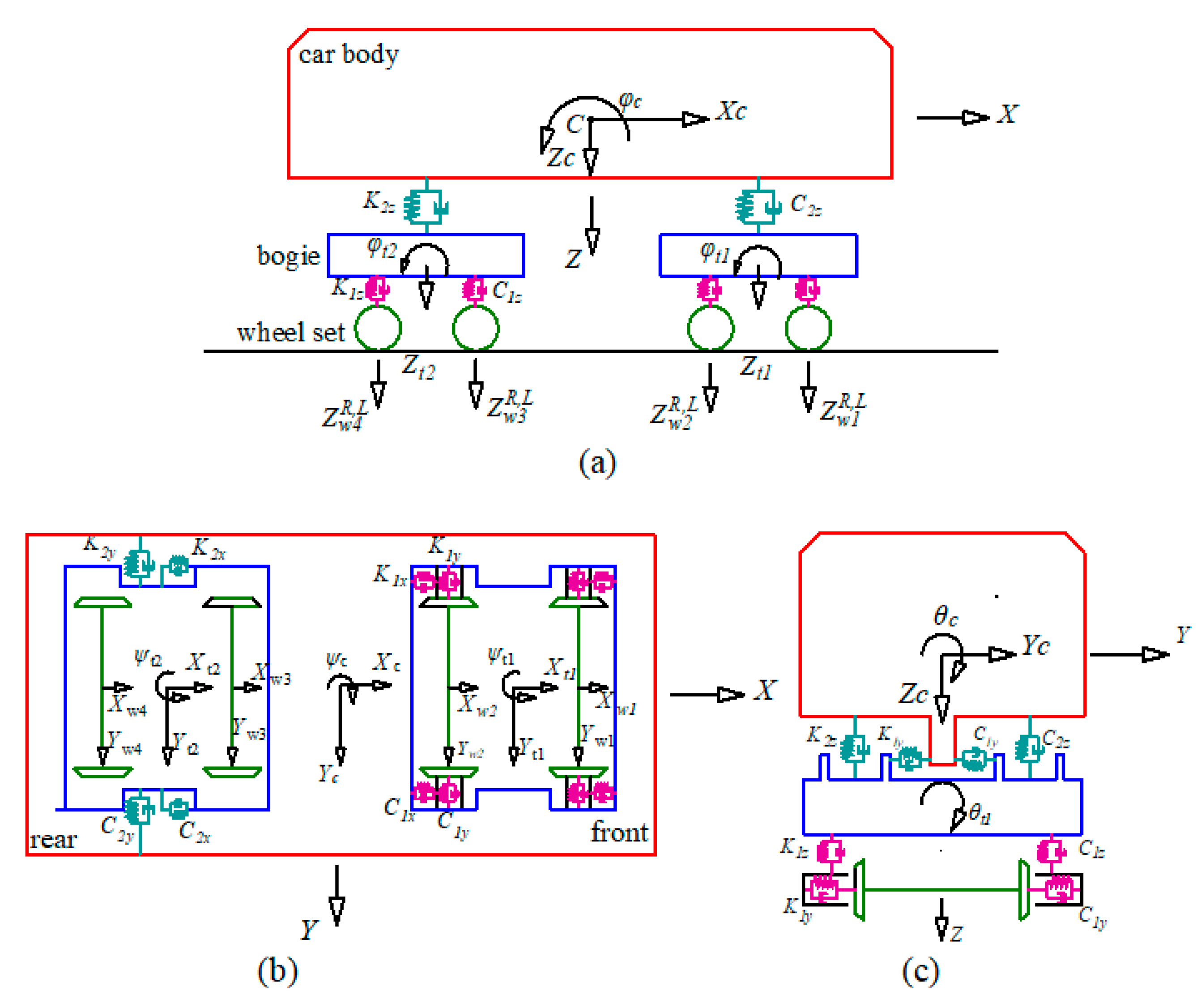
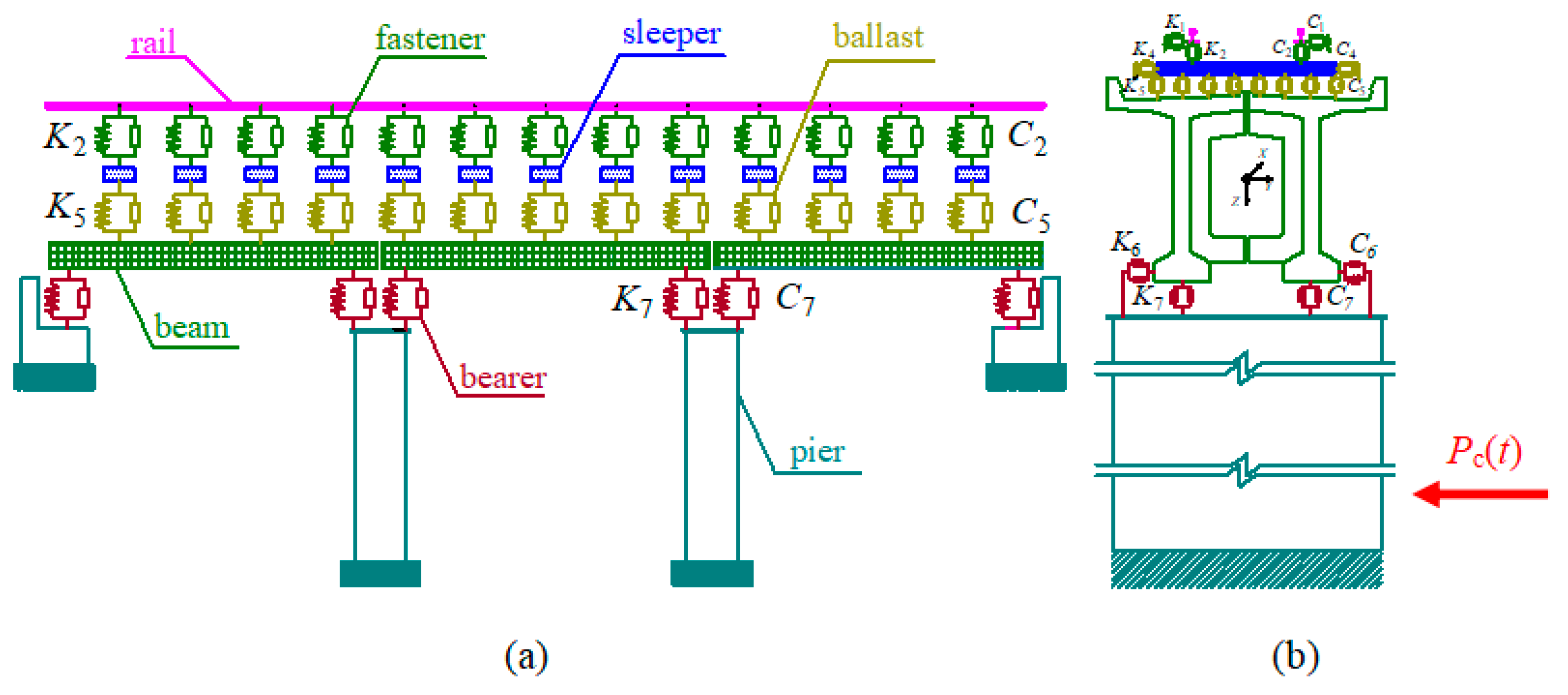
2.1. Model of FTTB System under Ship Impact
2.1.1. Model of FTTB System
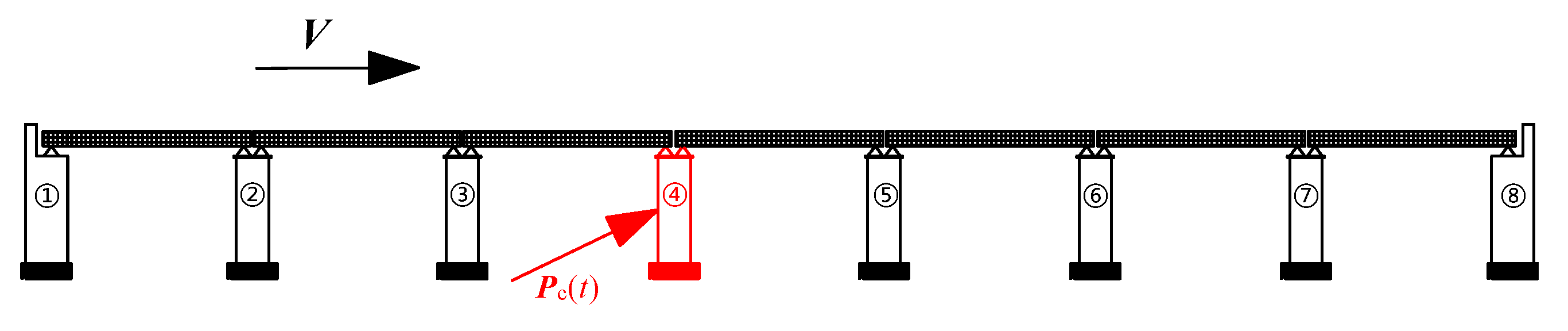
2.1.2. Simulation of Ship Impact
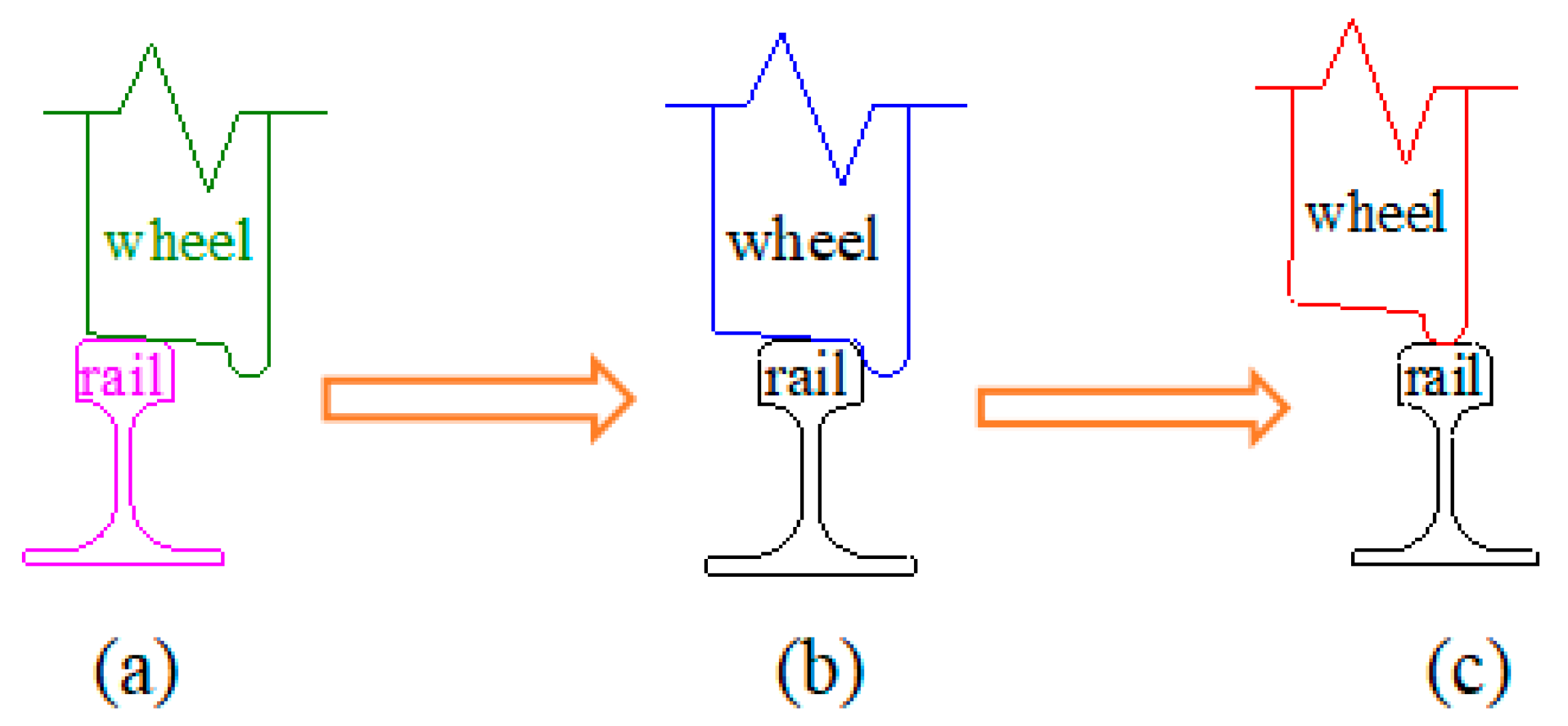
2.2. Calculation Method of Train Derailment Process on Bridge under Ship Impact
3. Results
3.1. Calculation of Train Derailment Process under Ship Impact
3.2. Influence of Impact Load on the Train Derailment Process
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Larry, D.; Olson, P.E. Dynamic Bridge Substructure Evaluation and Monitoring; US Federal Highway Administration: Washington, DC, USA, 2005. [Google Scholar]
- Wardhana, K.; Hadipriono, F.C. Analysis of recent bridge failures in the united states. J. Perform. Constr. Facil. 2003, 17, 144–150. [Google Scholar] [CrossRef] [Green Version]
- Wuttrich, R.; Wekezer, J.; Yazdani, N.; Wilson, C. Performance evaluation of existing bridge fenders for ship impact. J. Perform. Constr. Facil. 2001, 15, 17–23. [Google Scholar] [CrossRef]
- Chaoyi, X.; Nan, Z.; He, X. Dynamic analysis of a train-bridge system under vessel collision and running safety evaluation of its high-speed train. J. Vib. Shock. 2015, 34, 155–161. [Google Scholar]
- Hai, F.; Huiming, S.; Weiqing, L. Analysis of train derailment after hitting the pier of Tongling Yangtze River bridge combined road with railway. J. Railw. Eng. Soc. 2014, 9, 65–70. [Google Scholar]
- Wilson, C.M.D.; Yazdani, N.; Wekezer, J. Static finite-element analysis of bridge fenders for barge impact. J. Perform. Constr. Facil. 2001, 15, 90–95. [Google Scholar] [CrossRef]
- Consolazio, G.R.; Hendrix, J.; Mc Vay, M. Prediction of pier response to barge impacts with design-oriented dynamic finite element analysis. Transp. Res. Rec. 2004, 1868, 177–189. [Google Scholar] [CrossRef]
- Consolazio, G.R.; Cowan, D.R. Numerically efficient dynamic analysis of barge collisions with bridge piers. J. Struct. Eng. 2005, 131, 1256–1266. [Google Scholar] [CrossRef]
- Consolazio, G.R.; Davidson, M.T.; Cowan, D.R. Barge bow force-deformation relationships for barge-bridge collision analysis. Transp. Res. Rec. 2009, 2131, 3–14. [Google Scholar] [CrossRef]
- Davidson, M.T.; Consolazio, G.R.; Getter, D.J. Dynamic Amplification of Pier Column Internal Forces Due to Barge-Bridge Collision. Transp. Res. Rec. 2010, 2172, 11–22. [Google Scholar] [CrossRef]
- Yuan, P.; Harik, I.E. One-Dimensional Model for Multi-Barge Flotillas Impacting Bridge Piers. Comput.-Aided Civ. Infrastruct. Eng. 2008, 23, 437–447. [Google Scholar] [CrossRef]
- AASHTO. Guide Specification and Commentary for Vessel Collision Design of Highway Bridges; AASHTO: Washington, DC, USA, 1991. [Google Scholar]
- Sha, Y.; Hao, H. Laboratory tests and numerical simulation of barge impact on circular reinforced concrete piers. Eng. Struct. 2013, 46, 593–605. [Google Scholar] [CrossRef]
- Sha, Y.; Hao, H. Nonlinear finite element analysis of barge collision with a single bridge pier. Eng. Struct. 2012, 41, 63–76. [Google Scholar] [CrossRef]
- Fan, W.; Yuan, W.C. Shock spectrum analysis method for dynamic demand of bridge structures subjected to barge collisions. Comput. Struct. 2012, 90, 1–12. [Google Scholar] [CrossRef]
- Fan, W.; Yuan, W.C. Numerical simulation and analytical modeling of pile-supported structures subjected to ship collisions including soil-structure interaction. Ocean. Eng. 2014, 91, 11–27. [Google Scholar] [CrossRef]
- Gholipour, G.; Zhang, C.; Li, M. Effects of soil-pile interaction on the response of bridge pier to barge collision using energy distribution method. Struct. Infrastruct. Eng. 2018, 14, 1520–1534. [Google Scholar] [CrossRef]
- Gholipour, G.; Zhang, C.; Mousavi, A. Analysis of girder bridge pier subjected to barge collision considering the superstructure interactions: The case study of a multiple-pier bridge system. Struct. Infrastruct. Eng. 2019, 15, 392. [Google Scholar] [CrossRef]
- Yan, X.; Dun, Z. Train derailment on railway bridge caused by ship hitting pier. Foreign Bridges 2001, 4, 60–64. [Google Scholar]
- Chen, C. Study on Design Collision Force and Simulation of Damage for Bridge Subjected to Ship Impact; Tongji University Press: Shanghai, China, 2006. [Google Scholar]
- Junjie, W.; Cheng, C. Simulation of damage for bridge pier subjected to ship impact. Eng. Mech. 2007, 24, 156–160. [Google Scholar]
- Xia, C.Y.; Ma, Q.; Song, F.D.; Wu, X. Dynamic analysis of high-speed railway train-bridge system after barge collision. Struct. Eng. Mech. 2018, 67, 9–20. [Google Scholar]
- Gong, K.; Xiang, J.; Mao, J. Derailment precautions of freight train on bridge in heavy haul railway. J. Cent. South Univ. 2017, 48, 3406–3414. [Google Scholar]
- Xiang, J. Study on Mechanism and Analysis Theory of Train Derailment. Ph.D. Thesis, Central South University, Changsha, China, 2006. [Google Scholar]
- Zeng, Q.; Lou, P.; Xiang, J. The principle of total potential energy with stationary value in elastic system dynamics and its application to the analysis of vibration and dynamic stability. J. Huangzhong Univ. Sci. Technol. 2002, 19, 7–14. [Google Scholar]
- Zeng, Q.; Yang, P. The “Set-in-Right-Position” rule for forming structural matrices and the finite truss element method for space analysis of truss bridge. J. China Railw. Soc. 1986, 8, 48–59. [Google Scholar]
- National Railway Administration of the People’s Republic of China. Code for Design on Railway Bridge and Culvert; China Railway Publishing House: Beijing, China, 2017. [Google Scholar]
- British Standard BS EN1991-1-7, Eurocode 1-Actions on Structures General Action: Accidental Actions; The European Union: Brussels, Belgium, 2006.
- Xiang, J.; Zeng, Q. Analysis method of stability and critical speed for train-track(bridge) time-variable system under lateral vibration condition. J. Traffic Transp. Eng. 2011, 11, 19–24. [Google Scholar]
- National Bureau of Standards. Railway Vehicle-Specification for Evaluation the Dynamic Performance and Accreditation Test; Standards Press of China: Beijing, China, 2019.
- Xiao, X.-B. Study on High-Speed Train Derailment Mechanism in Severe Environment. Ph.D. Thesis, School of Transportation Engineering, Southwest Jiaotong University, Chengdu, China, 2013. [Google Scholar]
- Han, T.Y. No 120. Code for Rating Existing Railway Bridges; China Railway Publishing House: Beijing, China, 2016. [Google Scholar]
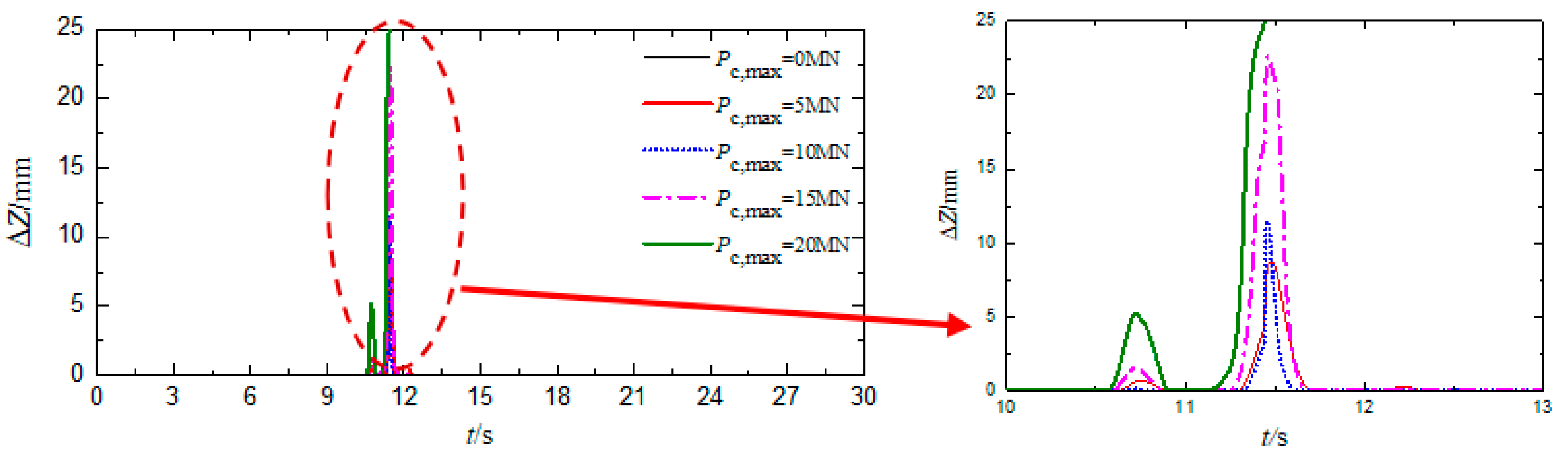
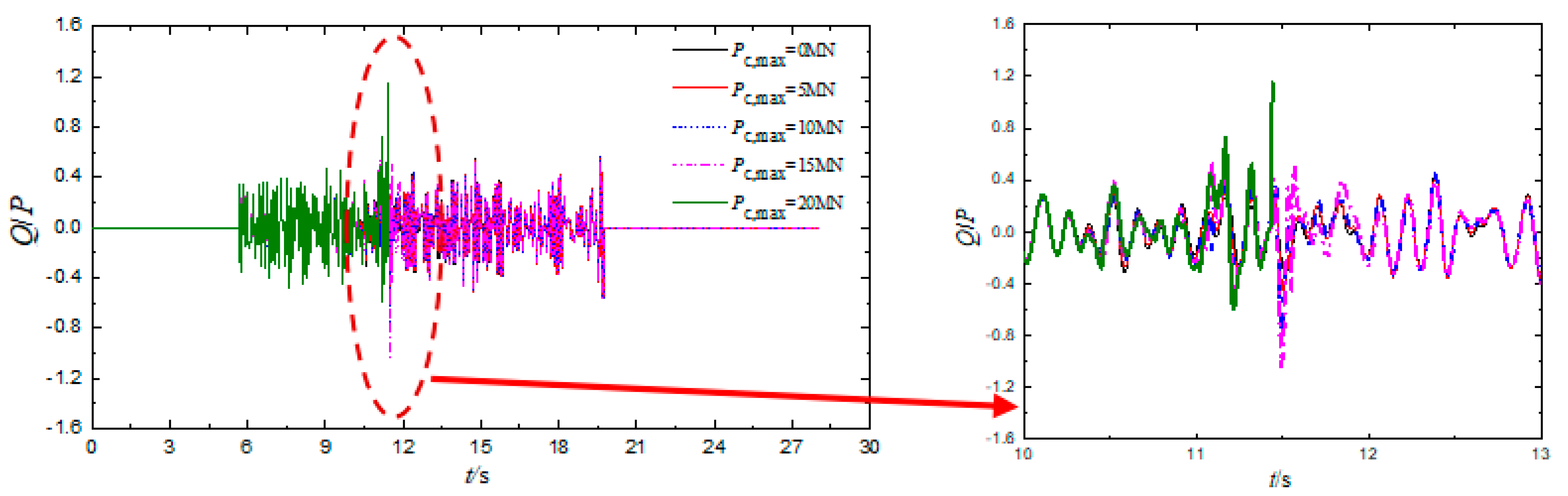
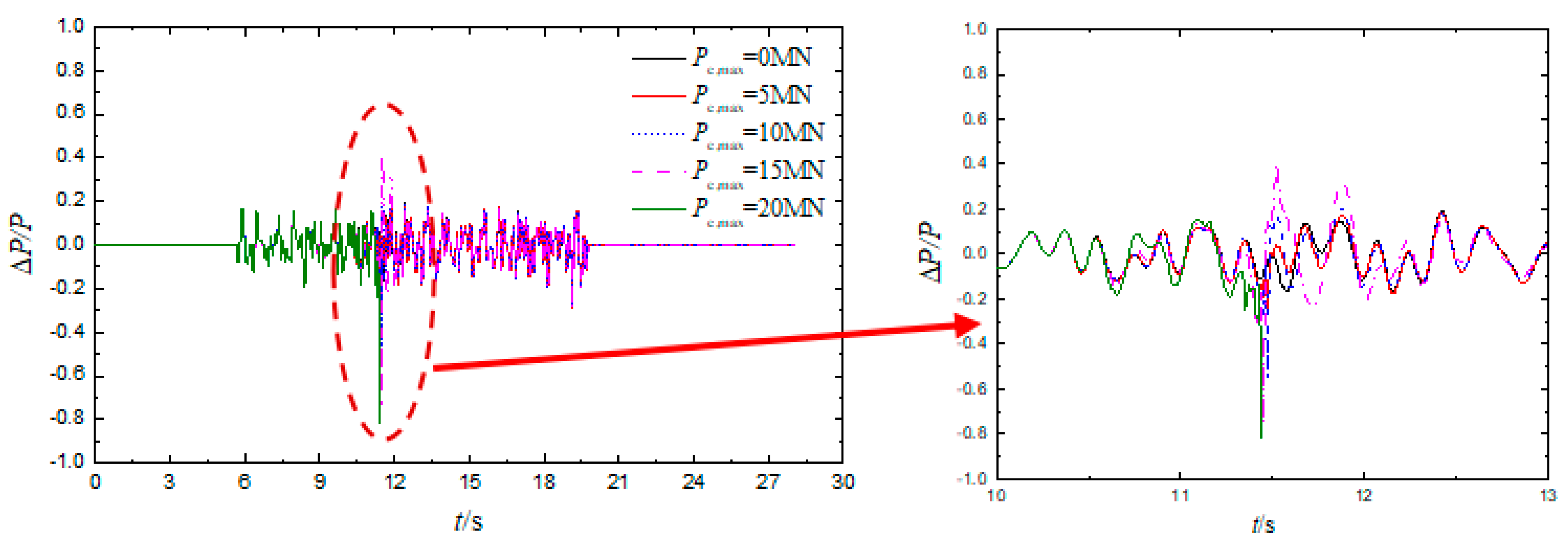
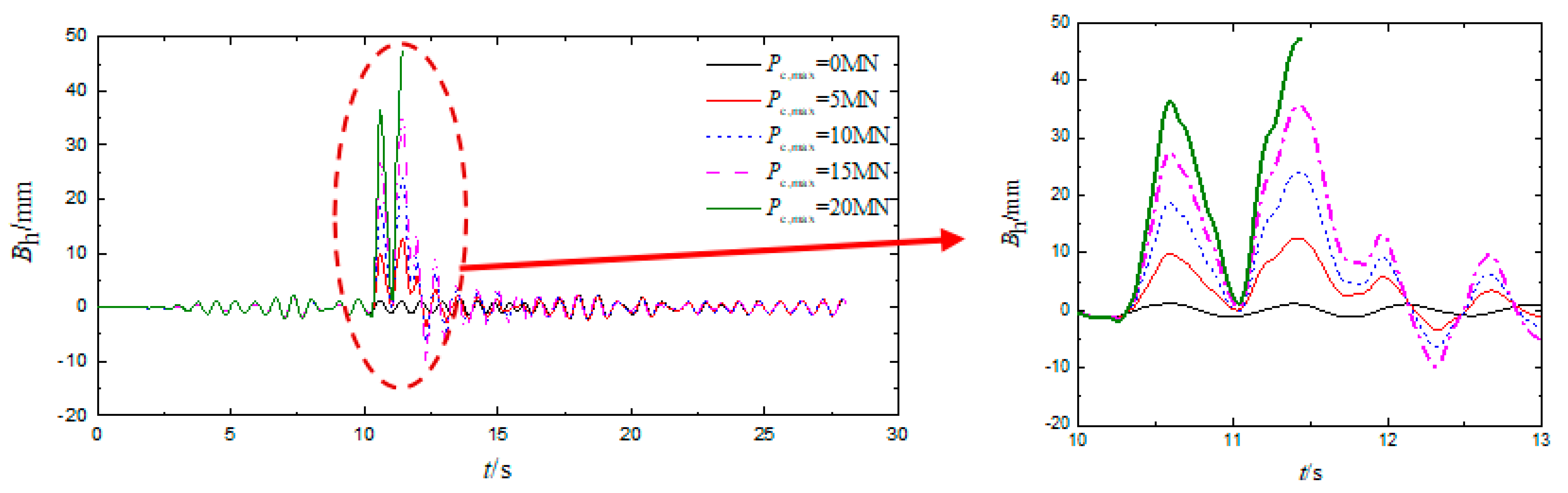
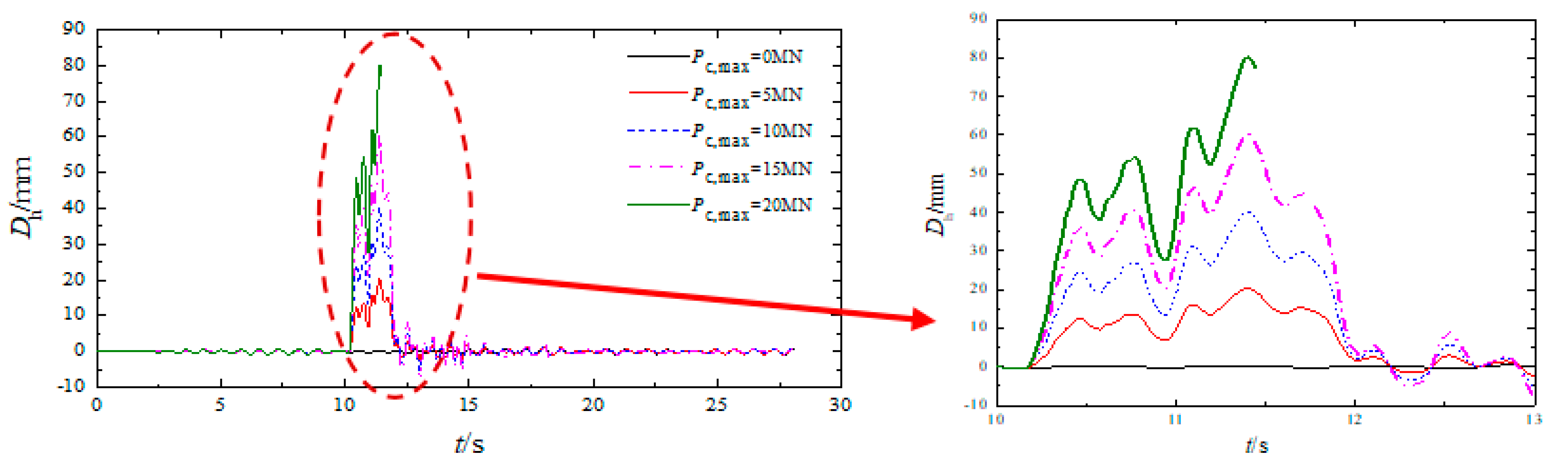
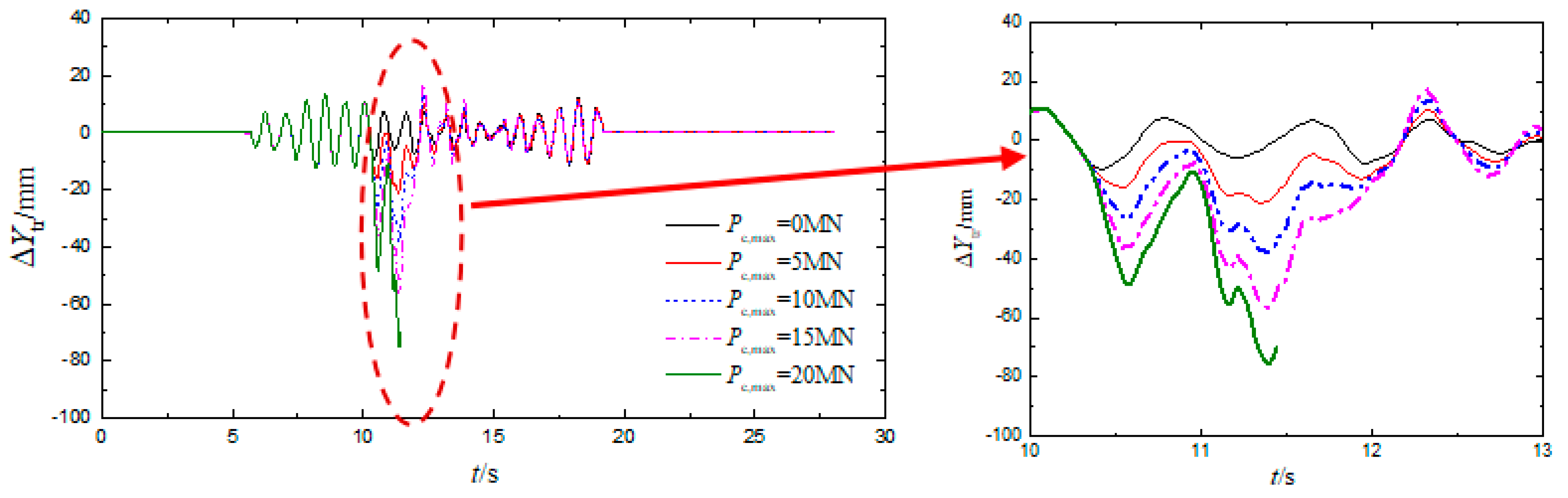
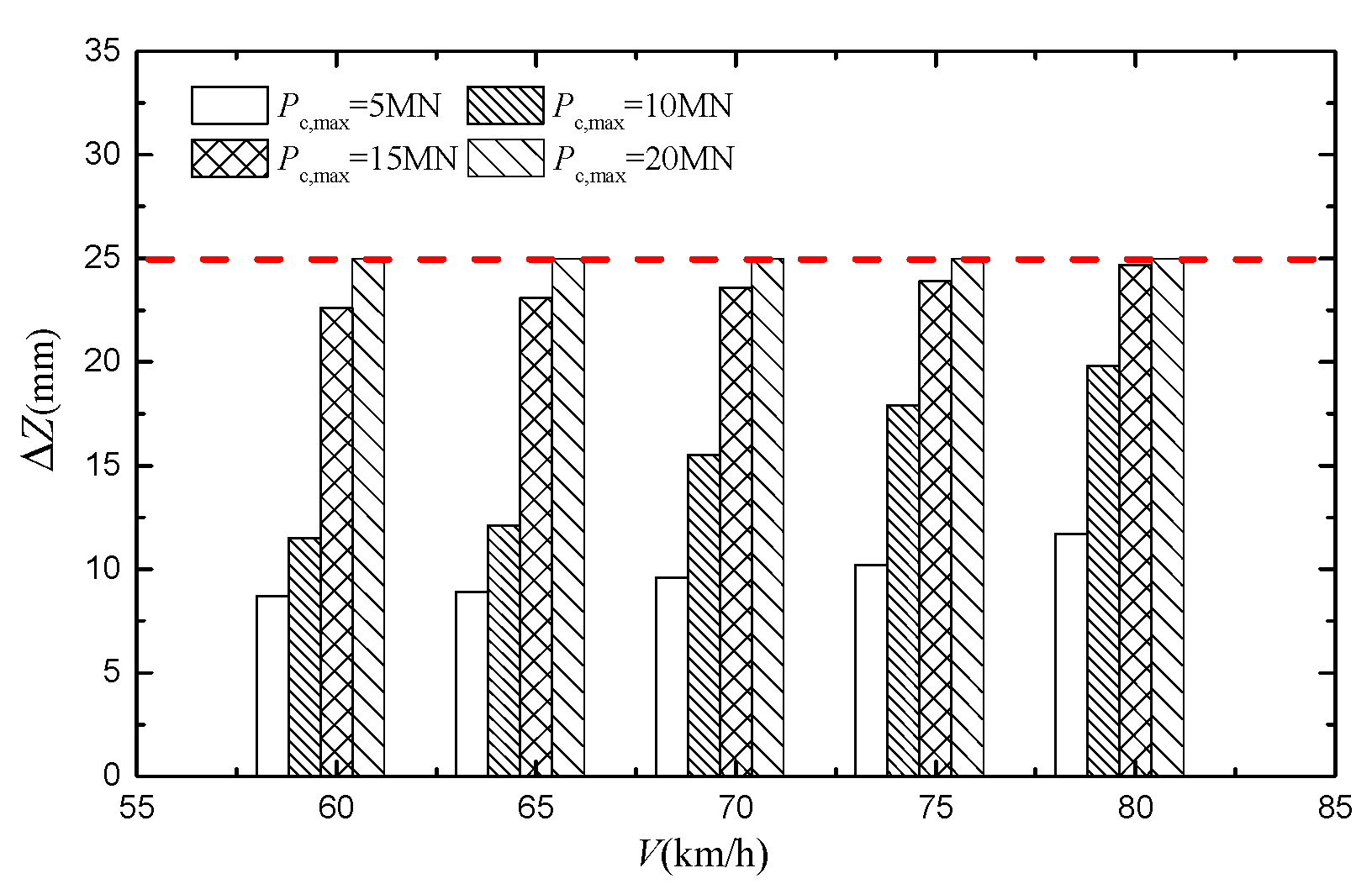
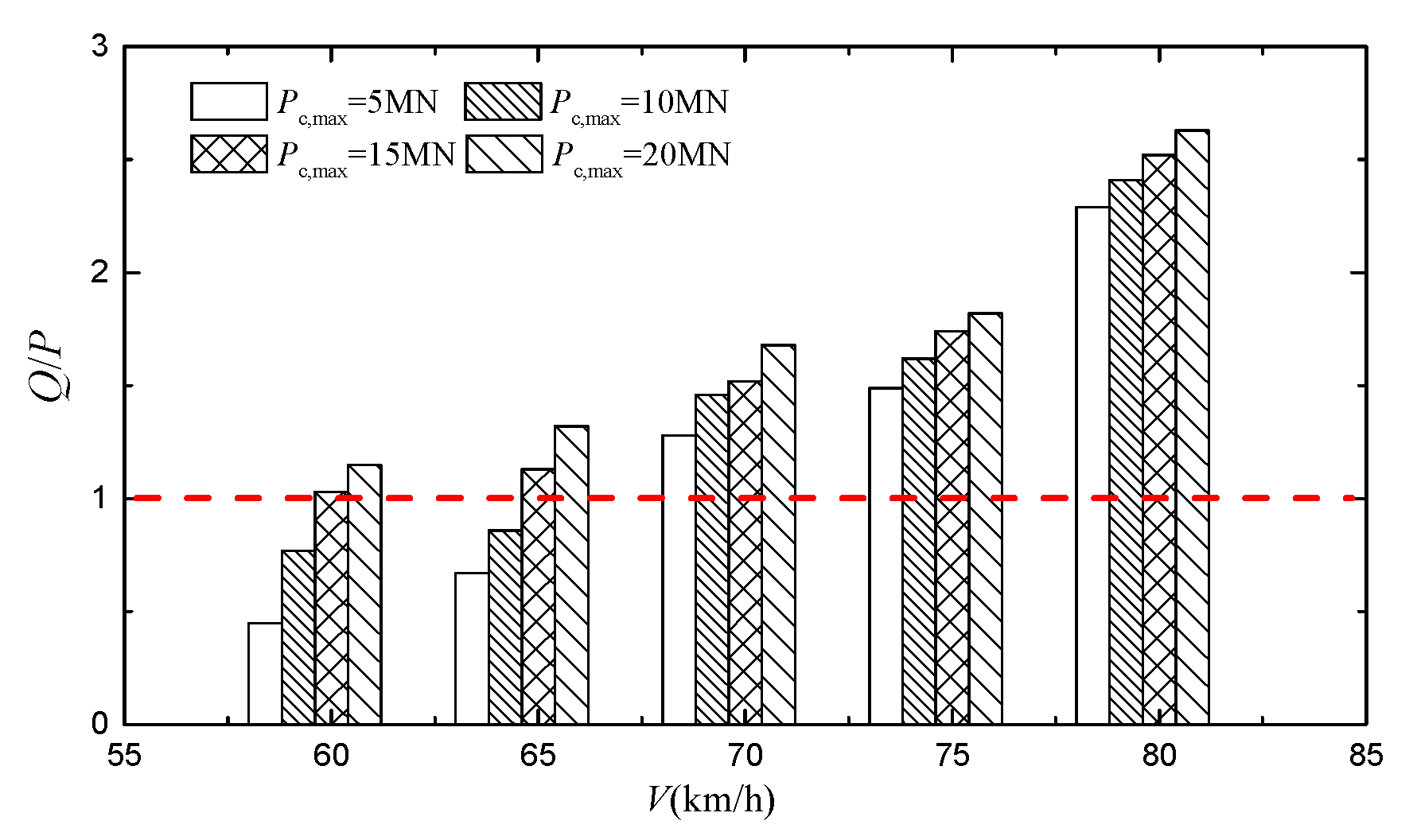
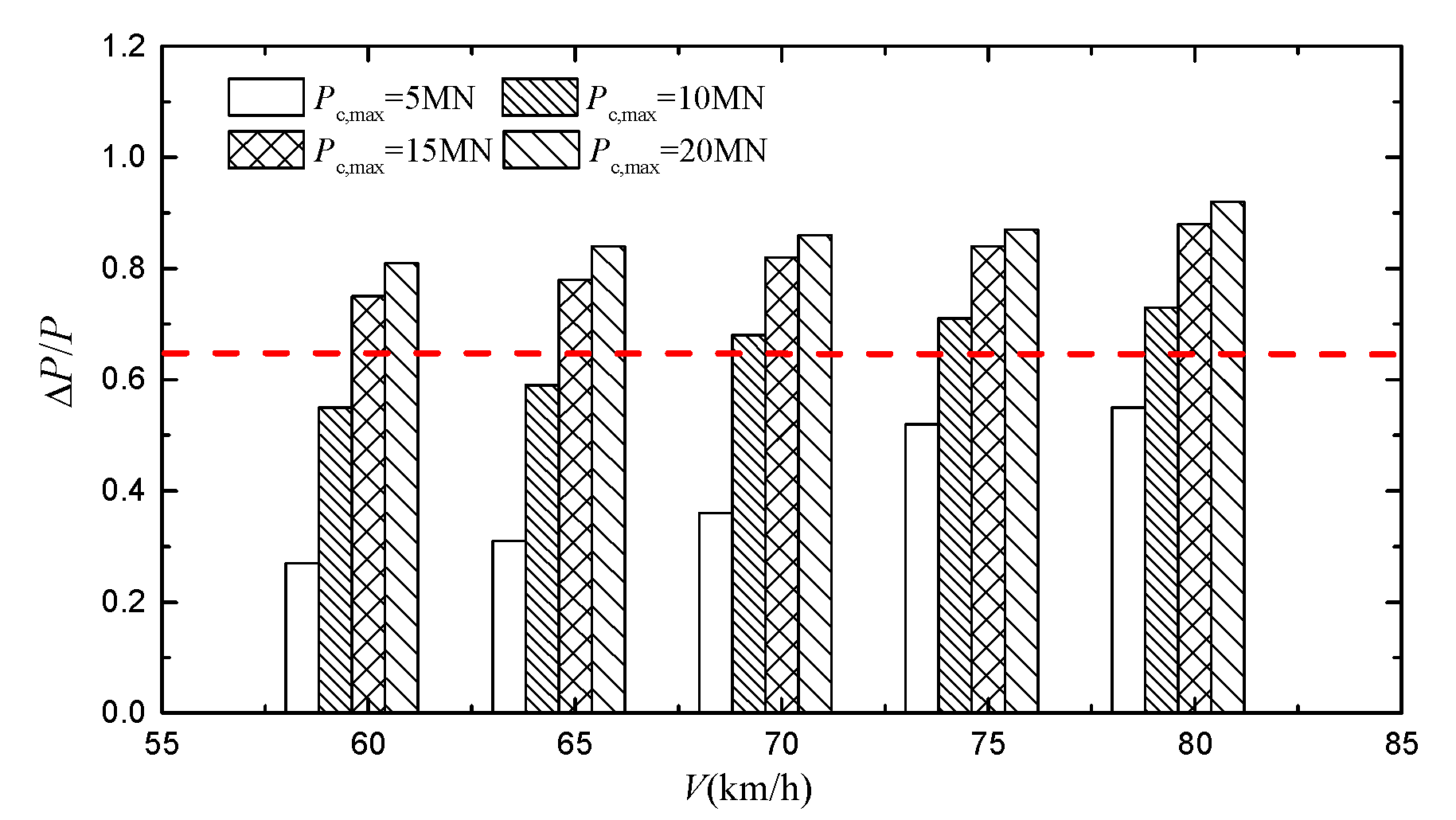
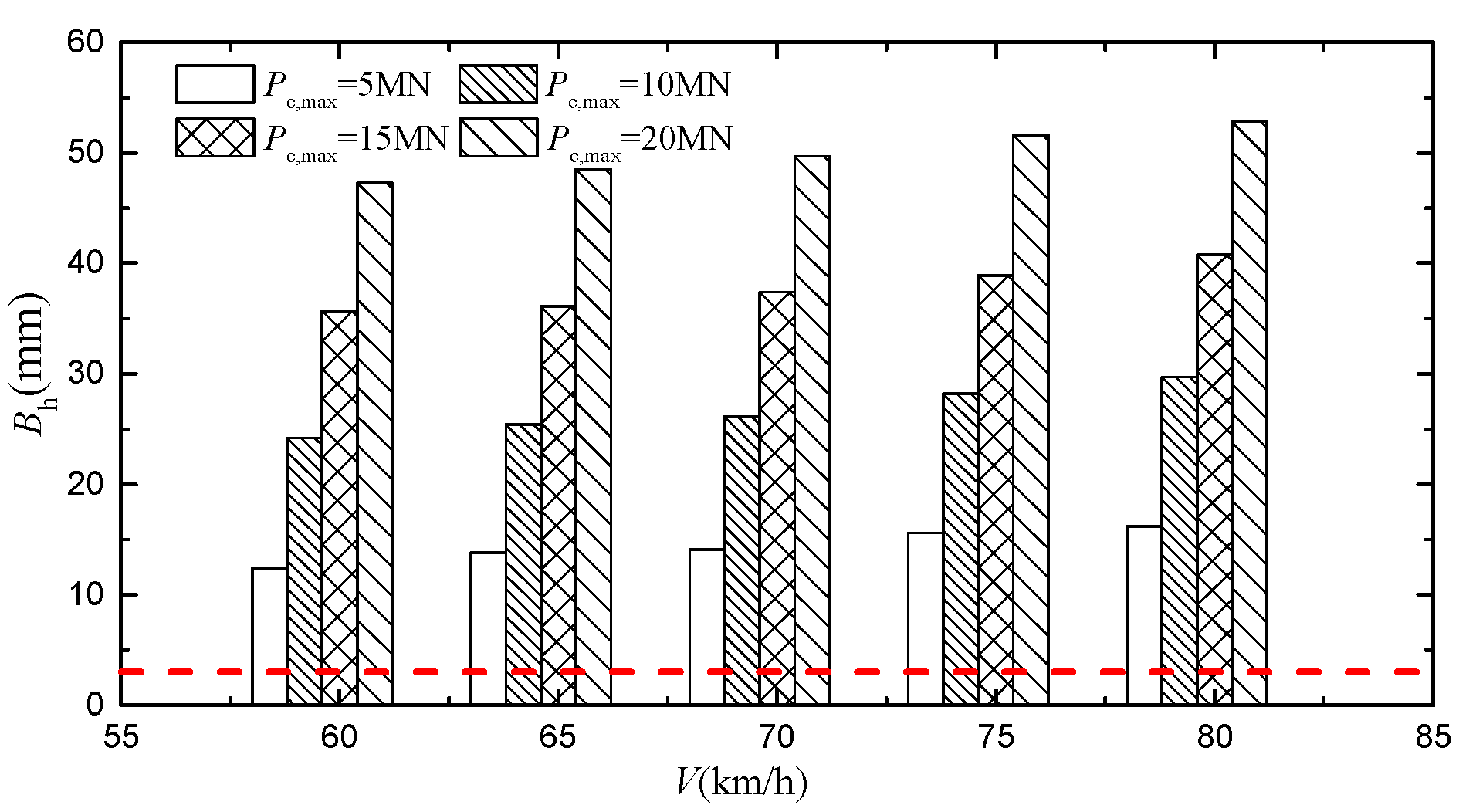
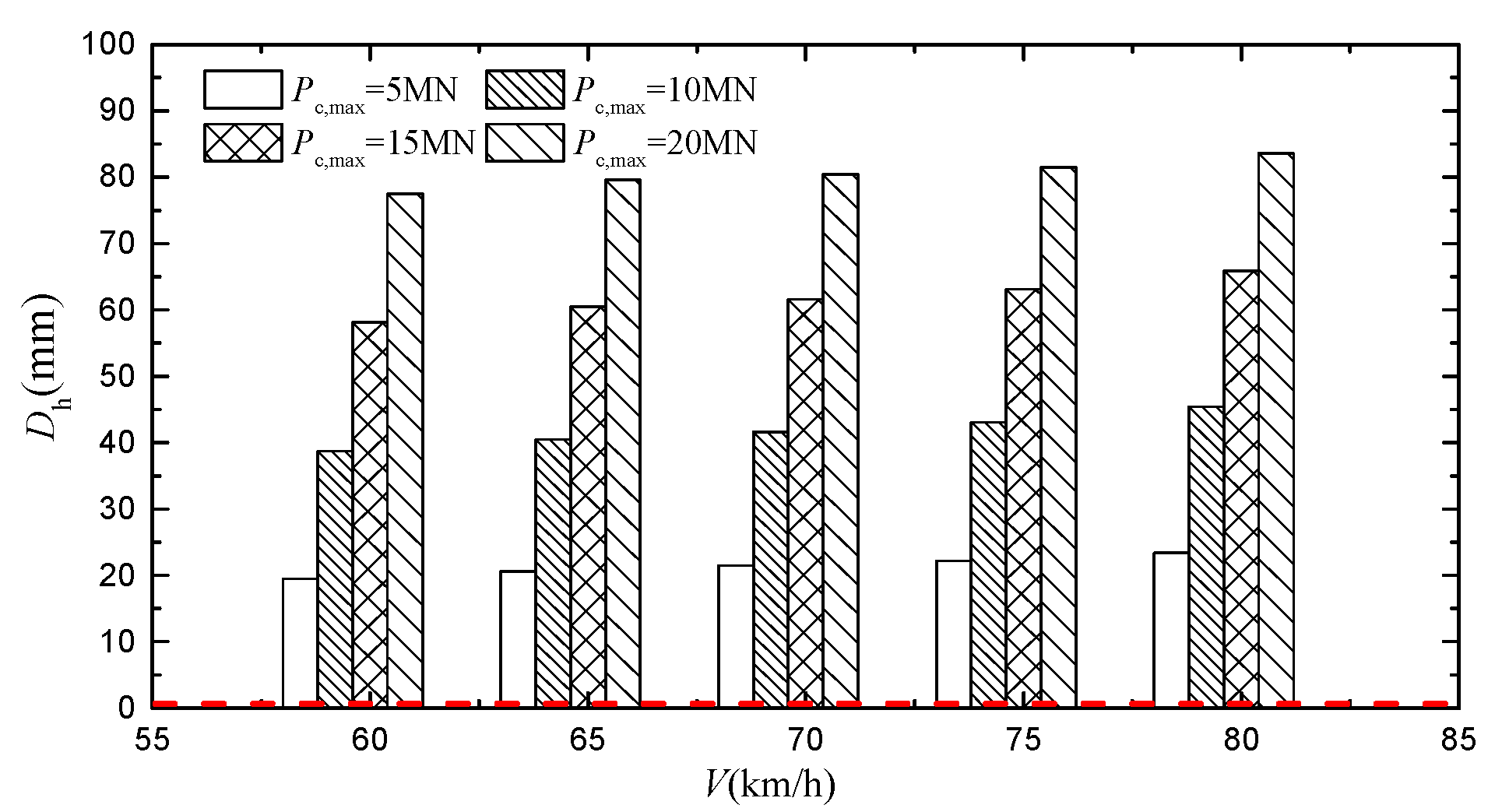
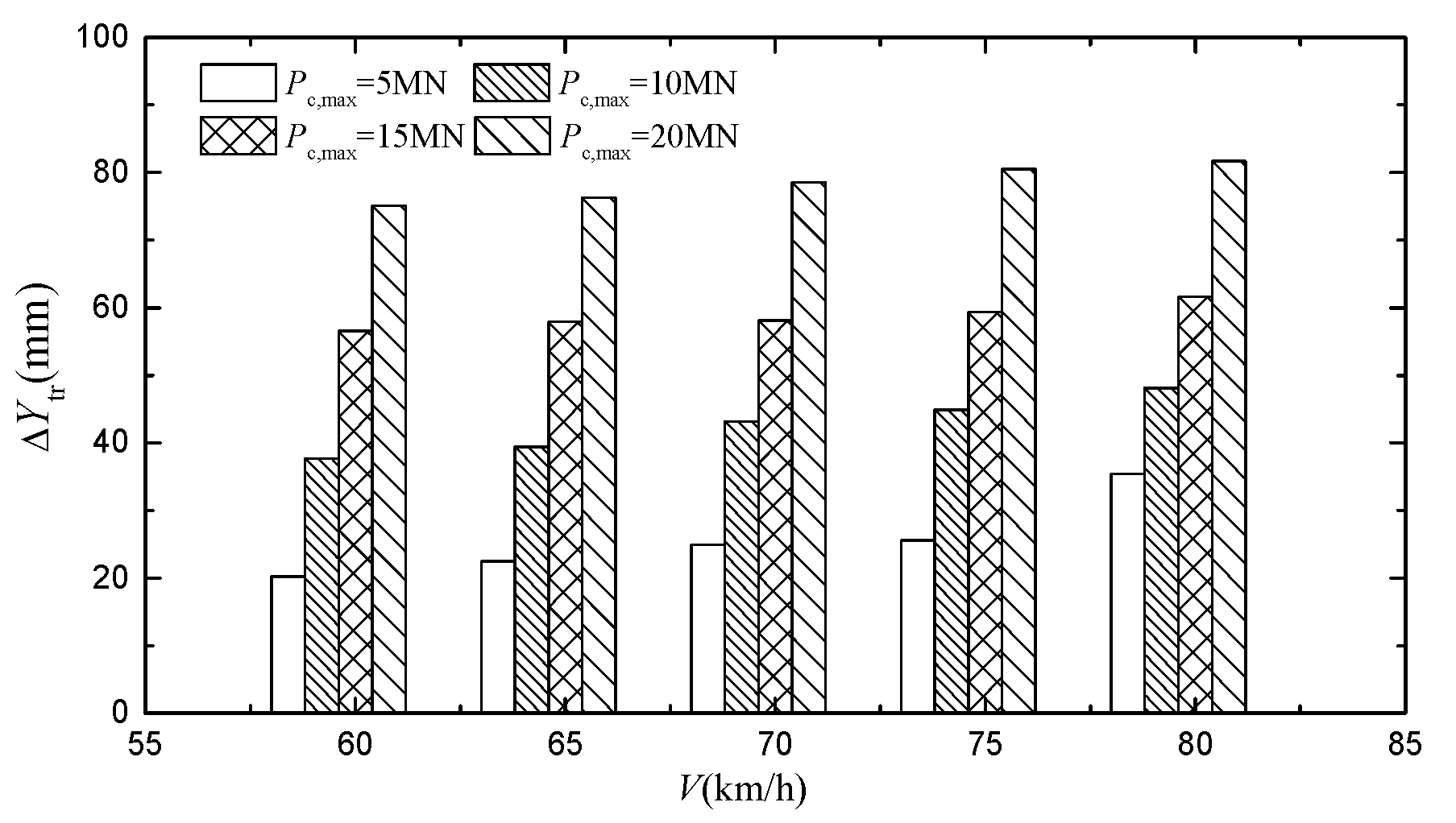
| V (km/h) | Pc,max (MN) | ΔZ (mm) | Derailment Wagon and Wheel | Q/P | ΔP/P | Bh (mm) | Dh (mm) | ΔYtr (mm) | ΔYtr/1.25 (mm) |
|---|---|---|---|---|---|---|---|---|---|
| 60 | 5 | 8.7 | No | 0.45 | 0.27 | 12.4 | 19.5 | 20.2 | --- |
| 10 | 11.5 | No | 0.77 | 0.55 | 24.2 | 38.7 | 37.7 | --- | |
| 15 | 22.6 | No | 1.03 | 0.75 | 35.7 | 58.1 | 56.5 | --- | |
| 20 | 25.0 | 7th wagon, 1st axletree, left wheel | 1.15 | 0.81 | 47.3 | 77.5 | 75.1 | 60.1 | |
| 65 | 5 | 8.9 | No | 0.67 | 0.31 | 13.8 | 20.6 | 22.5 | --- |
| 10 | 12.1 | No | 0.86 | 0.59 | 25.4 | 40.5 | 39.4 | --- | |
| 15 | 23.1 | No | 1.13 | 0.78 | 36.1 | 60.5 | 57.9 | --- | |
| 20 | 25.0 | 8th wagon, 1st axletree, left wheel | 1.32 | 0.84 | 48.5 | 79.6 | 76.3 | 61.0 | |
| 70 | 5 | 9.6 | No | 1.28 | 0.36 | 14.1 | 21.5 | 24.9 | --- |
| 10 | 15.5 | No | 1.46 | 0.68 | 26.1 | 41.6 | 43.2 | --- | |
| 15 | 23.6 | No | 1.52 | 0.82 | 37.4 | 61.6 | 58.1 | --- | |
| 20 | 25.0 | 9th wagon, 1st axletree, left wheel | 1.68 | 0.86 | 49.7 | 80.4 | 78.5 | 62.8 | |
| 75 | 5 | 10.2 | No | 1.49 | 0.52 | 15.6 | 22.2 | 25.6 | --- |
| 10 | 17.9 | No | 1.62 | 0.71 | 28.2 | 43.1 | 44.9 | --- | |
| 15 | 23.9 | No | 1.74 | 0.84 | 38.9 | 63.1 | 59.3 | --- | |
| 20 | 25.0 | 10th wagon, 1st axletree, left wheel | 1.82 | 0.87 | 51.6 | 81.5 | 80.5 | 64.4 | |
| 80 | 5 | 11.7 | No | 2.29 | 0.55 | 16.2 | 23.4 | 35.4 | --- |
| 10 | 19.8 | No | 2.41 | 0.73 | 29.7 | 45.1 | 48.1 | --- | |
| 15 | 24.7 | No | 2.52 | 0.88 | 40.8 | 65.9 | 60.6 | --- | |
| 20 | 25.0 | 11th wagon, 1st axletree, left wheel | 2.63 | 0.92 | 52.8 | 83.6 | 81.7 | 65.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, K.; Liu, L.; Yu, C.; Wang, C. Train Derailment Process Analysis on Heavy Haul Railway Bridge under Ship Impact. Symmetry 2021, 13, 2122. https://doi.org/10.3390/sym13112122
Gong K, Liu L, Yu C, Wang C. Train Derailment Process Analysis on Heavy Haul Railway Bridge under Ship Impact. Symmetry. 2021; 13(11):2122. https://doi.org/10.3390/sym13112122
Chicago/Turabian StyleGong, Kai, Linya Liu, Cuiying Yu, and Chen Wang. 2021. "Train Derailment Process Analysis on Heavy Haul Railway Bridge under Ship Impact" Symmetry 13, no. 11: 2122. https://doi.org/10.3390/sym13112122
APA StyleGong, K., Liu, L., Yu, C., & Wang, C. (2021). Train Derailment Process Analysis on Heavy Haul Railway Bridge under Ship Impact. Symmetry, 13(11), 2122. https://doi.org/10.3390/sym13112122





