Use of the Symmetries in the Study of Vibration Response of a Hollow Cylinder
Abstract
:1. Introduction
2. Materials and Methods
3. Use of FEM for the Study of a Hollow Cylinder
- -
- is the mass matrix;
- -
- the stiffness matrix.
4. Eigenvalues and Eigenmodes
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, D.; Zhou, C.; Rong, J. Free and forced vibration of repetitive structure. Int. J. Solids Struct. 2003, 40, 5477–5494. [Google Scholar] [CrossRef]
- Cai, C.; Wu, F. On the Vibration of RotationalPeriodic Structures. In Acta Scientiarum Naturalium Universitatis Sunyatseni; Sun Yat-sen University: Guangzhou, China, 1983; Volume 22, p. 109. [Google Scholar]
- Cai, C.; Cheung, Y.; Chan, H. Uncoupling of dynamic equations for periodic structures. J. Sound Vib. 1990, 139, 253–2630. [Google Scholar] [CrossRef]
- Chan, H.; Cai, C.; Cheung, Y. Exact Analysis of Structures with Periodicity Using U-Transformation; World Scientific Publication: Singapore, 1998. [Google Scholar]
- Evensen, D.A. Vibration Analysis of Multi-symmetric structures. AIAA J. 1976, 14, 446–453. [Google Scholar] [CrossRef]
- Meirovitch, L. Elements of Vibration Analysis, 2nd ed.; McGraww-Hill: New York, NY, USA, 1970. [Google Scholar]
- Wang, D.; Wang, C.C. Natural vibration of repetitive structures. Chin. J. Mech. 2000, 16, 85–95. [Google Scholar] [CrossRef]
- Zhong, W. The eigen-value problem of the chain of identical substructures and the expansion method solution lasted on the eigen-vectors. Acta Mech. Sin. 1991, 23, 72–81. [Google Scholar]
- Brillouin, L. Wave Propagation in Periodic Structures; Dover Publications: New York, NY, USA, 1946. [Google Scholar]
- Mead, D.J. A general theory of harmonic wave propagation in linear periodic systems with multiple coupling. J. Sound Vib. 1973, 27, 235–260. [Google Scholar] [CrossRef]
- Mead, D.J. Wave propagation and naturalmodes in periodic systems. I. Mono-coupled systems. J. Sound Vib. 1975, 40, 1–18. [Google Scholar] [CrossRef]
- Mead, D.J. Wave propagation and naturalmodes in periodic systems. II. Multi-coupled systems, with and without damping. J. Sound Vib. 1975, 40, 19–39. [Google Scholar] [CrossRef]
- Mead, D.J.; Bansal, A.S. Mono-coupled periodic systems with a single disorder: Free wave propagation. J. Sound Vib. 1978, 61, 481–496. [Google Scholar] [CrossRef]
- Gry, L.; Gontier, C. Dynamic modelling of railway track: A periodic model on a generalized beam formulation. J. Sound Vib. 1997, 199, 531–558. [Google Scholar] [CrossRef]
- Zhong, W.H.; Williams, F.W. On the direct solution of wave propagation for repetitive structures. J. Sound Vib. 1995, 181, 485–501. [Google Scholar] [CrossRef]
- Vlase, S.; Teodorescu-Drăghicescu, H.; Scutaru, L.M. On the Eigenvalues of the Elastic Systems with Some Symmetries. In Proceedings of the 6th International DAAAM Baltic Conference Industrial Engineering, Tallinn, Estonia, 24–26 April 2008. [Google Scholar]
- Vlase, S.; Paun, M. Vibration analysis of a mechanical system consisting of two identical parts. R. J. Tech. Sci. Appl. Mech. 2015, 60, 216–230. [Google Scholar]
- Kaveh, A.; Hamedani, K.B.; Joudaki, A.; Kamalinejad, M. Optimal analysis for optimal design of cyclic symmetric structures subject to frequency constraints. Structures 2021, 33, 3122–3136. [Google Scholar] [CrossRef]
- Vlase, S.; Marin, M.; Scutaru, M.L.; Pruncu, C. Vibration Response of a Concrete Structure with Repetitive Parts Used in Civil Engineering. Mathematics 2021, 9, 490. [Google Scholar] [CrossRef]
- Vlase, S.; Teodorescu, P.P. Elasto-Dynamics of a Solid with a general “Rigid” Motion using FEM Model. Part I. Theoretical Approach. Rom. J. Phys. 2013, 58, 872–881. [Google Scholar]
- Zhang, J.; Reynders, E.; De Roeck, G.; Lombaert, G. Model updating of periodic structures based on free wave characteristics. J. Sound Vib. 2019, 442, 281–307. [Google Scholar] [CrossRef]
- Wu, L.J.; Song, H.W. Band gap analysis of periodic structures based on cell experimental frequency response functions (FRFs). Acta Mech. Sin. 2019, 35, 156–173. [Google Scholar] [CrossRef]
- Ashari, A.K.; Stephen, N.G. On wave propagation in repetitive structures: Two forms of transfer matrix. J. Sound Vib. 2019, 439, 99–112. [Google Scholar] [CrossRef] [Green Version]
- Kaveh, A.; Joudaki, A. Matrix Analysis of Repetitive Circulant Structures: New-block and Near Block Matrices. Period. Polytech. Civ. Eng. 2019, 63, 687–694. [Google Scholar] [CrossRef] [Green Version]
- Rallu, A.; Hans, S.; Boutin, C. Asymptotic analysis of high-frequency modulation in periodic systems. Analytical study of discrete and continuous structures. J. Mech. Phys. Solids 2018, 117, 123–156. [Google Scholar] [CrossRef]
- Kaveh, A.; Zolghadr, A. Optimal design of cyclically symmetric trusses with frequency constraints using cyclical parthenogenesis algorithm. Adv. Struct. Eng. 2018, 21, 739–755. [Google Scholar] [CrossRef]
- Li, L.Y.; Cheng, B.W.; Zhang, Y.; Qin, H. Study of a smart platform based on backstepping control method. Earthq. Eng. Eng. Vib. 2017, 16, 599–608. [Google Scholar] [CrossRef]
- Viola, E.; Alessandro, M. Exact Analysis of Wave Motions in Rods and Hollow Cylinders. In Mechanical Vibration: Where Do We Stand? Elishakoff, I., Ed.; Springer: Berlin/Heidelberg, Germany; Wien: New York, NY, USA, 2006. [Google Scholar]
- Viola, E.; Alessandro, M.; Bartoli, I. Numerical Evaluation of Semi-analytical Finite Element (SAFE) Method for Plates, Rods and Hollow Cylinders. In Mechanical Vibration: Where Do We Stand? Elishakoff, I., Ed.; Spinger: Berlin/Heidelberg, Germany; Wien: New York, NY, USA, 2006. [Google Scholar]
- Viola, E.; Alessandro, M.; Bartoli, I. Semi-analytical Formulation for Guided Wave Propagation. In Mechanical Vibration: Where Do We Stand? Elishakoff, I., Ed.; Spinger: Berlin/Heidelberg, Germany; Wien: New York, NY, USA, 2006. [Google Scholar]
- Haris, C.M.; Crede, C.E. Shock and Vibration Handbook, 6th ed.; McGraw-Hill: New York, NY, USA, 2009. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Vlase, S. Elimination of Lagrangian Multipliers. Mech. Res. Commun. 1987, 14, 17–22. [Google Scholar] [CrossRef]
- Vlase, S. A Method of Eliminating Lagrangean Multipliers from the Equation of Motion of Interconnected Mechanical System. ASME Transaction. J. Appl. Mech. 1987, 54, 235–236. [Google Scholar] [CrossRef]
- Scutaru, M.L.; Vlase, S. Some Properties of Motion Equations Describing the Nonlinear Dynamical Response of a Multibody System with Flexible Elements. J. Appl. Math. 2012. [Google Scholar] [CrossRef] [Green Version]
- Vlase, S.; Teodorescu, P.P.; Itu, C.; Scutaru, M.L. Elasto-Dynamics of a Solid with a General “Rigid” Motion Using FEM Model. Part II. Analysis of a Double Cardan Joint. Rom. J. Phys. 2013, 58, 882–892. [Google Scholar]
- Vlase, S.; Dănășel, C.; Scutaru, M.L.; Mihălcică, M. Finite Element Analysis of a Two-Dimensional Linear Elastic Systems with a plane “Rigid Motion”. Rom. J. Phys. 2014, 59, 476–487. [Google Scholar]
- Vasile, O.; Vlase, S.; Nastac, C.; Scutaru, M.L. Experimental Analysis of a Mechanical System Composed by Two Identical Parts. Acta Technica Napocensis, Series-Applied Mathematics. Mech. Eng. 2018, 61, 333–338. [Google Scholar]
- Bakhvalov, N.S. Numerical Methods: Analysis, Algebra, Ordinary Differential Equations; MIR Publisher: Moscow, Russia, 1977. [Google Scholar]
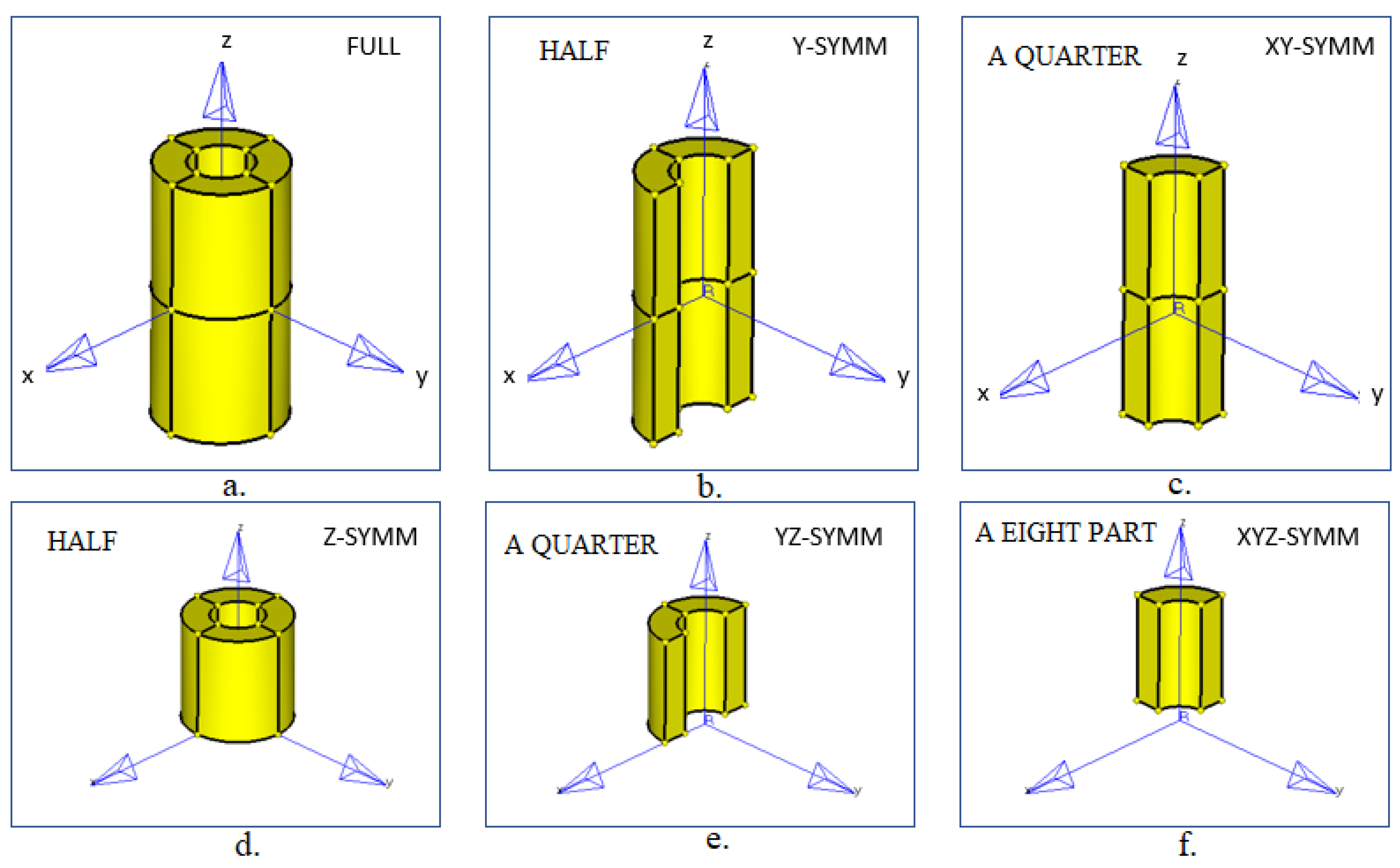
| Model | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Full | Half | Quarter | Half | Quarter | An Eighth | ||||||
 | 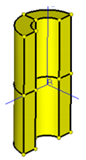 | 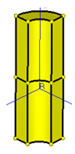 | 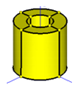 | 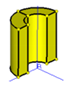 | 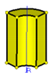 | ||||||
| Mode | Freq. * Hz | Mode | Freq. * Hz | Mode | Freq. * Hz | Mode | Freq. * Hz | Mode | Freq. * Hz | Mode | Freq. * Hz |
| 7;8 | 7970 | 4 | 7970 | 4 | 7970 | 2 | 7970 | ||||
 |  | 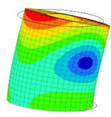 | 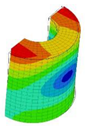 | ||||||||
| 9 | 7998 | ||||||||||
 | |||||||||||
| 10;11 | 10,055 | 5 | 10,055 | 2 | 10,055 | 6;7 | 10,055 | 3 | 10,055 | 1 | 10,055 |
 | 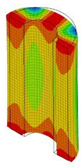 | 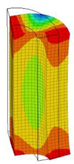 | 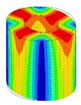 | 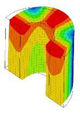 | 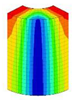 | ||||||
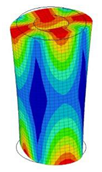
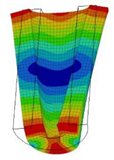
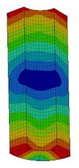
| 12;13 | 10,287 | 6 | 10,287 | 3 | 10,287 | ||||||
 |  |  | |||||||||
| 14;15 | 12,095 | 7 | 12,095 | 4 | 12,095 | 8;9 | 12,094 | 4 | 12,094 | 2 | 12,094 |
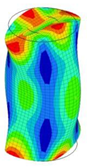 | 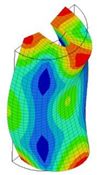 | 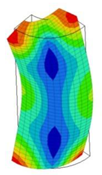 | 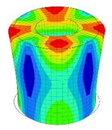 |  |  | ||||||
| 16;17 | 12,557 | 8 | 12,557 | ||||||||
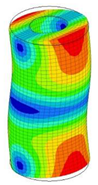 |  | ||||||||||
| 18 | 12,630 | 9 | 12,630 | 5 | 12,630 | 10 | 12,630 | 5 | 12,630 | 3 | 12,630 |
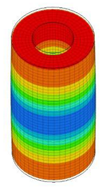 | 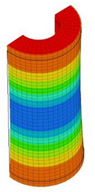 |  |  | 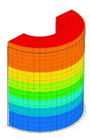 |  | ||||||
| 19 | 15,984 | 11 | 15,984 | ||||||||
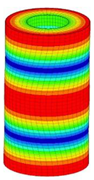 |  | ||||||||||
| 20;21 | 16,297 | 10 | 16,297 | 6 | 16,297 | ||||||
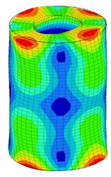 | 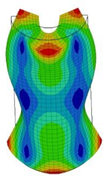 | 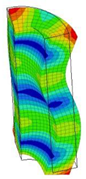 | |||||||||
| 22;23 | 17,204 | 11 | 17,204 | ||||||||
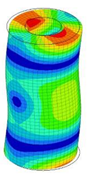 |  | ||||||||||
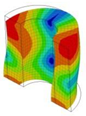
| 24;25 | 17,989 | 12 | 17,989 | 12;13 | 17,989 | 6 | 17,989 | ||||
 |  |  |  | ||||||||
| 26 | 20,815 | 13 | 20,815 | 7 | 20,815 | ||||||
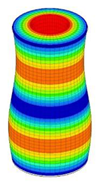 |  | 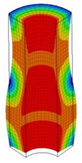 | |||||||||
| 27;28 | 21,977 | 14 | 21,977 | 8 | 21,977 | 14;15 | 21,977 | 7 | 21,977 | 4 | 21,977 |
 | 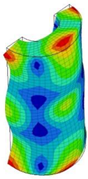 |  |  | 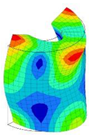 | 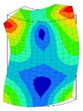 | ||||||
| 29 | 22,043 | 15 | 22,043 | 9 | 22,043 | 16 | 22,043 | 8 | 22,043 | 5 | 22,043 |
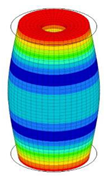 |  |  | 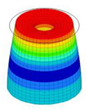 | 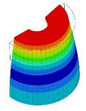 | 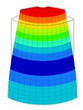 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Itu, C.; Vlase, S.; Marin, M.; Toderiță, A. Use of the Symmetries in the Study of Vibration Response of a Hollow Cylinder. Symmetry 2021, 13, 2145. https://doi.org/10.3390/sym13112145
Itu C, Vlase S, Marin M, Toderiță A. Use of the Symmetries in the Study of Vibration Response of a Hollow Cylinder. Symmetry. 2021; 13(11):2145. https://doi.org/10.3390/sym13112145
Chicago/Turabian StyleItu, Călin, Sorin Vlase, Marin Marin, and Ana Toderiță. 2021. "Use of the Symmetries in the Study of Vibration Response of a Hollow Cylinder" Symmetry 13, no. 11: 2145. https://doi.org/10.3390/sym13112145








