Author Contributions
Conceptualization, Z.K.; methodology, Z.K.; software, P.C., S.D. and Z.K.; validation, P.C., S.D. and Z.K.; formal analysis, P.C., S.D. and Z.K.; investigation, P.C., S.D. and Z.K.; resources, Z.K.; data curation, S.D. and Z.K.; writing—original draft preparation, P.C., S.D. and Z.K.; writing—review and editing, P.C., S.D. and Z.K.; visualization, P.C., S.D. and Z.K.; supervision, Z.K.; project administration, Z.K.; funding acquisition, Z.K. All authors have read and agreed to the published version of the manuscript.
Figure 1.
An analyzed dome: an axonometric view and the cross-section with the global coordinate systems. The dimensions are given in centimeters.
Figure 1.
An analyzed dome: an axonometric view and the cross-section with the global coordinate systems. The dimensions are given in centimeters.
Figure 2.
A projection of the shell with supports marked: the length of a single support zone is 1.0 m.
Figure 2.
A projection of the shell with supports marked: the length of a single support zone is 1.0 m.
Figure 3.
Modeling of the shell: (a) alignment to the top surface of the shell, (b) calculation model, (c) alignment to the middle surface of the shell, (d) calculation model, (e) alignment to the middle surface of the shell with the trim of the shell along the beam contour, and (f) the computational model.
Figure 3.
Modeling of the shell: (a) alignment to the top surface of the shell, (b) calculation model, (c) alignment to the middle surface of the shell, (d) calculation model, (e) alignment to the middle surface of the shell with the trim of the shell along the beam contour, and (f) the computational model.
Figure 4.
FE meshes adopted in the p1 model analysis: (a) FEAS—division into elements: 1482 nodes, 2486 elements; (b) ARSAP—division into elements: 3345 nodes, 4974 elements; (c) Abaqus—division into elements: 3462 nodes, 1571 elements.
Figure 4.
FE meshes adopted in the p1 model analysis: (a) FEAS—division into elements: 1482 nodes, 2486 elements; (b) ARSAP—division into elements: 3345 nodes, 4974 elements; (c) Abaqus—division into elements: 3462 nodes, 1571 elements.
Figure 5.
Model p3: (a) Abaqus—computational model p3 offset, nodes: 3312, shell elements: 1008, bar elements: 64, (b) Abaqus—computational model p3, nodes: 2900, shell elements: 812, bar elements: 116; (c) FEAS—computational model p3 (plan view)—2800: nodes, shell elements: 5400, members: 200; (d) ARSAP—computational model p3, nodes: 9190, shell elements: 3836, members: 360; (e) RFEM—computational model p3, nodes: 3780, shell elements: 3672, bar elements: 216.
Figure 5.
Model p3: (a) Abaqus—computational model p3 offset, nodes: 3312, shell elements: 1008, bar elements: 64, (b) Abaqus—computational model p3, nodes: 2900, shell elements: 812, bar elements: 116; (c) FEAS—computational model p3 (plan view)—2800: nodes, shell elements: 5400, members: 200; (d) ARSAP—computational model p3, nodes: 9190, shell elements: 3836, members: 360; (e) RFEM—computational model p3, nodes: 3780, shell elements: 3672, bar elements: 216.
Figure 6.
Deformation from self-weight: (a) ARSAP; (b) FEAS.
Figure 6.
Deformation from self-weight: (a) ARSAP; (b) FEAS.
Figure 7.
Deformation under the load on the top ring: (a) ARSAP; (b) FEAS.
Figure 7.
Deformation under the load on the top ring: (a) ARSAP; (b) FEAS.
Figure 8.
Deformation under the self-weight: Abaqus.
Figure 8.
Deformation under the self-weight: Abaqus.
Figure 9.
Deformation under the load on the top ring: FEAS.
Figure 9.
Deformation under the load on the top ring: FEAS.
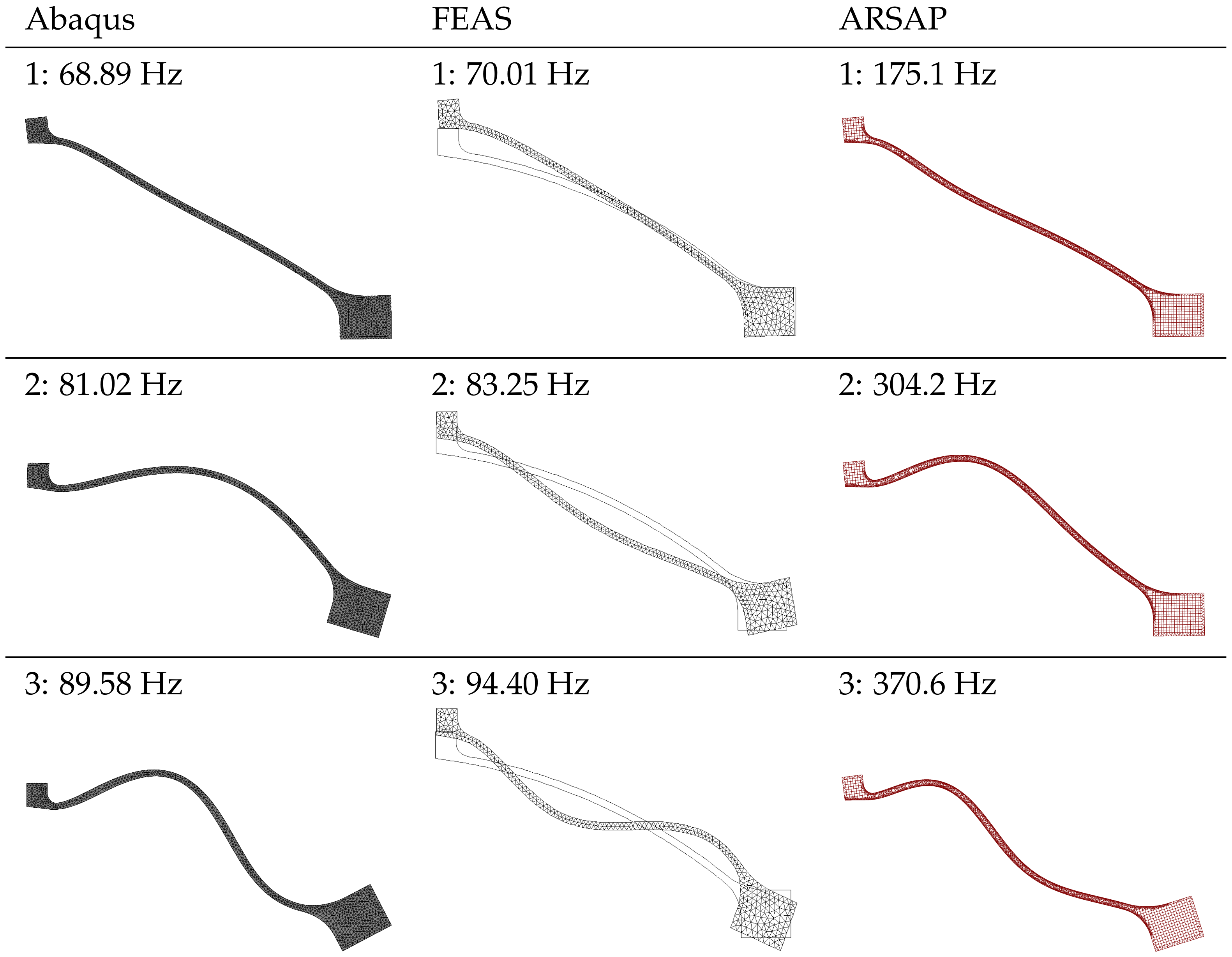
Figure 10.
Model p1: frequencies and modes of natural vibration.
Figure 10.
Model p1: frequencies and modes of natural vibration.
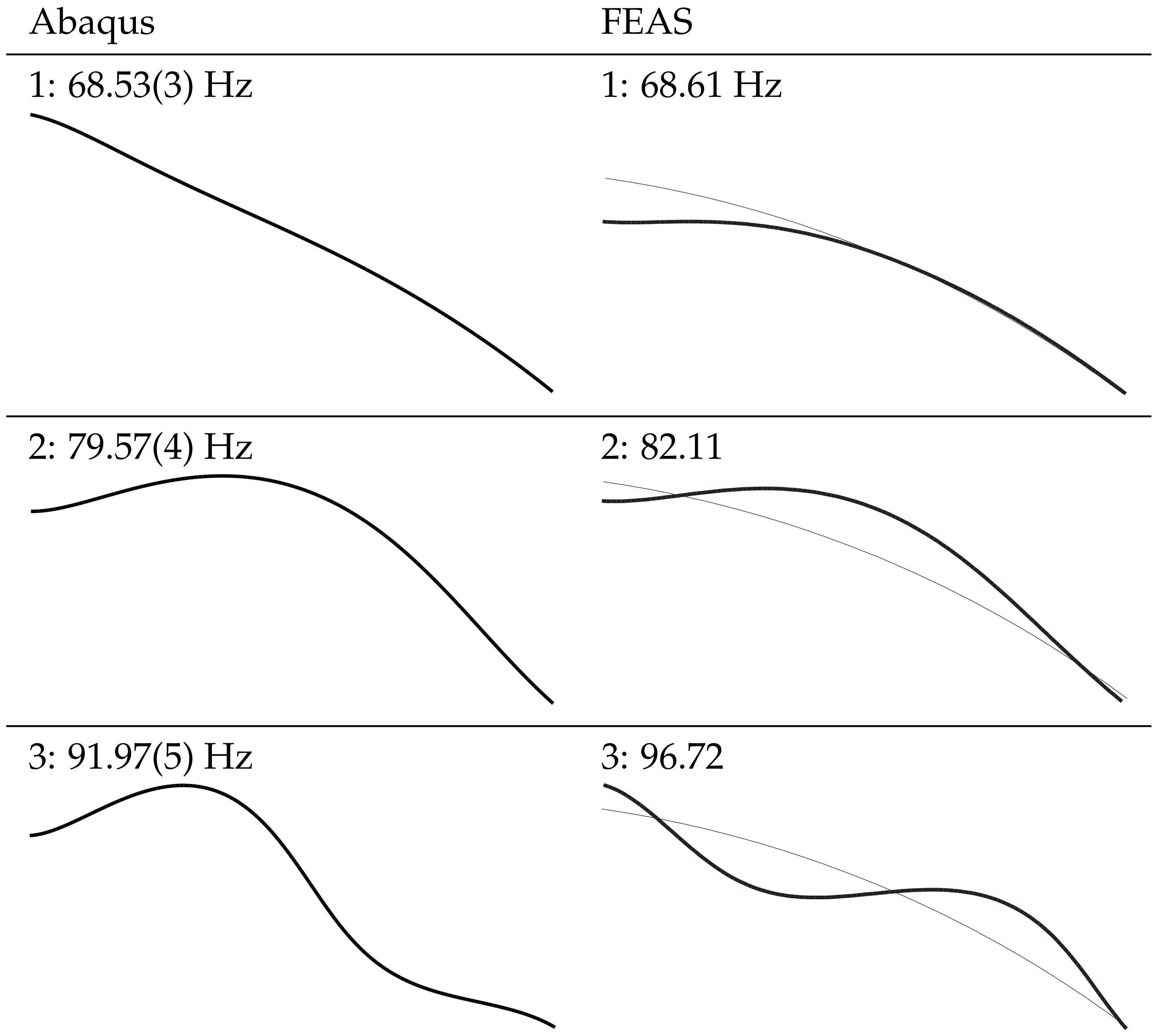
Figure 11.
Model p2: frequencies and modes of natural vibration.
Figure 11.
Model p2: frequencies and modes of natural vibration.
Figure 12.
Abaqus, the p3 model: first and third modes of natural vibration.
Figure 12.
Abaqus, the p3 model: first and third modes of natural vibration.
Figure 13.
FEAS, the p3 model: first and third modes of natural vibration.
Figure 13.
FEAS, the p3 model: first and third modes of natural vibration.
Figure 14.
ARSAP, the p3 model: first and third modes of natural vibration.
Figure 14.
ARSAP, the p3 model: first and third modes of natural vibration.
Figure 15.
RFEM, the p3 model: first and third modes of natural vibration.
Figure 15.
RFEM, the p3 model: first and third modes of natural vibration.
Figure 16.
Abaqus, the p4 model: first and third modes of natural vibration.
Figure 16.
Abaqus, the p4 model: first and third modes of natural vibration.
Figure 17.
FEAS, the p4 model: first and third modes of natural vibration.
Figure 17.
FEAS, the p4 model: first and third modes of natural vibration.
Figure 18.
ARSAP, the p4 model: first and third modes of natural vibration.
Figure 18.
ARSAP, the p4 model: first and third modes of natural vibration.
Figure 19.
RFEM, the p4 model: first and third modes of natural vibration.
Figure 19.
RFEM, the p4 model: first and third modes of natural vibration.
Table 1.
Summary of the presented calculation models.
Table 1.
Summary of the presented calculation models.
| Model | Shell Element | Bar Element | Coaxiality of Ring Bars | System |
|---|
| p3 | 8-node | 3-node | no, Figure 3f | Abaqus |
| offset | curved | curved | | |
| p3 | 8-node | 3-node | yes, Figure 3b | Abaqus |
| | curved | curved | | |
| p3 | 3-node flat | 2-node | yes, Figure 3b | FEAS |
| p3 | 4-node flat | 2-node | yes, Figure 3b | ARSAP |
| p3 | 4-node | 2-node | yes, Figure 3b | RFEM |
Table 2.
Summary of displacements and reactions: p1 model, self-weight.
Table 2.
Summary of displacements and reactions: p1 model, self-weight.
| | (m) | (kN) |
|---|
| Abaqus | −5.05 | 214.00 |
| FEAS | | 211.42 |
| ARSAP | | 211.02 |
Table 3.
Summary of displacements and reactions: p3 model, own weight.
Table 3.
Summary of displacements and reactions: p3 model, own weight.
| Model | System | (m) | (kN) |
|---|
| p3 | Abaqus | | 202.81 |
| offset | | | |
| p3 | Abaqus | | 220.40 |
| p3 | FEAS | | 202.68 |
| p3 | ARSAP | | 216.60 |
| p3 | RFEM | | 216.49 |
Table 4.
Summary of displacements (m) : self-weight.
Table 4.
Summary of displacements (m) : self-weight.
| System | p1 | p2 | | p3 | | p3 Offset | p4 | | p4 Offset |
|---|
| Abaqus | 5.05 | 5.75 | (1.10) | 5.75 | (1.10) | 5.39 | (1.03) | 7.55 | (1.44) | 6.82 | (1.30) |
| FEAS | 5.32 | 5.37 | (1.03) | 5.43 | (1.04) | | | 8.61 | (1.64) | | |
| ARSAP | 5.34 | | | 5.64 | (1.08) | | | 9.57 | (1.83) | | |
| Dlubal | | | | 5.64 | (1.08) | | | 8.48 | (1.62) | | |
| mean | 5.24 | | | 5.62 | (1.07) | | | 8.55 | (1.63) | | |
| STD | 0.13 | | | 0.12 | | | | 0.72 | | | |
| CoV | 0.03 | | | 0.02 | | | | 0.08 | | | |
Table 5.
Summary of displacements (cm): load on the upper ring.
Table 5.
Summary of displacements (cm): load on the upper ring.
| System | p1 | p2 | | p3 | | p3 Offset | p4 | | p4 Offset |
|---|
| Abaqus | 0.97 | 1.27 | (1.33) | 1.27 | (1.33) | 1.06 | (1.11) | 1.26 | (1.32) | 1.05 | (1.10) |
| FEAS | 0.95 | 1.01 | (1.06) | 1.15 | (1.20) | | | 1.22 | (1.28) | | |
| ARSAP | 0.95 | | | 1.30 | (1.36) | | | 1.29 | (1.35) | | |
| Dlubal | | | | 1.30 | (1.36) | | | 1.30 | (1.36) | | |
| mean | 0.96 | | | 1.26 | (1.31) | | | 1.27 | (1.33) | | |
| STD | 0.01 | | | 0.06 | | | | 0.03 | | | |
| CoV | 0.01 | | | 0.05 | | | | 0.02 | | | |
Table 6.
List of the first natural frequencies of the dome for the p1 model (Hz).
Table 6.
List of the first natural frequencies of the dome for the p1 model (Hz).
| System | | | | | |
|---|
| Abaqus | 68.89 | 81.02 | 89.58 | 114.7 | 160.8 |
| FEAS | 69.54 | 81.34 | 90.65 | 117.7 | 166.7 |
| ARSAP | 171.5 | 304.2 | 370.6 | 444.5 | 593.9 |
Table 7.
List of the first natural frequencies of the dome for the p1 model (Hz) calculated in the ARSAP system.
Table 7.
List of the first natural frequencies of the dome for the p1 model (Hz) calculated in the ARSAP system.
| System | | | | | |
|---|
| ARSAP (379 nodes) | 175.0 | 309.5 | 378.1 | 470.6 | 642.2 |
| ARSAP (940 nodes) | 172.1 | 305.0 | 371.7 | 451.0 | 608.1 |
| ARSAP (3345 nodes) | 171.5 | 304.2 | 370.6 | 444.5 | 593.9 |
Table 8.
List of the first natural frequencies of the dome for the p2 (Hz) model.
Table 8.
List of the first natural frequencies of the dome for the p2 (Hz) model.
| System | | | | | |
|---|
| Abaqus | 68.53(3) | 79.57(4) | 91.97(5) | 118.7(6) | 163.57(7) |
| FEAS | 68.61 | 82.11 | 96.72 | 116.8 | 144.1 |
Table 9.
List of the first natural frequencies of the dome for the p3 (Hz) model.
Table 9.
List of the first natural frequencies of the dome for the p3 (Hz) model.
| Model | System | | | | | |
|---|
| p3 | Abaqus | 61.57(4) | 69.10(6) | 79.24(7) | 83.24(9) | 85.99(10) |
| offset | | | | | | |
| p3 | Abaqus | 68.52(4) | 71.27(5) | 76.33(7) | 79.11(9) | 82.00(10) |
| p3 | FEAS | 7.70 | 35.00 | 68.04 | 68.50 | 69.27 |
| p3 | ARSAP | 32.89(2) | 68.01(3) | 69.70(4) | 70.86(6) | 75.51(7) |
| p3 | RFEM | 4.41 | 32.28 | 68.73 | 70.48 | 71.52 |
Table 10.
List of the first natural frequencies of the shell for the p3 offset model calculated in the Abaqus system using different FE types (Hz).
Table 10.
List of the first natural frequencies of the shell for the p3 offset model calculated in the Abaqus system using different FE types (Hz).
| Finite Elements | | | | | |
|---|
| S8R+B32 | 61.57(4) | 69.10(6) | 79.24(7) | 83.24(9) | 85.99(10) |
| S8R5+B32 | 61.24(4) | 69.09(6) | 79.16(7) | 83.26(9) | 85.86(10) |
| S4R+B31 | 62.17(4) | 69.63(6) | 79.65(7) | 83.63(9) | 87.14(10) |
| S4+B31 | 61.86(4) | 69.56(6) | 79.54(7) | 83.54(9) | 86.86(10) |
Table 11.
List of the first natural frequencies of the dome for the p4 model (Hz).
Table 11.
List of the first natural frequencies of the dome for the p4 model (Hz).
| System | | | | | |
|---|
| Abaqus | 56.55 | 57.80 | 57.87 | 59.42 | 69.86 |
| FEAS | 61.46 | 63.40 | 64.25 | 65.08 | 69.76 |
| ARSAP | 57.49 | 58.85 | 60.31(4) | 69.87(5) | 71.33(6) |
| RFEM | 53.31 | 54.47 | 56.6(4) | 70.53(5) | 71.81(6) |
Table 12.
List of the natural frequencies that correspond to the first rotationally symmetrical form of free vibration.
Table 12.
List of the natural frequencies that correspond to the first rotationally symmetrical form of free vibration.
| | p1 | p2 | | p3 | | p4 | |
|---|
| Abaqus | 68.9 | 68.5 | (0.99) | 68.5 | (0.99) | 69.9 | (1.01) |
| FEAS | 69.54 | 68.6 | (0.99) | 68.5 | (0.99) | 69.9 | (1.01) |
| ARSAP | 171.5 | | | 69.7 | (1.01) | 69.9 | (1.01) |
| Dlubal | | | | 68.7 | (0.99) | 70.5 | (1.02) |
| mean | 103.3 | | | 68.8 | (0.99) | 70.0 | (1.01) |
| STD | 48.2 | | | 0.47 | | 0.29 | |
| CoV | 0.47 | | | 0.01 | | 0.004 | |
| ref mean | 69.2 | | | | | | |