Machine Learning for Conservative-to-Primitive in Relativistic Hydrodynamics
Abstract
1. Introduction
2. Method
2.1. NN for EOS
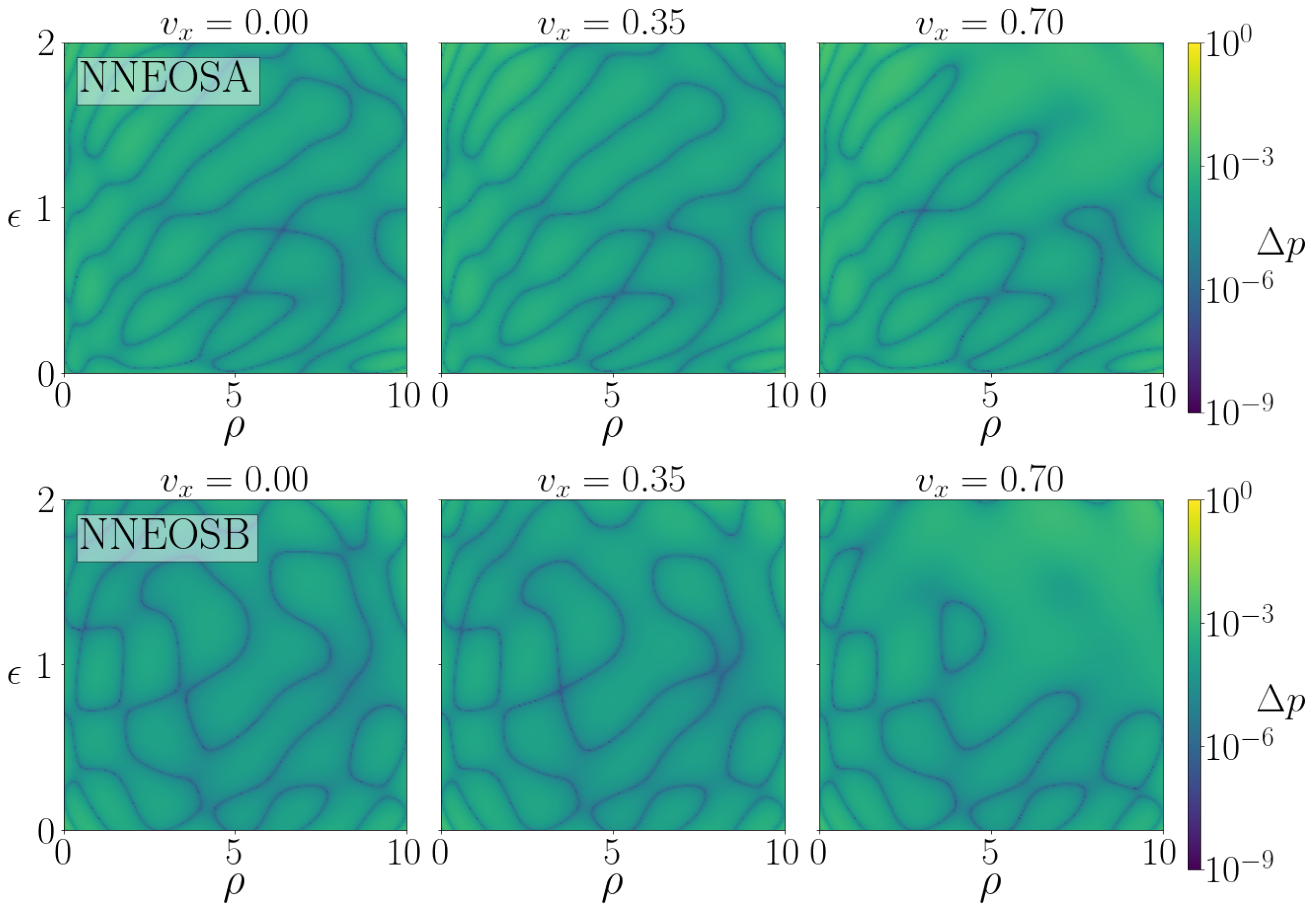
- NNEOSA
- Type A NN only outputs the pressure. Its gradient can be computed using the backpropagation algorithm, but the error of the derivatives is not taken into account during the training process.
- NNEOSB
- Type B NN has three output neurons, for the pressure and its derivatives respectively. Therefore, the loss of all three values is minimized simultaneously during training.
2.2. NN for C2P
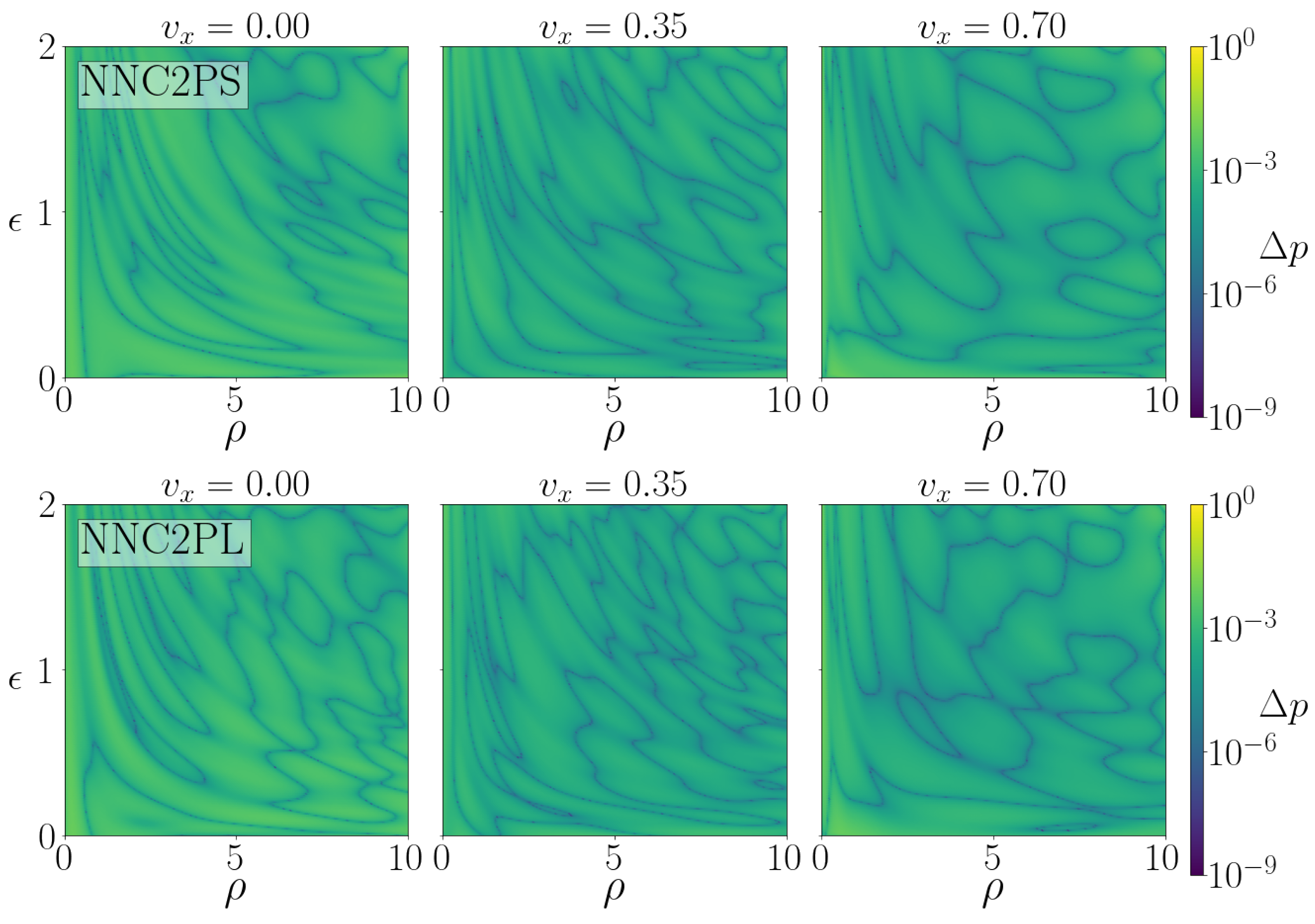
- NNC2PS
- Type S NN outputs the pressure from the conservative variable using a small number of neurons that still guarantee pressure errors of order ∼, as for the NNEOS.
- NNC2PL
- Type L NN has a larger size but it is otherwise identical to NNC2PS.
3. Results
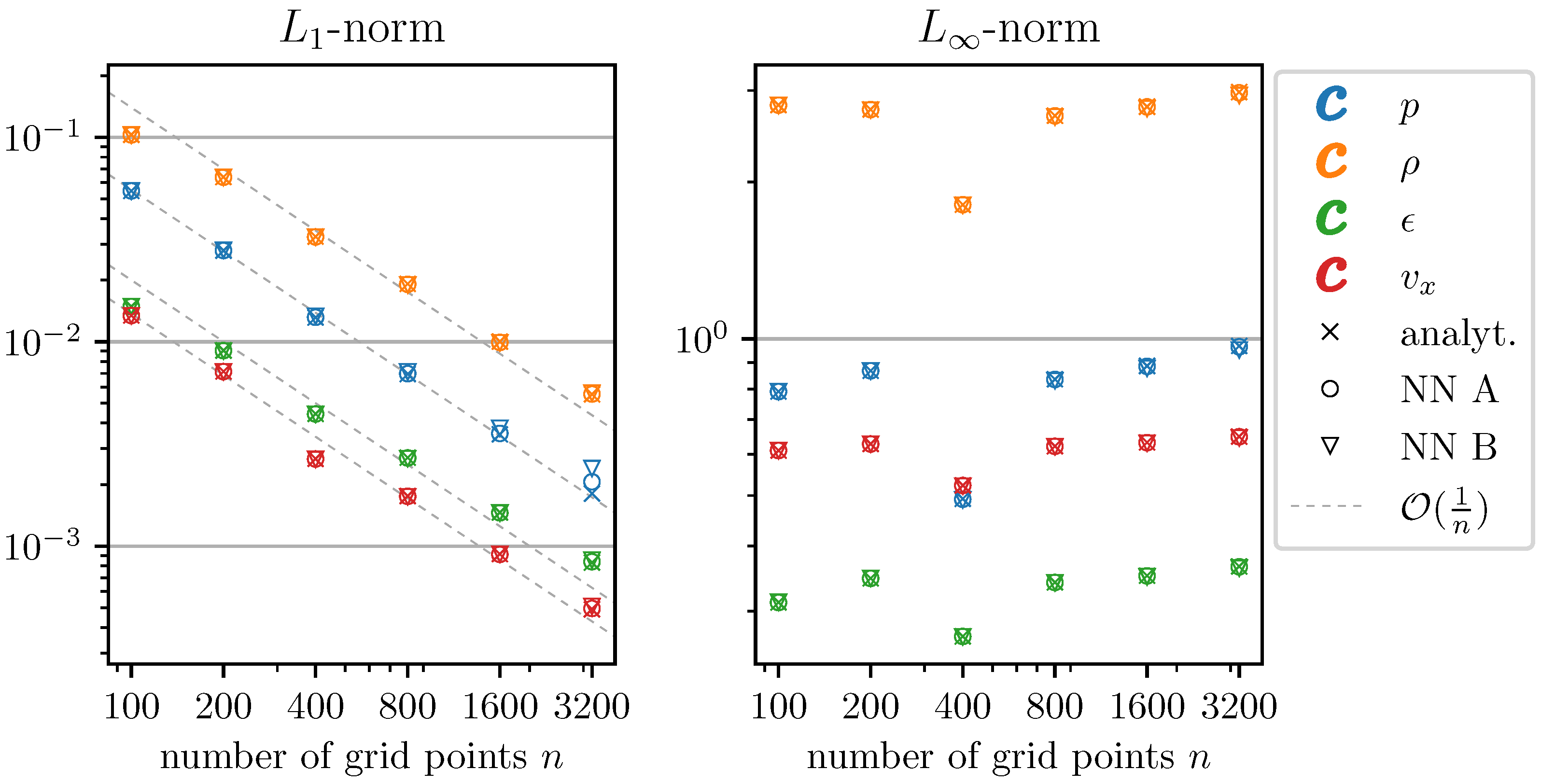
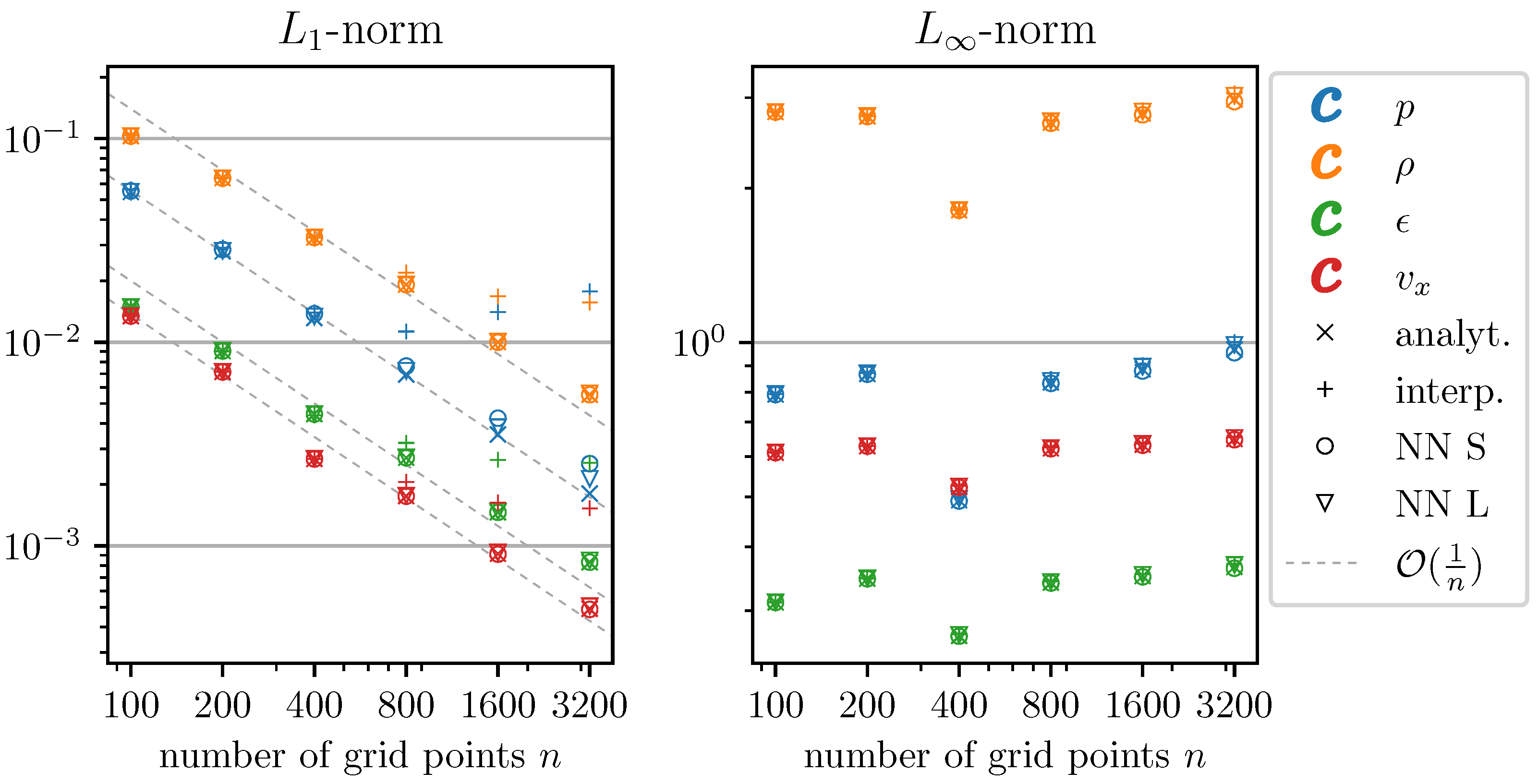
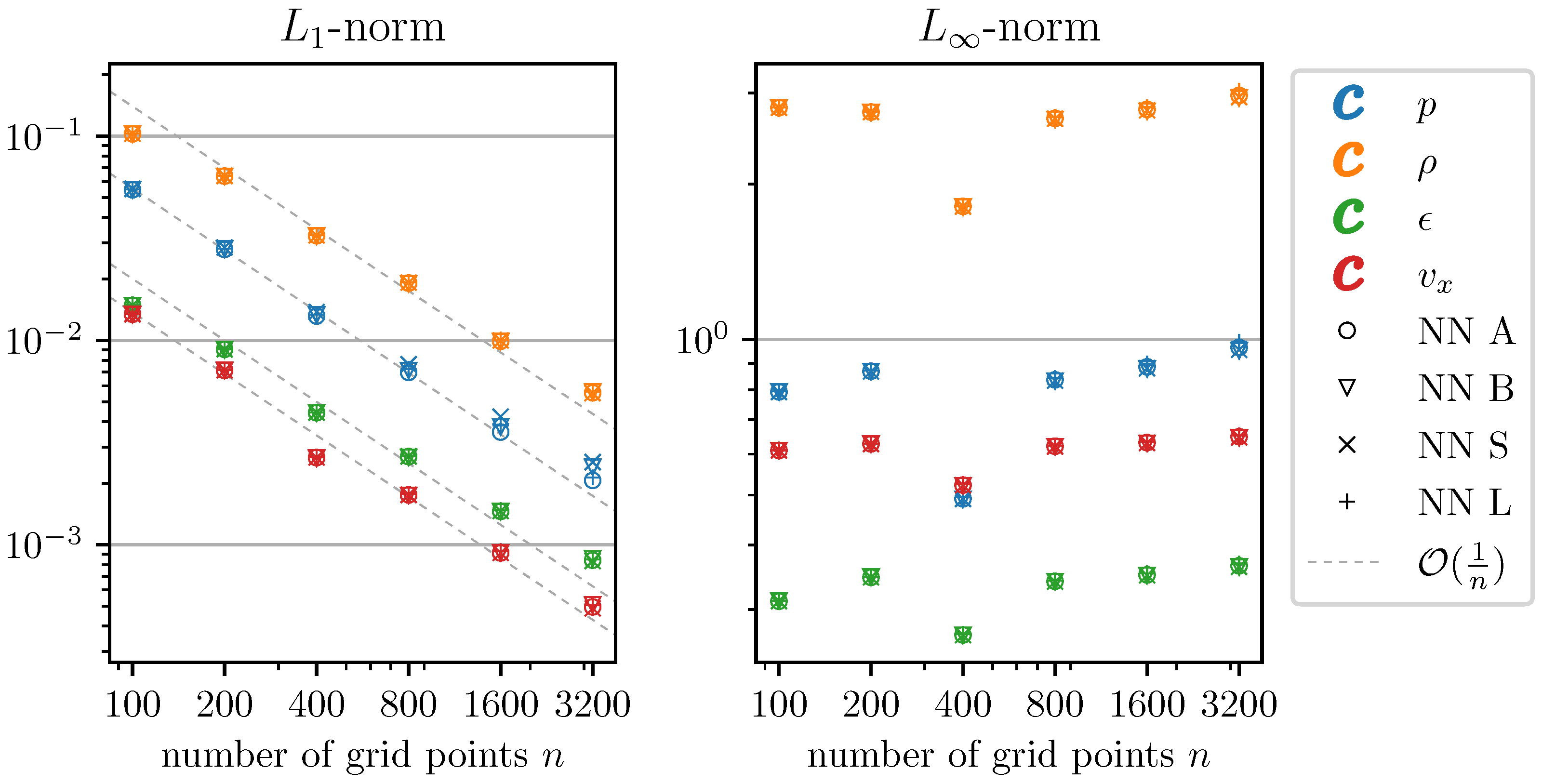
3.1. Accuracy and Timing of C2P
- The NR algorithm with the analytical EOS;
- The NR algorithm with the EOS in tabulated form;
- The NR algorithm with the NNEOSA and NNEOSB representation of the EOS;
- The NNC2PS and NNC2PL algorithms.
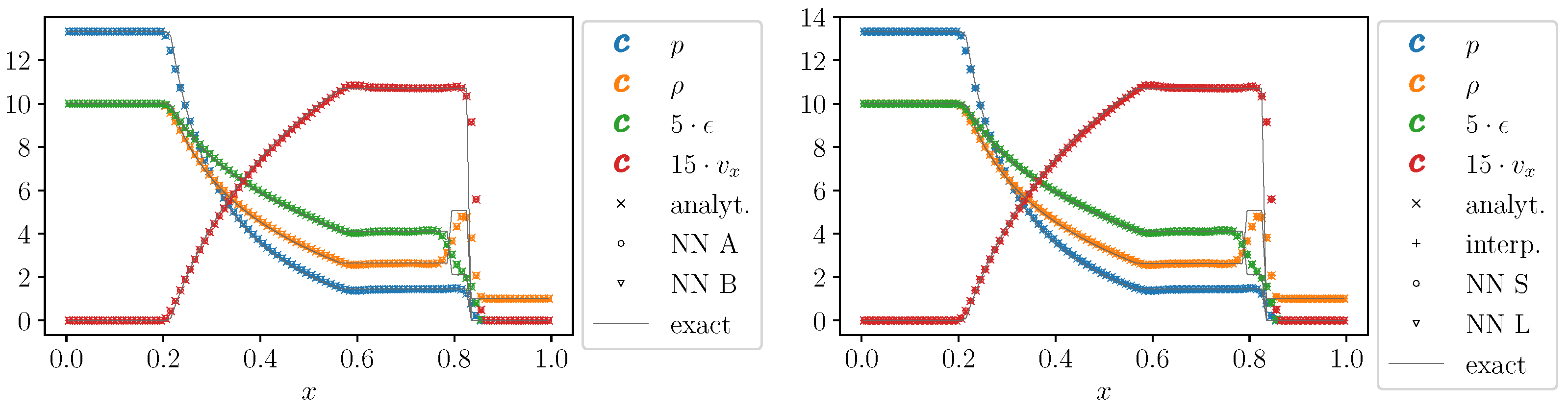
3.2. Shock Tube
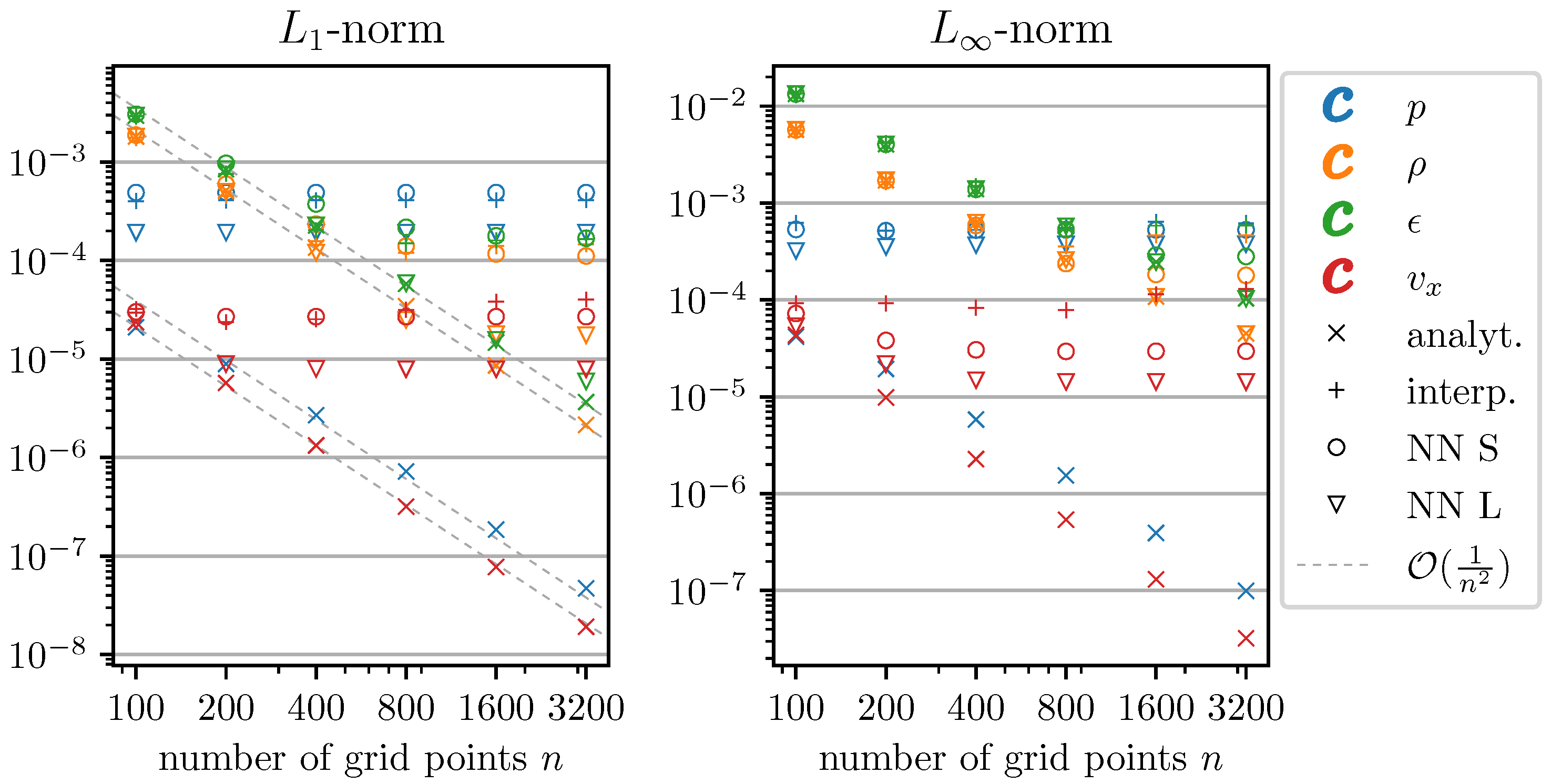
3.3. Smooth Sine-Wave
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| C2P | conservative-to-primitive |
| EOS | Equation of State |
| HRSC | High-resolution shock-capturing |
| NN | Neural network |
Appendix A. Conservative-to-Primitive Transformation
Appendix B. Examples of the Training of NN Representations
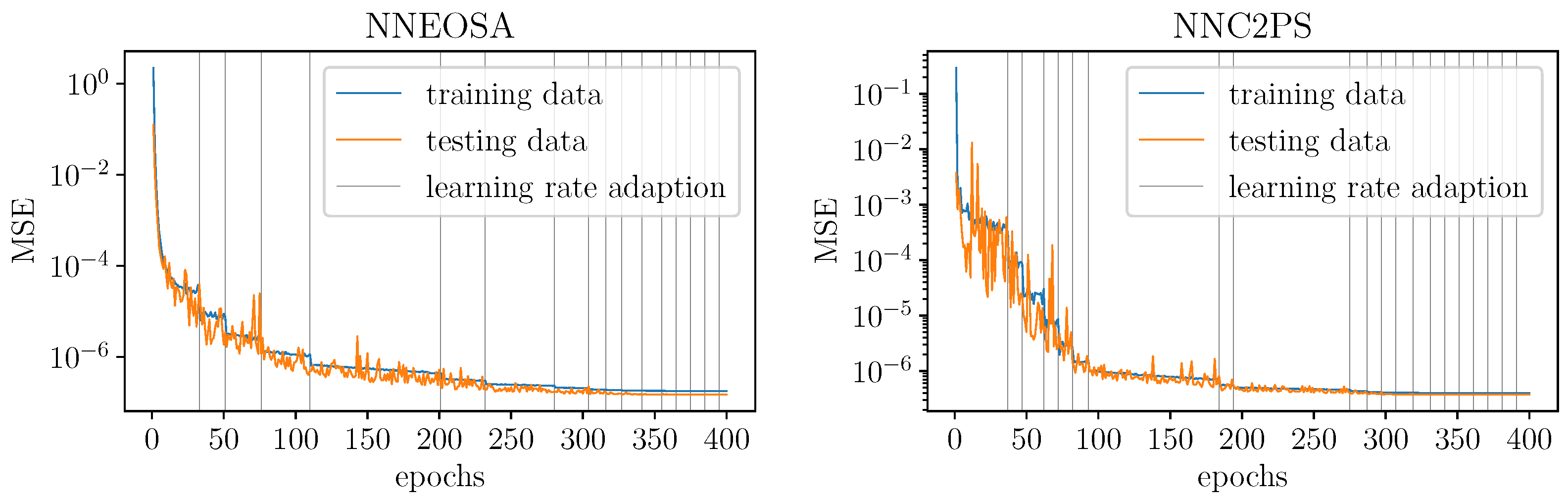
References
- Martí, J.M.; Müller, E. Numerical Hydrodynamics in Special Relativity. Living Rev. Relativ. 2003, 6, 7. [Google Scholar] [CrossRef] [PubMed]
- Timmes, F.X.; Swesty, F.D. The Accuracy, Consistency, and Speed of an Electron-Positron Equation of State Based on Table Interpolation of the Helmholtz Free Energy. Astrophys. J. Suppl. 2000, 126, 501–516. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Swesty, F.D. A Generalized equation of state for hot, dense matter. Nucl. Phys. 1991, A535, 331–376. [Google Scholar] [CrossRef]
- Anile, A.M. Relativistic Fluids and Magneto-Fluids: With Applications in Astrophysics and Plasma Physics; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar] [CrossRef]
- Toro, E.F. Riemann Solvers and Numerical Methods for Fluid Dynamics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- LeVeque, R.J. Finite Volume Methods for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Blandford, R.; Meier, D.; Readhead, A. Relativistic Jets from Active Galactic Nuclei. Ann. Rev. Astron. Astrophys. 2019, 57, 467–509. [Google Scholar] [CrossRef]
- Janka, H.T. Explosion Mechanisms of Core-Collapse Supernovae. Ann. Rev. Nucl. Part. Sci. 2012, 62, 407–451. [Google Scholar] [CrossRef]
- Font, J.A. Numerical hydrodynamics and magnetohydrodynamics in general relativity. Living Rev. Rel. 2007, 11, 7. [Google Scholar] [CrossRef]
- Radice, D.; Bernuzzi, S.; Perego, A. The Dynamics of Binary Neutron Star Mergers and GW170817. Ann. Rev. Nucl. Part. Sci. 2020, 70, 95–119. [Google Scholar] [CrossRef]
- Bernuzzi, S. Neutron Star Merger Remnants. Gen. Rel. Grav. 2020, 52, 108. [Google Scholar] [CrossRef]
- Noble, S.C.; Gammie, C.F.; McKinney, J.C.; Del Zanna, L. Primitive Variable Solvers for Conservative General Relativistic Magnetohydrodynamics. Astrophys. J. 2006, 641, 626–637. [Google Scholar] [CrossRef]
- Siegel, D.M.; Mösta, P.; Desai, D.; Wu, S. Recovery schemes for primitive variables in general-relativistic magnetohydrodynamics. Astrophys. J. 2018, 859, 71. [Google Scholar] [CrossRef]
- Kastaun, W.; Kalinani, J.V.; Ciolfi, R. Robust Recovery of Primitive Variables in Relativistic Ideal Magnetohydrodynamics. Phys. Rev. D 2021, 103, 023018. [Google Scholar] [CrossRef]
- Sekiguchi, Y.; Kiuchi, K.; Kyutoku, K.; Shibata, M. Dynamical mass ejection from binary neutron star mergers: Radiation-hydrodynamics study in general relativity. Phys.Rev. 2015, D91, 064059. [Google Scholar] [CrossRef]
- Foucart, F.; O’Connor, E.; Roberts, L.; Kidder, L.E.; Pfeiffer, H.P.; Scheel, M.A. Impact of an improved neutrino energy estimate on outflows in neutron star merger simulations. Phys. Rev. 2016, D94, 123016. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Hotokezaka, K.; Fromm, S.A.; Bernuzzi, S.; Roberts, L.F. Binary Neutron Star Mergers: Mass Ejection, Electromagnetic Counterparts and Nucleosynthesis. Astrophys. J. 2018, 869, 130. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Breschi, M.; Daszuta, B.; Endrizzi, A.; Logoteta, D.; Nedora, V.; Perego, A.; Radice, D.; Schianchi, F.; Zappa, F.; et al. Accretion-induced prompt black hole formation in asymmetric neutron star mergers, dynamical ejecta and kilonova signals. Mon. Not. Roy. Astron. Soc. 2020, 497, 1488–1507. [Google Scholar] [CrossRef]
- Nedora, V.; Bernuzzi, S.; Radice, D.; Daszuta, B.; Endrizzi, A.; Perego, A.; Prakash, A.; Safarzadeh, M.; Schianchi, F.; Logoteta, D. Numerical Relativity Simulations of the Neutron Star Merger GW170817: Long-Term Remnant Evolutions, Winds, Remnant Disks, and Nucleosynthesis. Astrophys. J. 2021, 906, 98. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA; London, UK, 2016. [Google Scholar]
- Mehta, P.; Bukov, M.; Wang, C.H.; Day, A.G.R.; Richardson, C.; Fisher, C.K.; Schwab, D.J. A high-bias, low-variance introduction to Machine Learning for physicists. Phys. Rep. 2019, 810, 1–124. [Google Scholar] [CrossRef] [PubMed]
- Schmidhuber, J. Deep Learning in Neural Networks: An Overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems 32; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E., Garnett, R., Eds.; Curran Associates, Inc.: New York, NY, USA, 2019; pp. 8024–8035. [Google Scholar]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- O’Connor, E.; Ott, C.D. A new open-source code for spherically symmetric stellar collapse to neutron stars and black holes. Class. Quantum Gravity 2010, 27, 114103. [Google Scholar] [CrossRef]
- Martí, J.M.; Müller, E. The analytical solution of the Riemann problem in relativistic hydrodynamics. J. Fluid Mech. 1994, 258, 317–333. [Google Scholar] [CrossRef]
- Mach, P. Analytic solutions of the Riemann problem in relativistic hydrodynamics and their numerical applications. Acta Phys. Pol. Proc. Suppl. 2009, 2, 575. [Google Scholar]
- Harten, A.; Lax, P.D.; van Leer, B. On Upstream Differencing and Godunov-Type Schemes for Hyperbolic Conservation Laws. SIAM Rev. 1983, 25, 35–61. [Google Scholar] [CrossRef]
- Wilson, J.R.; Mathews, G.J. Relativistic Numerical Hydrodynamics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef][Green Version]
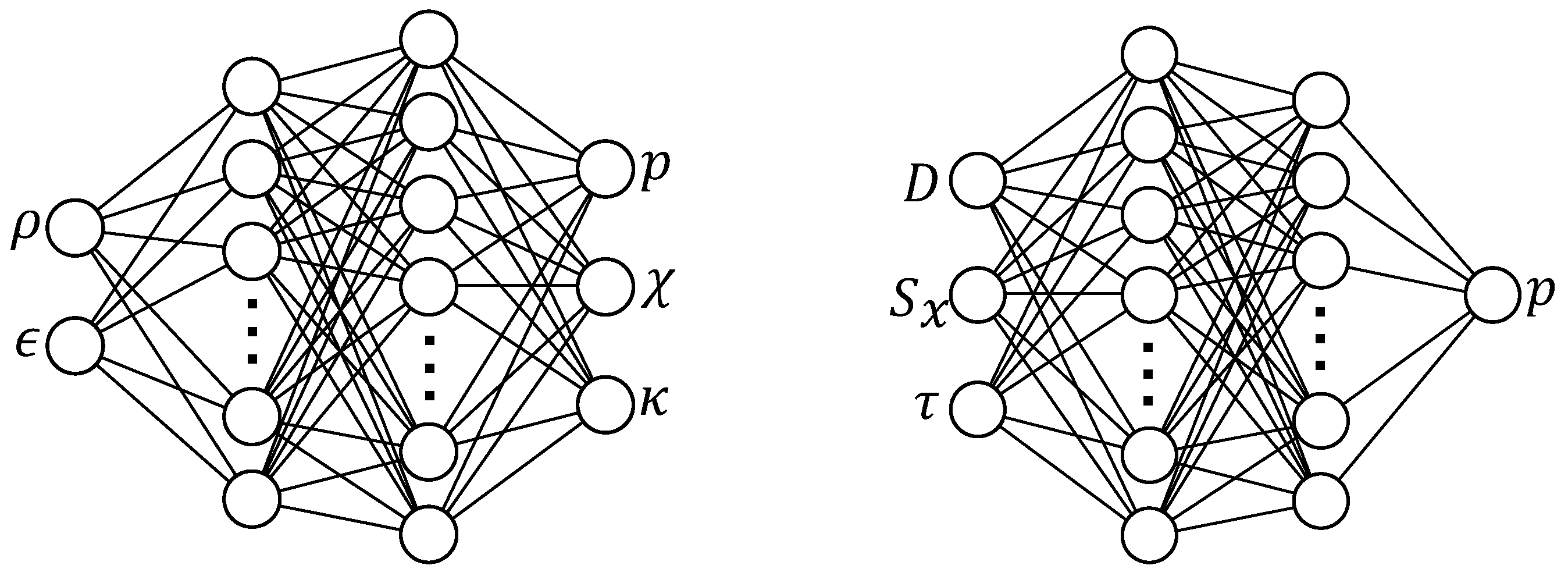
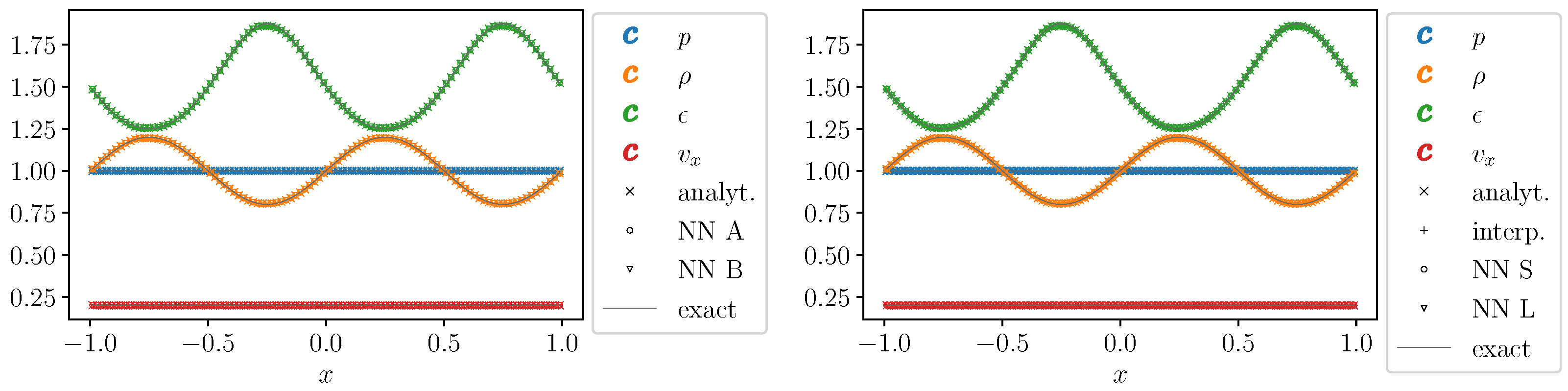


| Network | Size of H.L. | Error | Error | Error | ||||
|---|---|---|---|---|---|---|---|---|
| H.L. 1 | H.L. 2 | |||||||
| NNEOSA | 600 | 300 | ||||||
| NNEOSB | 400 | 600 | ||||||
| NNC2PS | 600 | 200 | - | - | - | - | ||
| NNC2PL | 900 | 300 | - | - | - | - | ||
| Grid Size | Analyt. | Interp. | NNEOSA | NNEOSB | NNC2PS | NNC2PL | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| [ s] | [ s] | [ s] | acc. | [ s] | acc. | [ s] | acc. | [ s] | acc. | |
| 100 | ||||||||||
| 200 | ||||||||||
| 400 | ||||||||||
| 800 | ||||||||||
| 1600 | ||||||||||
| 3200 | ||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dieselhorst, T.; Cook, W.; Bernuzzi, S.; Radice, D. Machine Learning for Conservative-to-Primitive in Relativistic Hydrodynamics. Symmetry 2021, 13, 2157. https://doi.org/10.3390/sym13112157
Dieselhorst T, Cook W, Bernuzzi S, Radice D. Machine Learning for Conservative-to-Primitive in Relativistic Hydrodynamics. Symmetry. 2021; 13(11):2157. https://doi.org/10.3390/sym13112157
Chicago/Turabian StyleDieselhorst, Tobias, William Cook, Sebastiano Bernuzzi, and David Radice. 2021. "Machine Learning for Conservative-to-Primitive in Relativistic Hydrodynamics" Symmetry 13, no. 11: 2157. https://doi.org/10.3390/sym13112157
APA StyleDieselhorst, T., Cook, W., Bernuzzi, S., & Radice, D. (2021). Machine Learning for Conservative-to-Primitive in Relativistic Hydrodynamics. Symmetry, 13(11), 2157. https://doi.org/10.3390/sym13112157







