Effects of the Tensor Force on the Ground Properties of Zr Isotopes

Abstract

The effects of the tensor force on the ground properties of Zr isotopes are studied in the framework of the Skyrme–Hartree–Fock approach. It is found that the tensor force strongly affects the ground state energies and the geometric symmetry properties, in particular for those isotopes near $N=60$ region. The effects are attributed to the fact that the tensor force enlarges the spin and pseudospin symmetry breaking and therefore results in a ∼2 MeV sub-shell gap between $d_{3/2}$ and $s_{1/2}$ single-particle levels.

1. Introduction

Although the tensor force has been introduced into the nuclear force by Yukawa when he proposed the meson exchange potential [1], it had been neglected for a long time in the effective interactions [2]. It was not until recent decades that the tensor force has regained tremendous interests due to its important role in the shape and magic number of atomic nuclei [3]. It was pointed out that the tensor force between two nucleons is repulsive when they are in the same spin direction whereas it is attractive when they are in different spin direction [3]. Such a feature affects the spin-orbit splitting and therefore changes the single-particle energies of the nuclei. The mean-field approaches use independent particle approximation that express the state of nuclei as a Slater determinant of single-particle levels, therefore the nuclear force can be expressed as low order of density matrix of reference states. The Skyrme interaction [4,5] is a widely used effective interaction model with zero-range density dependent force.

The tensor force has also been included in the existing Skyrme interactions [6,7,8]. The contribution of the nucleon–nucleon tensor interaction to single-particle energies with zero-range Skyrme potentials has been calculated in Ref. [6]. The Skx Skyrme parameters including the zero-range tensor terms with strengths calibrated to the finite-range results are refitted to nuclear properties as Skxta and Skxtb. The fits allow the zero-range proton-neutron tensor interaction as calibrated to the finite-range potential results, which gives the observed change in the single-particle gap $\epsilon \left(h_{11/2}\right)-\epsilon \left(g_{9/2}\right)$ going from ${}^{114}$Sn to ${}^{132}$Sn. Sets of ${\mathrm{T}}_{\mathrm{ij}}$ interactions was proposed in the Skyrme energy functional and the impacts of the tensor terms was analyzed on a large variety of observables in spherical mean-field calculations [7]. In Ref. [8], a new strategy of fitting the coupling constants in the Skyrme energy density functional was proposed, which shifts attention from the ground-state bulk to the single-particle properties by considering the isoscalar spin-orbit interaction and the tensor interaction [8]. It was demonstrated that the new strategy considerably and systematically improves basic single-particle properties including spin-orbit splittings and magic-gap energies. Based on $abinitio$ relativistic Brueckner–Hartree–Fock calculations for neutron-proton drops, SAMi-T was proposed to include the tensor term in the Skyrme functional to give standard nuclear properties as well as for spin and spinisospin properties [9]. In addition, there are similar strategies to introduce the tensor force in the finite-range Gogny [10] and M3Y interactions [11]. One notes that in the aforementioned work, the other parameters are refitted as well as the tensor parameters. Thus, it is difficult to know that whether the change of calculation results is pure from the tensor effect or not.

It is worth noting that there are two sets of parameters, SLy5 + T [12] and SIII + T [13], in which only the tensor force parameters are adjusted while the other Skyrme parameters are kept. Such kind of strategy can exhibit directly the tensor force effects. In Ref. [12], the parameters of the tensor force in SLy5 + T are fitted from the single-particle states in the N = 82 isotones and Z = 50 isotopes and the experimental isospin dependence of the spin-orbit splitting in these nuclei is very well accounted for when the tensor interaction is introduced. In Ref. [13], the role of the tensor part of the Skyrme interaction to the Hartree–Fock spin-orbit splitting in spherical spin unsaturated nuclei was reanalyzed based on SIII interaction. They made a new fit to the parameters of the tensor contribution to the spin-orbit coupling using data on $Z=82$ isotopes and $N=82$ isotones. The tensor force makes a dramatic difference to the single-particle energy difference between the $h_{11/2}$ and $g_{7/2}$ single-particle levels as well as the $i_{13/2}$ and $h_{9/2}$ single-particle levels. In both cases the calculation with the addition of the tensor force give a good description of the experimental data.

Recently, axial Hartree–Fock (HF) calculations using the semirealistic interaction M3Y-P6 have been carried out for Zr isotopes to focus on the role of the tensor force [14]. Specific attention has been paid to how the tensor component of the interaction affects the shape evolution in the Zr isotopes. There, spherical shapes are obtained for ${}^{86-96}$Zr and prolate deformations are obtained for ${}^{98-112}$Zr. However, as mentioned above, it is difficult to clarify how the tensor force affects the deformation of Zr isotopes with the M3Y interaction since the other parameters are refitted as well as the tensor parameters. Moreover, there are divergences shape evolution of Zr isotopes in the calculations without tensor contributions [15,16].

Therefore, the aim of this paper is to investigate the effects of tensor force on the ground properties of Zr isotopes, including the binding energies, the geometric symmetry properties (i.e., deformations), and the single-particle energy levels. We will adopt the deformed Skyrme–Hartree–Fock (SHF) approach [2,5,17] with SLy5 [12,18] and SIII [13,19] interactions.

The paper is organized as follows. In Section 2, a brief summary of the Skyrme interaction with the tensor force is given. The obtained results of the potential energy surfaces as well as the single-particle energy levels and the effects of the tensor force on them will be discussed in Section 3. Finally, a summary will be given in Section 4.

2. Theoretical Framework

The main purpose of the present work is to study the tensor effects on the binding energy and deformation of Zr isotopes in the framework of Skyrme–Hartree–Fock (SHF) approach [2,5,17].

The Skyrme effective interaction of two-body tensor force is written as [5,20]

$$\begin{array}{cc}\hfill V_T\left({\mathit{r}}_1,{\mathit{r}}_2\right)& =\frac{T}{2}\{\left[\left({\mathit{\sigma }}_1·{\mathit{P}}^{\prime }\right)\left({\mathit{\sigma }}_2·{\mathit{P}}^{\prime }\right)-\frac{1}{3}\left({\mathit{\sigma }}_1·{\mathit{\sigma }}_2\right){\mathit{P}}^{\prime 2}\right]\delta \left(\mathit{r}\right)\hfill \\ \hfill & +\delta \left(\mathit{r}\right)\left[\left({\mathit{\sigma }}_1·\mathit{P}\right)\left({\mathit{\sigma }}_2·\mathit{P}\right)-\frac{1}{3}\left({\mathit{\sigma }}_1·{\mathit{\sigma }}_2\right){\mathit{P}}^2\right]\}\hfill \\ \hfill & +U_{\mathrm{s}.\mathrm{o}}^{\left(q\right)}\{\left({\mathit{\sigma }}_1·{\mathit{P}}^{\prime }\right)\delta \left(\mathit{r}\right)\left({\mathit{\sigma }}_1·\mathit{P}\right)\hfill \\ \hfill & -\frac{1}{3}\left({\mathit{\sigma }}_1·{\mathit{\sigma }}_2\right)\left[{\mathit{P}}^{\prime }·\delta \left(\mathit{r}\right)\mathit{P}\right]\},\hfill \end{array}$$

(1)

where $\mathit{r}={\mathit{r}}_1-{\mathit{r}}_2$, ${\mathit{\sigma }}_i$ is the Pauli spin matrices for nucleons labeled as i = 1 or 2 and $\delta \left(\mathit{r}\right)$ is the Dirac delta function. The momentum operator $\mathit{P}=({\mathbf{\nabla }}_1-{\mathbf{\nabla }}_2)/\left(2i\right)$ acts on the right while ${\mathit{P}}^{\prime }=-({\mathbf{\nabla }}_1-{\mathbf{\nabla }}_2)/\left(2i\right)$ on the left.

The spin-orbit term $U_{\mathrm{s}.\mathrm{o}}^{\left(q\right)}$ reads [12]

$$U_{\mathrm{s}.\mathrm{o}}^{\left(q\right)}=\frac{W_0}{2r_q}\left(2\frac{d{\rho }_q}{d{r}_q}+\frac{d{\rho }_{q^{\prime }}}{d{r}_q}\right)+\left(\alpha \frac{J_q}{r_q}+\beta \frac{J_{q^{\prime }}}{r_q}\right),$$

(2)

where $W_0$ is the spin-orbit interaction strength for the nucleons as given in Refs. [5,21] and q and $q^{\prime }$ label for different isospin components. The spin-orbit densities for isospin component q,

$$\begin{array}{cc}\hfill J_q\left(r\right)& =\frac{1}{4\pi r_q^3}{\displaystyle \sum _i}{v}_i^2\left(2j_i+1\right)\hfill \\ \hfill & \times \left[j_i\left(j_i+1\right)-l_i\left(l_i+1\right)-\frac{3}{4}\right]R_i^2\left(r_q\right),\hfill \end{array}$$

(3)

is calculated from the corresponding occupation probability of each orbital $v_i^2$ and the radial part of the wave function $R_i\left(r_q\right)$. One notes that the first term of Equation (2) comes from the Skyrme spin-orbit interaction, whereas the second term comes from both the central exchange and the tensor contributions, that is, $\alpha ={\alpha }_C+{\alpha }_T$ and $\beta ={\beta }_C+{\beta }_T$ with [12]

$$\begin{array}{cc}\hfill & {\alpha }_C=\frac{1}{8}\left(t_1-t_2\right)-\frac{1}{8}\left(t_1{x}_1+t_2{x}_2\right),{\alpha }_T=\frac{5}{12}U,\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & {\beta }_C=-\frac{1}{8}\left(t_1{x}_1+t_2{x}_2\right),{\beta }_T=\frac{5}{24}(T+U).\hfill \end{array}$$

(5)

Beyond the nucleonic mean-field, pairing forces are taken into account within BCS approximation. We use a zero-range, density-dependent pairing force,

$$V=V_0\left[1-{\left(\frac{\rho \left(\mathit{r}\right)}{{\rho }_0}\right)}^{\gamma }\right]\delta \left(\mathit{r}\right),$$

(6)

with $V_0=680$ MeV ${\mathrm{fm}}^3$, $\gamma =1$, and ${\rho }_0=0.16$ fm${}^{-3}$ for the $Z=50$ isotopic chain [22].

In the calculations, to investigate the geometric symmetry properties of the nuclei, we assume axially-symmetric mean fields and the properties of axially-deformed nuclei are studied in cylindrical coordinates [23]. The optimal quadrupole deformation parameter

$${\beta }_2^{\left(q\right)}=\sqrt{\frac{\pi }{5}}\frac{{⟨2z^2-r^2⟩}_q}{{⟨z^2+r^2⟩}_q}$$

(7)

is calculated by minimizing the energy density functional. The absolute value of ${\beta }_2$ reflects the degree of axial deformation, in which ${\beta }_2=0$ indicates a spherical shape, a positive ${\beta }_2$ reflects a prolate shape along the z axis, and a negative ${\beta }_2$ reflects an oblate shape.

3. Results and Discussion

We investigate the Zr isotopes with even neutron number from $N=38$ to 72 by performing the deformed SHF + BCS calculations with and without tensor forces using the effective interactions SLy5 [12,18] and SIII [13,19].

Figure 1 shows the obtained potential energy surface as a function of deformation parameter ${\beta }_2$ for the selected isotopes ${}^{80}$Zr, ${}^{90}$Zr, ${}^{98}$Zr, and ${}^{104}$Zr as examples. One observes that the results of SLy5 (SLy5 + T) and SIII (SIII + T) parameters are more or less similar, except for the results of SLy5 + T and SIII + T in ${}^{104}$Zr, which is the last bound nucleus in the SIII + T calculation. We further checked the neighboring isotopes and also found that the potential energy surfaces around the minima obtained by the two sets of tensor parameters are quite similar. This indicates that the peculiar case in ${}^{104}$Zr” is not a systematic error in the calculations. Therefore, we will mainly focus on the results of SLy5 and SLy5 + T calculations to investigate the effects of the tensor force in Zr isotopes.

Figure 1. Potential energy surfaces as functions of deformation parameter ${\beta }_2$ for the selected isotopes ${}^{80}$Zr, ${}^{90}$Zr, ${}^{98}$Zr, and ${}^{104}$Zr calculated by the effective interactions SLy5 and SIII and with and without the tensor forces. All the energies are normalized with respect to the results of SLy5 calculation at ${\beta }_2=0$. The shifted energies have been labeled in each panel.

One observes from Figure 1 the tensor force plays different roles for different Zr isotopes. For ${}^{80}$Zr, the tensor force affects little at ${\beta }_2\approx 0$, but reduce the energy at large deformation near ${\beta }_2=0.4$. However, for ${}^{90}$Zr and ${}^{98}$Zr, the tensor force strongly affects the energy of spherical part. The energy correction is even up to ∼8 MeV. As a consequence, the shape of the ground state of ${}^{98}$Zr has been modified from oblate to spherical. This indicates that the tensor force can strongly affects the nuclear geometric symmetry properties.

The details of the calculated ground energies of Zr isotopes from $A=78$ to 112 are listed in Table 1. The corrections of ground state energies by the tensor force $\Delta E_T$ are defined as the energy difference between the calculations without and with the tensor force. They are all positive. Namely, the tensor force makes the nuclei more bound. They increase sharply from ${}^{86}$Zr to ${}^{88}$Zr and keep higher than 5 MeV in heavier isotopes. This indicates that the tensor force has a great impact on the energy shifts of Zr isotopes. This conclusion is consistent with that in the systematic investigation by the axial Hartree–Fock calculations with the M3Y-P6 semirealistic interaction in Ref. [14].

Table 1. Ground energies and deformations of Zr isotopes with the mass number from $A=78$ to 112 calculated by the effective interactions SLy5 and SIII and with and without the tensor forces in comparison with the available experimental data from Ref. [24]. The $\Delta E_T$ and $\Delta {\beta }_{2T}$ are the energy and the quadruple deformation corrections caused by the tensor force, respectively. Note that the ${}^{104}$Zr is the last bound nucleus in the SIII + T calculation.

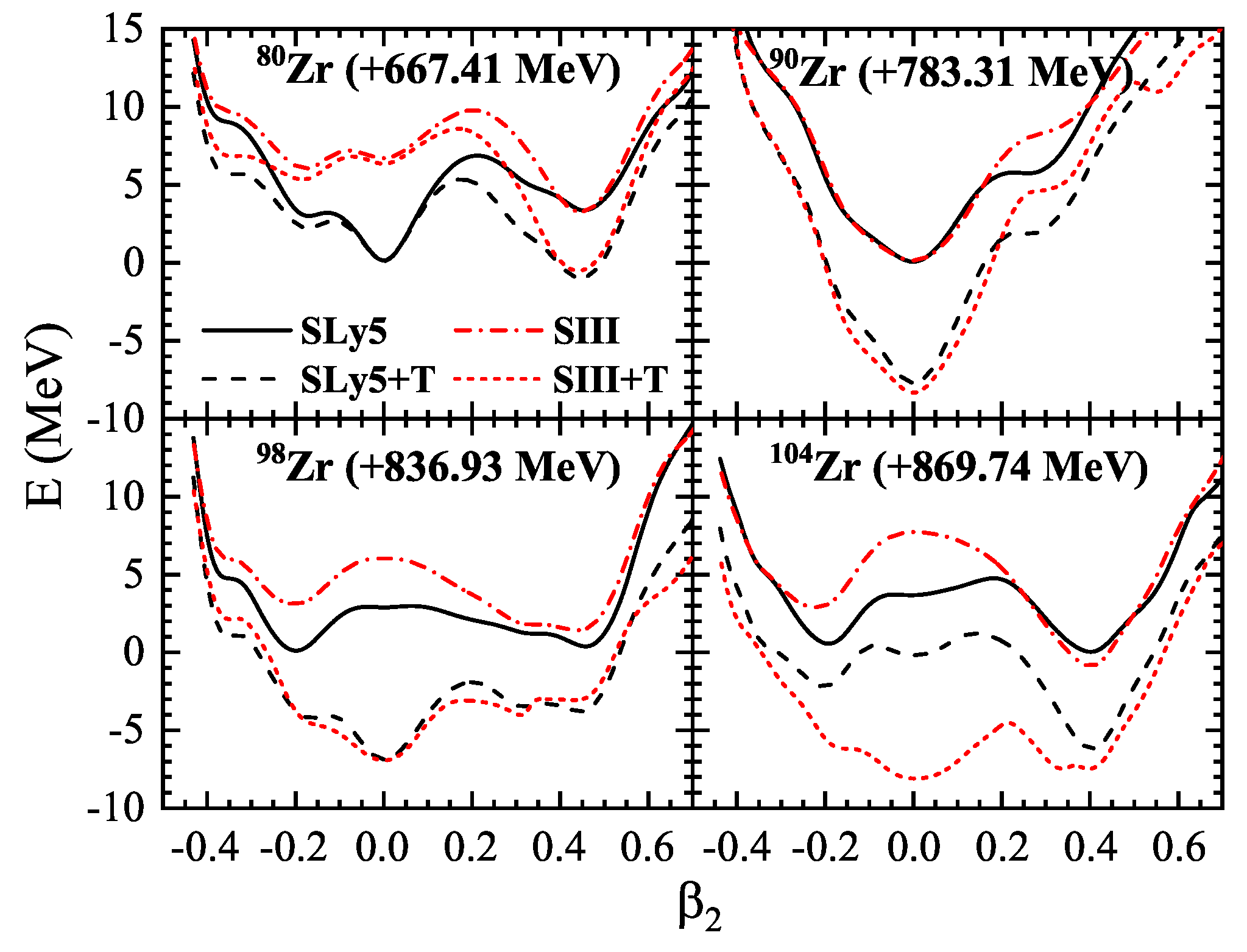
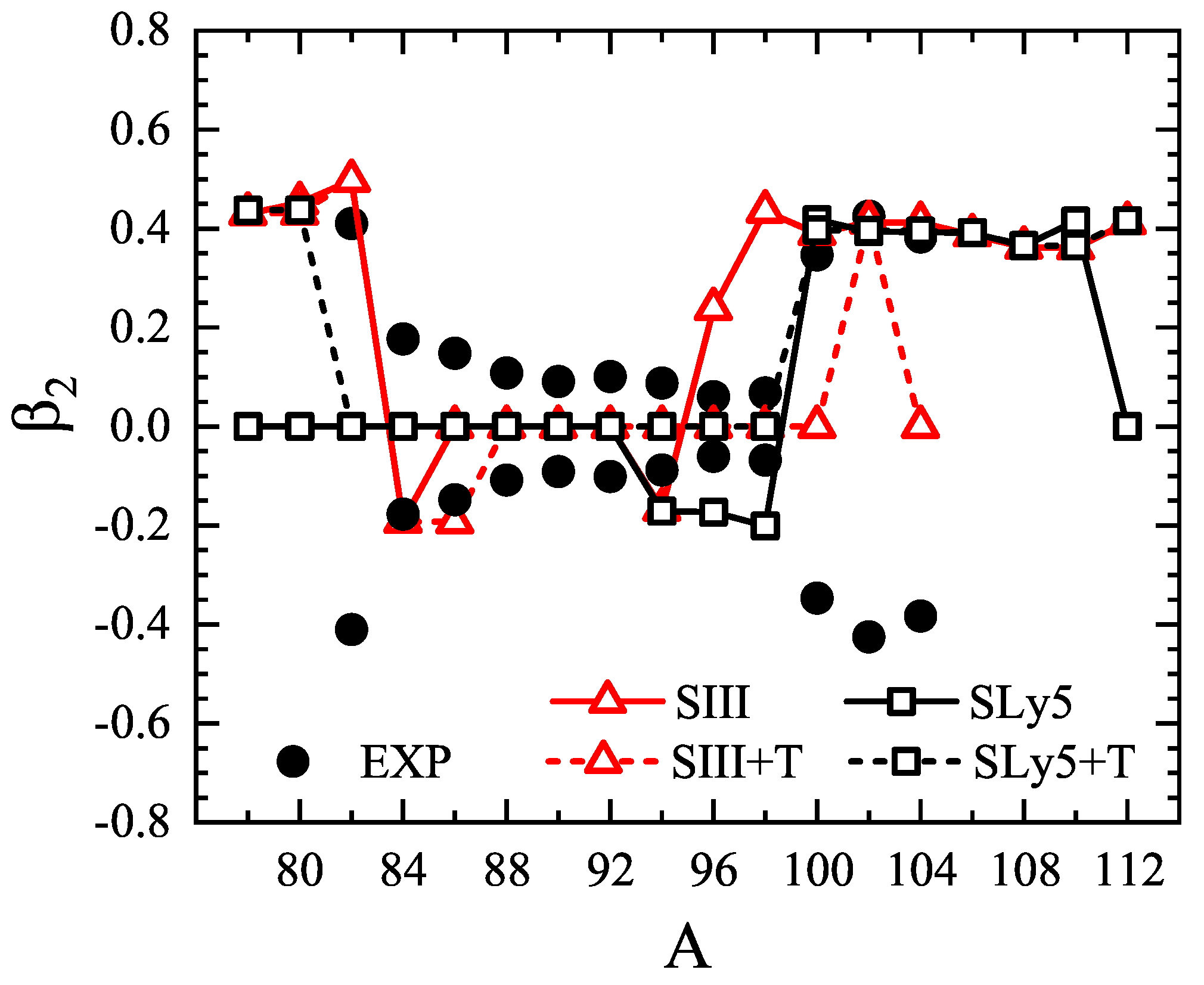
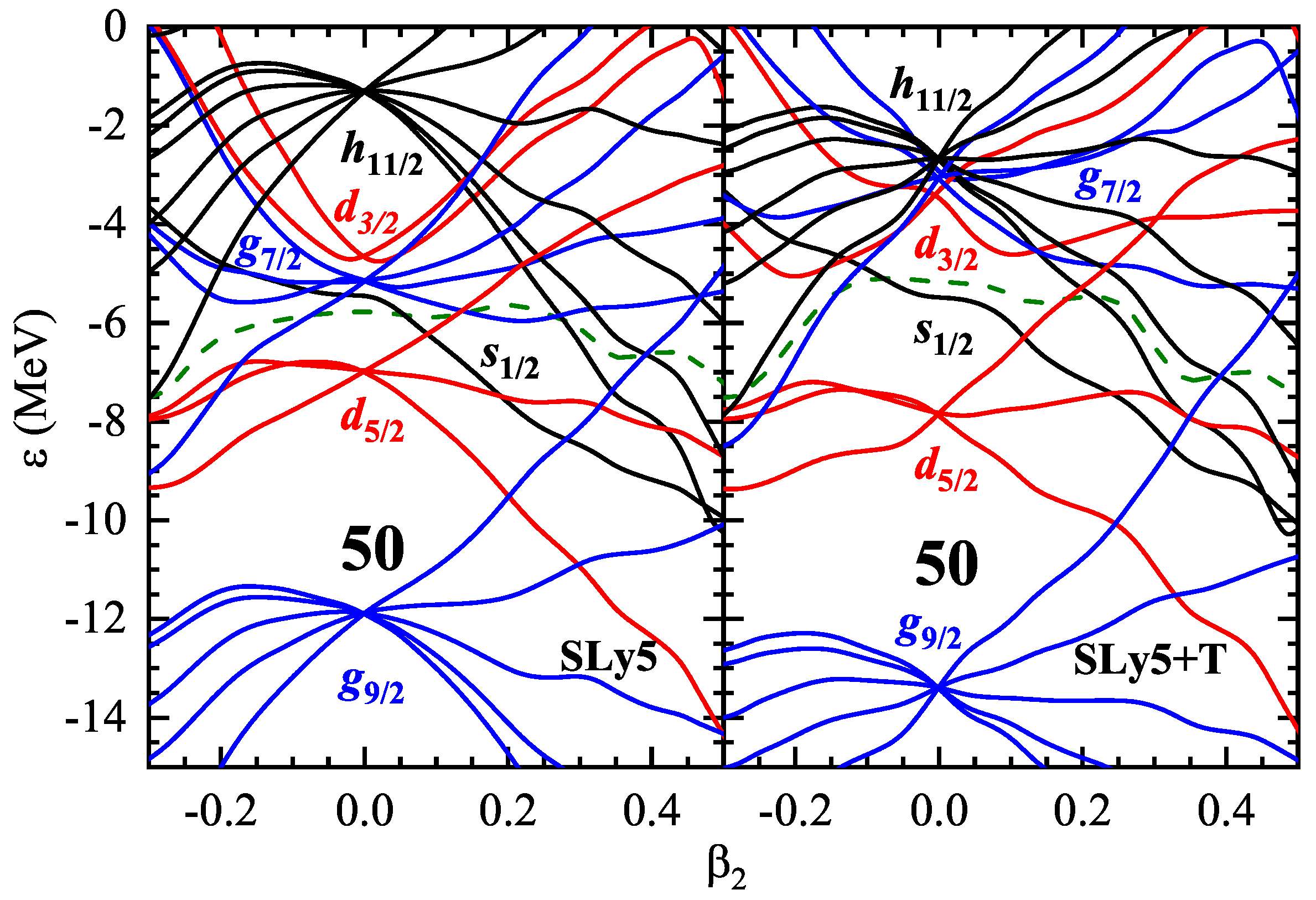
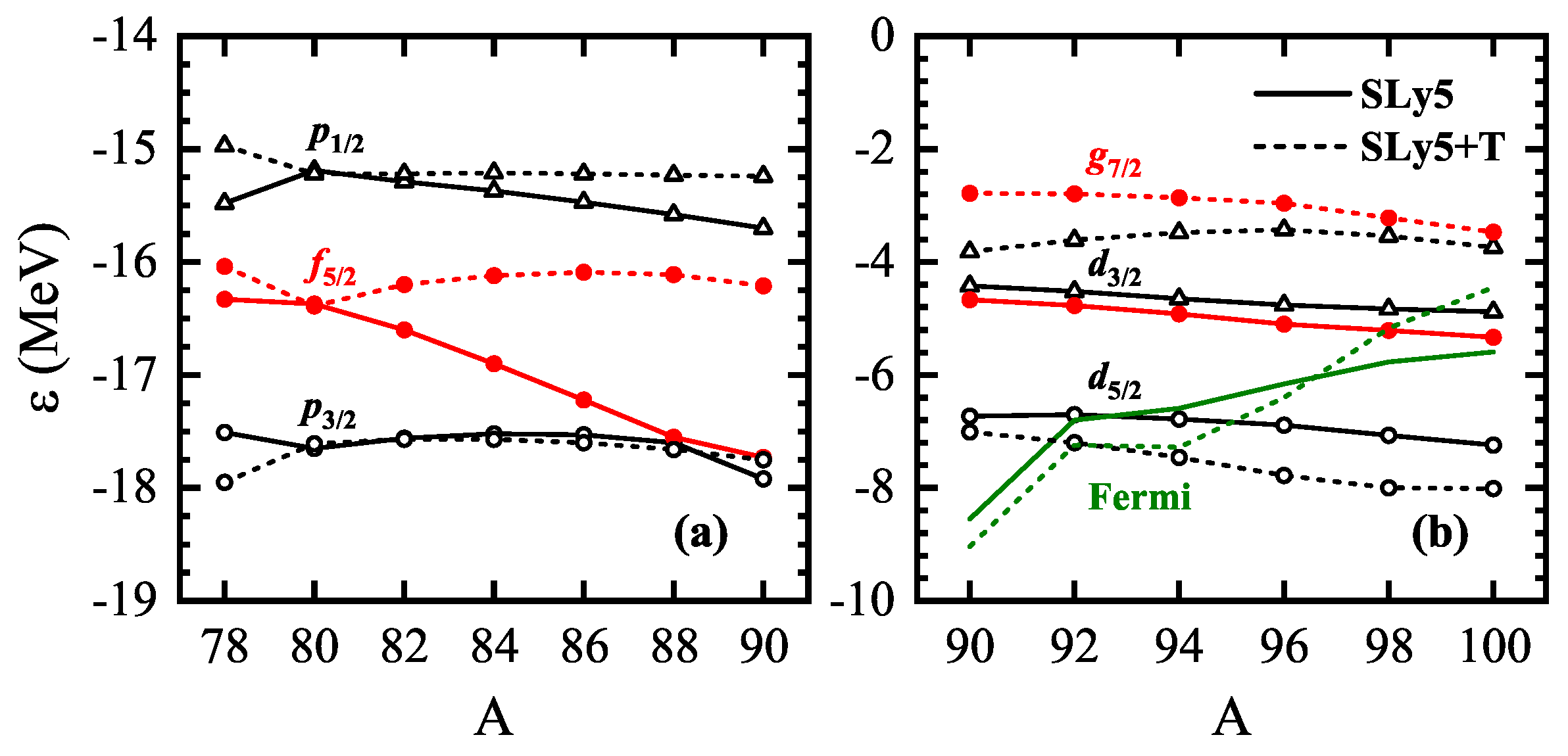
A	EXP		SIII		SIII + T		ΔET (MeV)	Δβ2T	SLy5		SLy5 + T		ΔET (MeV)	Δβ2T
	E (MeV)	|β2|	E (MeV)	β2	E (MeV)	β2			E (MeV)	β2	E (MeV)	β2
78	−639.132		−636.427	0.430	−639.855	0.431	3.428	−0.001	−637.427	0.000	−640.661	0.437	3.234	−0.437
80	−669.800		−664.182	0.452	−667.957	0.431	3.775	0.021	−667.414	0.000	−668.419	0.438	1.005	−0.438
82	−694.130	0.410	−	0.497	−692.171	0.497	3.824	0.000	−692.851	0.000	−693.300	0.000	0.449	0.000
84	−718.116	0.177	−712.633	−0.191	−715.485	−0.192	2.852	0.001	−716.920	0.000	−718.363	0.000	1.443	0.000
86	−740.804	0.148	−736.827	0.000	−740.734	−0.193	3.907	0.193	−739.946	0.000	−742.914	0.000	2.968	0.000
88	−762.608	0.108	−760.372	0.000	−766.122	0.000	5.750	0.000	−762.058	0.000	−767.126	0.000	5.068	0.000
90	−783.810	0.091	−783.208	0.000	−791.750	0.000	8.542	0.000	−783.312	0.000	−791.125	0.000	7.813	0.000
92	−799.664	0.101	−795.625	0.000	−805.141	0.000	9.516	0.000	−796.824	0.000	−805.279	0.000	8.455	0.000
94	−814.604	0.088	−808.942	−0.167	−818.705	0.000	9.763	−0.167	−810.369	−0.171	−819.428	0.000	9.059	−0.171
96	−828.672	0.060	−821.753	0.238	−832.329	0.000	10.576	0.238	−823.883	−0.173	−833.578	0.000	9.695	−0.173
98	−840.938	0.068	−835.513	0.435	−843.911	0.000	8.398	0.435	−836.928	−0.201	−843.916	0.000	6.988	−0.201
100	−852.215	0.347	−848.815	0.390	−855.218	0.000	6.403	0.390	−848.504	0.418	−853.926	0.397	5.422	0.021
102	−863.532	0.425	−860.238	0.413	−867.362	0.414	7.124	−0.001	−859.642	0.394	−865.111	0.396	5.469	−0.002
104	−873.808	0.383	−870.635	0.412	−877.852	0.000	7.217	0.412	−869.736	0.393	−875.940	0.395	6.204	−0.002
106	−882.768		−879.727	0.387					−879.096	0.391	−884.576	0.392	5.480	−0.001
108	−891.756		−888.413	0.362					−887.900	0.365	−892.488	0.366	4.588	−0.001
110	−899.470		−896.550	0.361					−894.903	0.415	−900.218	0.365	5.315	0.050
112	−906.528		−902.629	0.412					−901.789	0.000	−907.003	0.416	5.214	−0.416

In addition, we plot the ground state deformation ${\beta }_2$ of Zr isotope as a function of mass number in Figure 2. The corresponding ${\beta }_2$ values are also listed in Table 1. From Table 1 and Figure 2, one also finds that the deformation can be also affected by the tensor force. In some cases, the modifications are rather large even up to ∼$-0.4$ (cf. ${}^{78,80,112}$Zr in the SLy5 calculations). The modifications can improve the theoretical descriptions for some nuclei. For example, the shapes of ${}^{94-98}$Zr are changed from oblate in the SLy5 calculations to the spherical in the SLy5 + T calculations, becoming more closer to the experimental values. There are still some deviations between the theoretical and experimental results. The reasons might be attributed to that the shape fluctuations are not taken into account in the mean-field calculations.

Figure 2. The deformation parameter ${\beta }_2$ of Zr isotopes with the mass number from $A=78$ to 112 calculated by the effective interactions SLy5 and SIII and with and without the tensor forces in comparison with the available experimental data from Ref. [24]. Note that here for the experimental data we present both the positive and negative values, as their signs are not determined yet.

To understand the tensor effects on the binding energies and deformations, we show in Figure 3 the obtained neutron single-particle levels as a function of ${\beta }_2$ for the ${}^{98}$Zr calculated by SLy5 and SLy5 + T. The Fermi surface of ${}^{98}$Zr is close to $s_{1/2}$, $g_{7/2}$, and $d_{3/2}$ levels in the SLy5 result, thus the neutrons could occupy the deformed levels of $g_{7/2}$ and $d_{3/2}$ orbits under the pairing force. This is consistent with the fact that the shape of the ground state of ${}^{98}$Zr is deformed (cf. Figure 1). However, as seen from Figure 3b, the tensor force promotes the energies of $g_{7/2}$ and $d_{3/2}$ orbits. Namely, the tensor force not only enlarges the spin symmetry breaking ($d_{5/2}$ and $d_{3/2}$) but also enlarges the pseudospin symmetry breaking ($d_{5/2}$ and $g_{7/2}$). This leaves a ∼2 MeV energy gap between $d_{3/2}$ and $s_{1/2}$ and a sub-shell at $N=58$. As a consequence, the probability for neutrons occupying levels of $g_{7/2}$ and $d_{3/2}$ orbits is strongly suppressed and driven the ground state of ${}^{98}$Zr to the spherical shape as shown in Figure 1.

Figure 3. Partial neutron single-particle levels as a function of ${\beta }_2$ for ${}^{98}$Zr calculated by SLy5 and SLy5 + T. The Fermi surface is plotted in dashed line. The corresponding quantum numbers for the spherical case are labeled around ${\beta }_2=0$. The magic numbers in the spherical case and for finite deformation are also indicated. While the tensor force pushes up the energies of $d_{3/2}$ and $g_{7/2}$ orbits, it reverses their order, resulting in a sub shell of ∼2 MeV sub shell above the $s_{1/2}$ orbit.

The energies of spin and pseudospin partners in Zr isotopes at ${\beta }_2=0$ are shown in Figure 4. Orbits with larger orbital angular momentum l shift more, consistent with the axial Hartree–Fock calculations with the M3Y-P6 semirealistic interaction in Ref. [14]. There might be two reasons for this phenomenon. One is that the pseudospin partners come close to the Fermi surface and have larger occupation probabilities $v_i^2$. The other one is that the pseudospin partners have larger single-particle angular momentum. Both of them could have larger contributions on the spin-orbit density $J_q$ (cf. Equation (3)) and enlarge the tensor effects.

Figure 4. The energy of the neutron single-particle state of ${}^{78-90}$Zr (a) and ${}^{90-100}$Zr (b) at sphere ${\beta }_2=0$, respectively. Note that the Fermi surfaces of ${}^{78-90}$Zr, which locate above the $p_{1/2}$ levels, are not shown.

One further notices that not only the spin partner splitting but also the pseudospin partner splitting are enlarged by the tensor force. As can be seen in Figure 4a, the energy shift caused by the tensor force in the pseudospin partner $(p_{3/2},f_{5/2})$ is even much larger than the one in the spin partner $(p_{3/2},p_{1/2})$. This indicates the pseudospin symmetry is broken much more than the spin symmetry. Such effect is more significant in the larger mass region as shown in Figure 4b. The energies of $g_{7/2}$ and $d_{3/2}$ orbits, as pseudospin and spin partner of $d_{5/2}$ orbit respectively, are reversed by the tensor force, which makes a large energy gap between the Fermi surface and higher levels.

Such a rich phenomenon of single-particle levels near the Fermi surface induced by the tensor force is an important reason for the rich shape phenomenon in Zr isotopes (cf. Table 1 and Figure 2). For example, it was pointed out that the region of Zr isotopes with $A=90$–110 show a quantum phase transition phenomena and shape coexistence of prolate and triaxial shapes based on the large-scale Monte Carlo shell model calculations [25] and the interacting boson model with the configuration mixing method [26].

4. Summary

In conclusion, we have performed Skyrme–Hartree–Fock calculations to investigate the tensor effects on the ground properties for Zr isotopes. It is found that the tensor force strongly affects the potential energy surface and makes the nuclei more bound. The tensor force can strongly affect the nuclear geometric symmetry properties. The reason is attributed to the tensor force enlarging the spin and pseudospin symmetry breakings and results in a ∼2 MeV sub-shell gap between $d_{3/2}$ and $s_{1/2}$ single-particle levels in spherical deformation.

In Zr isotopes, the effects of the tensor force on the energy splitting of pseudospin partner bands are particularly important. The tensor force strongly shifts the single-particle energies of high-l orbits and therefore reverses $g_{7/2}$ and $d_{3/2}$ levels, which leads to the occurrence of a $N=60$ sub-shell gap.