Abstract
Particle Swarm Optimization (PSO) has been widely used to solve various types of optimization problems. An efficient algorithm must have symmetry of information between participating entities. Enhancing algorithm efficiency relative to the symmetric concept is a critical challenge in the field of information security. PSO also becomes trapped into local optima similarly to other nature-inspired algorithms. The literature depicts that in order to solve pre-mature convergence for PSO algorithms, researchers have adopted various parameters such as population initialization and inertia weight that can provide excellent results with respect to real world problems. This study proposed two newly improved variants of PSO termed Threefry with opposition-based PSO ranked inertia weight (ORIW-PSO-TF) and Philox with opposition-based PSO ranked inertia weight (ORIW-PSO-P) (ORIW-PSO-P). In the proposed variants, we incorporated three novel modifications: (1) pseudo-random sequence Threefry and Philox utilization for the initialization of population; (2) increased population diversity opposition-based learning is used; and (3) a novel introduction of opposition-based rank-based inertia weight to amplify the execution of standard PSO for the acceleration of the convergence speed. The proposed variants are examined on sixteen bench mark test functions and compared with conventional approaches. Similarly, statistical tests are also applied on the simulation results in order to obtain an accurate level of significance. Both proposed variants show highest performance on the stated benchmark functions over the standard approaches. In addition to this, the proposed variants ORIW-PSO-P and ORIW-PSO-P have been examined with respect to training of the artificial neural network (ANN). We have performed experiments using fifteen benchmark datasets obtained and applied from the repository of UCI. Simulation results have shown that the training of an ANN with ORIW-PSO-P and ORIW-PSO-P algorithms provides the best results than compared to traditional methodologies. All the observations from our simulations conclude that the proposed ASOA is superior to conventional optimizers. In addition, the results of our study predict how the proposed opposition-based method profoundly impacts diversity and convergence.
1. Introduction
Swarm intelligence (SI) is a subfield of artificial and natural (such as bees, ants, and fish) intelligence that studies how a group of agents might work together by utilizing self-organizing and sequencing. Simple independent agents provide the basis for emerging intelligence. SI contains a typical number of simple agents that interact with each other and their nature [1]. It is used to solve optimization problems in large search spaces that are challenging for mathematical and conventional computational techniques. Ant Colony Optimization (ACO) [2], Particle Swarm Optimization (PSO) [3], Artificial Bee Colony (ABC) [4], and Bat algorithm [5,6] are representative examples.
Particle Swarm Optimization (PSO) is widely used to find approximate solutions to problems of maximizing and minimizing numerical values that are very difficult or impossible. It is used to reduce slow convergence rate and local minima problems [7]. PSO has different numbers of particles in the population used to find optimal solutions. All particles have current velocity, current position, and personal best (Pbest) out of which the global best (gbest) is selected [8]. Particles are randomly initialized and used to verify the fitness value of each particle by using the fitness function. The values of velocity and position are updated upon each iteration. PSO Algorithm provides effective parameters to control exploration and exploitation. There are some limitations in standard PSOs such as premature convergence, local search ability, being heavily dependent on parameters settings, and being easily trapped in local optima. Researchers proposed various variants of PSOs such as adaptive parameter setting, mutation strategy [9], and opposition-based initialization in order to solve these issues. With the advent of PSO, new methods have also been proposed for solving global optimization problems in terms of solutions to the design artificial neural networks (ANNs), evolutionary computing fuzzy systems, evolutionary computing, and evolutionary computing. The PSO algorithm is commonly used to solve data classification problems, cost estimation, agriculture problems, planning, clustering engineering field problems, and real time problems.
In order to find an efficient solution in the current estimate and its corresponding opposite, they are given opposition-based learning (OBL) at the same time. This idea is inspired by real-world opposition objects and applied to an initial population that is randomly generated [10]. The opposite of each individual in the population participates in the computation of the opposite population. OBL is used to accelerate the search process of some well-known techniques of EC. The idea of OBL is applied in many ECs such as Artificial Neural Networks (ANN) [11] and Reinforcement Learning (RL) [12]; and optimization algorithms such as Bat algorithm [13], Grey Wolf Optimizer (GWO), Genetic Algorithms (GA) [14], Whale Optimization Algorithm (WOA), Differential Evolution (DE), Grasshopper optimization algorithm (GOA), Harmony Search (HS), and Particle Swarm Optimization (PSO) [15], etc.
Opposition-based learning is used to find optimal solutions and improve performance toward some optimal solutions. OBL is used in many fields such as the medical field to diagnose disease and the agriculture field to save water crop, to clarify soil, and to schedule agriculture work [16]. It also worked in the engineering field in terms of training machine tolerance processes and minimizing costs [17]. Different initialization techniques are used for initializing the initial population of the PSO algorithm. The distribution of random number generation has three main categories: quasi-random sequences [18], i.e., Sobol, Hamersley, Van der Corput, Halton, and Faure; probability sequences, i.e., Log-normal, Gamma, Beta, and Exponential; and pseudo-random sequences, i.e., Mersenne twister, Linear congruential generator, Multiply-with-carry, Threefry, and Philox [19]. Pseudo-random number generator (PRNG) is used as an initialization technique because it covers all search spaces. For a globally optimal solution, pseudo-random sequences perform better than quasi random sequences due to its variation in random number generation. We used various PRNG strategies (Mersenne twister, Linear congruential generator, Multiply-with-carry, Threefry, and Philox) for the initialization of the population.
In this paper, we proposed Philox with opposition-based PSO ranked inertia weight (ORIW-PSO-P) and Threefry with opposition-based PSO ranked inertia weight (ORIW-PSO-TF) for enhancing global search ability and balance between exploration and exploitation ability. ORIW-PSO-P and ORIW-PSO-TF combine two effective improvements: Philox and Threefry initialization with opposition-based learning and ranked inertia weight for individual particles. We have proposed the new pseudorandom initialization strategies called Philox and Threefry. PRNG-based Philox and Threefry are used to initialize the initial population, and opposite particles are generated through opposition-based learning. In addition, in this paper, the inertia weights of particles are adjusted by using opposite rank-based inertia weight used to balance exploration and exploitation. Through opposite rank-based inertia weight optimal particles that are close to the optimal position move slowly and fast-moving particles continuing far away from the optimal position of the swarm. At the same time, it enhances local and global search ability. We have compared novel techniques with basic random distribution and pseudo-random sequence families such as Mersenne twister, Linear congruential generator, and Multiply-with-carry sequence on several unimodal and multimodal benchmark functions. The experimental results showed that Philox with opposition-based PSO ranked inertia weight (ORIW-PSO-P) and Threefry with opposition-based PSO ranked inertia weight (ORIW-PSO-TF) outperform the other opposition-based particle swarm optimization algorithm ranked inertia weight (ORIW-PSO), Mersenne twister with opposition-based PSO ranked inertia weight (ORIW-PSO-MT), Linear congruential generator with opposition-based PSO ranked inertia weight (ORIW-PSO-LCG), and Multiply-with-carry with opposition-based PSO ranked inertia weight (ORIW-PSO-MWC). In this work, the design of an algorithm, a critical aspect of the symmetry concept, has been emphasized because it is very important for global optimization.
Therefore, in this paper, we propose a novel pseudo-random initialization strategy (Philox and Threefry) that uses the OBL scheme and opposition rank-based inertia weight scheme in order to overcome the drawbacks of PSO algorithms and help PSO conduct additional explorations in order to accelerate convergence. We used the proposed variants to train artificial neural networks on classification problems. In order to compare the results of the classifiers, fifteen datasets were extracted from the well known UCI repository. The results of the proposed variant are superior when compared to other variants. The main contributions of this paper are as follows:
- (1)
- Utilization of pseudo-random sequence Threefry and Philox for the initialization of the population;
- (2)
- To increase population diversity, opposition-based learning is used;
- (3)
- A novel introduction of opposition-based rank-based inertia weight in order to amplify the execution of standard PSO for the acceleration of convergence speed.
2. Literature Review
An improved PSO with OBL method by the authors in [20] is employed in particle Pbest position used to escape the local optima problem. Particles have increased probability in finding opposition to Pbest positions, whereas position is updated with respect to Pbest and velocity. The proposed method was tested on different benchmark functions and achieved better performance than other algorithms. Verma et al. [21] used an opposition-based technique and dimension-based approach in order to improve standard PSO performance. The initial particles are generated through OBL in order to increase the chance of reaching the optimal solution. Each dimension is taken into consideration one at a time for discovering the global optimal solution. A new variant of PSO called adaptive opposition-based particle swarm optimization (AOPSO) by the authors of [22] was proposed. Adaptive opposition-based learning (AOBL) is based on quasi-opposite number (QOBL) and quasi-reflection opposite number (QROBL). AOBL has better convergence than compared to OBL. A nonlinear inertia weight is used to balance exploration and exploitation problems. AOPSO algorithm is applied to improve radar network distribution and used to reduce the local minima problem. A modified Particle Swarm optimization on elite opposition-based learning (EOBL) is presented by Xu and Tang [23] for solving large scale optimization problem. The basic PSO shows some weakness on large scale optimization problem such as slow convergence, low accuracy, and being easily trapped in the local optima; therefore, a new variant was proposed. EOBL is used to generate the initial population in order to increase population diversity. The proposed algorithm shows better performance than many popular algorithms on optimization problems.
Opposition-based learning competitive PSO (OBL-CPSO) [24] was used for avoiding premature convergence. Two learning mechanisms were engaged including competitive swarm optimization (CSO) and OBL. In each competition, three particles were randomly selected. The best-fit particle is presented as the winner, and it moves directly toward the next iteration. The worst fit particles learn from the winner, and the medium fit particles take OBL and then move to the next iteration with updated velocities and positions. An opposition-based PSO with an adaptive mutation strategy (AMOPSO) was introduced by Dong et al. [25] in order to overcome premature and low convergence rates. Global adaptive mutation-selection (AMS) and adaptive nonlinear inertia weight (ANIW) strategies are used in it. Adaptive nonlinear inertia was adjusted with an inertia weight to balance local and global searches. The purpose of AMS is to conduct a search around the entire surface of the space in swarm by using adaptive distributed mutation in order to avoid being trapped in the local optima and to improve exploratory ability. In the proposed method [26], a uniformed opposition-based Particle Swarm Optimization (UOPSO) was used to improve the accuracy and stability of the solution. Population diversity increased through the utilization of OPSO. The velocity factor was replaced with an inertia weight used to increase convergence speed. An adaptive elite mutation selection strategy was used to avoid being trapped in local minima. Experiments show that the proposed algorithm has efficient accuracy and stability for large-scale problems and unimodal and multimodal problems. This paper introduces a newly improved PSO algorithm with two modifications: The first one is generalized opposition-based and the second one consists of a linear decreasing inertia weight [27]. By using the threshold value, the population is divided into two portions Best and Worst. The opposite particle is generated from the Worst swarm that is combined with the Best swarm. The linear decreasing inertia weight is used to overcome trapping into local minima. Experiment results show the superior performance of the proposed PSO than compared to PSO variants.
The authors implemented a new methodology of the bat algorithm based on the study of the collaboration of the opposite population and dynamic learning (CDLOBA). By using OBL, opposite individuals are generated from the population. It is possible that the new opposite individuals are better, and they are hired to obtain a new and better population by using competitive collaborative strategies [28]. A new variant of bat algorithm (BA) is called OBMLBA, and it was introduced in [29] to overcome the local optima problem and to improve convergence speed. In the proposed algorithm, OBL and Lévy Flight Local Search strategy is used on the modified bat algorithm. Levy flight is a local search-based algorithm that prevents becoming stuck in local optima. The Lévy flight Local Search strategy is applied on individuals, and OBL is then applied on it. OBL, when introduced to the bat algorithm, improves convergence and diversity capability. In [30], the authors presented a new mutation operator and EOBL in order to improve the modified bat algorithm. The Cauchy mutation is described as having a one-dimensional probability density function centered with respect to the original. The proposed invariant provides better convergence speed and diversity of the population. In [31], the authors proposed the BA based on OBL for the optimal design of circular mutation. In the given variant, the author used the opposition method for the initialization of the population. The opposition technique was used for balancing exploration and exploitation. The proposed approach provides better results than compared to BBO. The authors in [32] developed a modified bat algorithm (mBA) using EOBL and inertia weight. By using OBL, from the initial population, some of the selected elite individuals are generated with respect to the corresponding opposite individuals in the search space.
Wahab et al. [33] used a combination of ANN and PSO algorithm to damage identification in structures. This combination was used to overcome the limitations of ANN by applying gradient descent methods used to train the NN and reduces computational time. In order to evaluate the performance of the proposed technique, numerical models and experimental models using different damage conditions are used. ANN-PSO easily identified damaged location structures. The advanced PSO algorithm and Newton’s laws of motion known as centripetal accelerated particle swarm optimization (CAPSO) was presented in [34] in order to evolve ANN’s learning and accuracy. CAPSO algorithms are used to train the feedforward multi-layer neural network (FFNN) in order to solve the classification problem of the diagnosis of nine medical diseases. The CAPSO algorithm showed superior classification accuracy than compared to most of the famous algorithms with respect to the diagnosis of nine medical diseases. In [35], the authors introduced the training of Feed Forward Neural Networks (FFNN) with fuzzy adaptive particle swarm optimization (FA-PSO) for two purposes: classification and short term price forecasting (STPF). In the proposed algorithm, the dynamic inertia weight was replaced with inertia weight and avoided being stuck in local minima. FA-PSO was used to tune the weights and biases of the FFNN of the fixed architecture. The proposed algorithm was used to predict various price differences in the Spanish electricity market.
3. Methodology
In this paper, we proposed Philox with opposition-based PSO ranked inertia weight (ORIW-PSO-P) and Threefry with opposition-based PSO ranked inertia weight (ORIW-PSO-TF) algorithms in order to avoid the local optima problem and to create a balance between exploration and exploitation abilities. The proposed technique uses two features in standard particle swarm optimization: The first one is Philox and Threefry initialization techniques with opposition-based learning as an initialization strategy and the second one where the inertia weight is updated with ranked inertia weight for individual particles. Population initialization has been observed to play a vital role in the search process of metaheuristic algorithms. Different initialization techniques are used for initializing the initial population. The initial population has an efficient effect on the PSO algorithm. We used opposition-based learning with PRNG approaches in order to initialize the initial population. We proposed two new initialization strategies for pseudo-random Philox and Threefry.
In the proposed methodology, the main focus is the opposition-based initialization process, e.g., how it is executed and processed and what sort of results can it produce on common and generic functions. Opposition-based initialization is used to generate opposite populations, and the fittest individual is selected for the current population and opposition population. Based on a jumping rate (jumping probability), rather than generating a new population through the evolutionary process, the fittest and opposite populations are determined from the current population as well as from the opposite population. We used a 0.3 Jumping probability for the opposite population. It has to be pointed out here that while accumulating the opposite population for generation jumping, every variable is generated dynamically. These are the lowest and highest values for each variable in the current set, and they are used to compute opposite points instead of using defined boundary intervals. By using variables, we generated opposite points in which (minimum and maximum) values become increasingly smaller than the upper and lower bounds of the search space.
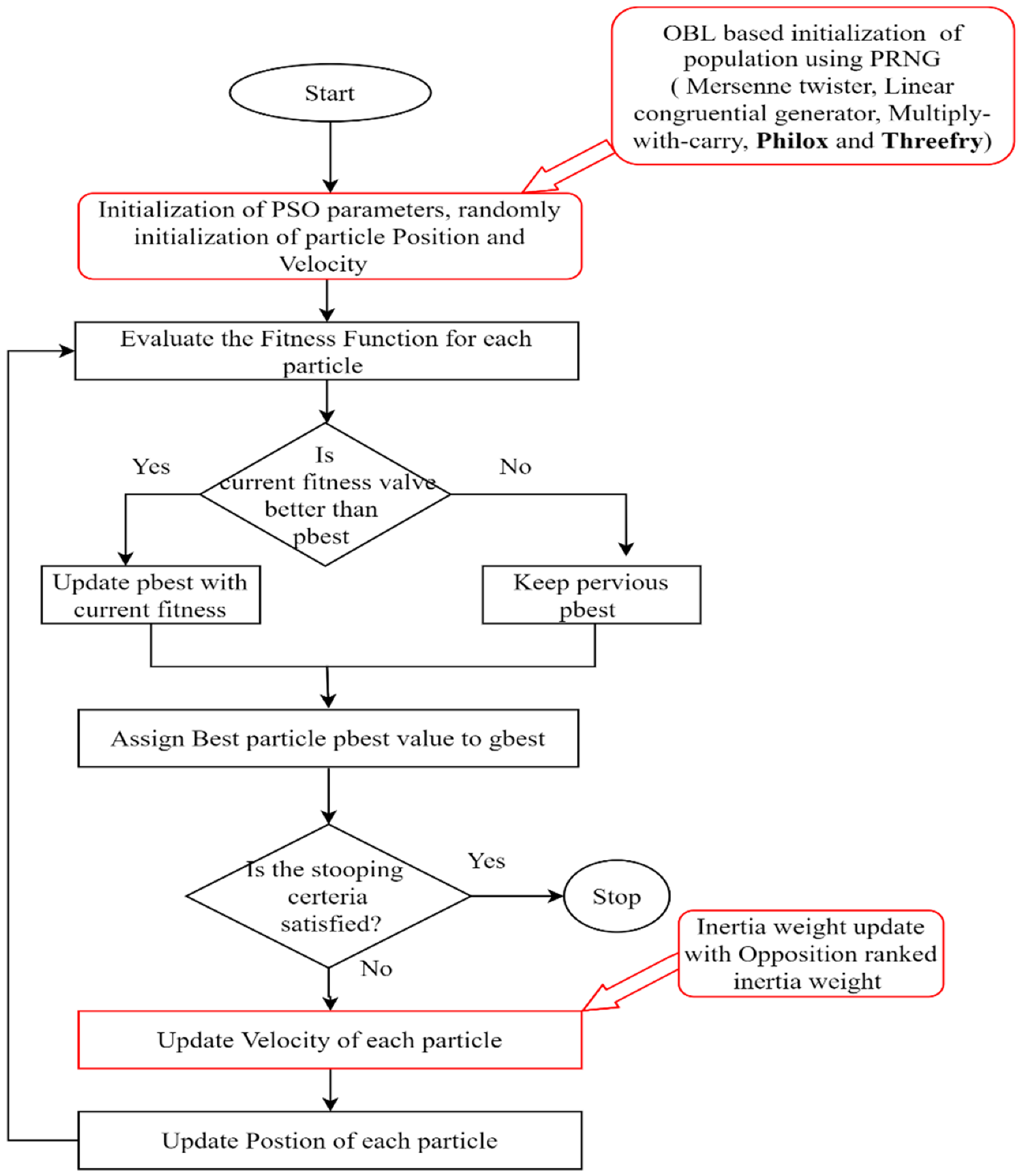
The opposition rank-based inertia weight approach is used to adjust particle inertia weights. It was adjusted on at the base of each particle with respect to the rank of its fitness value. The fittest individuals have minimum inertia weights, which moves slowly than compared to the lowest fittest individual. At the same time, it enhances local and global search abilities. Our proposed methodology is presented in Figure 1. The proposed algorithm shows efficient performance on several unimodal and multimodal complex benchmark functions.
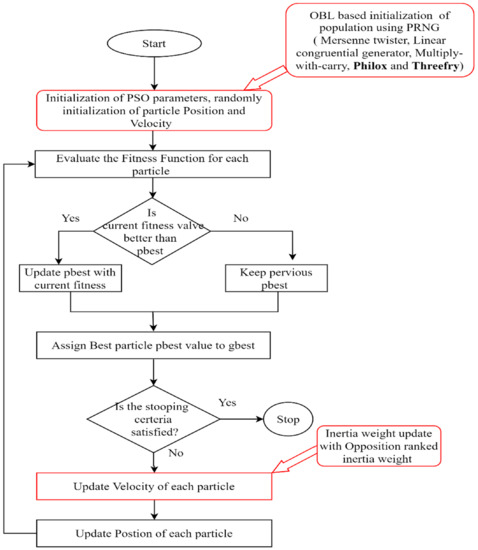
Figure 1.
Proposed methodology.
3.1. Random Number Generators for Initialization
The number occurs in a sequence in such a manner that it is impossible to predict the value on the bases of its past and present values, and the defined set of uniformly distributed numbers is known as Random number. On the basis of the probability density function, it generates a sequence. It is useful in statistical analysis, cryptography, probability theory, and the population initialization of optimization algorithms. Random numbers are generated by using the inbuilt library function Rand(xmin, xmax) by uniform distribution [36].
3.2. Pseudo-Random Number Generators for Initialization
A pseudo-random number generator (PRNG) is used to generate pseudo random sequences of numbers by using a deterministic algorithm. PRNG generated a numerical sequence resembling the properties of random numbers. It takes the seed value as the starting state, and many numbers can be generated within a short period time in this manner and can be reproduced when required if the seed value is known [37]. Therefore, the produced numbers are deterministic and efficient. Simulation and modeling applications are good applications of PRNGs where the same sequence can be used repeatedly. PRNG is not applicable in encryption and gambling because the numbers are required to be unpredictable. The pseudo-random number generator is used as an initialization technique because it covers all search spaces [38]. We used pseudo-random numbers for the initialization of the population that included Mersenne twister, Linear congruential generator, Multiply-with-carry, Threefry and Philox. Threefry and Philox are used for the first time for initialization in particle swarm optimization algorithms, and the show efficient convergence speed.
3.2.1. Mersenne Twisters
The Mersenne twister (MT) is an example of a PRNG that generates a random number by using the twister operation. MT uses the initial seed as input and is applied on the twister operation; however, in simple PRNG, the twister operation is not used [36]. Mersenne prime 219937 − 1 is a base version of MT and is used for general purposes.
3.2.2. Linear Congruential Generator
The linear congruential generator (LCG) is the oldest method and most popular PRNG algorithm. Through modular arithmetic, LCG generates a sequence of numbers that have sufficient randomness. LCG is an algorithm that generates a computed sequence of pseudo-random numbers with a partial discontinuous linear equation [39].
3.2.3. Multiply-with-Carry
Multiply-with-carry (MWC) uses an initial set of random integers from two to many thousand seed values for generating sequences. The range value of MWC is to , and long periods are required for generating a quick random sequence [40].
3.2.4. Threefry
Bulleted Threefry is based on the existing Threefish algorithm that shows high performance in graphics processing units (GPUs) and supports parallel system [41]. By using Threefry, we can easily generate a random sequence. Threefry consists of counter-based PRNGs that are derived from Threefish and is used in the Skein hash function. It is available in improved variants that can vary word sizes between 32 and 64 bits.
Threefry’s 32-bit word-size algorithm generates four numbers at a time as follows.
Here, vi,d into i, which is the random number obtained during d; the round is the key that is applied every fourth round. Each pair is mixed in each S-box by the following function:
where j = 1, 2.
R is a collection of constants, and << is the bitwise left rotation. The keys k0, …, 3 create a help key according to . After this, it rotates the keys according to the following.
The constant used to create the help key k4 purpose is in accordance with the creators in order to ensure that k4 cannot become 0.
3.2.5. Philox
Philox (non-cryptographic) shows high performance in graphic processing units (GPU) and the support parallel system. Philox (P) generates the well-defined random sequence [41]. Philox consists of counter-based PRNGs that use multiple instructions to scramble bits.
The processor’s word size is W, and the Philox S-box takes two words (L and R) from an N words block for W bits, and it is a standard Feistel function.
Philox-2_W-R bijection performs R rounds on a pair of W-bit inputs when N = 2. By using Threefish, the N-word inputs are swapped when N is larger then the P-box block before being imported into the N = 2 Philox S-box and multiplier M. The N = 2 element is constant. The N = 2 key is updated during each cycle based on the Weyl sequence.
3.3. Opposition Rank-Based Inertia Weight
Inertia weight (W) is an important factor in PSO algorithm that is used to balance exploration and exploitation. It is observed that the value of W provides quite good results when taken between 0.4 and 0.9. The previous velocity of a particle is controlled by using inertia weight. Opposition rank-based inertia weight is adjusted with respect to particle inertia weights according to their fitness value. The position of the particle is balanced such that the fittest particles move slowly, and the lowest fittest particle moves fast when compared to the fittest particle. The fittest particle is either current or their opposite. Inertia weight is adjusted on the basis of each particle and on the rank of its fitness value. The inertia weight of each particle is given by the following:
wheres R(i)(t) is the fitness rank of particle i. It is observed that the fittest particles (i.e., rank 1) have minimum inertia weights while the lowest fittest particle is set with the maximum inertia weight, which moves fast. The minimum inertia weight (Wmin) is set at 0.4, and the maximum inertia weight (Wmax) is set at 0.9.
3.4. Opposition-Based Learning
The idea of OBL is to work as real-world opposition similarly to how every person has an opposite person regardless of whether he is good or bad. The authors of [42] have presented a new opposition-based learning (OBL) scheme for machine learning. Let x be a real number that contains the interval x ∈ [a, b] and its opposite number is x’, which is defined as the following.
Let’s xi = (x1, x2, x3 …, xd) be points in the d dimension in the search space with interval xi belonging to {ai, bi}; thus, the opposite point is defined as follows.
The idea of OBL is that allows the given unknown function f(x) to be used with g(x), which is an evaluation function. It is used for initially guessing x and its corresponding opposite point is x’. For g(x) > g(x’), learning continues with x. OBL is used to accelerate the search process of some well-known techniques of EC.
4. Result and Discussion
In this section, the experimental results for the proposed pseudo-random number generator (Philox and Threefry) initialization schemes are used. All the suggested techniques and the standard PSO are implemented in MATLAB 2018 version. The system used for the experiments possessed the following specification: 2.00 GHz Core™ i3-5005U CPU processor. The standard benchmark function set is outlined in the table, and every function has a name, definition, and search space.
4.1. Parameter Setting
The parameters for simulation are considered as follows: The population size is 30, and dimensions are set as 10, 20, and 30 for all the functions. The numbers of dimensions 10, 20, and 30 are considered for Iteration 1000, 2000, and 3000, respectively. The inertia weight is set at Wmax = 0.9 and Wmin = 0.4, and the acceleration coefficient is set at C1 = C2 = 1.49 in order to produce good results. In order to obtain effective and impartial results, all the techniques used the same parameters, and these techniques are executed 10 times in order to compare their performance. The setting of parameters is shown in Table 1.

Table 1.
Experimental setting of parameters.
There is a set of standard benchmark functions over a continuous range of values available in the literature, and they are used to implement evolutionary computing algorithms. The purpose of the implementation of these test functions is to ensure the effectiveness and accuracy of the EA’s optimization algorithms. There is no standard list for all of these standard benchmark test functions; there may be many test functions available in different sources such as research-papers, textbooks, and certainly different websites. These test functions consist of great diversity in terms of separability, modality, and landscape in their properties, which render them more suitable for testing new algorithms in a unique manner that is not biased. A few functions are taken from a great list of these benchmark test functions for testing purpose. These functions have been used and validated by different researchers, which are provided in Table 2.

Table 2.
Standard benchmark functions and their optimal value.
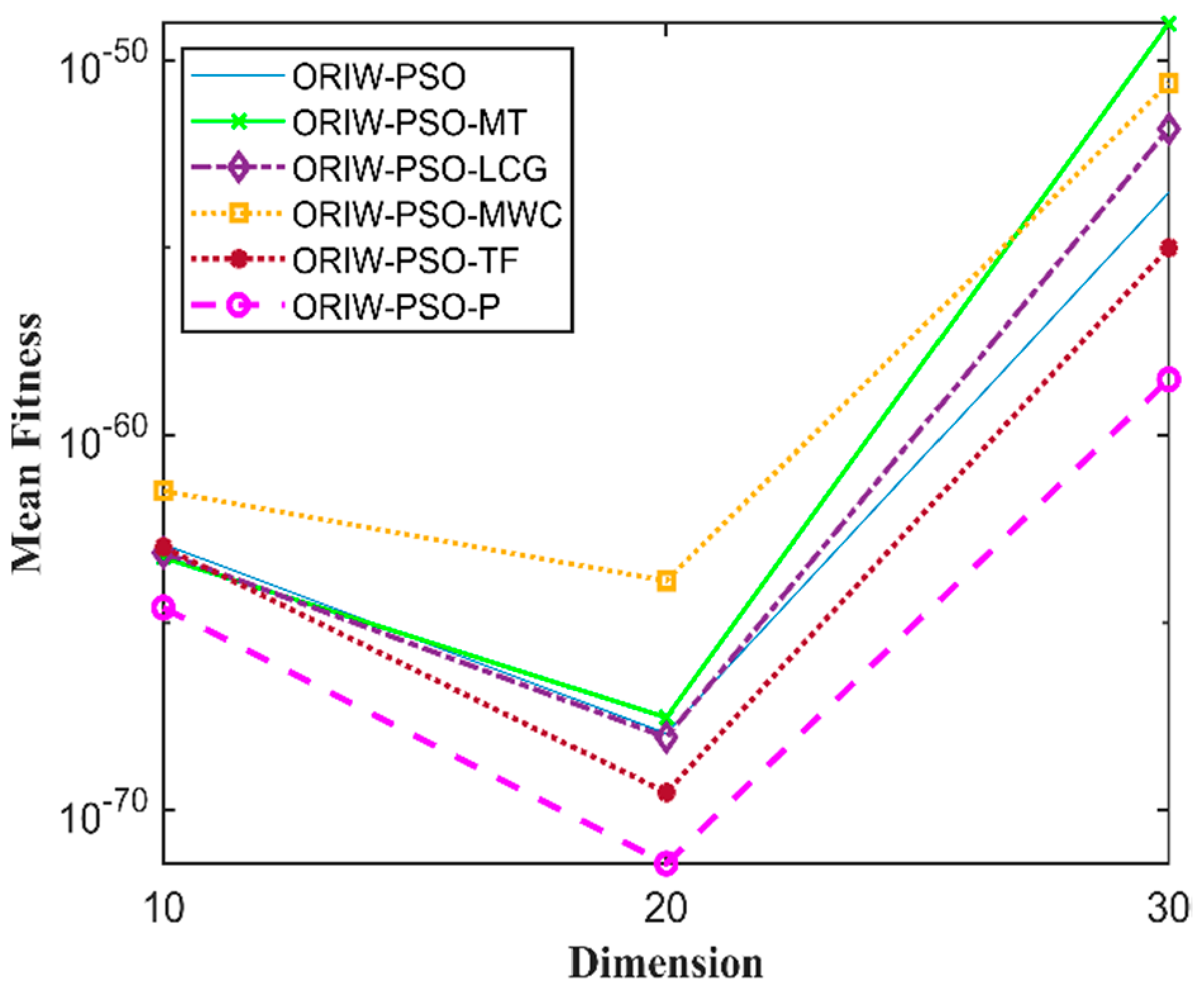
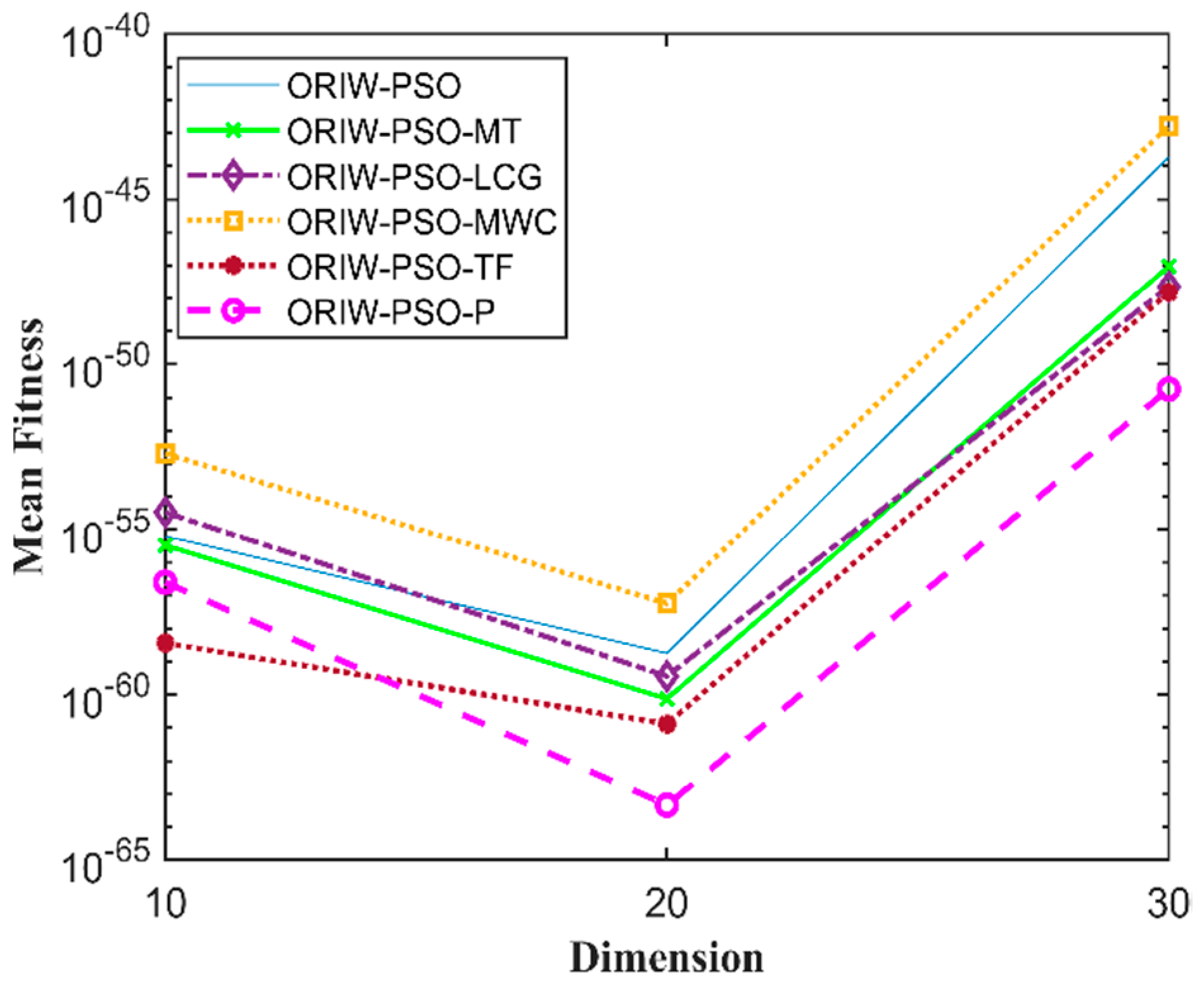
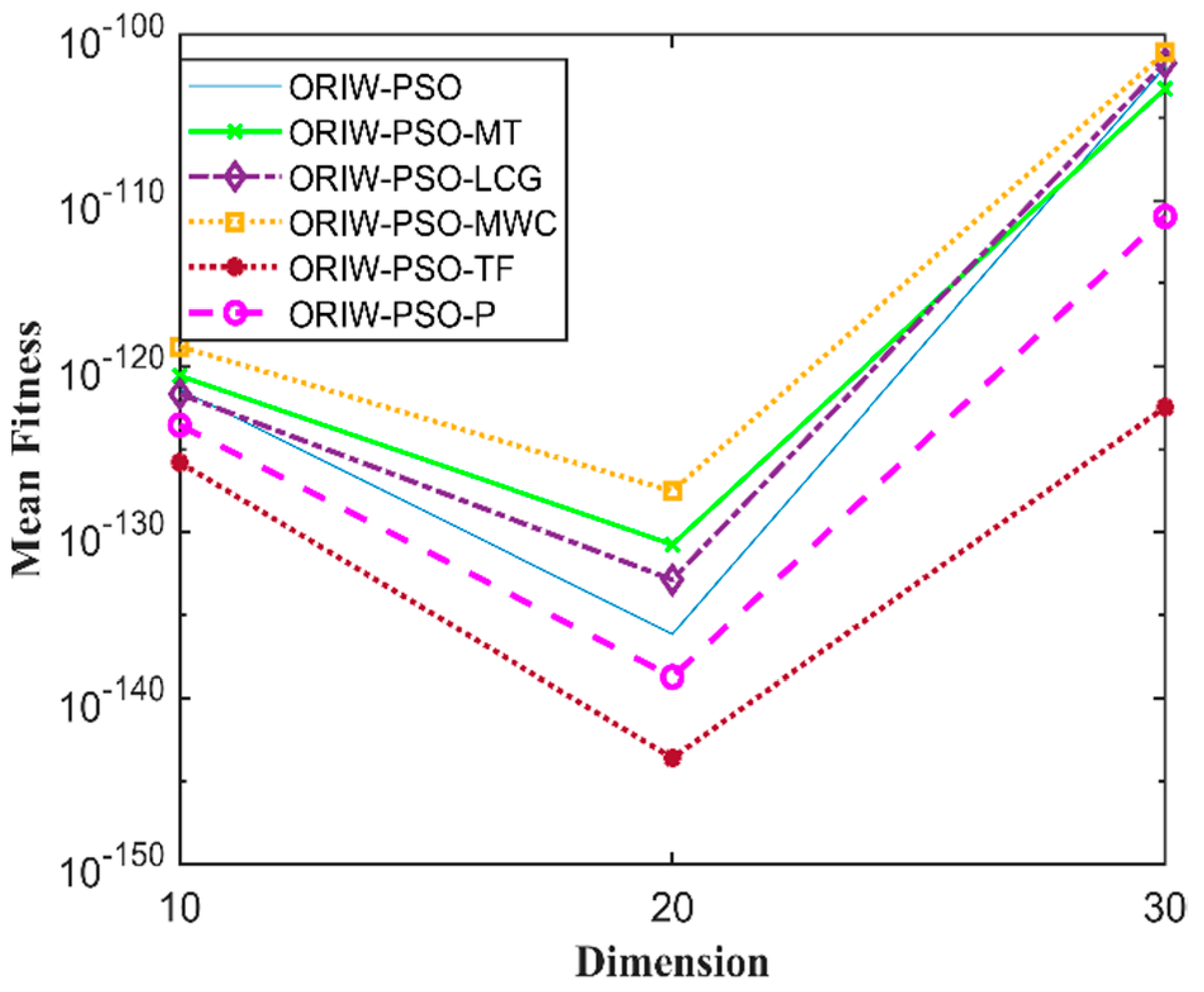
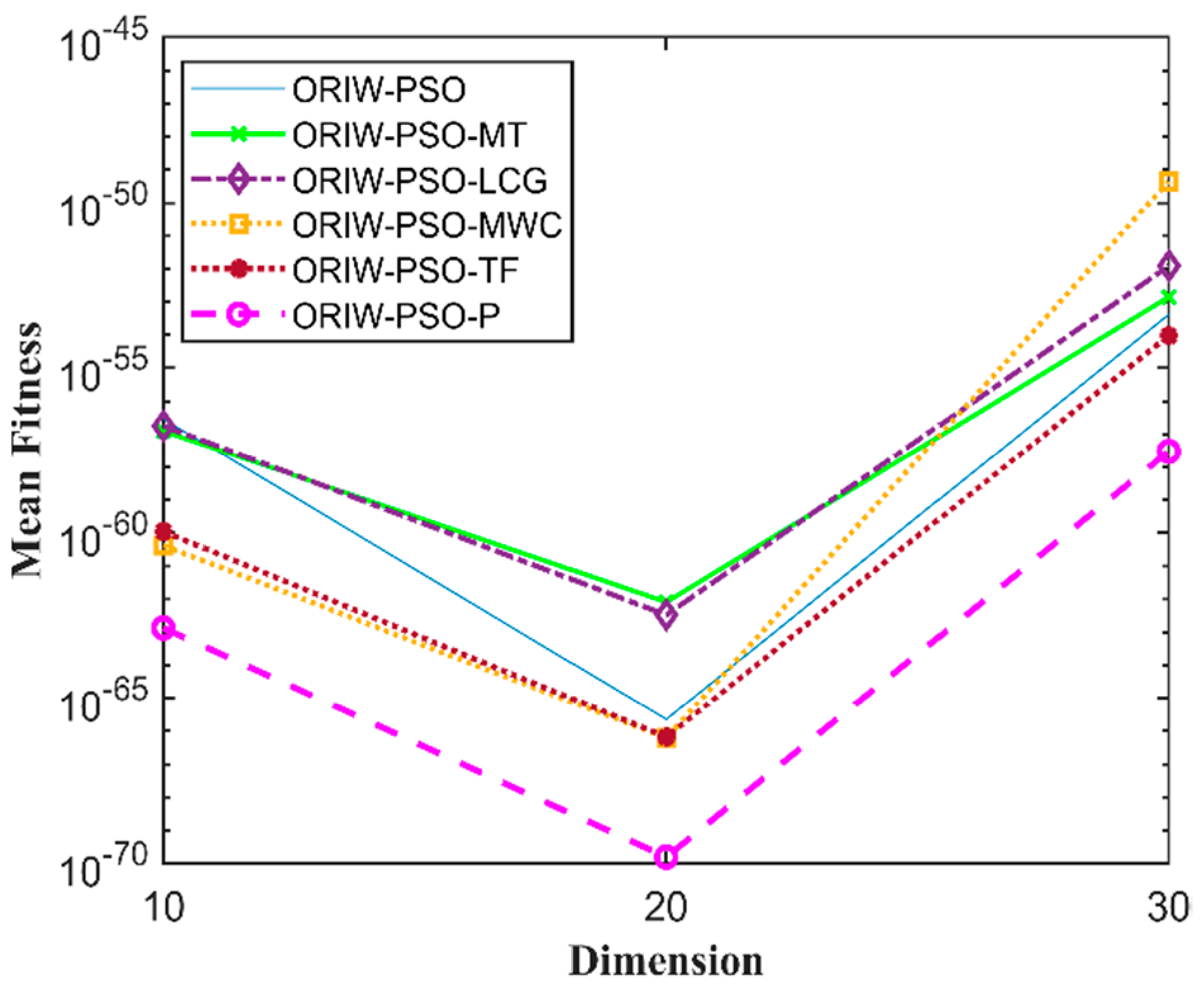
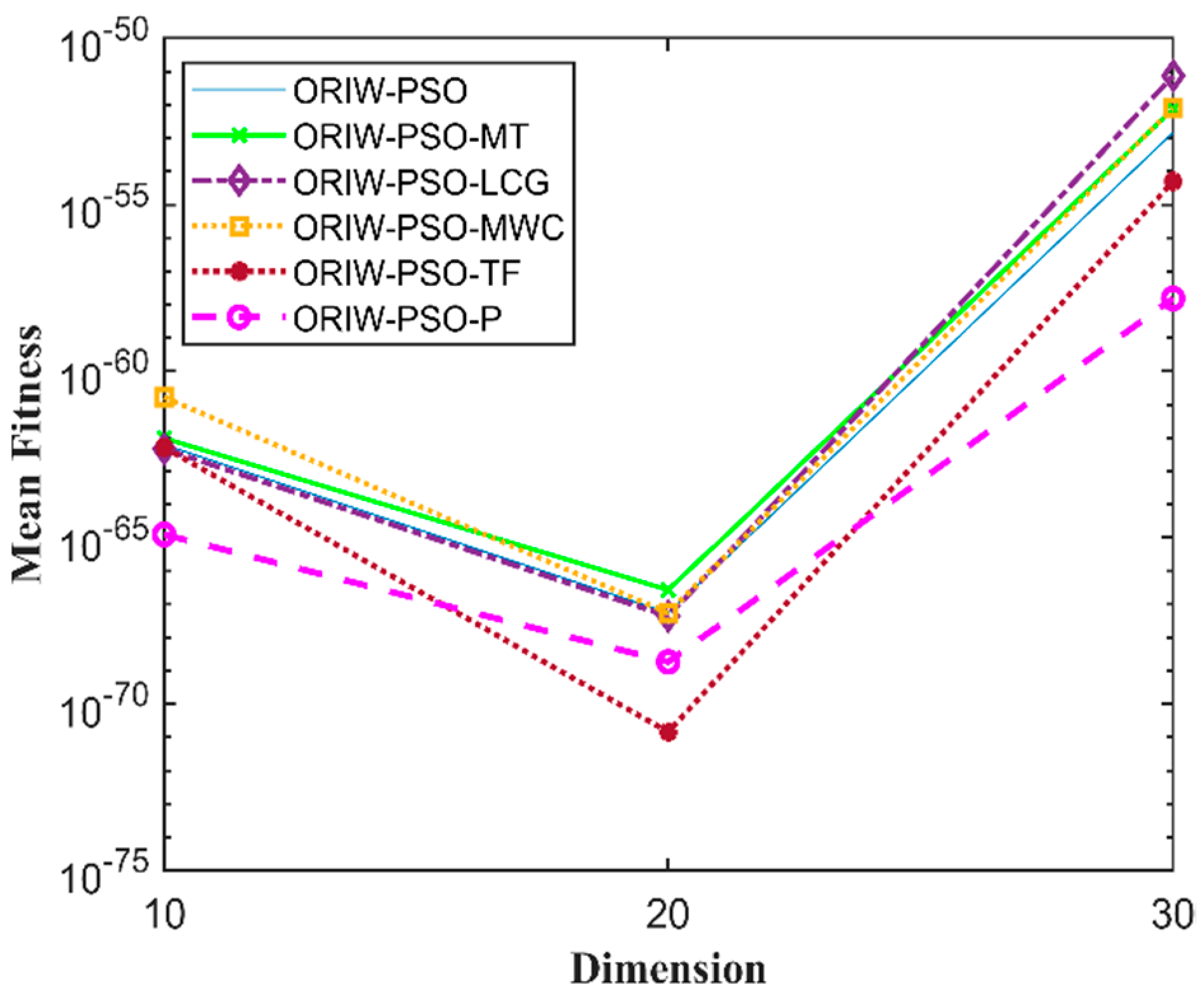
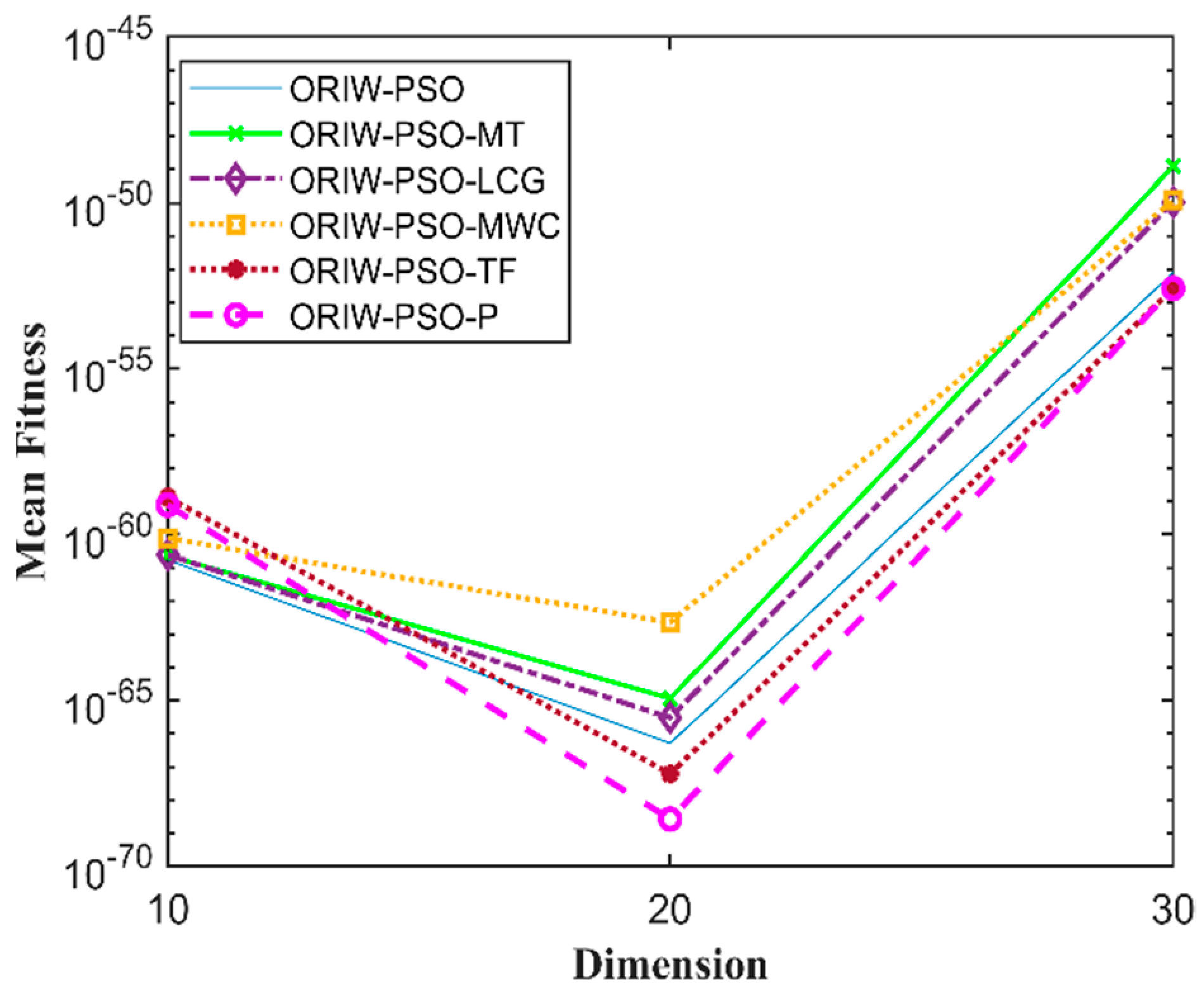
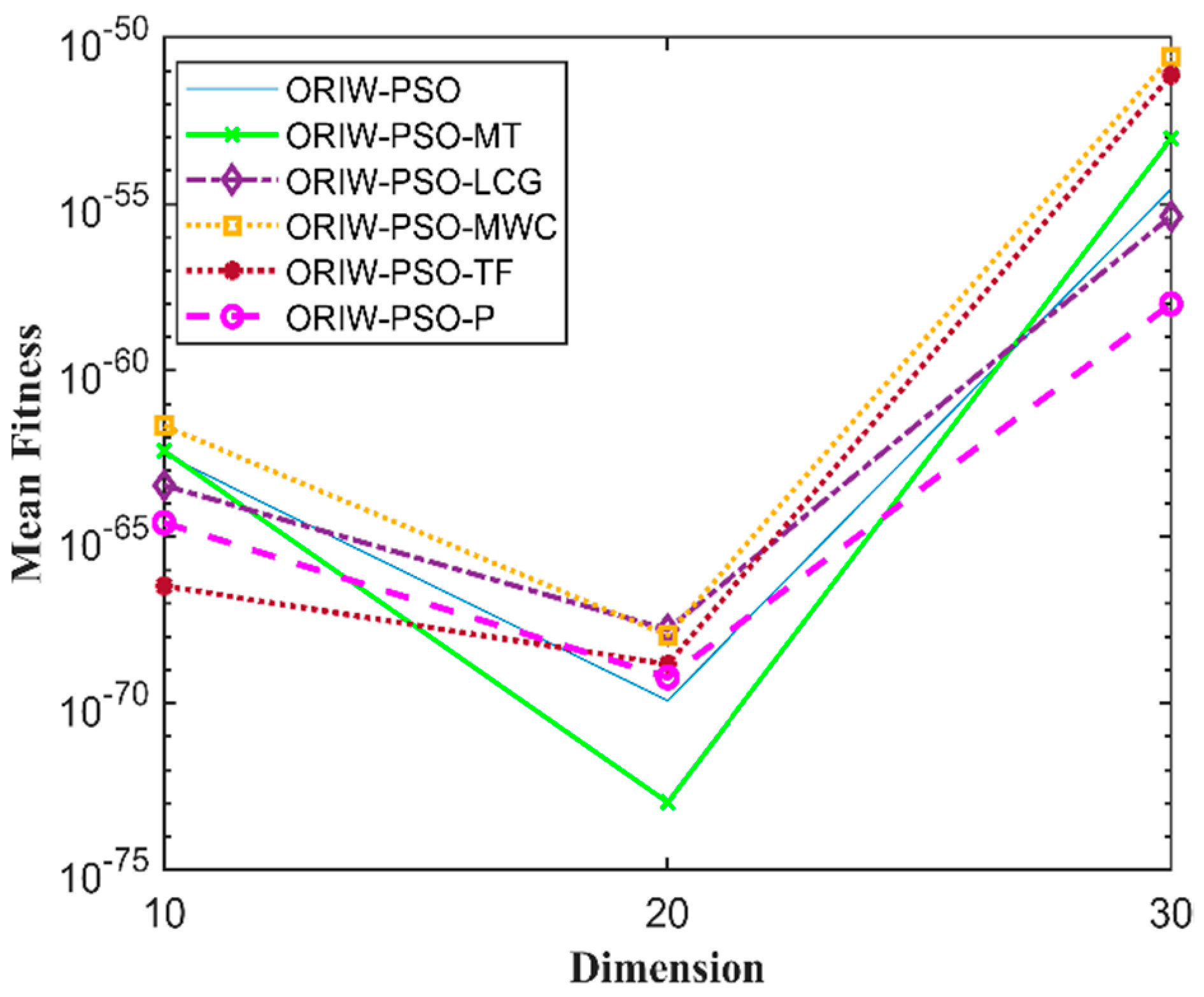
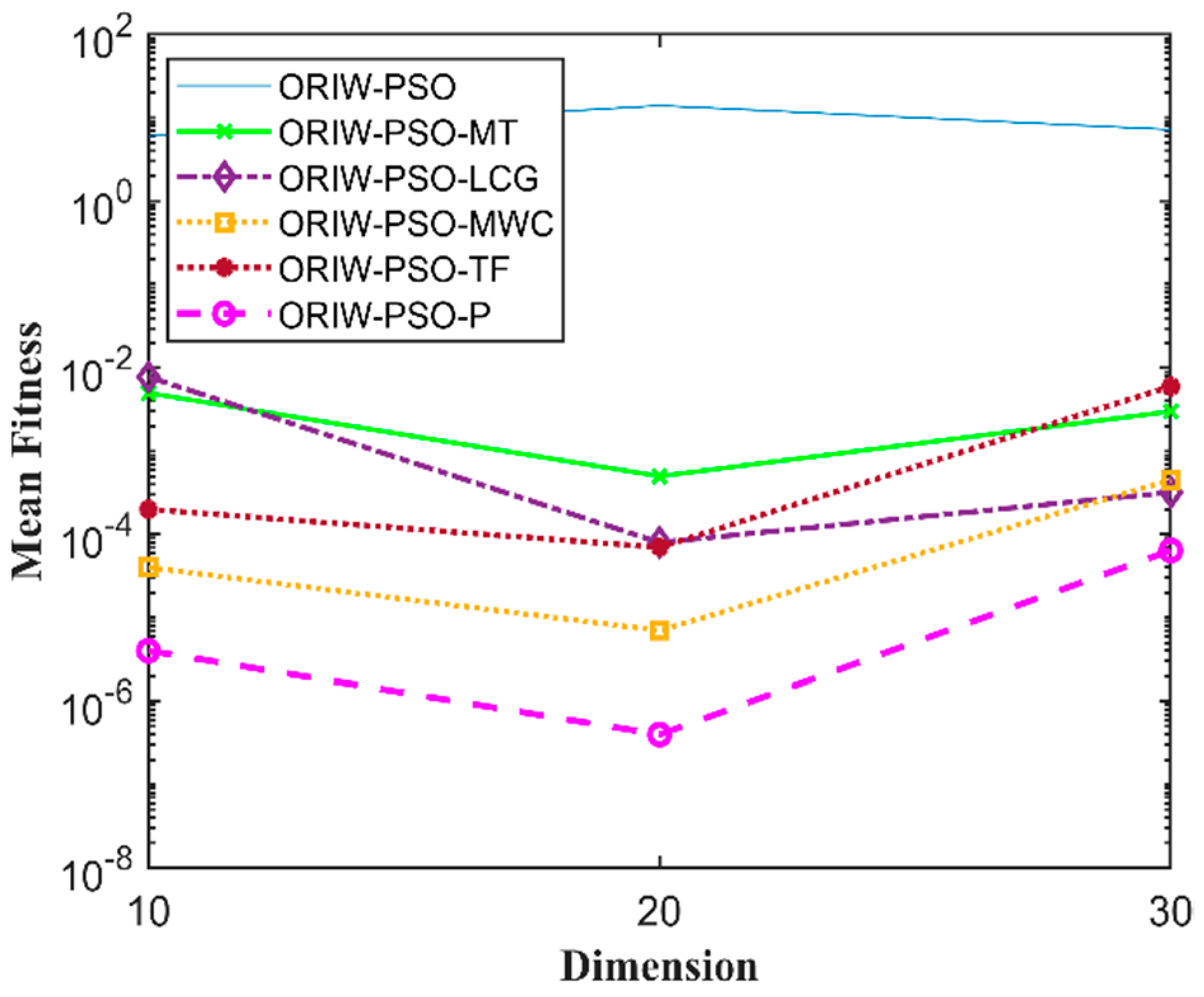
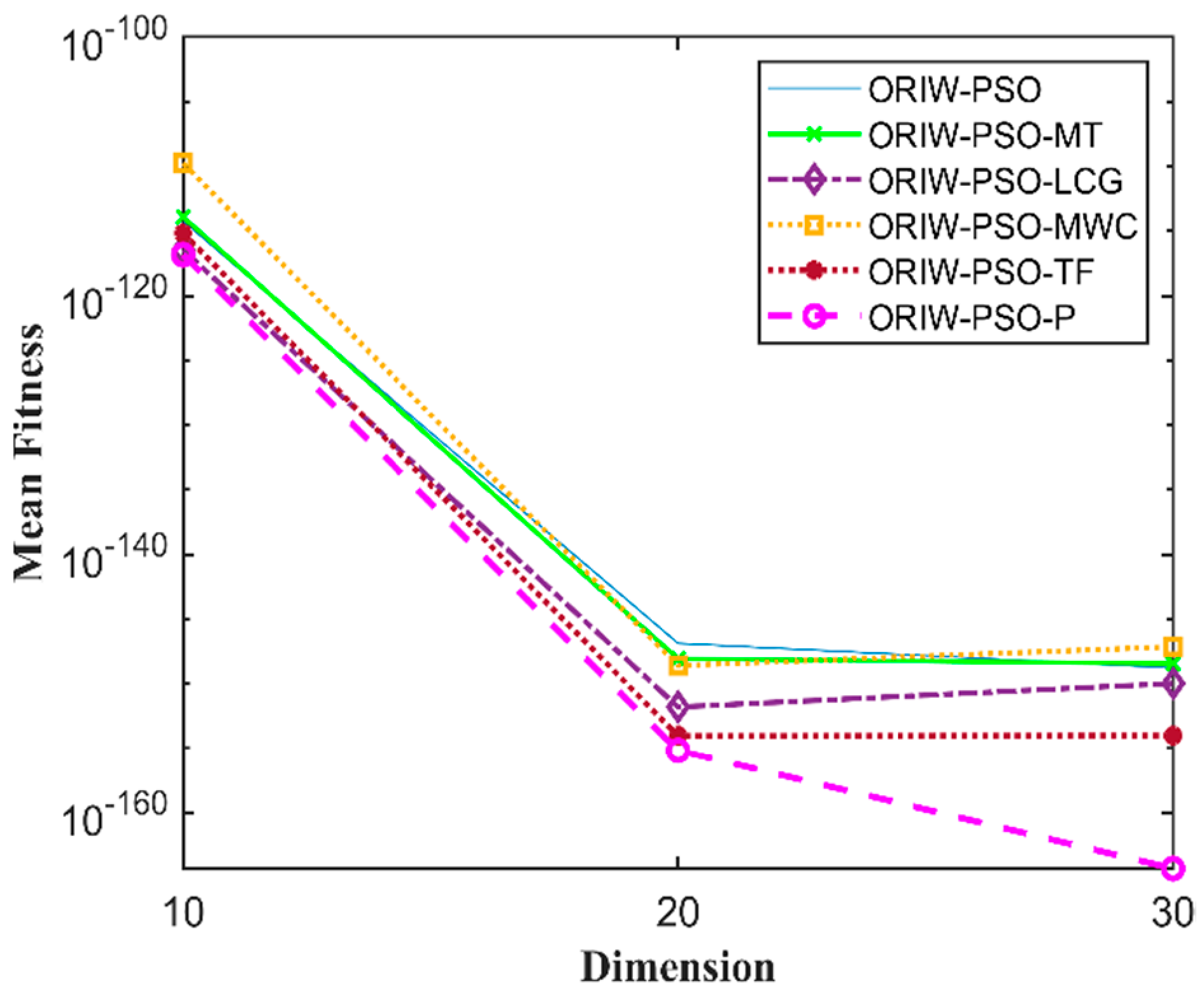
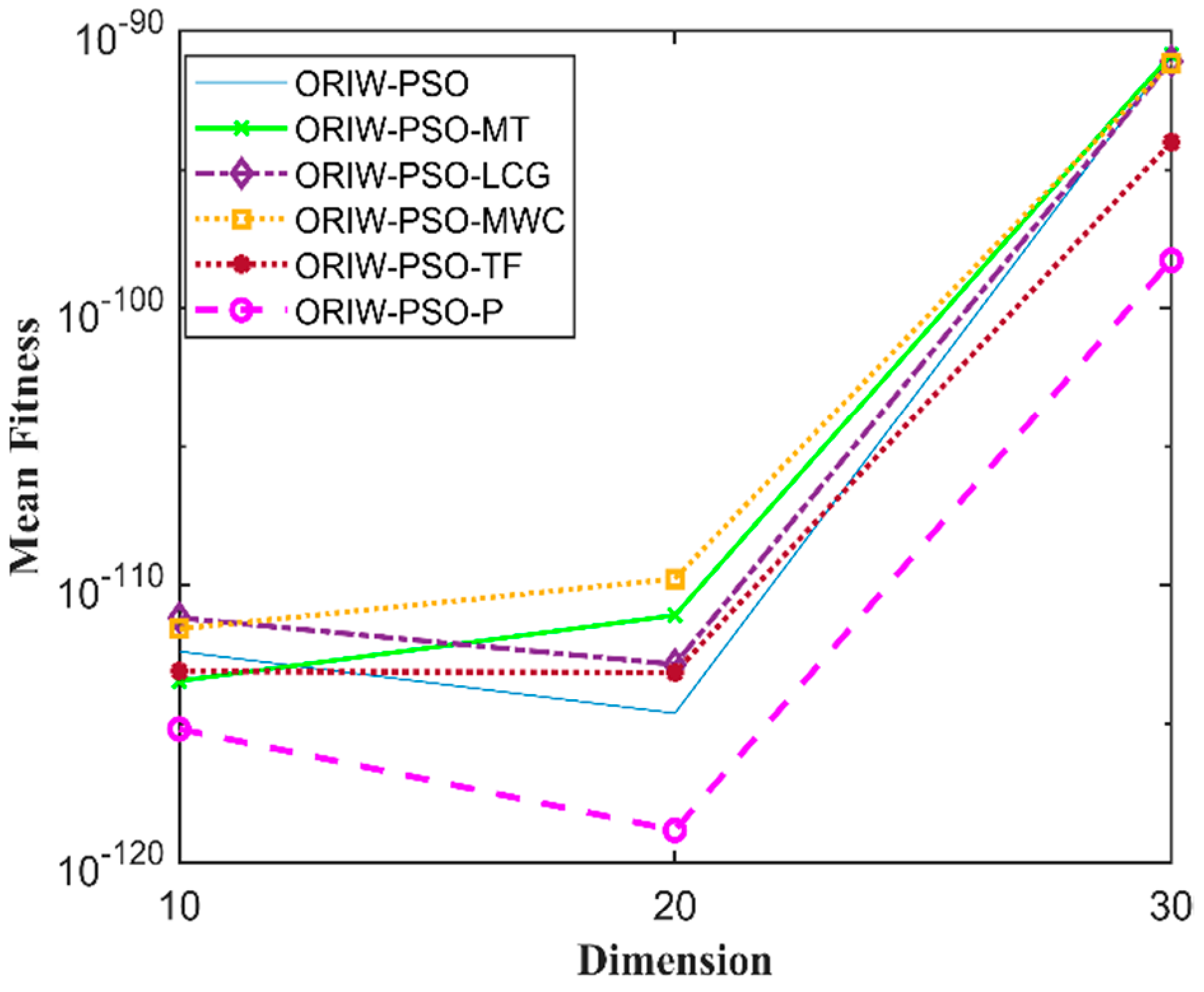
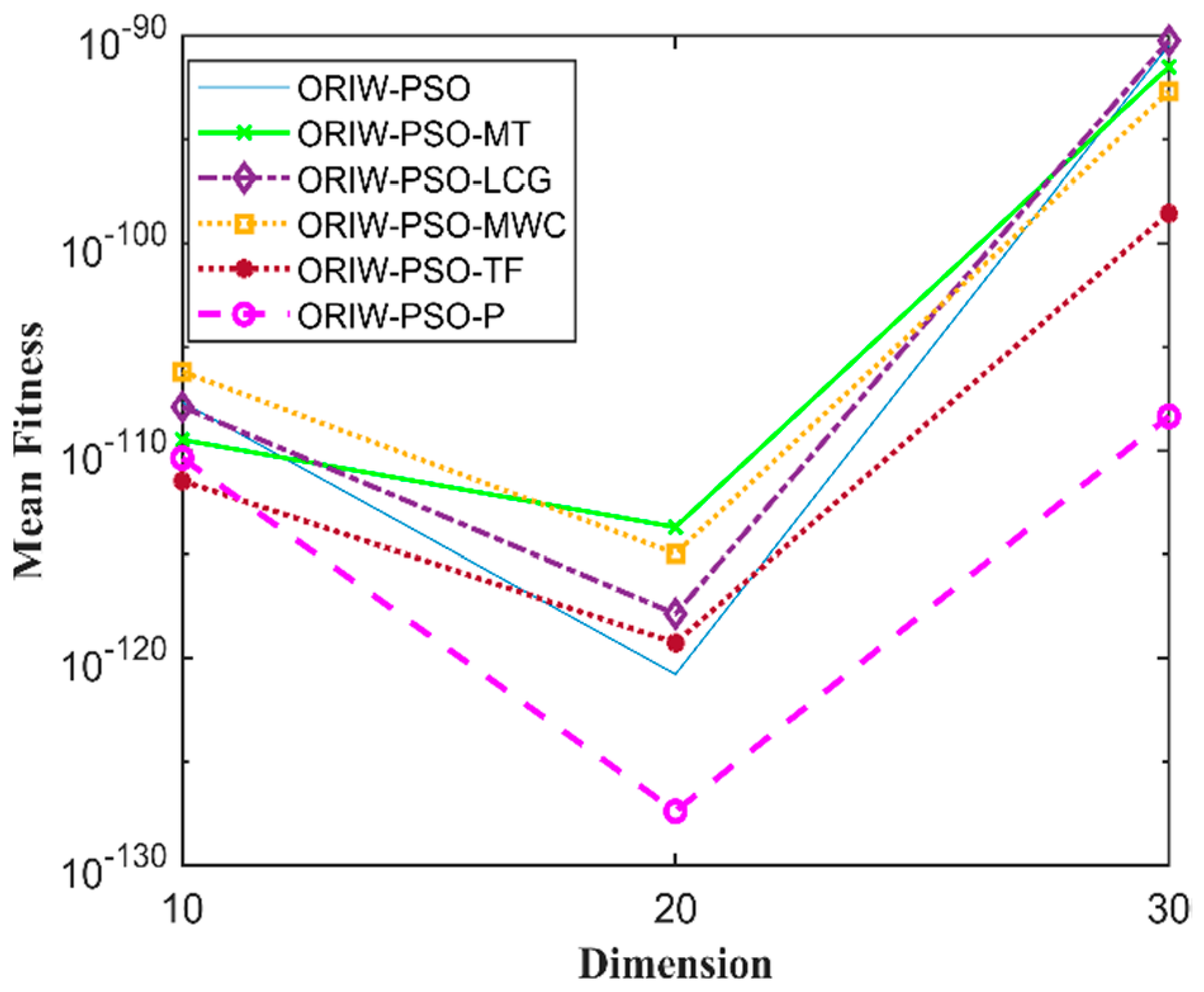
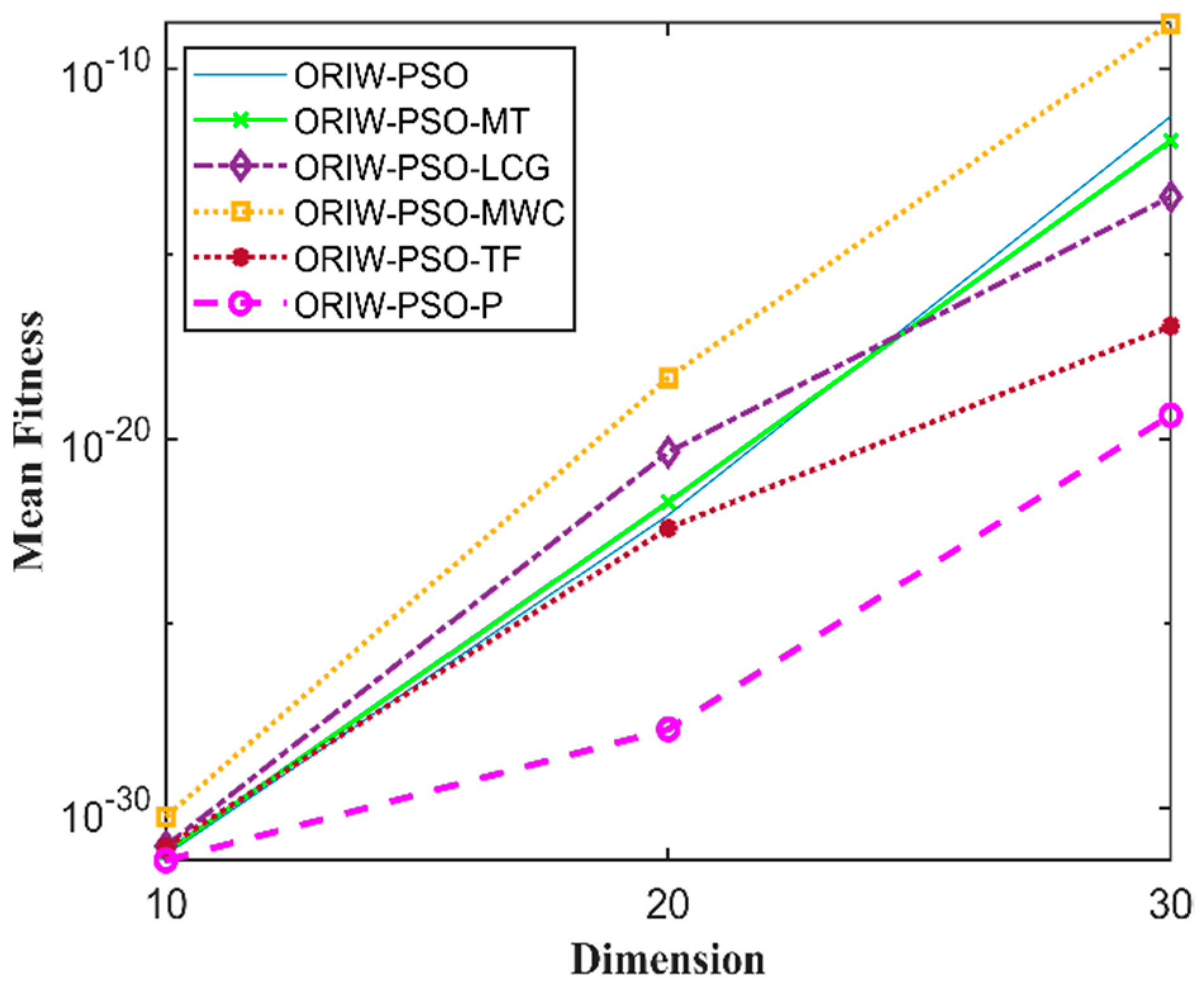
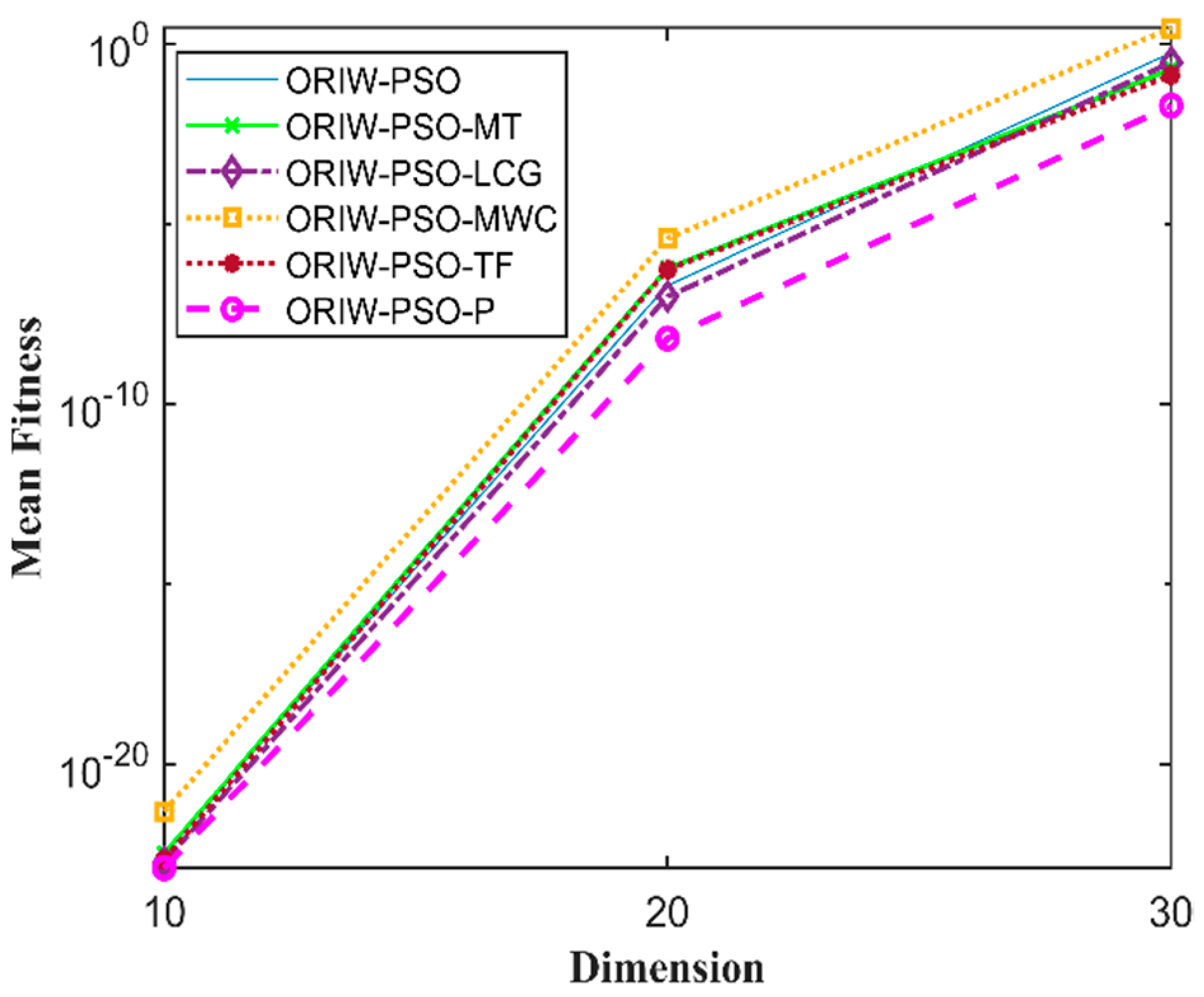
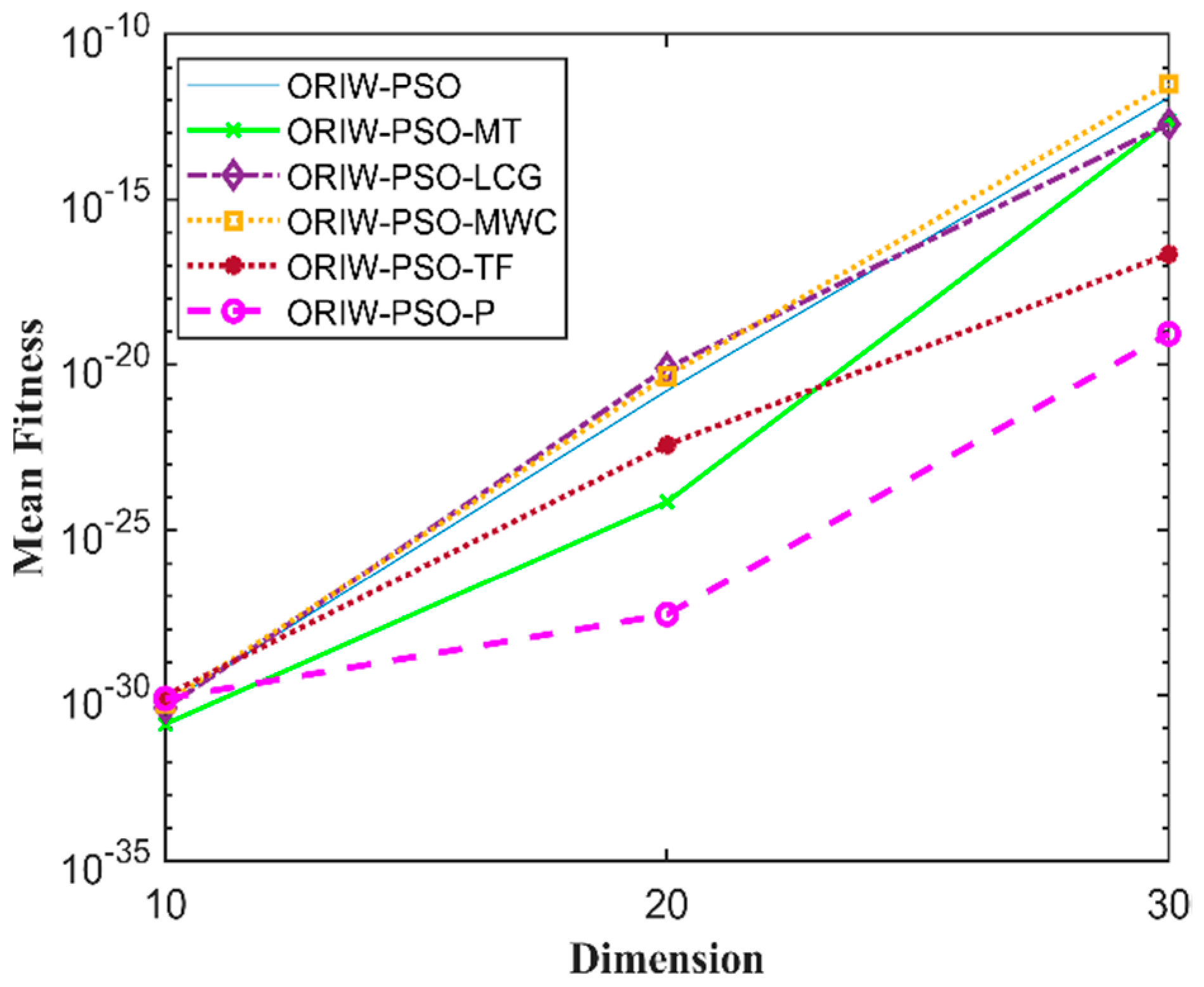
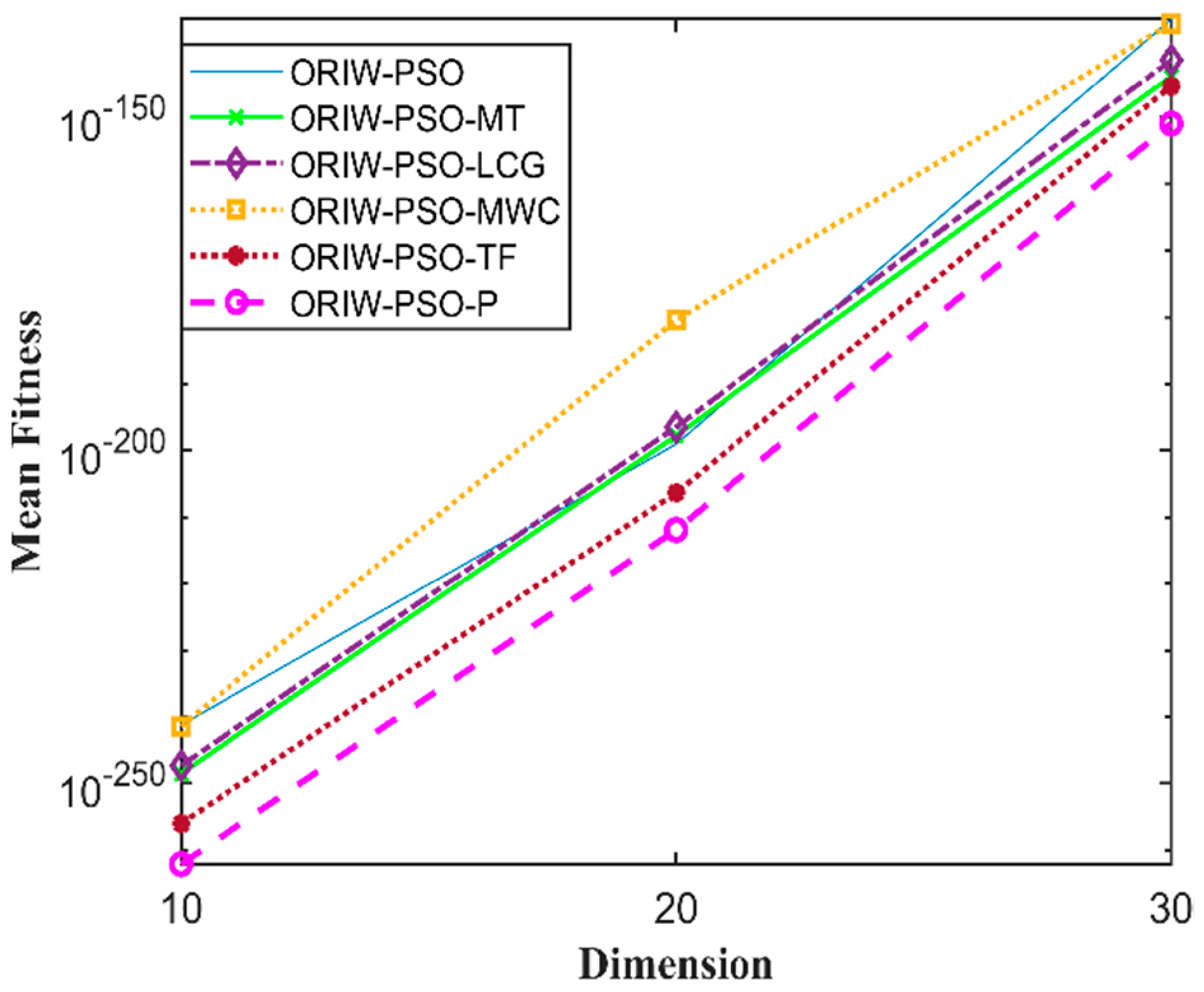
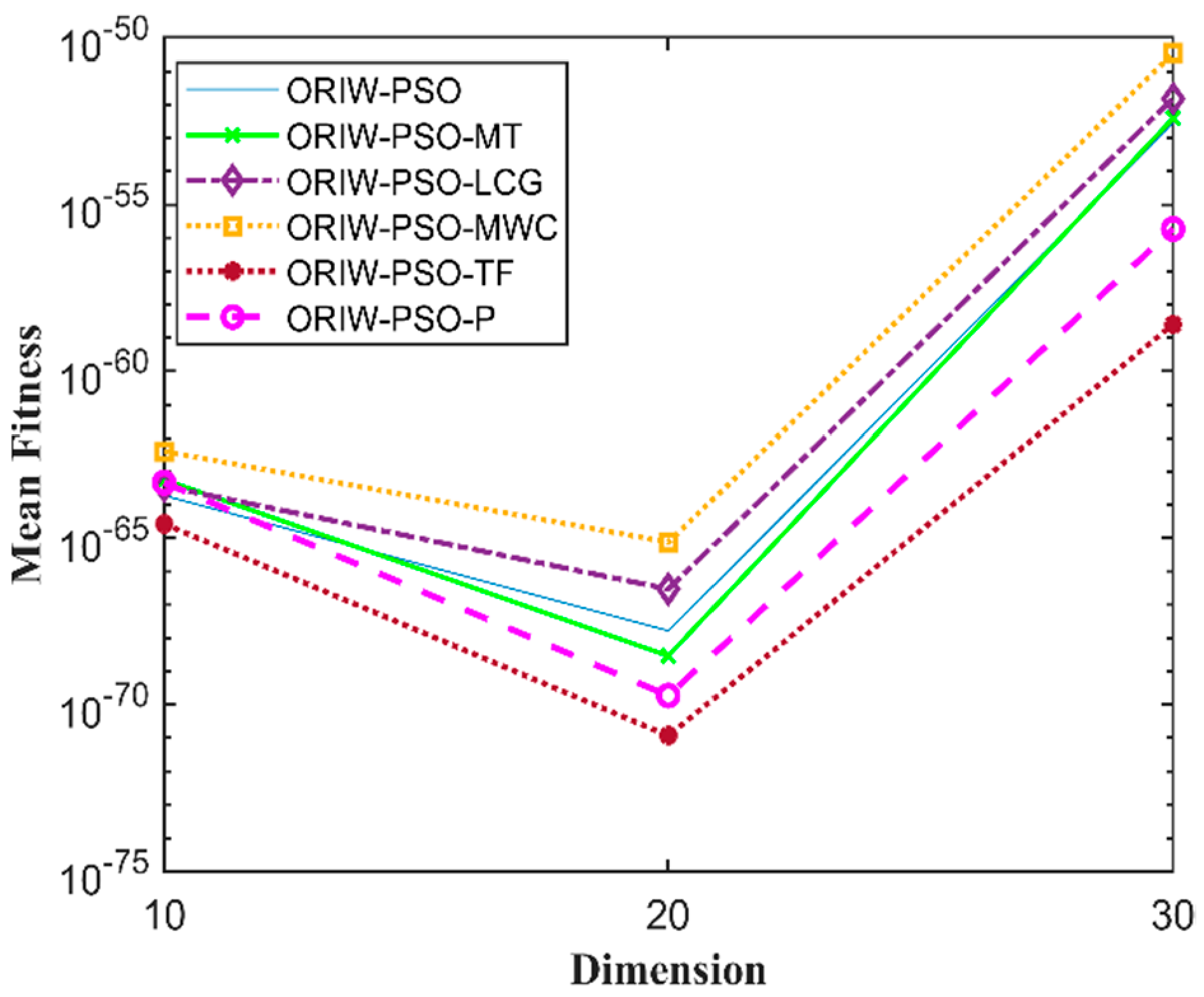
A comparison in the table has been carried out with other optimization algorithms, including opposition-based PSO ranked inertia weight (ORIW-PSO), Mersenne Twister with opposition-based PSO ranked inertia weight (ORIW-PSO-MT), Linear congruential generator with opposition-based PSO ranked inertia weight (ORIW-PSO-LCG), Multiply-with-carry with opposition-based PSO ranked inertia weight (ORIW-PSO-MWC), Threefry with opposition-based PSO ranked inertia weight (ORIW-PSO-TF), and Philox with opposition-based PSO ranked inertia weight (ORIW-PSO-P). ORIW-PSO-TF and ORIW-PSO-P is performing well on our specific function, and the winning result is highlighted in bold in Table 3. Our proposed variant ORIW-PSO-P and ORIW-PSO-TF really performed well on 10, 20, and 30 dimensions than compared to other variants. Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17 present the mean best fitness value of each test function.

Table 3.
Comparison of Mersenne twister, Linear congruential generator, Multiply-with-carry, Threefry, and Philox distribution with opposition-based PSO ranked inertia weight.
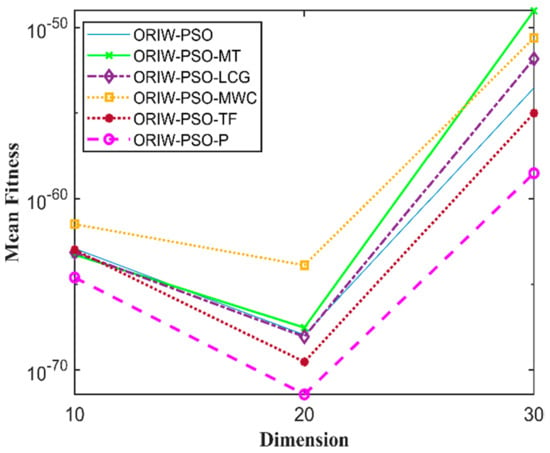
Figure 2.
Mean fitness of F1.
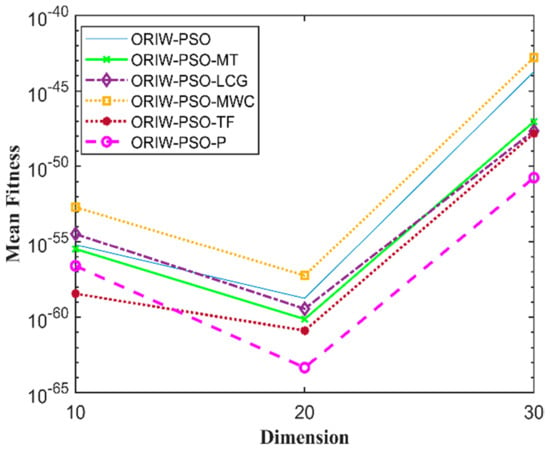
Figure 3.
Mean fitness of F2.
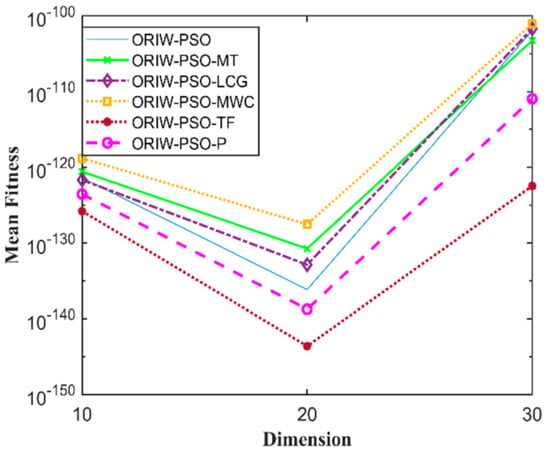
Figure 4.
Mean fitness of F3.
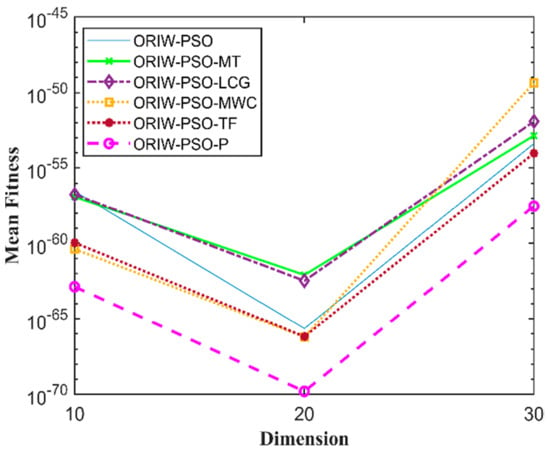
Figure 5.
Mean fitness of F4.
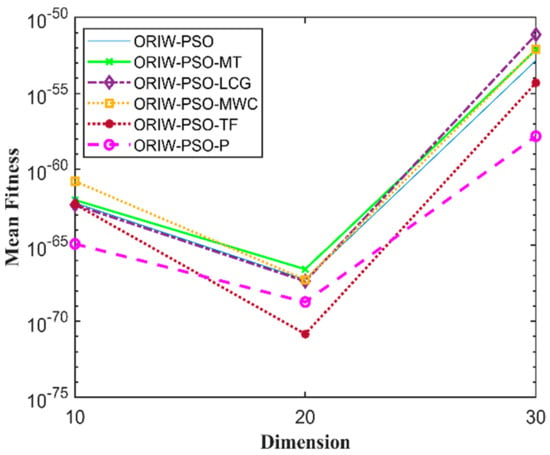
Figure 6.
Mean fitness of F5.
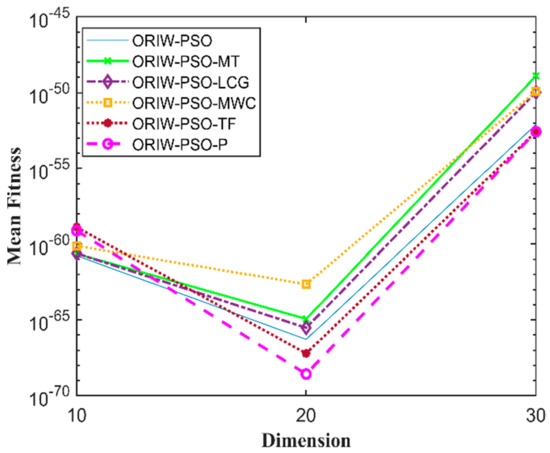
Figure 7.
Mean fitness of F6.
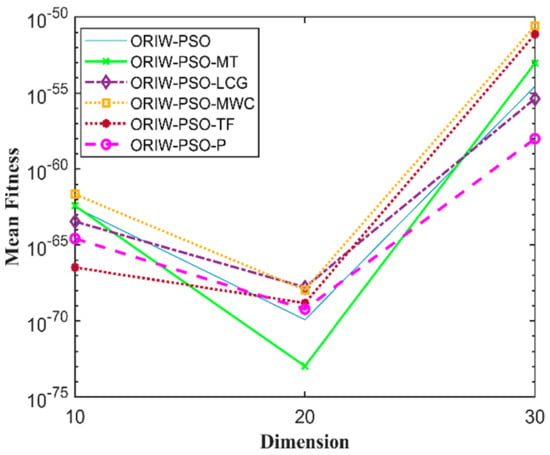
Figure 8.
Mean fitness of F7.
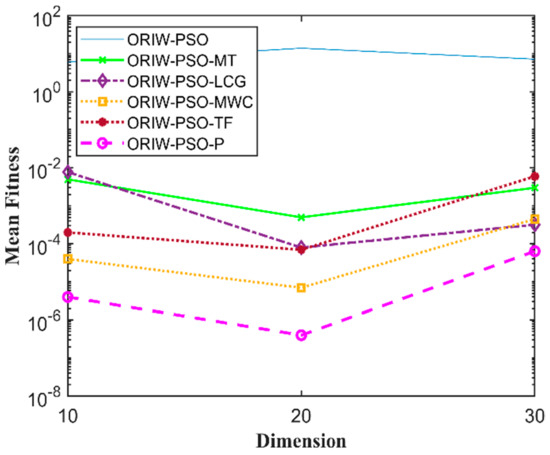
Figure 9.
Mean fitness of F8.
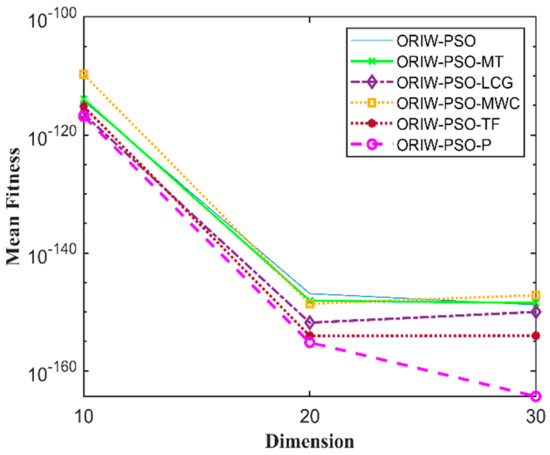
Figure 10.
Mean fitness of F9.
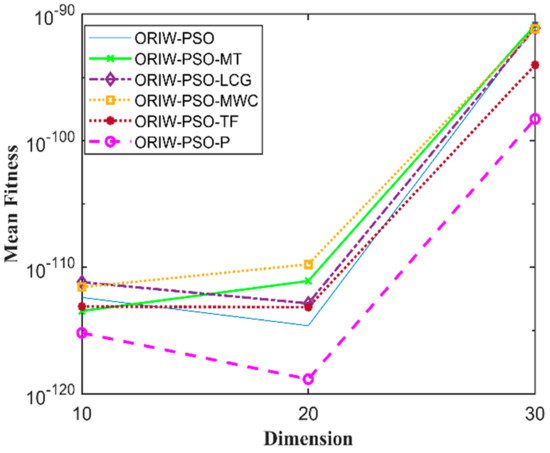
Figure 11.
Mean fitness of F10.
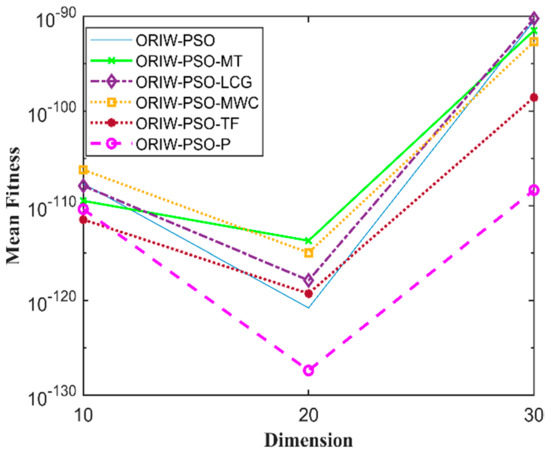
Figure 12.
Mean fitness of F11.
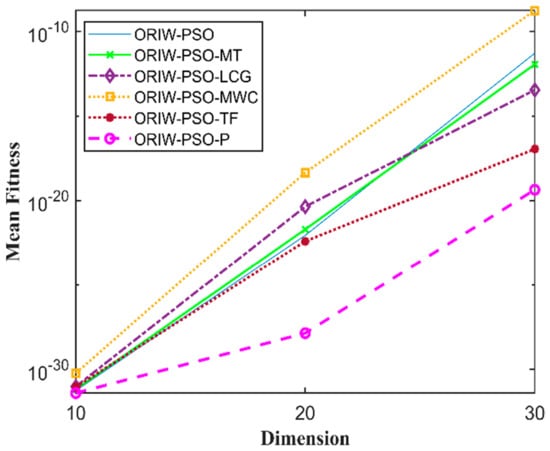
Figure 13.
Mean fitness of F12.
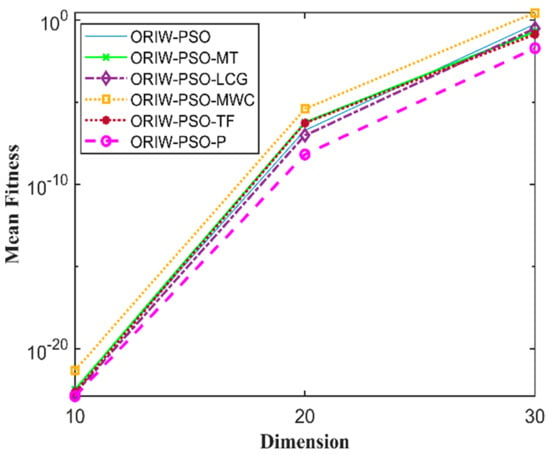
Figure 14.
Mean fitness of F13.
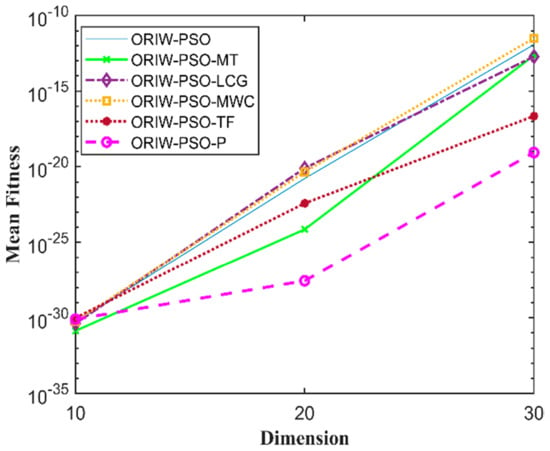
Figure 15.
Mean fitness of F14.
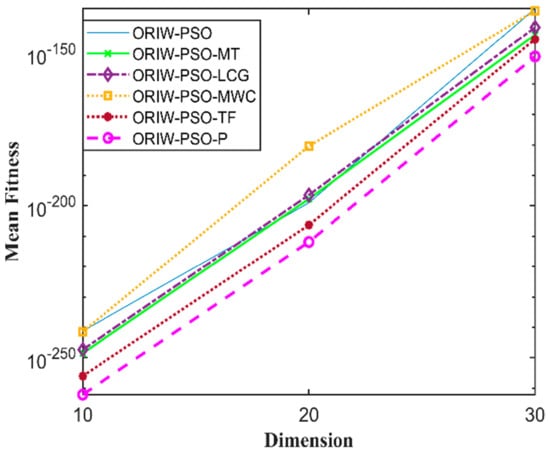
Figure 16.
Mean fitness of F15.
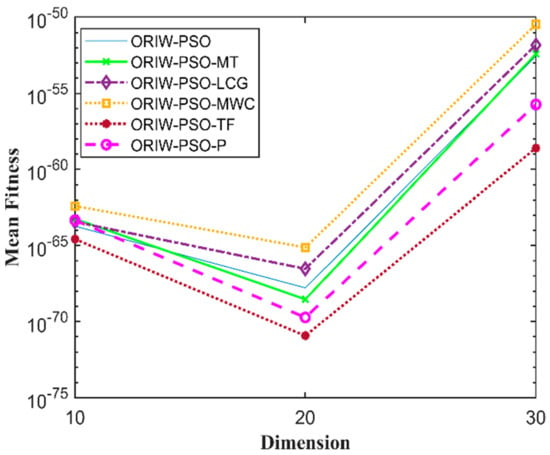
Figure 17.
Mean fitness of F16.
4.2. Statistical Test Results
The ANOVA test is used to measure the significance of different groups. One-way ANOVA is applied on the opposition-based particle swarm optimization algorithm ranked inertia weight (ORIW-PSO), Mersenne Twister with opposition-based PSO ranked inertia weight (ORIW-PSO-MT), Linear congruential generator with opposition-based PSO ranked inertia weight (ORIW-PSO-LCG), Multiply-with-carry with opposition-based PSO ranked inertia weight (ORIW-PSO-MWC), Threefry with opposition-based PSO ranked inertia weight (ORIW-PSO-TF), and Philox with opposition-based PSO ranked inertia weight (ORIW-PSO-P). Table 4 presents the results of ANOVA test.

Table 4.
ANOVA test on ORIW-PSO-P and all other variants on 30 dimension.
T-test with two samples assuming equal variance is applied on ORIW-PSO, ORIW-PSO-MT, ORIW-PSO-LCG, ORIW-PSO-MWC, ORIW-PSO-TF, and ORIW-PSO-P. Each variant is paired with ORIW-PSO-P. They are paired into (ORIW-PSO, ORIW-PSO-P), (ORIW-PSO-MT, ORIW-PSO-P), (ORIW-PSO-LCG, ORIW-PSO-P), (ORIW-PSO-MWC, ORIW-PSO-P), and (ORIW-PSO-TF, ORIW-PSO-P) in Table 5.

Table 5.
T-test on PRNG with opposition-based PSO ranked inertia weight with respect to ORIW-PSO-P 30 Dimension.
4.3. Data Classification
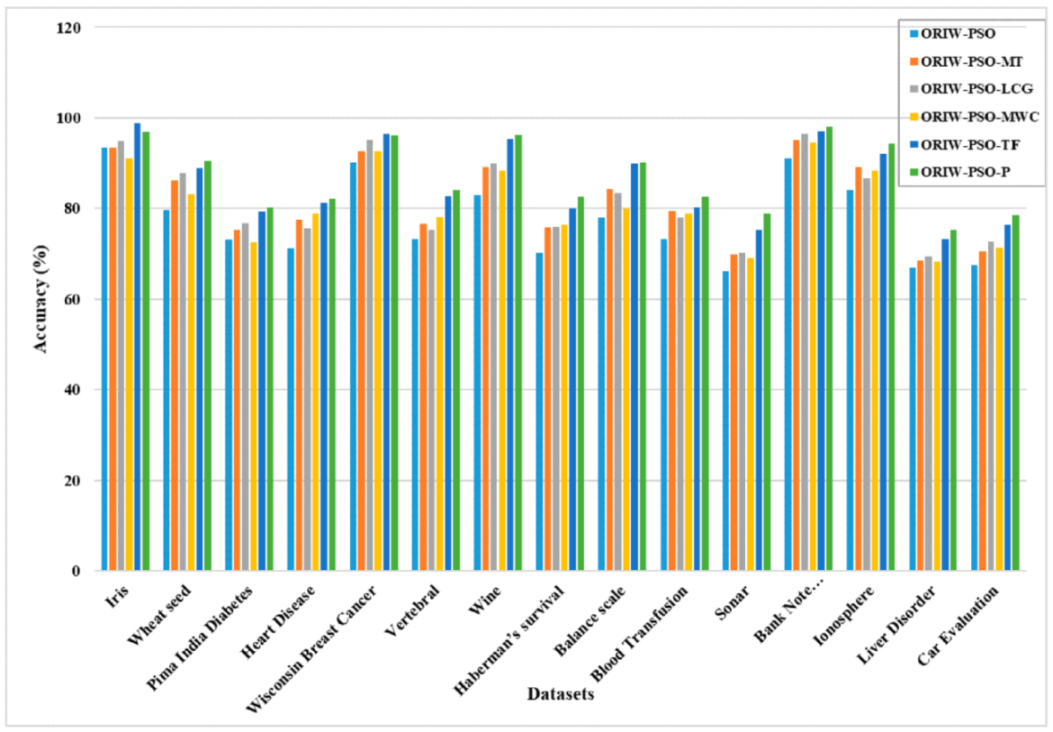
The feed forward neural network weights are trained on opposition-based particle swarm optimization algorithm ranked inertia weight (ORIW-PSO), Mersenne twister with opposition-based PSO ranked inertia weight (ORIW-PSO-MT), Linear congruential generator with opposition-based PSO ranked inertia weight (ORIW-PSO-LCG), Multiply-with-carry with opposition-based PSO ranked inertia weight (ORIW-PSO-MWC), Threefry with opposition-based PSO ranked inertia weight (ORIW-PSO-TF), and Philox with opposition-based PSO ranked inertia weight (ORIW-PSO-P). The datasets are divided into two portions: The training portion is divided at 70%, and the testing portion is divided at 30%. The proposed ORIW-PSOT-F, ORIW-PSO-P, and other neural network techniques were tested by using 15 standard benchmark datasets. The experimental results show that feedforward neural networks trained by the introduced approaches such as ORIWPSOTF and ORIWPSOP possess a positive ability in providing excellent results in data classification than compared to other improved variants.
We experimented with fifteen benchmark datasets (Iris, Wheat seed, Pima India Diabetes, Heart Disease, Wisconsin Breast Cancer, Vertebral, Wine, Haberman’s survival, Balance scale, Blood Transfusion, Sonar, Bank Note Authentication, Ionosphere, Liver Disorder, and Car Evaluation); these were extracted from the UCI repository. The summary of the dataset is present in Table 6, and accuracy results are presented in Table 7. Figure 18 show the result of accuracy. The initialization of the training weights occurs randomly in the interval [−50, 50].

Table 6.
Summary of datasets.

Table 7.
Accuracy results of FFNN classification of PRNG with opposition-based PSO ranked inertia weight.
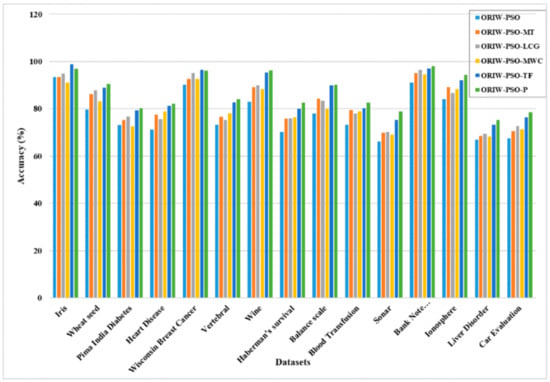
Figure 18.
Accuracy results.
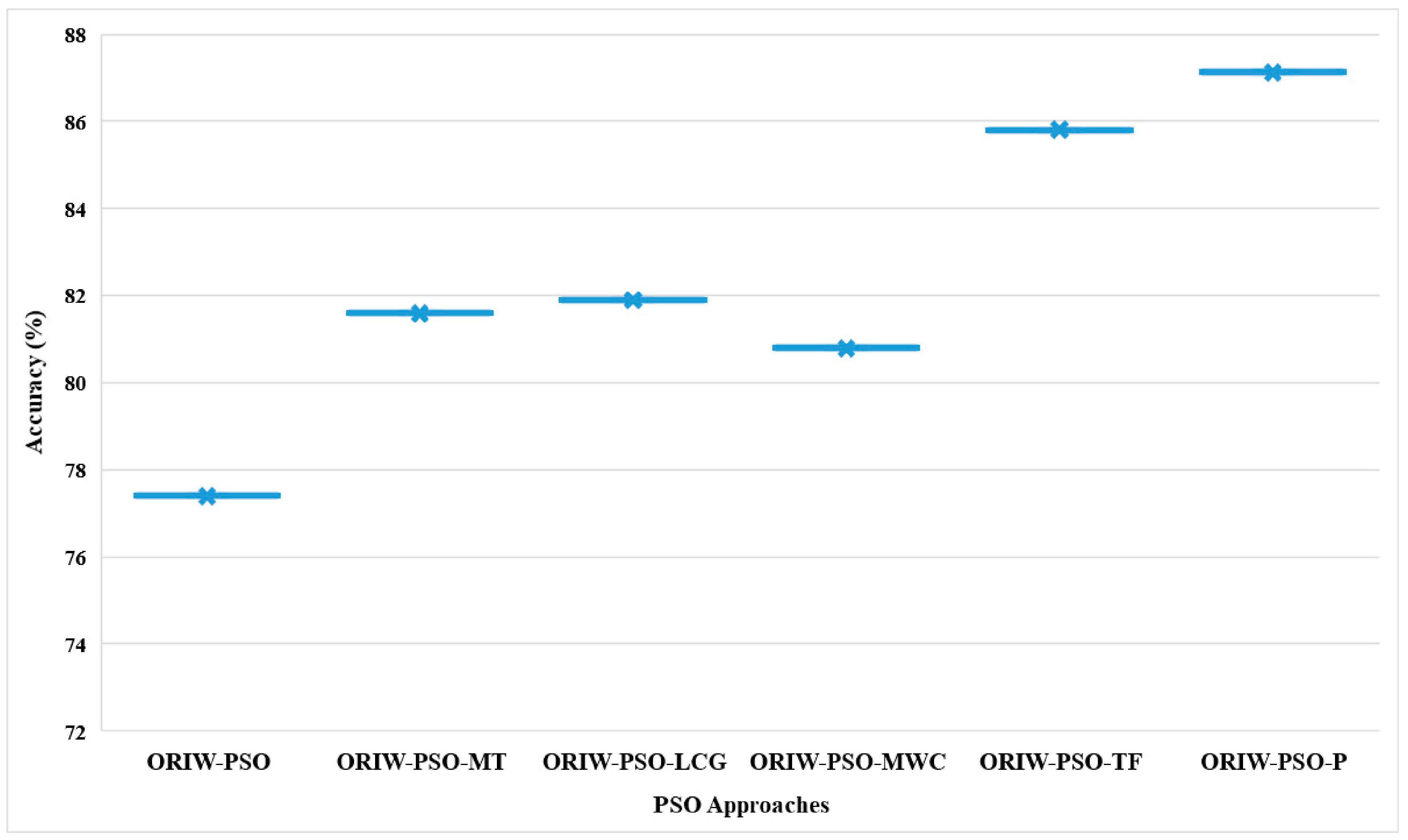
The classification results of six PSO approaches were tested by utilizing an ANOVA statistical test, and the one-way ANOVA test results are depicted in Table 8. The significance value is 0.04100 and is less than 0.05, which shows that there are significant differences between all PSO variants, with 95% confidence with respect to the results of the classification dataset using one-way ANOVA. Here, the significance is = 0.4100, and it is lower than the significance level threshold mentioned above. The results in Table 8 demonstrated that all variants of PSO are significantly different, with a confidence level of 95% [8]. Figure 19 shows a graph with the results of the one-way analysis of variance, and it is concluded that ORIW-PSO-TF and ORIW-PSO-P are perform significantly better than compared to the other variants of PSO. Based on the results in Figure 19, ORIW-PSO-TF and ORIW-PSO-P were shown to be statistically different from all PSO variants with a 95% confidence level. The graph results show that ORIW-PSO-TF and ORIW-PSO-P variants are significantly different from all other variants.

Table 8.
Accuracy results of FFNN classification of PRNG with opposition-based PSO ranked inertia weight.
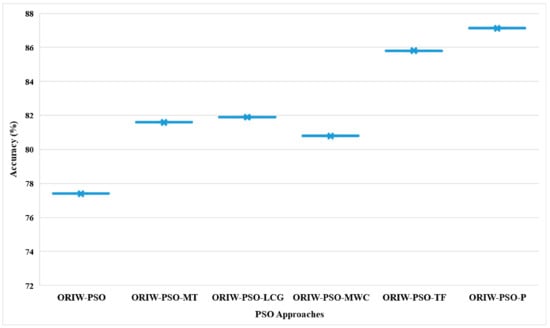
Figure 19.
One-way ANOVA test on mean testing accuracy results of PRNG with opposition-based PSO ranked inertia weight.
5. Conclusions
PSO is a nature-inspired algorithm that suffers from the problem of pre-mature convergence. Due to this problem, we proposed two newly improved variants of PSO termed as Threefry with opposition-based PSO ranked inertia weight (ORIW-PSO-TF) and Philox with opposition-based PSO ranked inertia weight (ORIW-PSO-P) by incorporating three modifications: Threefry and Philox pseudo sequences are used for initialization; opposition-based learning is used for initialization; and a novel introduction of opposition-based rank-based inertia weight is used to amplify the execution of standard PSO for the acceleration of convergence speed. The finding of the proposed variants is tested on sixteen benchmark functions and tested on the training of ANNs for data classification on real world datasets. The simulation results depict the effectiveness of the proposed variants (ORIW-PSO-TF) and (ORIW-PSO-P). The simulation results depict that the use of the pseudo-random generator family (Philox, Threefry, Mersenne Twister, Linear congruential generator, and Multiply-with-carry) maintains swarm diversity, finds optimal regions of swarm, and improves convergence speed. In this paper, we provided a comprehensive survey of the different PSO initialization opposition-based method on pseudo-random families such as Mersenne Twister (MT), Linear congruential generator (LCG), Multiply-with-carry (MWC), Threefry (TF), Philox (P), and uniform random distribution. The experimental results depict that the ORIW-PSO-P and ORIW-PSO-TF avoided being trapped in local optimal and enhanced convergence accuracy. For future investigations, our target is to research higher-dimensional problems and constrained optimization problems. Additionally, in this study, we have not modified any additional operators of algorithms such as mutation. However, it will be exciting to observe the impact of such operators with respect to low discrepancy sequences. The main purpose of this study also applies to other metaheuristic algorithms that develop future research directions with respect to our investigations.
Author Contributions
Formal analysis, D.B.R.; Investigation, W.H.B.; Methodology, K.N.; Resources, M.S.A.K.; Writing—review & editing, N.U.H. and A.A.A.I. All authors have read and agreed to the published version of the manuscript.
Funding
We would like to say thank you D. P. Kothari (IEEE Fellow & IEEE Access Journal, Senior Editor) for his valuable comments and suggestions on improving the paper. The manuscript APC is supported by Universiti Malaysia Sabah, Jalan UMS, 88400, Kota Kinabalu, Malaysia.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Slowik, A.; Kwasnicka, H. Nature Inspired Methods and Their Industry Applications-Swarm Intelligence Algorithms. IEEE Trans. Ind. Inform. 2018, 14, 1004–1015. [Google Scholar] [CrossRef]
- Blum, C. Ant Colony Optimization: Introduction and Recent Trends. Phys. Life Rev. 2005, 2, 353–373. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN‘95–International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Karaboga, D.; Basturk, B. A Powerful and Efficient Algorithm for Numerical Function Optimization: Artificial Bee Colony (ABC) Algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Bangyal, W.H.; Hameed, A.; Ahmad, J.; Nisar, K.; Haque, M.R.; Asri, A.; Ibrahim, A.; Rodrigues, J.J.P.C.; Khan, M.A.; Rawat, D.B.; et al. New Modified Controlled Bat Algorithm for Numerical Optimization Problem. Comput. Mater. Contin. 2021, 70, 2241–2259. [Google Scholar] [CrossRef]
- Yang, X.-S. A New Metaheuristic Bat-Inspired Algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Bangyal, W.H.; Nisar, K.; Asri, A.; Ag, B.; Haque, M.R.; Rodrigues, J.J.P.C.; Rawat, D.B. Comparative Analysis of Low Discrepancy Sequence-Based Initialization Approaches Using Population-Based Algorithms for Solving the Global Optimization Problems. Appl. Sci. 2021, 11, 7591. [Google Scholar] [CrossRef]
- Bangyal, W.H.; Hameed, A.; Alosaimi, W.; Alyami, H. A New Initialization Approach in Particle Swarm Optimization for Global Optimization Problems. Comput. Intell. Neurosci. 2021, 21, 17. [Google Scholar] [CrossRef] [PubMed]
- Bangyal, W.H.; Ahmed, J. An Improved Particle Swarm Optimization Algorithm with Chi-Square Mutation Strategy. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 481–491. [Google Scholar] [CrossRef]
- Nisar, K.; Sabir, Z.; Zahoor Raja, M.A.; Ibrahim, A.A.A.; Erdogan, F.; Haque, M.R.; Rodrigues, J.J.P.C.; Rawat, D.B. Design of Morlet Wavelet Neural Network for Solving a Class of Singular Pantograph Nonlinear Differential Models. IEEE Access 2021, 9, 77845–77862. [Google Scholar] [CrossRef]
- Bangyal, W.H.; Ahmad, J.; Shafi, I.; Abbas, Q. Forward only counter propagation network for balance scale weight & distance classification task. In Proceedings of the 2011 Third World Congress on Nature and Biologically Inspired Computing, Salamanca, Spain, 19–21 October 2011; IEEE: Salamanca, Spain, 2011; pp. 342–347. [Google Scholar]
- Arain, S.; Vryonides, P.; Nisar, K.; Quddious, A.; Nikolaou, S. Novel Selective Feeding Scheme Integrated with SPDT Switches for a Reconfigurable Bandpass-to-Bandstop Filter. IEEE Access 2021, 9, 25233–25244. [Google Scholar] [CrossRef]
- Bangyal, W.H.; Ahmad, J.; Rauf, H.T. Optimization of Neural Network Using Improved Bat Algorithm for Data Classification. J. Med. Imaging Health Inform. 2019, 9, 670–681. [Google Scholar] [CrossRef]
- Bangyal, W.H.; Ahmed, J.; Rauf, H.T. A Modified Bat Algorithm with Torus Walk for Solving Global Optimisation Problems. Int. J. BioInspired Comput. 2020, 15, 1–13. [Google Scholar] [CrossRef]
- Bangyal, W.H.; Ahmad, J.; Rauf, H.T.; Shakir, R. Evolving artificial neural networks using opposition based particle swarm optimization neural network for data classification. In Proceedings of the 2018 International Conference on Innovation and Intelligence for Informatics, Computing, and Technologies (3ICT), Zallaq, Bahrain, 18–19 November 2018; IEEE: Sakhier, Bahrain, 2018; pp. 1–6. [Google Scholar]
- Nisar, K.; Sabir, Z.; Zahoor Raja, M.A.; Ibrahim, A.A.A.; Rodrigues, J.J.P.C.; Khan, A.S.; Gupta, M.; Kamal, A.; Rawat, D.B. Evolutionary Integrated Heuristic with Gudermannian Neural Networks for Second Kind of Lane–Emden Nonlinear Singular Models. Appl. Sci. 2021, 11, 4725. [Google Scholar] [CrossRef]
- Waseem, Q.; Alshamrani, S.S.; Nisar, K.; Isni, W.; Wan, S. Future Technology: Software-Defined Network (SDN) Forensic. Symmetry 2021, 13, 767. [Google Scholar] [CrossRef]
- Ashraf, A.; Pervaiz, S.; Bangyal, W.H.; Nisar, K.; Asri, A.; Ibrahim, A.; Rodrigues, J.P.C.; Rawat, D.B. Studying the Impact of Initialization for Population-Based Algorithms with Low-Discrepancy Sequences. Appl. Sci. 2021, 11, 8190. [Google Scholar] [CrossRef]
- James, F. A Review of Pseudorandom Number Generators. Comput. Phys. Commun. 1990, 60, 329–344. [Google Scholar] [CrossRef] [Green Version]
- Si, T.; De, A.; Bhattacharjee, A.K. Particle swarm optimization with generalized opposition based learning in particle’s pbest position. In Proceedings of the 2014 International Conference on Circuits, Power and Computing Technologies (ICCPCT), Kumaracoil, India, 20–21 March 2014; IEEE: Nagercoil, India, 2014; pp. 1662–1667. [Google Scholar]
- Verma, O.P.; Gupta, S.; Goswami, S.; Jain, S. Opposition based modified particle swarm optimization algorithm. In Proceedings of the 8th International Conference on Computing, Communications and Networking Technologies, ICCCNT 2017, Delhi, India, 3–5 July 2017; IEEE: Delhi, India, 2017; pp. 1–6. [Google Scholar]
- Yy, M.; Jin, H.; Li, H.; Zhang, H.; Li, J. Adaptive opposition-based particle swarm optimization algorithm and application research. In Proceedings of the 2019 IEEE 4th International Conference on Signal and Image Processing (ICSIP), Wuxi, China, 19–21 July 2019; IEEE: Wuxi, China, 2019; pp. 518–523. [Google Scholar]
- Xu, H.H.; Tang, R.L. Particle swarm optimization with adaptive elite opposition-based learning for large-scale problems. In Proceedings of the 2020 5th International Conference on Computational Intelligence and Applications (ICCIA), Beijing, China, 19–21 June 2020; IEEE: Beijing, China, 2020; pp. 44–49. [Google Scholar]
- Zhou, J.; Fang, W.; Wu, X.; Sun, J.; Cheng, S. An opposition-based learning competitive particle swarm optimizer. In Proceedings of the 2016 IEEE Congress on Evolutionary Computation, CEC 2016, Vancouver, BC, Canada, 24–29 July 2016; IEEE: Vancouver, BC, Canada, 2016; pp. 515–521. [Google Scholar]
- Dong, W.; Kang, L.; Zhang, W. Opposition-Based Particle Swarm Optimization with Adaptive Mutation Strategy. IEEE Congr. Evol. Comput. 2017, 21, 5081–5090. [Google Scholar] [CrossRef]
- Kang, L. Uniform Opposition-Based Particle Swarm. In Proceedings of the 2018 9th International Symposium on Parallel Architectures, Algorithms and Programming (PAAP), Taipei, Taiwan, 26–28 December 2018; IEEE: Taipei, Taiwan, 2018; pp. 81–85. [Google Scholar]
- Farooq, M.U.; Ahmad, A.; Hameed, A. Opposition-based initialization and a modified pattern for Inertia Weight (IW) in PSO. In Proceedings of the 2017 IEEE International Conference on INnovations in Intelligent SysTems and Applications (INISTA), Gdynia, Poland, 3–5 July 2017; IEEE: Gdynia, Poland, 2017; pp. 96–101. [Google Scholar]
- Yong, J.; He, F.; Li, H.; Zhou, W. A Novel Bat Algorithm based on Collaborative and Dynamic Learning of Opposite Population. In Proceedings of the 2018 IEEE 22nd International Conference on Computer Supported Cooperative Work in Design, CSCWD 2018, Nanjing, China, 9–11 May 2018; IEEE: Nanjing, China, 2018; pp. 541–546. [Google Scholar]
- Shan, X.; Liu, K.; Sun, P.L. Modified Bat Algorithm Based on Lévy Flight and Opposition Based Learning. Sci. Program. 2016, 2016, 8031560. [Google Scholar] [CrossRef]
- Paiva, F.A.P.; Silva, C.R.M.; Leite, I.V.O.; Marcone, M.H.F.; Costa, J.A.F. Modified bat algorithm with cauchy mutation and elite opposition-based learning. In Proceedings of the 2017 IEEE Latin American Conference on Computational Intelligence (LA-CCI), Arequipa, Peru, 8–10 November 2017; IEEE: Arequipa, Peru, 2018; pp. 1–6. [Google Scholar]
- Ram, G.; Mandal, D.; Kar, R.; Ghoshal, S.P. Opposition-Based BAT Algorithm for Optimal Design of Circular and Concentric Circular Arrays with Improved Far- Fi Eld Radiation Characteristics. Int. J. Numer. Model. Electron. Netw. Devices Fields 2015, 30, 2087. [Google Scholar] [CrossRef]
- Haruna, Z. Development of a Modified Bat Algorithm using Elite Opposition—Based Learning. In Proceedings of the 2017 IEEE 3rd International Conference on Electro-Technology for National Development (NIGERCON), Owerri, Nigeria, 7–10 November 2017; IEEE: Owerri, Nigeria, 2017; pp. 144–151. [Google Scholar]
- Wahab, M.A.; Nguyen, H.X.; Roeck, G. De Damage Detection in Structures Using Particle Swarm Optimization Combined with Artificial Neural Network. Smart Struct. Syst. 2021, 1, 1–12. [Google Scholar]
- Beheshti, Z.; Mariyam, S.; Shamsuddin, H.; Beheshti, E.; Sophiayati, S. Enhancement of Artificial Neural Network Learning Using Centripetal Accelerated Particle Swarm Optimization for Medical Diseases Diagnosis. Soft Comput. 2014, 18, 2253–2270. [Google Scholar] [CrossRef]
- Yadav, A.; Peesapati, R.; Kumar, N. Electricity Price Forecasting and Classification Through Wavelet–Dynamic Weighted. IEEE Syst. J. 2017, 12, 3075–3084. [Google Scholar]
- Matsumoto, M. Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudo-Random Number Generator. ACM Trans. Model. Comput. Simul. 1998, 8, 3–30. [Google Scholar] [CrossRef] [Green Version]
- Carvajal, R.G.; Galan, J.; Torralba, A. Pseudo-Random Sequence Generators with Improved Inviolability Performance. IEE Proc.-Circuits Devices Syst. 2006, 152, 375–383. [Google Scholar]
- Boyar, J. Inferring Sequences Produced by Pseudo-Random Number Generators. J. ACM 1989, 36, 129–141. [Google Scholar] [CrossRef]
- Ecuyer, P.L. Tables of Linear Congruential Generators of Different Sizes and Good Lattice Structure. Math. Comput. 1999, 68, 249–260. [Google Scholar]
- Schroeder, M.R. Distribution Properties of Multiply-with-Carry Random Number Generators. Math. Comput. 1997, 66, 283–288. [Google Scholar]
- Salmon, J.K.; Moraes, M.A.; Dror, R.O.; Shaw, D.E.; York, N. Parallel Random Numbers: As Easy as 1, 2, 3. In Proceedings of the 2011 International Conference for High Performance Computing, Networking, Storage and Analysis, Seattle, WA, USA, 12–18 November 2011; 2011; pp. 1–12. [Google Scholar]
- Tizhoosh, H.R. Opposition-Based Learning: A New Scheme for Machine Intelligence. In Proceedings of the International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), Vienna, Austria, 28–30 November 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 695–701. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).