Eigenvalue-Based Spectrum Sensing with Small Samples Using Circulant Matrix
Abstract
:1. Introduction
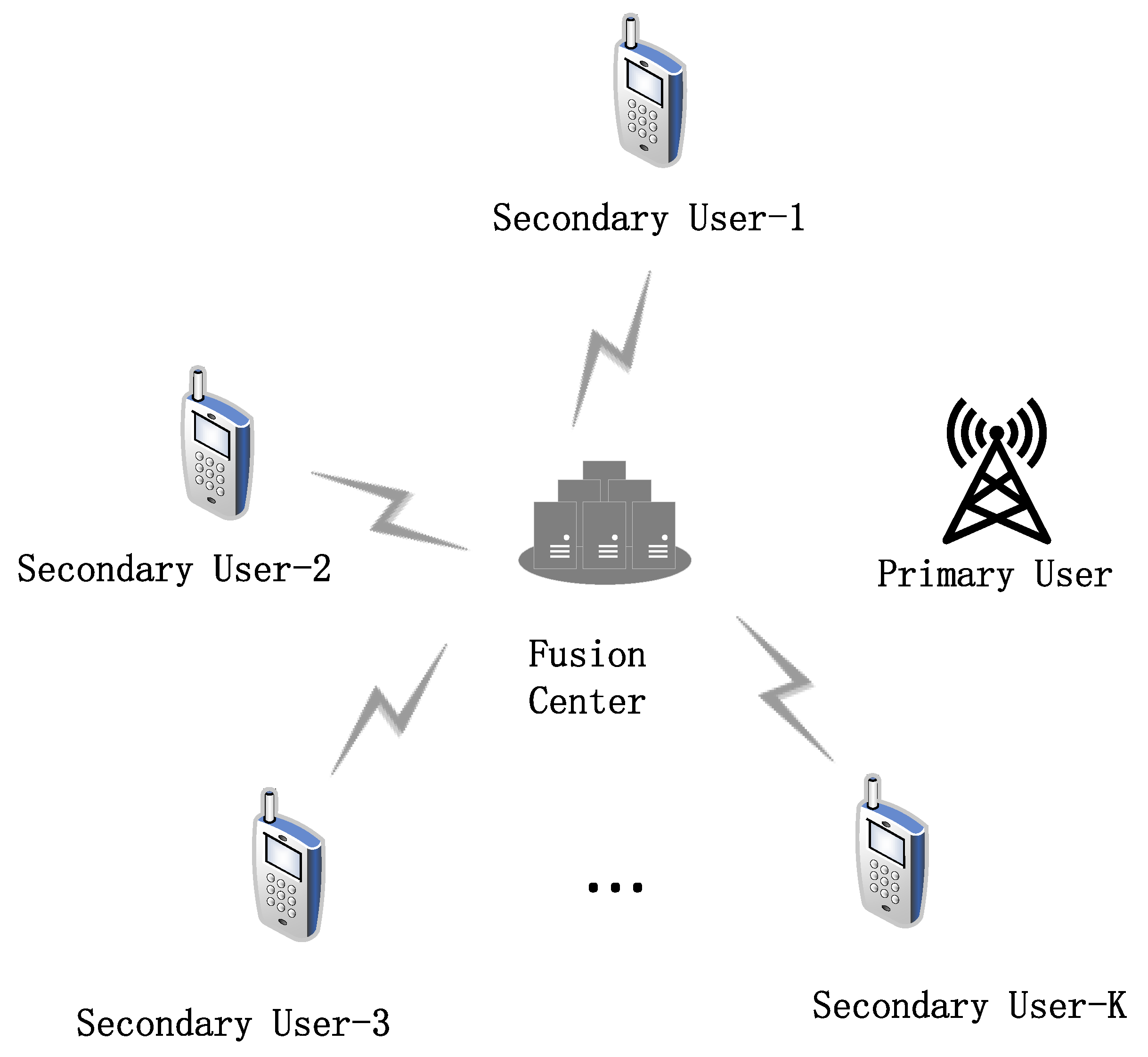
2. System Model
3. Proposed Detectors
3.1. The Average of Circulant Matrix
3.2. The Distribution of Eigenvalues of under the
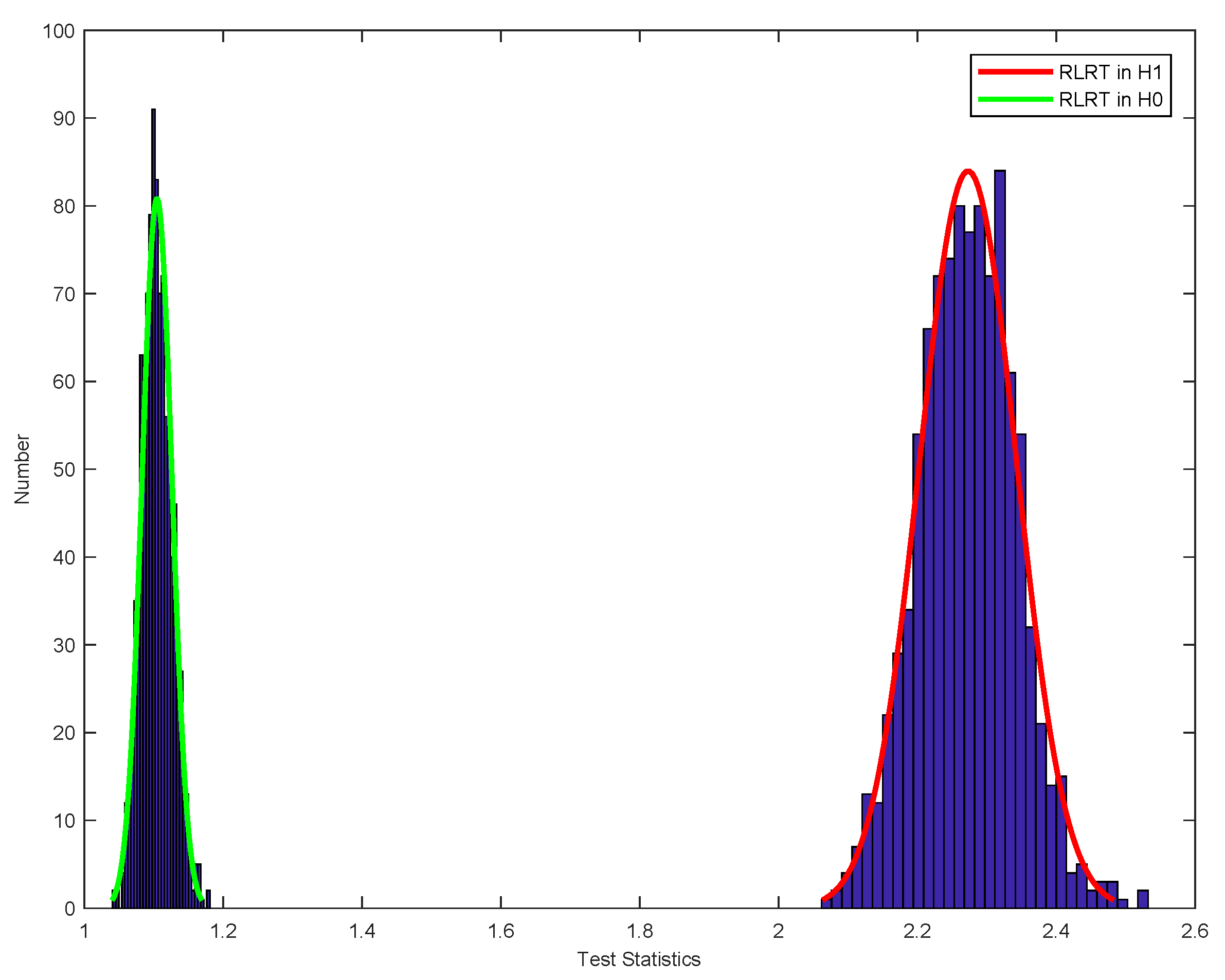
3.3. The Detector ACM-RLRT under Unknown Noise Variance
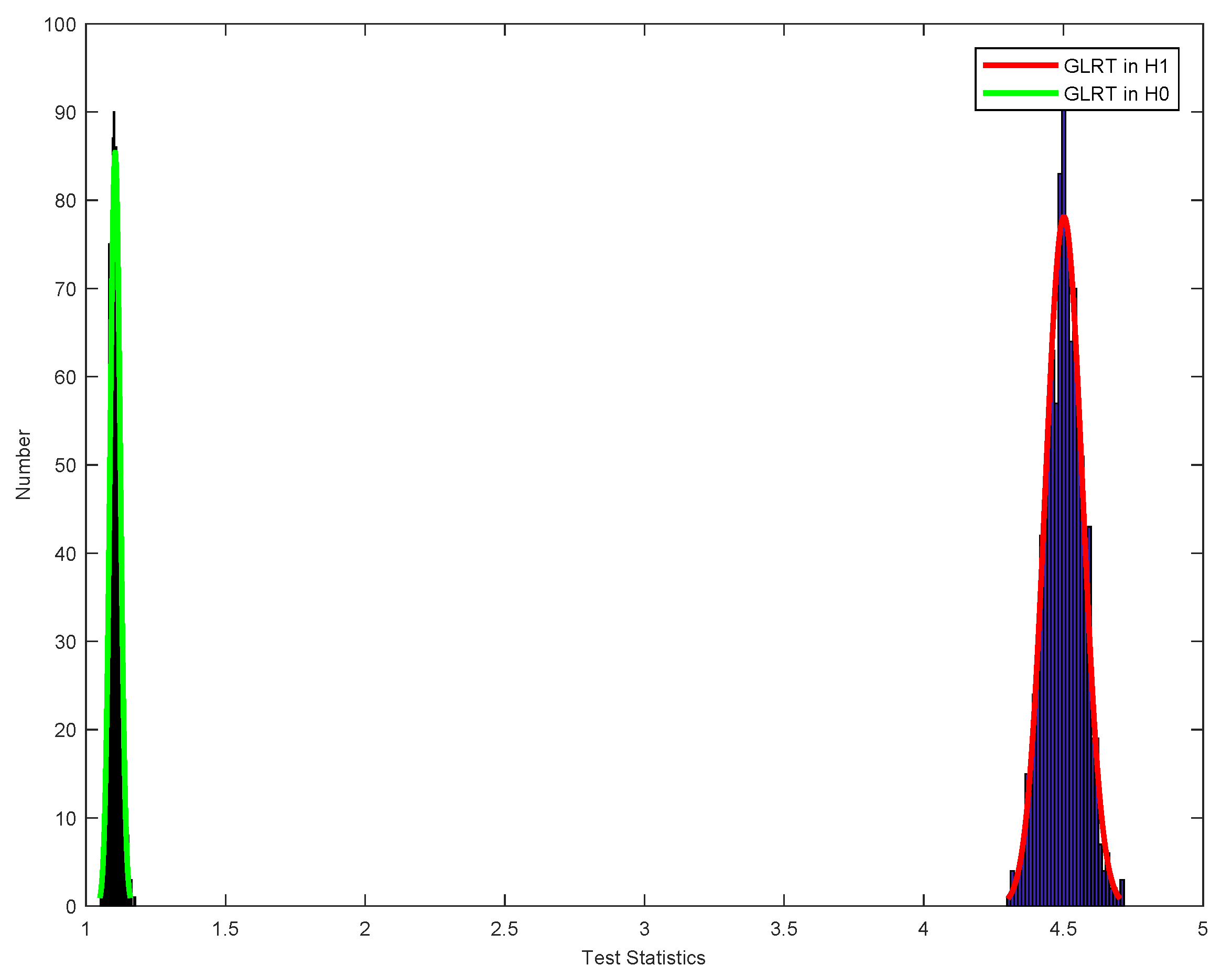
3.4. The Detector ACM-GLRT under Unknown Noise Variance
4. Performance Analysis
4.1. Performance Analysis of ACM-RLRT with Known Noise Variance
4.2. Performance Analysis of ACM-GLRT with Unknown Noise Variance
4.3. Computational Complexity
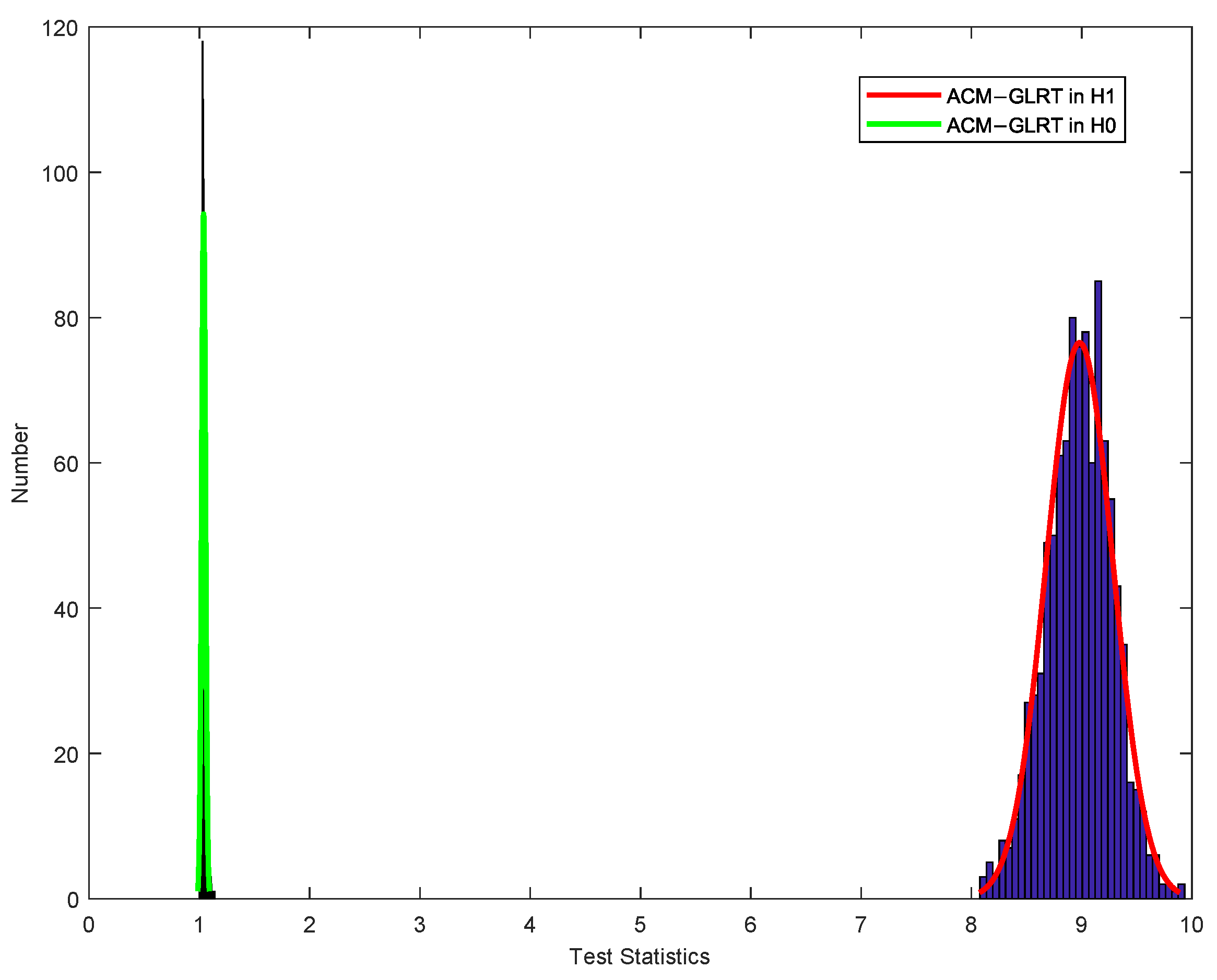
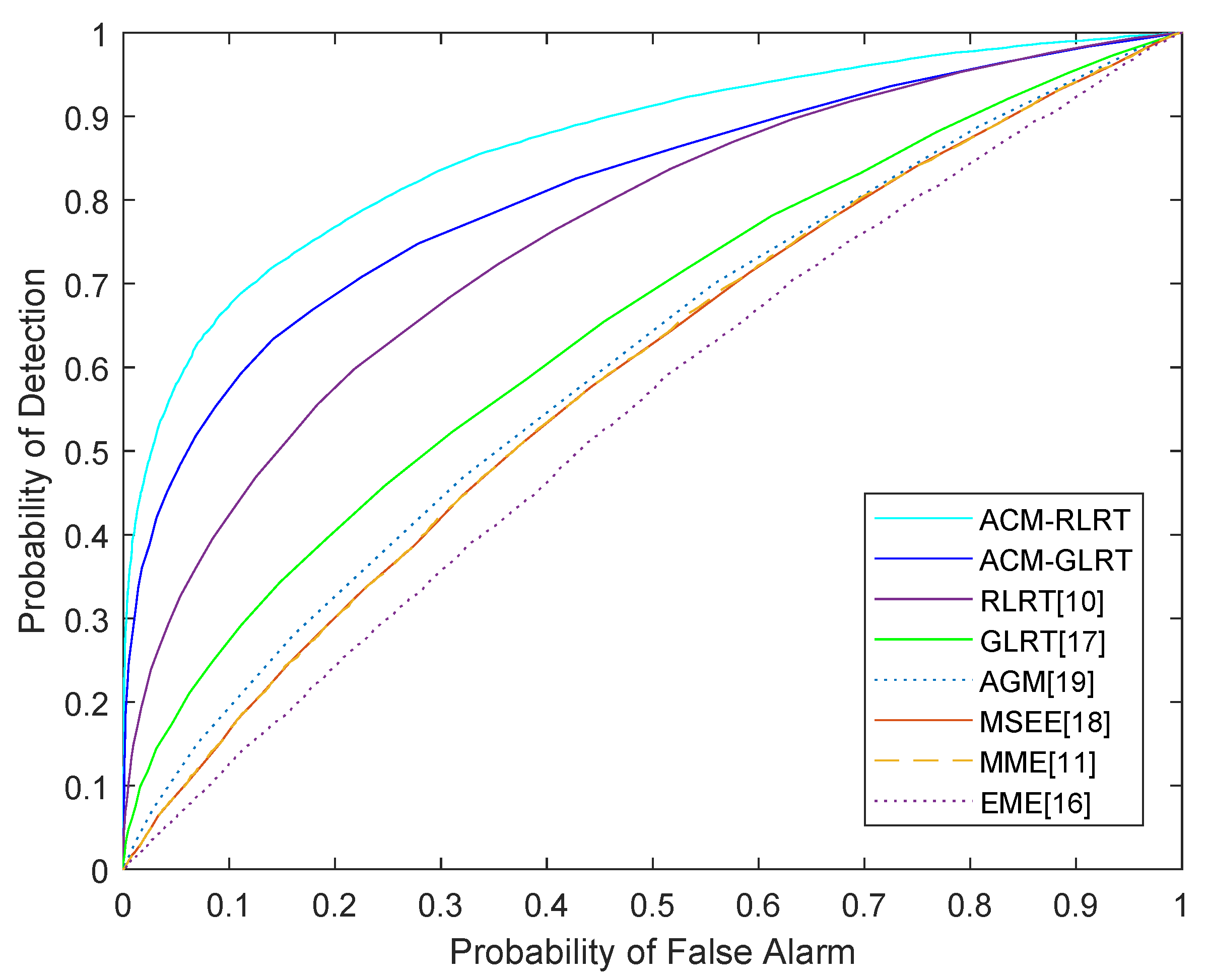
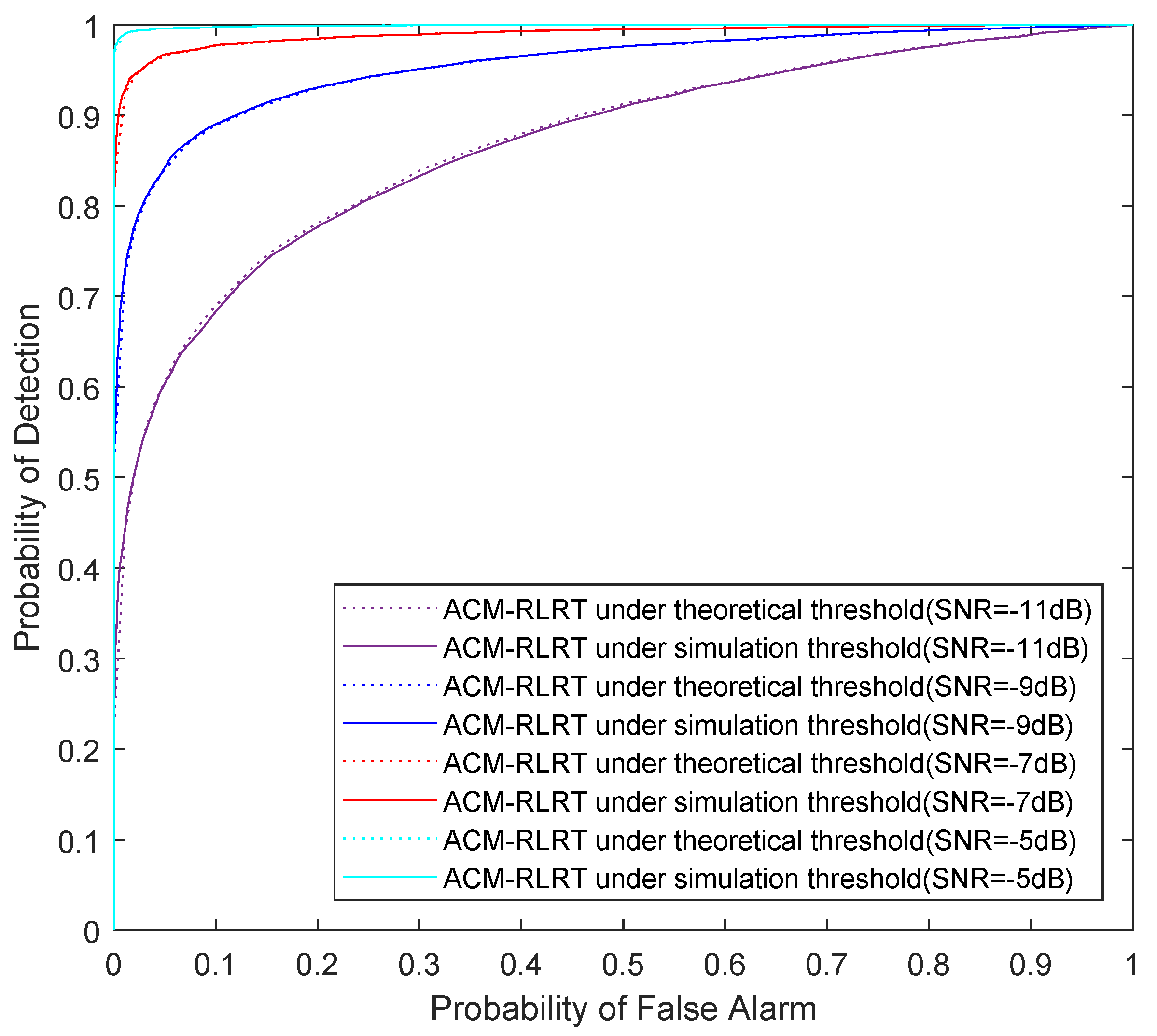
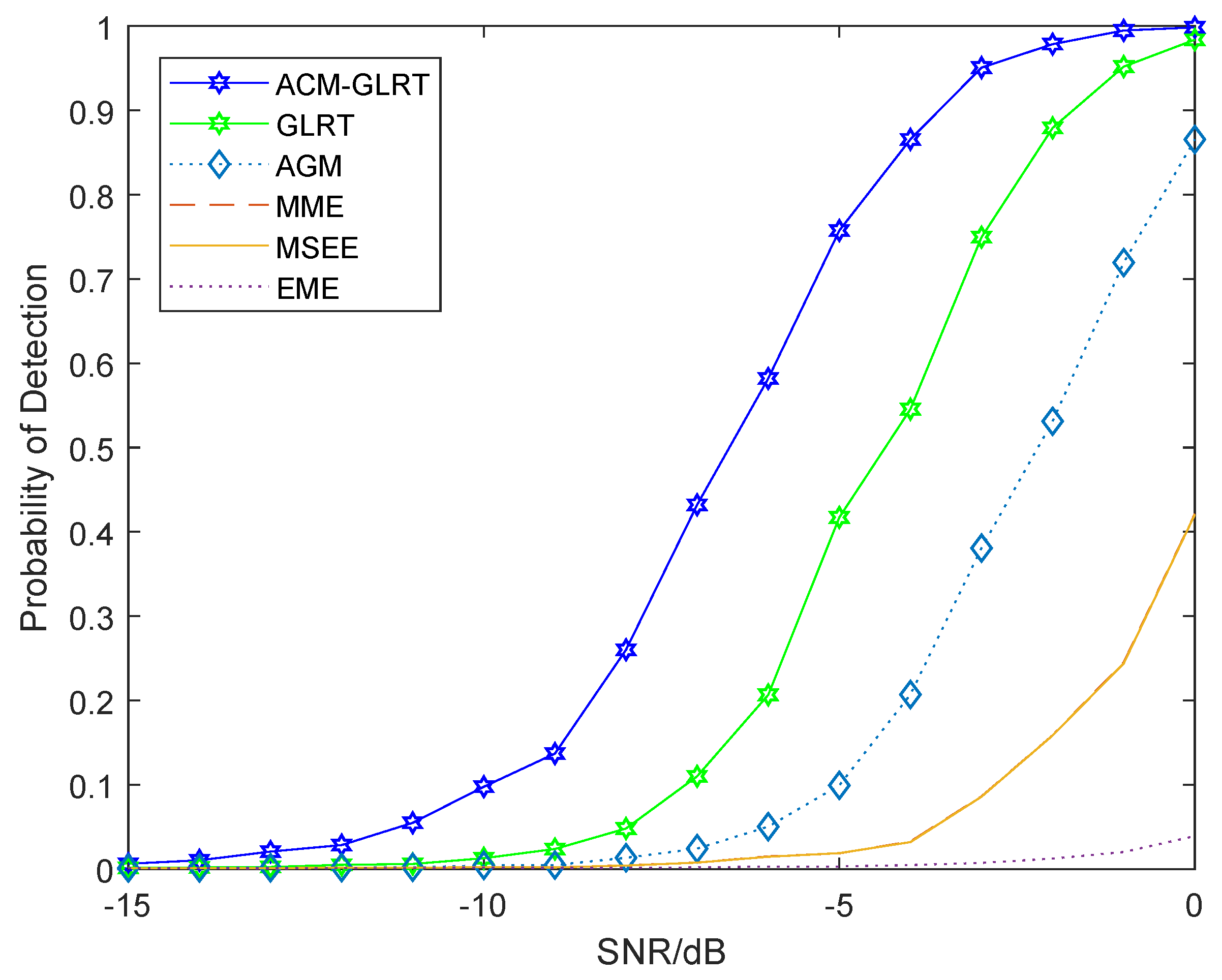
5. Simulation Results
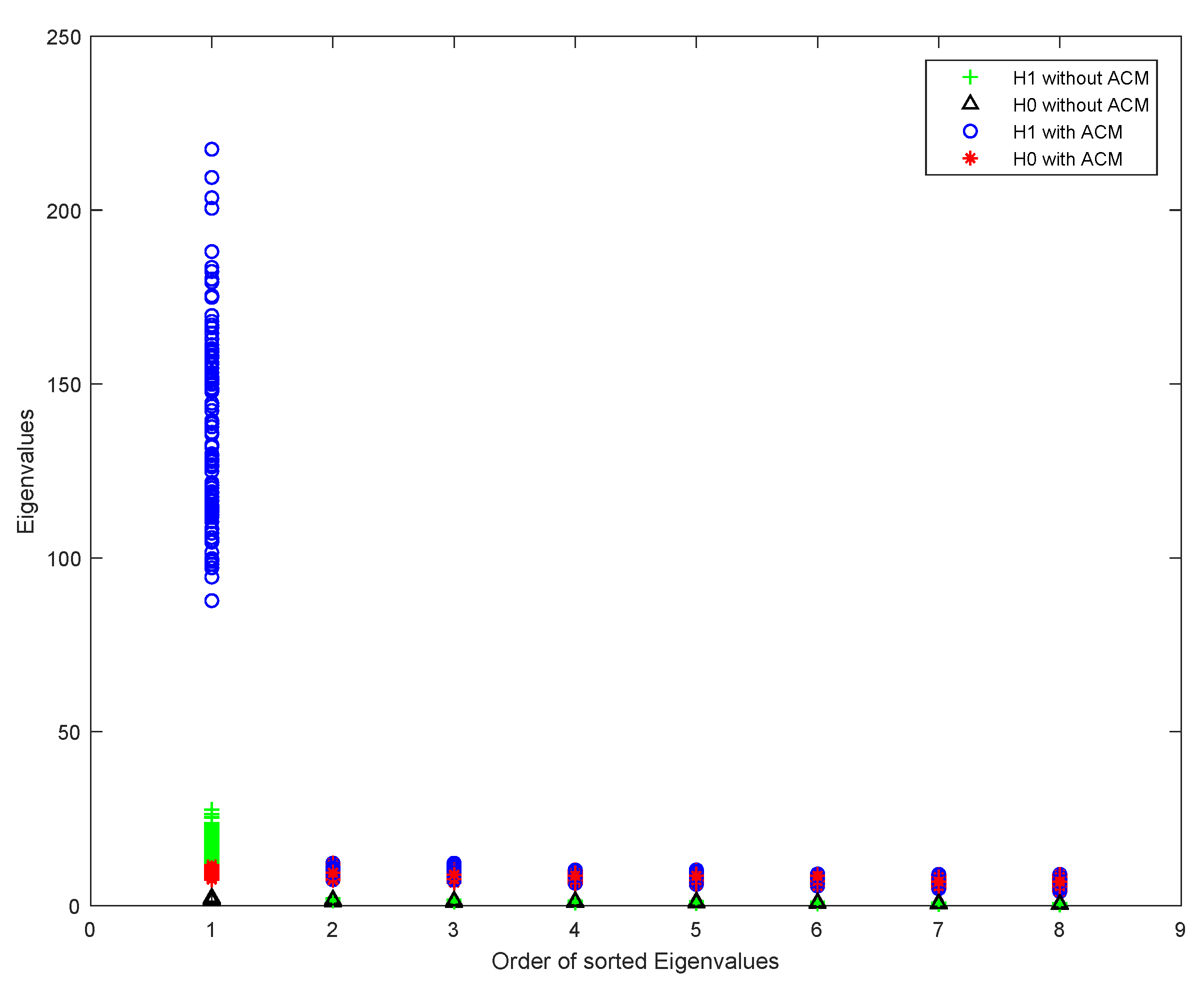
5.1. The Effect of Circulant Matrix on Eigenvalues of Covariance Matrix
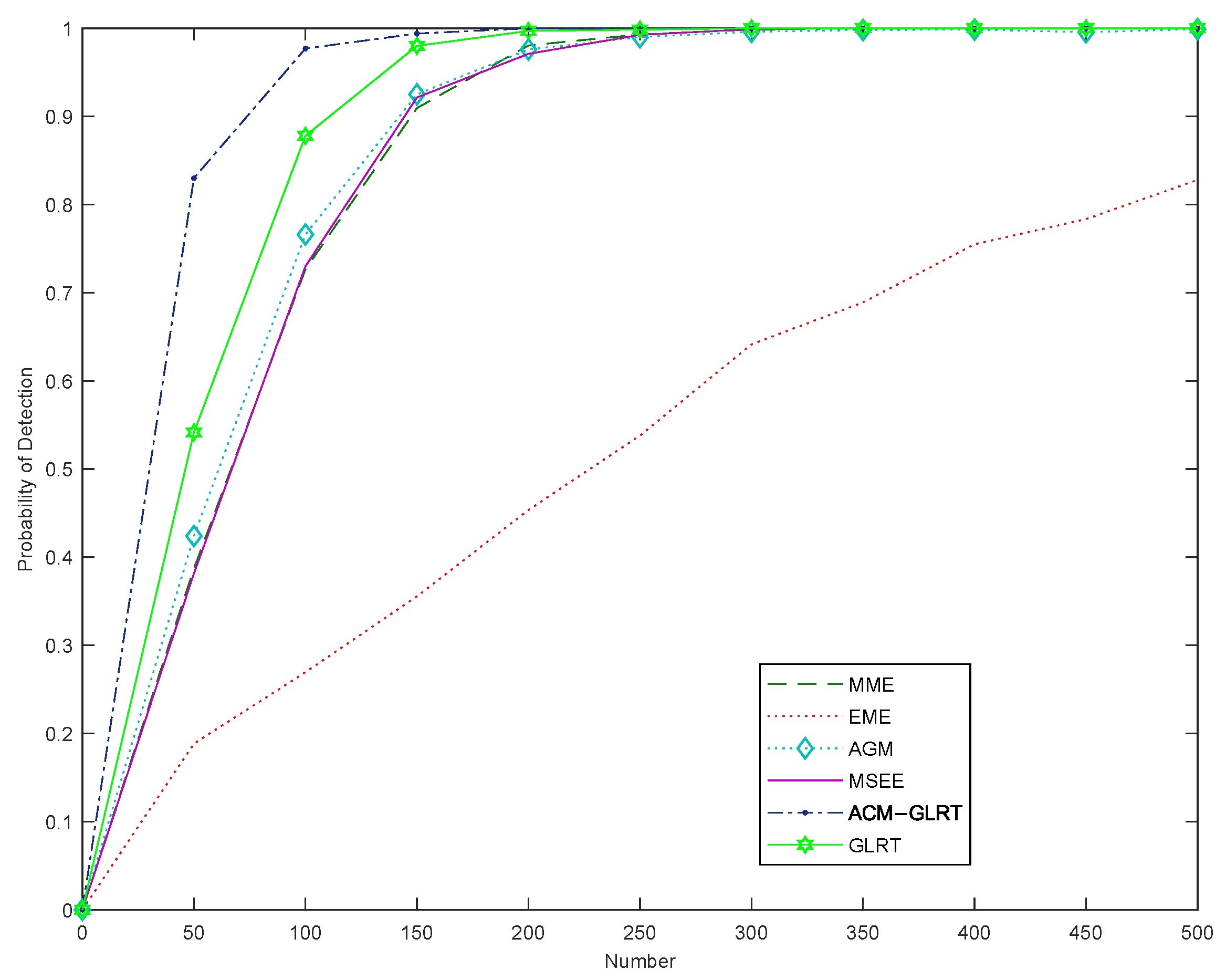
5.2. Receiver Operating Characteristic (ROC) Curve
5.3. SNR
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kale, R.S.; Wadhai, V.M.; Helonde, J.B.; Novel, T. Threshold Formulation for Energy Detection Method to Efficient Spectrum Sensing in Cognitive Radio. Sens. Image Process. 2018, 10, 25–35. [Google Scholar]
- Varalakshmi, L.M.; Sugumaran, K.; Tamilselvan, M. Matched Filter Based Spectrum Sensing on Cognitive Radio for OFDM WLANs. Int. Res. J. Eng. Technol. 2016, 3, 935–938. [Google Scholar]
- Sutton, P.D. Cyclostationary signatures in practical cognitive radio applications. IEEE J. Sel. Areas Commun. 2008, 26, 13–24. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Liu, X.; Liang, Y.-C. Maximum Eigenvalue-Based Goodness-of-Fit Detection for Spectrum Sensing in Cognitive Radio. IEEE Trans. Veh. Technol. 2019, 68, 7747–7760. [Google Scholar] [CrossRef]
- Kortun, A.; Ratnarajah, T.; Sellathurai, M.; Liang, Y.-C.; Zeng, Y. On the Eigenvalue-Based Spectrum Sensing and Secondary User Throughput. IEEE Trans. Veh. Technol. 2014, 63, 1480–1486. [Google Scholar] [CrossRef]
- Tsinos, C.G.; Berberidis, K. Decentralized Adaptive Eigenvalue Based Spectrum Sensing for Multiantenna Cognitive Radio Systems. IEEE Trans. Wirel. Commun. 2015, 14, 1703–1715. [Google Scholar] [CrossRef]
- Jain, S.A.; Deshmukh, M.M. Performance analysis of energy and eigenvalue based detection for spectrum sensing in Cognitive Radio network. In Proceedings of the International Conference on Pervasive Computing (ICPC), St. Louis, MO, USA, 23–27 March 2015. [Google Scholar]
- Ayeh, E.; Namuduri, K.; Li, X. Performance evaluation of eigenvalue based detection strategies in a sensor network. In Proceedings of the IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014. [Google Scholar]
- Nadler, B.; Penna, F.; Garello, R. Performance of Eigenvalue-Based Signal Detectors with Known and Unknown Noise Level. In Proceedings of the IEEE International Conference on Communications (ICC), Kyoto, Japan, 5–9 June 2011. [Google Scholar]
- Zeng, Y.; Liang, Y.-C. Maximum minimum eigenvalue detection for cognitive radio. In Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications(PIMRC), Athens, Greece, 3–7 September 2007. [Google Scholar]
- Hamid, M.; Bjorsell, N.; Ben Slimane, S. Signal Bandwidth Impact on Maximum-Minimum Eigenvalue Detection. IEEE Commun. Lett. 2015, 19, 395–398. [Google Scholar] [CrossRef]
- Wael, C.; Armi, N.; Rohman, B.P. Spectrum sensing for low SNR environment using maximum-minimum eigenvalue (MME) detection. In Proceedings of the International Seminar on Intelligent Technology and Its Applications (ISITIA), Lombok, Indonesia, 28–30 July 2016. [Google Scholar]
- Ali, S.S.; Zhao, W.; Jin, M.; Yoo, S.-J. Enhanced Maximum-Minimum Eigenvalue Based Spectrum Sensing. In Proceedings of the International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Korea, 16–18 October 2019. [Google Scholar]
- Chaurasiya, R.B.; Shrestha, R. Hardware-Efficient and Fast Sensing Time Maximum-Minimum-Eigenvalue-Based Spectrum Sensor for Cognitive Radio Network. IEEE Trans. Circuits Syst. 2019, 66, 142–149. [Google Scholar] [CrossRef]
- Ratnarajah, T.; Zhong, C.; Kortun, A.; Sellathurai, M.; Papadias, C.B. Complex random matrices and multiple-antenna spectrum sensing. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- Wang, P.; Fang, J.; Han, N.; Li, H. Multiantenna-Assisted Spectrum Sensing for Cognitive Radio. IEEE Trans. Veh. Technol. 2010, 59, 1791–1800. [Google Scholar] [CrossRef] [Green Version]
- Bouallegue, K.; Dayoub, I.; Gharbi, M.; Hassan, K. Blind Spectrum Sensing Using Extreme Eigenvalues for Cognitive Radio Networks. IEEE Commun. Lett. 2018, 22, 1386–1389. [Google Scholar] [CrossRef]
- Zhang, R.; Lim, T.J.; Liang, Y.-C.; Zeng, Y. Multi-antenna based spectrum sensing for cognitive radios: A GLRT approach. IEEE Trans. Commun. 2010, 58, 84–88. [Google Scholar] [CrossRef]
- Bianchi, P.; Debbah, M.; Maïda, M.; Najim, J. Performance of Statistical Tests for Single-Source Detection Using Random Matrix Theory. IEEE Trans. Inf. Theory 2011, 57, 2400–2419. [Google Scholar] [CrossRef] [Green Version]
- Lim, T.J.; Zhang, R.; Liang, Y.C.; Zeng, Y. GLRT-Based Spectrum Sensing for Cognitive Radio. In Proceedings of the IEEE Global Telecommunications Conference, New Orleans, LA, USA, 30 November–4 December 2008. [Google Scholar]
- Bai, Z.D. Methodologies in spectral analysis of large dimensional random matrices, a review. Stat. Sin. 1999, 9, 611–677. [Google Scholar]
- Tracy, C.A.; Widom, H. On orthogonal and symplectic matrix ensembles. Commun. Math. Phys. 1996, 177, 727–754. [Google Scholar] [CrossRef] [Green Version]
- Pollock, D.S.G. Circulant matrices and time-series analysis. Int. J. Math. Educ. 2002, 33, 213–230. [Google Scholar] [CrossRef]
- Rojo, O.; Rojo, H. Some results on symmetric circulant matrices and on symmetric centrosymmetric matrices. Linear Algebra Appl. 2004, 392, 211–233. [Google Scholar] [CrossRef] [Green Version]
- Priestley, M.B. Spectral Analysis and Time Series; CRC Press: Boca Raton, FL, USA, 1996; pp. 397–398. [Google Scholar]
- Lancaster, H.O. The chi-Squared Distribution. J. Oper. Res. Soc. 1970, 21, 383–384. [Google Scholar] [CrossRef]
- Balakrishnan, N.; Basu, B. Exponential Distribution: Theory, Methods and Applications, 1st ed.; Academic Press: London, UK, 1996; pp. 17–29. [Google Scholar]
- Stacy, E.W. A Generalization of the Gamma Distribution. Ann. Math. Stat. 1962, 33, 1187–1192. [Google Scholar] [CrossRef]
- Phillips, P.C.B. The True Characteristic Function of the F Distribution. Biometrika 1982, 69, 261–264. [Google Scholar] [CrossRef]
- Bowman, K.O.; Shenton, L.R.; Gailey, P.C. Distribution of the ratio of gamma variates. Commun. Stat. Simul. Comput. 1996, 27, 1–19. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, L.; Fu, Y.; Chen, Y.; Wang, X.; Zhang, X. Eigenvalue-Based Spectrum Sensing with Small Samples Using Circulant Matrix. Symmetry 2021, 13, 2330. https://doi.org/10.3390/sym13122330
Du L, Fu Y, Chen Y, Wang X, Zhang X. Eigenvalue-Based Spectrum Sensing with Small Samples Using Circulant Matrix. Symmetry. 2021; 13(12):2330. https://doi.org/10.3390/sym13122330
Chicago/Turabian StyleDu, Liping, Yuting Fu, Yueyun Chen, Xiaojian Wang, and Xiaoyan Zhang. 2021. "Eigenvalue-Based Spectrum Sensing with Small Samples Using Circulant Matrix" Symmetry 13, no. 12: 2330. https://doi.org/10.3390/sym13122330
APA StyleDu, L., Fu, Y., Chen, Y., Wang, X., & Zhang, X. (2021). Eigenvalue-Based Spectrum Sensing with Small Samples Using Circulant Matrix. Symmetry, 13(12), 2330. https://doi.org/10.3390/sym13122330





