On Stability Switches and Bifurcation of the Modified Autonomous Van der Pol–Duffing Equations via Delayed State Feedback Control

Abstract

This paper considers the Modified Autonomous Van der Pol–Duffing equation subjected to dynamic state feedback, which can well characterize the dynamic behaviors of the nonlinear dynamical systems. Both the issues of local stability switches and the Hopf bifurcation versus time delay are investigated. Associating with the $\tau$ decomposition strategy and the center manifold theory, the delay stable intervals and the direction and stability of the Hopf bifurcation are all determined. Specifically, the computation of purely imaginary roots (symmetry to the real axis), the positive real root formula for cubic equation and the sophisticated bilinear form of adjoint operators are proposed, which make the calculations mentioned in our discussion unified and simple. Finally, the typical numerical examples are shown to illustrate the correctness and effectiveness of the practical technique.

1. Introduction

Since the effective characterization of the nonlinear phenomenons, nonlinear electronic circuits have been extensively studied in the last decades by scientists, engineers and physicists [1]. The early substantial achievement can be seen in the Chua’s circuit in the mid-1960s. Since then, different nonlinear circuits were introduced by many scholars. For example, Shinriki et al. introduced a circuit representing the modified Van der Pol oscillator (MVPO) in [2]. King and Gaito derived a nonlinear circuit from the (MVPO) in [3]. Furthermore, Matouk et al. gave simple modification to the Van der Pol–Duffing circuit in [4]. It is noted that this circuit represents the autonomous Van der Pol–Duffing (AVPD) oscillator and is equivalent to Chua’s autonomous circuit but with a cubic nonlinear element.

Generally speaking, the Modified Autonomous Van der Pol–Duffing (MAVDP) equations is described by the following form:

$$\begin{array}{c}\dot{x}\left(t\right)=-\nu [x^3\left(t\right)-\mu x\left(t\right)-y\left(t\right)]\hfill \\ \dot{y}\left(t\right)=x\left(t\right)-\alpha y\left(t\right)-z\left(t\right)\hfill \\ \dot{z}\left(t\right)=\beta y\left(t\right)\hfill \end{array}$$

(1)

where $\alpha ,\beta ,\nu$ are all positive reals.

Indeed, the local codimension bifurcations are investigated in a Van der Pol–Duffing circuit with parallel resistor in [5]. In addition, a complete description of the regions with multiple small periodic solutions arise through the Hopf bifurcations has been provided. In [6], Fan investigated the existence of chaos in a modified Van der Pol–Duffing system by a rigorous verification by using topological horseshoe theory. Recently, the dynamics of a driven Van der Pol–Duffing oscillator circuit was investigated in [7]. Both the existence of higher-dimensional chaotic orbits and transient dynamics are addressed. Moreover, Han et al. propose two novel bursting patterns in modified Van der Pol–Duffing circuit system in [8]. These two bursting patterns are classified via “supHopf/supHopf” hysteresis loop. Meanwhile, by the multiple timescales method, the pure and impure quadratic damping of a hybrid Rayleigh–Van der Pol–Duffing oscillator are investigated in [9], and the various resonance states are considered exhaustively. A model of human walking is represented by a modification of hybrid Van der Pol–Duffing–Rayleigh oscillator in [10]. A stability analysis of the proposed oscillator has been performed by using the energy balance method and the Lindstedt–Poincare perturbation technique. A unified Van der Pol–Duffing circuit is used to design a memristor-based chaotic circuit by introducing an ideal and active flux-controlled memristor in [11]. Rajagopa et al. deal with a new modified hyperchaotic Van der Pol–Duffing (MVPD) snap oscillator in [12]. With the help of Lyapunov exponents, various dynamical properties are investigated. Both the stability analysis and the existence of the Hopf bifurcation is established. More recently, the generation mechanism of vibration in a driven Van der Pol–Duffing oscillator is explored in [13], and it is proved that the pitchfork bifurcation delay phenomenon deserves a prominent role in the occurrence of the mixed mode vibrations. A fractional order eco-epidemic model is addressed in [14], and the local stability analysis conditions for the existence of Hopf bifurcation are established.

For obtaining the desired dynamical behaviors, the original system in (1) can be subject to state feedback control in [15]. Moreover, the existing control methods can be classified, mainly, into two categories: the static state feedback control mode is the one in which the value of the input u at time t is a function of the value, at this time, of the state $x\left(t\right)$. In particular, one is interested in control laws of the form

$$u\left(t\right)=Kx\left(t\right)$$

Secondly, the dynamic state-feedback control mode is the one in which the value of the input u at time t is a function of the value, at this time, of the state $x\left(t\right)$ of a new input $x_t\left(\theta \right)$ and of a new set of state variables. In particular, the delayed state can be chosen as a candidate, and the control laws can be described by equations of the form

$$u\left(t\right)=K\left[x\right(t-\tau )-x(t\left)\right],\tau \ge 0.$$

To the best of the authors’ knowledge, the research on the mathematical model of MAVDP circuits with delayed feedback regulation are novelty ones, since the specific analysis of the intrinsic quality is benefit for the design of the physical circuit. It is especially suitable for the circuits with the time delay units, which are designed by the filters of T type LCL, as is pointed out in [16]. Meanwhile, the delayed circuits also can be viewed as nonlinear systems. It is worthy to analyze the dynamic nonlinear systems that are applicable for real world problems. In this paper, we will give a rigorous verification for stability switches and the Hopf bifurcation in the modified Van der Pol–Duffing system with delayed feedback. In sum, the novelties of this paper lie in the following aspects:

• Both the delay independent stable condition and the delay dependent stable interval of MAVPD in (2) are included in the framework of the $\tau$ decomposition method.
• Based on the adjoint operator theory, a lite bilinear form is introduced to reduce the amount of calculations on projection and adjoint eigenvectors.
• By solving the initial value problem of ordinary differential equation, a sophisticated procedure is addressed for the computation of Hopf bifurcation.

2. Problem Statement and Preliminaries

In this section, we state the MAVPD in a delay differential equation form and introduce the framework to deal with the issues of local analysis and the nonlinear dynamics. It includes the determination of the stability switches and the bifurcating periodic solutions associated with the $\tau$ decomposition technique and the center manifold theory.

Subjected to the dynamic state feedback control law, the original MAVPD equation in (1) can be written as

$$\begin{array}{c}\dot{x}\left(t\right)=-\nu [x^3-\mu x-y]+K[x(t-\tau )-x\left(t\right)]\hfill \\ \dot{y}\left(t\right)=x-\alpha y-z\hfill \\ \dot{z}\left(t\right)=-\beta y\hfill \end{array}$$

(2)

It is a conventional way to get the equilibrium points of system (2), and they are

$$\left\{\begin{array}{c}{E}_0=(0,0,0)\hfill \\ E_{+}=(\sqrt{\mu },0,\sqrt{\mu })\hfill \\ E_{-}=(-\sqrt{\mu },0,-\sqrt{\mu })\hfill \end{array}\right.,\mu >0\mathrm{and}{E}_0=(0,0,0),\mu <0.$$

(3)

With the notation of $X\left(t\right)={[x\left(t\right),y\left(t\right),z\left(t\right)]}^T$, the system (2) can be stated in the matrix form around the equilibrium point of $E_0$

$$\dot{X}=AX\left(t\right)+BX(t-\tau )+F\left(X\right)$$

(4)

with the corresponding Jacobian matrices such that

$$A=\left[\begin{array}{ccc}\mu \nu -K-3\nu x_0^2& \nu & 0\\ 1& -\alpha & -1\\ 0& \beta & 0\end{array}\right]\mathrm{and}B=\left[\begin{array}{ccc}K& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]\mathrm{and}F\left(X\right)=\left[\begin{array}{c}-\nu x^3\left(t\right)\\ 0\\ 0\end{array}\right].$$

(5)

There is no doubt that the local stability of the system is dependent on the linear part of (4), and the associating characteristic equation is

$$\begin{array}{c}CE\left(\lambda \right)={\lambda }^3+a{\lambda }^2+b\lambda +c-K({\lambda }^2+\alpha \lambda +\beta )e^{-\tau \lambda }\hfill \end{array}$$

(6)

with

$$\begin{array}{c}a=\alpha +K+3\nu x_0^2-\mu \nu ,\hfill \\ b=\beta +\alpha K+3\alpha \nu x_0^2-\alpha \mu \nu -\nu ,\hfill \\ c=\beta K+3\beta \nu x_0^2-\beta \mu \nu .\hfill \end{array}$$

(7)

The $\tau$ Decomposition Method

The $\tau$ decomposition method is a better choice for the local asymptotic stability analysis of systems with time delay. This technique treats the time delay as the variable parameter. In [17], this technique involves firstly dividing the delay $\tau$ axis into intervals, and the same stability character prevails within each interval. Then the crossing behaviors over the interval endpoints can determine the stability switches. Thus, there exist mainly two aspects of work. One is to calculate the interval endpoints on the delay axis, and the other is to determine whether the crossing of the endpoint is stable or not. The former one can resort to the computation of purely imaginary roots (PIR) of the system’s characteristic equation. The conjugate complex roots appear in pairs, i.e., they are symmetrical to the real axis in the complex plane. Thus, we can only consider the positive PIRs, and the later one is related to the cross directions around the PIRs. Fortunately, the number of PIRs of the transcendental equation is finite, and the cross direction on every PIR is independent of $\tau$. Now the corresponding results are introduced.

Lemma 1.

For the transcendental equation in (6), the purely imaginary roots (PIRs) are the positive real roots (PRRs) of auxiliary polynomial in ${\omega }^2$

$$W\left({\omega }^2\right)={\omega }^6+p{\omega }^4+q{\omega }^2+r$$

(8)

with

$$\begin{array}{c}p=a^2-2b-K^2\hfill \\ q=b^2-2ac+2K^2\beta -K^2{\alpha }^2\hfill \\ r=c^2-K^2{\beta }^2\hfill \end{array}.$$

(9)

Before we proceed, some simple trivial cases should be excluded by the following assumption.

Assumption 1.

The characteristic Equation (6) corresponds to no zero and multiple PIRs.

Further, the auxiliary polynomial in (8) tells us that the PIRs of (2) in (6) are quite related to the positive real roots (PRR) of cubic polynomial in (8). Thus, a targeted result on the positive real roots is deduced.

Lemma 2. 

For the cubic equation

$${\lambda }^3+p{\lambda }^2+q\lambda +r=0,$$

(10)

the positive real roots (PRR) are defined such that:

(i)

There is one distinct PRR, if and only if

$${\displaystyle r<0,\left\{\begin{array}{c}\mathsf{\Delta }>0\hfill \\ \mathsf{\Delta }<0,{\mathsf{\Delta }}_1<0\hfill \\ \mathsf{\Delta }=0,pq>0\hfill \end{array}\right\}}$$

(11)

and it is

$${\lambda }_1=S+T-\frac{p}{3}.$$

(12)

(ii)

There are two distinct PRRs, if and only if

$$\mathsf{\Delta }<0,{\mathsf{\Delta }}_2>0,r>0$$

(13)

and they are

$$\begin{array}{c}{\lambda }_2=wS+w^{2}T-\frac{p}{3}\hfill \\ {\lambda }_3=w^{2}S+wT-\frac{p}{3}.\hfill \end{array}$$

(14)

(iii)

There exist three distinct PRRs, if and only if

$$\mathsf{\Delta }<0,{\mathsf{\Delta }}_1>0,r<0$$

(15)

and they are (12) and (14), in which

$$\begin{array}{cc}w=\frac{-1+\sqrt{3}j}{2},\hfill & S=\sqrt[3]{-\frac{Q}{2}+\sqrt{\mathsf{\Delta }}},\hfill \\ P=q-\frac{p^2}{3},\hfill & T=\sqrt[3]{-\frac{Q}{2}-\sqrt{\mathsf{\Delta }}},\hfill \\ Q=r+\frac{2p^3}{27}-\frac{pq}{3},\hfill & {\mathsf{\Delta }}_1=-\frac{p}{3}-\sqrt{p^2-3q},\hfill \\ \mathsf{\Delta }=\frac{Q^2}{4}+\frac{P^3}{27},\hfill & {\mathsf{\Delta }}_2=-\frac{p}{3}+\sqrt{p^2-3q}.\hfill \end{array}$$

(16)

Proof. 

See in the Appendix A. □

Meanwhile, the issue of cross directions over PIRs is relatively concise according to the discussion in [18], and it is summarized in the next statement.

For convenience, we call those ${\omega }_i$s such that

$${\omega }_1>{\omega }_2>{\omega }_3$$

are the cross frequencies (CF). Moreover, the cross directions (CD) over those CFs are summarized below.

Remark 1.

As is clearly shown in [18], the CD at the largest CF of ${\omega }_1$ is always to the right (the unstable crossing), at ${\omega }_2$ is always to the left (the stable crossing), and at ${\omega }_3$ is still unstable crossing.

On the other hand, the eigen-decomposition theory tells us that, the divide of the subspace corresponding to PIR $j{\omega }_0$ needs the eigen-vector and the adjoint vector associating with $\pm j\omega$. Therefore, we first introduce a distinguished bilinear form for the eigenvalue decomposition in the analysis of nonlinear dynamics of (2).

Lemma 3.

For X and Y are the solutions of the linearized system in (2) and its adjoint system

$$\dot{Y}\left(s\right)=A^{T}Y\left(s\right)+B^{T}Y(s+\tau ),$$

(17)

respectively. The value of bilinear form

$$I={\overline{Y}}^T\left(0\right)X\left(0\right)+{\int }_{-\tau }^0{\overline{Y}}^T(\xi +\tau )BX\left(\xi \right)d\xi$$

(18)

can be called the inner product $<Y,X>$.

3. Main Results

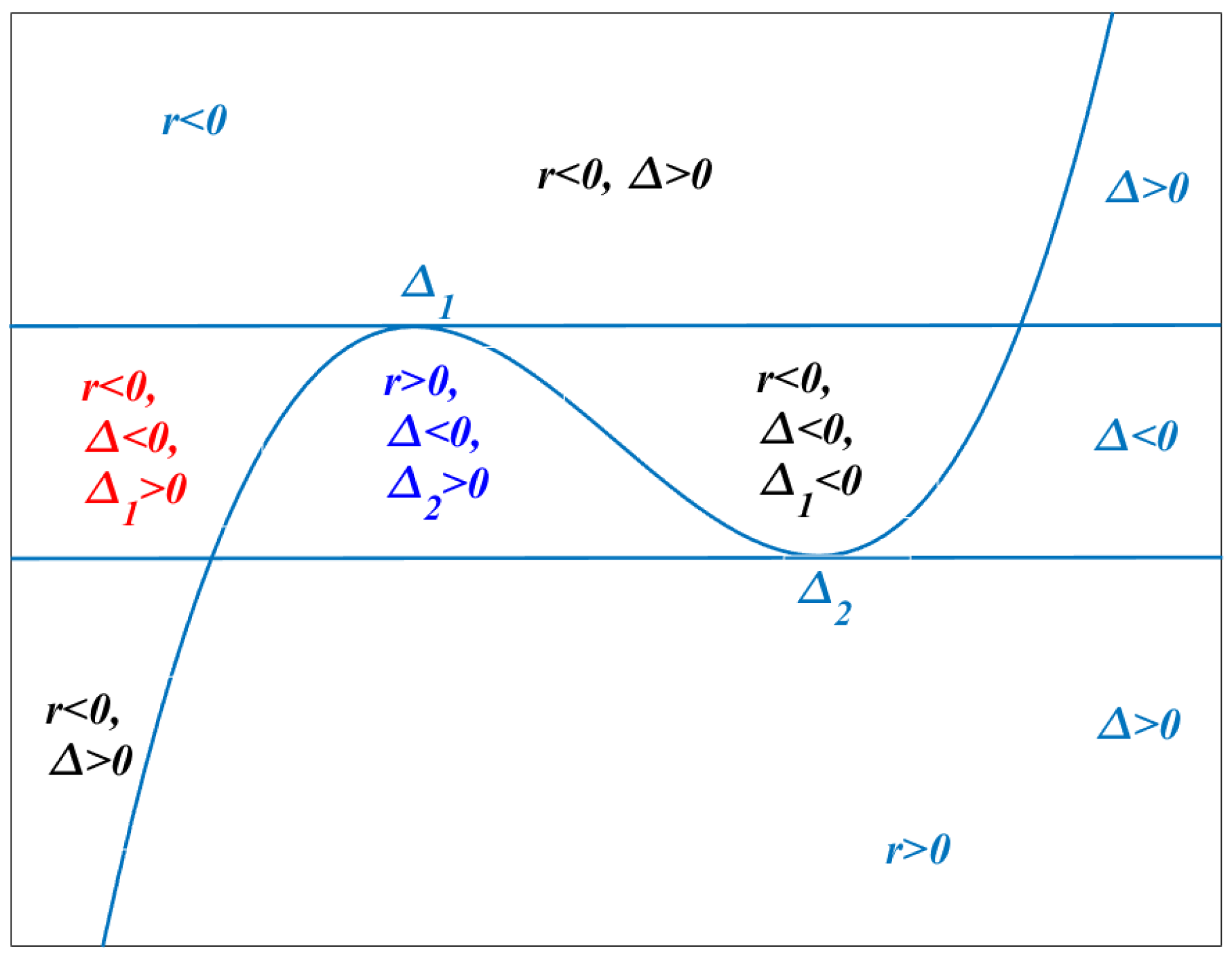
3.1. The Issue of Linear Analysis

In this section, the phenomenon of stability switch is investigated in a unified manner, and the occurrence of Hopf bifurcation is revealed as well.

Before we proceed, necessary statements and definitions should be introduced according to the discussion mentioned above.

As is indicated in Lemma 2, we can obtain all the PIRs analytically depending on the three number conditions. In practice, every $j{\omega }_i$ corresponds to a series of critical delays,

$$T_i=\left\{{\tau }_{ik}\left|{\tau }_{ik}={\tau }_{0i}+\frac{2k\pi }{{\omega }_i}\right.\right\},\begin{array}{c}i=1,2,3.\hfill \\ k=0,1,2,3,\cdots .\hfill \end{array}$$

(19)

with ${\tau }_{0i}=\frac{{\theta }_i}{{\omega }_i}$ being the smallest positive real such that

$${\displaystyle {\theta }_i=\left\{\begin{array}{c}\angle \left[\frac{\beta -{\omega }^2+\alpha \omega j}{c-a{\omega }^2+(b\omega -{\omega }^3)j}+\pi \right],0<\angle \frac{\beta -{\omega }^2+\alpha \omega j}{c-a{\omega }^2+(b\omega -{\omega }^3)j}<\pi \\ \angle \left[\frac{\beta -{\omega }^2+\alpha \omega j}{c-a{\omega }^2+(b\omega -{\omega }^3)j}-\pi \right],\pi <\angle \frac{\beta -{\omega }^2+\alpha \omega j}{c-a{\omega }^2+(b\omega -{\omega }^3)j}<2\pi \end{array}\right.}$$

(20)

Definition 1.

The MAVPD system is the initial stable means that the roots of the characteristic equation of the system in (6) are all with negative real parts when $\tau =0$.

Theorem 1.

For the initial stable MAVPD system in (2), the local dynamics satisfy:

(i) The delay dependent stable interval for $\tau \in [0,{\tau }_{10})$, with the one PIR condition in (11).

(ii) The delay $N+1$ dependent stable interval for N such that

$${\displaystyle max\left\{N\left|\frac{{\tau }_{2N}-{\tau }_{20}}{{\tau }_{1N}-{\tau }_{10}}<\frac{{\omega }_1}{{\omega }_2}\right.\right\},and}$$

$${\displaystyle max\left\{N\left|({\tau }_{2N}-{\tau }_{20}){\omega }_2<({\tau }_{1m}-{\tau }_{10}){\omega }_1+({\tau }_{3n}-{\tau }_{30}){\omega }_3\right.\right\}}$$

with the two and three PIRs conditions in (13) and (15), respectively, where $N=0,1,2,\cdots andm+n\le N$.

Moreover, there exists a Hopf bifurcation of system (2) when the delay passes through those critical delays ${\tau }_{ij}s$ from stable (unstable) interval into unstable (stable) interval.

Proof. 

Associating with the initial stable MAVPD and the one PIR condition which corresponds to unstable crossing, the system becomes unstable after ${\tau }_{10}$, and it will never return, for all the crossings associated with ${\omega }_1$ are unstable. Then, the result for only one delay interval is obtained. In the case of three-PIR condition, the delay stable intervals must satisfy

$${\displaystyle \frac{({\tau }_{2N}-{\tau }_{20}){\omega }_2}{2\pi }<\frac{({\tau }_{1m}-{\tau }_{10}){\omega }_1}{2\pi }+\frac{({\tau }_{3(N-m)}-{\tau }_{30}){\omega }_3}{2\pi }}$$

(21)

in which

$$\frac{({\tau }_{2N}-{\tau }_{20}){\omega }_2}{2\pi }$$

are the times of stable crossings and

$$\frac{({\tau }_{1m}-{\tau }_{10}){\omega }_1}{2\pi }+\frac{[{\tau }_{3(N-m)}-{\tau }_{30}]{\omega }_3}{2\pi }$$

are the times of unstable crossings. The condition of (21) guarantees the stable crossing comes before the unstable crossing. The two-PIR condition is a special case mentioned above. Therefore, we get the stability switches. □

Corollary 1.

For the intimal unstable MVPD system in (2), it is delay N interval dependent stable for N such that

$${\displaystyle max\left\{N\left|\frac{{\tau }_{2N}-{\tau }_{20}}{{\tau }_{1N}-{\tau }_{10}}<\frac{{\omega }_1}{{\omega }_2}\right.\right\},and}$$

$${\displaystyle max\left\{N\left|({\tau }_{2N}-{\tau }_{20}){\omega }_2<({\tau }_{1m}-{\tau }_{10}){\omega }_1+({\tau }_{3n}-{\tau }_{30}){\omega }_3\right.\right\}}$$

with the two- and three-PIR conditions in (13) and (15), respectively, where $N=0,1,2,\cdots andm+n\le N$.

Moreover, there exists a Hopf bifurcation of system (2) when the delay passes through those critical delays ${\tau }_{ij}s$ from stable (unstable) interval into unstable (stable) interval.

Remark 2.

With the discussion mentioned above, the Hopf bifurcation occurs when the delay passes through those critical delays $T_{ik}$ from stable (unstable) interval into unstable (stable) interval.

3.2. The Issue of Periodical Solutions

In this section, we will rescale the MAVPD equation in (2) by ${\displaystyle t_{new}=\frac{t_{old}}{\tau }}$. Then, the time delay is tacked with the bifurcating parameter, and we have

$$\dot{X}\left(t\right)=\tau AX\left(t\right)+\tau BX(t-1)+F\left(X_t\right)$$

(22)

with

$$F=\left[\begin{array}{c}-\tau \nu X_t^{\left(1\right)}{\left(0\right)}^3\\ 0\\ 0\end{array}\right]$$

The abstract differential equation is

$${\dot{X}}_t=L{X}_t+R{X}_t.$$

(23)

The linear operator L satisfies

$${\displaystyle L\phi \left(\theta \right)=\left\{\begin{array}{c}\frac{d\phi }{d\theta },-1\le \theta <0\\ {\int }_{-1}^{0}d\eta \left(s\right)\phi \left(s\right),\theta =0\end{array}\right.}$$

(24)

with

$$d\eta \left(\theta \right)=\tau \left[A\delta \right(\theta )+B\delta (\theta +1\left)\right],$$

and $\delta (·)$ is the Dirac delta function.

Then, the nonlinear part is as follows:

$$R{X}_t\left(\theta \right)=\left\{\begin{array}{c}\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right],-1\le \theta <0\\ \left[\begin{array}{c}{f}_1\\ 0\\ 0\end{array}\right],\theta =0\end{array}\right.$$

(25)

with $f_1=-\nu X_t^{\left(1\right)}{\left(0\right)}^3$.

Moreover, the linear operator L is adjoint with the operator of $L^{*}$ such that

$${\displaystyle L^{*}\psi \left(\theta \right)=\left\{\begin{array}{c}-\frac{d\psi }{d\theta },0<\theta \le 1\hfill \\ {\int }_{-1}^{0}d{\eta }^T\left(t\right)\psi (-t),\theta =0\hfill \end{array}\right.}$$

(26)

associating with the simplified inner product by Lemma 3,

$$<\psi ,\phi >={\overline{\psi }}^T\left(0\right)\left[I+e^{-j{\omega }_0}B\right]\phi \left(0\right).$$

(27)

Therefore, we can determine the adjoint vector for constructing the center manifold through the following statement.

Lemma 4.

The eigenvectors of linear operator L and its adjoint $L^{*}$ associate with $j{\omega }_0$ such that

$$q\left(\theta \right)=\left[\begin{array}{c}1\\ q_2\\ q_3\end{array}\right]e^{j{\omega }_0\theta }$$

(28)

and

$$q^{*}\left(s\right)=D\left[\begin{array}{c}1\\ q_2^{*}\\ q_3^{*}\end{array}\right]e^{j{\omega }_{0}s}$$

(29)

satisfying $<q,q^{*}>=1,<\overline{q},q^{*}>=0$, in which

$$\begin{array}{c}{q}_2=j{\omega }_0\chi ,\hfill \\ q_3=\tau \beta \chi ,\hfill \\ q_2^{*}=-j{\omega }_0\nu \overline{\chi },\hfill \\ q_3^{*}=-\tau \nu \overline{\chi }\hfill \\ D={\left[1+{\overline{q}}_2{q}_2^{*}+{\overline{q}}_3{q}_3^{*}+\tau K{e}^{j{\omega }_0}\right]}^{-1}\hfill \end{array}$$

(30)

with

$$\chi =\frac{\tau }{{\tau }^2\beta -{\omega }_0^2+\tau \alpha {\omega }_{0}j}.$$

Proof. 

As the eigenvector of differential operator L associating with $j{\omega }_0$ such that $Lq\left(\theta \right)=j{\omega }_{0}q\left(\theta \right)$, we have

$$q\left(\theta \right)=q\left(0\right)e^{j\omega \theta }.$$

Moreover, $Lq\left(0\right)={\int }_{-1}^{0}d\eta \left(s\right)q\left(s\right)=j{\omega }_{0}q\left(0\right)$ gives the matrix equation

$$\tau Aq\left(0\right)+\tau Bq\left(0\right)e^{-j{\omega }_0}=j{\omega }_{0}q\left(0\right).$$

Thus,

$$q\left(\theta \right)=\left[\begin{array}{c}1\\ \frac{j{\omega }_0\tau }{{\tau }^2\beta -{\omega }_0^2+\tau \alpha {\omega }_{0}j}\\ \frac{{\tau }^2\beta }{{\tau }^2\beta -{\omega }_0^2+\tau \alpha {\omega }_{0}j}\end{array}\right]e^{j{\omega }_0\theta }.$$

On the other hand, the adjoint matrix equation from (26) is

$$\tau A^T{q}_0^{*}\left(0\right)+\tau B^T{q}_0^{*}\left(0\right)e^{j{\omega }_0}=-j{\omega }_0{q}_0^{*}\left(0\right).$$

We obtain an adjoint eigenvector

$$q_0^{*}\left(s\right)=\left[\begin{array}{c}1\\ \frac{-\tau \nu {\omega }_{0}j}{{\omega }_0^2-{\tau }^2\beta +\tau \alpha {\omega }_{0}j}\\ \frac{-{\tau }^2\nu }{{\omega }_0^2-{\tau }^2\beta +\tau \alpha {\omega }_{0}j}\end{array}\right]e^{j{\omega }_{0}s}.$$

Additionally, the normalized eigenvector $q^{*}=D{q}_0^{*}$ should be such that $<q,D{q}_0^{*}>$$=1$, and we have

$$<q,q_0^{*}>=\left[{\overline{q_0^{*}}}^T\left(0\right)q\left(0\right)+e^{j{\omega }_0}{\overline{q_0^{*}}}^T\left(0\right)Bq\left(0\right)\right]=\frac{1}{\overline{D}}.$$

Thus,

$$D=\frac{1}{\overline{<q,q_0^{*}>}}=\frac{1}{\left(1+\overline{q_2}{q}_2^{*}+\overline{q_3}{q}_3^{*}+\tau K{e}^{j{\omega }_0}\right)},$$

and the orthogonality condition $<\overline{q},q^{*}>$$=0$ is easy to verify. □

Applying the eigen-decomposition technique, we adopt the notations in [19] to divide the solution space of (23) into the center manifolds and stable ones.

$$\left\{\begin{array}{ccc}z\left(t\right)\hfill & =& <q^{*},X_t>\hfill \\ w\left(t\right)\hfill & =& X_t-zq-\overline{z}\overline{q}\hfill \end{array}\right.$$

(31)

On the other, the center manifold theorem tells us that there exists a local manifold $w\left(t\right)$ such that

$$w(t,\theta )=\frac{1}{2}{w}_{20}\left(\theta \right)z^2+w_{11}\left(\theta \right)z\overline{z}+\frac{1}{2}{w}_{02}\left(\theta \right){\overline{z}}^2+\cdots$$

(32)

The evolution of z on t gives

$${\displaystyle \begin{array}{ccc}\dot{z}\left(t\right)\hfill & =& <q^{*},{\dot{X}}_t>=<q^{*},L{X}_t>+<q^{*},R{X}_t>=j{\omega }_{0}z\left(t\right)+{\overline{q^{*}}}^T\left(0\right)R{X}_t\left(0\right)\hfill \\ \hfill & =& j{\omega }_{0}z+\overline{D}\left[1\overline{q_2^{*}}\overline{q_3^{*}}\right]\left[\begin{array}{c}-\tau \nu X_t^{\left(1\right)}{\left(0\right)}^3\\ 0\\ 0\end{array}\right]\hfill \end{array}}$$

With the notation in (31), we have

$$\begin{array}{ccc}{X}_t^{\left(1\right)}{\left(0\right)}^3\hfill & =& {\left[z{q}^{\left(1\right)}\left(0\right)+\overline{z}{\overline{q}}^{\left(1\right)}\left(0\right)+\frac{1}{2}{w}_{20}^{\left(1\right)}\left(0\right)z^2+w_{11}^{\left(1\right)}\left(0\right)z\overline{z}+\cdots \right]}^3\hfill \end{array}$$

Therefore, we obtain

$$\dot{z}=j{\omega }_{0}z+\frac{1}{2}{g}_{20}{z}^2+g_{11}z\overline{z}+\frac{1}{2}{g}_{02}{\overline{z}}^2+\frac{1}{2}{g}_{21}{z}^2\overline{z}+\cdots$$

(33)

with

$$g_{20}=g_{11}=g_{02}=0,g_{21}=-6\tau \nu \overline{D}.$$

Remark 3.

For applying the Hassard formula in [19],

$${\displaystyle \left\{\begin{array}{c}{\mu }_2=-\frac{1}{2}\frac{\mathrm{Re}\left[g_{21}\right]}{{\alpha }^{\prime }\left({\tau }_0\right)}\hfill \\ {\tau }_2=-\frac{\mathrm{Im}\left[g_{21}\right]+2{\mu }_2{\omega }^{\prime }\left(0\right)}{2{\omega }_0}\hfill \\ {\beta }_2=\mathrm{Re}\left[g_{21}\right]\hfill \end{array}\right.}$$

(34)

with $C_1\left(0\right)=\frac{j}{2{\omega }_0}\left[g_{20}{g}_{11}-2|g_{11}{|}^2-\frac{1}{3}{\left|g_{02}\right|}^2\right]+\frac{g_{21}}{2}$. Accordingly, we have $C_1\left(0\right)=-3\tau \nu \overline{D}$ in our discussion.

Theorem 2.

In Formula (34), ${\mu }_2$ determines the direction of the Hopf bifurcation: if ${\mu }_2>0(<0)$, then the Hopf bifurcation is supercritical (subcritical); ${\beta }_2$ determines the stability of the bifurcating periodic solutions: the solutions are orbitally stable (unstable) if ${\beta }_2<0(>0)$; and ${\tau }_2$ determines the period of the bifurcating periodic solutions: the period increases (decreases) if ${\tau }_2>0(<0)$.

Based on all the discussion above, we can summarize the following unified Algorithm 1.

Algorithm 1 The calculations of the stability switches and Hopf bifurcation

1: Construct the auxiliary polynomial of (8) by Lemma 1.

2: Compute the PRRs of (10) by Lemma 2, and the critical delays $T_i$ in (19).

3: Determine the delay stable intervals by Theorem 1 and Corollary 1.

4: Compute the eigenvectors $q\left(\theta \right)$ and $q^{*}\left(s\right)$ in (28) and (29).

5: Determine $g_{21}$, substitute it into the Hassard formula in (34), and obtain ${\mu }_2,T_2,{\beta }_2$.

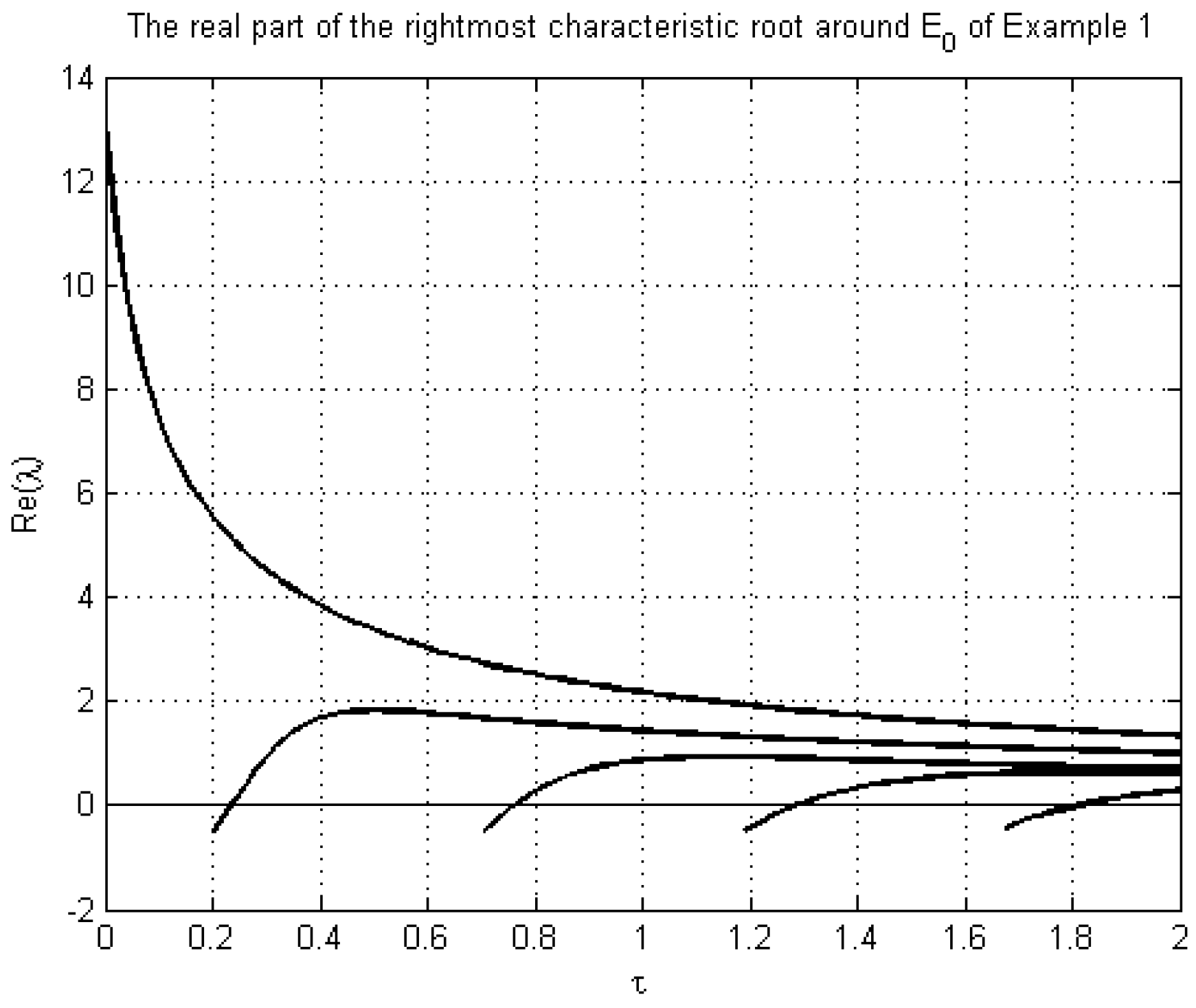
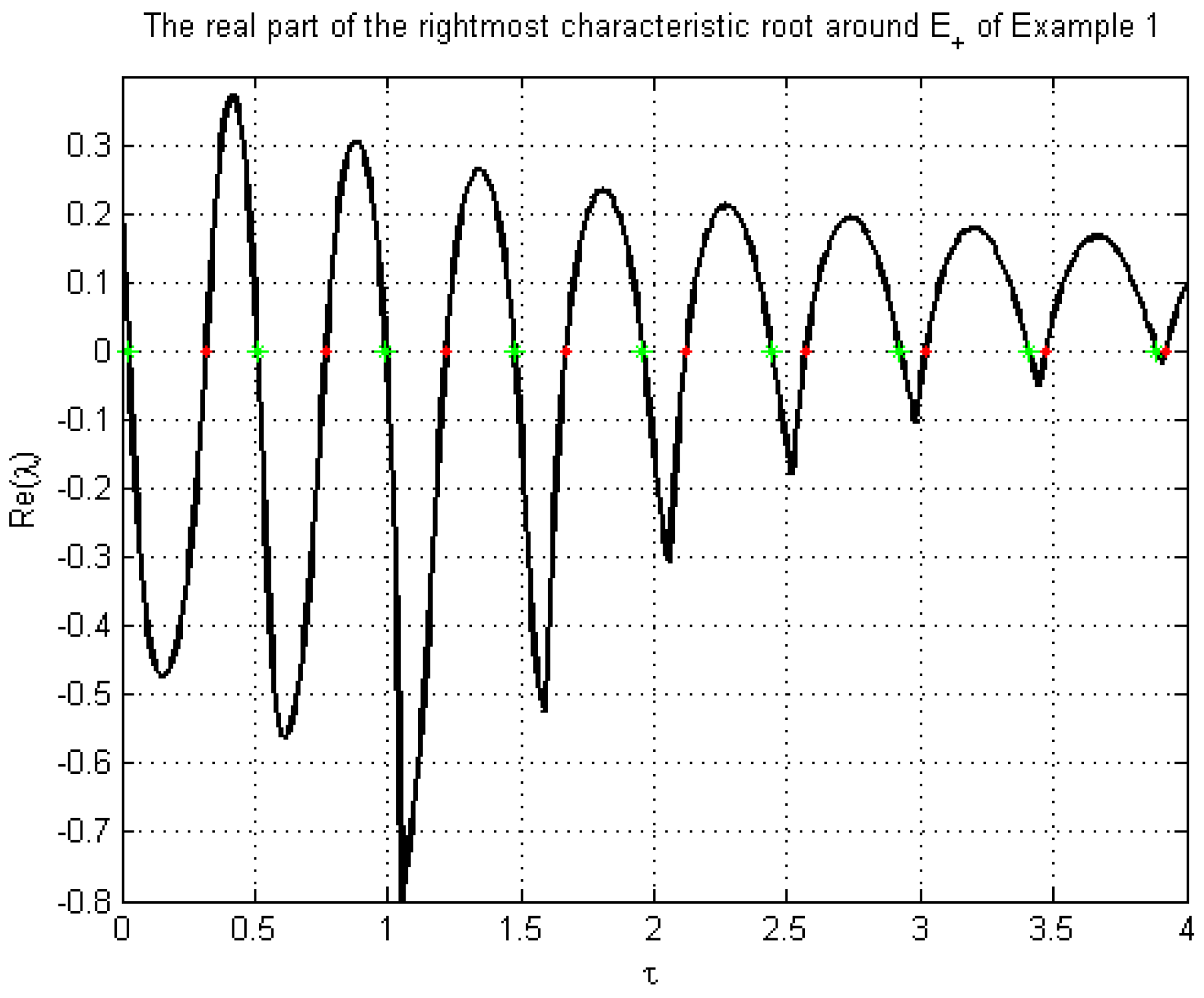
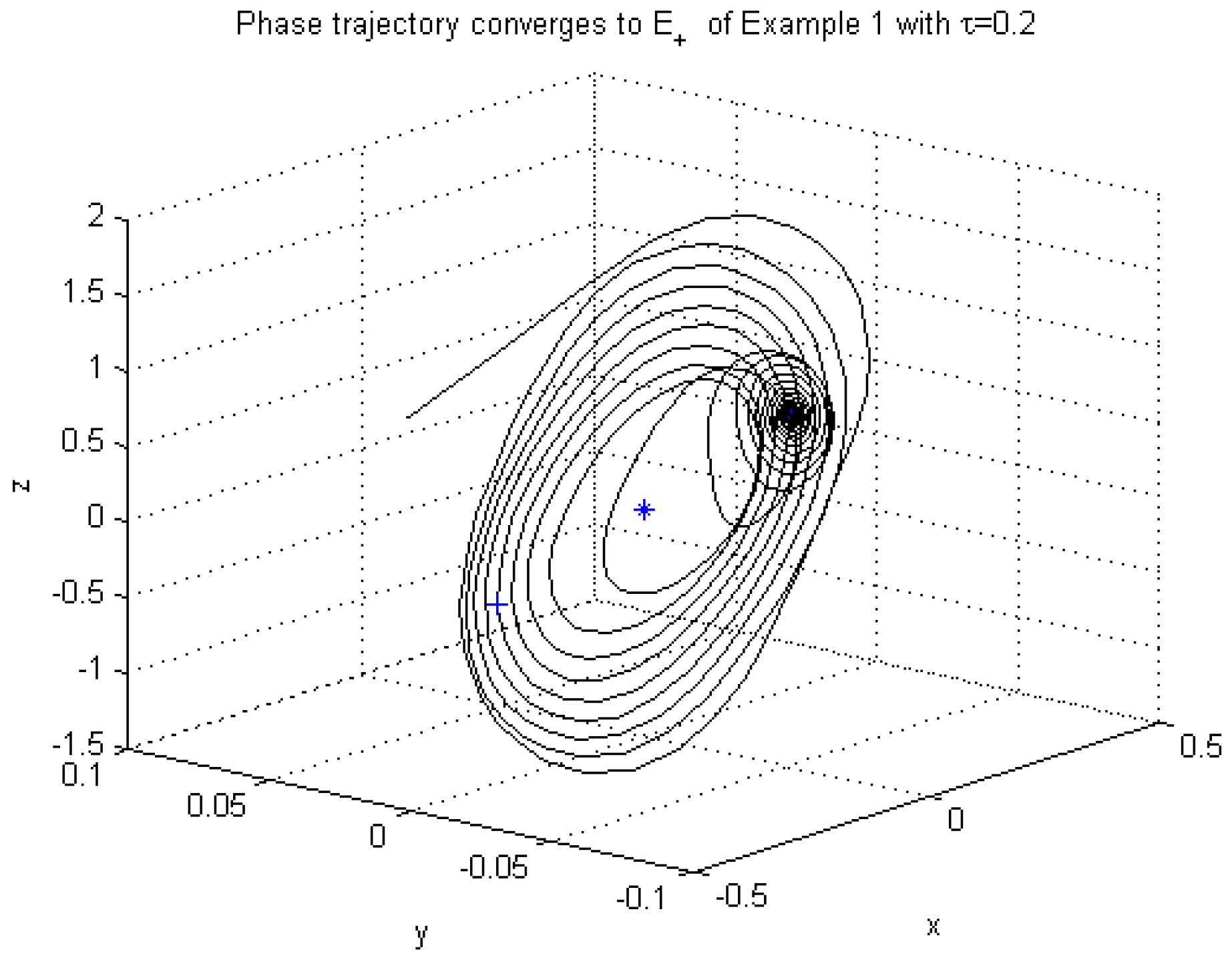
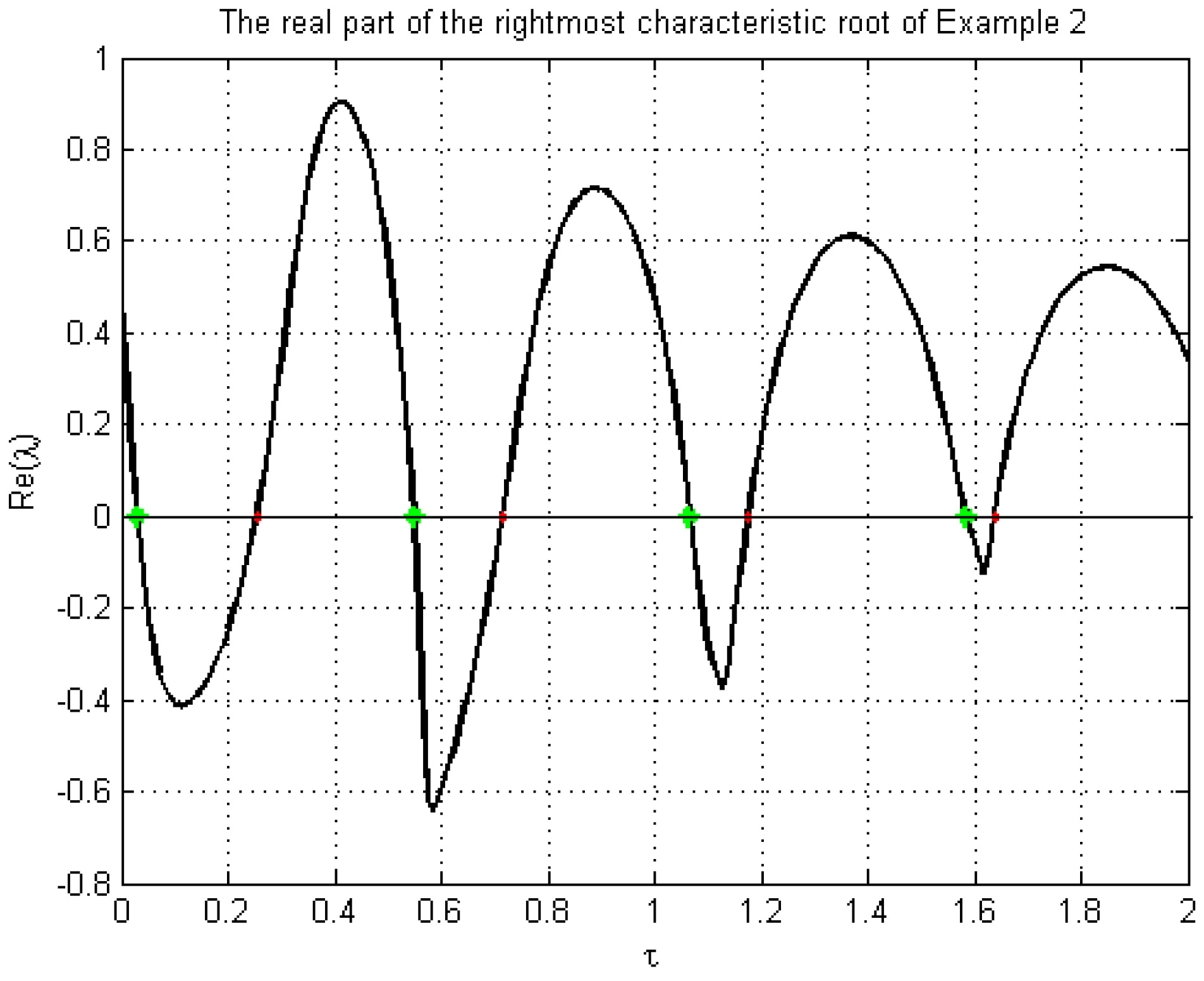
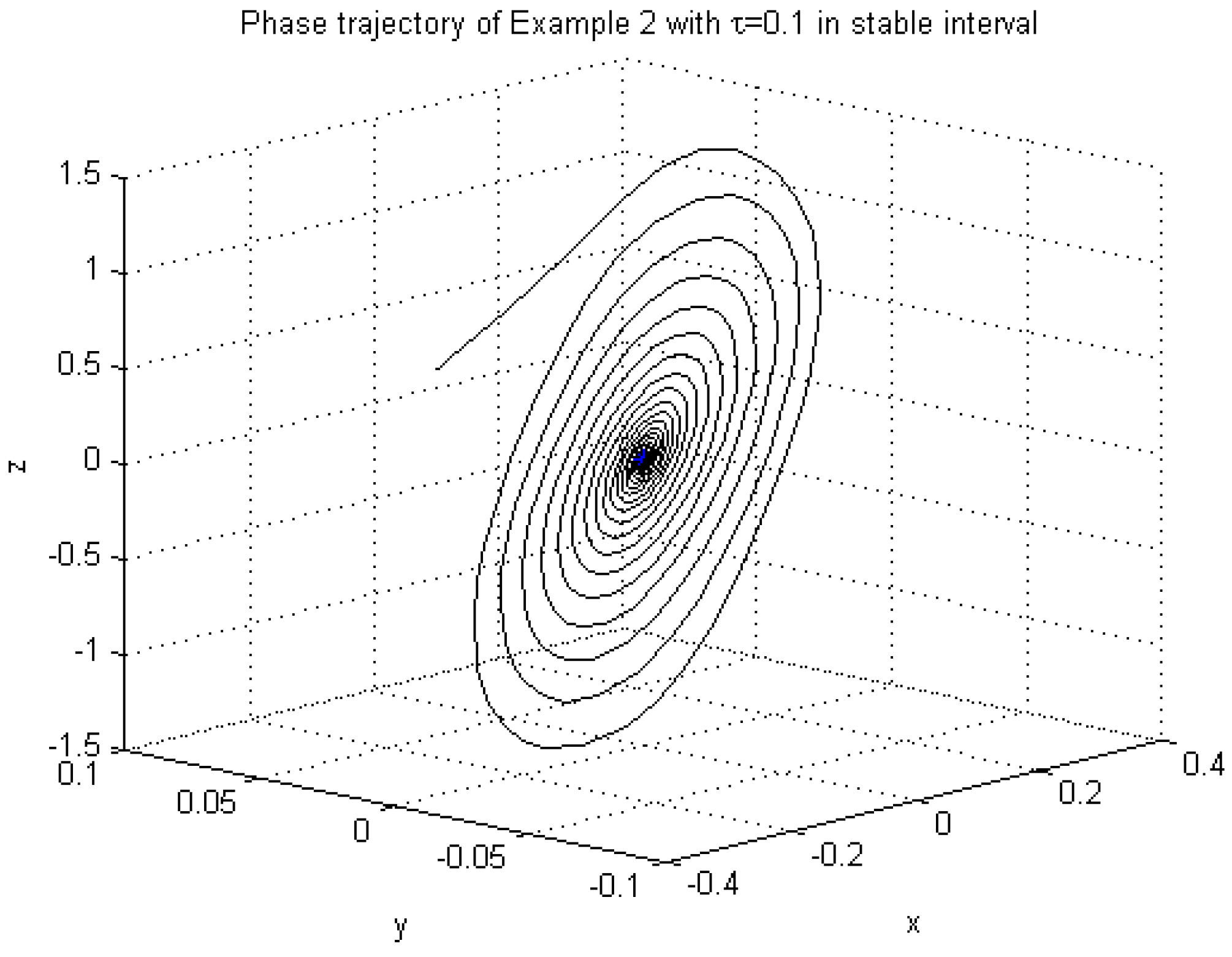
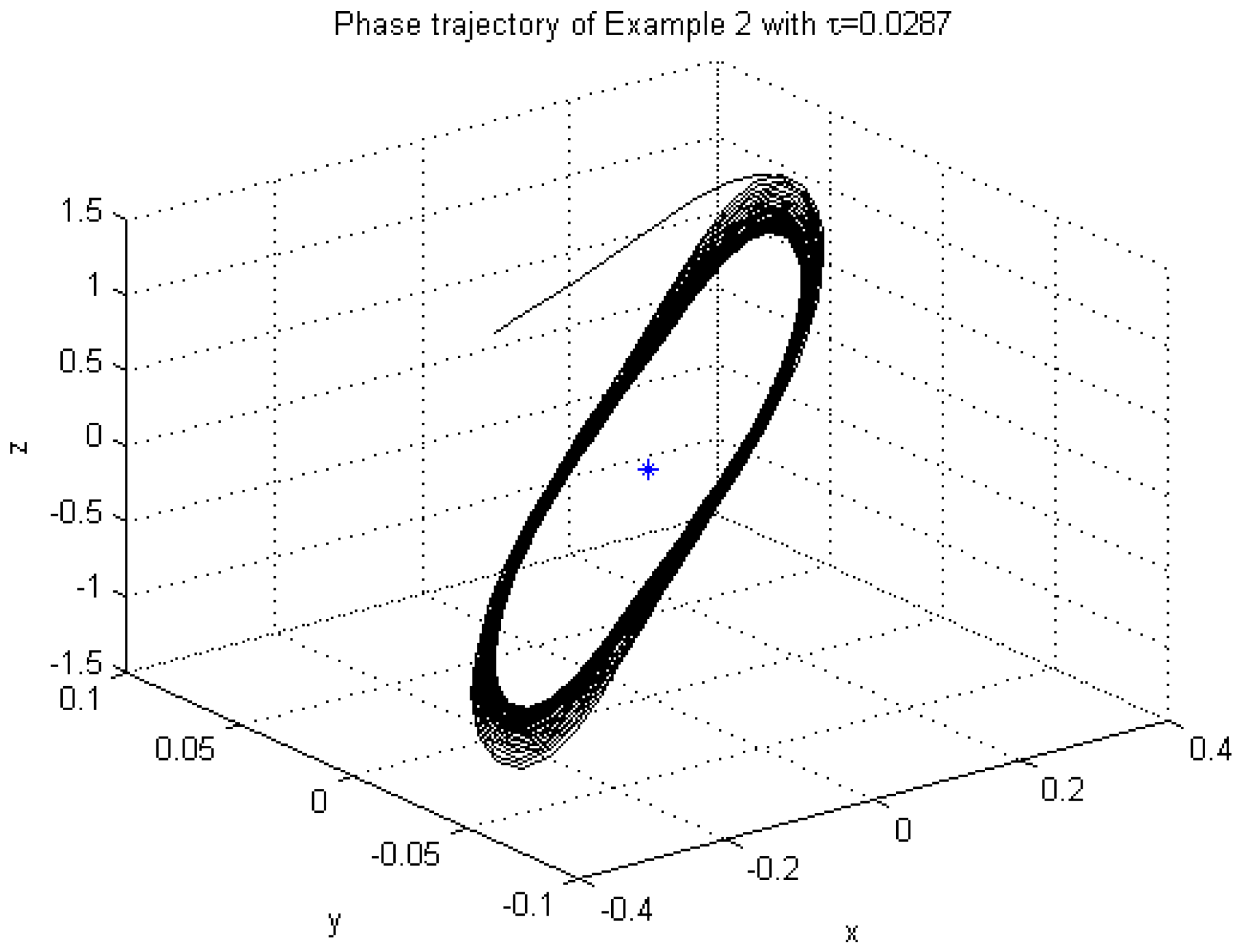
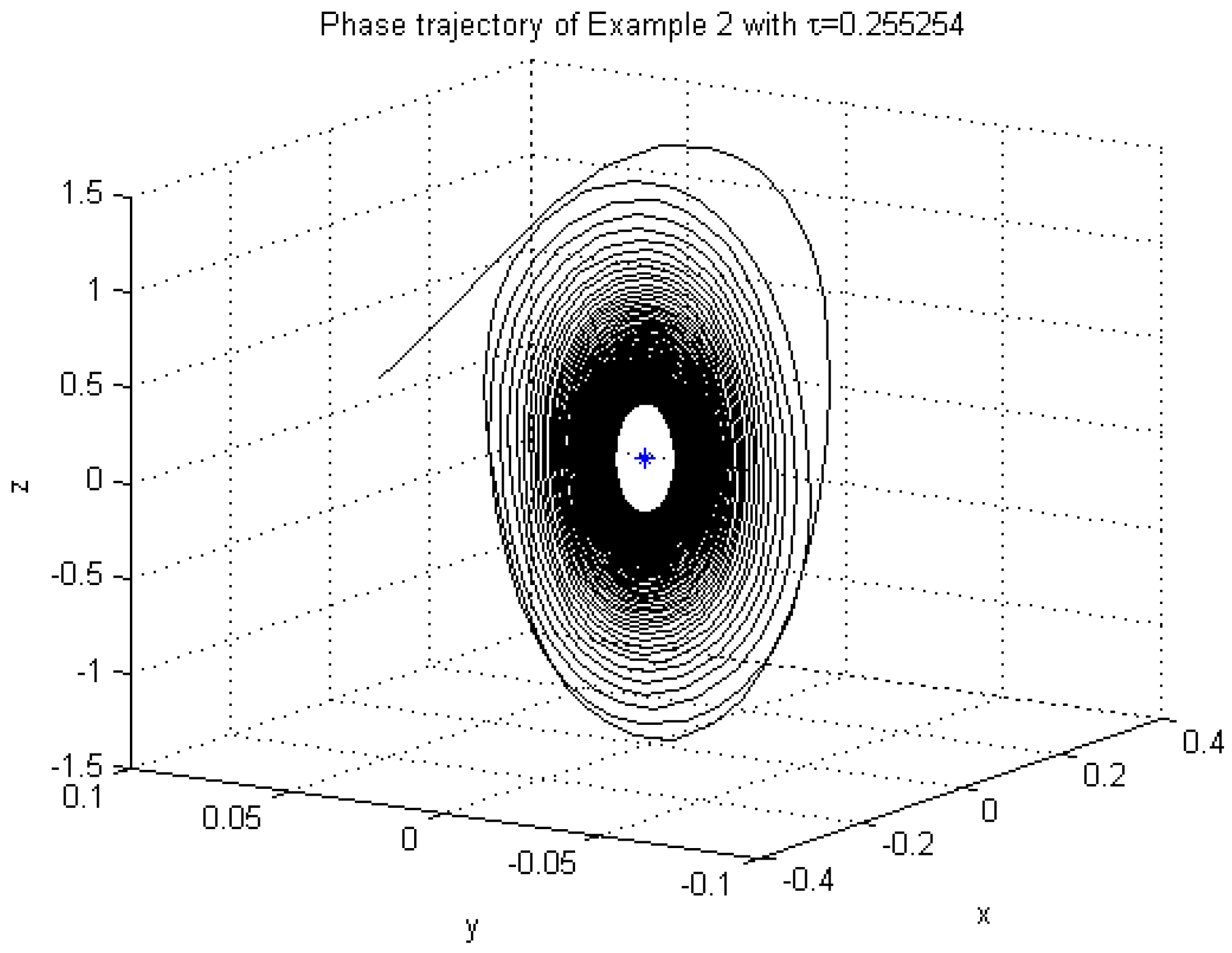
4. Numerical Examples

Example 1.

The first example comes from [4] with $\alpha =3,\beta =200,\mu =0.1,\nu =100$. Thus, the MAVPD with delayed feedback is

$$\begin{array}{c}\dot{x}\left(t\right)=-100[x^3-0.1x-y]+10[x(t-\tau )-x\left(t\right)]\hfill \\ \dot{y}\left(t\right)=x-1.6y-z\hfill \\ \dot{z}\left(t\right)=-200y\hfill \end{array}$$

(35)

It is easy to verify that there exist three equilibriums, which are mareked by blue symbols, and they are

$$(0,0,0),(\pm 0.3162,0,\pm 0.3162)$$

Firstly, we consider the origin point. The characteristic equation is

$$CE\left(\lambda \right)={\lambda }^3+3{\lambda }^2+100\lambda -(10{\lambda }^2+30\lambda +2000)e^{-\tau \lambda }$$

By Lemma 1, we can see that it has only one PIR with ${\omega }_{1}j=j11.9662$, and the critical delays are

$$T_1=\left\{{\tau }_{1k}\left|{\tau }_{1k}=0.2363+\frac{2k\pi }{11.9662}\right.\right\}$$

Unfortunately, all the critical delays correspond to the addition of unstable roots, which is shown in Figure 1. The curve is the rightmost root loci of the system in Example 1 around $E_0$. Since there exists a pair of symmetry conjugate roots with a positive real part for $\tau =0$, it adds two more symmetrical unstable roots for every critical delay. Thus, we conclude that the $E_0$ is an unstable equilibrium point for any $\tau \ge 0$.

Meanwhile, the characteristic equation around $E_{+}$ is

$$CE\left(\lambda \right)={\lambda }^3+33{\lambda }^2+190\lambda +6000-(10{\lambda }^2+30\lambda +2000)e^{-\tau \lambda }$$

There exist two PIRs with ${\omega }_{1}j=j13.9451$ (the unstable CF) and ${\omega }_{2}j=j13.0070$ (the stable CF). Accordingly, two series of critical delays are

$$T_1=\left\{{\tau }_{1k}\left|{\tau }_{1k}=0.31787+\frac{2k\pi }{13.9451}\right.\right\}\mathrm{and}$$

$$T_2=\left\{{\tau }_{2k}\left|{\tau }_{2k}=0.025+\frac{2k\pi }{13.0070}\right.\right\}$$

Thus, we obtain the stable switches intervals as follows:

$$\begin{array}{c}(0.0250,0.31787),(0.5081,0.7684),(0.9911,1.2190),(1.4742,1.6696),(1.9572,2.1201)\hfill \\ (2.4403,2.5707),(2.9234,3.0213),(3.4064,3.4718),(3.8895,3.9224),(4.3726,4.3730)\hfill \end{array}.$$

These stable intervals are also illustrated in Figure 2. They tell us that the equilibrium point $E+$ has ten times the stability switches versus time delay. In addition, we draw two phase trajectories with $\tau =0.2$ (stable) and $\tau =0.4$ (unstable) in Figure 3 and Figure 4, respectively.

It should be noted that every endpoint in the intervals mentioned above is a Hopf bifurcation point, and the bifurcation analysis is determined for Example 2 in a systematic manner.

Example 2.

This example is a constructed one like Example 1 with $\alpha =-0.1$. Then, there exists only one equilibrium point, $E_0=(0,0,0)$, and the associating characteristic equation is

$$CE\left(\lambda \right)={\lambda }^3+23{\lambda }^2+160\lambda +4000-(10{\lambda }^2+30\lambda +2000)e^{-\tau \lambda }$$

Lemma 1 tells us that the exponential polynomial has two PIRs, ${\omega }_{1}j=j13.6143$ and ${\omega }_{2}j=j12.1149$.

The critical delays are

$$T_1=\left\{{\tau }_{1k}\left|{\tau }_{1k}=0.255254+\frac{2k\pi }{13.6143}\right.\right\}\mathrm{and}$$

$$T_2=\left\{{\tau }_{2k}\left|{\tau }_{2k}=0.0287+\frac{2k\pi }{12.1149}\right.\right\}$$

Thus, we obtain the stable intervals,

$$(0.0287,0.255254),(0.5473,0.7168),(1.0660,1.1783),(1.5846,1.6398).$$

which are also shown in Figure 5. Moreover, we give the stable phase trajectory with $\tau =0.1$ in Figure 6, and the bifurcation phase trajectories in Figure 7 and Figure 8, respectively.

Subsequently, we choose ${\tau }_{10}=0.255254$ and ${\tau }_{20}=0.0287$ as the Hopf bifurcation points. At this time, the associating cross frequency (CF) is ${\omega }_1=13.6143$ and ${\omega }_2=12.1149$, respectively.

Associating with Lemma 4, Remark 3 and Theorem 2, for ${\tau }_{10}$, we obtain

$$\overline{D}=0.2256+0.2240j,g_{21}=-34.5439-34.3138j,C_1\left(0\right)=-17.2720-17.1569j,{\alpha }^{\prime }=6.04618,{\omega }^{\prime }=3.2116$$

Thus, we have

$$\begin{array}{c}{\mu }_2=2.8567\hfill \\ {\beta }_2=-345439\hfill \\ {\tau }_2=0.5863\hfill \end{array}$$

Moreover, for ${\tau }_{20}$, we obtain

$$\overline{D}=0.7873-0.0784j,g_{21}=-13.5601+1.3502j,C_1\left(0\right)=-6.7800+0.6751j,{\alpha }^{\prime }=-12.9115,{\omega }^{\prime }=8.3542$$

and

$$\begin{array}{c}{\mu }_2=-0.5251\hfill \\ {\beta }_2=-13.5601\hfill \\ {\tau }_2=0.3064\hfill \end{array}$$

5. Discussion

The Lorenz system, Chua’s circuit, Rossler system and the Van der Pol–Duffing equation are typical nonlinear systems. All of them can characterize the bifurcation and chaos behaviors. Indeed, they are intrinsic mathematical three-dimensional differential equations, or three-dimensional delay differential equations if there exists time delay in the states. Comparatively speaking, the nonlinear dynamics of delay differential equations are more rich than the ordinary ones. The methodology proposed in this work can be applied to other types of nonlinear circuit stems with minor changes, and more specific properties should be revealed.

6. Conclusions

In the paper, we have proposed a unified framework for dynamical analysis of the modified autonomous Van der Pol–Duffing equations. On one hand, the design of nonlinear circuits still needs much effort. For example, the different nonlinear parts lead to differential state response. On the other, our methodology can be improved to tackle some new nonlinear circuits. Therefore, we will pay much attention to the analysis of nonlinear dynamics among applicable circuits.