On Independent Secondary Dominating Sets in Generalized Graph Products

Abstract

In 2008, Hedetniemi et al. introduced $(1,k)$-domination in graphs. The research on this concept was extended to the problem of existence of independent $(1,k)$-dominating sets, which is an $\mathcal{NP}$-complete problem. In this paper, we consider independent $(1,1)$- and $(1,2)$-dominating sets, which we name as $(1,1)$-kernels and $(1,2)$-kernels, respectively. We obtain a complete characterization of generalized corona of graphs and G-join of graphs, which have such kernels. Moreover, we determine some graph parameters related to these sets, such as the number and the cardinality. In general, graph products considered in this paper have an asymmetric structure, contrary to other many well-known graph products (Cartesian, tensor, strong).

1. Introduction and Preliminary Results

In general, we will use the standard terminology and notation of graph theory (see [1]).

We consider only simple and undirected graphs. The graph $G=(\varnothing ,\varnothing )$ is an empty graph and G is trivial if it is empty or $\left|V\right(G\left)\right|=1$. If $\left|V\right(G\left)\right|\ge 2$, then G is nontrivial. We say that a subset $D\subseteq V\left(G\right)$ is dominating if every vertex of G is either in D or it is adjacent to at least one vertex of D. Dominating sets is one of the most intensively studied concepts in graph theory. Through decades, many new types of dominating sets have been introduced and researched; some recent results were obtained, for example, in [2,3,4,5].

A subset $S\subseteq V\left(G\right)$ is independent if no two vertices of S are adjacent in G. An independent set is maximal if it is not a proper subset of any other independent set. Maximum cardinality of an independent set in the graph G we denote by $\alpha \left(G\right)$, whereas minimum cardinality of a maximal independent set (or, equivalently, an independent dominating set) in G we denote by $i\left(G\right)$. By $\sigma \left(G\right)$ we denote the number of all maximal independent sets in G.

A subset J being dominating and independent is called a kernel of G. The concept of kernels was introduced by von Neumann and Morgenstern in digraphs in their research in game theory (see [6]). Since then, kernels in graphs were studied in the next decades, for examples, see [7,8,9,10]. The issue of the existence of kernels in undirected graphs is trivial, since every maximal independent set is a kernel.

However, if we place some additional restrictions on the subset of vertices, modifying the classical concepts of domination or independence, the problem of the existence becomes more complicated. By doing so, many types of kernels in undirected graphs were introduced and studied, for example, $(k,l)$-kernels [11,12,13], efficient dominating sets [14], restrained independent dominating sets [15], strong (1,1,2)-kernels [16], and many others.

Some types of kernels obtained in this way are related to multiple domination. This concept was introduced by J. F. Fink and M. S. Jacobson in [17]. For any integer $p\ge 1$, a subset $D\subseteq V\left(G\right)$ is called a p-dominating set of G if every vertex from $V\left(G\right)\backslash D$ has at least p neighbors in D. For $p=1$, we get the classical definition of the dominating set. If $p=2$, then we obtain the 2-dominating set. Based on the definition of the 2-dominating set in [18], A. Włoch introduced and studied the concept of a 2-dominating kernel. A set J is a 2-dominating kernel of a graph G if it is independent and 2-dominating.

In [19], Hedetniemi et al. introduced so-called secondary domination. For a positive integer k, we say that the set $D\in V\left(G\right)$ is $(1,k)$-dominating if for every $x\in V\left(G\right)\backslash D$ there exist distinct vertices $v,w\in D$ such that $xv\in E\left(G\right)$ and $d_G(x,w)\le k$. By combining this type of domination with independence, we obtain $(1,k)$-kernels, i.e., subsets, which are independent and $(1,k)$-dominating. Let us observe that $(1,1)$-kernels are equivalent to 2-dominating kernels. In general, the problem of the existence of secondary dominating kernels is $\mathcal{NP}$-complete (see [19,20]). Some problems concerning $(1,1)$-kernels in trees, graph products, and generalized Petersen graphs were considered in [20,21,22,23,24], while $(1,2)$-kernels were studied, among others, in [19,25].

In our considerations we will use the following notation:

• ${\sigma }_{(1,k)}\left(G\right)$ the number of all $(1,k)$-kernels in G.
• $j_{(1,k)}\left(G\right)$ the lower $(1,k)$-kernel number, i.e. minimum cardinality of a $(1,k)$-kernel in G.
• $J_{(1,k)}\left(G\right)$ the upper $(1,k)$-kernel number, i.e. maximum cardinality of a $(1,k)$-kernel in G.

This paper concerns the problem of the existence and the number of $(1,1)$-kernels and $(1,2)$-kernels in generalized graph products such as the generalized corona of graphs and the G-join of graphs. The main results of the paper are:

• Obtaining necessary and sufficient conditions for the existence of $(1,1)$-kernels and $(1,2)$-kernels as well as determining general formulas for parameters ${\sigma }_{(1,k)}$, $j_{(1,k)}$, and $J_{(1,k)}$ in the generalized corona.
• Giving complete characterization of the G-join with $(1,1)$-kernels and applying them to describe those kernels in other graph operations such as the join, the composition, and the duplication of vertices.

2. $(\mathbf{1},\mathbf{1})$-Kernels in the Generalized Corona of Graphs

In this section, we consider the problem of the existence and the number of $(1,1)$-kernels in the generalized corona of graphs. The classical definition of the corona of two graphs was introduced by R. Frucht and F. Harary in [26]. Problems of independence and domination in the generalized corona of graphs were considered in [10,27,28].

First, we give the definition of the generalized corona of graphs. Let G be a graph such that $V\left(G\right)=\{x_1,x_2,\dots ,x_n\}$, $n\ge 1$ and let $h_n={\left(H_i\right)}_{i\in \mathcal{I}}$ be a sequence of arbitrary graphs, where $\mathcal{I}=\{1,2,\dots ,n\}$ is the set of indices. The generalized corona of a graph G and the sequence $h_n$ is the graph $G\circ h_n$ such that $V(G\circ h_n)=V\left(G\right)\cup {\bigcup }_{i=1}^{n}V\left(H_i\right)$ and $E(G\circ h_n)=E\left(G\right)\cup {\bigcup }_{i=1}^{n}E\left(H_i\right)\cup {\bigcup }_{i=1}^n\{x_{i}y:y\in V\left(H_i\right)\}.$

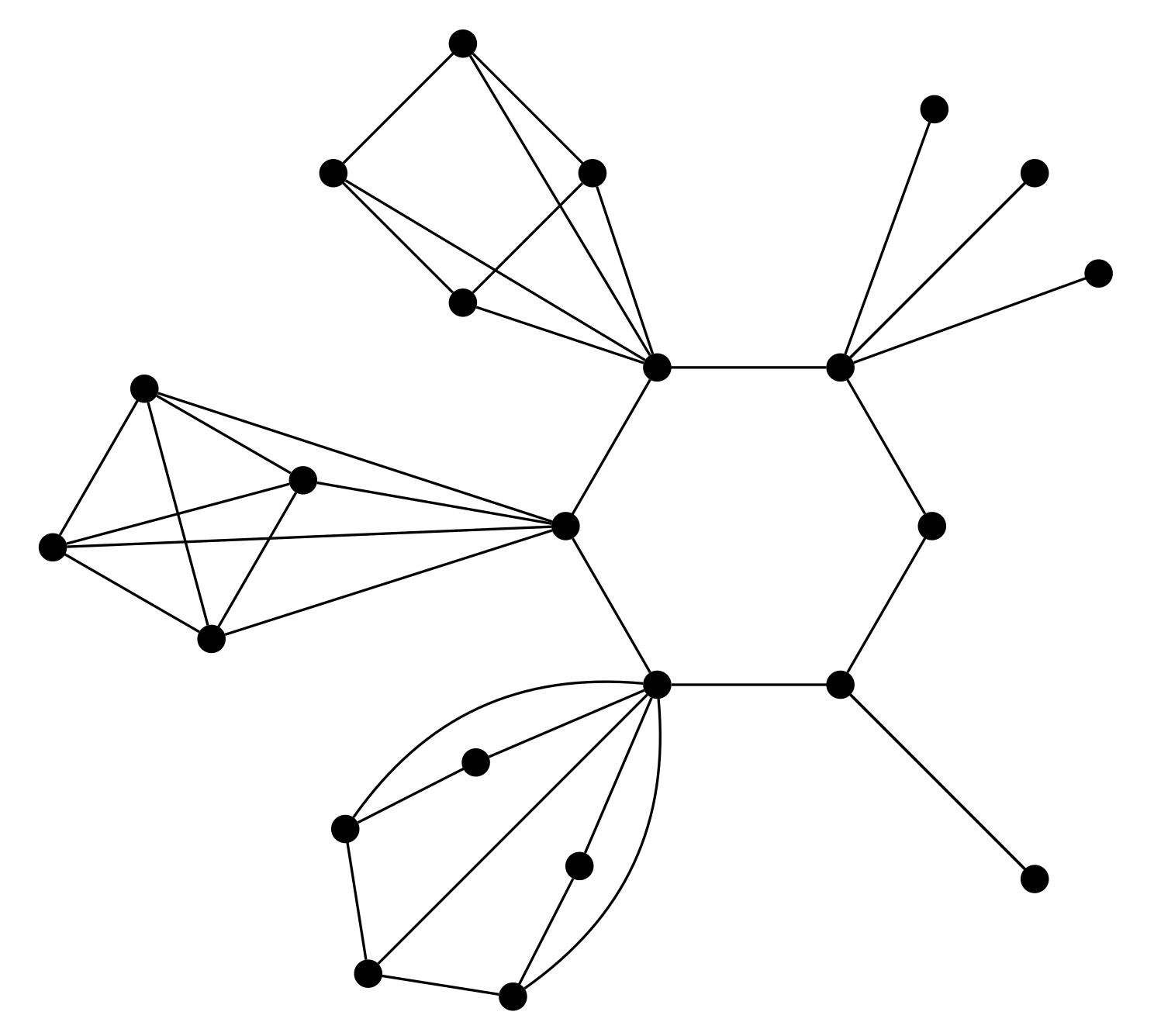
Figure 1 shows the generalized corona $C_6\circ (P_5,K_1,\varnothing ,N_3,C_4,K_4))$.

Now, we give necessary and sufficient conditions for the existence of $(1,1)$-kernels in the generalized corona of graphs, where all of the graphs from the sequence $h_n$ are nontrivial.

Theorem 1.

Let G be an arbitrary graph with $n\ge 1$ vertices and $h_n={\left(H_i\right)}_{i\in \mathcal{I}}$ be a sequence of n nontrivial graphs. The graph $G\circ h_n$ has a $(1,1)$-kernel if, and only if, all graphs $H_i$, $i\in \mathcal{I}$ have a $(1,1)$-kernel.

Proof. 

Assume that graphs $H_i$, $i\in \mathcal{I}$ have a $(1,1)$-kernel $J_i$. Since graphs $H_i$ are nontrivial, $\left|V\right(H_i\left)\right|\ge 2$. Thus, $|J_i|\ge 2$. We will show that for an arbitrary graph G of order $n\ge 1$, the set $J={\bigcup }_{i=1}^n{J}_i$ is a $(1,1)$-kernel of a graph $G\circ h_n$. From the definition of the generalized corona of graphs it follows that J is an independent set. Since $|J_i|\ge 2$, every vertex of a graph G has at least two neighbors in the set $J_i$. Hence, J is a $(1,1)$-kernel of a graph $G\circ h_n$.

Conversely, let us assume that a certain graph $G\circ h_n$, $n\ge 1$ has a $(1,1)$-kernel J. We will show that $J\cap V\left(G\right)=\varnothing$. Let $x_s\in V\left(G\right)$, $1\le s\le n$, and suppose by the contrary that $x_s\in J$. Then, $V\left(H_s\right)\cap J=\varnothing$. Since $\left|V\right(H_s\left)\right|\ge 2$, the set J is not 2-dominating, a contradiction with the assumption that J is a $(1,1)$-kernel. Hence, $J\cap V\left(G\right)=\varnothing$. Since the graph $G\circ h_n$ has a $(1,1)$-kernel J and $J\cap V\left(G\right)=\varnothing$, graphs $H_i$, $i\in \mathcal{I}$ must have a $(1,1)$-kernel $J_i$. Moreover, every vertex $x_i\in V\left(G\right)$ has at least two neighbors in the set $J_i$. Therefore, $|J_i|\ge 2$, and hence $\left|V\right(H_i\left)\right|\ge 2$, which ends the proof. □

Based on the proof of Theorem 1, the following corollary is obtained. It concerns the number of $(1,1)$-kernels in the generalized corona of graphs as well as the lower and upper $(1,1)$-kernel numbers.

Corollary 1.

Let G be an arbitrary graph with $n\ge 1$ vertices and $h_n={\left(H_i\right)}_{i\in \mathcal{I}}$ be a sequence of n nontrivial graphs. If graphs $H_i$ have a $(1,1)$-kernel, then

1.

${\sigma }_{(1,1)}(G\circ h_n)={\displaystyle \prod _{i=1}^n}{\sigma }_{(1,1)}\left(H_i\right),$

2.

$j_{(1,1)}(G\circ h_n)={\displaystyle \sum _{i=1}^n}{j}_{(1,1)}\left(H_i\right),$

3.

$J_{(1,1)}(G\circ h_n)={\displaystyle \sum _{i=1}^n}{J}_{(1,1)}\left(H_i\right).$

Now, let us consider the case where graphs from the sequence $h_n$ are arbitrary. Let $h_n={\left(H_i\right)}_{i\in \mathcal{I}}$ be a sequence of arbitrary graphs. In particular, graphs from the sequence $h_n$ can be trivial or empty. Let $\mathcal{I}={\mathcal{I}}_0\cup {\mathcal{I}}_1\cup {\mathcal{I}}_2$, where ${\mathcal{I}}_0=\{j\in \mathcal{I}:|V\left(H_j\right)|=0\}$, ${\mathcal{I}}_1=\{t\in \mathcal{I}:|V\left(H_t\right)|=1\}$, ${\mathcal{I}}_2=\{r\in \mathcal{I}:|V\left(H_r\right)|\ge 2\}$. We give the complete characterization of the generalized corona of graphs with a $(1,1)$-kernel.

Theorem 2.

Let G be an arbitrary graph with $n\ge 1$ vertices and $h_n={\left(H_i\right)}_{i\in \mathcal{I}}$ be a sequence of n arbitrary graphs. The graph $G\circ h_n$ has a $(1,1)$-kernel if, and only if, each graph $H_r$, $r\in {\mathcal{I}}_2$ has a $(1,1)$-kernel and the subgraph $\left(G\circ h_n\right)\backslash {\bigcup }_{r\in {\mathcal{I}}_2}\left(V\left(H_r\right)\cup \left\{x_r\right\}\right)$ has a $(1,1)$-kernel.

Proof. 

Let us assume that a certain graph $G\circ h_n$ has a $(1,1)$-kernel J. Then, each graph $H_r$, $r\in {\mathcal{I}}_2$ must have a $(1,1)$-kernel $J_r$ to 2-dominate vertices from the set $V\left(H_r\right)\backslash J_r$. Since $N_{G\circ h_n}\left[J_r\right]=V\left(H_r\right)\cup \left\{x_r\right\}$, $r\in {\mathcal{I}}_2$, the subgraph $\left(G\circ h_n\right)\backslash {\bigcup }_{r\in {\mathcal{I}}_2}\left(V\left(H_r\right)\cup \left\{x_r\right\}\right)$ must have a $(1,1)$-kernel.

Conversely, let us assume that each graph $H_r$, $r\in {\mathcal{I}}_2$ has a $(1,1)$-kernel $J_r$ and the subgraph $\left(G\circ h_n\right)\backslash {\bigcup }_{r\in {\mathcal{I}}_2}\left(H_r\cup \left\{x_r\right\}\right)$ has a $(1,1)$-kernel $J^{*}$. We will show that the set $J=J^{*}\cup {\bigcup }_{r\in {\mathcal{I}}_2}{J}_r$ is a $(1,1)$-kernel of the graph $G\circ h_n$. The independence of the set J follows from the definition of the generalized corona of graphs. Thus, it is sufficient to show that the set J is 2-dominating. Let $v\in V(G\circ h_n)\backslash J$. If $v\in V\left(H_r\right)\cup \left\{x_r\right\}$, $r\in {\mathcal{I}}_2$, then the vertex v is 2-dominated by the set $J_r$. If $v\in {\bigcup }_{k\in {\mathcal{I}}_0\cup {\mathcal{I}}_1}\left\{x_k\right\}$, then the vertex v has at least two neighbors in the set $J^{*}$. This means that the set J is a $(1,1)$-kernel of the graph $G\circ h_n$, which ends the proof. □

By the construction of $(1,1)$-kernels in the generalized corona of graphs shown in the proof above, we obtain the following corollary.

Corollary 2.

Let G be an arbitrary graph with $n\ge 1$ vertices and $h_n={\left(H_i\right)}_{i\in \mathcal{I}}$ be a sequence of n arbitrary graphs and let $G_1\cong \left(G\circ h_n\right)\backslash {\bigcup }_{r\in {\mathcal{I}}_2}\left(V\left(H_r\right)\cup \left\{x_r\right\}\right)$. If the graph $G\circ h_n$ has a $(1,1)$-kernel, then

1.

${\sigma }_{(1,1)}(G\circ h_n)={\sigma }_{(1,1)}\left(G_1\right)·{\displaystyle \prod _{r\in {\mathcal{I}}_2}}{\sigma }_{(1,1)}\left(H_r\right),$

2.

$j_{(1,1)}(G\circ h_n)=j_{(1,1)}\left(G_1\right)+{\displaystyle \sum _{r\in {\mathcal{I}}_2}}{j}_{(1,1)}\left(H_r\right),$

3.

$J_{(1,1)}(G\circ h_n)=J_{(1,1)}\left(G_1\right)+{\displaystyle \sum _{r\in {\mathcal{I}}_2}}{J}_{(1,1)}\left(H_r\right).$

Finally, we give another complete characterization of the generalized corona of arbitrary graphs.

Theorem 3.

Let G be an arbitrary graph with $n\ge 1$ vertices and $h_n={\left(H_i\right)}_{i\in \mathcal{I}}$ be a sequence of n arbitrary graphs. The graph $G\circ h_n$ has a $(1,1)$-kernel if, and only if, the following conditions hold:

(i) 

Each graph $H_r$, $r\in {\mathcal{I}}_2$ has a $(1,1)$-kernel.

(ii) 

The subgraph induced by the set $\{x_j:j\in {\mathcal{I}}_0\}$ has a $(1,1)$-kernel $J^{*}$.

(iii) 

For $t\in {\mathcal{I}}_1$ there exists $i\in {\mathcal{I}}_0$ such that $x_t{x}_i\in E\left(G\right)$ and $x_i\in J^{*}$.

Proof. 

Let us assume that a certain graph $G\circ h_n$ has a $(1,1)$-kernel J. Then, each graph $H_r$, $r\in {\mathcal{I}}_2$ must have a $(1,1)$-kernel $J_r$ to 2-dominate vertices from the set $V\left(H_r\right)\backslash J_r$. Thus, the condition (i) holds. We will show that the subgraph induced by the set $\{x_j:j\in {\mathcal{I}}_0\}$ has a $(1,1)$-kernel. If $x_i\in V\left(G\right)\cap J$, then $i\in {\mathcal{I}}_0$. Otherwise, the set J is not independent. Let $J^{*}=V\left(G\right)\cap J$. Since J is a $(1,1)$-kernel of the graph $G\circ h_n$, the set $J^{*}$ is a $(1,1)$-kernel of the subgraph induced by the set $\{x_j:j\in {\mathcal{I}}_0\}$. Hence, the condition (ii) holds. For all $t\in {\mathcal{I}}_1$, we have $|N_{G\circ h_n}\left(x_t\right)\cap (J\backslash V\left(G\right))|=1$. To 2-dominate vertices $x_t$, $t\in {\mathcal{I}}_1$ there must exist $x_i\in J^{*}$, $i\in {\mathcal{I}}_0$ such that $x_i{x}_t\in E\left(G\right)$. Thus, the condition (iii) holds.

Conversely, let us assume that conditions (i)–(iii) hold. We will show that the graph $G\circ h_n$ has a $(1,1)$-kernel $J={\bigcup }_{r\in {\mathcal{I}}_2}{J}_r\cup {\bigcup }_{t\in {\mathcal{I}}_1}V\left(H_t\right)\cup J^{*}$, where $J_r$ is a $(1,1)$-kernel of the graph $H_r$ for $r\in {\mathcal{I}}_2$ and $J^{*}$ is a $(1,1)$-kernel of the subgraph induced by the set $\{x_j:j\in {\mathcal{I}}_0\}$. The independence of the set J follows from the definition of $G\circ h_n$. Thus, it is sufficient to show that the set J is 2-dominating. Let $v\in V(G\circ h_n)\backslash J$. If $v\in V\left(H_r\right)\cup \left\{x_r\right\}$, $r\in {\mathcal{I}}_2$, then the vertex v is 2-dominated by the set $J_r$. If $v=x_t$, $t\in {\mathcal{I}}_1$, then the vertex v is 2-dominated by the set $V\left(H_t\right)\cup J^{*}$. If $v=x_j$, $j\in {\mathcal{I}}_0$, then the vertex v is 2-dominated by the set $J^{*}$. Hence, the set J is a $(1,1)$-kernel of the graph $G\circ h_n$, which ends the proof. □

Figure 2 shows the generalized corona $P_6\circ (P_5,K_1,\varnothing ,K_1,C_4,(K_1\cup C_4))$ and an example of a $(1,1)$-kernel in this graph.

3. $(\mathbf{1},\mathbf{2})$-Kernels in the Generalized Corona of Graphs

In this section, we study the existence of $(1,2)$-kernels in the generalized corona. Let $x\in V\left(G\right)$. The set $N_G^k\left(x\right)=\{v\in V\left(G\right):d_G(x,v)\le k\}$ we will refer to as the k-th weak neighborhood of the vertex x in the graph G. In particular, the set $N_G^2\left(x\right)$ we refer to as the second weak neighborhood of x.

Let $\mathcal{I}=\{1,2,\dots ,n\}$ be the set of indices. We denote as follows: by ${\mathcal{I}}_0$, the set $\{j\in \mathcal{I}:H_j=\varnothing \}$ and by ${\mathcal{I}}_K$, the set $\{j\in I:H_j\cong K_n,n\ge 2\}$. For simplicity, the subgraph of G induced by the set $\{x_j:j\in {\mathcal{I}}_0\}$, we denote by $G\left[{\mathcal{I}}_0\right]$.

Let us begin with proving lemmas, which will be helpful in our next considerations concerning the complete characterization of generalized corona with $(1,2)$-kernels.

Lemma 1.

Let J be a $(1,2)$-kernel in the generalized corona $G\circ h_n$. If $i\in \mathcal{I}\backslash {\mathcal{I}}_0$, then $x_i\notin J$.

Proof. 

Let J be a $(1,2)$-kernel. By contradiction, let us suppose that $i\in \mathcal{I}\backslash {\mathcal{I}}_0$ and $x_i\in J$. It follows that no vertex of the graph $H_i$ belongs to J. Moreover, for any $j\in \mathcal{I}$ such that $x_i{x}_j\in E\left(G\right)$, we have $x_j\notin J$. This means that for any vertex $y\in V\left(H_i\right)$, we have $N_{G\circ h_n}^2\left(y\right)\cap J=\left\{x_i\right\}$, which means that y is not $(1,2)$-dominated by J, a contradiction. □

Lemma 2.

Let $G\circ h_n$ have a $(1,2)$-kernel. If $i\in {\mathcal{I}}_K$, then there exists $j\in {\mathcal{I}}_0$ such that $x_i{x}_j\in E\left(G\right)$.

Proof. 

Let $G\circ h_n$ have a $(1,2)$-kernel J. For the sake of contradiction, let us assume that for some $i\in {\mathcal{I}}_K$, there is no $j\in {\mathcal{I}}_0$ such that $x_i{x}_j\in E\left(G\right)$. By Lemma 1, we know that $x_i\notin J$. Moreover, any other neighbor of $x_i$ in G also does not belong to J. This means that the intersection of sets $V\left(H_i\right)$ and J consists of unique vertex $y^{\prime }$, which dominates all other vertices of $V\left(H_i\right)$ and the vertex $x_i$, but it implies that for all vertices $y\in V\left(H_i\right)\backslash \left\{y^{\prime }\right\}$, we have $N_{G\circ h_n}^2\left(y\right)\cap J=\left\{y^{\prime }\right\}$, which means they are not $(1,2)$-dominated, a contradiction. □

Now, we are ready to present necessary and sufficient conditions for a generalized corona of graphs to have a $(1,2)$-kernel.

Theorem 4.

Let G be an arbitrary connected, nontrivial graph, $h_n={\left(H_i\right)}_{i\in \mathcal{I}}$ be a sequence of graphs such that ${\mathcal{I}}_0=\varnothing$. The generalized corona $G\circ h_n$ has a $(1,2)$-kernel if, and only if, ${\mathcal{I}}_K=\varnothing$.

Proof. 

First, we prove the sufficient condition. Let us assume that ${\mathcal{I}}_K=\varnothing$, i.e., for any $i\in \mathcal{I}$, the graph $H_i$ is not isomorphic to $K_n,n\ge 2$. In each graph $H_i$ we take an independent set of maximum cardinality and denote it by $J_i$. Let us consider the set $J={\bigcup }_{i=1}^n{J}_i$. Clearly, J is independent in $G\circ h_n$. We show that it is $(1,2)$-dominating. Let $v\in V(G\circ h_n)\backslash J$. First, let $v\in V\left(G\right)$; this means $v=x_i$ for some $i\in \mathcal{I}$. If $|J_i|\ge 2$, then the $x_i$ is $(1,1)$-dominated by $J_i$. If $|J_i|=1$, then $x_i$ is dominated by $J_i$ and there exists a path $x_i-x_j-J_j$ of length 2. Now, we assume that v belongs to $V\left(H_i\right)$ for some $i\in \mathcal{I}$. The set $J_i$ is dominating in $H_i$ and has at least two vertices, say $y_1,y_2$. This means v is dominated by at least one of them, say $y_1$ and, by the definition of generalized corona, there exists a path $v-x_i-y_2$. Hence, J is $(1,2)$-dominating.

To prove the necessary condition, let us suppose that $G\circ h_n$ has a $(1,2)$-kernel J. For the sake of contradiction, let ${\mathcal{I}}_K\ne \varnothing$. By Lemma 2, it means that ${\mathcal{I}}_0\ne \varnothing$. A contradiction with the assumption that ${\mathcal{I}}_0=\varnothing$ means that ${\mathcal{I}}_K=\varnothing$. □

From the proof of Theorem 4, we may conclude a corollary concerning the number of all $(1,2)$-kernels as well as lower and upper $(1,2)$-kernel numbers in some cases of generalized corona.

Corollary 3.

Let G be an arbitrary, connected, nontrivial graph with n vertices and $h_n={\left(H_i\right)}_{i\in \mathcal{I}}$ be a sequence of n arbitrary graphs such that $i\left(H_i\right)\ge 2$ for all $i\in \mathcal{I}$.

1.

${\sigma }_{(1,2)}(G\circ h_n)={\displaystyle \prod _{i=1}^n}\sigma \left(H_i\right),$

2.

$j_{(1,2)}(G\circ h_n)={\displaystyle \sum _{i=1}^n}i\left(H_i\right),$

3.

$J_{(1,2)}(G\circ h_n)={\displaystyle \sum _{i=1}^n}\alpha \left(H_i\right).$

Now, we consider a more general concept, i.e., we allow that graphs from the sequence $h_n$ can be empty.

Theorem 5.

Let G be an arbitrary connected non-empty graph, $h_n={\left(H_i\right)}_{i\in \mathcal{I}}$ be a sequence of graphs, and ${\mathcal{I}}_0\ne \varnothing$. The generalized corona $G\circ h_n$ has a $(1,2)$-kernel if, and only if, the subgraph $G\left[{\mathcal{I}}_0\right]$ has a maximal independent set S such that the following conditions hold:

(i) 

If $i\in {\mathcal{I}}_K$, then there exists $x_j\in S$ such that $x_i{x}_j\in E\left(G\right)$ and

(ii) 

For every vertex $x_k\in V\left(G\left[{\mathcal{I}}_0\right]\right)\backslash S$ at least one of the following conditions is satisfied:

(a) 

There exists $l\in \mathcal{I}\backslash {\mathcal{I}}_0$ such that $x_k{x}_l\in E\left(G\right)$.

(b) 

$x_k$ is $(1,2)$-dominated by the set S.

Proof. 

First, we will prove the sufficient condition. Let us assume that the subgraph $G\left[{\mathcal{I}}_0\right]$ has a maximal independent set S such that conditions (i) and (ii) are satisfied. We will show that $G\circ h_n$ has a $(1,2)$-kernel. If $i\notin {\mathcal{I}}_0$, then in the graph $H_i$ we take any independent set of the maximum cardinality and denote it by $J_i$. Let $J=\left({\bigcup }_{i\in \mathcal{I}\backslash {\mathcal{I}}_0}{J}_i\right)\cup S$. It is easy to see that J is independent. We will show it is $(1,2)$-dominating. Let us divide all vertices lying outside J into four cases.

First, let $i\in \mathcal{I}$ be such that the graph $H_i$ has at least two vertices and is not complete. Then, $x_i\in V\left(G\right)\backslash J$ is $(1,1)$-dominated by $J_i$ and for all $y\in V\left(H_i\right)\backslash J_i$, we have $\left|N_{G\circ h_n}^2\left(y\right)\cap J_i\right|\ge 2$.

Second, let $i\in \mathcal{I}$ be such that $H_i\cong K_1$. If the vertex $x_i$ has a neighbor $x_l\in V\left(G\right)$ such that $l\in \mathcal{I}\backslash {\mathcal{I}}_0$, then $\left|N_{G\circ h_n}^2\left(x_i\right)\cap (J_i\cup J_l)\right|\ge 2$. Therefore, let us suppose that for all j such that $x_j{x}_i\in E\left(G\right)$, we have $j\in {\mathcal{I}}_0$. If there exists $j\in S$ such that $x_i{x}_j\in E\left(G\right)$, then $x_i$ is $(1,1)$-dominated by the set $J_i\cup S$. Otherwise, by maximality of S in $G\left[{\mathcal{I}}_0\right]$ we obtain $\left|N_{G\circ h_n}^2\left(x_i\right)\cap (J_i\cup S)\right|\ge 2$. Hence, $x_i$ is $(1,2)$-dominated by J.

Third, let $i\in {\mathcal{I}}_K$. Then, by the condition (i), the vertex $x_i$ is $(1,1)$-dominated by the set $J_i\cup S$ and for all $y\in V\left(H_i\right)\backslash J_i$, we have $\left|N_{G\circ h_n}^2\left(y\right)\cap (J_i\cup S)\right|\ge 2$.

Fourth, let $i\in {\mathcal{I}}_0$. Then, by maximality of S in $G\left[{\mathcal{I}}_0\right]$ and the condition (ii), we have $\left|N_{G\circ h_n}^2\left(x_i\right)\cap S\right|\ge 2$ or $\left|N_{G\circ h_n}^2\left(x_i\right)\cap (S\cup J_l)\right|\ge 2$, where $l\in \mathcal{I}\backslash {\mathcal{I}}_0$ and $x_i{x}_l\in E\left(G\right)$.

This means that the set J is $(1,2)$-dominating in $G\circ h_n$, hence it is a $(1,2)$-kernel.

Now, we prove the necessary condition. Let us suppose that $G\circ h_n$ has a $(1,2)$-kernel J. For the sake of contradiction, let us assume that in the subgraph $G\left[{\mathcal{I}}_0\right]$, no maximal independent set satisfies both conditions (i) and (ii). This means that for every maximal independent set S of $G\left[{\mathcal{I}}_0\right]$:

• There exists $H_i\cong K_n,n\ge 2$ such that $x_i$ has no neighbor in S or
• There exists a vertex $x_k\in V\left(G\left[{\mathcal{I}}_0\right]\right)\backslash S$, which is neither $(1,2)$-dominated by S nor has a neighbor $x_l,l\in \mathcal{I}\backslash {\mathcal{I}}_0$.

Since the intersection of J and $V\left(G\left[{\mathcal{I}}_0\right]\right)$ must be a maximal independent set in $G\left[{\mathcal{I}}_0\right]$, we obtain that we always find at least one vertex $z\in V\left(H_i\right)\backslash J,i\in {\mathcal{I}}_K$, which is not $(1,2)$-dominated by J, or a vertex $x_k\in V\left(G\left[{\mathcal{I}}_0\right]\right)\backslash J$, which is not $(1,2)$-dominated by J. This is a contradiction with the fact that J is a $(1,2)$-kernel. Hence, there must exist a maximal independent set in $G\left[{\mathcal{I}}_0\right]$ satisfying both conditions (i) and (ii). □

Figure 3 presents the generalized corona $P_6\circ (P_4,K_1,\varnothing ,K_4,C_4,(P_2\cup C_3))$ with the $(1,2)$-kernel indicated by the green color.

4. $(\mathbf{1},\mathbf{1})$-Kernels in the G-Join of Graphs

In this section, we consider the problem of the existence and the number of $(1,1)$-kernels in the G-join of graphs. We will show that the existence of a $(1,1)$-kernel in the G-join of graphs does not require the existence of a $(1,1)$-kernel in all their factors.

Problems of the existence of different kinds of kernels in D-join of digraphs were considered in [29,30,31].

We provide the definition of the G-join of graphs. Let G be a graph such that $V\left(G\right)=\{x_1,x_2,\dots ,x_n\}$, $n\ge 2$ and let $h_n={\left(H_i\right)}_{i\in \mathcal{I}}$ be a sequence of arbitrary non-empty graphs, where $V\left(H_i\right)=\{y_1^i,y_2^i,\dots ,y_{p_i}^i\}$, $p_i\ge 1$, and $\mathcal{I}=\{1,2,\dots ,n\}$. The G-join of the graph G and the sequence $h_n$ is the graph $G\left[h_n\right]$ such that $V\left(G\left[h_n\right]\right)={\bigcup }_{i=1}^n\left(\left\{x_i\right\}\times V\left(H_i\right)\right)$ and $E\left(G\left[h_n\right]\right)=\{(x_s,y_j^s)(x_q,y_t^q);x_s=x_q$ and $y_j^s$.

Figure 4 shows the graph $C_6\left[(P_5,K_1,P_2,N_3,C_4,K_4)\right]$.

Some well-known graph products are specific cases of G-join. If $G\cong P_2$ and $h_n=(H_1,H_2)$, then we obtain a join of two graphs $H_1+H_2$. If $H_i\cong H$ for all $i\in \mathcal{I}$, then $G\left[h_n\right]$ is a composition of two graphs G and H. To obtain the next special case of G-join, let $X\subseteq V\left(G\right)$ and $X=\{x_i:i\in {\mathcal{I}}^{*}\subset \mathcal{I}\}$. If $H_j\cong K_1$ for all $j\in \mathcal{I}\backslash {\mathcal{I}}^{*}$ and $H_i\cong N_2$, $i\in {\mathcal{I}}^{*}$, then $G\left[h_n\right]$ is a duplication of the set X. In particular, if $|{\mathcal{I}}^{*}|=1$, then $G\left[h_n\right]$ is a duplication of the vertex $x_i$.

At first, we consider the case where all graphs from the sequence $h_n$ are nontrivial. The next theorem presents the complete characterization of the G-join of graphs having $(1,1)$-kernels when no graph from the sequence $h_n$ is trivial.

Theorem 6.

Let G be an arbitrary connected graph with $n\ge 1$ vertices and $h_n={\left(H_i\right)}_{i\in \mathcal{I}}$ be a sequence of n nontrivial graphs. The graph $G\left[h_n\right]$ has a $(1,1)$-kernel if, and only if, there exists a maximal independent set $J=\{x_i:i\in {\mathcal{I}}^{\prime }\subset \mathcal{I}\}$ of the graph G such that for all $i\in {\mathcal{I}}^{\prime }$ the graph $H_i$ has a $(1,1)$-kernel.

Proof. 

Let us assume that the graph $G\left[h_n\right]$ has a $(1,1)$-kernel $J^{*}$. We will show that in the set $J=\{x_i\in V\left(G\right)$: there exists $y_k^i\in V\left(H_i\right)$ such that $(x_i,y_k^i)$ is a maximal independent set. Let ${\mathcal{I}}^{\prime }=\{i\in \mathcal{I}:x_i\in J\}$. From the independence of the set $J^{*}$, it follows that the set J is independent. To prove that J is a maximal independent set, we will show that J is dominating. Let $x_t\in V\left(G\right)\backslash J$, $t\in \mathcal{I}\backslash {\mathcal{I}}^{\prime }$, then $\left(\left\{x_t\right\}\times V\left(H_t\right)\right)\cap J^{*}=\varnothing$. Hence, every vertex $(x_t,y_j^t)\notin J^{*}$, $1\le j\le p_t$ is adjacent to a vertex $(x_s,y_r^s)\in J^{*}$, $s\in {\mathcal{I}}^{\prime }$, $1\le r\le p_s$, thus $x_t{x}_s\in E\left(G\right)$. Therefore, the set J is dominating. This means that J is a kernel, so it is a maximal independent set. Since $G\left[h_n\right]$ has a $(1,1)$-kernel $J^{*}$, every graph $H_i$, $i\in {\mathcal{I}}^{\prime }$ must have a $(1,1)$-kernel $J_i$. By the assumption, graphs $H_i$, $i\in \mathcal{I}$ are nontrivial, hence $|J_i|\ge 2$.

Conversely, let us assume that the set J is a maximal independent set of a graph G and let ${\mathcal{I}}^{\prime }=\{i\in \mathcal{I}:x_i\in J\}$. Suppose that the set $J_i$, $i\in {\mathcal{I}}^{\prime }$ is a $(1,1)$-kernel of a graph $H_i$. Since the graph $H_i$, $i\in {\mathcal{I}}^{\prime }$ is nontrivial, $|J_i|\ge 2$. We will show that the set $J^{*}={\bigcup }_{i\in {\mathcal{I}}^{\prime }}\left(\left\{x_i\right\}\times J_i\right)$ is a $(1,1)$-kernel of a graph $G\left[h_n\right]$. It is easy to check that $J^{*}$ is independent. Let $(x_s,y_r^s)\in V\left(G\left[h_n\right]\right)\backslash J^{*}$ for $1\le s\le n$, $1\le r\le p_s$. If $x_s\in J$, then $x_s=x_k$ for some $k\in {\mathcal{I}}^{\prime }$. Hence, $y_r^s\notin J_k$, otherwise, $(x_s,y_r^s)\in J^{*}$. Therefore, for every vertex $y_r^s\notin J_k$, there exist at least two adjacent vertices in the set $J_k$. From the definition of the graph $G\left[h_n\right]$, it follows that the vertex $(x_s,y_r^s)$ is 2-dominated by the set $J^{*}$. Let $x_s\notin J$. Since J is a maximal independent set of a graph G, there exists the vertex from the set J adjacent to $x_s$. From the assumption that graphs $H_i$, $i\in \mathcal{I}$ are nontrivial, we obtain that there exist two vertices from the set $J^{*}$ adjacent to $(x_s,y_r^s)$. Hence, $J^{*}$ is a $(1,1)$-kernel of a graph $G\left[h_n\right]$, which ends the proof. □

By the construction of a $(1,1)$-kernel in the proof above, we obtain the value of parameters ${\sigma }_{(1,1)},j_{(1,1)},J_{(1,1)}$ in the graph $G\left[h_n\right]$.

Corollary 4.

Let G be an arbitrary connected graph with $n\ge 1$ vertices and $h_n={\left(H_i\right)}_{i\in \mathcal{I}}$ be a sequence of n nontrivial graphs having $(1,1)$-kernel. Let $\mathcal{J}=\{J_1,J_2,\dots ,J_t\}$, $t\ge 1$ be the family of maximal independent sets of a graph G and let $J_k=\{x_i:i\in {\mathcal{I}}_k\subset \mathcal{I}\}$, $k=1,2,\dots ,t$. Then,

1.

${\sigma }_{(1,1)}\left(G\left[h_n\right]\right)={\displaystyle \sum _{k=1}^t\prod _{i\in {\mathcal{I}}_k}}\sigma \left(H_i\right)$,

2.

$j_{(1,1)}\left(G\left[h_n\right]\right)=min\left\{{\displaystyle \sum _{i\in {\mathcal{I}}_k}}j\left(H_i\right):k=1,2,\dots ,t\right\}$,

3.

$J_{(1,1)}\left(G\left[h_n\right]\right)=max\left\{{\displaystyle \sum _{i\in {\mathcal{I}}_k}}J\left(H_i\right):k=1,2,\dots ,t\right\}.$

Finally, we consider a more general concept. Suppose that graphs from the sequence $h_n$ are arbitrary.

Theorem 7.

Let G be an arbitrary connected graph with $n\ge 1$ vertices and $h_n={\left(H_i\right)}_{i\in \mathcal{I}}$ be a sequence of n arbitrary non-empty graphs. The graph $G\left[h_n\right]$ has a $(1,1)$-kernel if, and only if, there exists a maximal independent set $J=\{x_i:i\in {\mathcal{I}}^{*}\subset \mathcal{I}\}$ of the graph G such that $H_i$, $i\in {\mathcal{I}}^{*}$ has a $(1,1)$-kernel. Moreover, if for some $j\in {\mathcal{I}}^{*}$, $H_j\cong K_1$, then every vertex adjacent to $x_j$ in a graph G is 2-dominated by the set J.

Proof. 

If all graphs $H_i$, $i\in \mathcal{I}$ are nontrivial, then we prove analogously as Theorem 6. Suppose that $H_m\cong K_1$, $m\in \tilde{\mathcal{I}}\subset \mathcal{I}$. Assume that the graph $G\left[h_n\right]$ has a $(1,1)$-kernel $J^{*}$. Let $J=\{x_i\in V\left(G\right)$ : there exists $y_k^i\in V\left(H_i\right)$ such that $(x_i,y_k^i)$ and let ${\mathcal{I}}^{*}=\{i\in \mathcal{I}:x_i\in J\}$. If $\tilde{\mathcal{I}}\cap {\mathcal{I}}^{*}=\varnothing$, then we prove analogously as Theorem 6. Suppose that $\tilde{\mathcal{I}}\cap {\mathcal{I}}^{*}\ne \varnothing$ and let $j\in \tilde{\mathcal{I}}\cap {\mathcal{I}}^{*}$. Let us consider the vertex $x_s\in N_G\left(x_j\right)$, $1\le s\le n$. Since $J^{*}$ is a $(1,1)$-kernel of the graph $G\left[h_n\right]$, every vertex $(x_s,y_r^s)$, $1\le r\le p_s$ is 2-dominated. This means that there exists at least one vertex $(x_t,y_u^t)$, $t\in {\mathcal{I}}^{*}$, $t\ne j$, $1\le u\le p_t$ adjacent to $(x_s,y_r^s)$ in the graph $G\left[h_n\right]$. Thus $x_s{x}_t\in E\left(G\right)$. Since $t\in {\mathcal{I}}^{*}$, the vertex $x_t\in J$. Hence, every vertex adjacent to $x_j$ in the graph G is 2-dominated by the set J.

Conversely, let J be a maximal independent set of a graph G and let ${\mathcal{I}}^{*}=\{i\in \mathcal{I}:x_i\in J\}$. Assume that the set $J_i$, $i\in {\mathcal{I}}^{*}$ is a $(1,1)$-kernel of the graph $H_i$. If $\tilde{\mathcal{I}}\cap {\mathcal{I}}^{*}=\varnothing$, then we prove analogously as Theorem 6. Let $\tilde{\mathcal{I}}\cap {\mathcal{I}}^{*}\ne \varnothing$. Suppose that every vertex adjacent to $x_j$, $j\in \tilde{\mathcal{I}}\cap {\mathcal{I}}^{*}$ is 2-dominated by the set J in the graph G. We will show that the set $J^{*}={\bigcup }_{i\in {\mathcal{I}}^{*}}\left(\left\{x_i\right\}\times J_i\right)$ is a $(1,1)$-kernel of the graph $G\left[h_n\right]$. From the definition of G-join, it follows that $J^{*}$ is independent. Let $(x_s,y_r^s)\in V\left(G\left[h_n\right]\right)\backslash J^{*}$ for $1\le s\le n$, $1\le r\le p_s$. If $x_s\in J$, then $x_s=x_k$ for some $k\in {\mathcal{I}}^{*}$. Then, $y_r^s\notin J_k$, otherwise, $(x_s,y_r^s)\in J^{*}$. Thus, for all vertices $y_r^s\notin J_k$ there exist at least two vertices in the set $J_k$ adjacent to $y_r^s$ in a graph G. Then, we obtain that the vertex $(x_s,y_r^s)$ is 2-dominated by $J^{*}$. Let $x_s\notin J$. Since J is a maximal independent set of the graph G, there exists at least one vertex $x_p\in J$, $p\in {\mathcal{I}}^{*}$ adjacent to $x_s$. If $|J_p|\ge 2$, then we obtain that there exist two vertices from $J^{*}$ adjacent to $(x_s,y_r^s)$. If $|J_p|=1$, then $p\in \tilde{\mathcal{I}}\cap {\mathcal{I}}^{*}$ and there exists at least one vertex $x_t$, $t\ne p$, $t\in {\mathcal{I}}^{*}$ adjacent to $x_s$ in the graph G. This means that there exist two vertices from the set $J^{*}$ adjacent to $(x_s,y_r^s)$ in the graph $G\left[h_n\right]$. Hence, $J^{*}$ is a $(1,1)$-kernel of the graph $G\left[h_n\right]$, which ends the proof. □

From Theorem 7, we obtain direct corollaries, concerning specific cases of the G-join.

Corollary 5.

Let $G,H$ be nontrivial graphs. The composition $G\left[H\right]$ has a $(1,1)$-kernel if, and only if, H has $(1,1)$-kernel.

Corollary 6.

The join $H_1+H_2$ has a $(1,1)$-kernel if, and only if, at least one of graphs $H_1,H_2$ has a $(1,1)$-kernel J such that $\left|J\right|\ge 2$.

Corollary 7.

Let $X\subseteq V\left(G\right),X\ne \varnothing$. The duplication $G^X$ has a $(1,1)$-kernel if, and only if, there exist a maximal independent set $J=\{x_j:j\in {\mathcal{I}}^{*}\subset \mathcal{I}\}$ such that if for some $j\in {\mathcal{I}}^{*},H_j\cong K_1$, then every vertex adjacent to $x_j$ in G is 2-dominated by the set J.

An example of a G-join with $(1,1)$-kernel is shown in Figure 5.

Finally, let us indicate that the problem of the existence of $(1,k)$-kernels in the G-join for $k=2$ has been solved by Michalski and Włoch in [25]. They also proved some results concerning parameters related to $(1,2)$-kernels in this product. In Figure 6, we present an example of a $(1,2)$-kernel in the graph $P_6\left((P_3,K_4,N_2,P_4,P_3,K_1)\right)$.

5. Concluding Remarks

In this paper, we discussed the problem of the existence of $(1,1)$ and $(1,2)$-kernels in generalized graph products, as well as determined parameters related to them. Together with results obtained in [25], this paper concludes the topic of $(1,1)$-kernels and $(1,2)$-kernels in generalized corona and G-join. Since the proven results are very general, they also solve the problem of the existence of secondary kernels in more specific cases, such as the composition of graphs, the duplication of the vertex, the classical join, and corona of two graphs. We showed that the asymmetry of these products is not an obstacle in finding complete characterizations. The main method used in proofs was thorough case analysis.

The problems analyzed in this paper are still open in a wide range of graph classes and we believe that the results presented here may be of major significance in exploring this field. One of the possibilities is obtaining complete characterizations of $(1,k)$-kernels in other graph products such as the Cartesian, tensor, and strong products. Some of these problems have been only partially solved in [19,21,23].